Influence of Compression Ratio on Combustion and Emission Characteristics of Hydrogen Internal Combustion Engines Under Different Excess Air Coefficients
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Setup
2.2. Numerical Models
2.2.1. One-Dimensional Simulation Model of Engine
- Based on experimental data (such as cylinder pressure curves and exhaust temperature), the correction coefficient C1 related to the combustion phase and the heat transfer multiplier are adjusted. Through iterative optimization, the simulated in-cylinder temperature and pressure are matched with the experimental values.
- C1 is dynamically adjusted according to the combustion phase (compression, combustion, expansion) to reflect the rapid heat release characteristics of hydrogen combustion. Considering hydrogen’s high thermal diffusivity, the heat transfer multiplier is set to 0.9–1.1 to correct the deviation of the traditional model for hydrogen.
- The convective heat transfer coefficient in the cylinder is calculated using the Woschni model and then substituted into the energy conservation equation to calculate the in-cylinder temperature distribution and wall heat loss.
2.2.2. Combustion Model
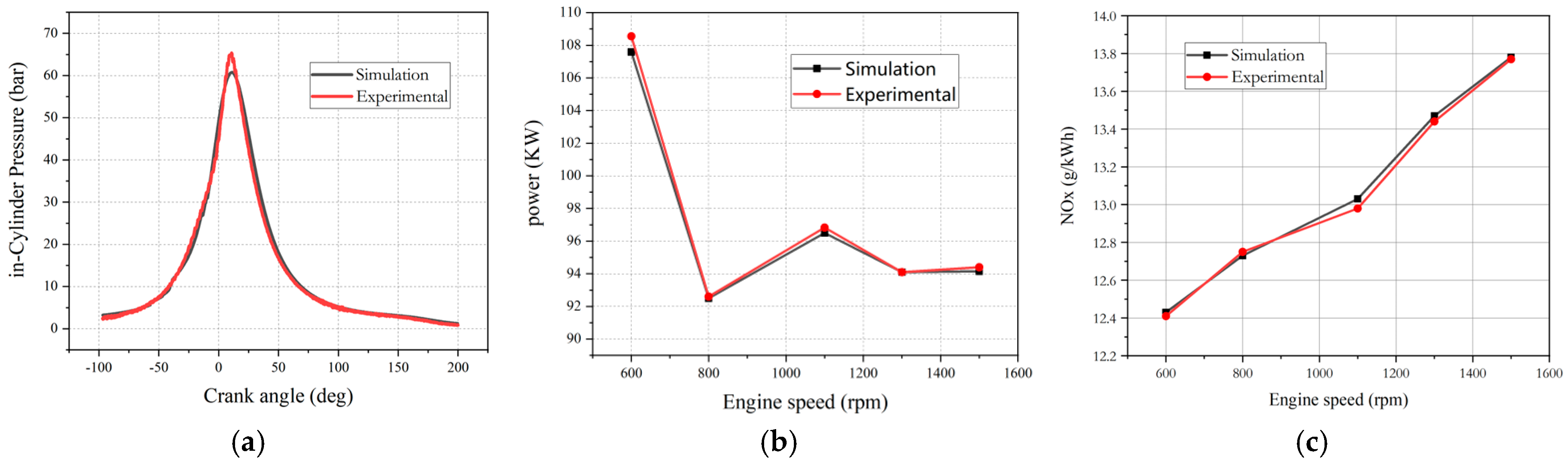
2.3. Model Validation
3. Results and Discussion
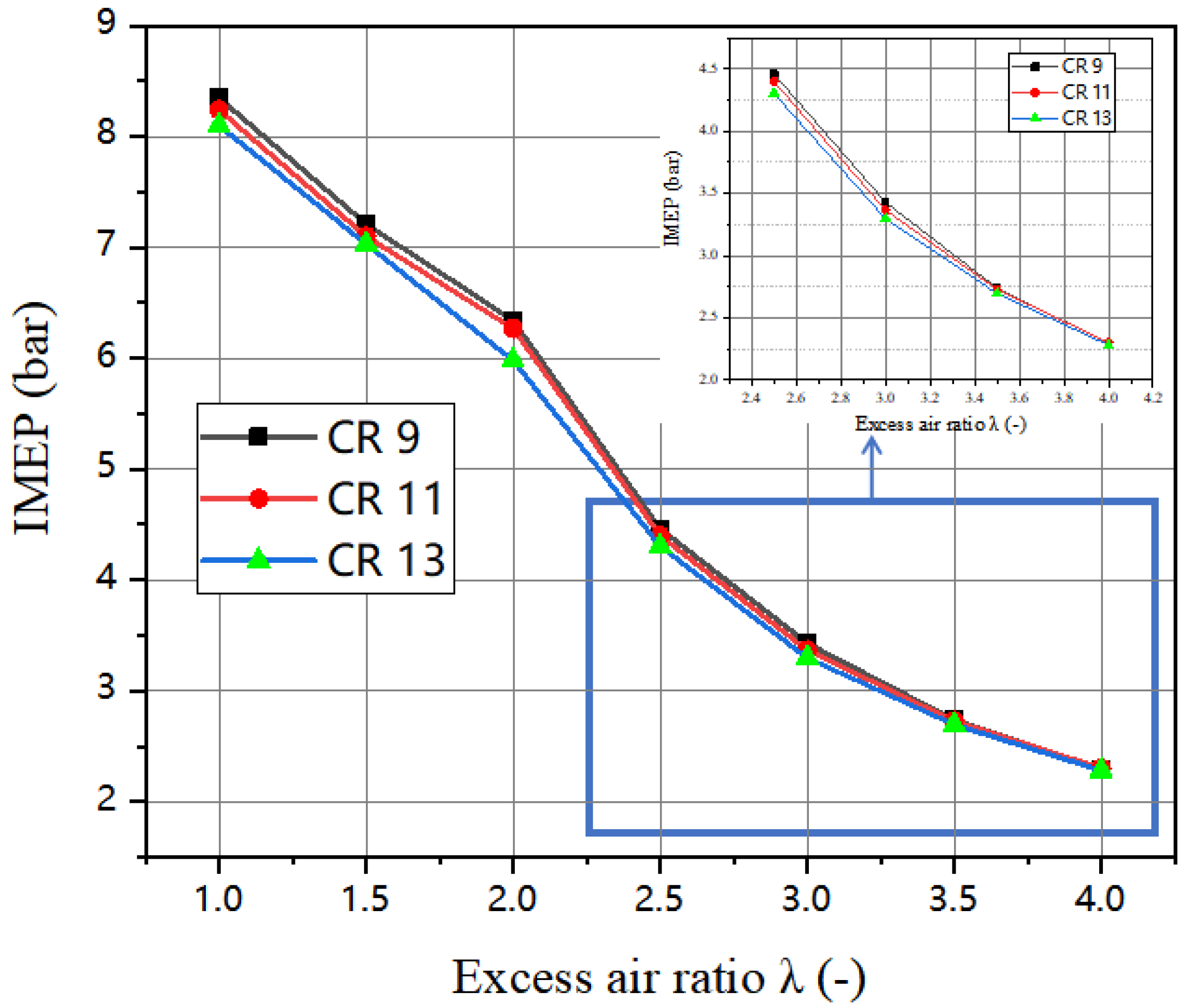
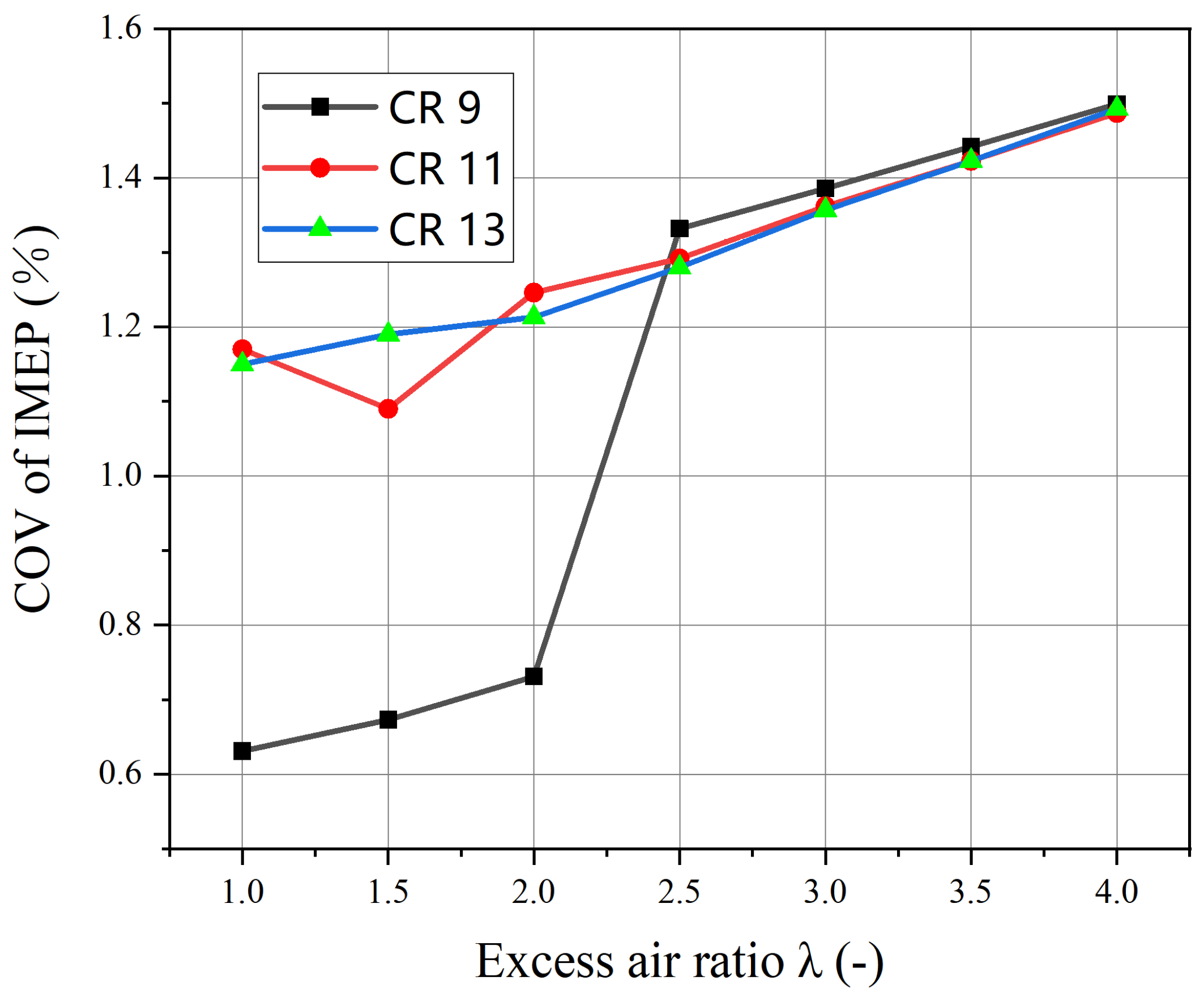
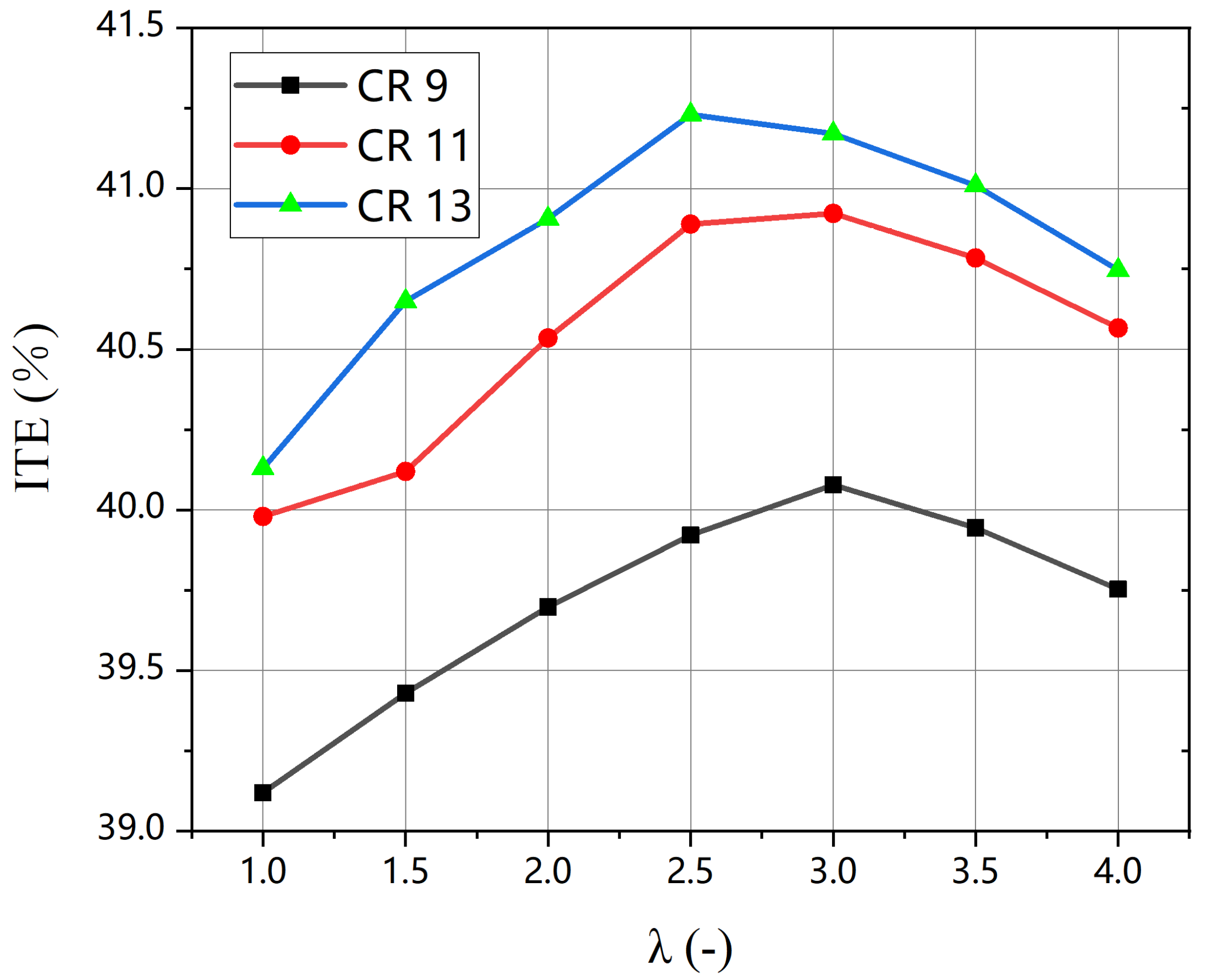
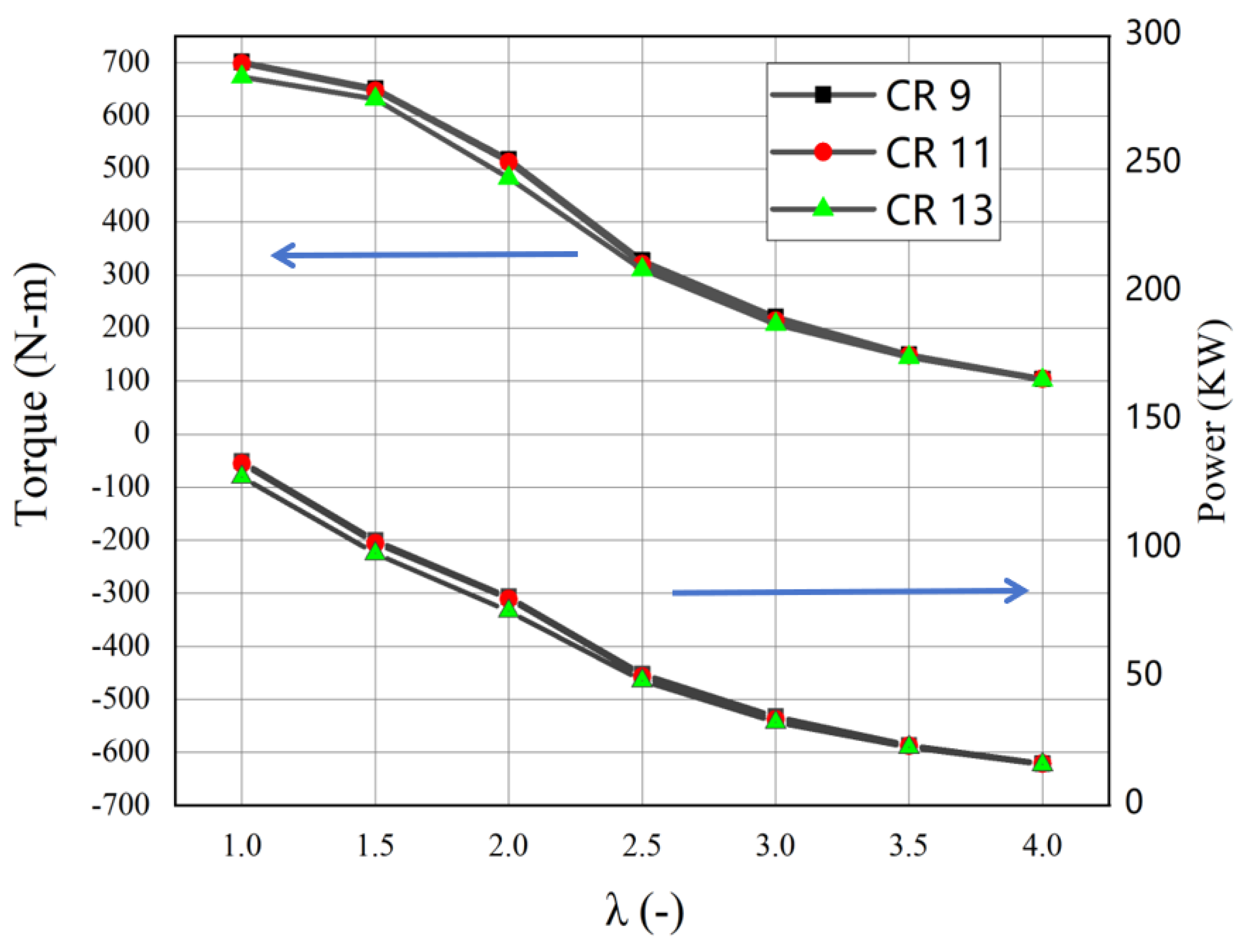
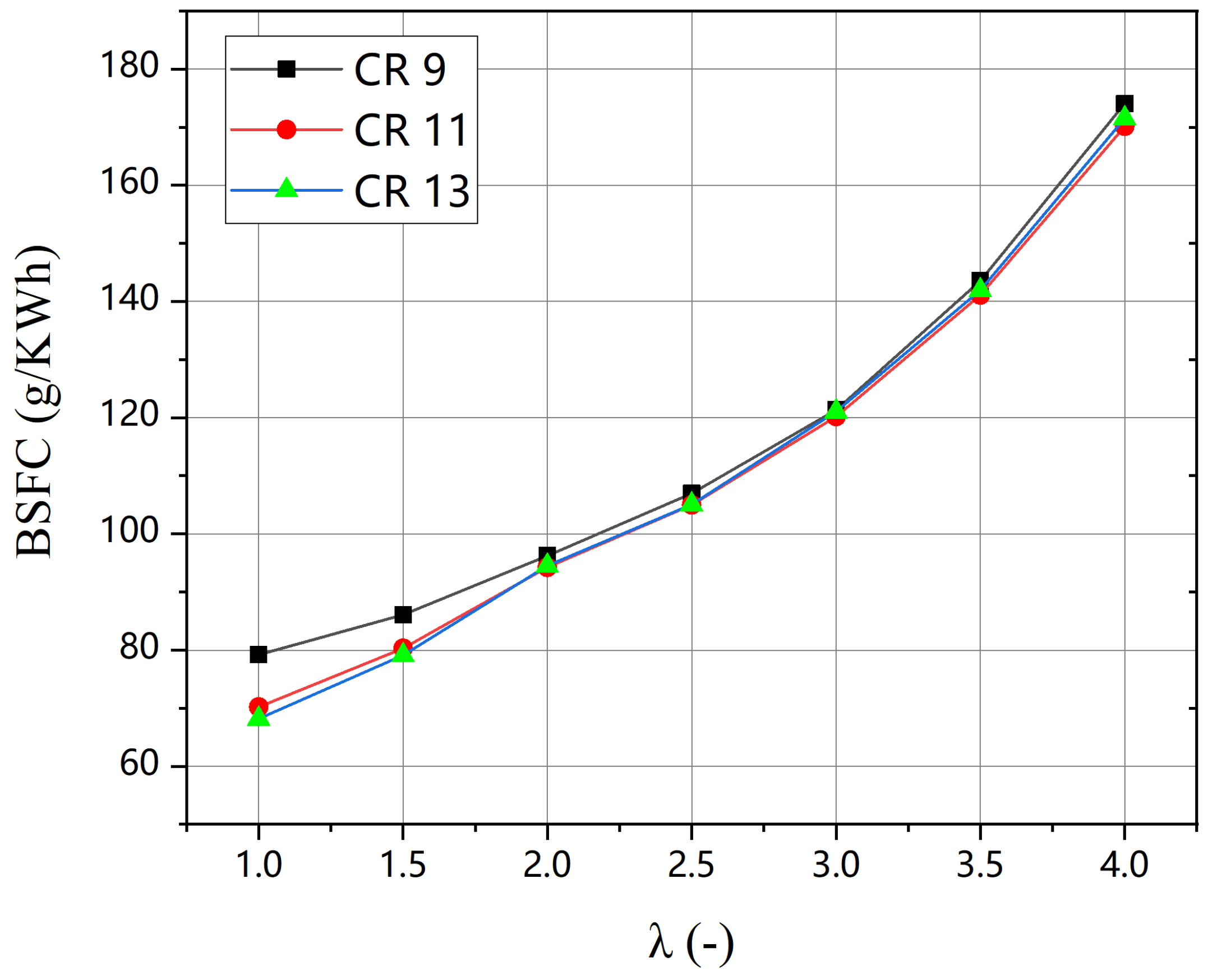
3.1. Engine Performance
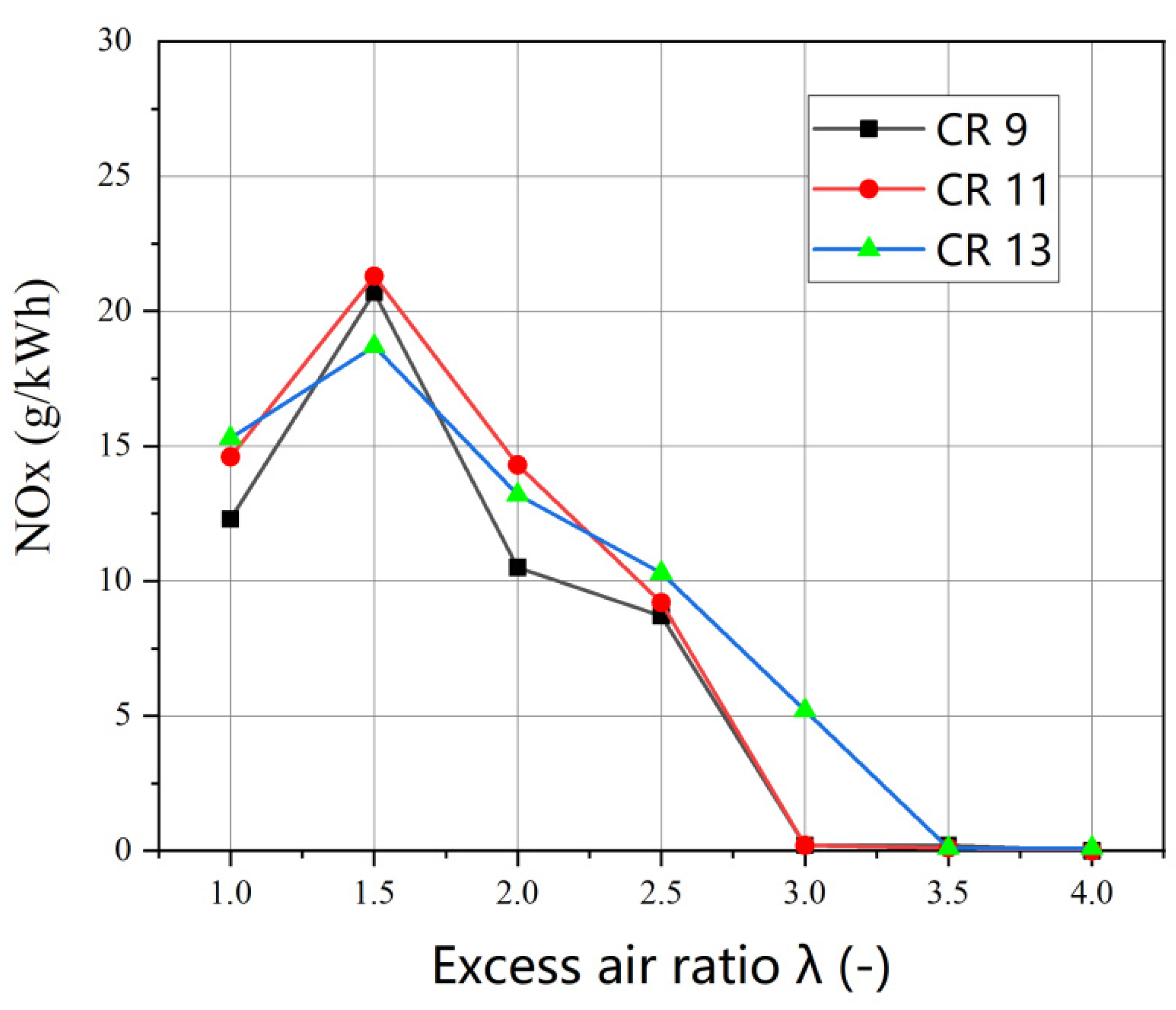
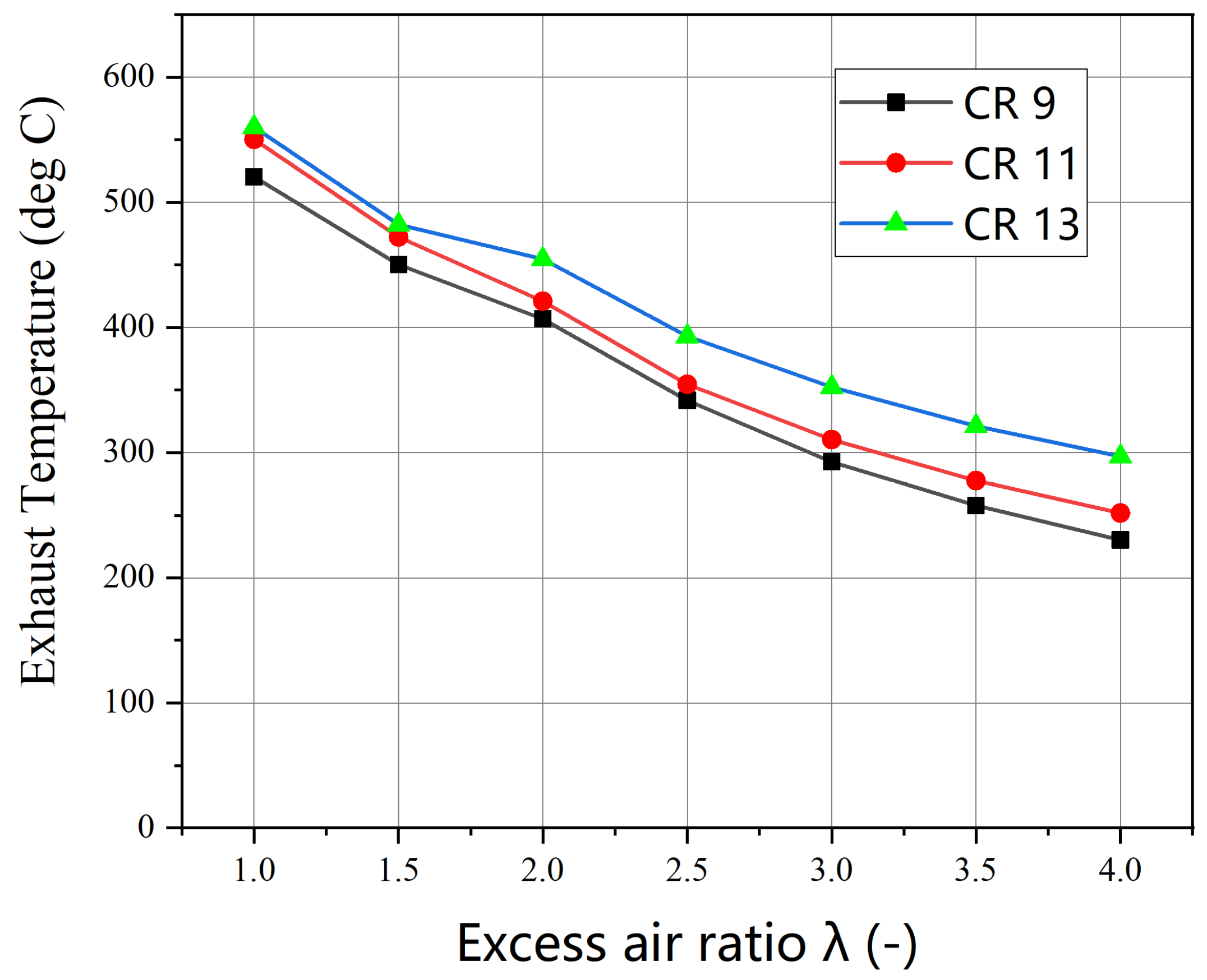
3.2. Engine Emissions
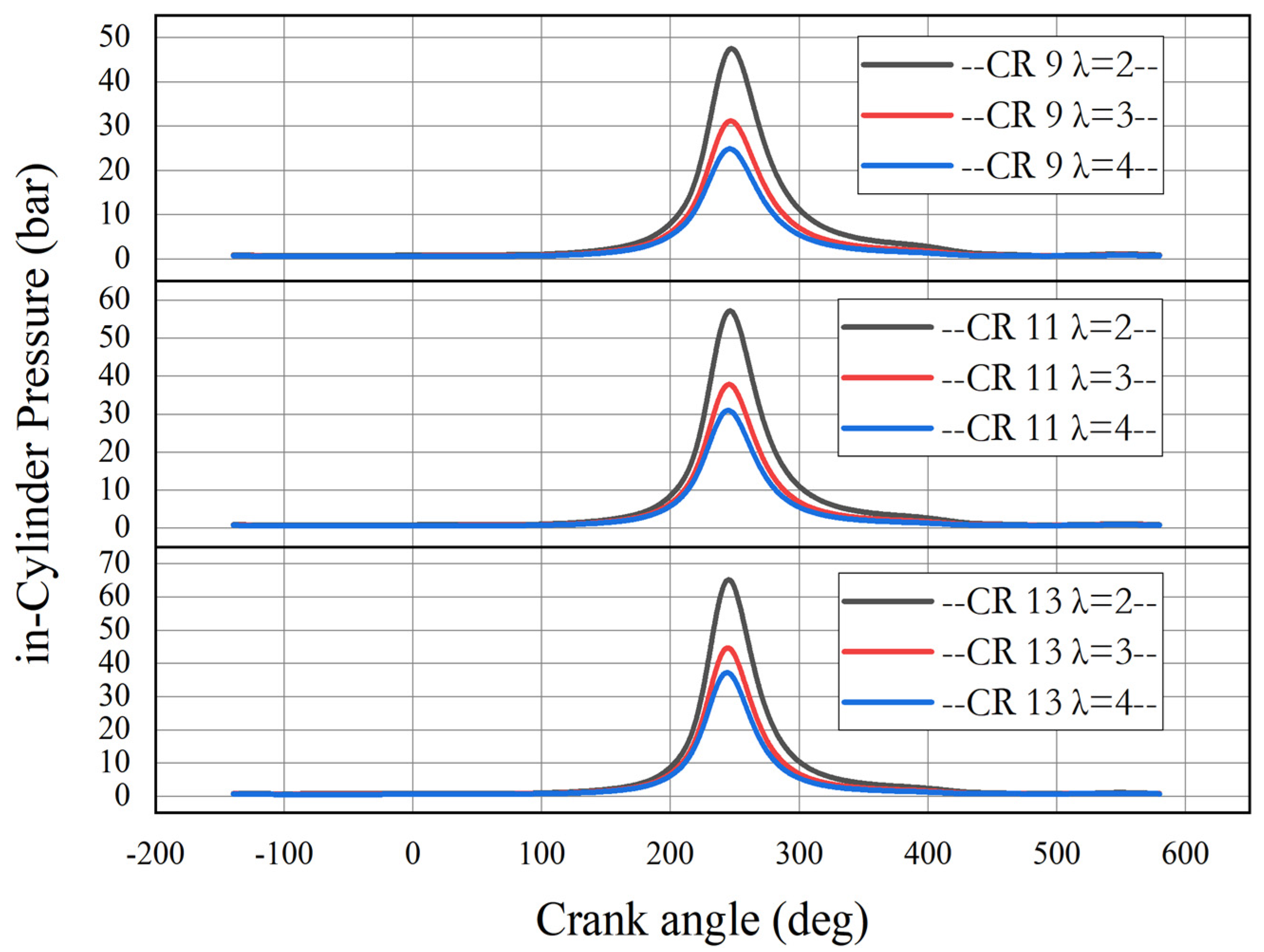
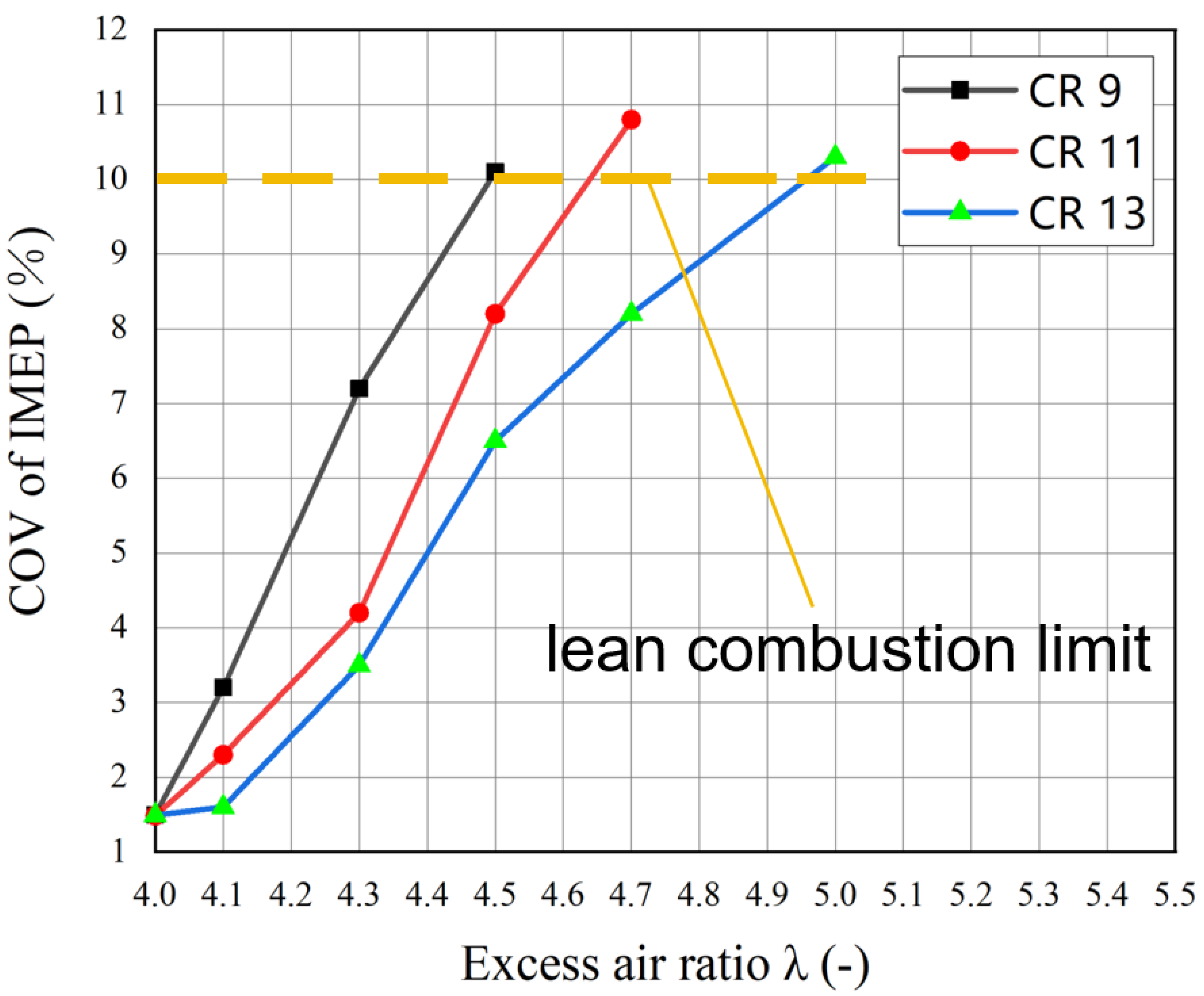
3.3. Combustion Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karlilar Pata, S.; Balcilar, M. Decarbonizing energy: Evaluating fossil fuel displacement by renewables in OECD countries. Environ. Sci. Pollut. Res. Int. 2024, 31, 31304–31313. [Google Scholar] [CrossRef]
- Fernandez-Dacosta, C.; Shen, L.; Schakel, W.; Ramirez, A.; Kramer, G.J. Potential and challenges of low-carbon energy options: Comparative assessment of alternative fuels for the transport sector. Appl. Energy 2019, 236, 590–606. [Google Scholar] [CrossRef]
- Folkson, R. Alternative Fuels and Advanced Vehicle Technologies for Improved Environmental Performance: Towards Zero Carbon Transportation; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Wang, L.; Song, R.; Zou, H.; Liu, S.; Zhou, L. Study on combustion characteristics of a methanol—Diesel dual-fuel compression ignition engine. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2008, 222, 619–627. [Google Scholar] [CrossRef]
- Utomo, O.; Abeysekera, M.; Ugalde-Loo, C.E. Optimal operation of a hydrogen storage and fuel cell coupled integrated energy system. Sustainability 2021, 13, 3525. [Google Scholar] [CrossRef]
- Yao, N.; Pan, W.; Zhang, J.; Wei, L. The advancement on carbon-free ammonia fuels for gas turbine: A review. Energy Convers. Manag. 2024, 315, 118745. [Google Scholar]
- Hosseini, S.E.; Butler, B. An overview of development and challenges in hydrogen powered vehicles. Int. J. Green Energy 2020, 17, 13–37. [Google Scholar]
- Das, L. Hydrogen engines: A view of the past and a look into the future. Int. J. Hydrogen Energy 1990, 15, 425–443. [Google Scholar]
- White, C.; Steeper, R.; Lutz, A.E. The hydrogen-fueled internal combustion engine: A technical review. Int. J. Hydrogen Energy 2006, 31, 1292–1305. [Google Scholar]
- Kawahara, N.; Tomita, E. Visualization of auto-ignition and pressure wave during knocking in a hydrogen spark-ignition engine. Int. J. Hydrogen Energy 2009, 34, 3156–3163. [Google Scholar]
- Hu, Z.; Yuan, S.; Wei, H.; Huang, Z.; Wei, H.; Chan, S.H.; Zhou, L. High-pressure injection or low-pressure injection for a direct injection hydrogen engine? Int. J. Hydrogen Energy 2024, 59, 383–389. [Google Scholar] [CrossRef]
- Boretti, A. Hydrogen internal combustion engines to 2030. Int. J. Hydrogen Energy 2020, 45, 23692–23703. [Google Scholar]
- Nguyen, D.; Kar, T.; Turner, J.W. Performance, Emissions, and Combustion Characteristics of a Hydrogen-Fueled Spark-Ignited Engine at Different Compression Ratios: Experimental and Numerical Investigation. Energies 2023, 16, 5730. [Google Scholar] [CrossRef]
- Lee, J.; Park, C.; Kim, Y.; Choi, Y.; Bae, J.; Lim, B. Effect of turbocharger on performance and thermal efficiency of hydrogen-fueled spark ignition engine. Int. J. Hydrogen Energy 2019, 44, 4350–4360. [Google Scholar]
- Poursadegh, F.; Brear, M.; Hayward, B.; Yang, Y. Autoignition, knock, detonation and the octane rating of hydrogen. Fuel 2023, 332, 126201. [Google Scholar] [CrossRef]
- Qiang, Y.; Jin, K.; Zhao, S.; Cai, J.; Su, F.; Wang, S.; Ji, C. Optimization of power performance and combustion stability of ultra-lean combustion in hydrogen fuel engines through combined turbulent jet ignition and variable valve timing. Fuel 2025, 381, 133493. [Google Scholar]
- Novella, R.; Gomez-Soriano, J.; González-Domínguez, D.; Olaciregui, O. Optimizing hydrogen spark-ignition engine performance and pollutants by combining VVT and EGR strategies through numerical simulation. Appl. Energy 2024, 376, 124307. [Google Scholar]
- Liu, X.R.; Li, G.X.; Hu, Y.P.; Bai, S.Z.; Deng, K.Y. In-Cylinder Heat Transfer Model for Diesel Engine Based on Improved Woschni Correlation. Appl. Mech. Mater. 2014, 538, 175–178. [Google Scholar]
- Kim, Y.-J.; Park, Y.-J.; Park, T.-J.; Lee, C.-E. Development of a Simulation Model for a New Rotary Engine to Optimize Port Location and Operating Conditions Using GT-POWER. Energies 2024, 17, 4732. [Google Scholar] [CrossRef]
- Brayek, M.; Driss, Z.; Jemni, M.A. Optimization of the Wiebe Function Parameters and a New Function for the Filling Coefficient for Dual-Fuel Engines. In International Conference on Wave Mechanics and Vibrations; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1196–1206. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar]
- Wang, W.; Mai, Z.; Yao, X.; Tang, C.; Huang, Z. Towards optimized excess air ratio and substitution rate for a dual fuel HPDI engine. Appl. Therm. Eng. 2024, 253, 123797. [Google Scholar]
- Gang, H.; Lang, L.; Ye, T.; Wei, Z. Combustion flow field structure and performance in hydrogen-fueled scramjet. J. Aerosp. Power 2023, 38, 2177–2185. [Google Scholar]
- Xu, Z. Effect of Compression Ratio on the Performance of Direct-Injection Hydrogen Engines. Trends Renew. Energy 2024, 10, 283–300. [Google Scholar] [CrossRef]
- Babayev, R.; Morén, M.; Johansson, B. Comparative Computational Study of Hydrogen and Natural Gas in Heavy-Duty Compression-Ignition Engines: Combustion Characteristics, Thermal Efficiency, and Local Pollutant and Greenhouse Gas Emissions. In Thermal Efficiency, and Local Pollutant and Greenhouse Gas Emissions; SSRN: Rochester, NY, USA, 2025. [Google Scholar]
- Liang, Y.; Wang, Z.; Dong, D.; Wei, W.; Zhang, H.; Li, G.; Zhang, Z. Effects of hydrogen volume fraction, air fuel ratio, and compression ratio on combustion and emission characteristics of an SI ammonia-hydrogen engine. Energy 2024, 308, 132858. [Google Scholar]
- Goldwitz, J.A. Combustion Optimization in a Hydrogen-Enhanced Lean Burn SI Engine. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Batool, S.; Naber, J.D.; Shahbakhti, M. Data-driven modeling and control of cyclic variability of an engine operating in low temperature combustion modes. IFAC-PapersOnLine 2021, 54, 834–839. [Google Scholar]
- Domínguez, V.M.; Hernández, J.J.; Ramos, Á.; Rodríguez-Fernández, J. Role of the Compression Ratio in Dual-Fuel Compression Ignition Combustion with Hydrogen and Methanol. Energy Fuels 2024, 38, 19127–19136. [Google Scholar]
- De Bellis, V.; Piras, M.; Bozza, F.; Malfi, E.; Novella, R.; Gómez-Soriano, J.; Olcina-Girona, M. Development and validation of a phenomenological model for hydrogen fueled PFI internal combustion engines considering Thermo-Diffusive effects on flame speed propagation. Energy Convers. Manag. 2024, 308, 118395. [Google Scholar]
- Wang, Y.; Zhang, L.; Zhou, C.; Guo, X.; Xing, K.; Huang, H. Numerical Study on the Potential of Stratified Mixture to Improve Thermal Efficiency and Reduce Carbon Emissions in High-Speed Gasoline Direct Injection Engine. J. Eng. Gas Turbines Power 2024, 146, 121015. [Google Scholar]
- Issa, A.N.; Kim, J.K.; Chun, K.W.; Choi, J.-H.; Lee, W.-J. Investigation of an optimal exhaust gas recirculation rate on a four-stroke spark-ignited LPG engine. J. Energy Inst. 2025, 120, 102048. [Google Scholar] [CrossRef]
- Baigang, S.; Lingzhi, B.; Qinghe, L. Development and trends of direct injection hydrogen internal combustion engine technology. J. Automot. Saf. Energy 2021, 12, 265. [Google Scholar]
- Silveira, J.; Fagundez, J.; Garlet, R.; Martins, M.; Salau, N.; Lanzanova, T. Hydrogen-fueled PFI SI engine investigation for near-zero NOx emissions in de-throttled and supercharged ultra-lean burn conditions. Int. J. Hydrogen Energy 2024, 91, 800–813. [Google Scholar]
- Liebau, M.; Suprun, W.; Kasprick, M.; Gläser, R. Transition Metal Oxides Supported on TiO2 as Catalysts for the Low-Temperature Selective Catalytic Reduction of NO x by NH3. Catalysts 2024, 15, 22. [Google Scholar] [CrossRef]
- Boretti, A. Electric turbochargers in hydrogen internal combustion engines powered hybrid electric vehicles: Advancing performance, efficiency, and sustainability. Int. J. Hydrogen Energy 2025, 103, 690–700. [Google Scholar] [CrossRef]
- Park, C.; Jang, I.; Lee, J.; Kim, M.; Park, C.; Kim, Y.; Choi, Y. Effect of a Compression Ratio Increase and High-Flow-Rate Injection on the Combustion Characteristics of an Ammonia Direct Injection Spark-Ignited Engine. J. Mar. Sci. Eng. 2025, 13, 268. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Le, M.D. Effects of compression ratios on combustion and emission characteristics of SI engine fueled with hydrogen-enriched biogas mixture. Energies 2022, 15, 5975. [Google Scholar] [CrossRef]
- Sadeq, A. Combustion Advancements: From Molecules to Future Challenges; Independently Published: Chicago, IL, USA, 2023. [Google Scholar]




| Parameters | Value |
|---|---|
| Cylinder diameter × stroke/mm × mm | 130 × 161 |
| Rated power/kW | 324–368 |
| Rated speed or nominal speed/r·min−1 | 1900 |
| Maximum torque/Nm | 2020–2320 |
| Torque peak rpm/r·min−1 | 1100–1500 |
| Engine displacement/L | 12.82 |
| Parameter | CR = 9 | CR = 11 | CR = 13 |
|---|---|---|---|
| ITE Peak (%) | 40.1 (λ = 3) | 40.8 (λ = 3) | 41.25 (λ = 3) |
| BSFC Minimum (g/kWh) | 80.1 (λ = 1) | 70.7 (λ = 1) | 68.7 (λ = 1) |
| Peak IMEP (bar) | 8.43 (λ = 1) | 8.32 (λ = 1) | 8.14 (λ = 1) |
| NOx Peak (g/kWh) | 22.4 (λ = 1.5) | 21.6 (λ = 1.5) | 18.6 (λ = 1.5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, D.; Liu, Y.; Zhang, Y. Influence of Compression Ratio on Combustion and Emission Characteristics of Hydrogen Internal Combustion Engines Under Different Excess Air Coefficients. Energies 2025, 18, 1656. https://doi.org/10.3390/en18071656
Lou D, Liu Y, Zhang Y. Influence of Compression Ratio on Combustion and Emission Characteristics of Hydrogen Internal Combustion Engines Under Different Excess Air Coefficients. Energies. 2025; 18(7):1656. https://doi.org/10.3390/en18071656
Chicago/Turabian StyleLou, Diming, Yixuan Liu, and Yunhua Zhang. 2025. "Influence of Compression Ratio on Combustion and Emission Characteristics of Hydrogen Internal Combustion Engines Under Different Excess Air Coefficients" Energies 18, no. 7: 1656. https://doi.org/10.3390/en18071656
APA StyleLou, D., Liu, Y., & Zhang, Y. (2025). Influence of Compression Ratio on Combustion and Emission Characteristics of Hydrogen Internal Combustion Engines Under Different Excess Air Coefficients. Energies, 18(7), 1656. https://doi.org/10.3390/en18071656





