Energy Efficiency and the Transition to Renewables—Building Communities of the Future
Abstract
:1. Introduction
- Using realistic, actual hourly demand data for the community.
- Using hourly power demand–supply matching for all hours of the year.
- Introducing feasible energy efficiency and conservation measures to reduce the power demand.
- Introducing the concept of elasticity coefficients that quantitatively describe tradeoffs between efficiency and power capacity increases.
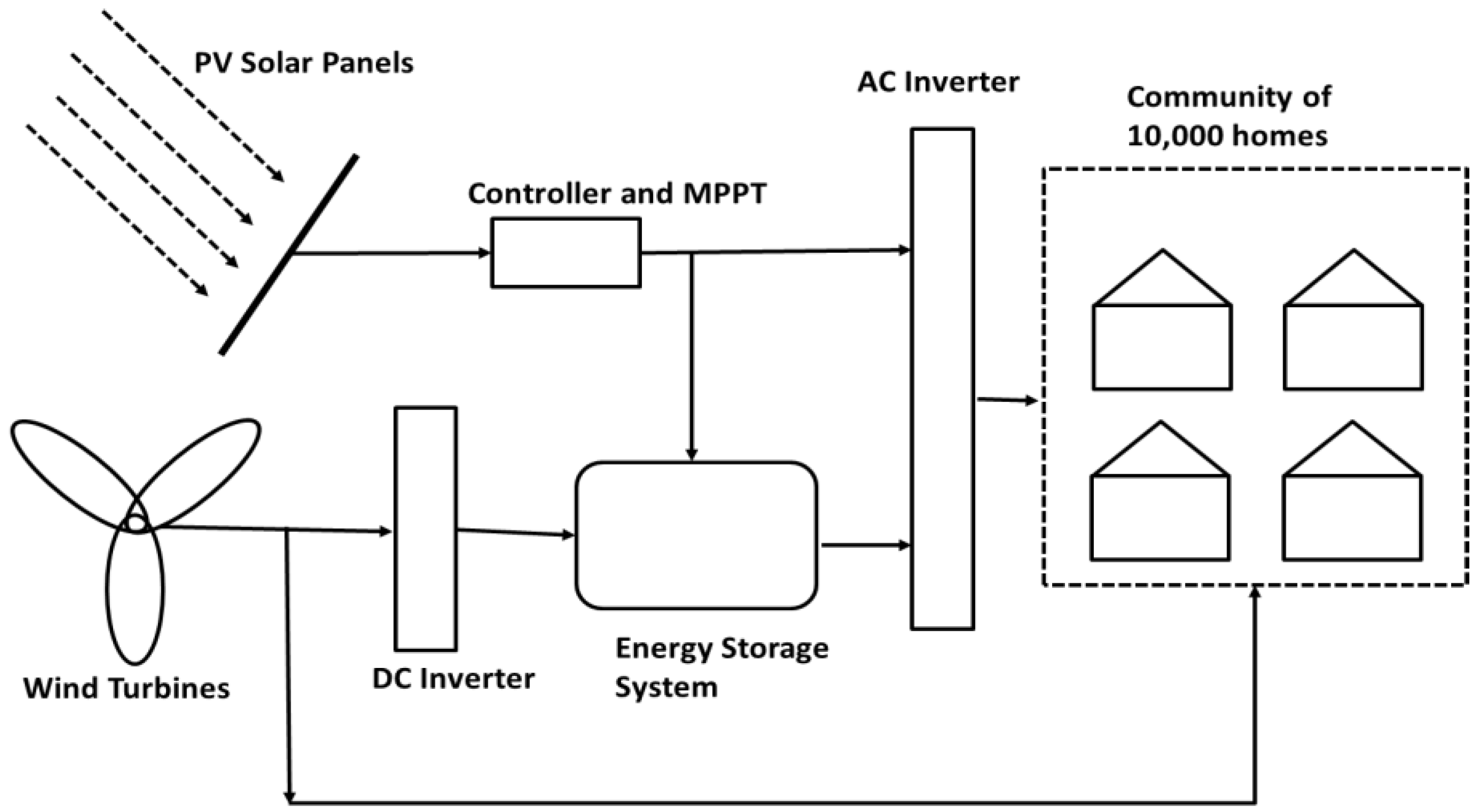
2. A Community of Buildings with Zero Carbon Emissions
- Larger energy generation and storage systems are more efficient and cheaper (per unit power and energy generated). The system’s operation and maintenance costs are spread over a larger population.
- A recent study found that shared, community-based solar projects expand renewable energy access to more diverse and less affluent populations [31].
- It is cheaper to install energy efficiency systems in new homes, which are designed for such systems, than to refurbish older homes.
- When uniform energy efficiency systems are applied to a large number of buildings, significant economies of scale are realized.
- The region is endowed with significant renewable energy resources. The average solar irradiance is higher than 220 W/m2. Wind power availability is high, especially in the panhandle and the coastal areas, where average velocities are more than 12 m/s.
- In 2023, the growing wind farms in the region generated approximately 108 TWh of electric energy, more than any other state in the USA [28].
- The regional energy needs are very high.
- The energy needs and general demand trends are similar to those of the entire southern region of the USA.
- Actual hourly demand data are available for an entire year.
3. Governing Equations and Solution
Solving the Governing Equations
- An initial wind power capacity was stipulated for the supply of wind power. This was treated as a parameter in the calculations. Based on this, the wind energy supply was computed for all hours of the year.
- A quantity of stored energy (in hydrogen mass) ES0 at the beginning of the first hour of the year was stipulated.
- The two values from steps 1 and 2 were recorded in a computer program that also included (for the entire community): the hourly a-c demand; the hourly total electric energy demand; and the heating demand for space heating in the winter and hot water throughout the year.
- An area, A, of the PV system was assumed. Based on the local irradiance, the hourly PV energy generation was computed and added to the hourly wind energy generation.
- Equations (4) and (5) for the surplus or deficit of energy were solved, and the two quantities were sequentially calculated for all hours of the year, starting at hour 1 and ending at hour 8760.
- At the end of the calculations, the stored energy at the end of the year, ES8760, was computed. ES8760 was compared to the originally stipulated value ES0 in step 2. If ES0 < ES8760, additional energy is needed, and A is increased. If ES0 > ES8760, the area A is decreased. Steps 5 and 6 were repeated with the new value for the required PV area A until ES0 = ES8760. The last value was the required PV area. In combination with the wind power capacity, stipulated in step 1, the two renewable energy sources (supplemented with the storage system) generated sufficient energy for the entire year.
- The correct value for ES0, which was stipulated in step 2, was calculated in a second iteration, which made use of the minimum energy storage condition that the energy storage system must contain sufficient energy/hydrogen to satisfy the entire demand for the next ten days (240 h), even when zero additional power is generated. Thus, ES0 was modified until its correct value indicated that the minimum stored energy constraint was satisfied.
4. Results and Discussion
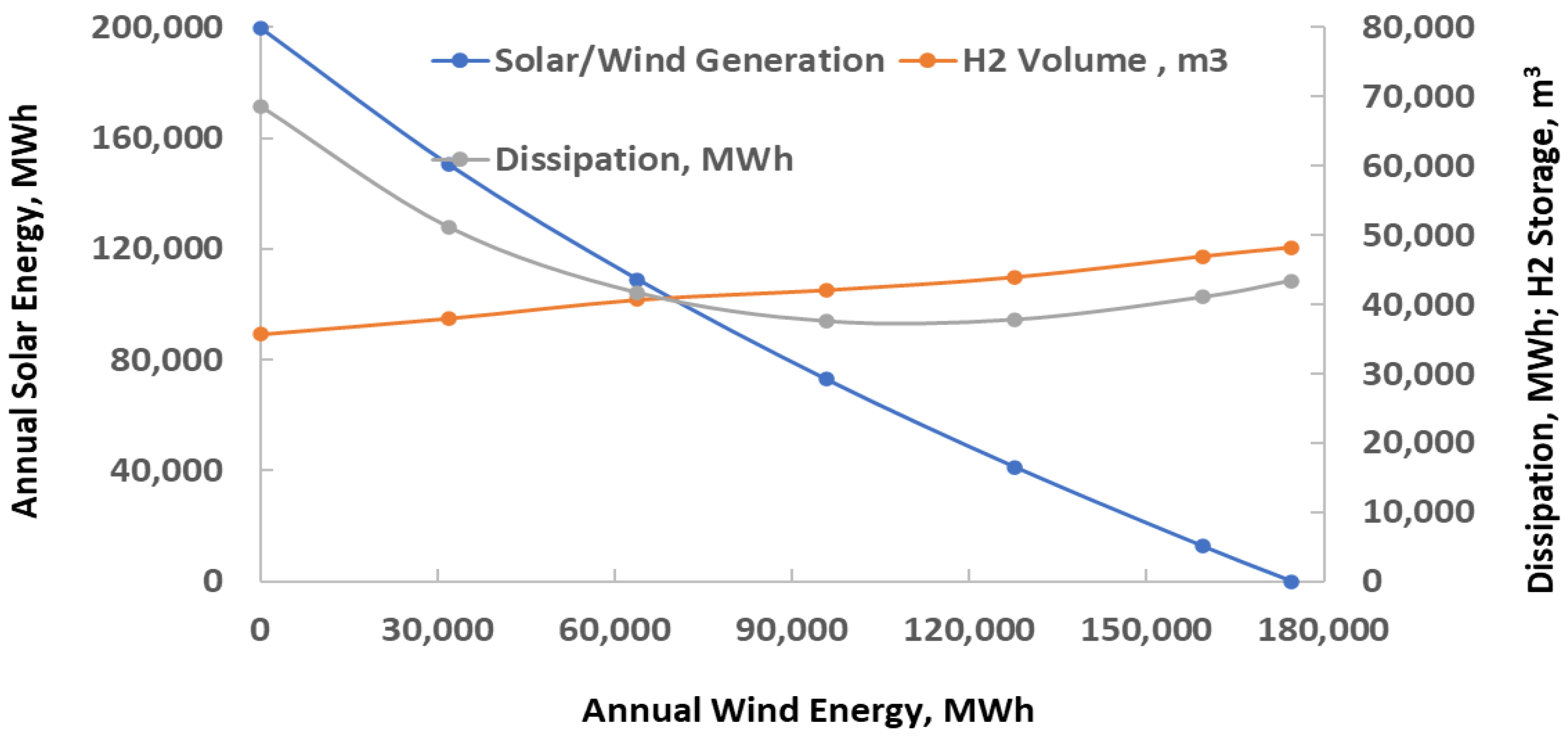
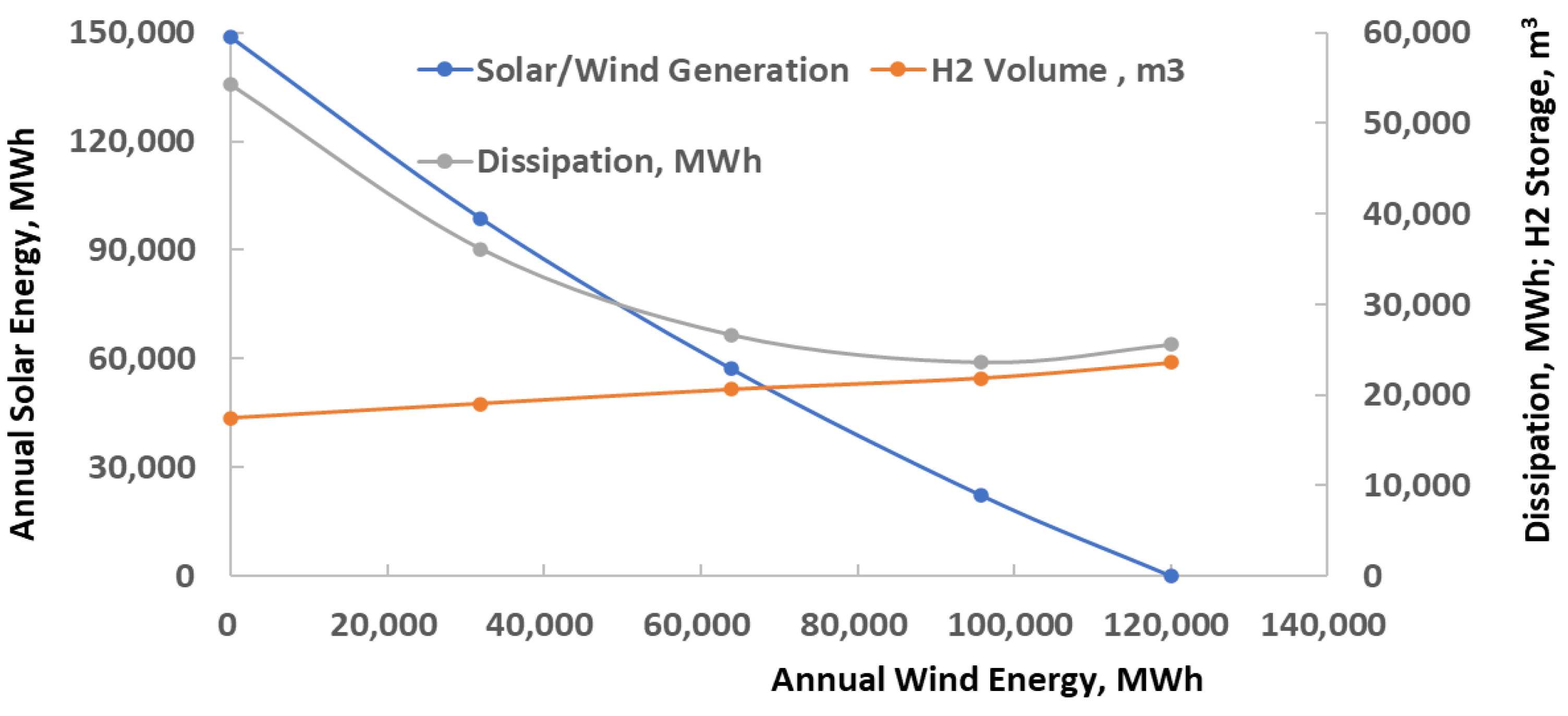
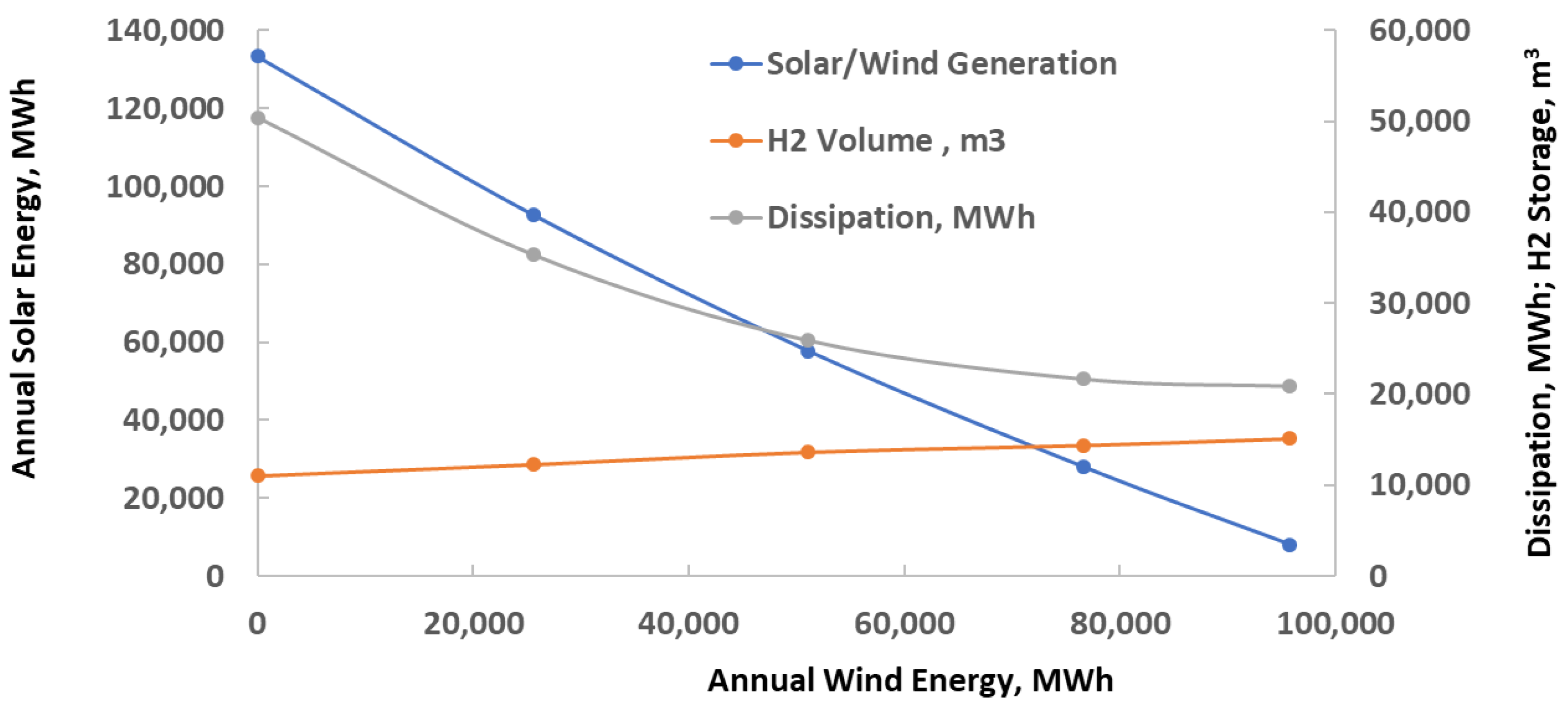
4.1. Case A: Electricity Source Substitution with Renewables
4.2. Case B: Electricity and Natural Gas Substitution with Renewables
5. Elasticity Coefficients for Transition
6. A Note on Cost
7. Conclusions
- Advance local regulations that would encourage new housing developments to install adequate insulation (in attics and windows), as well as efficient GSHP units for a-c and heat pumps.
- Promote the dual use of a-c units and heat pumps instead of piping natural gas to homes.
- Offer incentives for efficiently built housing developments to become grid independent by storing part of the electric energy generated by renewable energy sources.
- When hydrogen generation and storage equipment reach the markets, advance regulations for all new housing developments to become grid-independent and operate their own electricity microgrids.
- Offer incentives for existing buildings to significantly improve their insulation and the efficiency of their a-c units.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- IEA. Energy Efficiency Market Report—2013; IEA Publications: Paris, France, 2013. [Google Scholar]
- Michaelides, E.E. Energy, the Environment and Sustainability; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- IEA. Net Zero Roadmap: A Global Pathway to Keep the 1.5 °C Goal in Reach—2023 Update; IEA Publications: Paris, France, 2023. [Google Scholar]
- IEA. World Energy Investment 2024; 2024 IEA Publications: Paris, France, 2024. [Google Scholar]
- IPCC. Climate Change 2022: Mitigation of Climate Change. 2022. Available online: https://www.ipcc.ch/report/ar6/wg3/ (accessed on 12 February 2025).
- IEA. Key World Energy Statistics 2021; IEA Press: Paris, France, 2021. [Google Scholar]
- Matthew, C. The multiple benefits of current and potential energy efficiency policies. A Scott. Isl. Case Study. Energy Policy 2024, 187, 114032. [Google Scholar] [CrossRef]
- Watson, S.D.; Lomas, K.J.; Buswell, R.A. How will heat pumps alter national half hourly heat demands? Empirical modelling based on GB field trials. Energy Build. 2021, 238, 110777. [Google Scholar] [CrossRef]
- Kokoni, S.; Leach, M. Policy mechanisms to support heat pump deployment: A UK case study based on techno-economic modelling. Renew. Sustain. Energy Transit. 2021, 1, 100009. [Google Scholar] [CrossRef]
- Yushchenko, A.; Patel, M.K. Cost-effectiveness of energy efficiency programs: How to better understand and improve from multiple stakeholder perspectives? Energy Policy 2017, 108, 538–550. [Google Scholar] [CrossRef]
- Palma, P.; Gouveia, J.P.; Barbosa, R. How much will it cost? An energy renovation analysis for the Portuguese dwelling stock. Sustain. Cities Soc. 2022, 78, 103607. [Google Scholar] [CrossRef]
- Kirme, S.K.; Kapse, V.S. A comprehensive review of residential building energy efficiency measures in India. Energy Build. 2024, 319, 114537. [Google Scholar] [CrossRef]
- Tsvetkov, P.; Samuseva, P.; Nikolaychuk, L. The research of the impact of energy efficiency on mitigating greenhouse gas emissions at the national level. Energy Convers. Manag. 2024, 314, 118671. [Google Scholar] [CrossRef]
- Otrachshenko, V.; Hartwell, C.A.; Popova, O. Energy efficiency, market competition, and quality certification: Lessons from Central Asia. Energy Policy 2023, 177, 113539. [Google Scholar]
- Galvin, R. The economic losses of energy-efficiency renovation of Germany’s older dwellings: The size of the problem and the financial challenge it presents. Energy Policy 2024, 184, 113905. [Google Scholar]
- Sieger, L.; Weber, C. Inefficient markets for energy efficiency?—The efficiency premium puzzle in the German rental housing market. Energy Policy 2023, 183, 113819. [Google Scholar]
- Mihai, S.; Yaqoob, M.; Dang, H.V.; Davis, W.; Towakel, P.; Mohsin, R.; Karamanoglu, M.; Barn, B.; Shetve, D.; Prasad, R.; et al. Digital Twins: A Survey on Enabling Technologies, Challenges, Trends and Future Prospects. IEEE Commun. Surv. Tutor. 2022, 24, 2255–2291. [Google Scholar] [CrossRef]
- Sayed, A.N.; Bensaali, F.; Himeur, Y.; Dimitrakopoulos, G.; Varlamis, I. Enhancing building sustainability: A Digital Twin approach to energy efficiency and occupancy monitoring. Energy Build. 2025, 328, 115151. [Google Scholar] [CrossRef]
- Hernández, D.; Siegel, E. Energy insecurity and its ill health effects: A community perspective on the energy-health nexus in New York City. Energy Res. Soc. Sci. 2019, 47, 78–83. [Google Scholar] [CrossRef] [PubMed]
- Drehobl, A.; Ross, L.; Ayala, R. How High Are Household Energy Burdens? American Council for an Energy-Efficient Economy (ACEEE): Washington, DC, USA, 2020. [Google Scholar]
- IEA. World Energy Outlook; IEA Publications: Paris, France, 2024. [Google Scholar]
- California ISO (CAISO), 2016, Fast Facts—What the Duck Curve Tells Us About Managing a Green Grid, Report Comm PR/2016. Available online: https://www.caiso.com/library (accessed on 12 February 2025).
- Freeman, E.; Occello, D.; Barnes, F. Energy Storage for Electrical Systems in the USA. AIMS Energy 2016, 4, 856–875. [Google Scholar] [CrossRef]
- Stamatellou, A.-M.; Stamatelos, T. The Implications of Long-Term Local Climate Change for the Energy Performance of an nZEB Residential Building in Volos, Greece. Energies 2025, 18, 1032. [Google Scholar] [CrossRef]
- Baumann, C.; Wohlgenannt, P.; Streicher, W.; Kepplinger, P. Optimizing Heat Pump Control in an NZEB via Model Predictive Control and Building Simulation. Energies 2024, 18, 100. [Google Scholar] [CrossRef]
- Michaelides, E.E. Thermodynamics, Energy Dissipation, and Figures of Merit of Energy Storage Systems—A Critical Review. Energies 2021, 14, 6121. [Google Scholar] [CrossRef]
- ERCOT. 2024. Available online: https://www.ercot.com/gridinfo/generation (accessed on 28 September 2024).
- Hadjipaschalis, I.; Poullikkas, A.; Efthimiou, V. Overview of current and future ES technologies for electric power applications. Renew. Sustain. Energy Rev. 2009, 13, 1513–1522. [Google Scholar] [CrossRef]
- Huggins, R.A. Energy Storage—Fundamentals, Materials and Applications, 2nd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- O’Shaughnessy, E.; Barbose, G.; Kannan, S. Evaluating community solar as a measure to promote equitable clean energy access. Nat. Energy 2024, 9, 955–963. [Google Scholar] [CrossRef]
- UN-Habitat. 2024. Available online: https://www.weforum.org/agenda/2024/06/global-housing-crisis-practical-solutions/ (accessed on 28 September 2024).
- Texas. 2024. Available online: https://www.texasstandard.org/stories/texas-population-growth-census-suburban-kaufman-county-dfw-metroplex/ (accessed on 28 September 2024).
- EIA. Household Energy Use in Texas; US Energy Information Administration, US Department of Energy Publications: Washington, DC, USA, 2024. Available online: https://www.eia.gov/state/analysis.php?sid=TX (accessed on 28 September 2024).
- Wang, R.; He, Z.; Zhai, X.; Lu, S. Application and Performance Evaluation of Key Technologies in Green Buildings. Energies 2024, 17, 6418. [Google Scholar] [CrossRef]
- Moghimi, S.M.; Gulliver, T.A.; Thirumarai Chelvan, I.; Teimoorinia, H. Resource Optimization for Grid-Connected Smart Green Townhouses Using Deep Hybrid Machine Learning. Energies 2024, 17, 6201. [Google Scholar] [CrossRef]
- Ochsner, K. Geothermal Heat Pumps—A Guide for Planning and Installing; Earthscan: London, UK, 2008. [Google Scholar]
- Aguilar, R.S.; Michaelides, E.E. Microgrid for a Cluster of Grid Independent Buildings Powered by Solar and Wind Energy. Appl. Sci. 2021, 11, 9214. [Google Scholar] [CrossRef]
- Szpilko, D.; Fernando, X.; Nica, E.; Budna, K.; Rzepka, A.; Lăzăroiu, G. Energy in Smart Cities: Technological Trends and Prospects. Energies 2024, 17, 6439. [Google Scholar] [CrossRef]
- Dubey, S.; Sarvaiya, N.J.; Sheshadri, B. Temperature dependent Photovoltaic (PV) efficiency and its effect on PV production in the world—A review. Energy Procedia 2013, 33, 311–321. [Google Scholar] [CrossRef]
- Wilcox, S. National Solar Radiation Database 1991–2010 Update: User’s Manual; Technical Report NREL/TP-5500-54824.2012. Available online: https://www.nrel.gov/docs/fy12osti/54824.pdf (accessed on 2 March 2025).
- Michaelides, E.E. Energy Storage—The Key to Renewable Energy Transition; CRC Press: Boca Raton, FL, USA, 2025; in print. [Google Scholar]
- de Oliveira, C.C.; Vaz, I.C.M.; Ghisi, E. Retrofit strategies to improve energy efficiency in buildings: An integrative review. Energy Build. 2024, 321, 114624. [Google Scholar] [CrossRef]
- Leonard, M.D.; Michaelides, E.E. Grid-independent residential buildings with renewable energy sources. Energy 2018, 148, 448–460. [Google Scholar] [CrossRef]
- Zakeri, B.; Syri, S. Electrical ES systems: A comparative life cycle cost analysis. Renew. Sustain. Energy Rev. 2015, 42, 569–596. [Google Scholar] [CrossRef]
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A comprehensive review of stationary energy storage devices for large scale renewable energy sources grid integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Available online: https://www.energy.gov/eere/solar/solar-photovoltaic-system-cost-benchmarks (accessed on 2 March 2025).
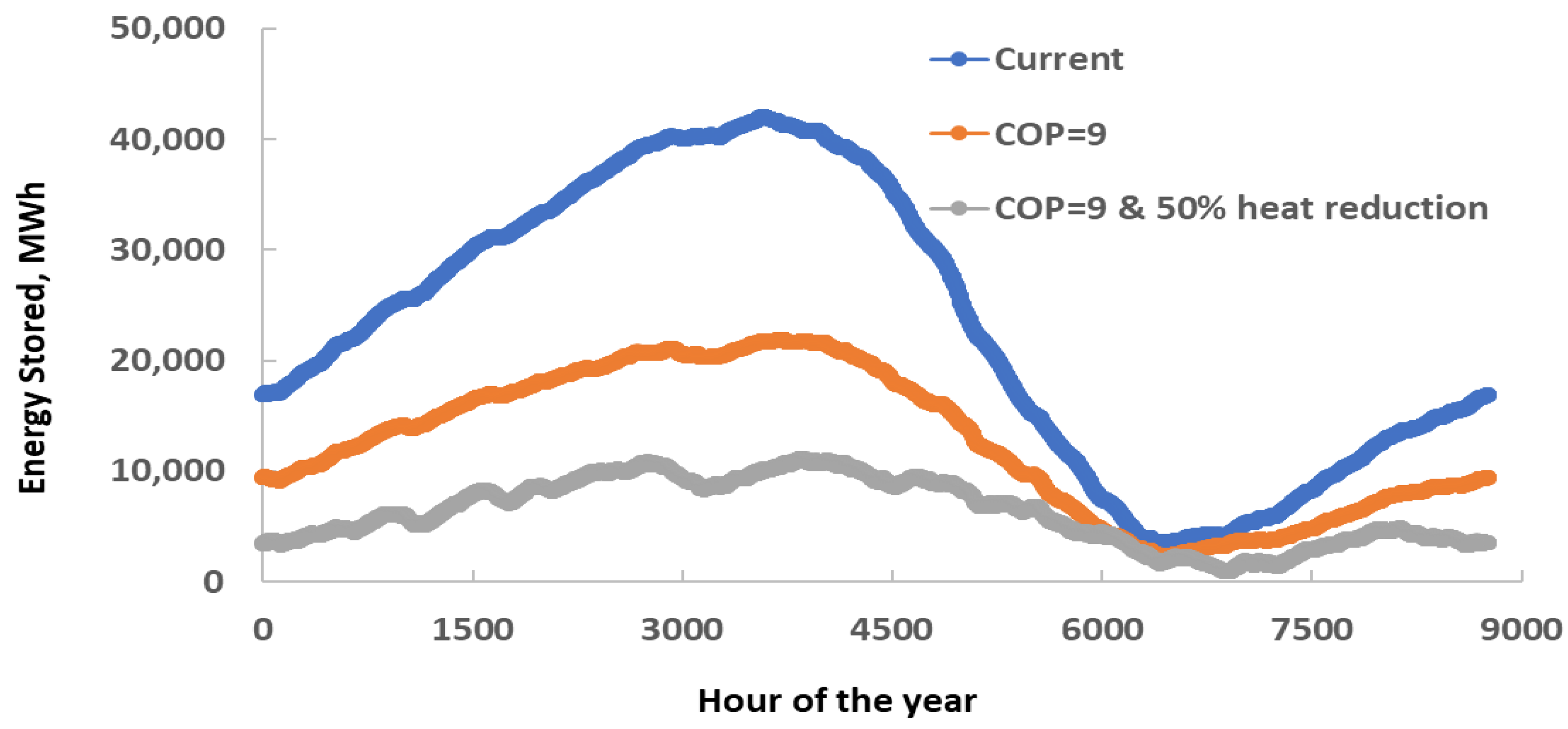

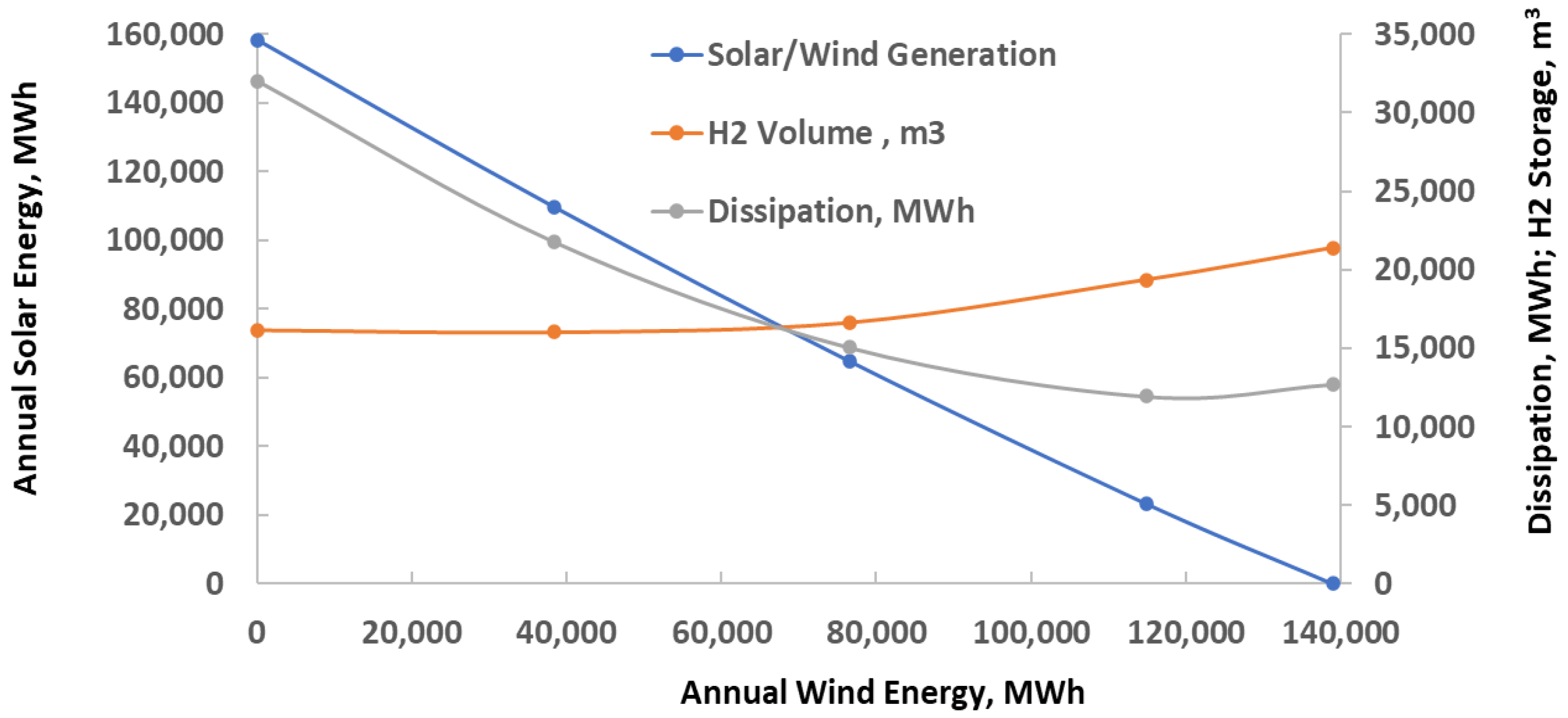


| Power Reduction, kW | Annual Energy Reduction, MWh | Storage Reduction, m3 | Dissipation Reduction, MWh | |
|---|---|---|---|---|
| COP 3.5 to 5 | 10,390 | 16,875 | 6452 | 4884 |
| COP 5 to 7 | 5041 | 8187 | 3175 | 2191 |
| COP 7 to 9 | 2774 | 4506 | 1691 | 1175 |
| 50% heat & COP = 9 | 9557 | 15,522 | 5476 | 3863 |
| Power Reduction, kW | Annual Energy Reduction, MWh | Storage Reduction, m3 | Dissipation Reduction, MWh | |
|---|---|---|---|---|
| COP 3.5 to 5 | 17,447 | 28,336 | 4536 | 4585 |
| COP 5 to 7 | 9099 | 14,778 | 2309 | 2168 |
| COP 7 to 9 | 5459 | 8866 | 1323 | 1567 |
| 50% heat & COP = 9 | 5056 | 8212 | 1235 | 1463 |
| Without Efficiency Measures, 1000 $US | With All Efficiency Measures, 1000 $US | |
|---|---|---|
| Efficiency Measures | 0.0 | 68.3 |
| Installed Renewable Power | 26.1 | 9.6 |
| Energy Storage | 135.2 | 35.5 |
| Fuel Cells | 11.6 | 4.3 |
| Total Investment | 172.9 | 117.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michaelides, E.E. Energy Efficiency and the Transition to Renewables—Building Communities of the Future. Energies 2025, 18, 1778. https://doi.org/10.3390/en18071778
Michaelides EE. Energy Efficiency and the Transition to Renewables—Building Communities of the Future. Energies. 2025; 18(7):1778. https://doi.org/10.3390/en18071778
Chicago/Turabian StyleMichaelides, Efstathios E. 2025. "Energy Efficiency and the Transition to Renewables—Building Communities of the Future" Energies 18, no. 7: 1778. https://doi.org/10.3390/en18071778
APA StyleMichaelides, E. E. (2025). Energy Efficiency and the Transition to Renewables—Building Communities of the Future. Energies, 18(7), 1778. https://doi.org/10.3390/en18071778






