Research on the Magnetic Integration of Inductors for High-Power DC Transformers—A Case Study on Electric Roadways
Abstract
:1. Introduction
2. Topology of the DC Transformer for Electrified Roads
3. Dual Inductor Magnetic Integration Solution
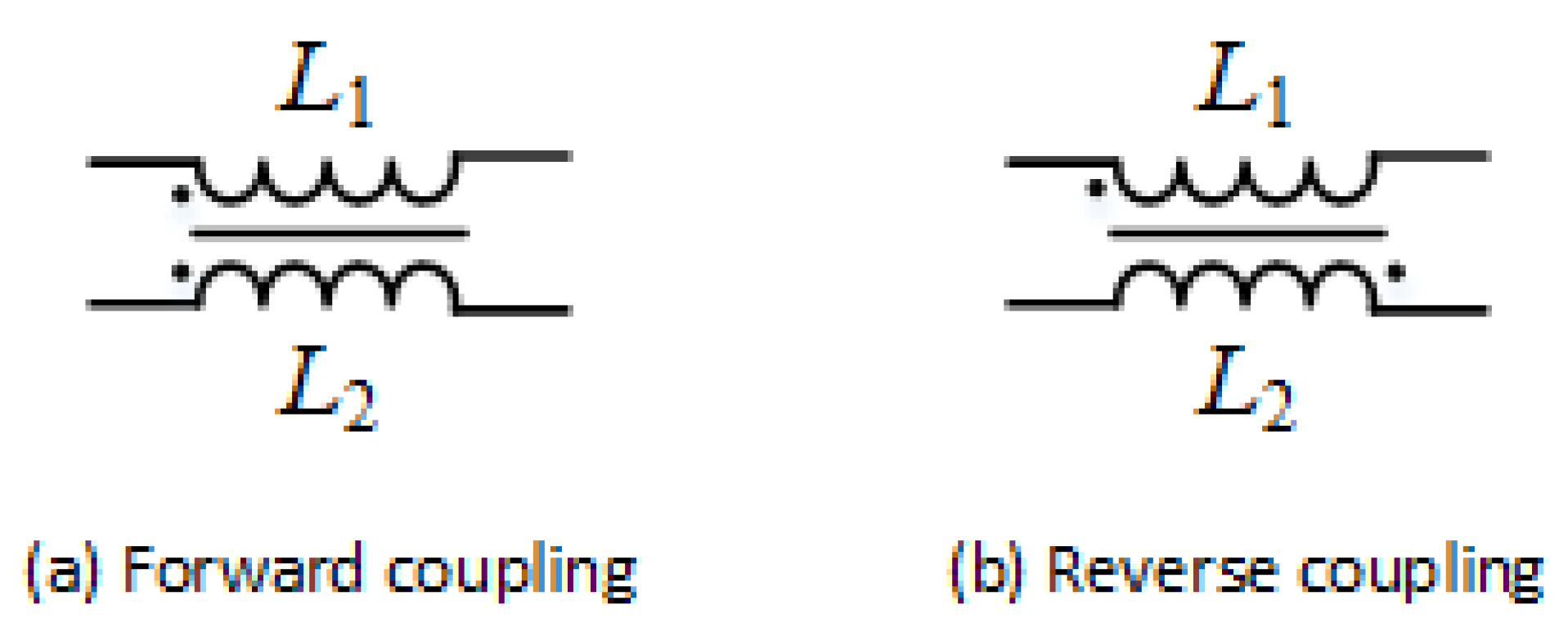
3.1. Decoupling Topology Selection
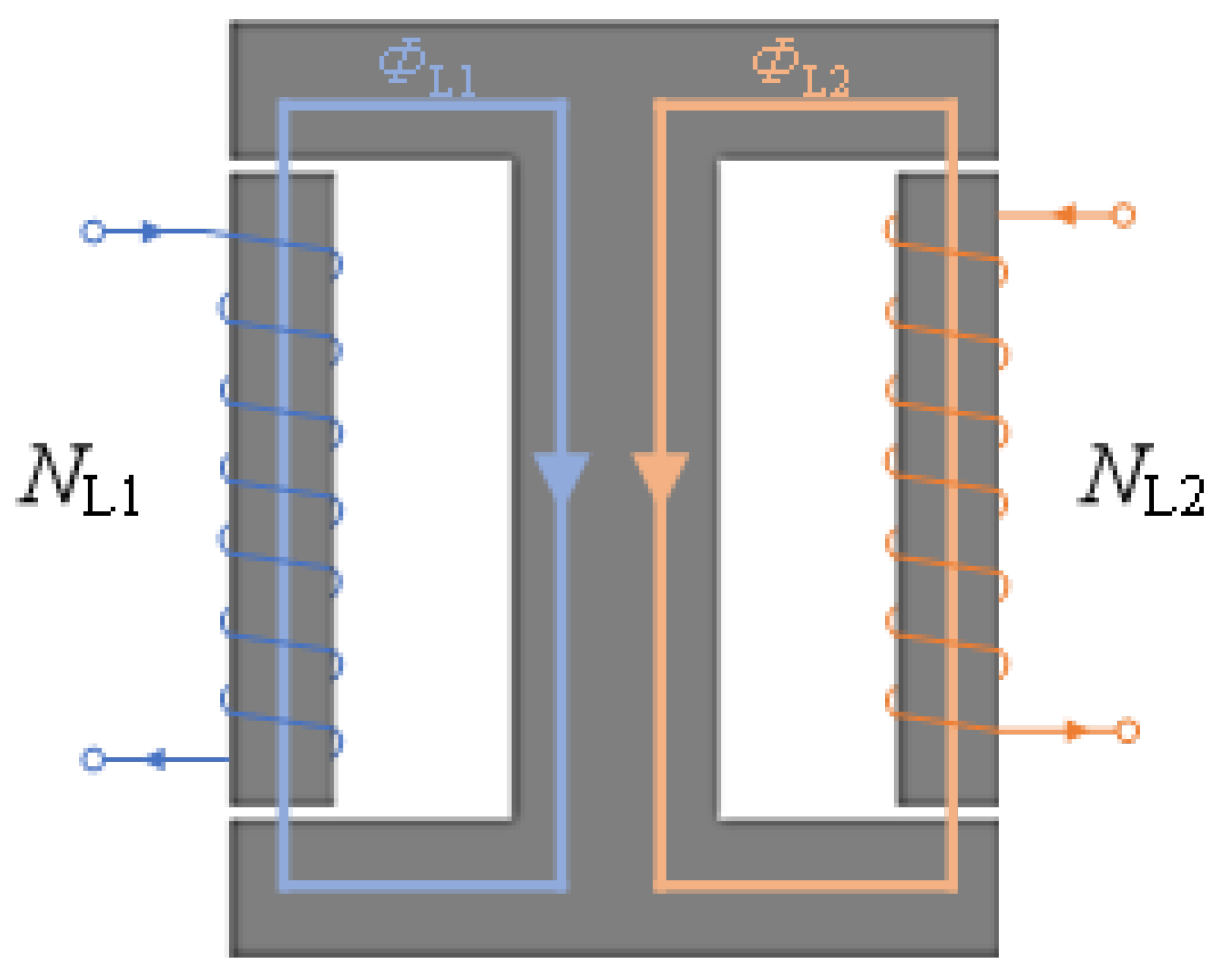
3.2. Magnetic Integration Inductor Design
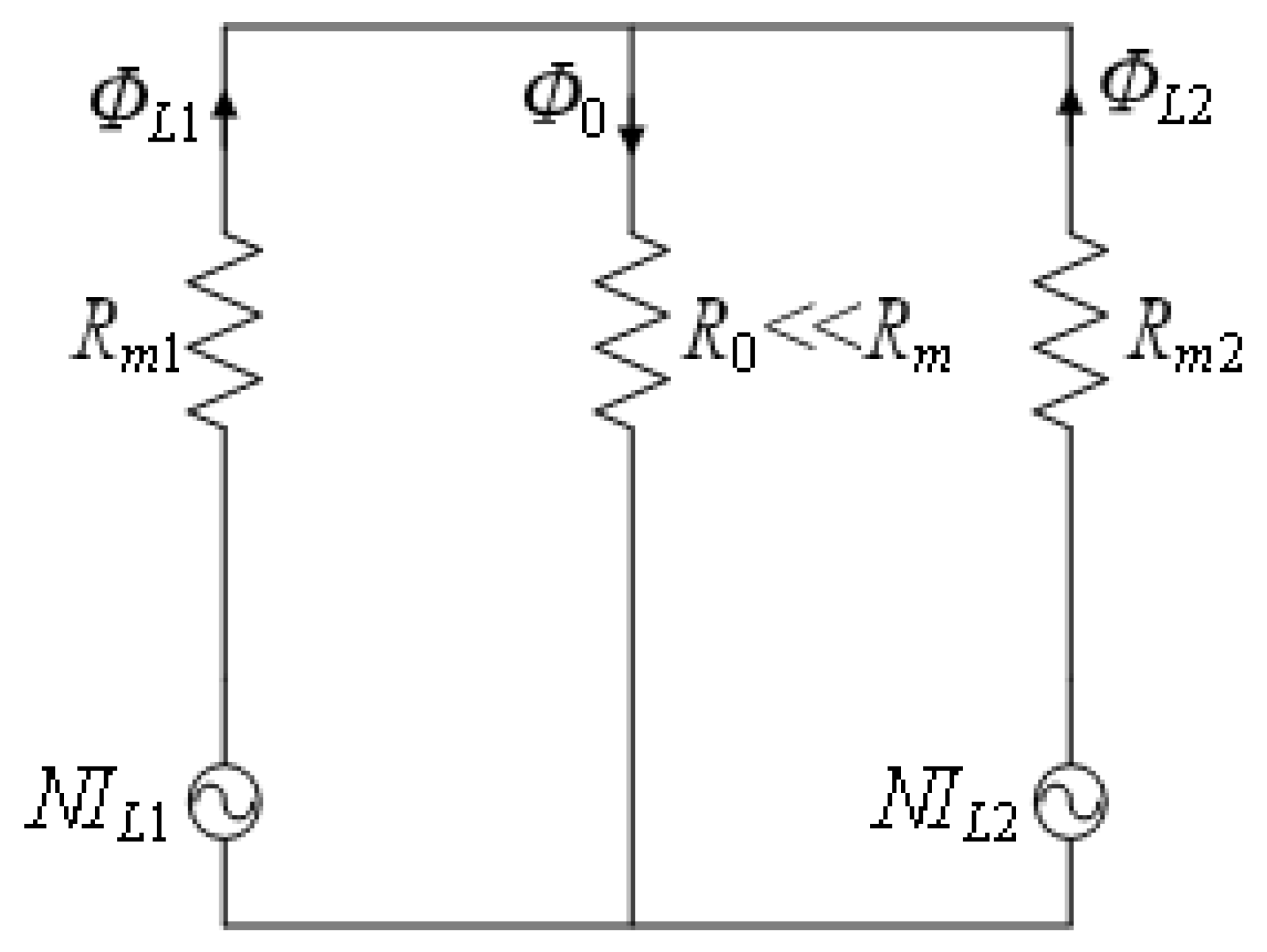
3.2.1. Basic Principles
3.2.2. Design Specifications and Boundary Conditions
3.2.3. IGSE Loss Model
3.2.4. Temperature Rise Magnetic Flux Density Limitation
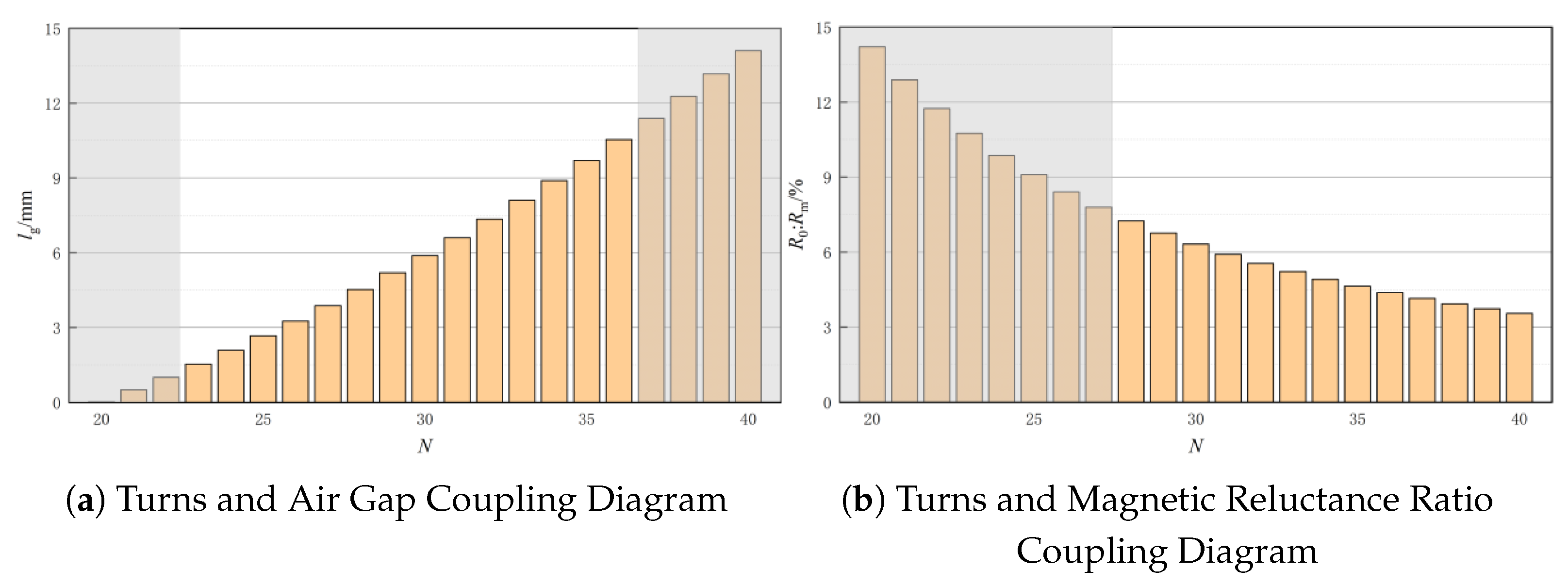
3.2.5. Selection of Winding Turns
3.2.6. Insulation Design
3.3. Magnetic Integration Scheme Simulation and Prototype Testing
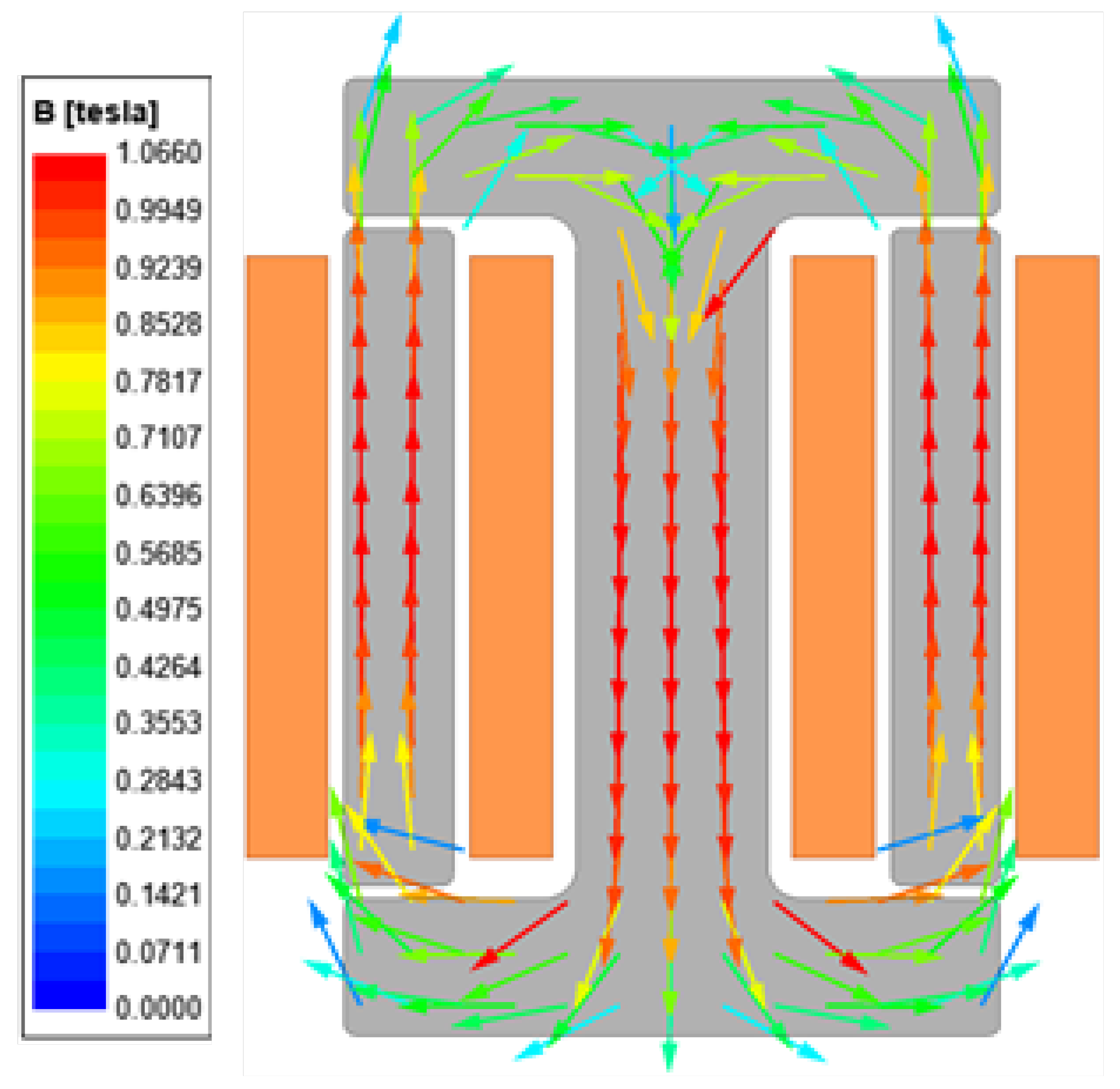
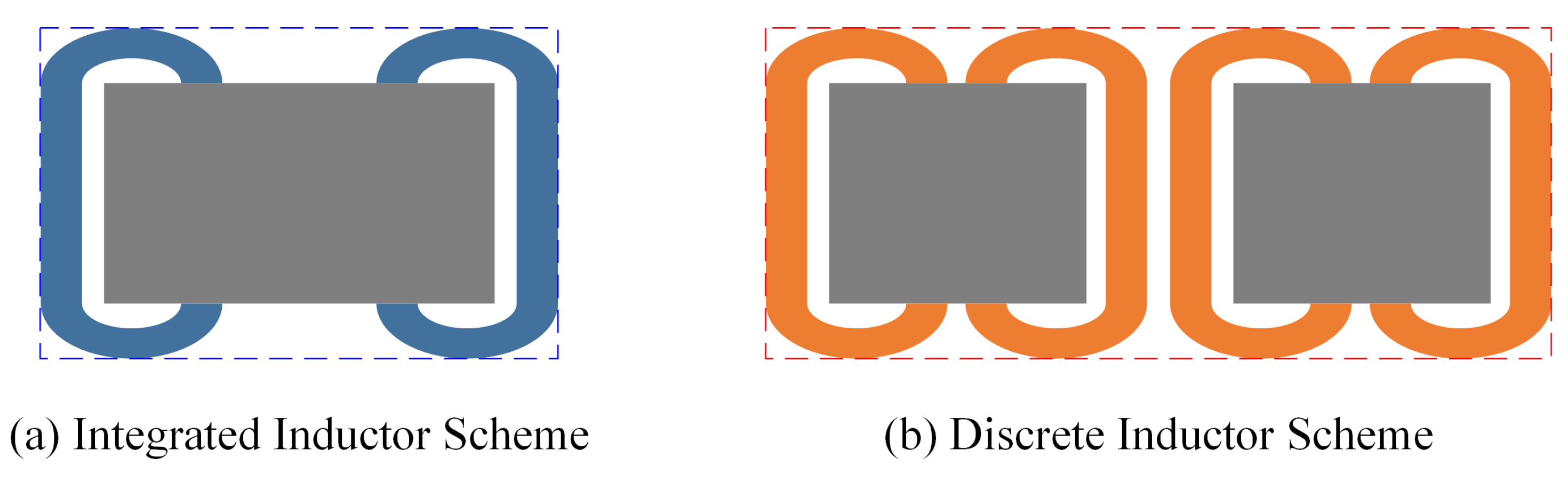
3.3.1. Magnetic Integration Scheme
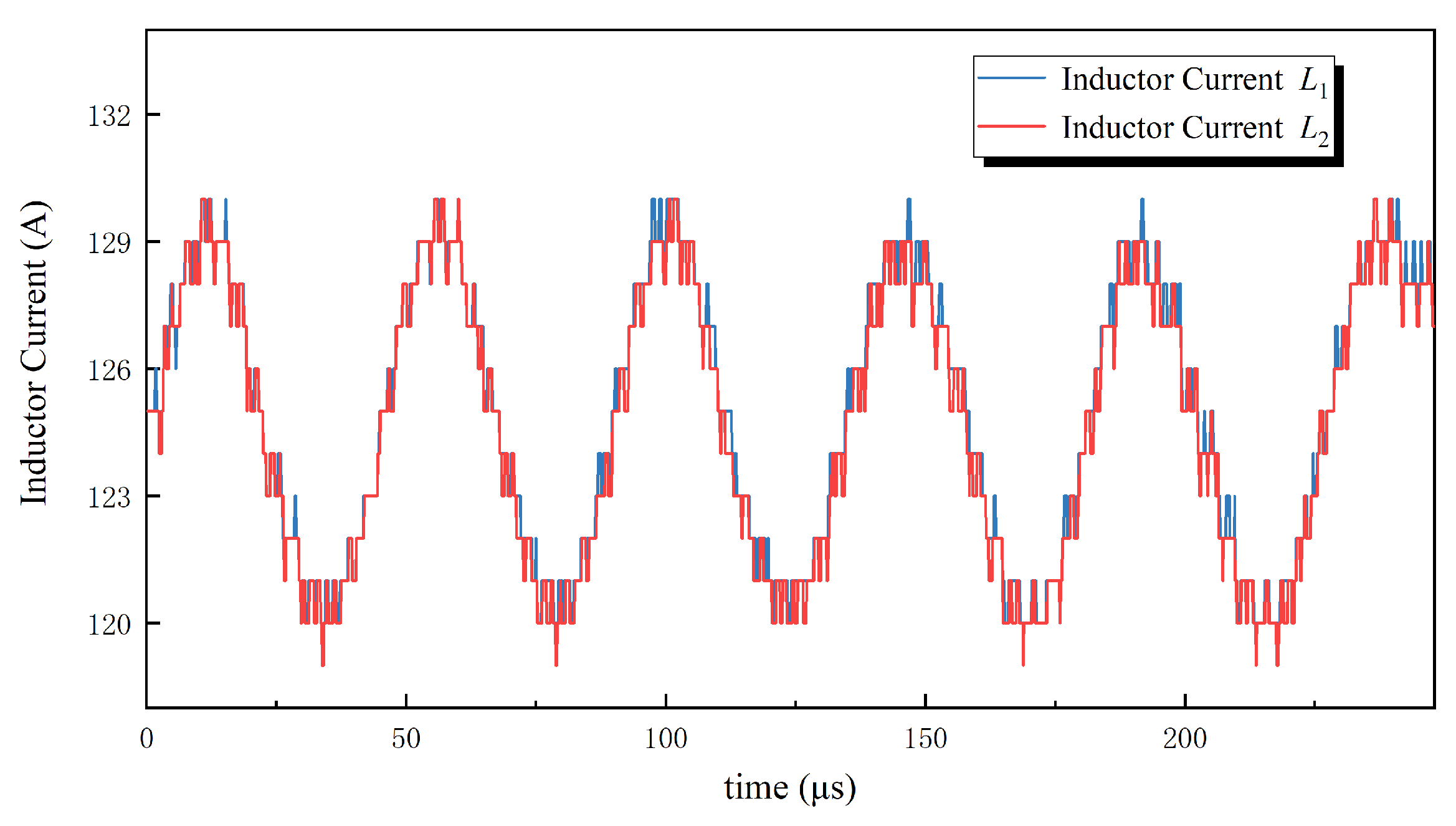
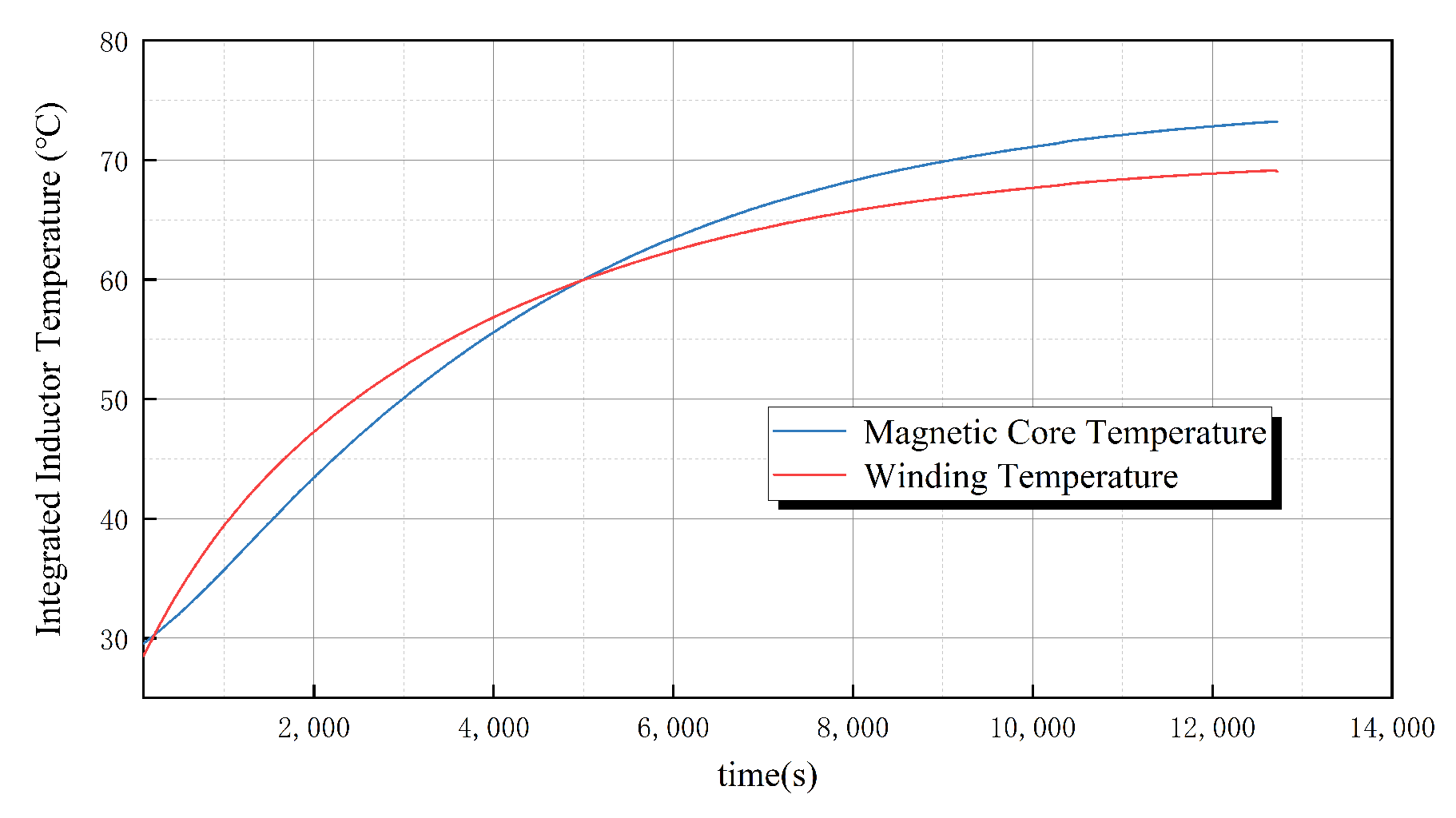
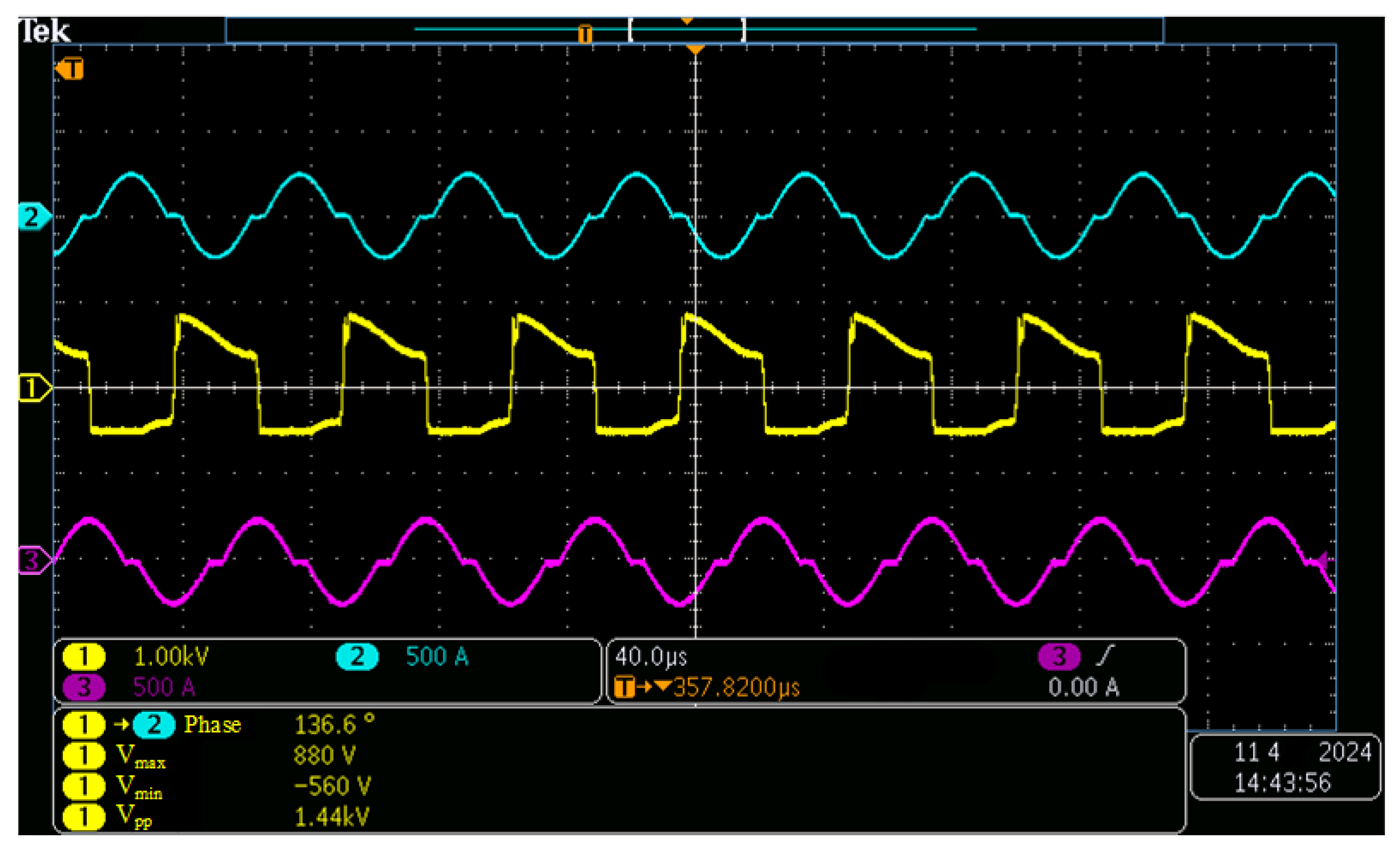
3.3.2. Prototype Testing and Verification
3.3.3. Comparison
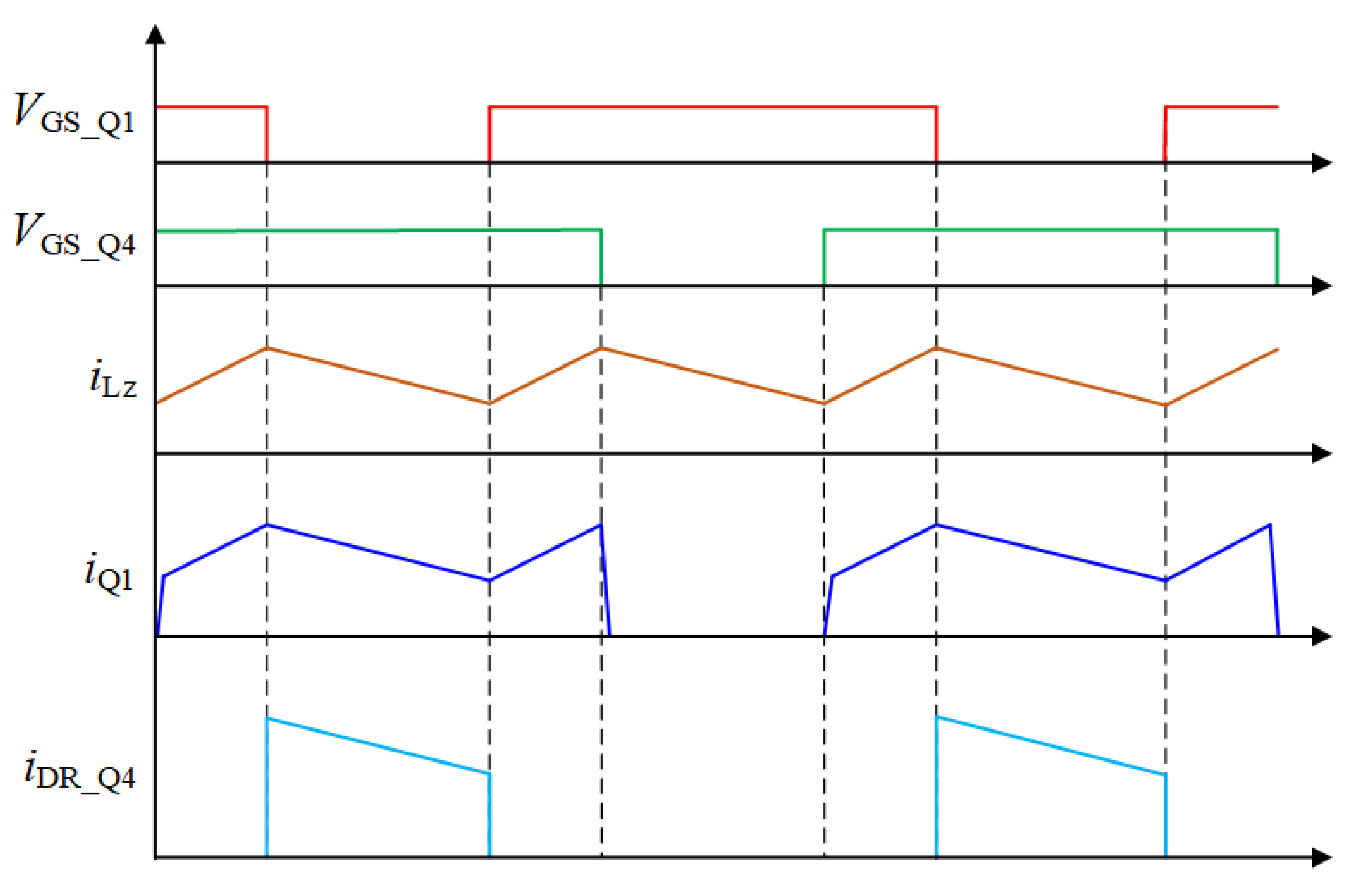
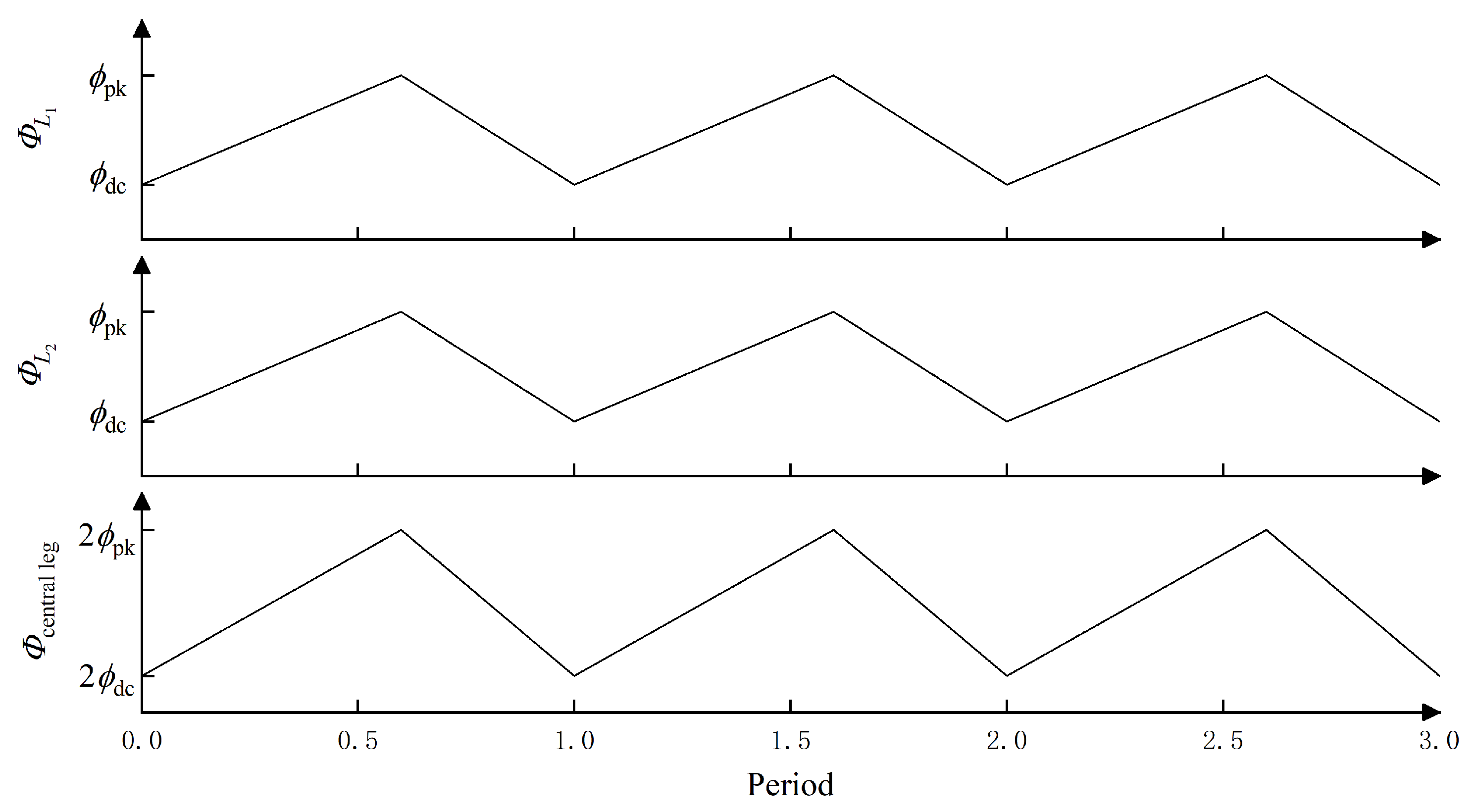
3.4. Optimization of Magnetic Integration Based on Interleaved Parallel Control
4. Conclusions
- Volume and area reduction: The magnetic integration inductor scheme for the DC-DC converter, validated through simulations and experiments, shows that compared to discrete inductors, it can effectively reduce the overall volume by 7.93% and the footprint by 38.62%, enhancing the module’s overall lightweight and compact design.
- Further optimization with interleaved control: Building on the magnetic integration scheme, the use of interleaved parallel control allows the magnetic integration inductor scheme to achieve a 19.74% reduction in overall volume and a 46.49% reduction in footprint compared to discrete inductors. This significantly decreases the inductor and overall module volume and mass.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Taylor, N.; Kringos, N. Electrification of roads: Opportunities and challenges. Appl. Energy 2015, 150, 109–119. [Google Scholar]
- Wang, D.; Ye, C.; Lv, H.; Meng, L.; Tang, F.; Ni, Y.; Liu, P. Dielectric model of asphalt pavement materials towards the future electrified road. Philos. Trans. R. Soc. A 2023, 381, 20220164. [Google Scholar]
- Pei, Y.; Chen, F.; Ma, T.; Gu, G. A comparative review study on the electrified road structures: Performances, sustainability, and prospects. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 62, p. 106185. [Google Scholar]
- Ze-dong1, Z.; Hao, L.; Yong-dong, L.; Zheng, X. Electrical Highway Application. China J. Highw. Transp. 2019, 32, 132–141. [Google Scholar]
- Olovsson, J.; Taljegard, M.; Von Bonin, M.; Gerhardt, N.; Johnsson, F. Impacts of electric road systems on the german and swedish electricity systems—An energy system model comparison. Front. Energy Res. 2021, 9, 631200. [Google Scholar] [CrossRef]
- Ahmed, M.H.; Lee, F.C.; Li, Q. Two-stage 48-V VRM with intermediate bus voltage optimization for data centers. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 702–715. [Google Scholar] [CrossRef]
- Liu, Q.; Qian, Q.; Ren, B.; Xu, S.; Sun, W.; Yang, L. A two-stage buck–boost integrated LLC converter with extended ZVS range and reduced conduction loss for high-frequency and high-efficiency applications. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 9, 727–743. [Google Scholar]
- Fu, M.; Fei, C.; Yang, Y.; Li, Q.; Lee, F.C. Optimal design of planar magnetic components for a two-stage GaN-based DC–DC converter. IEEE Trans. Power Electron. 2018, 34, 3329–3338. [Google Scholar] [CrossRef]
- Yang, F.; Ruan, X.; Yang, Y.; Ye, Z. Interleaved critical current mode boost PFC converter with coupled inductor. IEEE Trans. Power Electron. 2011, 26, 2404–2413. [Google Scholar]
- Chen, W.; Lee, F.C.; Zhou, X.; Xu, P. Integrated planar inductor scheme for multi-module interleaved quasi-square-wave (QSW) DC/DC converter. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Record (Cat. No. 99CH36321), Charleston, SC, USA, 1 July 1999; Volume 2, pp. 759–762. [Google Scholar]
- Wong, P.L.; Wu, Q.; Xu, P.; Yang, B.; Lee, F.C. Investigating coupling inductors in the interleaving QSW VRM. In Proceedings of the APEC 2000, Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No. 00CH37058), New Orleans, LA, USA, 6–10 February 2000; Volume 2, pp. 973–978. [Google Scholar]
- Cheng, D.W.; Wong, L.P.; Lee, Y.S. Design, modeling, and analysis of integrated magnetics for power converters. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, (Cat. No. 00CH37018), Galway, Ireland, 23–23 June 2000; Volume 1, pp. 320–325. [Google Scholar]
- Deng, C.; Li, S.; Tang, J. A review of flexible multilayer foil integration technology for passive components. IEEE Trans. Power Electron. 2021, 36, 13025–13038. [Google Scholar]
- Mohamadi, M.; Mazumder, S.K.; Kumar, N. Integrated magnetics design for a three-phase differential-mode rectifier. IEEE Trans. Power Electron. 2021, 36, 10561–10570. [Google Scholar]
- Sun, X.; Zhu, H.; Meng, D.; Li, X.; Wang, B. Research on magnetic integration and loss optimal control of four-port energy router. CSEE J. Power and Energy Systems. 2024, 2, 1–12. [Google Scholar]
- Inoue, S.; Itoh, K.; Ishigaki, M.; Sugiyama, T. Integrated magnetic component of a transformer and a magnetically coupled inductor for a three-port DC-DC converter. IEEJ J. Ind. Appl. 2020, 9, 713–722. [Google Scholar]
- Karlsson, A.; Alaküla, M. Energy supply to buses on a conductive electric road: An evaluation of charger topologies and electric road characteristics. World Electr. Veh. J. 2021, 12, 241. [Google Scholar] [CrossRef]
- Swaminathan, N.; Cao, Y. An overview of high-conversion high-voltage DC–DC converters for electrified aviation power distribution system. IEEE Trans. Transp. Electrif. 2020, 6, 1740–1754. [Google Scholar] [CrossRef]
- Venkatachalam, K.; Sullivan, C.R.; Abdallah, T.; Tacca, H. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters. In Proceedings of the 2002 IEEE Workshop on Computers in Power Electronics, Mayaguez, PR, USA, 3–4 June 2002; pp. 36–41. [Google Scholar]
- Barg, S.; Ammous, K.; Mejbri, H.; Ammous, A. An improved empirical formulation for magnetic core losses estimation under nonsinusoidal induction. IEEE Trans. Power Electron. 2017, 32, 2146–2154. [Google Scholar]
- Zhou, Y.; Zhu, W.B.; Tong, G.H. A core loss calculation method for DC/DC power converters based on sinusoidal losses. IEEE Trans. Power Electron. 2023, 38, 692–702. [Google Scholar]
- Zhanlei, L.; Lingyu, Z.; Cao, Z.; Yongliang, D.; Yukun, Z.; Shengchang, J.I. Accurate Ferrite Core Loss Model Based on CNN-BiLSTM and Few-Shot Transfer Learning Prediction Method. High Volt. Eng. 2024, 50, 4487–4498. [Google Scholar]
- Pilato, G.; Vitale, G.; Vassallo, G.; Scirè, D. Neural modeling of power nonlinear inductors by the E-α Net network. Nonlinear Dyn. 2024, 112, 17069–17086. [Google Scholar] [CrossRef]

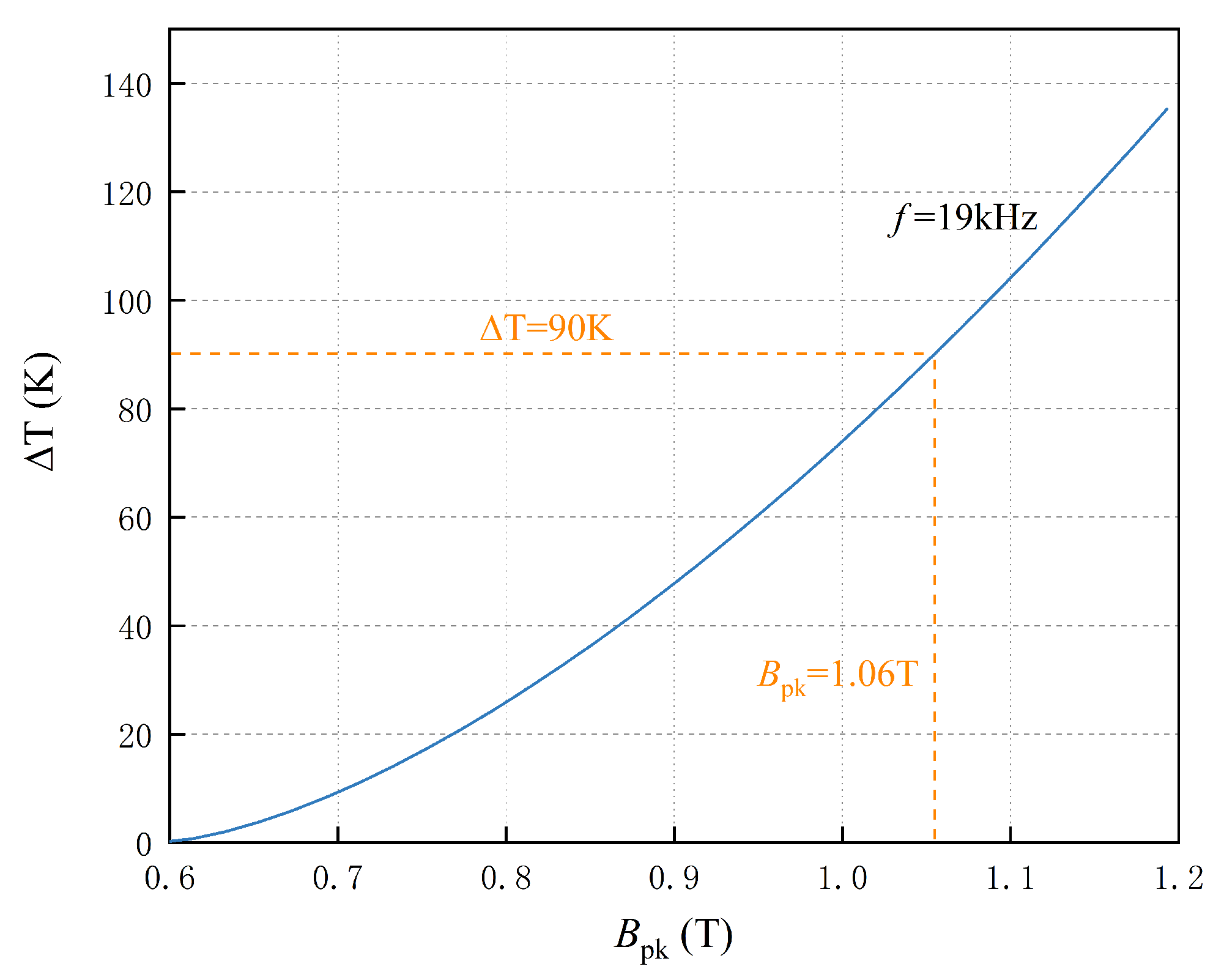


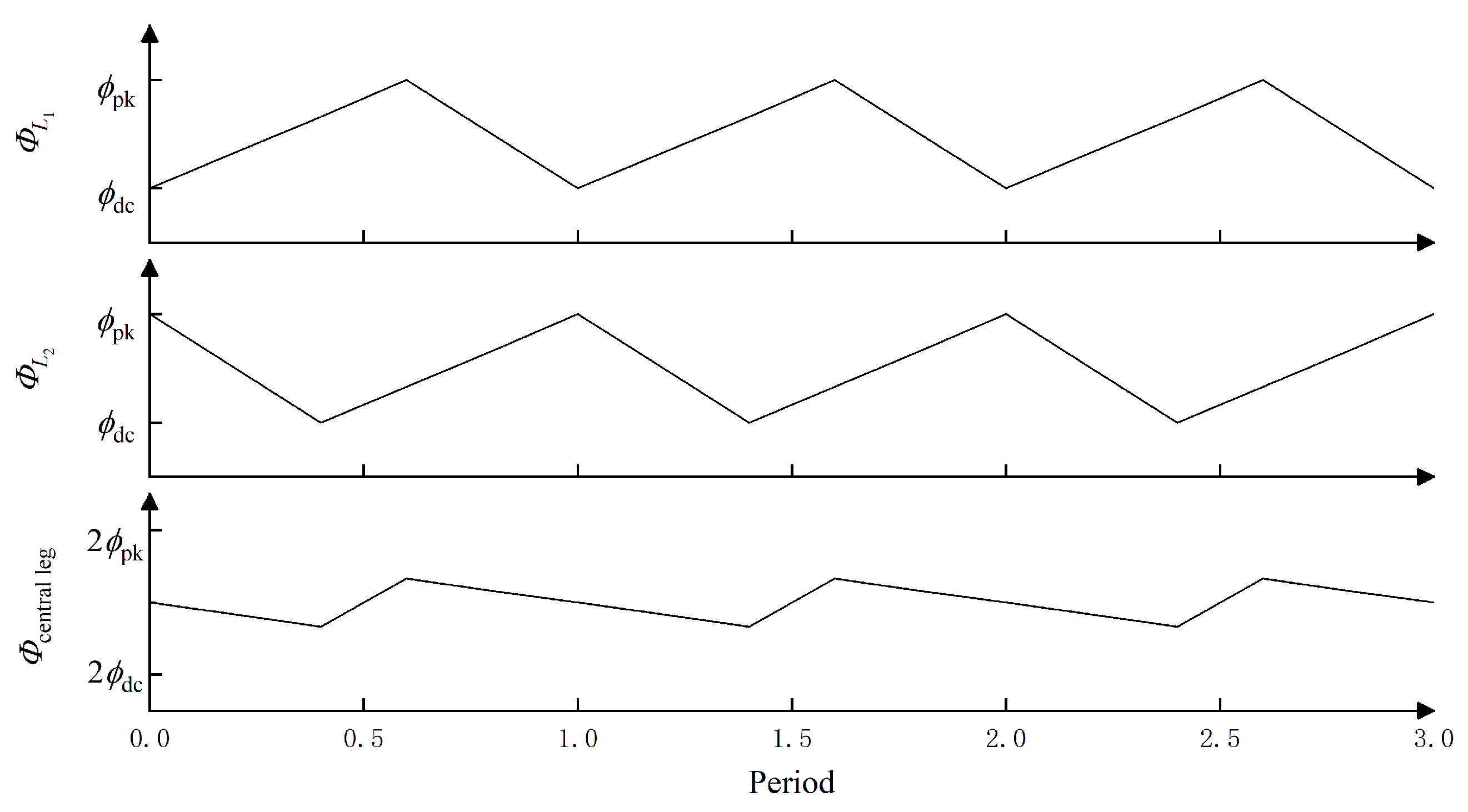
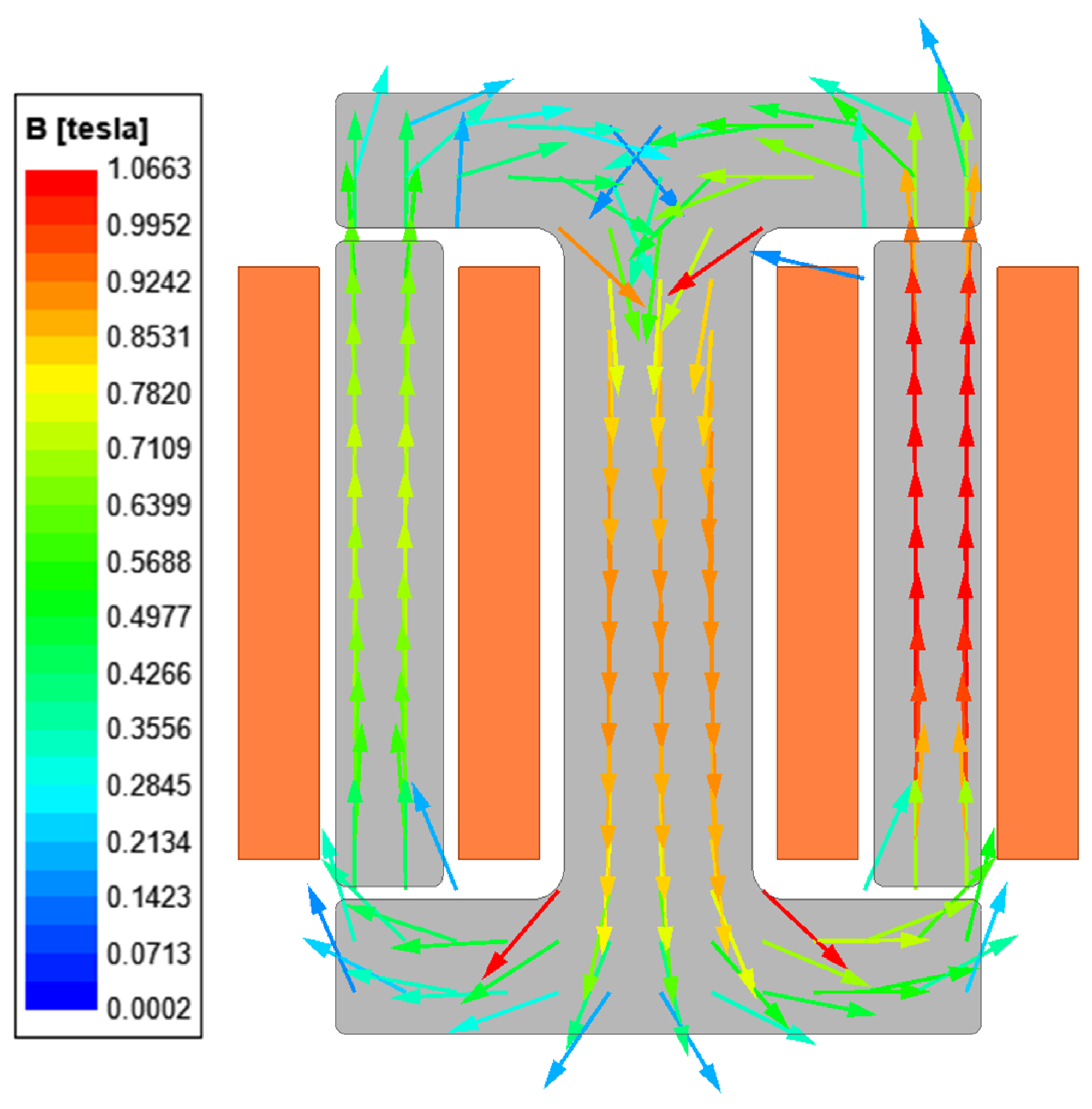

| Parameters | Value |
|---|---|
| Rated power | 150 kW |
| Range of input voltage | 1500–2000 V DC |
| Range of output voltage | 500–750 V DC |
| Efficiency | >96% |
| Frequency | 19 kHz |
| Parameters | Value |
|---|---|
| Inductance | mH (−5–20%) |
| Operating frequency | 19 kHz |
| Operating voltage | 700–2000 V DC |
| Rateing current | 150 A |
| Saturation current | ≥1.5 |
| Maximum current | 180 A |
| Withstand voltage level | ≥6000 V |
| Operating environment tempreture | °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Wang, H.; Cai, F.; Xie, W.; Zeng, Y. Research on the Magnetic Integration of Inductors for High-Power DC Transformers—A Case Study on Electric Roadways. Energies 2025, 18, 1859. https://doi.org/10.3390/en18071859
Li B, Wang H, Cai F, Xie W, Zeng Y. Research on the Magnetic Integration of Inductors for High-Power DC Transformers—A Case Study on Electric Roadways. Energies. 2025; 18(7):1859. https://doi.org/10.3390/en18071859
Chicago/Turabian StyleLi, Biyu, Hu Wang, Fenglin Cai, Wei Xie, and Yang Zeng. 2025. "Research on the Magnetic Integration of Inductors for High-Power DC Transformers—A Case Study on Electric Roadways" Energies 18, no. 7: 1859. https://doi.org/10.3390/en18071859
APA StyleLi, B., Wang, H., Cai, F., Xie, W., & Zeng, Y. (2025). Research on the Magnetic Integration of Inductors for High-Power DC Transformers—A Case Study on Electric Roadways. Energies, 18(7), 1859. https://doi.org/10.3390/en18071859







