Simulation of Molten Carbonate Fuel Cell with Dry Reforming of Methane (DR-MCFC)
Abstract
:1. Introduction
2. Reactions in DR-MCFC
2.1. Reactions of DRM
2.2. Reaction Fluxes in DRM
2.3. Reactions of Molten Carbonate Fuel Cell
3. Gas Properties
3.1. Gas Flow Characteristics
3.2. Heat Generation in DRM
3.3. Heat Generation in MCFC
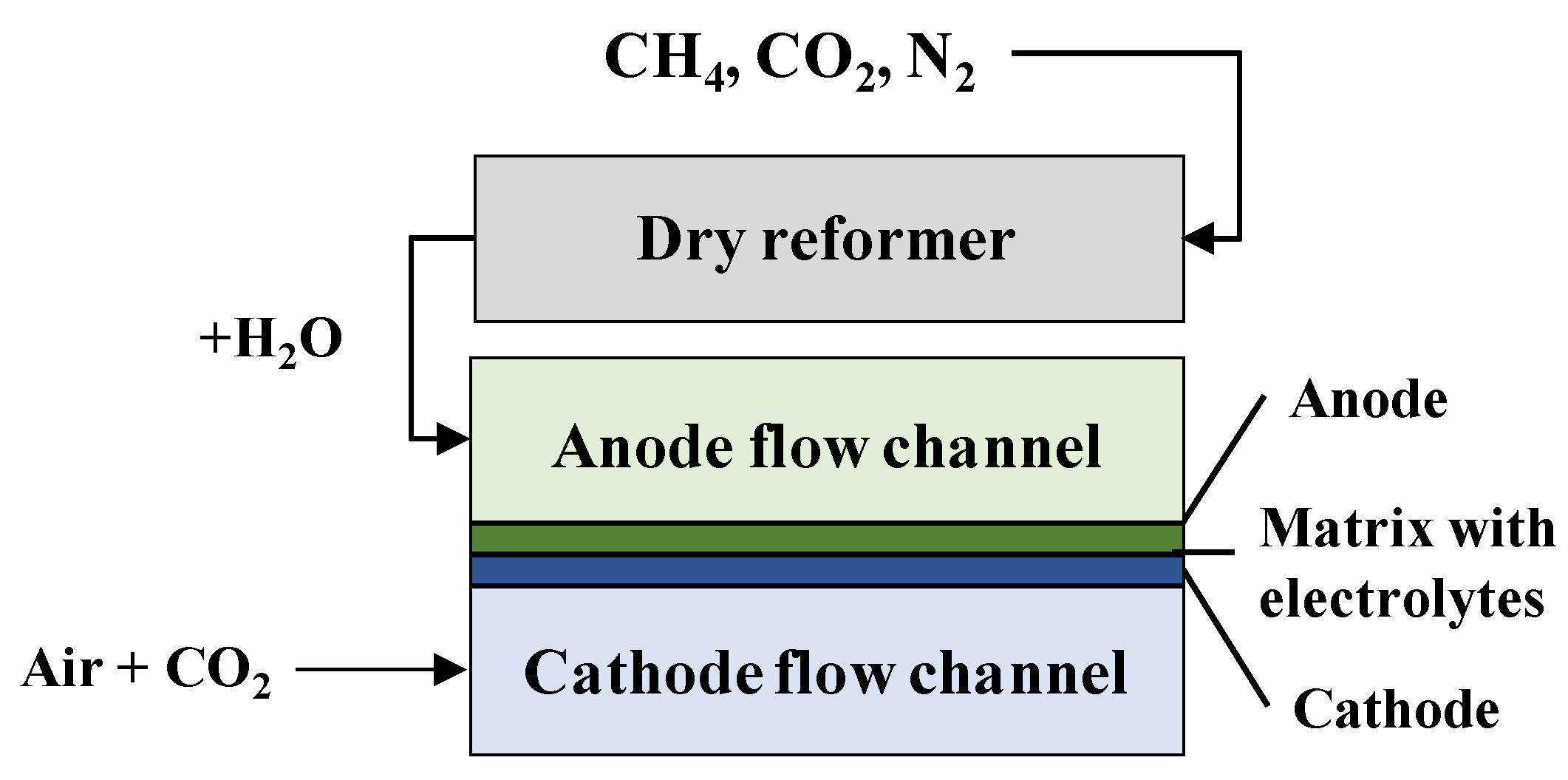
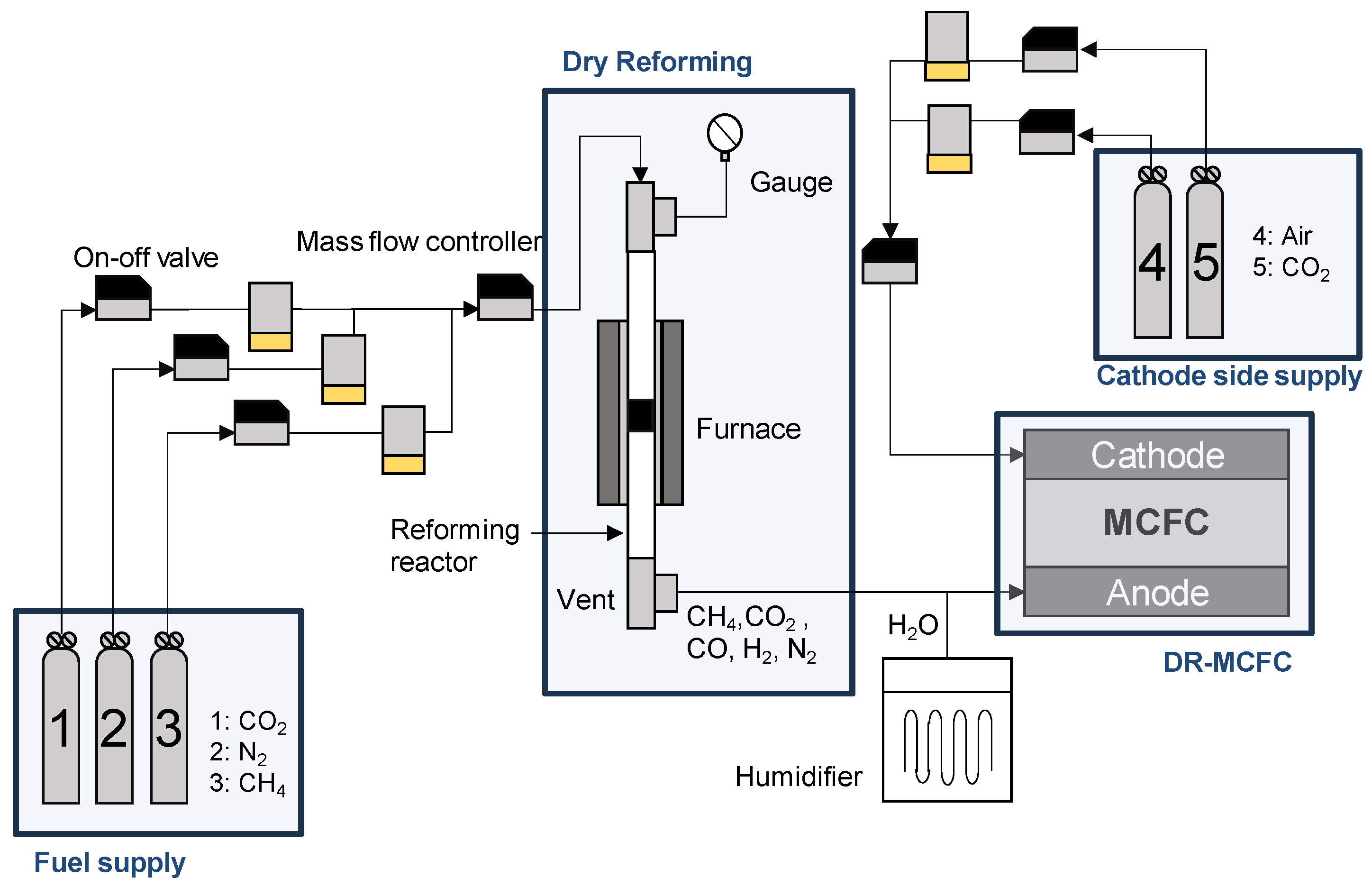
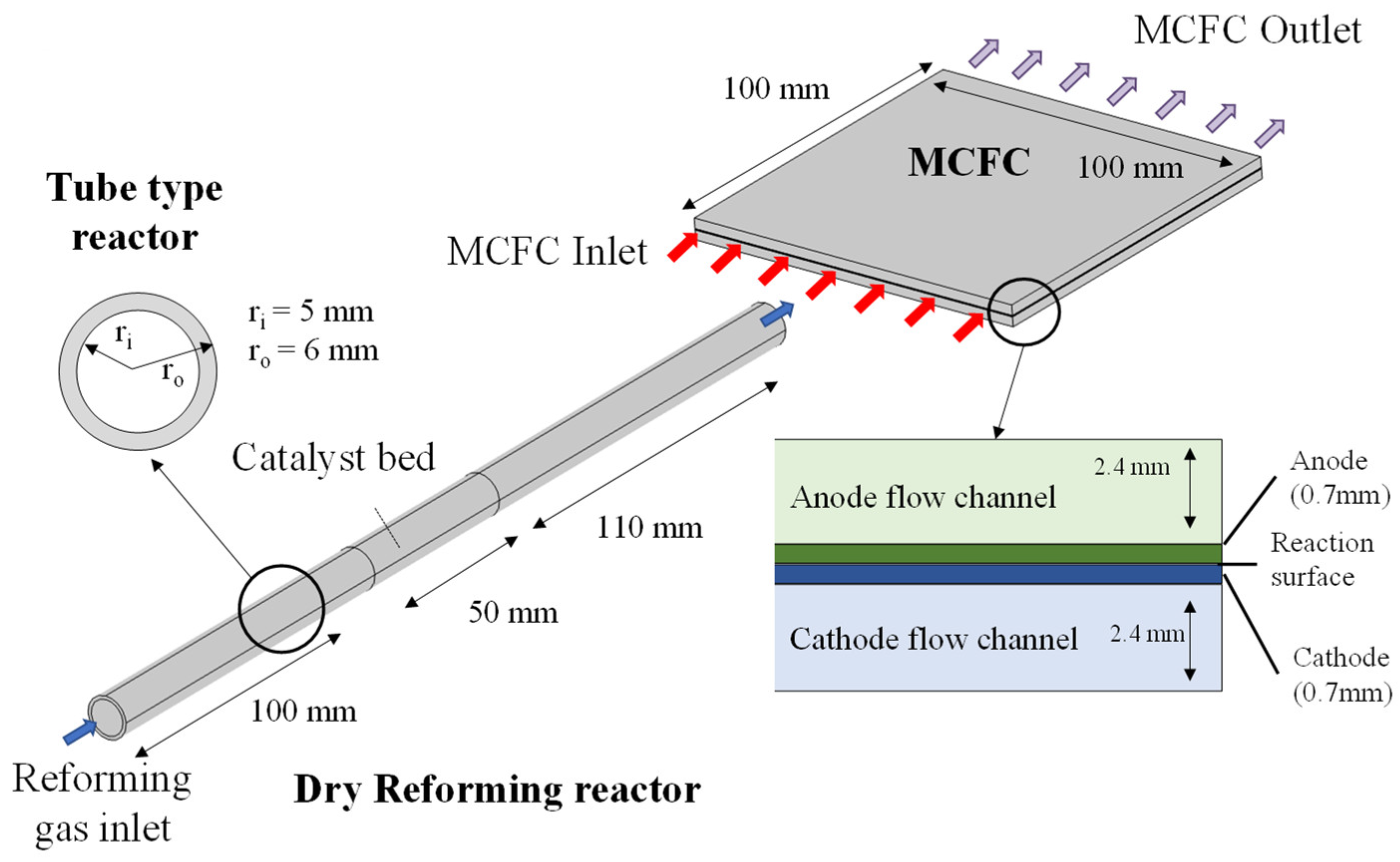
4. Simulation Model of DR-MCFC
4.1. Simulation Model
4.2. Simulation Conditions
5. Simulation of MCFC with Dry Reforming
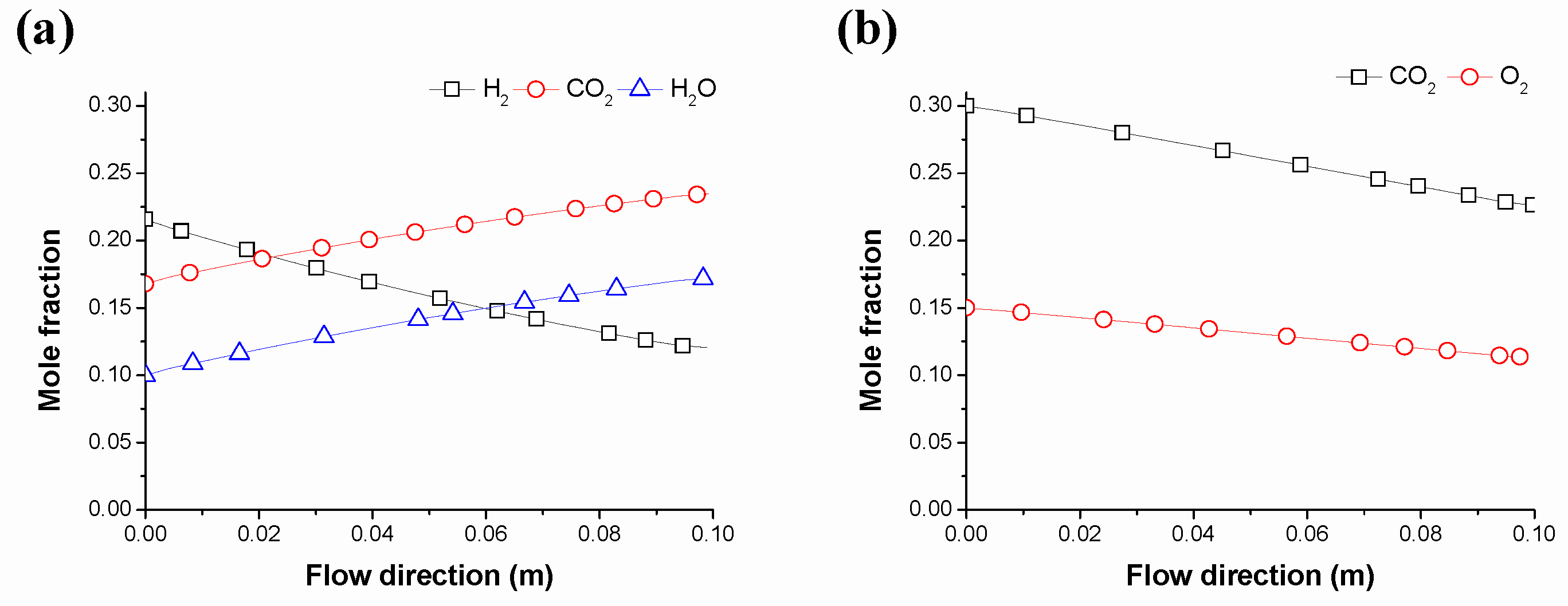
5.1. Operation Conditions for Different Gas Input Conditions
5.2. Comparison of Fuel Cell Performances
6. Discussion on DR-MCFC Operating Conditions
7. Conclusions
- (1)
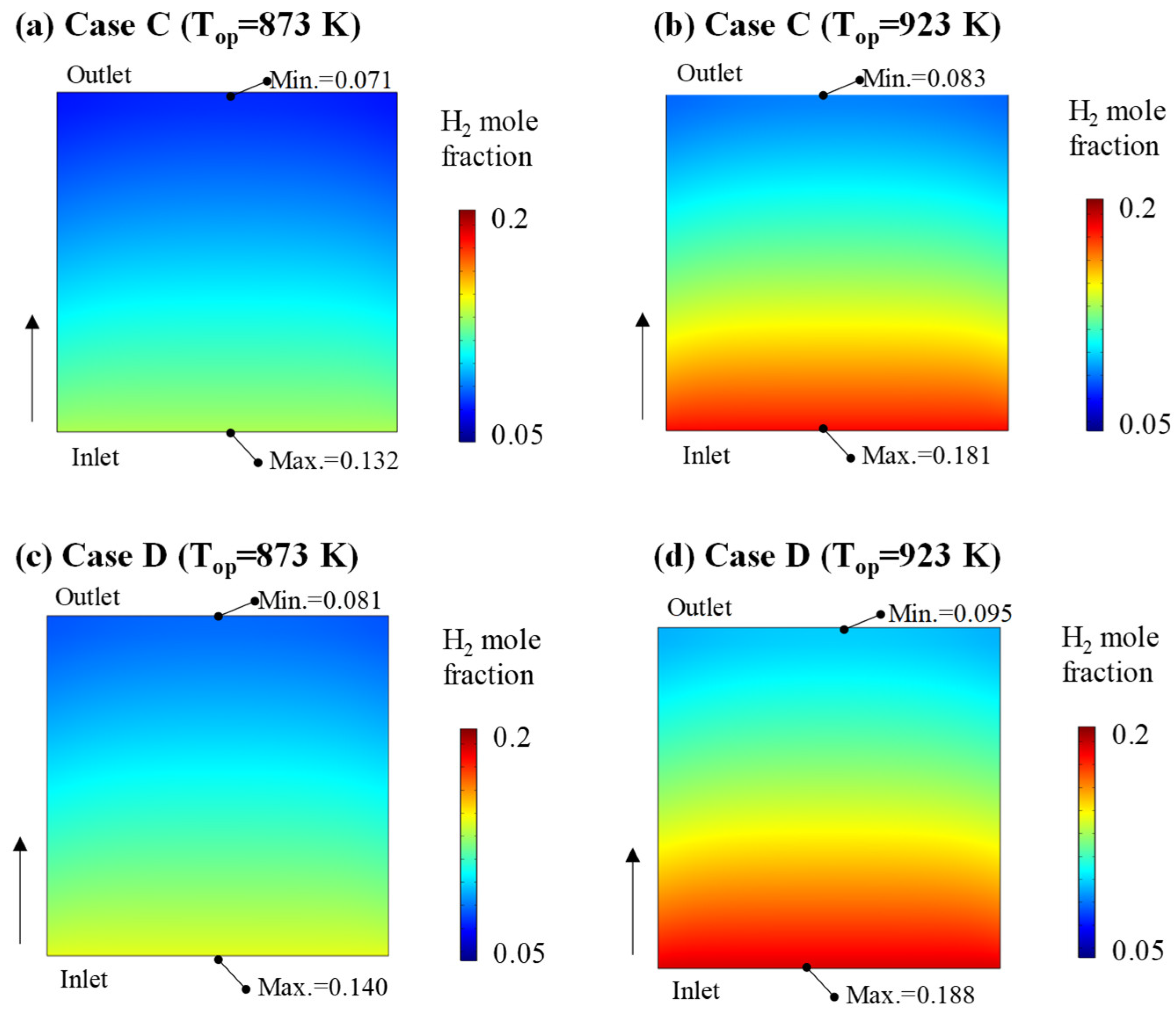
- Dry reforming was examined under various gas input conditions and operating temperatures, and its impact on the connected fuel cell was evaluated. The resulting mole fraction of H2 after dry reforming ranged from 0.181 to 0.214, directly influencing fuel cell performance. Consequently, the average current density of the fuel cell at a cell voltage of 0.8 V varied between 1321.5 and 1444.9 A·m−2, which was up to 27.07% lower than that of a conventional MCFC at 923 K due to the reduced hydrogen concentration in the anode;
- (2)
- For the same gas composition, the reforming reaction became more active as the gas flow rate decreased. For this reason, the mole fraction of H2 and the current density increased at the inlet of the MCFC. However, the current density difference between the inlet and outlet decreased as the flow rate increased. Therefore, higher gas flow rates are advantageous for long-term operation;
- (3)
- More H2 was produced as the operating temperature increased in the dry reformer. In addition, the activation resistance and ohmic resistance decreased as the operating temperature increased in the MCFC. Therefore, MCFCs must be operated at higher temperatures to improve their reforming efficiency and performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Reaction rate | |
| Reaction rate of gas component | |
| Density of catalyst | |
| Effectiveness factor | |
| Correction factor | |
| Cell voltage | |
| Nernst voltage , | |
| Resistance of anode | |
| Resistance of cathode | |
| Internal cell resistance | |
| Reaction rate of WGS | |
| Velocity of mixture gas | |
| Permeability of porous media | |
| Coefficient of dynamic viscosity | |
| Length of porous media | |
| Pressure drop of porous media | |
| Viscosity of gas component | |
| Temperature | |
| Mole fraction of gas component | |
| Molecular weight of gas component | |
| Mass fraction of gas component | |
| Thermal diffusion coefficient | |
| Binary diffusivity of multicomponent | |
| Specific diffusion volume of component | |
| Effective diffusivity of multicomponent | |
| Porosity of porous layer | |
| Tortuosity of porous layer | |
| Thermal conductivity of gas | |
| Thermal conductivity of mixture gas | |
| Heat capacity of gas | |
| Heat capacity of mixture gas | |
| Heat energy of RWGS |
Appendix A
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Species | Aμ | Bμ | Cμ |
|---|---|---|---|
| CH4 | 3.844 | 0.401 | −1.43 |
| CO2 | 11.336 | 0.499 | −1.09 |
| N2 | 42.606 | 0.475 | −9.88 |
| CO | 23.811 | 0.539 | −1.54 |
| H2 | 27.758 | 0.212 | −3.28 |
| O2 | 44.224 | 0.562 | −1.13 |
| H2O | −32.826 | 0.429 | −1.62 |
| Diffusion Volumes | |||
|---|---|---|---|
| C | 15.9 | O | 6.11 |
| H | 2.31 | N | 4.54 |
| H2 | 6.12 | CO2 | 26.9 |
| N2 | 18.5 | CO | 18.0 |
| O2 | 16.3 | H2O | 13.1 |
| Species | Ak | Bk | Ck |
|---|---|---|---|
| CH4 | −0.00935 | 1.40 | 3.32 |
| CO2 | −0.01183 | 1.02 | −2.22 |
| N2 | 0.00309 | 7.59 | −1.10 |
| CO | 0.0150 | 8.27 | −1.91 |
| H2 | 0.0395 | 4.59 | −6.49 |
| O2 | 0.00121 | 8.62 | −1.33 |
| H2O | 0.00053 | 4.71 | 4.96 |
| Species | AC | BC | CC | DC | EC |
|---|---|---|---|---|---|
| CH4 | 34.942 | −4.00 | 1.92 | 1.53 | 3.93 |
| CO2 | 27.437 | 4.23 | −1.96 | 4.00 | −2.99 |
| N2 | 29.342 | −3.54 | 1.01 | −4.31 | 2.59 |
| CO | 29.556 | −6.58 | −1.22 | 2.26 | |
| H2 | 25.399 | 2.02 | −3.85 | −3.19 | |
| O2 | 29.526 | −8.90 | 3.81 | −3.26 | |
| H2O | 33.933 | −8.42 | 2.99 | −1.78 | 3.69 |
References
- Dicks, A.L. Hydrogen generation from natural gas for the fuel cell systems of tomorrow. J. Power Sources 1996, 61, 113–124. [Google Scholar] [CrossRef]
- Slinn, M.; Kendall, K.; Mallon, C.; Andrews, J. Steam reforming of biodiesel by-product to make renewable hydrogen. Bioresour. Technol. 2008, 99, 5851–5858. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.-Y.; Kim, K.-J.; Kim, B.-J.; Hong, G.-R.; Jang, W.-J.; Bae, J.W.; Park, Y.-K.; Jeon, B.-H.; Roh, H.-S. From gray to blue hydrogen: Trends and forecasts of catalysts and sorbents for unit process. Renew. Sustain. Energy Rev. 2023, 186, 113635. [Google Scholar] [CrossRef]
- Ming, Q.; Healey, T.; Allen, L.; Irving, P. Steam reforming of hydrocarbon fuels. Catal. Today 2002, 77, 51–64. [Google Scholar] [CrossRef]
- Takeguchi, T.; Kani, Y.; Yano, T.; Kikuchi, R.; Eguchi, K.; Tsujimoto, K.; Uchida, Y.; Ueno, A.; Omoshiki, K.; Aizawa, M. Study on steam reforming of CH4 and C2 hydrocarbons and carbon deposition on Ni-YSZ cermets. J. Power Sources 2002, 112, 588–595. [Google Scholar] [CrossRef]
- Gao, J.; Hou, Z.; Lou, H.; Zheng, X. Chapter 7—Dry (CO2) Reforming. In Fuel Cells: Technologies for Fuel Processing; Shekhawat, D., Spivey, J.J., Berry, D.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 191–221. [Google Scholar]
- Usman, M.; Wan Daud, W.M.A.; Abbas, H.F. Dry reforming of methane: Influence of process parameters—A review. Renew. Sustain. Energy Rev. 2015, 45, 710–744. [Google Scholar] [CrossRef]
- Jang, W.-J.; Shim, J.-O.; Kim, H.-M.; Yoo, S.-Y.; Roh, H.-S. A review on dry reforming of methane in aspect of catalytic properties. Catal. Today 2019, 324, 15–26. [Google Scholar] [CrossRef]
- Guczi, L.; Stefler, G.; Geszti, O.; Sajó, I.; Pászti, Z.; Tompos, A.; Schay, Z. Methane dry reforming with CO2: A study on surface carbon species. Appl. Catal. A Gen. 2010, 375, 236–246. [Google Scholar] [CrossRef]
- Kim, G.S.; Lee, B.Y.; Ham, H.C.; Han, J.; Nam, S.W.; Moon, J.; Yoon, S.P. Highly active and stable Sr0.92Y0.08Ti1−xRuxO3−d in dry reforming for hydrogen production. Int. J. Hydrogen Energy 2019, 44, 202–212. [Google Scholar] [CrossRef]
- Lee, B.; Lee, S.; Lim, H. Numerical modeling studies for a methane dry reforming in a membrane reactor. J. Nat. Gas Sci. Eng. 2016, 34, 1251–1261. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Eppinger, T.; Kraume, M. Detailed numerical simulations of catalytic fixed-bed reactors: Heterogeneous dry reforming of methane. Chem. Eng. Sci. 2015, 122, 197–209. [Google Scholar] [CrossRef]
- Jun, Y.-B.; Park, J.-H.; Kim, H.-S.; Jung, K.-S.; Yoon, S.-P.; Lee, C.-W. A simulation model for ruthenium-catalyzed dry reforming of methane (DRM) at different temperatures and gas compositions. Int. J. Hydrogen Energy 2024, 49, 786–797. [Google Scholar] [CrossRef]
- Tomczyk, P. MCFC versus other fuel cells—Characteristics, technologies and prospects. J. Power Sources 2006, 160, 858–862. [Google Scholar] [CrossRef]
- Randström, S.; Lagergren, C.; Capobianco, P. Corrosion of anode current collectors in molten carbonate fuel cells. J. Power Sources 2006, 160, 782–788. [Google Scholar] [CrossRef]
- Kulkarni, A.; Giddey, S. Materials issues and recent developments in molten carbonate fuel cells. J. Solid State Electrochem. 2012, 16, 3123–3146. [Google Scholar] [CrossRef]
- Pfafferodt, M.; Heidebrecht, P.; Sundmacher, K.; Würtenberger, U.; Bednarz, M. Multiscale Simulation of the Indirect Internal Reforming Unit (IIR) in a Molten Carbonate Fuel Cell (MCFC). Ind. Eng. Chem. Res. 2008, 47, 4332–4341. [Google Scholar] [CrossRef]
- Freni, S. Rh based catalysts for indirect internal reforming ethanol applications in molten carbonate fuel cells. J. Power Sources 2001, 94, 14–19. [Google Scholar] [CrossRef]
- Freni, S.; Maggio, G. Energy balance of different internal reforming MCFC configurations. Int. J. Energy Res. 1997, 21, 253–264. [Google Scholar] [CrossRef]
- Jarchlouei, M.A.; Chitsaz, A.; Mahmoudi, S.M.S.; Rosen, M.A.; Bafekr, S.H. Gibbs energy minimization using Lagrange method of undetermined multipliers for electrochemical and thermodynamic modeling of a MCFC with internal steam reforming. Energy Convers. Manag. 2021, 228, 113594. [Google Scholar] [CrossRef]
- Szablowski, L.; Dybinski, O.; Szczesniak, A.; Milewski, J. Mathematical Model of Steam Reforming in the Anode Channel of a Molten Carbonate Fuel Cell. Energies 2022, 15, 608. [Google Scholar] [CrossRef]
- d’Amore, F.; Pereira, L.M.C.; Campanari, S.; Gazzani, M.; Romano, M.C. A novel process for CO2 capture from steam methane reformer with molten carbonate fuel cell. Int. J. Hydrogen Energy 2023, 48, 37366–37384. [Google Scholar] [CrossRef]
- Chitsaz, A.; Bafekr, S.H.; Holagh, S.G. Exergy and environmental assessments of the performance of a molten carbonate fuel cell cogeneration plant: External steam reforming against internal steam reforming. Fuel Commun. 2023, 16, 100092. [Google Scholar] [CrossRef]
- Di Carlo, A.; Bocci, E.; Dell’Era, A. Comparison by the use of numerical simulation of a MCFC-IR and a MCFC-ER when used with syngas obtained by atmospheric pressure biomass gasification. Int. J. Hydrogen Energy 2011, 36, 7976–7984. [Google Scholar] [CrossRef]
- Kim, Y.J.; Lee, M.C. Comparison of thermal performances of external and internal reforming molten carbonate fuel cells using numerical analyses. Int. J. Hydrogen Energy 2017, 42, 3510–3520. [Google Scholar] [CrossRef]
- Jung, K.-S.; Zhang, K.; Lee, C.-W. Simulation of Internal Manifold-Type Molten Carbonate Fuel Cells (MCFCs) with Different Operating Conditions. Energies 2023, 16, 2700. [Google Scholar] [CrossRef]
- Freni, S.; Maggio, G.; Cavallaro, S. Ethanol steam reforming in a molten carbonate fuel cell: A thermodynamic approach. J. Power Sources 1996, 62, 67–73. [Google Scholar] [CrossRef]
- Leto, L.; Dispenza, C.; Moreno, A.; Calabrò, A. Simulation model of a molten carbonate fuel cell–microturbine hybrid system. Appl. Therm. Eng. 2011, 31, 1263–1271. [Google Scholar] [CrossRef]
- Benguerba, Y.; Dehimi, L.; Virginie, M.; Dumas, C.; Ernst, B. Modelling of methane dry reforming over Ni/Al2O3 catalyst in a fixed-bed catalytic reactor. React. Kinet. Mech. Catal. 2015, 114, 109–119. [Google Scholar] [CrossRef]
- Richardson, J.T.; Paripatyadar, S.A. Carbon dioxide reforming of methane with supported rhodium. Appl. Catal. 1990, 61, 293–309. [Google Scholar] [CrossRef]
- Snoeck, J.W.; Froment, G.F.; Fowles, M. Steam/CO2 Reforming of Methane. Carbon Filament Formation by the Boudouard Reaction and Gasification by CO2, by H2, and by Steam: Kinetic Study. Ind. Eng. Chem. Res. 2002, 41, 4252–4265. [Google Scholar] [CrossRef]
- Snoeck, J.W.; Froment, G.F.; Fowles, M. Kinetic Study of the Carbon Filament Formation by Methane Cracking on a Nickel Catalyst. J. Catal. 1997, 169, 250–262. [Google Scholar] [CrossRef]
- De Groote, A.M.; Froment, G.F. Simulation of the catalytic partial oxidation of methane to synthesis gas. Appl. Catal. A Gen. 1996, 138, 245–264. [Google Scholar] [CrossRef]
- Wolf, T.L.; Wilemski, G. Molten Carbonate Fuel Cell Performance Model. J. Electrochem. Soc. 1983, 130, 48. [Google Scholar] [CrossRef]
- Yuh, C.Y.; Selman, J.R. The Polarization of Molten Carbonate Fuel Cell Electrodes: I. Analysis of Steady-State Polarization Data. J. Electrochem. Soc. 1991, 138, 3642. [Google Scholar] [CrossRef]
- Kim, Y.J.; Chang, I.G.; Lee, T.W.; Chung, M.K. Effects of relative gas flow direction in the anode and cathode on the performance characteristics of a Molten Carbonate Fuel Cell. Fuel 2010, 89, 1019–1028. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. An equilibrium theory for catalytic steam reforming in membrane reactors. Chem. Eng. Sci. 2017, 160, 291–303. [Google Scholar] [CrossRef]
- Yaws, C.L. Chemical Properties Handbook, 1st ed.; McGraw-Hill Education: New York, NY, USA, 1999. [Google Scholar]
- Carr, N.L.; Kobayashi, R.; Burrows, D.B. Viscosity of Hydrocarbon Gases Under Pressure. J. Pet. Technol. 1954, 6, 47–55. [Google Scholar] [CrossRef]
- Aydın, Ö.; Kubota, A.; Tran, D.L.; Sakamoto, M.; Shiratori, Y. Designing graded catalytic domain to homogenize temperature distribution while dry reforming of CH4. Int. J. Hydrogen Energy 2018, 43, 17431–17443. [Google Scholar] [CrossRef]
- Mason, E.A.; Saxena, S.C. Approximate Formula for the Thermal Conductivity of Gas Mixtures. Phys. Fluids 1958, 1, 361–369. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lim, C.-Y.; Lee, C.-W. Design of Cell Frame Structure of Unit Cell for Molten Carbonate Fuel Cell Using CFD Analysis. Trans. Korean Hydrog. New Energy Soc. 2018, 29, 56–63. [Google Scholar] [CrossRef]
- Lu, Y.; Jia, D.; Gao, F.; Hu, T.; Chen, Z. First-principle calculations of the thermal properties of SrTiO3 and SrO(SrTiO3)n (n = 1, 2). Solid State Commun. 2015, 201, 25–30. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lee, M.; Lee, M.-J.; Chang, S.-C.; Yoon, S.-P.; Ham, H.C.; Han, J. Effect of the flow directions on a 100 cm2 MCFC single cell with internal flow channels. Int. J. Hydrogen Energy 2016, 41, 18747–18760. [Google Scholar] [CrossRef]
- Rexed, I. Applications for Molten Carbonate Fuel Cells. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]


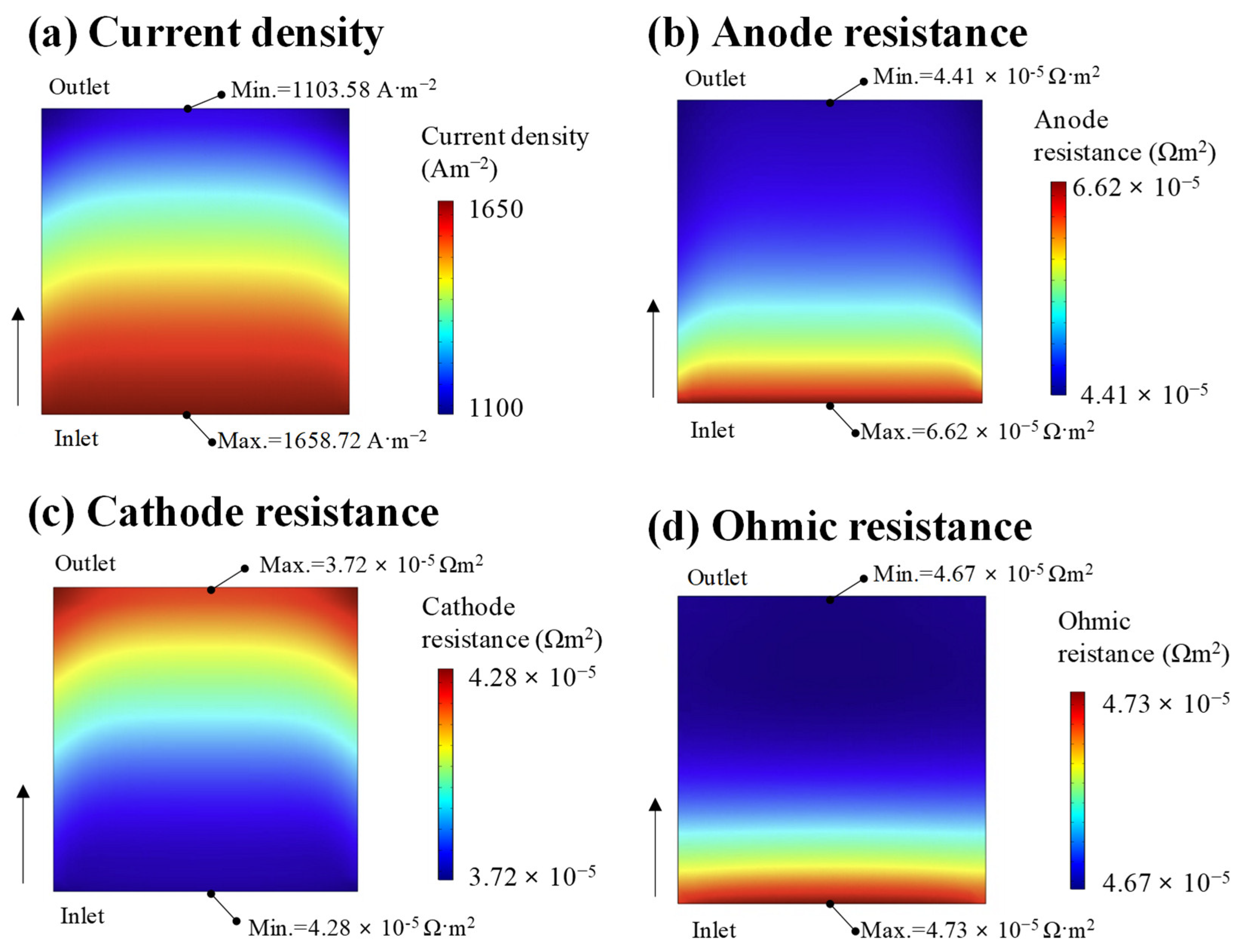
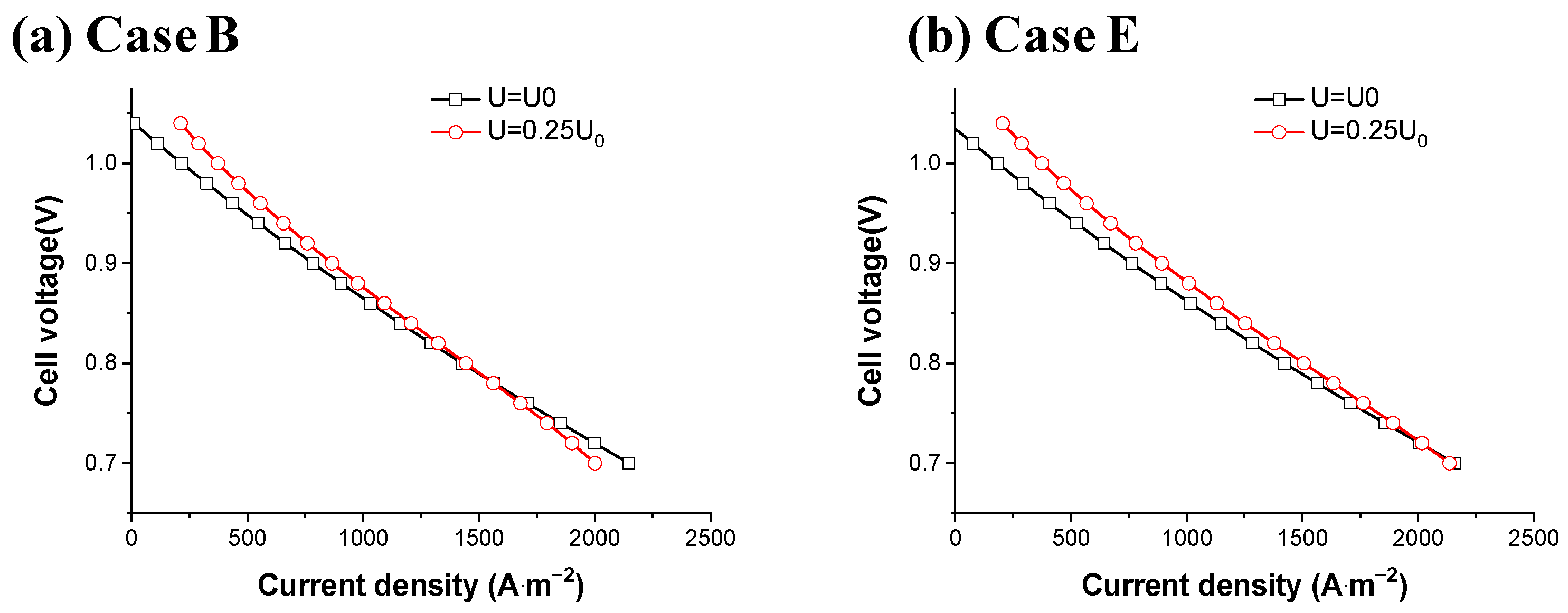


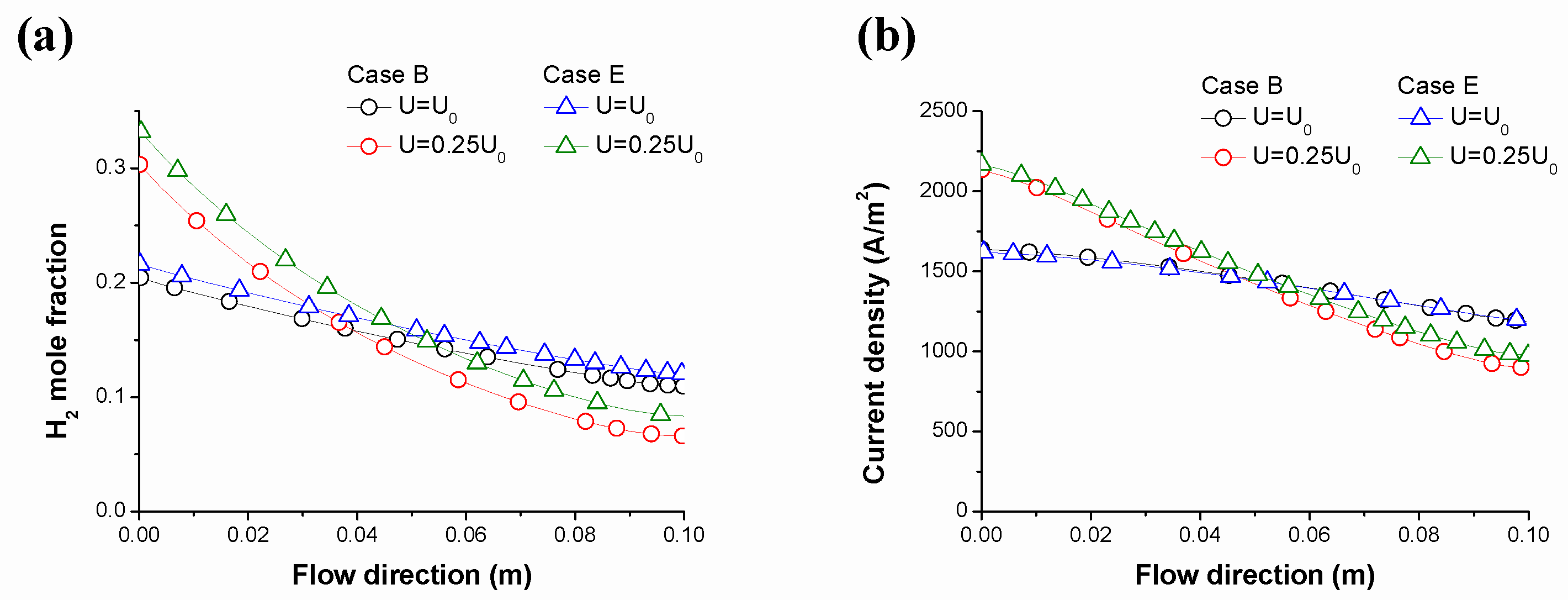
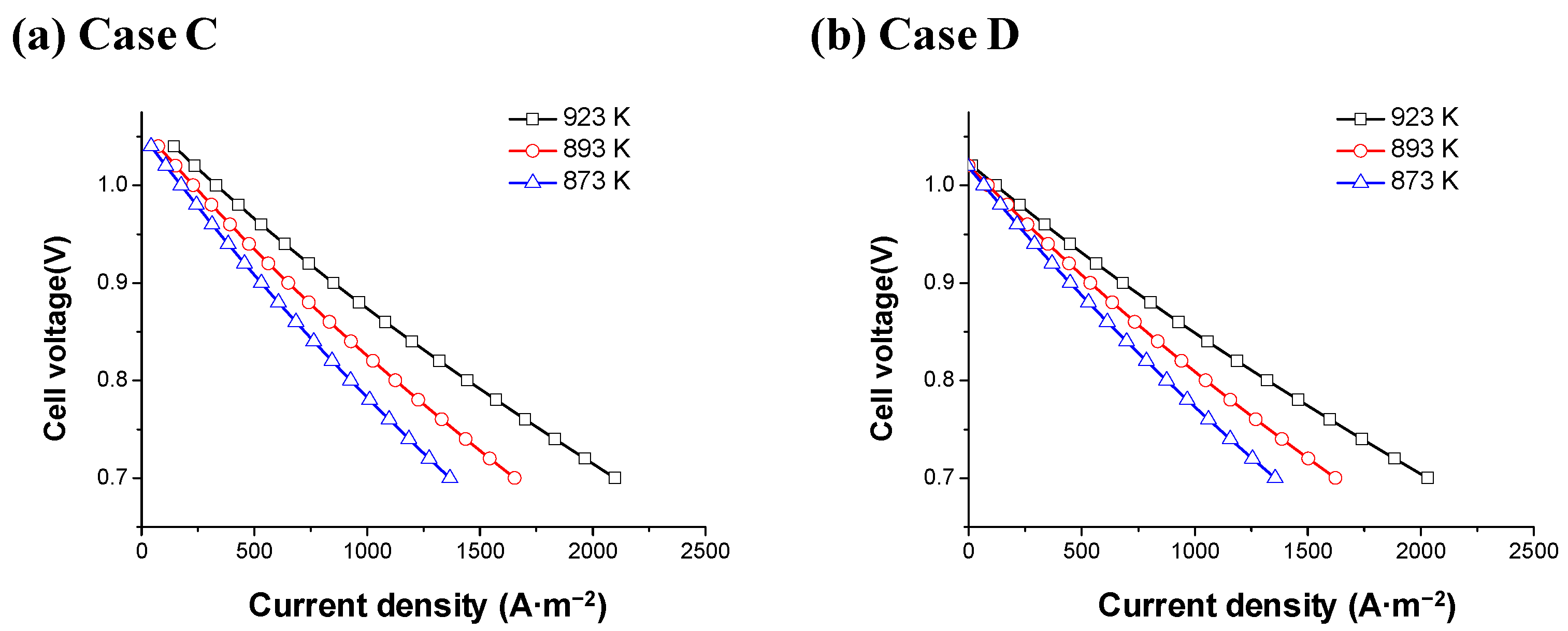


| Fuel Type | Current Density | Cell Voltage | Operating Temperature | Cell Area | Reference |
|---|---|---|---|---|---|
| Direct H2 | 1200 A·m−2 | 0.83 V | 921 K (Average) | Not available | [24] |
| Direct H2 | 1200 A·m−2 | 0.826 V | 843 K | 1 m2 | [25] |
| Direct H2 | 1805.7 A·m−2 | 0.8 V (Single cell) | 923 K | 0.01 m2 | [26] |
| Ethanol Reforming | 1900 A·m−2 | 0.578 V | 923 K | Unit area | [27] |
| Steam Reforming | 1900 A·m−2 | 0.526 V | 923 K | Unit area | [27] |
| Steam Reforming | 1380 A·m−2 | 0.8 V | 905 K (Average) | Not available | [24] |
| Steam Reforming | 1550 A·m−2 | 0.793 V | 893 K | 0.771 m2 | [28] |
| Steam Reforming | 1200 A·m−2 | 0.799 V | 843 K | 1 m2 | [25] |
| Steam Reforming | 1100 A·m−2 | 0.775 V | 923 K | 0.01 m2 | [20] |
| Steam Reforming | 100 A·m−2 (Approximate value) | 0.8 V (Single cell) | 923 K | 0.002025 m2 | [21] |
| Steam Reforming | 1100 A·m−2 | 0.834 V | 923 K | 0.01 m2 | [23] |
| Steam Reforming | 1481 A·m−2 | 0.78 V | 923 K | 0.0647 m2 | [26] |
| Species | Reaction Fluxes |
|---|---|
| H2 | |
| H2O | |
| CH4 | |
| CO | |
| CO2 | |
| C |
| Properties | SS316L | Anode (Ni-Cr Alloy) | Cathode (Nickel Oxide) | Electrolyte (Li/K)2CO3 |
| Density [kg·m−3] | 8000 | 8220 | 6794 | 1914 |
| Heat Capacity [J·mol−1·K−1] | 500 | 444 | 44,352 | 4000 |
| Thermal conductivity [W·m−1·K−1] | 25 | 25 | 5.5 | 2 |
| Porosity | 0.7 | 0.6 | 0.7 | - |
| Variable | Specification | |
|---|---|---|
| Fuel gas composition (CH4:CO2:N2) | Case A | 0.25:0.25:0.5 |
| Case B | 0.33:0.33:0.33 | |
| Case C | 0.4:0.2:0.4 | |
| Case D | 0.2:0.4:0.4 | |
| Case E | 0.4:0.4:0.2 | |
| Operating temperature (Top) | 873, 893, and 923 K | |
| Gas flow rate (U) | 6 × 10−5 m3·s−1 | |
| Operating pressure | 1.013 × 105 Pa | |
| Cathode gas composition | Air/CO2 = 0.7:0.3 | |
| CH4 | CO2 | N2 | CO | H2 | H2O | |
|---|---|---|---|---|---|---|
| Case A | 0.087 | 0.087 | 0.357 | 0.184 | 0.185 | 0.1 |
| Case B | 0.130 | 0.131 | 0.230 | 0.204 | 0.205 | 0.1 |
| Case C | 0.198 | 0.055 | 0.285 | 0.180 | 0.181 | 0.1 |
| Case D | 0.050 | 0.193 | 0.283 | 0.187 | 0.188 | 0.1 |
| Case E | 0.166 | 0.167 | 0.134 | 0.216 | 0.214 | 0.1 |
| Case A | Case B | Case C | Case D | Case E | Conventional MCFC | |
|---|---|---|---|---|---|---|
| OCV (V) | 1.058 | 1.042 | 1.080 | 1.022 | 1.034 | 1.064 |
| Average current density at 0.8 V (A·m−2) | 1420.5 | 1427.7 | 1444.9 | 1321.5 | 1422.2 | 1805.7 |
| Case A | Case B | Case C | Case D | Case E | Conventional MCFC | |
|---|---|---|---|---|---|---|
| Nernst loss | 23.3% | 21.8% | 24.8% | 21.0% | 20.8% | 18.7% |
| Anode polarization | 28.6% | 27.3% | 29.2% | 27.7% | 26.5% | 14.8% |
| Cathode polarization | 21.9% | 23.2% | 21.1% | 23.4% | 24.1% | 31.5% |
| Ohmic loss | 26.2% | 27.7% | 25.0% | 28.0% | 28.6% | 35.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, K.-S.; Jun, Y.-B.; Yoon, J.-S.; Yoon, S.-P.; Lee, C.-W. Simulation of Molten Carbonate Fuel Cell with Dry Reforming of Methane (DR-MCFC). Energies 2025, 18, 1863. https://doi.org/10.3390/en18071863
Jung K-S, Jun Y-B, Yoon J-S, Yoon S-P, Lee C-W. Simulation of Molten Carbonate Fuel Cell with Dry Reforming of Methane (DR-MCFC). Energies. 2025; 18(7):1863. https://doi.org/10.3390/en18071863
Chicago/Turabian StyleJung, Kyu-Seok, Young-Bae Jun, Jung-Sik Yoon, Sung-Pil Yoon, and Chang-Whan Lee. 2025. "Simulation of Molten Carbonate Fuel Cell with Dry Reforming of Methane (DR-MCFC)" Energies 18, no. 7: 1863. https://doi.org/10.3390/en18071863
APA StyleJung, K.-S., Jun, Y.-B., Yoon, J.-S., Yoon, S.-P., & Lee, C.-W. (2025). Simulation of Molten Carbonate Fuel Cell with Dry Reforming of Methane (DR-MCFC). Energies, 18(7), 1863. https://doi.org/10.3390/en18071863







