Cross-Seasonal Storage of Flue Gas Waste Heat from Power Plants Based on Soil Heat Storage Using Buried Pipes: Geotechnical Thermal Response Experiment
Abstract
:1. Introduction
2. Materials and Methods
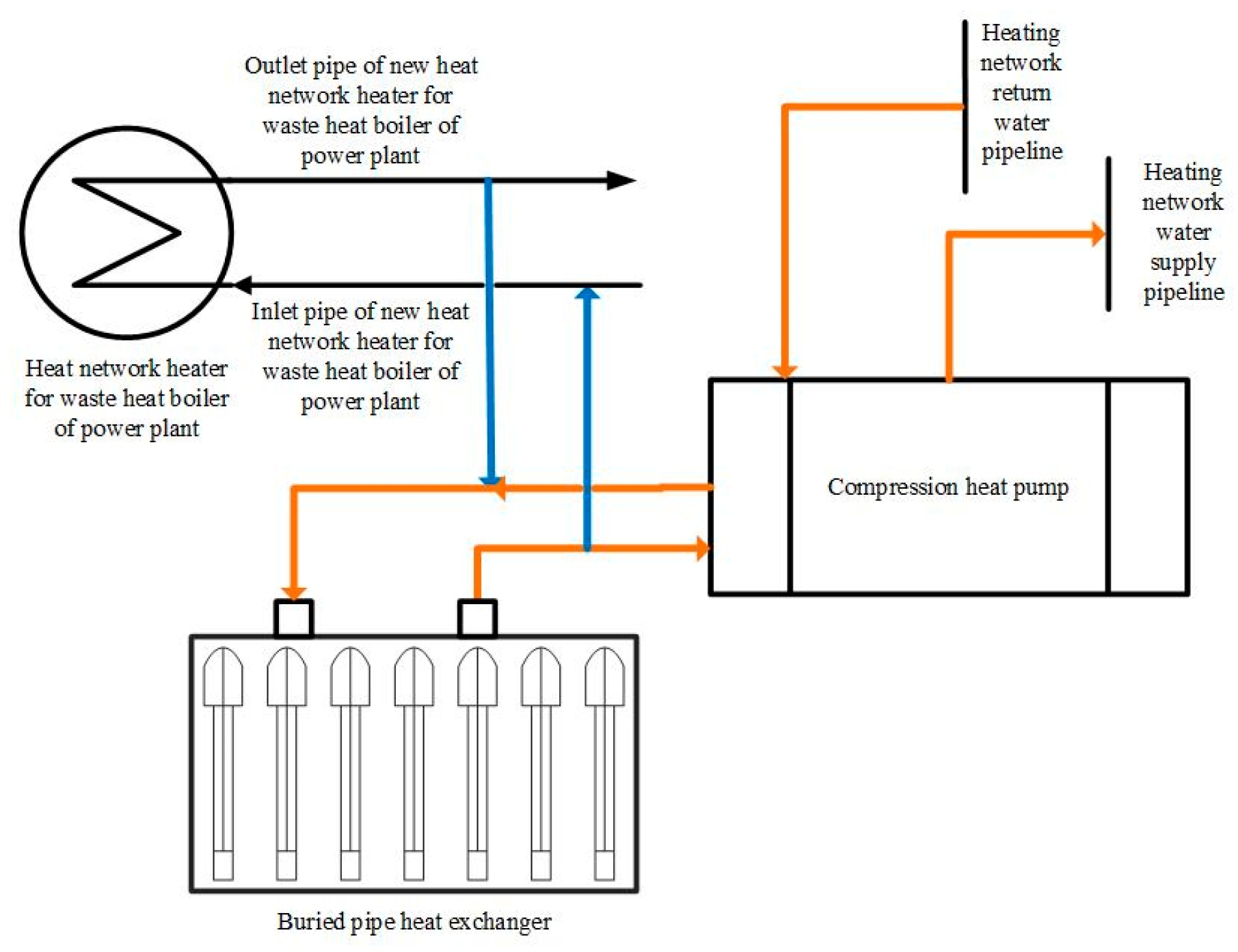
2.1. Experimental Method
2.2. Apparatus and Procedure
- (1)
- Field investigation and drilling plan preparation: Conducting an on-site investigation is a necessary preparation condition before conducting thermal response testing. We determine the number and location of test holes, as well as the required cable models and lengths, based on the actual situation, terrain, topography, and water and electricity conditions of the project site. The relevant technical parameters of the experimental well are shown in Table 1.
- (2)
- Drilling and recording vertical strata data: Before conducting the thermal response test, the drilled rock layer data are recorded during the process of opening the test well, and an outer-rock-layer data map of the rock and soil is drawn in the vertical direction.
- (3)
- The buried pipe is placed, and the test well is backfilled after the placement. Special backfill material is used to fill the casing and surrounding soil of the jacketed heat exchanger. After the backfilling, the test well is left for at least 48 h to keep the drilling medium and backfill material temperatures as consistent as possible with the original ground temperature.
- (4)
- The experimental site is leveled to ensure that the experimental equipment is placed flat, facilitating the operation of the experiment. The equipment is transported to the edge of the borehole, minimizing the length of exposed pipelines and minimizing heat loss caused by pipelines. During the process of connecting equipment and drilling, unnecessary bends, valves, and reducers are reduced. The exposed parts of the equipment are insulated with material with a thickness generally greater than 20 mm.
- (5)
- Commissioning the test system: Connecting the testing equipment to external conditions such as water and electricity follows a particular order. First, the water is generally connected, and then the electricity. The equipment is then connected to the buried pipe and the water replenishment pipe. After the water pipe equipment is connected and checked for leaks, the power electricity is connected to the project site, and the equipment is debugged.
- (6)
- The insulated high-level water tank is filled with water, and the vent valve is opened. We use the height difference between the water tank and the vent valve to discharge the air inside the circulation pipeline and then connect the power supply to confirm its safety. The circulating water pump is turned on to keep the water inside the pipeline in a circulating state, and the automatic vent valve discharges the residual gas in the pipeline. Due to the large water capacity of sleeve-type buried pipe systems, the continuous process of circulating water for exhaust is relatively lengthy, usually lasting about 3 h. When the circulating water flow is stable, and there is no gas discharge from the automatic vent valve, the test state can be entered.
- (7)
- After the gas is completely discharged, we keep the water pump running and turn on a paperless recorder to record the original soil temperature.
- (8)
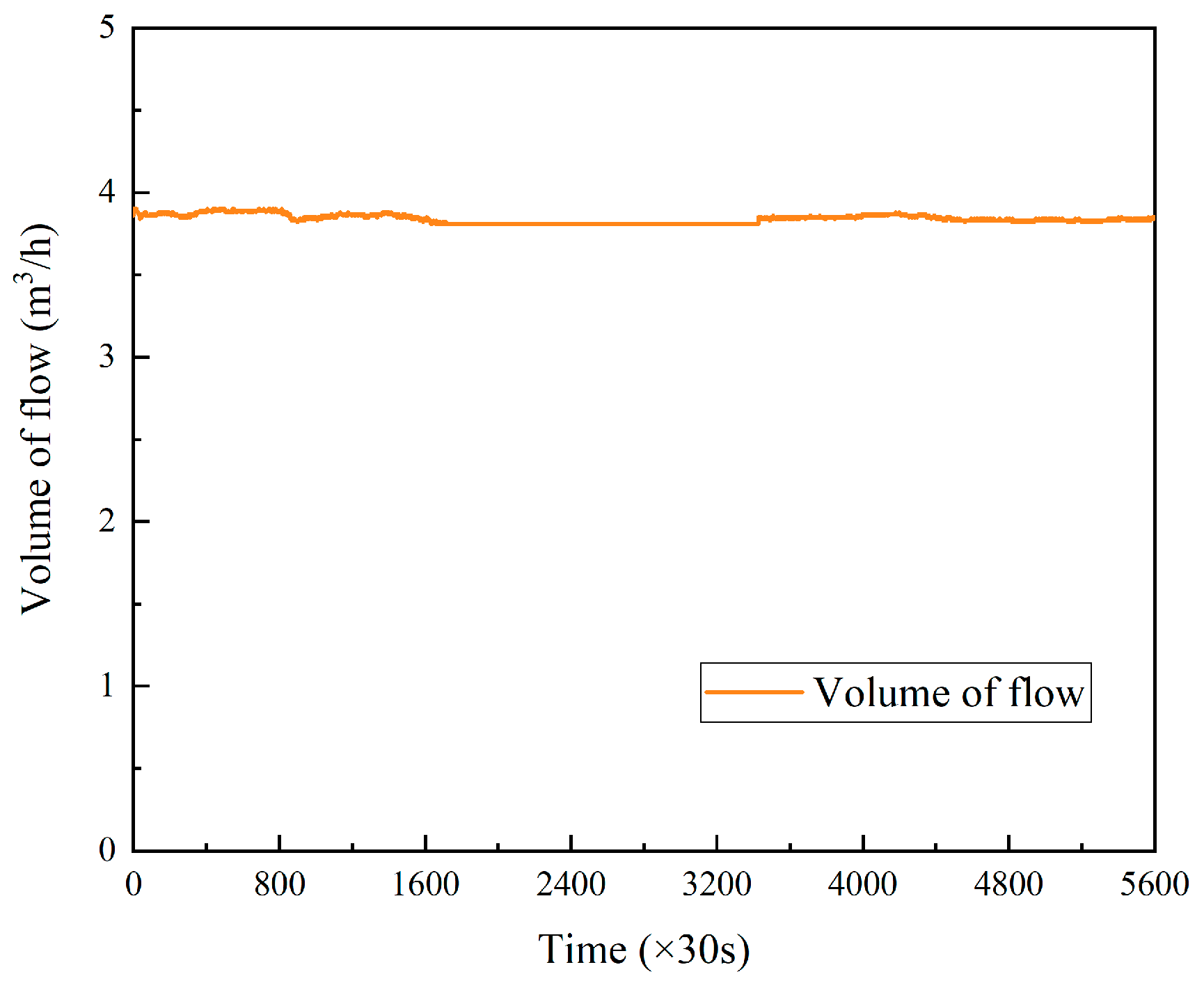
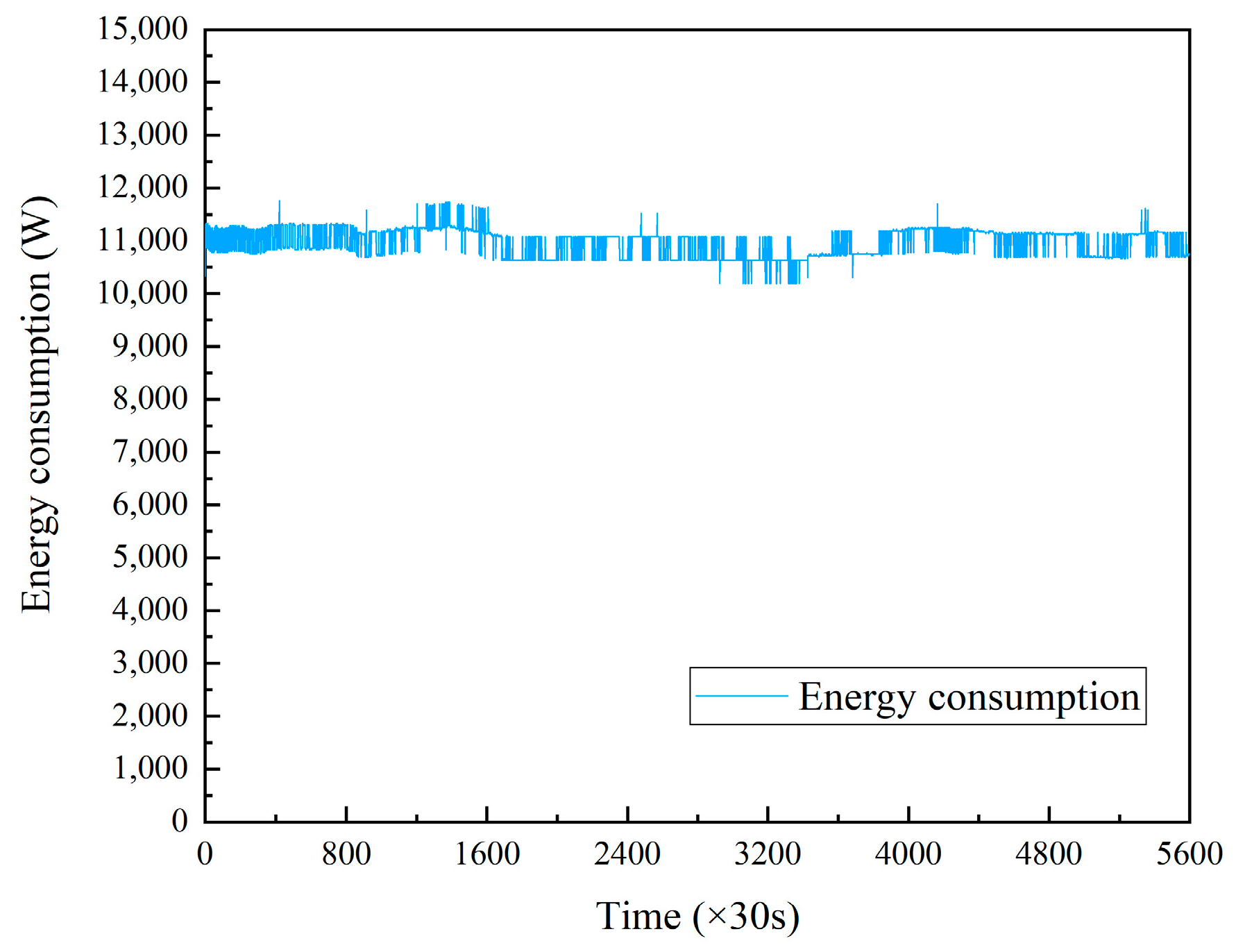
- After the initial ground temperature test of the rock and soil, the electric heater is turned on while keeping the circulating water pump turned on, and stable power heating is carried out on the circulating water while maintaining the voltage and current. At this time, the volume average circulating flow rate of the circulating medium is 4 m3/h. We then use a recorder to document the inlet and outlet temperature, flow rate, heating power, pressure, and other data from the heat exchanger. The data collection time interval is 30 s, and the testing time is no less than 48 h. The temperature fluctuation in the local buried pipe return water compared with 12 h ago is no greater than 1 °C. The data from the recorder are then exported for storage.
- (9)
- After the test, the closing order is reversed from the opening order. After exporting the data from the paperless recorder, the recorder is closed, and the circulating water pump is turned off. The geotechnical thermal response experimental equipment is then dismantled.
- (10)
- The data from the paperless recorder are analyzed and processed to ascertain the comprehensive thermal property parameters of the test well in the plot.
2.3. Experimental Uncertainty Analysis
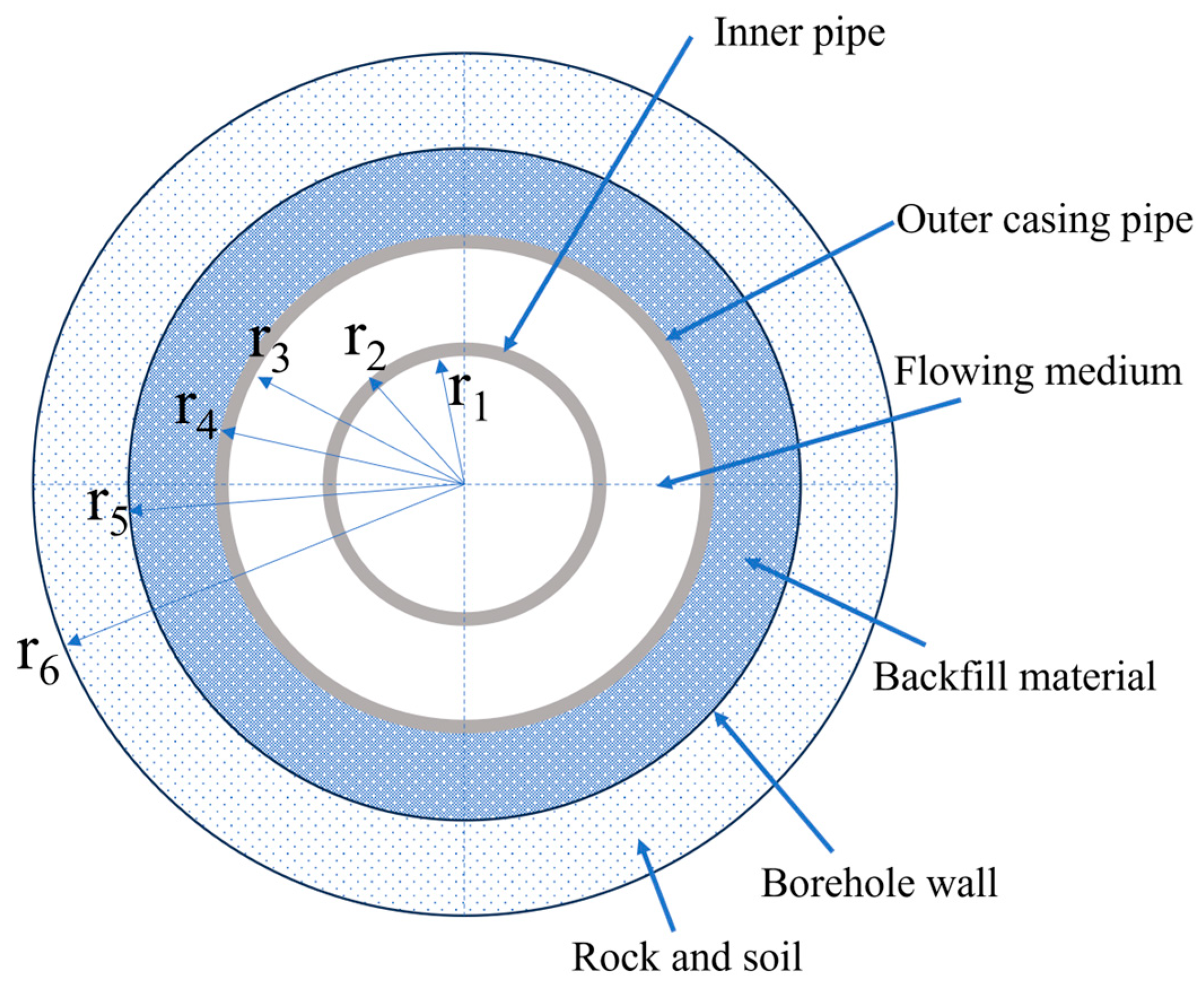
2.4. Data Processing
- (1)
- The thermal properties of backfill materials and surrounding rock and soil are uniform and consistent, and their thermal properties parameters do not vary with changes in radial and vertical dimensions;
- (2)
- There is no thermal conduction in the vertical direction; that is, heat transfer is a two-dimensional problem along the radial direction of the buried pipe;
- (3)
- The temperature of the fluid inside the buried pipe is uniform, and the heat return problem of the fluid inside and outside the casing in the casing-shaped buried pipe heat exchanger is not considered;
- (4)
- There is no contact thermal resistance between the contact surfaces; that is, there is no contact gap between materials.
3. Results
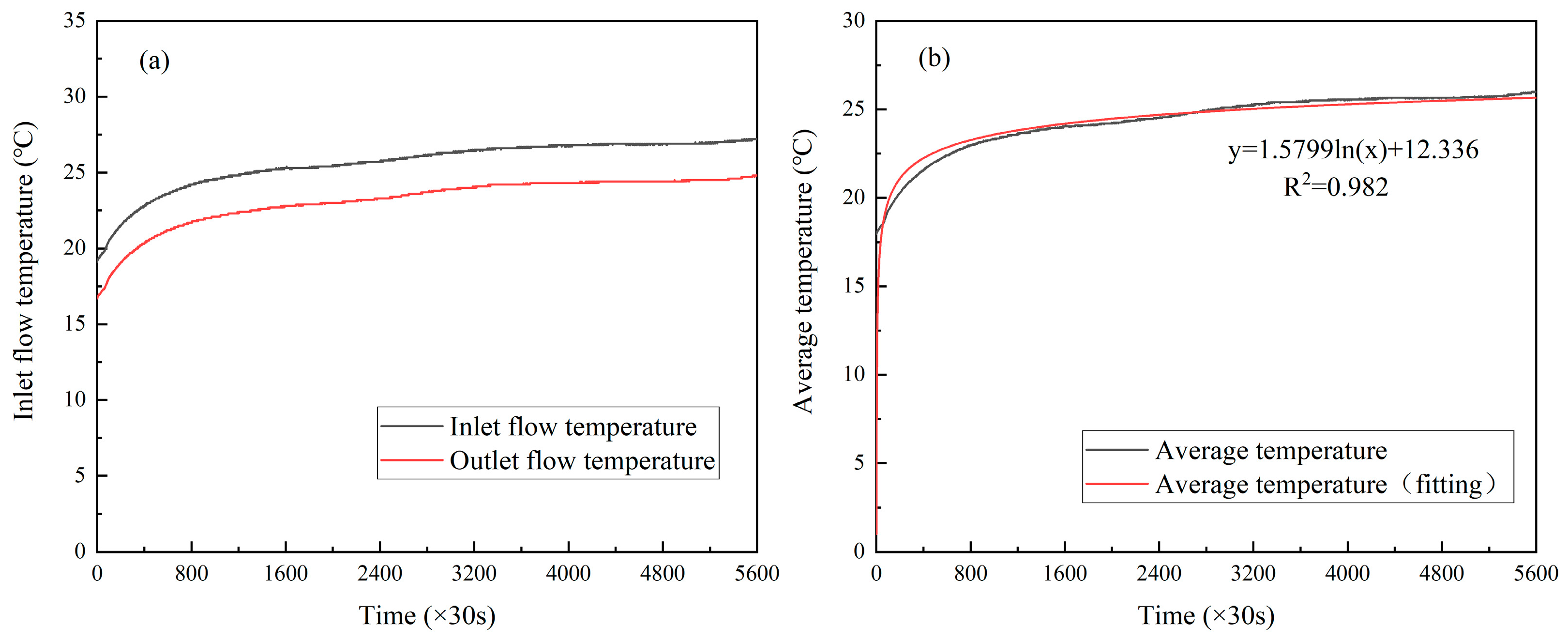
3.1. Soil Geological Composition and Initial Average Temperature
3.2. Soil Thermophysical Properties
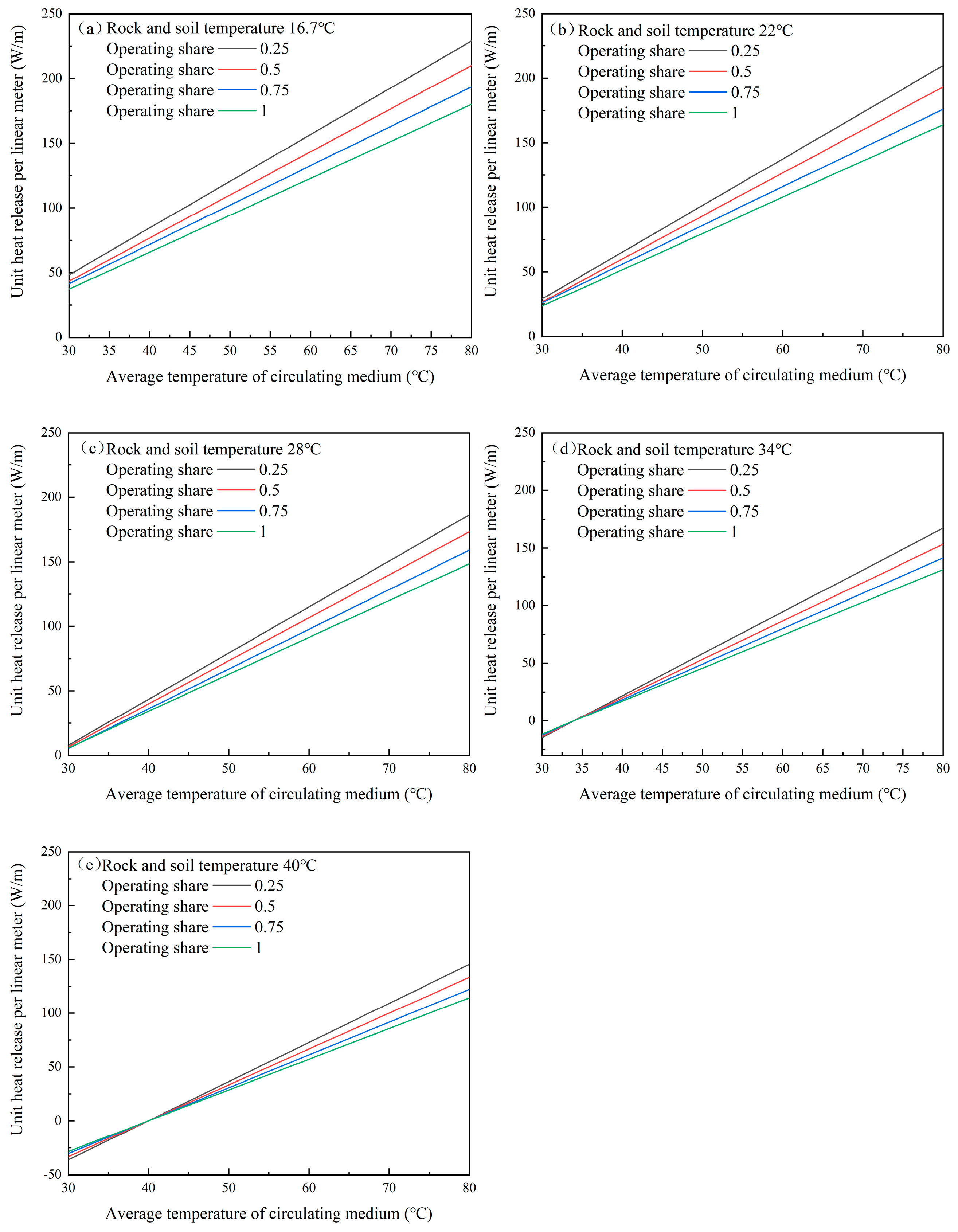
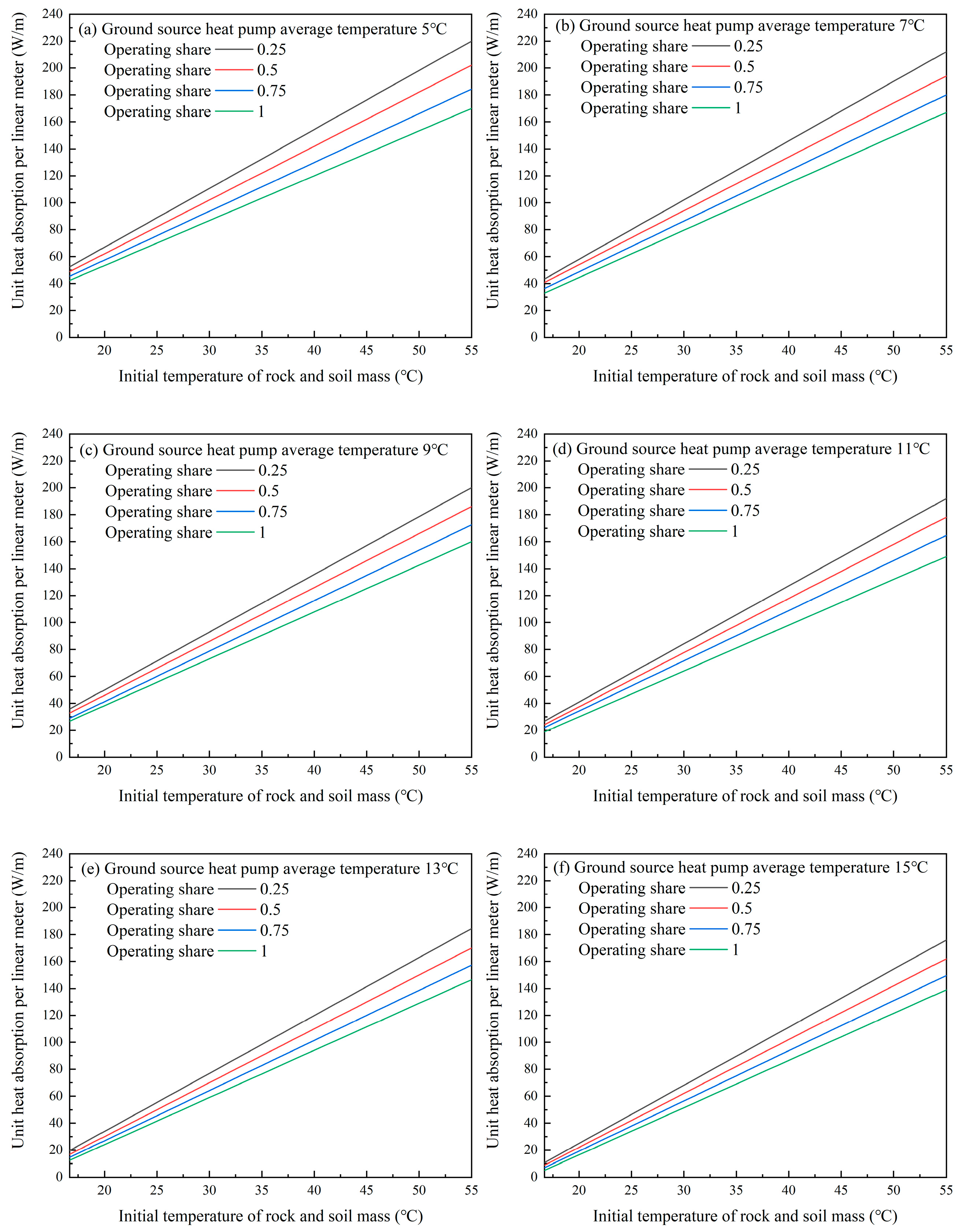
3.3. Analysis of Heat Transfer Capacity of Buried Pipe Heat Exchanger
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UTES | Underground thermal energy storage |
| DOAJ | Energy conservation and energy storage |
| WTES | Water tank thermal energy storage |
| GWTS | Gravel–water pit thermal energy storage |
| ATES | Aquifer thermal energy storage |
| BTES | Buried pipe thermal energy storage |
| λ | Thermal conductivity |
| Cv | Volumetric specific heat capacity |
| R | Thermal resistance of the unit length of the hole |
References
- Administration, N.E. Renewable Energy Generation Increased by 20% Year-on-Year in the First Three Quarters. Available online: https://www.nea.gov.cn/ (accessed on 11 December 2024).
- Statistics, N.B.O. Annual Data. Available online: https://www.stats.gov.cn (accessed on 9 December 2022).
- Reed, A.L.; Novelli, A.P.; Doran, K.L.; Ge, S.; Lu, N.; McCartney, J.S. Solar district heating with underground thermal energy storage: Pathways to commercial viability in North America. Renew. Energy 2018, 126, 1–13. [Google Scholar] [CrossRef]
- IEA. Technology Collaboration Programme-Energy Storage Through Energy Conservation. Available online: https://iea-eces.org/news/annual-report-2018 (accessed on 18 July 2018).
- Giordano, N.; Comina, C.; Mandrone, G.; Cagni, A. Borehole thermal energy storage (BTES). First results from the injection phase of a living lab in Torino (NW Italy). Renew. Energy 2016, 86, 993–1008. [Google Scholar] [CrossRef]
- Hendriks, M.M.; Velvis, H. Operational management of large scale UTES systems in Hospitals. In Proceedings of the Innostock 2012 the 12th International Conference on Energy Storage, Lleida, Spain, 16–18 May 2012. [Google Scholar]
- Nubicker, J.; Mangold, D.; Heidemann, W.; Müller-Steinhagen, H. Solar Assisted District Heating System with Duct Heat Store in Neckarsulm-Amorbach (Germany). In Proceedings of the Proceedings ISES Conference 2003, Göteborg, Sweden, 14–19 June 2003. [Google Scholar]
- Baser., T.; McCartney., J.S. Development of a Full-Scale Soil-Borehole Thermal Energy Storage System. In Proceedings of the IFCEE 2015, San Antonio, TX, USA, 17–21 March 2015; pp. 1608–1617. [Google Scholar]
- Hawes, D.W.; Feldman, D.; Banu, D. Latent heat storage in building materials. Energy Build. 1993, 20, 77–86. [Google Scholar] [CrossRef]
- Hesaraki, A.; Holmberg, S.; Haghighat, F. Seasonal thermal energy storage with heat pumps and low temperatures in building projects—A comparative review. Renew. Sustain. Energy Rev. 2015, 43, 1199–1213. [Google Scholar] [CrossRef]
- Lundh, M.; Dalenbäck, J.O. Swedish solar heated residential area with seasonal storage in rock: Initial evaluation. Renew. Energy 2008, 33, 703–711. [Google Scholar] [CrossRef]
- Sibbitt, B.; McClenahan, D.; Djebbar, R.; Thornton, J.; Wong, B.; Carriere, J.; Kokko, J. The Performance of a High Solar Fraction Seasonal Storage District Heating System–Five Years of Operation. Energy Procedia 2012, 30, 856–865. [Google Scholar] [CrossRef]
- Xu, L.; Torrens, J.I.; Guo, F.; Yang, X.; Hensen, J.L.M. Application of large underground seasonal thermal energy storage in district heating system: A model-based energy performance assessment of a pilot system in Chifeng, China. Appl. Therm. Eng. 2018, 137, 319–328. [Google Scholar] [CrossRef]
- Zhao, J.; Chen., Y.; Li., X. Optimization for heat storage operating modes based on simulation of seasonal underground storage of solar-GSHP system. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2007, 34, 74–77. [Google Scholar] [CrossRef]
- Han, M.; Qu., H.; Li., X.; Zhao., J.; Cui, J. Theoretical research on underground heat storage performance of ground coupled heat pump system with seasonal storage. J. Sol. Energy 2008, 29, 920–926. [Google Scholar] [CrossRef]
- Liu, X. Underground Heat Transfer Analysis and Engineering Application of Based on Seasonal Solar Thermal Storage Underground Pipe; Shandong Jianzhu University: Jinan, China, 2016. [Google Scholar]
- Han, M. Heat Transfer Analysis of Buried Pipes Underground Seasonal Thermal Storage; Shandong Jianzhu University: Jinan, China, 2013. [Google Scholar]
- Zhang, W. Study on the Seasonal Soil Heat Storage Characteristics in a Solar Ground Coupled Heat Pump System in Severe Cold Areas; Harbin Institute of Technology: Harbin, China, 2010. [Google Scholar]
- Wang, X. Operating Characteristics and Optimization of the Solar-Ground Coupled Heat Pump System with Seasonal Storage; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Chen, Y. Research on the Mode Selection of Ground-Source Sides of Solar Groud-Source Heat Pump Air Conditioning System; Hebei University of Technology: Tianjin, China, 2016. [Google Scholar]
- Wang, M. Research on the Control Strategy of Solar-Ground Source Heat Pump System; Hebei University of Technology: Tianjin, China, 2016. [Google Scholar]
- Yang, W.; Chen., Z.; Si., M. Underground energy storage and release characteristics of ground source heat pump with seasonal energy storage. J. Southeast Univ. (Nat. Sci. Ed.) 2010, 40, 973–978. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger., J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]



| Item Name | Technical Parameters of Test Hole |
|---|---|
| Heat exchanger form | Coaxial deep well heat exchanger |
| Drilling depth (m) | 300 |
| Depth of pipe in hole (m) | 280 |
| Drilling diameter (mm) | 150 |
| Outer-casing pipe parameters (mm) | Φ108 × 4.0 |
| Outer-casing pipe material | Q235, hot-dip galvanizing |
| Inner pipe parameters (mm) | De40 × 3.7 |
| Inner pipe material | Pert |
| Backfill material | Raw slurry + yellow sand backfill |
| Installation method of outer-casing pipe | Weighted |
| Test pressure | Stabilizes at 0.5 MPa for two hours |
| Uncertainty Control Link | Uncertainty Control Measures |
|---|---|
| Temperature sensor | A class A PT100 platinum resistance sensor is used, the temperature range is 0~40 °C, and the uncertainty is controlled within ±0.1 °C. |
| Flow sensor | High-precision turbine flow sensor with an uncertainty rating of ±0.5% is used. |
| Circulating water pump | A variable-frequency pump is adopted. |
| Pipe insulation | A 20 mm rubber plastic insulation layer is used. |
| Global uncertainty control of system parameters | By integrating the accuracy of the temperature and flow measurements and taking various measures, system uncertainty is controlled within ±5%. |
| Error Type | Test Platform System Error | Test Environment Error |
|---|---|---|
| Error composition | Test equipment includes an electric heater, water tank, replenishment tank, frequency converter, water pump, thyristor, and electric heating tube | Test environment error includes drilling depth, pipe laying depth, and test temperature |
| Error value | 3% | 1.5% |
| Error calculation | 4.5% < 5%, requirement met | |
| Drilling Depth (m) | Geological Composition |
|---|---|
| 0~−3 | Miscellaneous fill; backfill; a large amount of gravel and brick; miscellaneous fill at the surface; various waste, including domestic waste and construction waste; loose structure; and uneven soil. |
| −3~−57 | Pebble mixed with coarse sand—gray, black, brown, wet–saturated, and dense; maximum particle size, Dmax = 12 cm; general particle size, D, is 4~8 cm. |
| −57~−150 | Gravelly sandstone partially mixed with mudstone, mainly comprising siliceous gravel; red-yellow, yellow, and other colors; wet, medium dense–dense, filled with medium coarse sand; low compressibility; continuous distribution. |
| −150~−200 | Conglomerate mixed with coarse sand; gray, black, brown, and other colors; wet–saturated, dense; maximum particle size, Dmax = 8 cm; general particle size, D, is 1~5 cm. |
| −200~−300 | Gravelly sandstone, partially mixed with mudstone, mainly composed of siliceous gravel; red-yellow, yellow, and other colors; wet, medium dense–dense, filled with medium coarse sand; low compressibility; continuous distribution. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Liu, M.; Shen, Y.; Zheng, L.; Fang, X.; Ma, S. Cross-Seasonal Storage of Flue Gas Waste Heat from Power Plants Based on Soil Heat Storage Using Buried Pipes: Geotechnical Thermal Response Experiment. Energies 2025, 18, 2191. https://doi.org/10.3390/en18092191
Yang F, Liu M, Shen Y, Zheng L, Fang X, Ma S. Cross-Seasonal Storage of Flue Gas Waste Heat from Power Plants Based on Soil Heat Storage Using Buried Pipes: Geotechnical Thermal Response Experiment. Energies. 2025; 18(9):2191. https://doi.org/10.3390/en18092191
Chicago/Turabian StyleYang, Fan, Ming Liu, Yu Shen, Lijun Zheng, Xinyue Fang, and Siming Ma. 2025. "Cross-Seasonal Storage of Flue Gas Waste Heat from Power Plants Based on Soil Heat Storage Using Buried Pipes: Geotechnical Thermal Response Experiment" Energies 18, no. 9: 2191. https://doi.org/10.3390/en18092191
APA StyleYang, F., Liu, M., Shen, Y., Zheng, L., Fang, X., & Ma, S. (2025). Cross-Seasonal Storage of Flue Gas Waste Heat from Power Plants Based on Soil Heat Storage Using Buried Pipes: Geotechnical Thermal Response Experiment. Energies, 18(9), 2191. https://doi.org/10.3390/en18092191







