Stability Proxies for Water-in-Oil Emulsions and Implications in Aqueous-based Enhanced Oil Recovery

Abstract

Several researchers have proposed that mobility control mechanisms can positively contribute to oil recovery in the case of emulsions generated in Enhanced-Oil Recovery (EOR) operations. Chemical EOR techniques that use alkaline components or/and surfactants are known to produce undesirable emulsions that create operational problems and are difficult to break. Other water-based methods have been less studied in this sense. EOR processes such as polymer flooding and LoSal^TM injection require adjustments of water chemistry, mainly by lowering the ionic strength of the solution or by decreasing hardness. The decreased ionic strength of EOR solutions can give rise to more stable water-in-oil emulsions, which are speculated to improve mobility ratio between the injectant and the displaced oil. The first step toward understanding the connection between the emulsions and EOR mechanisms is to show that EOR conditions, such as salinity and hardness requirements, among others, are conducive to stabilizing emulsions. In order to do this, adequate stability proxies are required. This paper reviews commonly used emulsion stability proxies and explains the advantages and disadvantage of methods reviewed. This paper also reviews aqueous-based EOR processes with focus on heavy oil to contextualize in-situ emulsion stabilization conditions. This context sets the basis for comparison of emulsion stability proxies.

1. Introduction

This succinct review concentrates on crude oil-water emulsions stability proxies in the context of enhanced-oil recovery (EOR). If emulsions can act as mobility control agents, as hypothesized in this article, physicochemical conditions arising from injection of EOR fluid slugs into reservoirs are of the upmost relevance, if these conditions favor emulsion formation and stabilization. The issue of emulsion formation is set aside and we concentrate on issues of stability and consequently on stability proxies. Emulsions naturally arise in oilfield operations and understanding of stabilizing mechanisms is important [1]. Figure 1 is a cartoon of the evolution steps that emulsions typically follow toward phase separation: (1) creaming or sedimentation, depending on the density contrast between the continuous and dispersed phases; (2) flocculation; (3) coalescence; (4) phase separation. Emulsions can lose significant structural integrity, through coalescence, before any phase separation occurs.

Figure 1. Steps toward phase separation in oil-water emulsions.

Figure 1. Steps toward phase separation in oil-water emulsions.

Breaking oil-in-water emulsions associated with chemical processes such as surfactant-polymer and alkaline-surfactant-polymer flooding is relevant for the success of the EOR process [2,3], as these emulsions can be very stable. Hirasaki et al. [3] indicate that asphaltene layers at water drop interfaces are the main contributing agent in the majority of cases. The conditions established by the injection of surfactants and alkalis, on one hand, and polymers on the other hand, are conducive to stabilize emulsions as a result of electrostatic and steric effects. Emulsion breakers are often necessary/required to induce significant phase separation as to attain the required product quality.

Colloid and Interface Science plays an important role in EOR [4]. The accepted wisdom in EOR at the microscale is to reduce the interfacial tension of water/oil interfaces to mobilize capillary trapped oil through either interfacial active agents, e.g., surfactants, or by reaching miscibility, e.g., miscible gas or solvent flooding. On the other hand, prevention of fingering or unstable displacement to improve sweep efficiency traditionally relies on either reducing displaced-phase viscosity (as in heating methods or solvent mixed with the oil) or increased injectant viscosity (or non-Newtonian behavior). Sweep efficiency can be attained through deep conformance technologies. We argue that conditions originated in EOR designs that substantially impact water-oil interfacial tension might produce dispersion that can exert mobility control.

Evidence of Emulsions Conformance Effects: Heavy-Oil EOR

Oil-sand EOR more clearly illustrates the possible impact of mobility control or conformance by emulsions on oil recovery. Oil sand recovery using non-thermal methods is attractive for thin reservoirs that are not commercially viable via thermal methods [5]. The required concentration of commercial polymers (HPAM) for effective mobility control turns EOR processes based on polymer injection unviable for recovery of very viscous oils. The issue of mobility ratio or control arises because viscous water has much lower viscosity than heavy oil and consequently the displacement front develops fingers and oil recovery is generally poor. Alkali-surfactant (AS) flooding has been shown to be a potential viable technology for EOR in heavy-oil reservoirs [5,6,7,8,9,10]. However, in the absence of a thickening agent such as polymers, the increase in water saturation as water displaces oil only worsens the mobility control issue. This in principle should deteriorate in presence of surfactants and alkalis, because the drop in the water-oil interfacial tension should mobilize trapped oil and further increase water saturation. The question is, how does AS improve mobility ratio?

Bryan and Kantzas [6] state that emulsification, entrainment and entrapment of dispersed phase and wettability reversal mechanisms can contribute to oil recovery during the injection of alkaline agents and surfactants in heavy-oil reservoirs. Recovery in chemical flooding of heavy-oil reservoirs have been shown to depend on flow rate, and consequently on the shear rate [5,6,7,8,9,10]. This is consistent with capillary number dependencies associated with emulsion flow [11]. At low capillary number, defined as ratio between viscous forces to capillary forces approaching zero, or equivalently at low flow rates, interfacial forces dominate flow in porous media. Cobos et al. [11] carried out flow of oil-in-water emulsions in quartz microcapillaries with a converging section, as a means to physically simulate a pore-throat, and found that the pressure-drop was a strong function of capillary number and drop diameter to pore-throat diameter ratio. More precisely, according to Cobos et al. [11], when the capillary number is less than 10⁻², pressure drop fluctuations and average pressure drop depend strongly on oil-water interfacial characteristics, but as the flow rate increases droplets do not significantly control pressure responses and mobility control is expected to decrease. This is because the capillary pressure drop necessary to overcome mobilization of emulsion drops is easily overcome by viscous pressure drops at the pore scale. Liu et al. [12,13] studied optimal conditions for formation of emulsions for recovery of heavy oil in Western Canada in surfactant enhanced alkaline flooding. Lei et al. [14] developed a mathematical model to study the effect of emulsification on recovery during alkaline-surfactant-polymer (ASP) flooding. A good match with experimental results is found by including emulsion drop entrainment and entrapment in ASP flooding models.

Figure 2 illustrates the proposed improved recovery mechanism for heavy oil recovery based on alkaline floods, as we interpret it. As water fingers through, water-in-oil emulsions might be produced by mechanisms such as snap-off. If water droplets are of a size similar or larger than typical pore-throats, then, capillary pressure will trap water droplets and block further displacement, deviated water flow to other unswept areas of the porous medium. Although the purpose of this article is not to prove the mechanism associated with emulsion flow, the proposed mechanism is plausible and explains pressure drops observed in laboratory experiments (see discussion in this section). This mechanism can in fact operate similarly for oil-in-water emulsions.

Figure 2. Proposed enhanced-oil recovery (EOR) mechanism by flow of in-situ emulsions. Water drops are represented in black. Filtration is representative of capillary trapped drops.

Figure 2. Proposed enhanced-oil recovery (EOR) mechanism by flow of in-situ emulsions. Water drops are represented in black. Filtration is representative of capillary trapped drops.

Pressure response in a number of low-salinity flooding experiments is consistent with in situ formation of dispersed phases that have the ability to produce partial plugging of the porous media ([15], and references therein). If drops in an emulsion exhibit a size similar to typical pore throats, reduction in water mobility is expected, particularly for oil-in-water emulsions, with the resulting increase in pressure drop. This might also be expected with formation of bridges in fines migration. However, bridging of solid particles leads to more permanent formation damage and we speculate that emulsions or lamellar phases more adequately explain the pressure drop observed in low salinity waterflooding. Ours and one more recent study [16,17] shows changes in stability as a function of water-oil ratio and salinity in the presence of demulsifiers.

There is enough peer-reviewed evidence showing that macro-emulsions, or fluid-fluid dispersions not in thermodynamic equilibrium in contrast with micro-emulsions, contribute positively to a number of EOR processes [18,19,20,21]. In order to elucidate how emulsions contribute to recovery, their stability must be determined under physicochemical conditions defined by EOR injection schemes. In other words, in order to test the hypothesis that emulsions contribute to recovery for a given EOR process, EOR conditions that favor macro-emulsion stability must be examined. This situation is common to several aqueous-based injection schemes in traditional chemical flooding, but processes such as steam flooding might also lead to low-salinity conditions, which favor water-in-oil emulsion formation [22]. The focus of emulsion stability has been on the production side, mainly due to product quality issues, e.g., separator design or demulsifier screening [22,23]. Although no standard is available at present [22], the fact is that several methods rely on phase separation to quantify emulsion stability. In contrast, methods such as tracking evolution of drop-size distribution [24], can relate to pore-level mobility control mechanisms. In this article, we describe a number of stability proxies and provide a rationale for the choice of method for evaluating the impact of emulsions on EOR process efficiency. It is only when emulsions can travel through the pore space reasonably unscathed that their effect on displacement efficiency can be observed.

This article is organized as follows. After this introduction, the main section of this article describes stability controlling agents, followed by emulsion stability proxies. A discussion section provides a summary of method comparison. Closing remarks are provided as the closing section.

2. Stabilizing Agents

2.1. Introduction

This section covers two important aspect of emulsion stability. The first one refers to what controls emulsion stability. Although continuous phase viscosity plays an important role in this regard, we concentrate on interfacial controls. Two groups of naturally occurring agents are discussed here. Due to their importance, emulsions stabilized by particles are reviewed first. These correspond to the so-called Pickering emulsions [25]. The second type of agents is linked to organic fractions of the crude oil, namely asphaltenes, resins and organic acids.

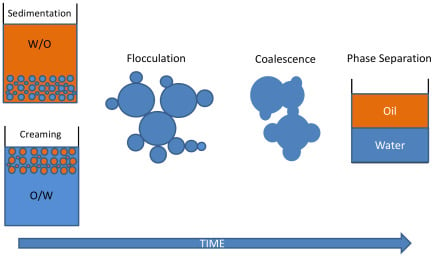
2.2. What Controls Emulsion Stability?

2.2.1. Solid-Stabilized Emulsions: Pickering Emulsions

Chemical flooding often requires injecting soft (low hardness or low divalent cation concetration) and fresh (low total dissolved solid, TDS, fraction) aqueous phase to enhanced polymer rheological behavior [26]. On the other hand, divalent cation concentration, a direct application of low-ionic strength solutions is the so-called low-salinity waterflooding, which has been cited as responsible for fines migration [27]. Fines have been considered contributors to recovery mechanisms in low-salinity waterflooding [27]. A different mechanism relates to fluid-fluid interfacial changes, not necessarily connected to fines transport, which may lead to the stabilization of lamellas and emulsions. The presence of particles of near-neutral wettability can lower interfacial and lead to stabilization of emulsions. These Pickering emulsions refer to particle-stabilized dispersions, named after S.U. Pickering, who first discovered at the dawn of the 20th century that suitable particles can stabilize oil droplets in water [25]. Solid particles, which must be smaller than the droplet size, can adsorb onto the interface between oil and water, providing a steric barrier, minimizing the interface interaction by volume exclusion to stabilize the emulsion [28]. A number of particles of varied affinity for the different phases can be used to stabilize Pickering emulsions, such as clays and silica, among others. The same holds for foams, as particles can accommodate at the water-air interface [28,29]. Pickering emulsions are of interest in a number of areas outside the realm of the oil industry [30,31]. This type of emulsions exhibits original rheological properties as well as considerable kinetic stability.

Particle morphology can alter wettability and in this respect, smooth particles tend to be more hydrophobic [32]. The wettability (three-phase contact angle) of the solids is a key factor in their potential to stabilize emulsions. Arditty et al. [30] show that silica particles, with surfaces treated for wettability alteration, can be used to stabilize either O/W (partially hydrophilized silica) or W/O emulsions (hydrophobized silica). As a rule of thumb, the continuous phase of the emulsion is normally the one in which the particles are preferentially dispersed [31]. However, this is not always true, for example, hydrophilic particles stabilize O/W emulsions if they are small and their surfaces are not modified, but they stabilize W/O emulsions if dried and added to an asphaltene-containing oleic phase [33].

The impact of calcium on bitumen drop surfaces in the presence of montmorillonite (M) was investigated by Moran et al. [34] (in 2006). They suggest that CaM aggregates can irreversibly reside on a (negatively charged) bitumen drop surface and apparently be responsible for the surface plastic behavior of bitumen drops. The adsorption of particles at an interface is irreversible in practical terms, because the detachment energy is larger than thermal fluctuation [29]. This is because the interfacial energy reduction by replacing fluid-fluid interfacial area with suitable particles lowers the total energy of the system to a significant extent. The removal of particles requires restoring fluid-fluid interfaces that demand thermodynamic work. The rheology of high concentration emulsions reflects the rigidity of the surface, which is not controlled by interfacial tension [30].

Regarding flow behavior of Pickering emulsions, Yaghi [35] found that adding solids to the Newtonian or non-Newtonian emulsions of three oils results in a shear thinning behavior, with the relative viscosity increasing with the addition of solids. The relative viscosity of oil-in-water emulsions in the presence of solids varies with solids concentration, dispersed phase volume fraction, shear rate and oil viscosity.

A number of factors impact the stability of Pickering emulsions [29,36,37]:

• Composition of the oleic phase. This includes asphaltene content and polarity of this fraction of the oil phase. Resins and waxes can also play an important role.
• Particle type. Hydrophobicity, size distribution and concentration appear to impact emulsion stability.
• Phase volume fractions. The general observation is that the most abundant phase usually becomes the continuous phase. Phase inversion occurs at a given phase concentration. In oil producing wells, as watercut reaches high values, O/W emulsions become more frequently encountered [38].
• Salinity of the brine phase. It is apparent that the overall Total Dissolved Solid concentration (TDS) impacts stability. However, the concentration of divalent cations appears to impact the stability of Pickering emulsions even more so that monovalent cations.
• pH of the aqueous phase. Yan and Masliyah [39] show that pH changes the wettability of clay particles and alters the droplet size. The value of pH also alters the surface charge of particles.
• Temperature.
• Stress conditions (pressure).

Regarding the composition of the crude oil, McLean and Kilpatrick [40] studied the role of asphaltenes and their interactions with the resins and surrounding crude medium in forming interfacial films leading to emulsion stability. Asphaltene along with resins, as naturally existing component in oil, can serve as powerful emulsion stabilizers. Although we do not usually ascribe asphaltene and resins to Pickering emulsion, they may provide the same effect as the solid particles by forming steric barrier between droplets, provided cross-linked asphaltene clusters are large enough. They determined that pH affected emulsion stability in a significant way. These authors attribute this result to increased charge densities at high pH (10–12) by polarization of the polar groups, consequently destroying mechanical properties of the interfacial film. Lower pH results (neutral to acidic) hints on the effect of acidic components of the oils. They concluded that emulsion stability is governed by the state of solubility of the asphaltenes. We speculate that if asphaltenes are destabilized, they will form nanoclusters or even microscale clusters, which might eventually drop out of solution. These colloidal “particles” sit at the interface and might act as stabilizing particles. Grutters et al. [41] carried out experiments to evaluate the role of asphaltenes in the stabilization of W/O emulsions in a 20 API° crude oil with the viscosity approximately 70 cP at 25 °C. They argue that the observed loss of stability when asphaltenes are precipitated could be related to decreased viscosity of the continuous phase. Moreover, they point out that polar resins, such as napthenic acids, play an important role in stabilizing the emulsions in their experiments.

Solid-stabilized emulsions represent a challenge during the production of bitumen from Canadian Athabasca oil sands, in terms of water-bitumen separation process [42]. Clays, mainly montmorillonite and kaolinite, have been identified as significant contributors to the stability of bitumen emulsions. These particles tend to stabilize water-in-oil emulsions that are not easily separated by mechanical or chemical means. Sztukowski et al. [43] indicate that kaolinite has been identified as one of the most common clay minerals in oil-sands reservoirs and Kaolin clays with adsorbed asphaltenes have been identified as emulsion stabilizers. Liu et al. [41] used zeta potential distribution measurements to study the interaction between bitumen and clay in aqueous solutions. In the absence of calcium, a mixture of bitumen emulsion and montmorillonite or kaolinite clay suspensions shows a bimodal zeta potential distribution. This is an indicator of the weak interaction between the two and a poor drop coating. Calcium suppresses the zeta potential for all the three components. When calcium is added to a mixture containing up to 1 mM calcium concentration, the potential distribution became unimodal, as opposed to results for kaolinite. From these results, one might infer that aqueous phase composition could lead to fine migration events in enhanced-oil recovery operations, which, depending on the ionic makeup of the water phase, might impact the effect of particles as stabilizing agents.

Yan and Masliyah [39] studied the effect of pH on adsorption and desorption of clay particles at oil-water interface. Kaolinite clay particles treated with asphaltenes were used for this purpose. When kaolinite is treated this way, heavy organic fractions adsorb on the clay surfaces, changing their character toward oil-wetting. Under similar emulsification conditions, higher pH of the brine results in larger diameter of the oil droplet. At pH 7, the creamed emulsions were redispersed into the aqueous phase at a different pH. The clays desorbed from the oil surface at pH greater than 6, but adsorbed onto the oil droplet surface at pH < 6. Asphaltene treatment leads to wettability changes of the clay surfaces. Micropipette experiments demonstrate the formation of a viscoplastic skin on the surface of bitumen droplets in aqueous environments with dispersed clays [44]. In these experiments, oil or bitumen droplets are pushed out through capillary tubes (micropipettes) in a selected aqueous phase to exposed oil (bitumen) drops to the selected brine. If observed under optical microscopy, the stability of droplets can be inferred from lack of coalescence when two droplets are pushed against each other. Also, the formation of an organic/inorganic skin on the droplets surface can be visually demonstrated when the oil is sucked back in the micropipettes. Increased interfacial plasticity is prominent in deionized water with montmorillonite and calcium present. Process water for the same clay and high concentration of calcium does not lead to the same plastic behavior of the droplet skin. A modified micropipette experiment is used to evaluate the interfacial rheology in similar bitumen systems [34,44]. In this experiment, a micromanipulator is used to stretch one drop between a micropipette and a measuring cantilever, enabling rheological experiment to be conducted on one bitumen drop. The plastic behavior observed in previous experiments is confirmed in these rheological tests.

Ngai et al. [45] used stimulus-sensitive microgel particles as emulsifier. The resulting emulsions were responsive to pH, ionic strength and temperature changes which lead to changes in particles charge and hydrophobicity. Stable oil-in-water (octanol in water) emulsions were generated at high pH, while lowering pH to below 6.0 led to continuous coarsening of the emulsions. Tight packing of the particles at the highly charged oil-water interface suggests capillary attraction [46]. This capillary attraction arises from liquid-filled pore space between flocculated droplets and the continuous phase outside the porous medium formed by surface-occupying particles. Energy would be required to removed particles, as interfaces (menisci) must be deformed (removed). The higher the work required the more stable the particle-stabilized emulsion is. In microgel dispersions, high salt concentration reduces particle activity at the interface, leaving oil droplets unprotected [45]. On the other hand, Ngai et al. [45] argue that reduced average emulsion drop size caused by increased concentration of microgel particles can be explained by the augmented coverage of the surface.

Yang et al. [47] studied the stability of paraffin-water emulsions, stabilized with positively-charged plate-like layered double hydroxides particles. They determined the effect of pH on the stability of this type of Pickering emulsions. They argue that the adsorption of particles at interfaces may be controlled by adjusting the electrostatic interaction between particles and the interface without changing hydrophobicity, which is thought to be a main controlling factor of emulsion type and stability. Electrostatic interactions are altered by changes in pH of the continuous phase, by addition of concentrated aqueous solutions of either NaOH or HCl under a N2 atmosphere. Zeta potential measurements were carried out as characterization of the surface charge of the particles. Based on arguments of reduction of interfacial energy ($E=-\pi R^2{\gamma }_{ow}{\left(1-\cos \theta \right)}^2$), where R, γ_ow and θ represent particle radius, oil-water interfacial tension and three phase contact angle respectively , the so-called attachment energy, it is argued that a reduction in particle surface charge (or zeta potential) would lead to flocculation and therefore would increase attachment energy. The small influence observed is due to the kinetic control of the adsorption process. Increased stability with increased particle concentration is due to better surface coverage, according to Yang et al.

Generally, the most stable emulsions are found when interfaces are stabilized by the smallest particles. A wide particle size distribution may potentially lead to less stable emulsions, if larger particles occupy interfacial areas, but do not contribute to the stability of these regions. Emulsion stability appears to increase with increasing solids concentration [32], and emulsion type could be inversed when the solid concentration is increased. Sztukowski and Yarranton [43] studied W/O emulsion stability with clays. They used heptane, toluene, asphaltenes as model fluids and native solids extracted from oilfield operations. They found that a combination of asphaltene and fine solids (submicron scale) coverage produced the most stable emulsions. They argue that fine solids compete with asphaltenes to adsorb at the interface and that a coverage of the interface by asphaltenes between 60 to 80% and the remaining area covered by fine solids leads to the greatest stability. Coarser solids (above 1 µm) can indeed stabilize emulsions, but only if they are in sufficiently high concentration. Apparently, asphaltene coverage does not contribute to stability in the case of coarse solids. Coarse solids tend to form bridges between droplets, particularly when they are present at high concentration.

Formation of particle networks has been determined by X-ray microscopy [48]. These networks could indeed alter the rheology of the continuous phase, but this is probably insufficient to justify the stability of emulsions in these environments. The structure and strength of particle networks are very sensitive to ionic strength and pH of the solution. A combination of surface coverage by solid particles and hindrance of drop coalescence by these networks (and likely increase in viscosity of the continuous phase) may lead to better stability of emulsions. Horozov and Binks [49] speculate that two general mechanisms of emulsion stabilization by solid particles exist, first is steric stabilization of emulsion droplets covered by coherent particle layers and second is stabilization by particle bridges when the droplets are sparsely covered.

In summary, inorganic particles play an important role in stabilizing emulsions. At low ionic strength, aqueous solutions such as those in low-salinity flooding or polymer injection, clays and other fines can be released. These particles, as evidence reviewed here shows, can serve to stabilize emulsions, but this stabilization depends on particle wettability, which in turn is affected by interaction with asphaltenes, solution pH, surface charge and particle size. These factors appear to be the main controls for particles as stabilizers. Steric effects as well as capillary attraction (of the droplet surface covering particles) are important emulsion stability mechanisms. However, it is unclear how wax or asphaltene aggregates facilitate emulsions stabilization. Proxies of stability would be more adequate if they are able to reflect interfacial behavior, rather than only phase separation.

2.2.2. Organic Crude Oil Components

In this section, we review the proposed roles of organic components of crude oil in emulsion stabilization. Solubility classes, namely resulting from the application of a SARA (Saturated, Aromatic, Resins and Asphaltenes) analysis or variations of this technique is used to separate crude oil fractions to classify them. The interplay between resins and asphaltenes has been frequently used to explain emulsion stability. Additionally, the acid fraction of crude oils has been associated with emulsion stability through formation of complexes that adhere to interfaces. We highlight a few references that provide insight into stabilization mechanisms.

2.2.2.1. Asphaltenes

Asphaltenes are operationally defined in terms of solubility in different solvents and represent a group of components insoluble in low-molecular weight normal alkanes like n-pentane and n-heptane but soluble in aromatics like benzene and toluene. In general, asphaltenes are chemically composed of polynuclear aromatic rings, aliphatic rings and chains, and heteroatoms such as nitrogen, oxygen, sulfur, and various metals (vanadium, nickel, iron, copper, etc.).

Asphaltene is an amphiphilic material and plays a very important role in stabilizing crude oil emulsions. It is speculated that the rigidity of the asphaltene cross-linked film on the interface leads to high emulsion stability [40] instead of providing a steric barrier, because the asphaltene interfacial films appear to be only in the order of 2–10 nm thick [50]. In spite of its importance, asphaltene is among the least understood deposits occurring in the oil field due to its high polydispersity and chemical variability at the molecular level [51]. The typical, if at all, asphaltene molecule is flat or planar because the interconnection of the aromatic carbon rings, with content that typically falls between 40–60% of asphaltene, and a corresponding H/C atomic ratio of 1.0–1.2. This has a significant impact on asphaltene physical chemistry, aggregation, solubility, and interfacial film formation [52]. The association of asphatenes is driven by several intermolecular interactions, including electrostatic ones, van der Waals or dispersion forces between aromatic rings, intermolecular charge transfer, exchange-repulsion interaction, and hydrogen bonding [53].

McAuliffe et al. observed that crude-oil-in-water emulsions can be easily prepared using some asphaltic crude oils and dilute solutions of sodium hydroxide [54]. The asphaltenic material from the oil adsorbs slowly and irreversibly and forms rigid skins of water-in-oil emulsions in competition with surfactant-like species, which is fast and reversible [55]. Sztukowski et al. indicate that asphaltene properties have a significant impact on emulsion stability even for emulsions partially stabilized by solids, and asphaltenes with a larger molar mass make more stable emulsion [36]. Emulsions with particles and asphaltenes combined can be much more stable than those stabilized by asphaltenes alone, provided that all the adsorption sites on the particle surface are saturated with asphaltene [32,33]. Generally speaking, the crude oil with higher asphaltene concentration can make more stable emulsions [16,56]. However, Sztukowski et al. [36] observed that for emulsions prepared with asphaltenes and no solids, the stability decreases as the asphaltene concentration increases. They explained this result by arguing that the asphaltenes may contain a small amount of a component that reduces emulsion stability and at low concentrations, there may be too little of this component to affect emulsion behavior [43]. Xu et al. [57] found in their “wash test” that only a small fraction of the total asphaltenes is involved in formation of droplet covering skin or coating.

2.2.2.2. Resins

Resins, together with asphaltenes, affect emulsion stability via interfacial action. Resin-solvated asphaltenic aggregates are able to adsorb to the interface more quickly than larger pure asphaltenic aggregates to improve stability, but will reduce the emulsion stability when resins become the primary adsorbent in the monolayer by reptation through the consolidated asphaltene network. The reason for resin to be able to displace the asphaltene from the interface is that resin is more surfactant like than asphaltenes and is thermodynamically favorable to adsorb on the interface to minimize the surface free energy at longer times [58].

2.2.2.3. Organic Acids

Naphthenic and other naturally occurring fatty acids from the crude oil do not seem to stabilize emulsions alone [33]. Naphthenic acids can form neutralization products with saline water. Naphthenic acids and their naphthenates can accumulate at the interface between the oil and water phase and stabilize emulsions due to their amphiphilic property. Brandal et al. [59] investigated the interactions between naphthenic acids and divalent metal cations across model oil-alkaline water interfaces by correlating changes in dynamic interfacial tension (IFT). Their results show that the dynamic IFT strongly depends on naphthenic acid structure, type of divalent cation, and the concentration of the compounds as well as the pH of the aqueous phase. The divalent cations in the aqueous phase can react with saturated naphthenic acids and cause mostly a permanent lowering of the IFT. This drop in IFT can lead to increase emulsion stability, which might explain why the divalent cations are more effective than monovalent ones at stabilizing emulsion.

Mohammed and Sorbie [60] describe analytical procedures to extract and characterize naphthenic acid content and type from naphthenate deposits. They use electrospray mass spectroscopy and atmospheric pressure chemical ionization to discern different classes of families of acids from the extracted material. It turns out that Na-naphthenates do not form precipitate-like deposits, but they still contribute to emulsion “problems”. These naphthenates are emulsion-like. Ca-napthenate, on the other hand, forms solid deposits that contribute to impair oil production through emulsion formation as well as deposits. Mohammed and Sorbie [61] later present a thermodynamic model describing calcium naphthenate precipitation. Extraction (partition) experiments show that most of the acid remains in the oil phase (95%). The model results qualitatively agree with experimental results, including a maximum in the Ca-naphthenate mass at a watercut in the range of 60–70%.

Despite all the extensive reports on the importance of asphaltenes and resins, and organic acids, in emulsion stability, it is not completely clear how these organic acids or the solubility classes contribute to stability. Naphthenic acids appear to be conducive to stability through the formation of interfacially active complexes with cations in aqueous solution. These cations tend to express two distinct classes of naphthenates, either emulsion-like or solid-like, which might explain observations regarding emulsion stability for some oils [62]. It is important to indicate that organic acids in oil are part of the resin fraction, in general, and therefore altering their conformation or content can affect the configuration of polar groups such as asphaltenes. What seems clear is that polar fractions of crude oils, namely asphaltene and resin, are needed to impart stability to emulsions, in the absence of other interfacially active agents.

3. Stability Proxies

This section discusses a number of stability proxies commonly used to characterize emulsion stability. Some of these proxies are more commonly used, while others have been more recently developed or are not common place in applications. We concentrate on droplet-size distribution methods, because they better represent proxies of coalescence, but discuss a number of other methods for completeness.

3.1. Droplet Size Distribution Based Methods

3.1.1. Nuclear Magnetic Resonance (NMR)

NMR spectroscopy is based on the interaction between nuclear spins and radiofrequency signals when the nuclear spins are exposed to an external static magnetic field. The energy release through several relaxation mechanisms involves several relaxation rates. The proximity to interfaces affects relaxation mechanisms and therefore this can be used as proxy for drop size. The sensitivity of NMR depends on the strength of the external magnetic field and the nuclear moment, which in itself is a function of magnetogyric ratio. The structure of organic of molecules or the diffusion coefficient can be determined [63,64].

Emulsion studies using NMR technique rely on signal attenuation due to random motion of the molecules when two magnetic field gradients are imposed on the system since the NMR signal intensity becomes directly proportional to the number of nuclei producing it. This method is called NMR pulsed field gradient-spin echo (PFG-SE) and was first demonstrated by Tanner and Stejskal [65] to measure the free unrestricted self diffusion of molecules. The signal attenuation for a single diffusing molecule is described by:

$$\frac{S}{S_0}=\exp \left(-D{\left(\gamma g\delta \right)}^2\left(\mathrm{\Delta }-\frac{\delta }{3}\right)\right)$$

(1)

where D is the self-diffusion coefficient of the relevant molecules ($\frac{c{m}^2}{s}$) and Δ, δ and g are the temporal duration between application of the two magnetic field gradients (s), the duration of a single magnetic field gradient (s) and the strength of the magnetic field gradient ($\frac{T}{cm}$), respectively. γ (T⁻¹S⁻¹) is the gyro-magnetic ratio of the nucleus being studied (hydrogen, in the application discussed in this review [66].

Equation (1) can be used in a homogeneous system with no barriers for diffusion. In the case of water-in-oil emulsions, molecular diffusion is restricted to the spherical cavity represented by water droplets. By varying the duration of the applied magnetic field gradient it is possible to observe the effect of the cavity wall on diffusion and consequently cavity dimensions [67]. To estimate the droplet diameter, two approaches are usually followed [66]:

I. 

Gaussian phase distribution model (GPD)

This method was first formulated by Murday and Cotts [68] and assumes diffusion following the gradient pulses is Gaussian phase distributed. The signal attenuation for the spherical cavity has a complex relationship with the radius of the sphere (droplet radius).

II. 

Short Gradient Pulse (SGP) model

This model assumes that the duration of the applied magnetic field gradient is zero. In the equations describe magnetic responses, the radius of the emulsion droplet is the only free parameter and all other parameters are determined in the experiment. Since emulsions are generally polydispersed, echo signals coming from different droplet sizes are superimposed. This can be solved by assuming the distribution function for droplet size. The measured signal in this case can be defined by the following integral:

$$\frac{S}{S_0}=\frac{{\displaystyle {\int }_0^{\infty }{a}^{3}P\left(a\right)R\left(g,\delta ,a,\mathrm{\Delta }\right)\text{d}a}}{{\displaystyle {\int }_0^{\infty }{a}^{3}P\left(a\right)\text{d}a}}$$

(5)

where R(g,δ,a,Δ) is the signal attenuation function and P(a) is the droplet size distribution function. Typically, a log-normal distribution function is used to describe the size distribution of the emulsions [65]. This restriction results in the loss of the actual size distribution of the emulsion. Therefore some alternative methods have been developed that do not assume any predetermined distribution function for the system and yield more general information about droplet size distributions [66,67,68,69].

Another important issue to be considered is self diffusion of droplets due to their Brownian motion, which is not considered in the aforementioned method. The attenuation of NMR signal can be due to restricted molecular diffusion within the droplets or to the diffusion of droplets by themselves. This was studied by Garasanin et al. [70].

NMR is a non-invasive, non-destructive technique that can be used for high concentration emulsions, avoiding dilution. Since this method does not rely on the transparency of the continuous phase, NMR can produce size distributions in opaque systems such as water-in-crude oil emulsions. One of the first applications of this method for sizing water-in-crude oil emulsion was conducted by Balinov et al. [71]. In their study, NMR self-diffusion technique was used to determine water–in-crude oil emulsion droplet size, in addition to investigating the effect of aging, volume fraction of dispersed phase and the addition of demulsifier on droplet size. It was shown that results were in good agreement with parallel studies performed using optical microscopy. In another study [72], NMR pulsed field gradient with diffusion editing (PFG-DE) was utilized to quantify drop size distributions of brine/crude oil emulsions. The drop size distributions obtained from this technique were compared to results from the traditional pulsed field gradient (PFG) technique. The PFG-DE technique does not assume a form of the drop size distribution. An algorithm for the selection of the optimal parameters to use in a PFG-DE measurement is described in the reference [72]. Finally, the PFG-DE technique is shown to have the ability to resolve a bimodal drop-size distribution. The typical droplet size measurable with this technique is 0.3–20 µm for oil-in-water emulsions and 1–20 µm for water-in-oil emulsions. For most cases, bias due to droplet diffusion is negligible, but for small droplet sizes and low viscosity continuous phases this can have larger effect. High resolution NMR generally improved the sensitivity particularly for small droplet sizes [73].

3.1.2. Near-Infrared Spectroscopy (NIR)

NIR spectroscopy relies on the absorption of near-infrared radiation, resulting in molecular vibration and also molecular light scattering that leads to intensity attenuation. NIR region covers the electromagnetic spectrum between mid-infrared and the visible region, i.e., the wavelength range 780–2526 nm.

Application of NIR spectroscopy for droplet size measurement in emulsions is based on light- scattering theories [74]. According to this theory, the intensity of a beam of light is exponentially attenuated while traversing a distance L through a particular medium. If multiple scattering is negligible, attenuation can be calculated by the following equation [75]:

$$\frac{I}{I_0}=\exp \left(-{\alpha }_{ext}L\right)$$

(7)

$${\alpha }_{ext}=N\left(C_{abs}+C_{sca}\right)=N{C}_{ext}$$

(8)

where $\frac{I}{I_0}$ is the ratio between the intensity of scattered light and the incoming light, C_ext, C_abs and C_sca, are the extinction, absorption and scattering cross sections , respectively. L is the sample thickness and N is the number of particle per unit volume. Expressions for absorption and scattering cross-sections have been developed to describe the extinction upon the chemical composition of the particles, their size, orientation and shape, the surrounding medium, the number of particles, the polarization state and the frequency of the incident beam. Mathematical calculations have been performed by Rayleigh, Mie and Frauhhofer among others [76].

According to Rayleigh scattering, scatter intensity is a strong function of the droplets radius and the wavelength as described by the following equation [75]:

$$\frac{I}{I_0}\propto {\left(\frac{\pi }{\lambda }\right)}^4\frac{r^6}{L^2}$$

(9)

where r is the droplet radius and λ is the wavelength. Since water droplets in crude oil emulsions are usually about the same size or larger than the NIR wavelength and also water is a high absorbing compound, one may conclude that the Rayleigh scattering theory no longer applies [74]. For larger droplets, Mie theory may be applied, but refractive index data are required [77].

Water droplets radii can be extracted indirectly in NIR spectroscopy. It turns out that larger droplets scatter light more effectively than smaller ones with consequent decrease in absorbance, which can be seen in the shift in the baseline of the spectra [75].

NIR spectroscopy is a simple, low time-consuming method that can provide a variety of characteristics on a system from a single spectrum without consuming additional sample. However, there are some disadvantages related to this method such as required reference technique to build up calibration routines [73], insensitivity to minor constituents, broad absorption band, although multivariate techniques mitigate this problem [78,79,80].

3.1.3. Acoustic and Electro-Acoustic Techniques

These techniques are based on the interaction between ultrasound pulses and particles or droplets when sound waves travel through the dispersion. The frequency range is usually between 0.1–200 MHz.

A brief description of attenuation mechanisms follows [73,81]:

• Viscous losses to shear waves generated by the particles oscillating in the acoustic pressure field. This is important mostly for particles smaller than the wavelength of ultrasound.
• Thermal mechanism. This is thermodynamic in nature and relates to resonance of sound waves in particles, which converts acoustic energy to thermal and causes attenuation of sound waves. This is important for deformable, soft particles, including emulsion droplets.
• Scattering mechanisms due to diffraction, reflection and refraction phenomena when sound waves interact with particles. This mechanism does not convert acoustic energy into other kinds of energy, but due to changes in direction, a portion of the wave cannot reach the transducer and as a result cannot be detected. At higher concentration particle-particle interaction and multiple scattering have to be considered.
• Intrinsic absorption of ultrasound by particles and medium due to interaction at the molecular level, which is not related to the particles size.
• Structural mechanism causes the acoustic attenuation in some structural network of particles.
• Electrokinetic mechanisms due to the interaction of ultrasound with electrical double layer of particles. Its contribution to acoustic attenuation is negligible, but this is the basis for electroacoustic.

There is no theory that can take into account all of the six mechanisms, but by simplification, a model to calculate the sound speed and acoustic attenuation can be obtained.

There are two ultrasound-based techniques applicable to characterizing colloidal systems. The first one, “acoustic”, deals only with the acoustic properties of the dispersion such as attenuation and sound velocity. It can provide reliable particle size information of the dispersion with a wide range of concentration and also provides information about the microstructure of dispersed phase. The second technique is electroacoustics, which relates to the coupling between the acoustic wave and electric properties of the dispersion, by applying an electric field. Electroacoustic techniques can provide particle size information as well as zeta potential [81]. There are two different approaches depending on the different fields used to generate the driving force. In the first, sound energy is applied to the dispersion and an electric field results from the vibration of the electric double layers of particles. This is called colloid vibration current or potential (CVC or CVP). In the second one, an applied electric field causes the generation of sound energy and is called electrokinetic sound amplitude (ESA). From ESA response, dynamic mobility can be determined. The magnitude of dynamic mobility yields information about the zeta potential and the phase angle of mobility yields information related to size. Lower phase angle corresponds to smaller particles. This phase angle varies approximately from 0 to 45° [82].

There are few studies reported in the literature relevant to the study of water-in-crude oil emulsions using the electroacoustic techniques. Electroacoustic technique based on colloid vibration potential (CVP) is effective to monitor the rate and extent of coalescence in water-in-crude oil emulsions, and to evaluate the effectiveness of additives to break the emulsion and optimize their concentration [83]. Marques and coworkers study electrical charging of oil droplets due to asphaltene adsorption in toluene-in-water emulsions, using the electroacoustic technique based on ESA. After establishing a direct relationship between the ESA signal and the asphaltene content, they concluded that the contribution of asphaltenes to the emulsion stability is based, in principle, on both mechanisms: steric and electrostatic [83].

3.1.4. Microscopy

Microscopy is one of the oldest techniques used to provide direct observation of dispersed phase size and shape in a dispersion. The most significant development in this area has been transmission electron microscopy (TEM) and more recently scanning electron microscopy (SEM). The problems with optical microscopy are its limited resolution and also the difficulty in observing objects smaller than the wavelength of visible light. Several studies have compared microscopy-based methods to the other aforementioned alternatives. Generally, the comparison favors microscopy, except for the objection related to labor intensity [73,84].

Optical microscopy usually combines the magnification of a microscope with the image acquisition capability of a digital camera. It provides a direct estimate of particle size, shape and dispersion quality. However, its accuracy is highly dependent on calibration, proper focusing and concentration of the dispersed phase in the sample [73]. The observation of particles or droplets with an optical microscope is limited by the two following factors:

• The resolution of the microscope, which refers to the ability to discriminate between two closely spaced points in the field of view of the microscope. Light waves emanating from two neighboring points can interfere with one another to produce a diffraction pattern of alternate light and dark bands especially when the distance between the points is comparable with the wavelength of the light being used. If these two points are the opposite edges of a particle, then the particle appears as an object of indeterminate shape surrounded by a dark rings [85]. Hence, the operational size domain is limited by the wavelength of the applied light and known as the Rayleigh limit [54]. The resolving power, d_p, of a microscope can be calculated by:

  $$d_p\approx \frac{\lambda }{\left[n_0\sin \theta \right]}$$

  (10)

  where n₀ the refractive index of the medium and θ is the half angle subtended by the microscope objective at the focal plane. n₀sinθ is known as the numerical aperture (N.A.). Applying a light with the lower wavelength or increasing the refractive index or θ, decrease d_p, and improve resolution. Usually, visible light is used but by filling the region between the lens and the sample with the transparent oil (immersion oil) instead of air, the refractive index increases. Using wide angle lenses is also helpful, but the angle is limited by other optical problems like spherical and chromatic aberration [85].
• Optical properties of the sample. Sample must be transparent and the continuous phase and the droplets must have different optical properties to make them optically distinguishable such as different refractive indices and different colors [54].

Optical microscopy has been used to determine size distribution or the average size diameter of emulsions as proxy of the effect of asphaltene, waxes and fine solid particles on emulsion stability [64,86,87,88,89,90]. Eley et al. [87] studied emulsions of simulated sea water and three crude oils and in a model oil consisting of n-heptane,m-xylene and asphaltenes by optical microscopy to obtain droplet diameters. They found a log-normal distribution function fitted their results [87]. The use of a computerized microscope image analysis technique to determine the droplet size distribution in emulsion samples has been studied by Jokela et al. [91]. In their study, particle size distributions of standard polystyrene latex particles and a crude oil-in-water emulsion obtained using this technique were compared with those obtained using Coulter counting and a laser diffraction method. Satisfactory agreement between all three methods was found [91]. Also, other studies droplet size has been measured using microscopy techniques to investigate demulsification process to investigate the effect of the demulsifying process, aging and demulsifiers on emulsion stability [92], to calculate interfacial areas and film thickness [90]. In the following the principles of the above mentioned techniques are described briefly.

Transmission Electron Microscopy (TEM) method relies on the wave nature of the electron Resolution of this method can be limited by electron wavelength but, in practice, the limit is set by the performance of the magnetic lenses and the maintenance of stable magnetic fields. In this method a focused electron beam of sufficient energy passes through the sample in a vacuum chamber. Electrons are absorbed or scattered by various part of the sample in proportion to the local electron density, and the remainder are transmitted. An electromagnetic objective lens, collect the transmitted electron and magnifies the image of the sample into the object plane of a magnetic projector lens system, which induces the further magnification as it projects the electrons onto a fluorescent screen. The main problem concerns the preparation of the sample in a way that allows one to transfer it to the evacuated chamber of the microscope and be examined without undergoing changes in structure such as electrostatic charging, shrinkage and distortion [73,85].

In Scanning Electron Microscopy (SEM), a high energy electron beam is focused on a specimen and subsequently raster scanned over a rectangular area. The low velocity secondary electrons that are emitted as a result are drawn towards a collector grid and fall onto a sensitive detector. The output from this detector is used to modulate the intensity of an electron beam in a cathode ray tube. The beam itself is made to scan the surface of the cathode ray tube (CRT) in synchronism with the scanning of the sample by the primary electron beam. The result is a reconstructed image on the CRT with high magnification, resolution and depth of field. Since secondary electrons are emitted at low voltage, they can be easily deflected to follow curved paths to the collector. The electrons emerging from parts that are out of the line-of-sight are also collected and contribute to the striking realism of the three dimensional image [85]. The effective magnification is about 10–100,000× and at 1000× magnification depth of field is about 30 μm and resolution is about 0.005 μm. The size range that can be detected by SEM is 10–500 μm. Also, with additional solid state X-ray detectors, elemental analysis can be performed at local spots of the surface of the particles [73]. More recent developments are the scanning transmission electron microscope (STEM), and scanning tunneling microscope (STM). More information about these two technologies can be found in [85]. This method has the restriction related to the performance under vacuum similar to TEM and also particle surface should be conductive during analysis. Otherwise, the bombardment with electrons leads to a local high concentration of electrons which is called hot spots and can be observed as a very bright spots on the image [73].

3.1.5. Light Scattering and Diffraction

This method is based on the interaction between the electromagnetic (light) waves and the particles. On the basis of scattering theory [85], there are several methods to calculate the particle or droplet size of the dispersions such as laser diffraction and dynamic light scattering.

In Laser Diffraction or static light scattering method sample is illuminated by monochromic laser light and the scattered light intensity is measured on a series of detectors positioned at different angles mostly in the forward direction. The measured signals would be converted into a particle size distribution using a model base matrix, which contains the calculated intensities at all detector elements per unit volume of spherical particles for each size class of particles. The intensity data to size distribution conversion is biased by the conversion method used [73].

In Dynamic Light Scattering (DLS), dynamic changes of the scattered light intensity are measured at a given angle and as a function of time. This procedure is affected by the fact that re-radiated light from moving particle has different frequency from that of the incident light when it is observed by the stationary observer [73]. This frequency can increase or decrease depending on whether the particle is moving towards or away from the observer. Intensity alteration is then converted to a mean translational diffusion coefficient which is a function of particle size through the Stokes-Einstein equation. Hence, the hydrodynamic radius of particle can be calculated, provided that at high concentration particle-particle interaction has to be taken into account [85].

These techniques have been used in different emulsion studies to determine the mean diameter and obtain droplet size distribution of water in crude oil emulsion [93,94,95], and also to investigate the coalescence of water in crude oil emulsion [96].

3.1.6. Small Angle Neutron Scattering

Small Angle Neutron Scattering (SANS) involves scattering of a beam of neutron by the sample and measuring the intensity of the scattered neutron as a function of scattering angle [97]. SANS is used for studying the structure of the material on length scale of 10 to 1000 A$°$, and has been applied to study different problems such as polymer conformation and morphology, biological structure and the size, shape and orientation of the component [97]. In this method, scattering takes place from aggregates of atoms not from individual atoms, therefore the structural information is coarser than the atomic level [97].

The generalized equation for the SANS from any sample is [94]:

$$\frac{\text{d}\sigma \left(Q\right)}{\text{d}\mathrm{\Omega }}=N_p{V}_p^2{\overline{\rho }}_p^{2}P\left(Q\right)S\left(Q\right)$$

where N_p is the number of identical particles, each of volume V_p, Q is $\frac{4\pi \left(\sin {\theta }_p\right)}{\lambda }$, where 2θ is the scattering angle and λ is the wavelength of the neutron. ${\overline{\rho }}_p^2$ is the particle contrast, P(Q) is the shape factor or form factor and S(Q) is the interparticle structure factor. These last three terms provide the information regarding the size, shape and interactions of the scattering particles [97]. The technique of “contrast variation” is responsible for the success of SANS. Contrast variation method is based on the definition of “contrast (∆ρ)”, which is the difference between particle and solvent average scattering density [97]. According to Porod’s law, the contrast relates to the specific surface area of the particle by [98]:

$$\left(\frac{S}{V}\right)=\pi \frac{P_{Porod}}{2\pi {\left(\mathrm{\Delta }\rho \right)}^2}$$

where S and V are the surface area and volume of the particles, respectively. P_Porod is the plateau value of the I × Q⁴ vs. Q plot, and I is the scattering intensity. Specific surface area can be used to calculate the radius of the particle R_ave$)$, assuming that particles have spherical geometry, which is the case in water-in-oil emulsions, according to [98]:

$$\left(\frac{S}{V}\right)=\frac{3\phi }{R_{ave}}\left(\frac{z+1}{z+3}\right)$$

where φ is the volume fraction of particles and z is he polydispersity index.

Small angle neutron scattering technique has been used by several researchers to study the size and composition of the asphaltene aggregates and also to study structure, thickness and composition of interfacial films at the water- crude oil interface [98,99,100,101,102,103].

3.1.7. Differential Scanning Calorimetry

Differential Scanning Calorimetry (DSC) is a thermal technique used to characterize emulsions. In the DSC technique, the heat exchange between a sample and a reference is monitored as a function of time or temperature [104,105]. In fact, in this method, information about droplet size is obtained based on the solidification or melting properties of the droplets while temperature is scanning down below the freezing point or up above the melting point of water. In principal, when water-in-crude oil emulsion is cooled down below the water freezing point, ice nucleation occurs inside droplets and formation of “ice germs” induces freezing [105]. Theoretically, the radius of the germ, which is supposed to be spherical, could be related to temperature and water droplet radius, as controlled by capillary phenomena [105].

The relation between water droplet radius R and the freezing temperature T is as follow [106]:

$$R^3=0.69\frac{3\dot{T}}{4\pi {\displaystyle {\int }_{T_f}^{T}A\cdot \exp \left[-\frac{16\pi {\gamma }^3{V}_S}{3L_f^2{\ln }^2\left(\frac{T}{T_f}\right)}\frac{1}{KT}\right]\text{d}T}}$$

where $\dot{T}$ is the rate of temperature change (K·s⁻¹), A is the preexponential factor in the expression of the nucleation rate (s⁻¹m⁻³), k is the Boltzman constant (N·m·K⁻¹), γ (N·m⁻¹) is the interfacial tension between water and ice germ, V_S (m³·mol⁻¹) is the molar volume of the germ, L_f (N·m·mol⁻¹) is the molar melting heat and T_f (K) is the melting temperature.

Since it is impossible to obtain some of the parameter in the above equation, such as interfacial tension, by a direct determination method, an empirical correlation between R and T is necessary to generate the calibration curve. For this purpose, droplet size required to be obtained by another analytical technique and be correlated to the freezing temperature obtained from DSC thermal analysis [105,106].

There are several studies reported in the literature that have applied DSC to determine emulsion type, water content in water-in-oil emulsions, emulsion stability, the ratio of dispersed water and the presence of additives [105,106,107,108].

3.2. Phase Separation Based Methods

This type of methods relies on measuring the amount or fraction of resolved phases naturally separating from emulsion breakup or by external forcing. The paradigmatic example of this is the bottle test [22,23]. The volume of the dispersed phase separated from the emulsion as a function of time can be used as proxy of stability. In this method, the smaller the “resolved” volume of dispersed phase (with respect to the original volume), the more stable the emulsion is, provided separation conditions are comparable, namely acceleration [22]. There is an ASTM standard (ASTM 4007) for determining the bottom sediments and water in an emulsion. Kokal and Wingrove [23] present a method denominated emulsion separation index, which determines the effectiveness of emulsion breakers. Though a variety of stability proxies based on bottle tests are available, there is no accepted standard protocol for emulsion stability determination based on bottle test. Bottle test is a controlled analog of gravitational settlers [109]. Bottle test are usually inadequate for very tight/stiff emulsions, because phase separation cannot be induced under gravity segregation or even commonly found centrifuges. Much higher acceleration in ultra-centrifuges can induce coalescence, but final separation might be difficult to attain, rendering the proxy inaccurate. Additionally, when the interface between the resolved and continuous phases is not sharply defined (observed), bottle tests become unusable.

3.3. Electro-Coalescence

Electric grids or electro-coalescers provide an effective means for breaking emulsions [22]. Electric methods offer a possible consistent method for determining w/o emulsion stability by measuring the critical electric field (CEF) [16,110]. The proposed mechanism consists of polarization of water droplets under the action of the electric field to form chains of droplets spanning the gap between the electrodes [47]. As the field increases, the compression of the interfacial film causes it to rupture and the current increases sharply as a result. If current is tracked as a function of the applied voltage, a CEF value can be defined as the ratio between the critical voltage and the electrode separation gap at which the current abruptly increases [16]. One implication of interface rupture and water percolation spanning between electrodes is the alteration of the emulsion structure. This in turn introduces the possibility of using rheological methods to determine stability.

4. Discussion

Table 1 lists methods reviewed in this article. The comparison among methods can be established by looking at the advantages (Pros) and disadvantages (Cons) of the different methods. The table also shows what each method is more likely to reflect, in references to Figure 1. As can be easily noticed in the table, methods based on size distribution require an external driving force to induce coalescence and phase separation, which for weak emulsions is gravity. While this might appear simple, for instance for microscopy methods, the challenge is to produce statistically equivalent samples for comparison purposes. This problem has been encountered before and a full description of one such a procedure can be found in reference [24]. In this sense, if for example centrifugal force is used to induce coalescence, all the drop-size distribution methods will have a similar pitfall as bottle tests. This means that stiff emulsions might need to rely on electromagnetic methods (electrocoalescence) or ultracentrifugation. On the other hand, methods that result too complex might be impractical. This includes SANS, and light diffraction for W/O emulsions, unless a proper solvent is found to suspend the dispersed phase without modifying the size distribution. For clean oils, this is not generally a problem, but for crude oils, the damage to optical windows is likely. Methods that require complex interpretation models, such as electroacoustics and NIR might also be impractical, due to calibration needs. In our opinion, NMR and optical microscopy, if properly combined with centrifuging and proper sampling procedures may be appropriate to analyze emulsions produced in EOR operations. Electrorheology is a newcomer in the list, but has high potential. Further development of this method is required, but as in the case of microscopy, small volume sample is appropriate.

One important consideration must be brought up. If interfacial mechanisms must be understood, then techniques such as electrorheology, NMR and NIR might be preferable, because they are able to provide additional information about the system. One distinction between EOR methods that favor the use of surfactants, which generally stabilize microemulsion phases and later macroemulsions, as opposed to say low salinity water flooding, is that in the latter method accumulation of naturally occurring crude oil material accumulates at the interface and stabilizes the emulsions without significant changes in interfacial tension [62]. In order to understand how these organic fractions in the oil are conducive to stability, stability proxies that provide more detailed information about the interface are needed.

Table 1. Comparison of emulsion stability proxies described in this paper.

Basis	Method	Pros	Cons	Separation Step	EOR Applicability
Size Distribution	NMR (Nuclear Magnetic Resonance)	Easy to implement and fast. Non-invasive and non-destructive. Rich in useful information such as diffusion and compositional analysis.	Significant preparation steps are needed and interpretation can be complex. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable
	NIR (Near-infrared Spectroscopy)	Simple and fast.	Reference and calibration techniques are required. Insensitive to minor constituents. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable
	Acoustic and Electro-Acoustic	Relatively simple to operate. It is not sensitive to optical density.	Large amount of sample and a complex interpretation model. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable if significant volume of sample is available.
	Microscopy	Direct observation	TEM and SEM are too complex. Optical microscopy is time consuming, except for automated systems. Dark emulsions are problematic. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable if automated methods are developed, but unless contrast techniques are used (fluorescence), not good for dark emulsions.
	Light Scattering and diffraction	DLS requires small sample volume. Both are simple. Fast and reliable.	DLS works well for small drop size and mostly for oil-in-water. LD needs a special solvent for W/O. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	DLS can be used for microemulsions (O/W). Light diffraction works well with macroemulsions.
	SANS (Small Angle Neutron Scattering)	Good for interfacial studies	It provides specific surface area rather than size. Complex technique. It requires specialized facility and preparation time.	Coalescence	Too complex to be practical.
DSC	Differential Scanning Calorimetry	Simple to set up and relatively fast. Small sample volume.	A drop radius-freezing temp. calibration curves is needed. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Not applicable as phase behavior (e.g., surfactants) depends on temperature
Gravity	Bottle Tests (Phase Separation)	Simple to implement and some standard techniques are available, but not directly as proxy of stability	Requires extreme accelerations (forces) for stiff emulsions, not attainable in traditional systems. Inaccurate and requires relatively large sample volume.	Phase Separation	Applicable, if emulsions can be broken.
Electric Cond.	Electro-coalescence	Relatively fast. Small sample volume can be used. It can provide significant volume of information. Very stiff emulsions can be studied.	Information on water content and size distribution may be needed to compare emulsions.	Coalescence	Applicable, but the technique is not as developed as other methods.

Table 1. Comparison of emulsion stability proxies described in this paper.

Basis	Method	Pros	Cons	Separation Step	EOR Applicability
Size Distribution	NMR (Nuclear Magnetic Resonance)	Easy to implement and fast. Non-invasive and non-destructive. Rich in useful information such as diffusion and compositional analysis.	Significant preparation steps are needed and interpretation can be complex. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable
	NIR (Near-infrared Spectroscopy)	Simple and fast.	Reference and calibration techniques are required. Insensitive to minor constituents. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable
	Acoustic and Electro-Acoustic	Relatively simple to operate. It is not sensitive to optical density.	Large amount of sample and a complex interpretation model. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable if significant volume of sample is available.
	Microscopy	Direct observation	TEM and SEM are too complex. Optical microscopy is time consuming, except for automated systems. Dark emulsions are problematic. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Applicable if automated methods are developed, but unless contrast techniques are used (fluorescence), not good for dark emulsions.
	Light Scattering and diffraction	DLS requires small sample volume. Both are simple. Fast and reliable.	DLS works well for small drop size and mostly for oil-in-water. LD needs a special solvent for W/O. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	DLS can be used for microemulsions (O/W). Light diffraction works well with macroemulsions.
	SANS (Small Angle Neutron Scattering)	Good for interfacial studies	It provides specific surface area rather than size. Complex technique. It requires specialized facility and preparation time.	Coalescence	Too complex to be practical.
DSC	Differential Scanning Calorimetry	Simple to set up and relatively fast. Small sample volume.	A drop radius-freezing temp. calibration curves is needed. An external driving force is required for stiff emulsions, e.g., centrifugal force.	Coalescence	Not applicable as phase behavior (e.g., surfactants) depends on temperature
Gravity	Bottle Tests (Phase Separation)	Simple to implement and some standard techniques are available, but not directly as proxy of stability	Requires extreme accelerations (forces) for stiff emulsions, not attainable in traditional systems. Inaccurate and requires relatively large sample volume.	Phase Separation	Applicable, if emulsions can be broken.
Electric Cond.	Electro-coalescence	Relatively fast. Small sample volume can be used. It can provide significant volume of information. Very stiff emulsions can be studied.	Information on water content and size distribution may be needed to compare emulsions.	Coalescence	Applicable, but the technique is not as developed as other methods.

5. Concluding Remarks

A review of literature discussing conditions that favor emulsion stability has been completed in this article. Organic polar fractions of the crude oils represented by asphaltene and resin contribute significantly to stability, but mechanisms are still debatable. For particle-stabilized system, particle wettability, surface charge, pH and size seem the main controlling variables.

We have reviewed a variety of methods to determine emulsions stability. Some of these methods relying on direct observation of droplets are more applicable to relatively transparent or translucent dispersions, such as optical microscopy, while others are only proxies of emulsion stability, as they do not measure directly coalescence or phase separation. Electrorheology and other related methods have emerged in more recent times as promising alternatives. However, further investigation is required to understand what these methods really reflect, in regards to emulsion stability. Low-field NMR has a number of advantages, such as being non-invasive and non-destructive as well as being able to provide system characteristics, e.g., restricted diffusion response, that makes it a technique of choice.

Enhanced-oil recovery (EOR) might often times impose physico-chemical conditions conducive to emulsion stability, in particular in low-salinity waterflooding and polymer injection. In this sense, the hypothesis of emulsions contributing positively to EOR mechanisms is compatible with conditions imposed by a number of recovery methods. Stability proxies such as low-field NMR, (electro-) rheologically based methods and optical techniques seem appropriate choices to investigate emulsion stability under EOR conditions. Obtaining the drop-size distribution occurring in EOR processes can be very powerful, especially if done in-situ, because it might be possible to determine if the drop size will produce adequate pore-level conformance. On the other hand, the implication of using methods such as NMR (high- or low-field) and electrorheology is the possibility of better investigation of the stabilization mechanism. In particular, for severely tight/stiff emulsions, electromagnetic methods might offer the only alternative to determine stability. This would also contribute to the development of better electrocoalescers, particularly if alternate current systems were used, because additional interfacial effects can be exploited.