Calculation of the Arc Velocity Along the Polluted Surface of Short Glass Plates Considering the Air Effect
Abstract
:1. Introduction
2. Electric Field for Maintaining Arc Movement


3. Arc Force Analysis and Velocity Calculation
3.1. Force Analysis of the Arc

3.1.1. The Forward Electric Field Force
3.1.2. The Forward Airflow Pressure Force
3.1.3. Backward Air Resistance
- (1)
- When the resultant force is larger than the air resistance ΔF > 0, then g < (ρ0/η – 1)/2, and the arc moves forward.
- (2)
- When the resultant force is equal to or smaller than the air resistance ΔF ≤ 0, then g ≥ (ρ0/η – 1)/2, the arc is extinguished or remains static.
3.2. Arc Velocity Calculation
3.2.1. Velocity Caused by the Electric Field Force
3.2.2. Velocity Caused by Airflow Pressure
3.2.3. Velocity Caused by Air Resistance
3.3. Calculation Results
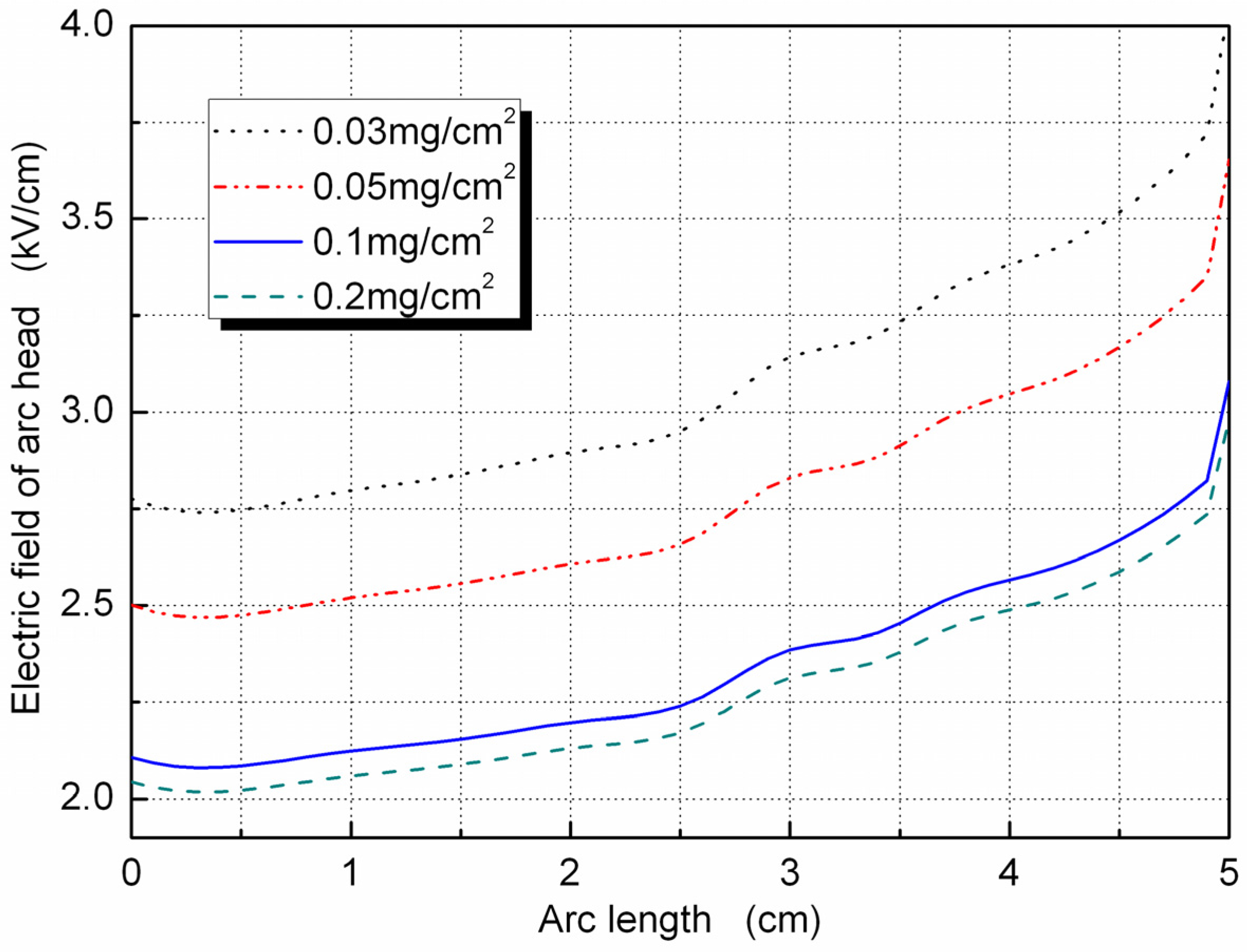
3.3.1. Electric Field of the Arc Head

| ESDD (mg/cm2) | γ (μS·cm−1) | Uc (kV) |
|---|---|---|
| 0.03 | 3.6 | 10.44 |
| 0.05 | 5.5 | 9.17 |
| 0.1 | 11 | 7.45 |
| 0.2 | 20 | 5.57 |
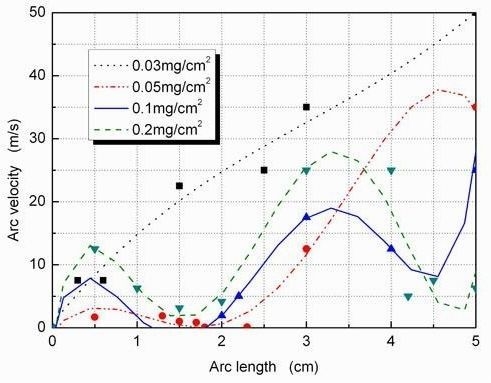
3.3.2. The Arc Velocity

4. Test Specimens, Setups and Procedures
4.1. Test Specimens and Setups

4.2. Test Procedures
5. Analysis and Discussion

5.1. Arc Velocity


5.2. The Temperature Effect on the Arc Velocity
6. Conclusions
- (1)
- Based on the image method and the collision ionization theory, the electric field of the arc needed to keep moving with different degrees of pollution was calculated.
- (2)
- Considering the electric force stressed on the charged particle in the electric field and the effect of airflow and ambient air on the moving arc, the characteristics of arc velocity along the polluted insulation surface were investigated.
- (3)
- Based on force analysis, a mathematical expression was presented, which allows one to evaluate the propagation velocity of the arc along the polluted surface. Only the physical parameters, such as the degree of pollution, insulation plate length, and critical flashover voltage were offered.
- (4)
- The electric fields of the arc head and arc velocities with degrees of pollution of 0.03, 0.05, 0.1, and 0.2 mg/cm2 were calculated, and an experiment was carried out. At the ESDD of 0.03 mg/cm2, the proposed model was consistent with the experiment. When the ESDD exceeds 0.2 mg/cm2, the airflow caused by thermal buoyancy hindered the arc from moving towards the arc head because of the large current and arc radius, and the reduced arc velocity.
- (5)
- The velocity, which was not a fixed value, changed with the variations in the degree of pollution and the electrode gap. No matter what type of electrode from which the arc developed from, no obvious difference in arc velocity at the same degree of pollution and electrode gap.
Acknowledgments
References
- Subba Reddy, B.; Kumar, U. Enhancement of surface flashover performance of high voltage ceramic discinsulators. J. Mater. Eng. Perform 2011, 20, 24–30. [Google Scholar]
- Su, H.; Jia, Z.; Guan, Z.; Li, L. Mechanism of contaminant accumulation and flashover of insulator in heavily polluted coastal area. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1635–1641. [Google Scholar] [CrossRef]
- El-A Slama, M.; Beroual, A.; Hadi, H. Analytical computation of discharge characteristic constants and critical parameters of flashover of polluted insulators. IEEE Trans. Electr. Insul. 2010, 17, 1764–1771. [Google Scholar]
- Jiang, X.; Yuan, J.; Shu, L.; Zhang, Z.; Hu, J.; Mao, F. Comparison of DC pollution flashover performances of various types of porcelain, glass, and composite insulators. IEEE Trans. Power Deliv. 2008, 23, 1183–1190. [Google Scholar] [CrossRef]
- Dhahbi-Megriche, N.; Beroual, A.; Krähenbühl, L. A new proposal model for flashover of polluted insulators. J. Phys. D: Appl. Phys. 1997, 30, 889–894. [Google Scholar] [CrossRef]
- Waters, R.T.; Haddad, A.; Griffiths, H.; Harid, N.; Sarkar, P. Partial-arc and spark models of the flashover of lightly polluted insulators. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 417–424. [Google Scholar] [CrossRef]
- Gençoglu, M.T.; Cebeci, M. The pollution flashover on high voltage insulators. Electr. Power Syst. Res. 2008, 78, 1914–1921. [Google Scholar] [CrossRef]
- Li, X.; Chen, D.; Wu, Y.; Dai, R. A comparison of the effects of different mixture plasma properties on arc motion. J. Phys. D: Appl. Phys. 2007, 40, 6982–6988. [Google Scholar] [CrossRef]
- Shrzan, K.L.; Moro, F. Concentrated discharges and dry bands on polluted outdoor insulators. IEEE Trans. Power Deliv. 2007, 22, 466–471. [Google Scholar] [CrossRef]
- Balmain, K.G.; Gossland, M.; Reeves, R.D.; Kuller, W.G. Optical measurement of the velocity of dielectric surface arcs. IEEE Trans. Nuclear Sci. 1982, 29, 1615–1617. [Google Scholar] [CrossRef]
- Li, S.; Zhang, R.; Tan, K. Measurement of dynamic potential distribution during the propagation of a local arc along a polluted surface. IEEE Trans. Electr. Insul. 1990, 25, 757–761. [Google Scholar] [CrossRef]
- Larigaldie, S. Mechanisms of spark propagation in ambient air at the surface of a charged dielectric. II. Theoretical modeling. J. Appl. Phys. 1987, 61, 102–108. [Google Scholar] [CrossRef]
- Kotsonis, M.; Ghaemi, S.; Veldhuis, L.; Scarano, F. Measurement of the body force field of plasma actuators. J. Phys. D: Appl. Phys. 2011, 44, 045204. [Google Scholar] [CrossRef]
- Boylett, F.D.A.; Maclean, I.G. The propagation of electric discharges across the surface of an electrolyte. Proc. R. Soc. Lond. A 1971, 324, 469–489. [Google Scholar] [CrossRef]
- Feng, C.; Ma, X. Introduction of Engineering Electromagnetic Field; Higher Education Press: Beijing, China, 2000; pp. 40–43. [Google Scholar]
- Rethfeld, B.; Wendelstorf, J.; Klein, T.; Simon, G. A self-consistent model for the cathode fall region of an electric arc. J. Phys. D: Appl. Phys. 1996, 29, 121–128. [Google Scholar] [CrossRef]
- Li, C.; Zhang, L.; Qian, S. Calorifics; Higher Education Press: Beijing, China, 1978; pp. 111–116. [Google Scholar]
- Yao, Z.; Zhen, X.; Feng, X. Physical Electronics; Xi’an Jiaotong University Press: Xi’an, China, 1991; pp. 145–146. [Google Scholar]
- Li, C.; Zhang, L.; Qian, S. Thermotics; Higher Education Press: Beijing, China, 1978; p. 114. [Google Scholar]
- Li, C.; Fu, B. Application Chemistry Manual; Chemical Industry Express: Beijing, China, 2007; pp. 102–162. [Google Scholar]
- Dai, G. Heat Transfer, 2nd ed.; Higher Education Press: Beijing, China, 1999; pp. 188–206. [Google Scholar]
- Compilation Team of Common Chemistry Handbook. Common Chemistry Handbook; Geological Press: Beijing, China, 1997; pp. 86–87. [Google Scholar]
- Yang, B.; Liu, X.; Dai, Y. High Voltage Technology; Chongqing University Press: Chongqing, China, 2001; p. 5. [Google Scholar]
- Jolly, D.C. Contamination flashover, Part I: Theoretical aspects. IEEE Trans. Appar. Syst. 1972, 91, 2437–2442. [Google Scholar] [CrossRef]
- Fulcheri, L.; Rollier, J.-D.; Gonzalez-Aguilar, J. Design and electrical characterization of a low current-high voltage compact arc plasma torch. Plasma Sources Sci. Technol. 2007, 16, 183–192. [Google Scholar] [CrossRef]
- Benilov, M.S. Understanding and modeling plasma-electrode interaction in high-pressure arc discharges: A review. J. Phys. D: Appl. Phys. 2008, 41, 144001. [Google Scholar] [CrossRef]
- Roth, J.R. Plasma Engineering in Industry: Principles; Institute of Physics Publishing: Bristol, UK, 1995; Volume I, Chapter 10. [Google Scholar]
- Zhang, Z.; Qiao, Z. Viscous Fluid Mechanics; National Defense Industrial Press: Beijing, China, 1989; pp. 1–6. [Google Scholar]
- Wilkins, R. Flashover voltage of high-voltage insulators with uniform surface-pollution films. Proc. Inst. Electr. Eng. 1971, 116, 457–465. [Google Scholar] [CrossRef]
- Aydogmus, Z.; Cebeci, M. A new flashover dynamic model of polluted HV insulators. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 577–584. [Google Scholar] [CrossRef]
- Guan, Z.; Zhang, R. Calculation of dc and ac flashover voltage of polluted insulators. IEEE Trans. Electr. Insul. 1990, 25, 723–729. [Google Scholar] [CrossRef]
- IEC 60507:1991. Artificial pollution tests on high-voltage insulators to be used on dc systems. International Electrotechnical Commission: Geneva, Switzerland, 2008.
- IEEE Standard Techniques for High-Voltage Testing. IEEE Std.-4, 1995. Available online: http://dc317.4shared.com/doc/ETJq1s_H/preview.html (accessed on 21 March 2012).
- Artificial pollution testing of HVDC insulators: Analysis of factors influencing performance. Electra 1992, 140, 98–113.
- Xu, G. The Principle and Application of High-Voltage Circuit Breaker; Tsinghua University Press: Beijing, China, 2000; pp. 287–289. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sima, W.; Guo, F.; Yang, Q.; Yuan, T. Calculation of the Arc Velocity Along the Polluted Surface of Short Glass Plates Considering the Air Effect. Energies 2012, 5, 815-834. https://doi.org/10.3390/en5030815
Sima W, Guo F, Yang Q, Yuan T. Calculation of the Arc Velocity Along the Polluted Surface of Short Glass Plates Considering the Air Effect. Energies. 2012; 5(3):815-834. https://doi.org/10.3390/en5030815
Chicago/Turabian StyleSima, Wenxia, Fusheng Guo, Qing Yang, and Tao Yuan. 2012. "Calculation of the Arc Velocity Along the Polluted Surface of Short Glass Plates Considering the Air Effect" Energies 5, no. 3: 815-834. https://doi.org/10.3390/en5030815
APA StyleSima, W., Guo, F., Yang, Q., & Yuan, T. (2012). Calculation of the Arc Velocity Along the Polluted Surface of Short Glass Plates Considering the Air Effect. Energies, 5(3), 815-834. https://doi.org/10.3390/en5030815