Effect of Smart Rotor Control Using a Deformable Trailing Edge Flap on Load Reduction under Normal and Extreme Turbulence
Abstract
:1. Introduction
2. NREL 5 MW UpWind Reference Wind Turbine Model
| Properties | Parameters |
|---|---|
| Rating | 5 MW |
| Rotor orientation, configuration | Upwind, 3 Blades |
| Basic control | Variable speed, collective pitch |
| Rotor, hub diameter | 126 m, 3 m |
| Hub height | 90 m |
| Cut-in, rated, cut-out wind speed | 3 m/s, 11.4 m/s, 25 m/s |
| Cut-in, rated rotor speed | 6.9 rpm, 12.1 rpm |
3. Aerodynamics of Deformable Trailing Edge Flap
3.1. Aerodynamic Parameters of DTEF



3.2. Unsteadiness Evaluation of DTEF

| Mean wind speed [m/s] | NTM, steady proportion (%) | ETM, steady proportion (%) |
|---|---|---|
| 4 | 96.45 | 97.09 |
| 8 | 97.40 | 97.85 |
| 12 | 99.04 | 99.17 |
| 16 | 99.18 | 99.27 |
| 20 | 99.26 | 99.35 |
| 24 | 99.35 | 99.41 |
4. Smart Rotor Control System Design
4.1. Basic Control Design
4.2. DTEF Control Design

5. Simulation Results and Analysis
5.1. External Conditions for Simulations
| Mean wind speed [m/s] | 4 | 8 | 12 | 16 | 20 | 24 |
|---|---|---|---|---|---|---|
| Turbulence intensity for NTM | 30.1 | 20.3 | 17.0 | 15.4 | 14.4 | 13.8 |
| Turbulence intensity for ETM | 62.7 | 35.0 | 25.8 | 21.2 | 18.4 | 16.5 |
5.2. Effects of Smart Rotor Control on Blades
5.2.1. Normal Turbulence Results

| My1 | ||||||||||||||
| BC | BC + FC | BC + FC + CFC | ||||||||||||
| [m/s] | Std [106 NM] | Std [106 NM] | Reduction std [%] | Reduction DEL [%] | Std [106 NM] | Reduction std [%] | Reduction DEL [%] | |||||||
| 4 | 0.54 | 0.52 | 3.7 | 2.1 | 0.52 | 3.7 | 2.1 | |||||||
| 8 | 1.25 | 1.17 | 6.4 | 10.0 | 1.17 | 6.4 | 10.0 | |||||||
| 12 | 2.08 | 1.89 | 9.1 | 19.0 | 1.81 | 12.9 | 22.8 | |||||||
| 16 | 2.15 | 1.81 | 15.8 | 14.6 | 1.73 | 19.5 | 9.4 | |||||||
| 20 | 2.26 | 1.85 | 18.1 | 19.6 | 1.80 | 20.4 | 19.1 | |||||||
| 24 | 2.58 | 2.20 | 14.7 | 7.8 | 2.18 | 15.5 | 13.6 | |||||||
| BTd1 | ||||||||||||||
| BC | BC + FC | BC + FC + CFC | ||||||||||||
| [m/s] | Std [106 NM] | Std [106 NM] | Reduction [%] | Std [106 NM] | Reduction [%] | |||||||||
| 4 | 0.32 | 0.3 | 6.3 | 0.3 | 6.3 | |||||||||
| 8 | 0.73 | 0.63 | 13.7 | 0.63 | 13.7 | |||||||||
| 12 | 1.29 | 1.15 | 10.9 | 1.11 | 13.9 | |||||||||
| 16 | 1.27 | 1.10 | 13.4 | 1.07 | 15.7 | |||||||||
| 20 | 1.27 | 1.10 | 13.4 | 1.08 | 15.0 | |||||||||
| 24 | 1.44 | 1.31 | 9.0 | 1.30 | 9.7 | |||||||||
5.2.2. Extreme Turbulence Results

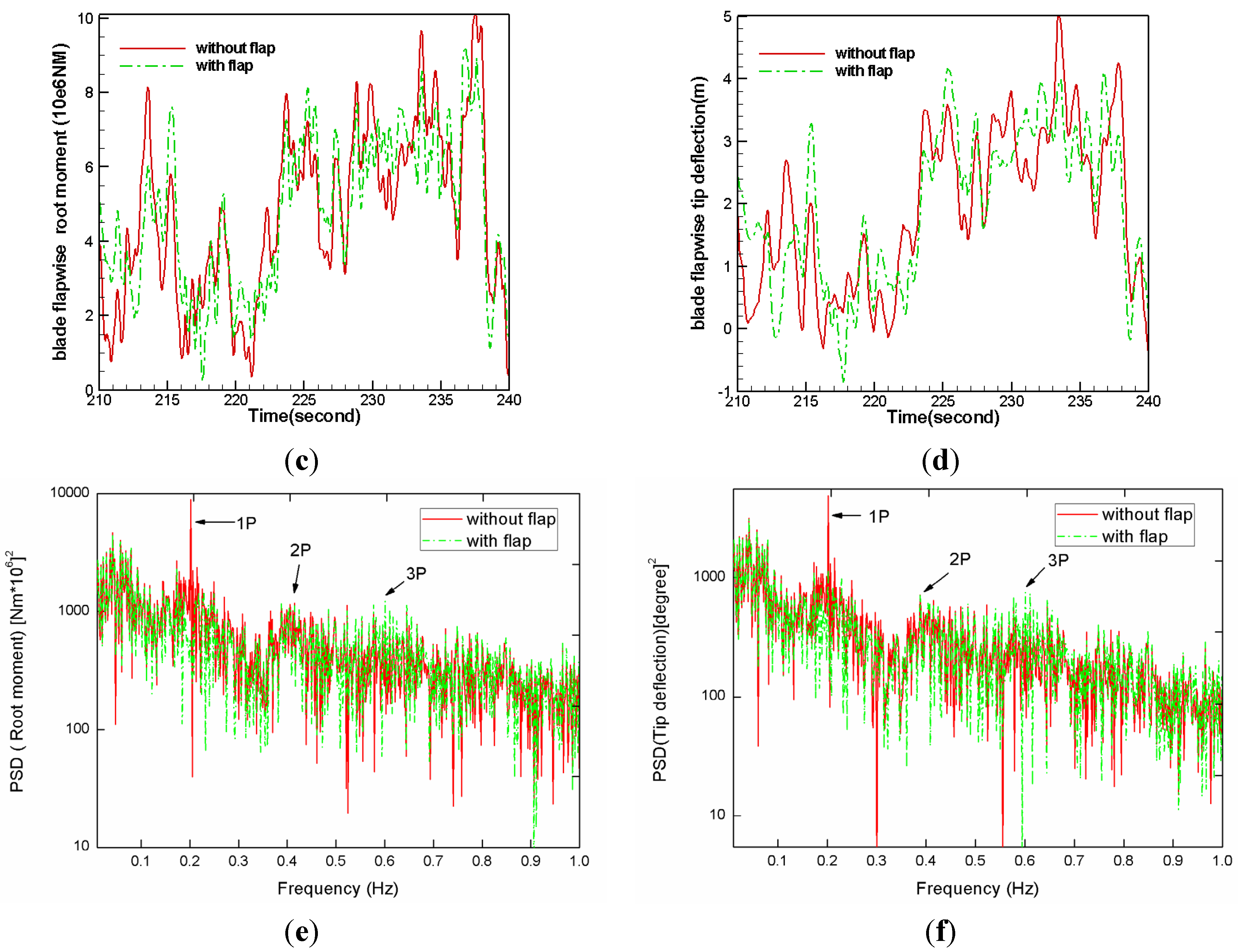
| My1 | ||||||||||||||
| BC | BC + FC | BC + FC + CFC | ||||||||||||
| [m/s] | Std [106 NM] | Std [106 NM] | Reduction std [%] | Reduction DEL [%] | Std [106 NM] | Reduction std [%] | Reduction DEL [%] | |||||||
| 4 | 1.04 | 0.95 | 8.7 | 22.2 | 0.95 | 8.7 | 22.2 | |||||||
| 8 | 2.04 | 1.93 | 5.4 | 13.1 | 1.93 | 5.4 | 13.1 | |||||||
| 12 | 2.52 | 2.31 | 8.3 | 18.6 | 2.23 | 11.5 | 19.6 | |||||||
| 16 | 2.67 | 2.38 | 10.9 | 13.5 | 2.28 | 14.6 | 9.6 | |||||||
| 20 | 2.60 | 2.26 | 13.1 | 17.2 | 2.21 | 15.0 | 19.1 | |||||||
| 24 | 2.82 | 2.48 | 12.1 | 8.5 | 2.46 | 12.8 | 12.0 | |||||||
| BTd1 | ||||||||||||||
| BC | BC + FC | BC + FC + CFC | ||||||||||||
| [m/s] | Std [106 NM] | Std [106 NM] | Reduction [%] | Std [106 NM] | Reduction [%] | |||||||||
| 4 | 0.58 | 0.53 | 8.6 | 0.53 | 8.6 | |||||||||
| 8 | 1.14 | 1.05 | 7.9 | 1.05 | 7.9 | |||||||||
| 12 | 1.53 | 1.39 | 9.2 | 1.36 | 11.1 | |||||||||
| 16 | 1.59 | 1.45 | 8.8 | 1.40 | 11.9 | |||||||||
| 20 | 1.47 | 1.34 | 8.8 | 1.32 | 10.2 | |||||||||
| 24 | 1.59 | 1.47 | 7.5 | 1.47 | 7.5 | |||||||||
5.3. Effects of Smart Rotor Control on Power and Tower Load
| NTM | ||||||
| [m/s] | 4 | 8 | 12 | 16 | 20 | 24 |
| Mean generator power | 1.1 | −5.3 | 0.019 | 0 | 0 | 0.016 |
| FA tower root moment | −1.6 | 1.3 | 1.7 | 3.4 | 5.7 | 5.0 |
| FA tower top deflection | −1.7 | 1.9 | 3.0 | 6.2 | 9.7 | 8.3 |
| ETM | ||||||
| [m/s] | 4 | 8 | 12 | 16 | 20 | 24 |
| Mean generator power | 3.7 | 1.0 | 0.017 | 0.03 | 0 | 0.018 |
| FA tower root moment | −1.0 | 1.0 | 1.3 | 3.2 | 5.7 | 4.8 |
| FA tower top deflection | 0 | 1.8 | 2.8 | 5.8 | 9.8 | 7.8 |
5.4. Effects of Smart Rotor Control on Power and Pitch System Using the Collective DTEF Deployment Angle
| NTM | |||||
| [m/s] | 12 | 16 | 20 | 24 | |
| Pitch Angle Std | FC | 5.8 | 0.5 | −1.0 | −0.4 |
| FC + CFC | 6.1 | 7.8 | 3.7 | 2.5 | |
| Generator power std | FC | 0.1 | 0.1 | −2.7 | −2.9 |
| FC + CFC | 3.2 | 3.0 | 3.2 | 0.4 | |
| ETM | |||||
| [m/s] | 12 | 16 | 20 | 24 | |
| Pitch Angle Std | FC | 1.2 | −0.03 | −1.2 | −0.7 |
| FC + CFC | 5.6 | 5.8 | 3.1 | 2.1 | |
| Generator power std | FC | −0.1 | −0.8 | −2.5 | −3.0 |
| FC + CFC | 0.8 | 2.9 | 3.6 | 0.8 | |

6. Conclusions
- (1)
- A new aero-servo-elastic platform, based on FAST/Aerodyn and Matlab/Simulink codes, was successfully built to implement smart rotor control using DTEF.
- (2)
- Using the newly developed smart rotor control, fluctuating aerodynamic load on blades was effectively reduced under NTM and ETM turbulence conditions. Maximum reduction in flapwise root moment and tip deflection was up to 20.4% and 15.7%, respectively, for NTM, and up to 15.0% and 11.9%, respectively, for ETM.
- (3)
- Load reduction on blades with the smart rotor control system also had positive effect on tower load and power generation.
- (4)
- Adoption of a collective flap angle might assist in reducing power fluctuation and reducing wear on the pitch control system.
Acknowledgments
References
- Musial, M.; Butterfield, S. Energy from offshore wind. In Proceedings of Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006.
- Fichaux, N.; Beurskens, J.; Jensen, P.H.; Wilkes, P. Design Limits and Solutions for Very Large Wind Turbines—A 20 MW Turbine Is Feasible; UpWind Report; European Wind Energy Association: Brussels, Belgium, 2011. [Google Scholar]
- Veers, P.S.; Ashwill, T.D.; Sutherland, H.J.; Laird, D.L.; Lobitz, D. Trends in the design, manufacture and evaluation of wind turbine blades. Wind Energy 2003, 6, 245–259. [Google Scholar] [CrossRef]
- Barlas, T.K.; van Kuik, G.A.M. State of the art and prospectives of smart rotor control for wind turbines. J. Phys. Conf. Ser. 2007, 75, 1–20. [Google Scholar] [CrossRef]
- Collis, S.S.; Joslin, R.D.; Seifert, A.; Theofilis, V. Issues in active flow control: Theory, control, simulation and experiment. Prog. Aerosp. Sci. 2004, 40, 237–289. [Google Scholar] [CrossRef]
- Chopra, I. Review of state of art of smart structures and integrated systems. Am. Inst. Aeronaut. Astronaut. J. 2002, 40, 2145–2187. [Google Scholar] [CrossRef]
- Migliore, P.G.; Quandt, G.A.; Miller, L.S. Wind Turbine Trailing Edge Aerodynamic Brake; NREL/TP—441-7805; Technical Report; NREL: Washington, DC, USA, 1995. [Google Scholar]
- Stuart, J.G.; Wright, A.D.; Butterfield, C.P. Considerations for an Integrated Wind Turbine Controls Capability at the National Wind Technology Center: An Aileron Control Case Study for Power Regulation and Load Mitigation. NREL/TP—440-21335. In Proceedings of American Wind Energy Association (AWEA) Conference, Denver, CO, USA, 23–27 June 1996.
- Barlas, T.K.; van Kuik, G.A.M. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Basualdo, S. Load alleviation on wind turbine blades using variable airfoil geometry. Wind Eng. 2005, 29, 169–182. [Google Scholar] [CrossRef]
- Troldborg, N. Computational study of the Risø-B1-18 airfoil with a hinged flap providing variable trailing edge geometry. Wind Eng. 2005, 29, 89–113. [Google Scholar] [CrossRef]
- Van Wingerden, J.W.; Hulskamp, A.; Barlas, T.; Houzager, I.; Bersee, H.; van Kuik, G.; Verhaegen, M. Two-degree-freedom active vibration control of a prototyped “smart” rotor. IEEE Trans. Control Syst. Technol. 2011, 19, 284–296. [Google Scholar] [CrossRef]
- Hulskamp, A.W.; van Wingerden, J.W.; Barlas, T.; Champliaud, H.; van Kuik, G.A.M.; Bersee, H.E.N.; Verhaegen, M. Design of a scaled wind turbine with a smart rotor for dynamic load control experiments. Wind Energy 2011, 14, 339–354. [Google Scholar] [CrossRef]
- Baek, P. Unsteady Flow Modeling and Experimental Verification of Active Flow Control Concepts for Wind Turbine Blades. Ph.D. Thesis, Technical University of Denmark, Roskilde, Denmark, 2011. [Google Scholar]
- Lackner, M.A.; van Kuik, G. A comparison of smart rotor control approaches using trailing edge flaps and individual pitch control. Wind Energy 2010, 13, 117–134. [Google Scholar] [CrossRef]
- Lackner, M.A.; van Kuik, G. The performance of wind turbine smart rotor control approaches during extreme loads. J. Solar Energy Eng. 2010, 132, 011008:1–011008:8. [Google Scholar] [CrossRef]
- Wilson, D.G.; Berg, D.E.; Barone, M.F.; Berg, J.C.; Resor, B.R.; Lobitz, D.W. Active aerodynamic blade control design for load reduction on large wind turbines. In Proceedings of European Wind Energy Conference & Exhibition, Marseille, France, 16–19 March 2009.
- Wilson, D.G.; Resor, B.R.; Berg, D.E.; Barlas, T.K.; van Kuik, G.A.M. Active aerodynamic blade distributed flap control design procedure for load reduction on the UPWind 5 MW wind turbine. In Proceedings of 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010.
- Andersen, P.B. Advanced Load Alleviation for Wind Turbines Using Adaptive Trailing Edge Flaps: Sensoring and Control. Ph.D. Thesis, Technical University of Denmark, Roskilde, Denmark, 2010. [Google Scholar]
- Jonkman, J.; Buhl, M.L. FAST User’s Guide; NREL/EL-500-29798; Technical Report; NREL: Golden, CO, USA, 2005. [Google Scholar]
- Laino, D.J.; Hansen, A.C. AeroDyn User’s Guide; Technical Report; NREL: Salt Lake City, UT, USA, 2002. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060; Technical Report; NREL: Golden, CO, USA, 2009. [Google Scholar]
- Van Rooij, R.P.J.O.M. Modification of the Boundary Layer Calculation in RFOIL for Improved Airfoil Stall Prediction; Report IW-96087R; Technical Report; Delft University of Technology: Delft, The Netherland, 1996. [Google Scholar]
- Abbott, I.H.; von Doenhoff, A.E. Theory of Wind Sections-Including a Summary of Airfoil Data; Dover Publications Inc.: New York, NY, USA, 1959; p. 587. [Google Scholar]
- Kooijman, H.J.T.; Lindenburg, C.; Winkelaar, D.; van der Hooft, E.L. DOWEC 6 MW Pre-Design: Aeroelastic Modelling of the DOWEC 6 MW Pre-Design in PHATAS; DOWEC-F1W2-HJK-01-046/9; Technical Report; Energy Center of the Netherlands: Petten, The Netherlands, 2003. [Google Scholar]
- National Renewable Energy Lab., NWTC Design Codes (AirfoilPrep); NREL: Golden, CO, USA, 2004. Available online: http://wind.nrel.gov/designcodes/preprocessors/airfoilprep/ (accessed on 11 November 2010).
- Johnson, S.J.; van Dam, C.P.; Berg, D.E. Active Load Control Techniques for Wind Turbines; SAND 2008-4809; Technical Report for Sandia National Laboratories: Albuquerque, NM, USA, 2008. [Google Scholar]
- Andersen, P.B.; Gaunaa, M.; Bak, C.; Hansen, M.H. A dynamic stall model for airfoils with deformable trailing edges. Wind Energy 2009, 12, 734–751. [Google Scholar] [CrossRef]
- Gaunaa, M. Unsteady two-dimensional potential-flow model for thin variable geometry airfoils. Wind Energy 2010, 13, 167–192. [Google Scholar] [CrossRef]
- Bir, G. Multiblade coordinate transformation and its application to wind turbine analysis. NREL/CP-500-42553. In Proceedings of ASME Wind Energy Symposium, Reno, NV, USA, 7–10 January 2008.
- Van Engelen, T.G.; van def Hooft, E.L. Individual Pitch Control Inventory; ECN Report No. ECN-C-03-138; ECN Windenergie: Petten, The Netherlands, 2005. [Google Scholar]
- Van Engelen, T.G. Design model and load reduction assessment for multi-rotational mode individual pitch control (Higher Harmonics Control). In Proceedings of European Wind Energy Conference & Exhibition, Athens, Greece, 27 February–2 March 2006.
- Bossayni, E.A. Individual blade pitch control for load reduction. Wind Energy 2003, 6, 119–128. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. PID Control: New Identification and Design Methods; Lan Kingstong Publishing Services: Nottingham, UK, 2005. [Google Scholar]
- Wind Turbines—Part 1: Design Requirements; IEC 61400-1 Ed.3; International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Jonkman, B.J. Turbsim User’s Guide; Version 1.50; NREL/TP-500-46198; Technical Report for NREL: Golden, CO, USA, 2009. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yu, W.; Zhang, M.M.; Xu, J.Z. Effect of Smart Rotor Control Using a Deformable Trailing Edge Flap on Load Reduction under Normal and Extreme Turbulence. Energies 2012, 5, 3608-3626. https://doi.org/10.3390/en5093608
Yu W, Zhang MM, Xu JZ. Effect of Smart Rotor Control Using a Deformable Trailing Edge Flap on Load Reduction under Normal and Extreme Turbulence. Energies. 2012; 5(9):3608-3626. https://doi.org/10.3390/en5093608
Chicago/Turabian StyleYu, Wei, Ming Ming Zhang, and Jian Zhong Xu. 2012. "Effect of Smart Rotor Control Using a Deformable Trailing Edge Flap on Load Reduction under Normal and Extreme Turbulence" Energies 5, no. 9: 3608-3626. https://doi.org/10.3390/en5093608
APA StyleYu, W., Zhang, M. M., & Xu, J. Z. (2012). Effect of Smart Rotor Control Using a Deformable Trailing Edge Flap on Load Reduction under Normal and Extreme Turbulence. Energies, 5(9), 3608-3626. https://doi.org/10.3390/en5093608




