Operating Point Optimization of a Hydrogen Fueled Hybrid Solid Oxide Fuel Cell-Steam Turbine (SOFC-ST) Plant

Abstract

This paper presents a hydrogen powered hybrid solid oxide fuel cell-steam turbine (SOFC-ST) system and studies its optimal operating conditions. This type of installation can be very appropriate to complement the intermittent generation of renewable energies, such as wind generation. A dynamic model of an alternative hybrid SOFC-ST configuration that is especially suited to work with hydrogen is developed. The proposed system recuperates the waste heat of the high temperature fuel cell, to feed a bottoming cycle (BC) based on a steam turbine (ST). In order to optimize the behavior and performance of the system, a two-level control structure is proposed. Two controllers have been implemented for the stack temperature and fuel utilization factor. An upper supervisor generates optimal set-points in order to reach a maximal hydrogen efficiency. The simulation results obtained show that the proposed system allows one to reach high efficiencies at rated power levels.

1. Introduction

Distributed generation of electricity is becoming increasingly important within the energy generated worldwide. In particular, Europe nowadays gets approximately 20% of its electricity from renewable energy sources, including 5.3% from wind energy [1], totaling an installed capacity of 106,040 MW by the end of 2012 [2]. In order to continue the development and deployment of renewable energy technologies, the EU adopted in 2009 its Renewable Energy Directive. According to it, 14% of the total electricity consumption of the EU will come from wind energy by 2020.

In particular, wind power provides advantages over other power generation systems, such as non-use of cooling water or the lack of carbon dioxide emissions. However, a high level penetration of wind power in the overall electrical system also causes a series of new problems and challenges to be tackled. One of the disadvantages of wind power is its intermittent nature, which means that the system must have additional generation reserves. To cope with this problem, a combination of wind power generation complemented with hydrogen production (electrolyzer) and fuel cell power generation—a wind-to-hydrogen system—would considerably improve the security of supply to the grid [3,4,5].

In this context, high-temperature solid oxide fuel cell (SOFCs), directly fed with hydrogen, which is supplied by an electrolyzer, seems to be an appropriate fuel cell type to complement the intermittent generation of wind farms. Some of the features of SOFCs are the following:

• Suitable for all sizes, 2 kW to multi-MW [6,7,8,9];
• Compared to low-temperature fuel cells, they can achieve higher electric efficiencies [10,11];
• Compared to other fuel cell technologies, SOFC systems are projected to have the lowest system capital cost [10,12];
• The high operating temperature (typically 1073 to 1323 K for high temperature SOFCs) allows the use of most of the waste heat for co-generation or in bottoming cycles (BCs), increasing in this way its efficiency by over 60% [13]. Besides that, high operating temperature SOFCs, compared to low-temperature ones, allow direct internal processing of fuels;
• Typical response times of SOFCs, on the order of minutes, could be seen as a drawback for their integration in wind farms. However, in the case of grid connected wind farms, there can be no doubt that wind-to-hydrogen systems are a real step toward the attenuation of the intermittent nature of wind power.

The literature presents plenty of models of SOFCs complemented with BCs based on gas turbines (SOFC-GT) fueled with different types of hydrocarbons (e.g., natural gas, methane) [14,15,16,17,18,19,20] or even SOFC-GT-ST [21] or biofuels (alcohols) [22,23]. Although each system has its particular design, it can be said that they have the following common features:

• When fueled with gases different from ${\mathrm{H}}_2$, or even $\mathrm{CO}$, they require a pre-reformer in order to transform the input combustible in a valid fuel for the SOFC, like ${\mathrm{H}}_2$ or $\mathrm{CO}$, and these processes are endothermic;
• In these cases, the anode waste gases are a combination of non-reformed and non-utilized fuels, as ${\mathrm{H}}_2$, ${\mathrm{CH}}_4$, $\mathrm{CO}$, ${\mathrm{CO}}_2$, etc. Usually, non-utilized fuel present in SOFC exhaust gases is combusted in a burner, and given their high output temperature, they are used to feed a gas turbine (GT).

In contrast, less works can be found in the literature regarding hydrogen directly fed SOFC systems. In [24], an exergy analysis is performed in order to explore the effect of current density and temperature for hydrogen and methane fuels. Results show that first and second law efficiencies for hydrogen are $50.97\%$ and $52.8$%; for methane, under the same settings, these efficiencies are $62.19\%$ and $59.96$%, respectively. The performance of SOFCs operating on hydrogen and ethanol has been also compared in [25].

Regarding hybrid systems, in [13], a performance study of a SOFC-GT designed for methane as fuel, when it is operated with non-designed fuels, is carried out. This research work shows that, when the hybrid system operates with hydrogen, the net power output decreases to 70% of the one obtained with methane. In [22], several biofuels—namely methane, ethanol, methanol, hydrogen and ammonia—are evaluated exergetically with respect to their performance at the system level (SOFC-GT) and, also, including system components, like heat exchangers, gas turbine, burner, compressor and the stack. One of the conclusions extracted from this work is that with this system configuration, the hydrogen fed system has the lowest energy efficiency (70%), compared with that of methane (78%), which is the most efficient one.

In general, it has been observed that all hydrogen fueled systems obtain the lowest efficiency compared with other fuels. The main reason is that hydrogen reforming is not necessary and, as consequence, all the heat produced by the exothermic process has to be carried away by increasing the incoming flows. This results in high cathodic flows and, correspondingly, high parasitic losses [13,22,24]. However, given the good prospects of hydrogen as a future universal fuel [26], it seems important to optimize SOFC systems fueled with this gas. These systems have their own peculiarities, namely, a lack of any pre-reformer—as mentioned above—and the composition of residual anode gases, which is a combination of just ${\mathrm{H}}_2$ and water steam, where non-reacted ${\mathrm{H}}_2$ can be easily recycled [27].

This paper aims to present an alternative hybrid system configuration based on an SOFC in order to suit better the characteristics of Hydrogen as a combustible. The key features of the proposed system can be summarized as follows:

• The SOFC is confined in a hot box in order to capture the heat produced during its operation. This high temperature waste heat is recovered by means of a bottoming cycle based on a steam turbine and a synchronous generator. In this way, the proposed system improves the efficiency of the SOFC;
• The proposed system allows an accurate control of temperature, T, of SOFC (even working at part-load) by regulating the fluid flow of the waste heat recovering system. With this solution, optimal operation of the system is achieved and, in addition, increasing SOFC incoming flows is not necessary, which is the usual way for temperature control in several hydrogen fed SOFCs and, also, the main cause of heat losses;
• ${\mathrm{H}}_2$ is recycled from anode residual gases and re-used in the fuel cell; hence, it is possible to work under variable ${\mathrm{H}}_2$ utilization factors, u, and this has been chosen as one of the optimization variables for the proposed system;
• A two level control structure is proposed for the optimal management of the SOFC-ST system. At the upper level, a supervisory controller generates set-points to the lower level ones, in order to achieve optimal fuel efficiency for a given power demand. At the lower levels, SOFC stack temperature and fuel utilization controllers have been developed.

2. Model Description

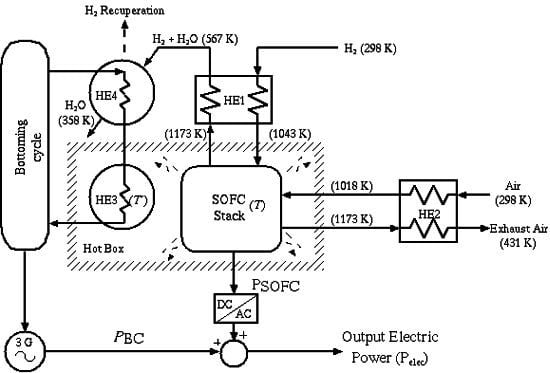
The proposed system (Figure 1) consists of a 120 kW rated thermally insulated SOFC (inside a hot box) plus a BC, which is fed with the waste heat stream extracted from the insulated system. Two counter-flow heat exchangers (HE1 and HE2) preheat the SOFC inputs, namely hydrogen and air. The excess heat from the hot box is extracted through HE3 and is injected to the BC, where the recovered waste heat stream $Q_{\mathrm{BC}}$ is transformed into electric power $P_{\mathrm{BC}}$ by means of a steam turbine (ST) and a synchronous generator.

In addition, the fluid of the BC is pre-heated by another heat exchanger (HE4), which mainly acts as a condenser of the steam leaving the SOFC. In this way, the global system electric power output $P_{\mathrm{elec}}$ is the sum of the electric power given by the SOFC—including the corresponding DC/AC converter—and the electrical power obtained from the bottoming cycle $P_{\mathrm{BC}}$.

The main objective of the SOFC-ST system is the optimal management of all variables in order to achieve the maximum fuel efficiency. For this purpose, a control-oriented dynamic lumped model using fundamental equations of chemical reactions, electrochemistry and thermodynamics has been developed for the SOFC stack. Heat exchangers have been designed by means of the logarithmic mean temperature difference method (LMTD) method, assuming that the stack operates at 1173 K, $0.65$ utilization factor and rated output power. Under any other operating condition, heat exchanger performance has been predicted using the ε-NTUmethod. Finally, the BC is modeled as a first-order dynamic system, and the remaining elements are supposed to be ideal.

This system can be inserted into a renewable generation plant, such as a wind farm, where the hydrogen generated during off-peak hours will source the fuel cell in order to get a more stable generation of the whole hybrid system. All the modeling has been written as a C-MEXS-function and executed from within Matlab-Simulink^®.

Figure 1. The proposed hybrid solid oxide fuel cell-steam turbine (SOFC-ST) system. The figure indicates the design temperatures of gases and steams at different stages of the process.

Figure 1. The proposed hybrid solid oxide fuel cell-steam turbine (SOFC-ST) system. The figure indicates the design temperatures of gases and steams at different stages of the process.

2.1. Model Assumptions

The general considerations and assumptions in the model are:

• The stack is fed with hydrogen and air;
• The system is not pressurized, thus standard pressure has been considered for the anodeand cathode;
• Chemical components, except water, behave as ideal gases at the operating temperatures and pressures of the SOFC-ST system [28];
• All the physical variables are assumed to be uniform over the SOFC [29];
• The gas temperatures within the SOFC are assumed to be the same as the solid; i.e., the thermal inertia of gases is neglected [29];
• The temperature of the SOFC stack is assumed to be unique, and this is the controlled variable, T;
• The temperature at the hot side of HE3 is assumed to be unique, and this is described as $T^{\prime }$ in the thermal model;
• All heat exchangers operate in steady conditions;
• Ancillary supplies, such as compressors and blowers of gases, have not been considered.

2.2. SOFC Electrochemical Model

The electrochemical oxidation of ${\mathrm{H}}_2$ takes place at the anode side according to Equation (1). This reaction requires oxygen ions, which are released by the reduction reaction of ${\mathrm{O}}_2$ taking place at the cathode side of SOFC, Equation (2). Combining the two half reactions, the overall electrochemical reaction can be obtained as shown in Equation (3):

$$\begin{array}{cc}\hfill {\mathrm{H}}_2+{\mathrm{O}}^{2-}& ⟺{\mathrm{H}}_2\mathrm{O}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \frac{1}{2}{\mathrm{O}}_2+2{\mathrm{e}}^{-}& ⟺{\mathrm{O}}^{2-}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\mathrm{H}}_2+\frac{1}{2}{\mathrm{O}}_2+2{\mathrm{e}}^{-}& ⟺{\mathrm{H}}_2\mathrm{O}\hfill \end{array}$$

(3)

The whole process of the formation of water, Equation (3), is entirely exothermic, and its enthalpy of formation is $\Delta \overline{h_f}$ (Table 1). This enthalpy is the heat that would be produced by burning the fuel, and the convention is that it is negative when energy is released [9]. When the product water is considered steam, $\Delta \overline{h_f}$ is known as the lower heating value (LHV). Therefore, to get a good comparison with other fuel-using technologies, the efficiency of fuel cells is usually defined as:

$${\eta }_{\mathrm{SOFC}}=\frac{W_{\mathrm{elec}}}{-\Delta \overline{h_{\mathrm{f}}}}$$

(4)

where $W_{\mathrm{elec}}$ is the electrical energy produced per mol of fuel.

Table 1. Electrochemical parameters.

Parameter	Symbol	Value
Enthalpy of formation (J mol${}^{-1}$)	$\Delta \overline{h_{\mathrm{f}}}$	$-241.83\times {10}^3$
Gibbs free energy at $1,273$ K and std. press.(J mol${}^{-1}$)	$\Delta \overline{g_{\mathrm{f}}}$	$-177.4\times {10}^3$
Faraday constant (C mol${}^{-1}$)	F	96485
Gas constant (J mol${}^{-1}$ K${}^{-1}$)	R	$8.314$

Table 1. Electrochemical parameters.

Parameter	Symbol	Value
Enthalpy of formation (J mol${}^{-1}$)	$\Delta \overline{h_{\mathrm{f}}}$	$-241.83\times {10}^3$
Gibbs free energy at $1,273$ K and std. press.(J mol${}^{-1}$)	$\Delta \overline{g_{\mathrm{f}}}$	$-177.4\times {10}^3$
Faraday constant (C mol${}^{-1}$)	F	96485
Gas constant (J mol${}^{-1}$ K${}^{-1}$)	R	$8.314$

Keeping in mind that the maximum electrical energy available is equal to the change in Gibbs free energy, there is a limit to the efficiency, which is defined by:

$${\eta }_{\max }=\frac{\Delta \overline{g_{\mathrm{f}}}}{\Delta \overline{h_{\mathrm{f}}}}\times 100\%$$

(5)

For instance, at 1273 K and standard pressure ($\Delta \overline{g_{\mathrm{f}}}=-177.4\mathrm{kJ}{\mathrm{mol}}^{-1}$), the maximum efficiency limit of a hydrogen fuel cell, relative to LHV, is $\frac{-177.4}{-241.83}\times 100\%=77.98\%$.

The electromotive force (EMF) or open circuit voltage (OCV) of fuel cells, i.e., the maximum voltage that could be generated, can be calculated based on $\Delta \overline{g_f}$ as follows [9]:

$$E=\frac{-\Delta \overline{g_{\mathrm{f}}}}{2F}$$

(6)

For example, at 1273 K and standard pressure:

$$E=\frac{177.4\times {10}^3[\mathrm{J}/\mathrm{mol}]}{2·96485[\mathrm{C}/\mathrm{mol}]}=0.92\left[\mathrm{V}\right]$$

(7)

The pressure and concentration of reactants affects the Gibbs free energy and, thus, the voltage in Equation (6). This effect is expressed by the Nernst equation, which can be given in many forms. If the water product is in the form of steam, then at standard pressure:

$$E=E^0+\frac{RT}{2F}ln\left(\frac{\frac{P_{{\mathrm{H}}_2}}{P^0}·{\left(\frac{P_{{\mathrm{O}}_2}}{P^0}\right)}^{\frac{1}{2}}}{\frac{P_{{\mathrm{H}}_2\mathrm{O}}}{P^0}}\right)$$

(8)

If all pressures are given in bars, then $P^0=1$ and Equation (8) simplifies to:

$$E=E^0+\frac{RT}{2F}ln\left(\frac{P_{{\mathrm{H}}_2}·{P_{{\mathrm{O}}_2}}^{\frac{1}{2}}}{P_{{\mathrm{H}}_2\mathrm{O}}}\right)$$

(9)

where $P_{{\mathrm{H}}_2}$, $P_{{\mathrm{O}}_2}$ and $P_{{\mathrm{H}}_2\mathrm{O}}$ are partial pressures and $E^0$ is the reference voltage at standard pressure in V calculated as follows [30]:

$$E^0\left(T\right)=1.2723\left[\mathrm{V}\right]-2.7645\times {10}^{-4}[\mathrm{V}/\mathrm{K}]T$$

(10)

where T is the temperature of the SOFC in K.

Equations (6), (8) and (9) are different expressions of OCV. However, when a fuel cell supplies a load, a voltage drop occurs, and the output voltage is a function of electrical current. The voltage/current characteristic for fuel cells results from the Nernst equation and three major irreversibilities, namely, activation, ohmic and concentration polarizations. However, for tubular SOFCs, concentration polarization is negligible [9,30], and it has not been considered in the current model.

2.2.1. Activation Polarization

This is caused by the slowness of reactions taking place on the surface of electrodes. A proportion of the generated voltage is lost in driving the chemical reaction that transfers the electrons to or from the electrode. The Butler-Volmer equation is used to calculate the respective overpotential of anode and cathode; in the context of a fuel-cell, this equation looks like [24,31]:

$${\eta }_{\mathrm{Act}}=\frac{RT}{\beta n_{\mathrm{e}}F}{sinh}^{-1}\left(\frac{i}{2i_0}\right)$$

(11)

where i is the current density through the fuel cell and $i_0$ is the exchange current density, which is obtained as:

$$i_0=Aexp\left(\frac{E_{\mathrm{Act}}}{RT}\right)$$

(12)

and all parameter values are given in Table 2.

2.2.2. Ohmic Polarization

This voltage drop is the straightforward resistance to the flow of electrons through the material and the various interconnections, as well as the resistance to the flow of ions through the electrolyte. This voltage drop obeys Ohm’s law and can be written as:

$${\eta }_{\mathrm{Ohm}}=I{R}_{\mathrm{Ohm}}$$

(13)

where I is the whole current through the fuel cell.

For lumped modeling purposes, a global $R_{\mathrm{Ohm}}$ has been considered for the entire fuel cell, as a function of stack temperature T. This function has been chosen using experimental data given in [30,32], and it is expressed as:

$$R_{\mathrm{Ohm}}=R_{T_0}exp\left(\alpha \left(\frac{1}{T_0}-\frac{1}{T}\right)\right)$$

(14)

Table 2. Designed model operational parameters. SOFC, solid oxide fuel cell; BC, bottoming cycle; HE3, heat exchanger no. 3.

Parameter	Symbol	Value
Pre-exponential factor (kA cm${}^{-2}$)	A	$101.2$
Activation energy of electrochemical reaction (J mol${}^{-1}$)	$E_{\mathrm{Act}}$	$120\times {10}^3$
Coefficient of charge transfer	β	$0.5$
Number of electrons transferred	$n_{\mathrm{e}}$	2
Resistance at $T_0$ temperature (Ω)	$R_{{\mathrm{T}}_0}$	$0.2$
Temperature coefficient (K)	α	$-2870$
Reference temperature (K)	$T_0$	923
Number of cell in series in fuel stack	$N_0$	384
Thermal capacitance of SOFC stack (kJ K${}^{-1}$)	C	450
Thermal capacitance of HE3 (kJ K${}^{-1}$)	$C^{\prime }$	45
Heat transfer thermal resistance (K kW${}^{-1}$)	$R^{\prime }$	$43.65$
Time constant of BC (s)	${\tau }_{\mathrm{BC}}$	100
Energy efficiency of BC	${\eta }_{\mathrm{BC}}$	$0.25$
Energy efficiency of DC/AC converter	${\eta }_{\mathrm{DCAC}}$	$0.95$

Table 2. Designed model operational parameters. SOFC, solid oxide fuel cell; BC, bottoming cycle; HE3, heat exchanger no. 3.

Parameter	Symbol	Value
Pre-exponential factor (kA cm${}^{-2}$)	A	$101.2$
Activation energy of electrochemical reaction (J mol${}^{-1}$)	$E_{\mathrm{Act}}$	$120\times {10}^3$
Coefficient of charge transfer	β	$0.5$
Number of electrons transferred	$n_{\mathrm{e}}$	2
Resistance at $T_0$ temperature (Ω)	$R_{{\mathrm{T}}_0}$	$0.2$
Temperature coefficient (K)	α	$-2870$
Reference temperature (K)	$T_0$	923
Number of cell in series in fuel stack	$N_0$	384
Thermal capacitance of SOFC stack (kJ K${}^{-1}$)	C	450
Thermal capacitance of HE3 (kJ K${}^{-1}$)	$C^{\prime }$	45
Heat transfer thermal resistance (K kW${}^{-1}$)	$R^{\prime }$	$43.65$
Time constant of BC (s)	${\tau }_{\mathrm{BC}}$	100
Energy efficiency of BC	${\eta }_{\mathrm{BC}}$	$0.25$
Energy efficiency of DC/AC converter	${\eta }_{\mathrm{DCAC}}$	$0.95$

2.2.3. Output Voltage of SOFC

According to the previous considerations, the output stack voltage of the modeled system will therefore be:

$$V_{\mathrm{SOFC}}=N_0(E-{\eta }_{\mathrm{Act}})-{\eta }_{\mathrm{Ohm}}$$

(15)

where $N_0$ is the number of cells in series.

2.2.4. Fuel Utilization Factor

The fuel utilization factor of a fuel cell, u, is defined as the ratio between the fuel flow that reacts and the fuel flow injected to the stack. That is to say:

$$u=\frac{({\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}-{\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{out}})}{{\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}}$$

(16)

where ${\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}$ and ${\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{out}}$ are, respectively, the input and output molar flow rates of hydrogen to the fuel stack. Alternatively, it can be shown [28] that u can be expressed in terms of the SOFC current I as follows:

$$u=\frac{2K_{\mathrm{r}}I}{{\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}}$$

(17)

where $K_{\mathrm{r}}$ is a constant defined for modeling purposes whose value is $N_0/4F$ [mol/(s A)].

By means of Equation (17), u can be determined on-line as ${\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}$, and I are deemed readily measurable. Hence, it is possible to continuously track the value of u.

2.3. SOFC Electrochemical Model Validation

Experimental data from the literature [33] have been used to validate the SOFC model. Figure 2 shows the experimental data of cell voltage and power density for different temperatures compared with simulation results obtained from the developed SOFC model. For all current densities, the maximum error is under 5%, but in actual operation, the fuel cell never exceeds a current density of 200 mA/cm${}^2$ (which corresponds with the maximum real power, 120 kW), and in this range, the simulation errors are under 2%, which is perfectly acceptable to ensure the good results of the work.

Figure 2. Comparison between simulation and experimental data of a prototyped $2.2$ cm diameter, 150 cm active length tubular cell at 1173 K, 1213 K and 1273 K fueled with 89% ${\mathrm{H}}_2$ + 11% ${\mathrm{H}}_2\mathrm{O}$, fuel utilization factor of 85%, and air as the oxidant (4 stoichs). (a) Cell voltage vs current density; (b) Power density vs current density.

Figure 2. Comparison between simulation and experimental data of a prototyped $2.2$ cm diameter, 150 cm active length tubular cell at 1173 K, 1213 K and 1273 K fueled with 89% ${\mathrm{H}}_2$ + 11% ${\mathrm{H}}_2\mathrm{O}$, fuel utilization factor of 85%, and air as the oxidant (4 stoichs). (a) Cell voltage vs current density; (b) Power density vs current density.

2.4. Thermal Model of the Hybrid System

The thermal model of the hybrid system depicted in Figure 1 includes the behavior of the SOFC, heat exchangers and the bottoming cycle. It has been assumed that the remaining elements are ideal and do not have heat losses to the surroundings.

2.4.1. SOFC Thermal Model

The research objectives determine the complexity and the dimension of models. In this way, on the one hand, models based on distributed parameters allow a detailed analysis of the geometry and operating conditions of the stack [34,35]. On the other hand, control-oriented lumped models can be found in the literature in which it is assumed that all the SOFC has a unique temperature [36,37,38].

In this work, it has been assumed that the hot box has been designed in order to facilitate a convenient heat transfer between the SOFC (whose temperature is represented by T) and the temperature at the hot side of HE3 (denoted by $T^{\prime }$), which will feed the BC.

The dynamic lumped model of the SOFC stack temperature, T, can be found by performing an energy balance around the entire fuel cell [39,40]:

$$C\frac{dT}{dt}=\sum _{i=1}^n{\dot{n}}_i^{\mathrm{in}}{C}_{p,i}{T}_{\mathrm{in}}-\sum _{i=1}^n{\dot{n}}_i^{\mathrm{out}}{C}_{p,i}T-u·{\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}\Delta \overline{h_{\mathrm{f}}}-P_{\mathrm{SOFC}}-Q_{\mathrm{SOFC}}$$

(18)

where C is the thermal capacitance of stack materials, ${\dot{n}}_i{C}_{p,i}$ are the molar flow heat capacities of input and output flow components, $u·{\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}$—following (16)—represents the molar flow of ${\mathrm{H}}_2$ that effectively reacts inside the SOFC and $T_{\mathrm{in}}$ is the input temperature of the input gases—obtained at each simulation step, after a previous performance evaluation of HE1 and HE2. Additionally, $\Delta \overline{h_{\mathrm{f}}}$ denotes the enthalpy of the formation of reaction (3)—which is a negative value—$P_{\mathrm{SOFC}}$ is the output electric power of the fuel cell and $Q_{\mathrm{SOFC}}$ is the loss heat flow of the SOFC extracted from the hot box through HE3. In order to parametrize the thermal behavior of open-loop system, results from [41] have been considered. All parameter values of the thermal model have been resumed in Table 2.

Since the proposed system has the SOFC thermally insulated, it is necessary to extract the heat produced by the fuel cell ($Q_{\mathrm{SOFC}}$) in order to control its temperature. The corresponding control is designed in Section 4.1.

Figure 3 shows the power distribution of the system under typical operating conditions. The importance of the heat (mainly latent) of the output steam of HE1can be observed. Due to this fact, the BC recovers this heat by means of the condenser, HE4, which is used to pre-heat the thermal fluid flowing through the circuit, HE4-HE3-BC.

Figure 3. Power distribution in the modeled SOFC when working at full load (120 kW), $T=900{}^{\circ }$C, u = 0.80.

Figure 3. Power distribution in the modeled SOFC when working at full load (120 kW), $T=900{}^{\circ }$C, u = 0.80.

2.4.2. Heat Transmission Modeling

In order to model the heat transferred from the SOFC to the BC, an equivalent circuit based on the thermal-electric analogy (as shown in Figure 4) is assumed.

Figure 4. Electric analogous circuit of SOFC-Steam Turbine (ST) heat transmission dynamics.

Figure 4. Electric analogous circuit of SOFC-Steam Turbine (ST) heat transmission dynamics.

In this circuit, the heat flow is analogous to the electrical current, while the temperature is analogous to the voltage. The heat extracted from the SOFC stack (at a temperature, T) is represented by thermal source $Q_{\mathrm{SOFC}}$. All heat transfer mechanisms between the SOFC stack and HE3 are expressed by the thermal resistance, $R^{\prime }$. Condensers at nodes T and $T^{\prime }$ indicate the thermal capacitances of the SOFC stack (C) and heat exchanger HE3 ($C^{\prime }$). Additionally, the heat flow to the BC by the recuperation fluid (having a final temperature, $T^{\prime }$) is represented by the thermal sink $Q_{\mathrm{BC}}$ and, finally, the heat recuperated by means of the condenser HE4 is represented by the thermal source $Q_{Cond}$. Parameter values of the equivalent circuit have been resumed in the Table 2.

Nodal equations of the circuit presented in Figure 4 are given next:

$$\begin{array}{ccc}\hfill Q_{\mathrm{SOFC}}& =& TCp+\frac{T-T^{\prime }}{R^{\prime }}\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill \frac{T-T^{\prime }}{R^{\prime }}+Q_{Cond}& =& Q_{\mathrm{BC}}+T^{\prime }{C}^{\prime }p\hfill \end{array}$$

(20)

From this system of equations, the Laplace transform of the SOFC stack temperature can be calculated as:

$$T\left(p\right)=\frac{Q_{\mathrm{SOFC}}(R^{\prime }{C}^{\prime }p+1)+(Q_{Cond}-Q_{\mathrm{BC}})}{p\left[R^{\prime }C{C}^{\prime }p+(C+C^{\prime })\right]}$$

(21)

and as a consequence, it is possible to obtain:

$${\left.\frac{T\left(p\right)}{Q_{\mathrm{BC}}\left(p\right)}\right|}_{Q_{\mathrm{SOFC}}=0,Q_{Cond}=0}=\frac{-1}{p\left[R^{\prime }C{C}^{\prime }p+(C+C^{\prime })\right]}=G\left(p\right)$$

(22)

where the minus sign denotes that the heat stream to the BC has a negative effect on T. This particular transfer function will be used to design the parameters of the controller presented in Section 4.1.

2.4.3. Heat Exchangers

In the proposed system, four heat exchangers are used to preheat SOFC input gases (HE1, HE2) and to recover the waste heat streams from the SOFC stack (HE3, HE4). When modeling the heat exchangers, it has been assumed that:

• The heat exchanger is well insulated, so that heat loss to the surroundings is negligible and, thus, heat transfer from the hot fluid is equal to the heat transfer to the cold fluid;
• Changes in the kinetic and potential energies of fluid streams are negligible;
• There is no fouling;
• Fluid properties, except heat capacities, are constant.

In the SOFC-ST hybrid system proposed in this work, heat exchangers HE1 and HE2 (Figure 1) are used to preheat ${\mathrm{H}}_2$ and the air, respectively. The logarithmic mean temperature difference method (LMTD) has been used to design these heat exchangers, namely, the overall heat transfer coefficient, U, and the area of the inner surface, $A_{HE}$, assuming $0.85$ thermal effectiveness. These values have been calculated in nominal conditions: SOFC inlet gases at standard temperature and pressure (STP) conditions; SOFC operates at 900 ${}^{\circ }$C; a fuel utilization $u=0.65$ and a nominal value of the current of the SOFC, that is to say, $I=I_{\mathrm{nom}}$.

The enthalpy of gases (${\mathrm{N}}_2$, ${\mathrm{O}}_2$, ${\mathrm{H}}_2$) are supposed to be temperature-dependent and have been calculated with polynomial equations defined in [42]. On the other hand, the water enthalpy up to 1073 K has been calculated based on functions defined by the International Association on Properties of Water and Steam Industrial Formulation [43]; beyond this value, polynomial equations defined in [42] have been used, which means that the calculation of heat exchangers has been iterative.

The condenser, HE4, has been modeled as a heat exchanger with a thermal effectiveness of $0.90$, where the enthalpy of the water is used up to its condensation, so has the output water temperature has been designed at 85 ${}^{\circ }$C.

Once having the design parameters at nominal conditions, to calculate the outlet temperatures of the fluids in each exchanger and the efficiency in any other operating conditions, the ε-NTU method has been used. Taking into account the variability of the heat capacities of the different components, another iterative algorithm has been implemented in the simulation platform, in order to have an updated performance evaluation for each heat exchanger at every simulation step.

2.4.4. Bottoming Cycle Modeling

The modeling of the BC is a simple first order system, whose input is $Q_{\mathrm{BC}}$, and the output is AC electric power:

$$P_{\mathrm{BC}}\left(p\right)=\frac{Q_{\mathrm{BC}}}{p{\tau }_{\mathrm{BC}}+1}·{\eta }_{\mathrm{BC}}$$

(23)

where $P_{\mathrm{BC}}$ is the BC output electric power and ${\eta }_{\mathrm{BC}}$ and ${\tau }_{\mathrm{BC}}$ are, respectively, the energy efficiency [44] and the time constant [45] of the whole BC (heat exchangers, turbine and generator).

Finally, the total electric power of the hybrid SOFC-ST system is:

$$P_{elec}=P_{\mathrm{SOFC}}·{\eta }_{\mathrm{DCAC}}+P_{\mathrm{BC}}$$

(24)

where it has been assumed that the power electronics DC to AC converter has an efficiency of ${\eta }_{\mathrm{DCAC}}=0.95$.

3. Operating Point Analysis

By means of the dynamic model of SOFC-ST developed in the previous section, multiple steady state operating points have been calculated in simulations carried out in the Matlab-Simulink^® environment. In all cases the electric power generated by the SOFC, BC and the hybrid system (SOFC + BC), as well as the global efficiency of the whole system have been analyzed in order to find the optimal operating point of the plant in the function of T and u.

The considered ranges for both variables were as follows:

• T, normal working values between 1073 K and 1323 K;
• u, limited between $0.65$ and $0.85$.

Knowing that a too high operating temperature may degrade the materials and a too low temperature impairs power output [46], temperature limits have been chosen on the basis of the technical information of SOFC [11]. Regarding fuel utilization, this parameter has been fixed by two limits: (1) model assumptions made for the developed dynamic model guarantee good results for $u\ge 0.65$ [28]; (2) overused fuel—if u increases beyond a value ($0.90$), the cells may suffer from fuel starvation and become permanently damaged [47].

3.1. Effect of Temperature

A steady-state analysis has been developed at three constant temperatures, namely, 1073 K, 1173 K and 1273 K for the whole range of working electric current. Figure 5a shows the effect of T (remaining u constant, $u=0.7$) on the output power of SOFC and the output power of BC. On the one hand, for low currents, the maximum $P_{\mathrm{SOFC}}$ is obtained for lower temperatures (1073 K–1173 K); however, as from 250 A, the slope of the 1073 K curve decreases sharply. This loss of power is due to the rise of activation polarization (negative polarization) for lower temperatures. On the other hand, for high current levels (as from 400 A), maximum output power is achieved at 1273 K. The most homogeneous behavior for the whole electric current range is obtained for the case of 1173 K. In the case of the BC, the answer is the opposite, i.e., for lower currents, a better system performance is obtained at higher temperatures and vice versa; for high current intensities, the maximum $P_{\mathrm{BC}}$ is accomplished at 1073 K. This behavior is explained by a reduction of the conversion efficiency of SOFC (more irreversibilities) at reduced temperatures, growing in this way the heat flow of the stack, $Q_{\mathrm{SOFC}}$, and, as a consequence, increasing $P_{\mathrm{BC}}$.

Finally, results obtained for total output power $P_{\mathrm{elec}}$ are also shown in Figure 5a. It can be seen that the negative effect of activation polarizations over SOFC power outputs for lower temperatures is partially offset by a better $P_{\mathrm{BC}}$, and as a result, total output power response is better compared with $P_{\mathrm{SOFC}}$ for lower temperatures. Thus, the $P_{\mathrm{elec}}$ performance of the hybrid system is more homogeneous than $P_{\mathrm{SOFC}}$ regarding temperature. Directly related with the results obtained for $P_{\mathrm{elec}}$, in Figure 5b is displayed the global efficiency for the three temperatures. For low currents (up to 250 A), the best result is for the 1073 K temperature, but as from this point, efficiency decreases sharply. Comparing the two remaining curves (1173 K and 1273 K), a better performance for 1173 K can be observed (almost two points higher for low temperatures), but the difference lowers as the current increases. It can be concluded that the performance of the whole system is better for lower temperatures, but there is a turning point, given the negative effect of activation polarization.

Figure 5. Power output and efficiency of the modeled hybrid system in a range of T between 1073 K and 1273 K ($u=0.70$). (a) Different power outputs of the system vs. current intensity; (b) Efficiency of the system vs. current intensity.

Figure 5. Power output and efficiency of the modeled hybrid system in a range of T between 1073 K and 1273 K ($u=0.70$). (a) Different power outputs of the system vs. current intensity; (b) Efficiency of the system vs. current intensity.

3.2. Effect of Fuel Utilization

Steady-state analysis has been developed at three constant values of u, namely, $0.65$, $0.75$ and $0.85$, for the whole range of working electric current. In Figure 6a, the effect of u can be seen (remaining T constant, $T=1273$ K) on the output power of SOFC and the output power of BC. It can be observed that lowering u produces an increase of $P_{\mathrm{SOFC}}$; this is due to a higher voltage output and, therefore, a decrease of irreversibilities in the SOFC for lower utilization factors. The opposite behavior is observed for $P_{\mathrm{BC}}$. On the one hand, this is a direct consequence of lowering irreversibilities and, thus, reducing $Q_{\mathrm{SOFC}}$, and on the other hand, a lower utilization factor supposes an increased fuel inflow; therefore, the need for more energy to heat it up and the less residual heat to feed the BC. As was the case with lowering temperatures, the negative effect of increasing u is partially offset by the better performance of $P_{\mathrm{BC}}$.

Figure 6. Power output and efficiency of modeled hybrid system in a range of fuel utilization factors between $0.65$ and $0.85$ ($T=1173$ K). (a) Different power outputs of the system vs. current intensity; (b) Efficiency of the system vs. current intensity.

Figure 6. Power output and efficiency of modeled hybrid system in a range of fuel utilization factors between $0.65$ and $0.85$ ($T=1173$ K). (a) Different power outputs of the system vs. current intensity; (b) Efficiency of the system vs. current intensity.

Regarding total output power $P_{\mathrm{elec}}$, also shown in Figure 6a, it can be observed that the best results are obtained for $u=0.65$ for the whole range of currents. This is also reflected in the global efficiencies depicted in Figure 6b for the three values of u. It can be seen that they are three parallel curves. Therefore, it can be concluded that optimal u at analyzed $T=1273$ K, for all ranges of currents, is unique, $u=0.65$.

3.3. Operating Point Optimization

After analyzing the effect of variables T and u, in this section, the optimal operating point has been searched for as the SOFC conditions that lead to the maximal system electric power output per burned Hydrogen fuel unit, that is to say:

$$\underset{T,u}{max}\left(\frac{P_{elec}}{u·{\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}}\right)$$

(25)

where the independent variables are the SOFC temperature, $T\in \left[1073,1323\right]$ K, and the utilization factor, $u\in \left[u_{min},0.85\right]$. In this last expression, $u_{min}$ represents the minimum allowable fuel utilization factor for the SOFC stack, and the constrained optimization problem has been solved three times, for $u_{min}=0.65,0.70,0.75$.

In all cases, the maximum efficiency is obtained with the lower fuel utilization factor. This fact might also be deduced from Figure 6, where the constant u curves are parallel among them.

Figure 7 presents the optimal efficiency vs. the generated power and the corresponding operating conditions of the temperature and fuel utilization factors needed to achieve it. For example, the maximum theoretical efficiency that the SOFC-ST system will have when it generates $120\mathrm{kW}$ is $66\%$ for $u=0.65$ and $T=900{}^{\circ }$C.

Figure 7. Optimal efficiency of the overall system and the optimal SOFC operating temperatures as a function of the minimum allowable fuel utilization factor.

Figure 7. Optimal efficiency of the overall system and the optimal SOFC operating temperatures as a function of the minimum allowable fuel utilization factor.

As regards temperature, it can be observed that maximum efficiencies for the whole range of working currents is obtained for $T\in \left[800,950\right]$ ${}^{\circ }$C. Regarding the fuel utilization factor, it can be also concluded that after decreasing its value by $0.05$, the overall system efficiency increases $0.8$ points and that this involves a 2 K SOFC temperature increase.

The real efficiency value will be affected by the considered model assumptions, such as not taking into account ancillary supplies; however, it must be pointed out that the obtained conclusions for working point optimization, regarding the fuel utilization factor and temperature, are not affected by these assumptions.

4. SOFC Controllers

In view of the obtained results in the optimal operating point analysis, a two-level control structure has been defined for the hybrid system. In the upper level, a supervisory controller, given the electric power that must generate the SOFC-ST, defines optimal operating set-points of T and u in order to optimizeits efficiency.

In order to achieve the optimal set-points, two feedback controllers, one for the SOFC temperature and the other for the control of the fuel utilization, operate at the lower level of the proposed control structure. Simulations have been carried out assuming that the minimum allowable fuel utilization factor for the SOFC is $u_{min}=0.70$.

4.1. Temperature Control of SOFC

In the literature, very complex temperature control strategies have been proposed for traditional non-hydrogen fueled hybrid SOFC-GT systems. In [48], a strategy for changing shaft speed and fuel flow is proposed. In [49], fuel cell temperature is controlled by a bypass valve around the recuperator. By releasing excess heat to the exhaust, the bypass valve provides the control means to avoid the self-exciting behavior of system temperature and stabilizes the temperature. In this way, more complicated control strategies are also found based on adaptive fuzzy controllers [50] or even based on a dynamic radial basis function (RBF) neural network [46].

In the current work, the control of the temperature, T, of the SOFC has been implemented by controlling the heat flowing from the SOFC to the BC. In this control, the manipulable variable is the flow of the thermal fluid through HE4-HE3-BC.

In the controller, the measured SOFC temperature (T) is compared with the reference temperature $T_{\mathrm{Ref}}$, and the difference between them is the input to one proportional-integer (PI) controller—designed by means of the pole assignment method, with set-point weighting—which generates $Q_{BC}$ control inputs that are reached by adapting the flow through HE4 and HE3.

The transfer function of the system, $G\left(p\right)$, is taken from Equation (22). The enthalpies of SOFC input and output streams in Equation (18) have been considered as load disturbances to the thermal model.

Figure 8 presents the behavior of the proposed SOFC stack temperature controller, following optimal references fixed by the supervisory controller. The power reference, as seen in Figure 9, is a power demand change to the SOFC-ST system, from 80 kW to 120 kW, with a slope of $0.2$ kW/s, and a return again to 80 kW after 400 s with the same slope. In Figure 8 (upper), it can be observed how the evolution of the temperature reference for optimal efficiency is related to the power reference, with a rise from 1120 K to 1170 K. The controlled temperature tracks its reference well; at the end of the upslope, there is a small overshooting of less than 10 K, and the reference is achieved again after 200 s. In the same Figure (lower), the recovered heat ($Q_{\mathrm{BC}}$) for the bottoming cycle is shown. It can be seen that when targeted temperature decreases, the recovered heat is maximum, but when temperature is rising, recovered heat flow decreases, until it become zero, and remains there for approximately 200 s. Given that the BC time constant is 100 s, the time required to completely stop the turbine is 400 s; therefore, in the simulated case, the turbine will not stop. Nevertheless, in order to avoid the turbine of BC stopping risk, a secure limit for load rising must be imposed on the system.

Figure 8. Temperature tracking and recovered heat ($Q_{\mathrm{BC}}$) of the developed control for the optimal operating point.

Figure 8. Temperature tracking and recovered heat ($Q_{\mathrm{BC}}$) of the developed control for the optimal operating point.

Figure 9. Power reference to the SOFC-ST system.

Figure 9. Power reference to the SOFC-ST system.

4.2. Fuel Utilization Factor Control

The aim of this control is to keep the SOFC working with a fuel utilization factor, u, which leads to the optimal operation of the SOFC-ST. Based on the electric power that must generate the SOFC, the controller calculates the electric current and, as a consequence—given $u_{\mathrm{ref}}$—the value of the hydrogen injected that is calculated by Equation (17). An input-linearization scheme based on a non-linear digital PI controller with anti-windup guarantees that the electrovalve gives the desired ${\dot{n}}_{{\mathrm{H}}_2}^{\mathrm{in}}$ to the fuel cell.

Figure 10 shows an almost total tracking of u to the reference given by the supervisory controller, that is to say, $u_{ref}=u_{min}=0.70$. In the same Figure (lower), the injected hydrogen flow can be seen.

Figure 10. Utilization factor tracking of the developed control for the optimal operating point.

Figure 10. Utilization factor tracking of the developed control for the optimal operating point.

5. Conclusions

This paper presents a hybrid system SOFC-ST as an alternative to SOFC-GT, usually used for this type of fuel cell. The waste heat stream to the BC is extracted from two heat sources. The first one is the excess heat from the SOFC stack, and the second is the recuperation of the latent heat of the water steam exhausted from the SOFC.

Based on the dynamic model developed for the hybrid system that includes the SOFC, HE, BC and heat transfer phenomena, the effect of temperature and fuel utilization in system behavior has been analyzed. Furthermore, the optimal operating conditions that achieve the maximum efficiency for each electric power to be generated have been defined.

Taking into account the recycling of the non-burned hydrogen, it has been observed that the maximum efficiency is obtained when the utilization factor is minimal. Due to this fact, in order to obtain the optimum performance, only the temperature of the SOFC needs to be adjusted dynamically. For the case of the 120 kW rated SOFC studied in this work, the optimal efficiency under nominal output power is reached when the utilization factor is $0.65$ and the working temperature is $900{}^{\circ }$C.

Finally, the proposed control system has a two-level structure. The lower level control reaches to operate the overall system at the desired operating conditions (namely, the stack temperature and fuel utilization factor). Additionally, the upper level supervisory controller generates set-points to thelow-level ones for an optimal management of the process. After all the proposed arrangements, a maximal hydrogen efficiency is assured.