Formation and Dissociation of Methane Hydrates from Seawater in Consolidated Sand: Mimicking Methane Hydrate Dynamics beneath the Seafloor

Abstract

Methane hydrate formation and dissociation kinetics were investigated in seawater-saturated consolidated Ottawa sand-pack under sub-seafloor conditions to study the influence of effective pressure on formation and dissociation kinetics. To simulate a sub-seafloor environment, the pore-pressure was varied relative to confining pressure in successive experiments. Hydrate formation was achieved by methane charging followed by sediment cooling. The formation of hydrates was delayed with increasing degree of consolidation. Hydrate dissociation by step-wise depressurization was instantaneous, emanating preferentially from the interior of the sand-pack. Pressure drops during dissociation and in situ temperature controlled the degree of endothermic cooling within sediments. In a closed system, the post-depressurization dissociation was succeeded by thermally induced dissociation and pressure-temperature conditions followed theoretical methane-seawater equilibrium conditions and exhibited excess pore pressure governed by the pore diameter. These post-depressurization equilibrium values for the methane hydrates in seawater saturated consolidated sand-pack were used to estimate the enthalpy of dissociation of 55.83 ± 1.41 kJ/mol. These values were found to be lower than those reported in earlier literature for bulk hydrates from seawater (58.84 kJ/mol) and pure water (62.61 kJ/mol) due to excess pore pressure generated within confined sediment system under investigation. However, these observations could be significant in the case of hydrate dissociation in a subseafloor environment where dissociation due to depressurization could result in an instantaneous methane release followed by slow thermally induced dissociation. The excess pore pressure generated during hydrate dissociation could be higher within fine-grained sediments with faults and barriers present in subseafloor settings which could cause shifting in geological layers.

1. Introduction

Methane hydrates remain a fascinating area of research both as a scientific curiosity as well as a potential source of methane, the principle component of natural gas hydrates. Several studies have been performed to investigate methane hydrate growth in porous media. Handa and Stupin [1] reported pressure-temperature (P-T) profiles for the hydrate-ice-gas and hydrate-liquid-water-gas for methane and propane hydrates in 70 Å radius silica gel pores. Under confinement, these pore hydrates were found to be finely dispersed and less stable than bulk hydrate. Uchida et al. [2,3] measured hydrate dissociation conditions in Vycor glass sediment of 100 Å, 300 Å, and 500 Å pores. The hydrate dissociation in pores smaller than 300 Å differed from the dissociation of bulk hydrates. A similar shift in hydrate stability for pore radii between 0.9 Å and 251 Å was observed by Seshadri et al. [4], Anderson et al. [5,6,7] and Ostergaard et al. [8]. Anderson et al. [7] found the equilibrium conditions to be a strong function of pore diameter for methane, carbon dioxide, and methane-carbon dioxide hydrates. Smith et al. [9,10] found higher hydrate equilibrium pressure in silica gel pores of 20, 30, 50 and 75 Å nominal radii than that for bulk hydrates of methane, propane and carbon dioxide.

Madden et al. [11] concluded that methane in the form of free gas bubbles provides additional gas-liquid interface and accelerates hydrate formation within sediments such as Ottawa sand containing Snomax (a nucleation enhancer), Black sand (<500 μm gain size) and permafrost sediments from the Hot Ice-1 GIP, Alaska, AK, USA. Riestenberg et al. [12] also investigated the effect of colloids on the equilibrium conditions for methane hydrate by bubbling methane gas through pure water, 200 mg/L bentonite solution and 34 g/L silica suspension. The hydrate formation pressures were found to be significantly lower for bentonite solution than that for pure water, where dissociation conditions were unchanged by colloids. However, Turner et al. [13] found no equilibrium temperature shift for methane hydrates formed in Adriatic sandstone with an average pore radius of 550 Å. The hydrate equilibrium temperature shift with pore radii was computed to be negligible with radii larger than 600 Å (0.06 µm). This sensitivity analysis assumed the wetting angle of the interface between hydrate crystal and water to be 0° (perfect wetting).

Sun et al. [14] used the multi-step heating dissociation method to determine the stability conditions of methane hydrate formed within 50 cm³ sediments hosting 16 cm³ pore-seawater. Although the sediment sample composed of silty and fine sand (4–250 µm) extracted from the Shenhu region in the South China Sea, sediments were unconsolidated in all measurements. Similarly, Saw et al. [15] performed experiments with synthetic seawater in an autoclave apparatus. They observed a range of dissociation enthalpies depending upon the pressure, temperature, and salinity of the system. Whilst they found that higher temperatures and salinity result in lower dissociation enthalpies, no consolidated sediments were used.

To give an improved basis for predicting actual behavior of hydrates in an oceanic environment, this study investigated the stability of methane hydrates during formation, followed by thermally induced dissociation under sub-seafloor conditions mimicked in a laboratory with natural sand as the host, confining pressure, seawater, and representative P-T conditions. Applying a confining pressure to sediments in these experiments was essential to simulate sub-seafloor conditions under which a majority of methane hydrates are naturally found. Hydrate dissociation was carried out at different temperatures to study the preferential formation/dissociation locations of methane hydrates within the sand-pack, degree of cooling due to their dissociation and equilibrium conditions during dissociation. These equilibrium P-T data were used to compute the enthalpy of dissociation of methane hydrates from consolidated and seawater saturated sand.

2. Experimental

The Flexible Integrated Study of Hydrates (FISH) unit, located at Brookhaven National Laboratory, was used to study sub-seafloor methane hydrate formation and dissociation kinetics in the laboratory setting. In natural environments, sediment porosity decreases due to overburden pressure (compaction) which may affect methane saturation in sub-seafloor hydrate deposits. The accurate representation of such a system will be the application of overburden pressure on a sediment sample. The Temco core holder (Core Laboratories, Houston, TX, USA), used in this study could hold a core sample (maximum 5.1 cm diameter and 15.2 cm length) in a gas impermeable rubber sleeve. The annulus gap around the rubber sleeve was filled with a fluid which applied radial pressure on the sleeve and sample, simulating reservoir overburden pressure. In a typical experiment, dried and weighed Ottawa sand F110 (average grain diameter: 110 µm) obtained from the U.S. Silica Company (Frederick, MD, USA), was loaded into the rubber sleeve after attaching the bottom end-cap assembly and three thermocouples into the main body of the core holder. Three 0.3 cm pressure taps fitted with thermocouples, located at 2.5, 7.6 and 12.7 cm along the sand-pack length were used for temperature measurements at different radial positions (boundary, half-radius and center) within the sand-pack (Figure 1).

Figure 1. Thermocouple arrangement for Temco core sleeve for hydrate formation/dissociation of Experiments 1–6 with seawater which are shown below.

Figure 1. Thermocouple arrangement for Temco core sleeve for hydrate formation/dissociation of Experiments 1–6 with seawater which are shown below.

Two porous plastic filters (GenPore, Reading, PA, USA, 5.1 cm diameter, 0.6 cm thickness) with 50 µm average pore diameter were placed above and below the sand-pack to avoid sand entry into fluid lines. The specifications the core holder and sediments properties are summarized in Table 1. For the present F110 Ottawa sand system with 38.67% porosity, 110 µm average grain diameter and 10.44 MPa confining pressure, Kozeny’s equation [16] and empirical relation by Hogentogler and Barber [17] yield the pore diameters as 46.23 µm and 58.65 µm, respectively.

Table 1. Specifications of core holder and properties of sand-pack.

Core holder	Core holder type	Temco DCHR-2.0 (Core Laboratories, Houston, TX, USA)
	Core holder volume	308.9 cm3
	Core diameter	5.1 cm
	Core length	15.2 cm
	Temperature ports	3 (at 2.5, 7.6 and 12.7 cm)
Sediment	Sediment type	520.34 g of Ottawa Sand F110 (Average grain diameter—110 μm)
	Sediment bulk density	1.625 g/cm3
	Volume of filters	12 cm3
	Volume of sand	296 cm3
	Mass of sand packed	520.34 g
	Sediment packing density	1.728 g/cm3
	Sediment porosity	38.67%
	Seawater salinity	28.05%
	Seawater saturation	≈100%

Table 1. Specifications of core holder and properties of sand-pack.

Core holder	Core holder type	Temco DCHR-2.0 (Core Laboratories, Houston, TX, USA)
	Core holder volume	308.9 cm3
	Core diameter	5.1 cm
	Core length	15.2 cm
	Temperature ports	3 (at 2.5, 7.6 and 12.7 cm)
Sediment	Sediment type	520.34 g of Ottawa Sand F110 (Average grain diameter—110 μm)
	Sediment bulk density	1.625 g/cm3
	Volume of filters	12 cm3
	Volume of sand	296 cm3
	Mass of sand packed	520.34 g
	Sediment packing density	1.728 g/cm3
	Sediment porosity	38.67%
	Seawater salinity	28.05%
	Seawater saturation	≈100%

Once the desired confining pressure equilibrated in about 12 h, seawater sampled from the Long Island Sound was charged into the sand-pack through the line extending from the bottom distributor until multiple pore volume of seawater flowed out of the top distributor to ensure 100% water saturation within sand-pack. The salinity of this filtered seawater was determined using a titration method at 28.05%. Methane of 99.99% purity was charged at a controlled flow rate (<2000 cm³/min) until a desired pore pressure was established. Methane charging was followed by cooling the cell down to the experimental temperature at constant rate (1.5 K/h) with a water bath surrounding the entire core-holder. Hydrate formation was continued until pore pressure reached a constant value, hydrate equilibrium pressure. During dissociation, the cell was depressurized, in 0.69–1.38 MPa increments, till the pressure was totally relieved. Each depressurization event resulted in sediment cooling caused by the endothermic dissociation of hydrates. During each depressurization event and once gas (methane) evolution ceased (8–10 s), the system outlet valve was closed and the sediments were allowed to warm up to the experimental temperature. This allowed initiating successive depressurization events at a constant temperature. The cell pressure, confining pressure and three thermocouple responses were monitored throughout the experiment with a Labview interface. The constant confining pressure was applied on the sand-pack throughout the experiment. Experimental confining pressure and sand-pack P-T conditions used in the hydrate formation events and successive pressure drops employed during dissociation are listed in Table 2.

Table 2. Summary of operating conditions utilized in hydrate formation/dissociation experiments with seawater and methane.

Experiment	Formation conditions		Confining pressure (MPa)	Dissociation pressure drops (MPa)
	P (MPa)	T (K)
1	8.59	277.2	10.44	0.53, 0.58, 0.62, 0.51, 0.52, 0.52, 0.52, 0.52, 0.52, 0.52, 0.52, 0.52, 0.54, 0.52, 0.52, 0.52, 0.76
2	9.25	277.2	10.44	0.69, 0.69, 0.92, 0.69, 0.69, 0.69, 0.69, 0.67, 0.72, 0.70, 0.58, 0.71, 0.72, 0.87
3	9.41	277.2	10.44	0.58, 0.69, 0.69, 0.69, 0.69, 0.70, 0.69, 0.70, 0.68, 0.68, 0.69, 0.69, 0.66, 0.92
4	9.06	275.2	10.44	0.74, 0.66, 0.68, 0.64, 0.69, 0.68, 0.69, 0.69, 0.68, 0.71, 0.68, 0.69, 0.70, 0.68, 0.70, 0.87
5	9.27	279.2	10.44	0.59, 0.73, 0.69, 0.70, 0.69, 0.70, 0.75, 0.70, 0.71, 0.71, 0.70, 0.65, 0.70, 0.70, 0.69, 0.70, 0.70, 0.65, 0.89
6	9.27	281.2	10.44	0.70, 0.70, 0.70, 0.70, 0.70, 0.70, 0.70, 0.72, 0.72, 0.70, 0.71, 0.76, 0.68, 0.90

Table 2. Summary of operating conditions utilized in hydrate formation/dissociation experiments with seawater and methane.

Experiment	Formation conditions		Confining pressure (MPa)	Dissociation pressure drops (MPa)
	P (MPa)	T (K)
1	8.59	277.2	10.44	0.53, 0.58, 0.62, 0.51, 0.52, 0.52, 0.52, 0.52, 0.52, 0.52, 0.52, 0.52, 0.54, 0.52, 0.52, 0.52, 0.76
2	9.25	277.2	10.44	0.69, 0.69, 0.92, 0.69, 0.69, 0.69, 0.69, 0.67, 0.72, 0.70, 0.58, 0.71, 0.72, 0.87
3	9.41	277.2	10.44	0.58, 0.69, 0.69, 0.69, 0.69, 0.70, 0.69, 0.70, 0.68, 0.68, 0.69, 0.69, 0.66, 0.92
4	9.06	275.2	10.44	0.74, 0.66, 0.68, 0.64, 0.69, 0.68, 0.69, 0.69, 0.68, 0.71, 0.68, 0.69, 0.70, 0.68, 0.70, 0.87
5	9.27	279.2	10.44	0.59, 0.73, 0.69, 0.70, 0.69, 0.70, 0.75, 0.70, 0.71, 0.71, 0.70, 0.65, 0.70, 0.70, 0.69, 0.70, 0.70, 0.65, 0.89
6	9.27	281.2	10.44	0.70, 0.70, 0.70, 0.70, 0.70, 0.70, 0.70, 0.72, 0.72, 0.70, 0.71, 0.76, 0.68, 0.90

3. Results and Discussions

3.1. Effect of Pore-Pressure/Consolidation on Kinetics of Methane Hydrate Formation

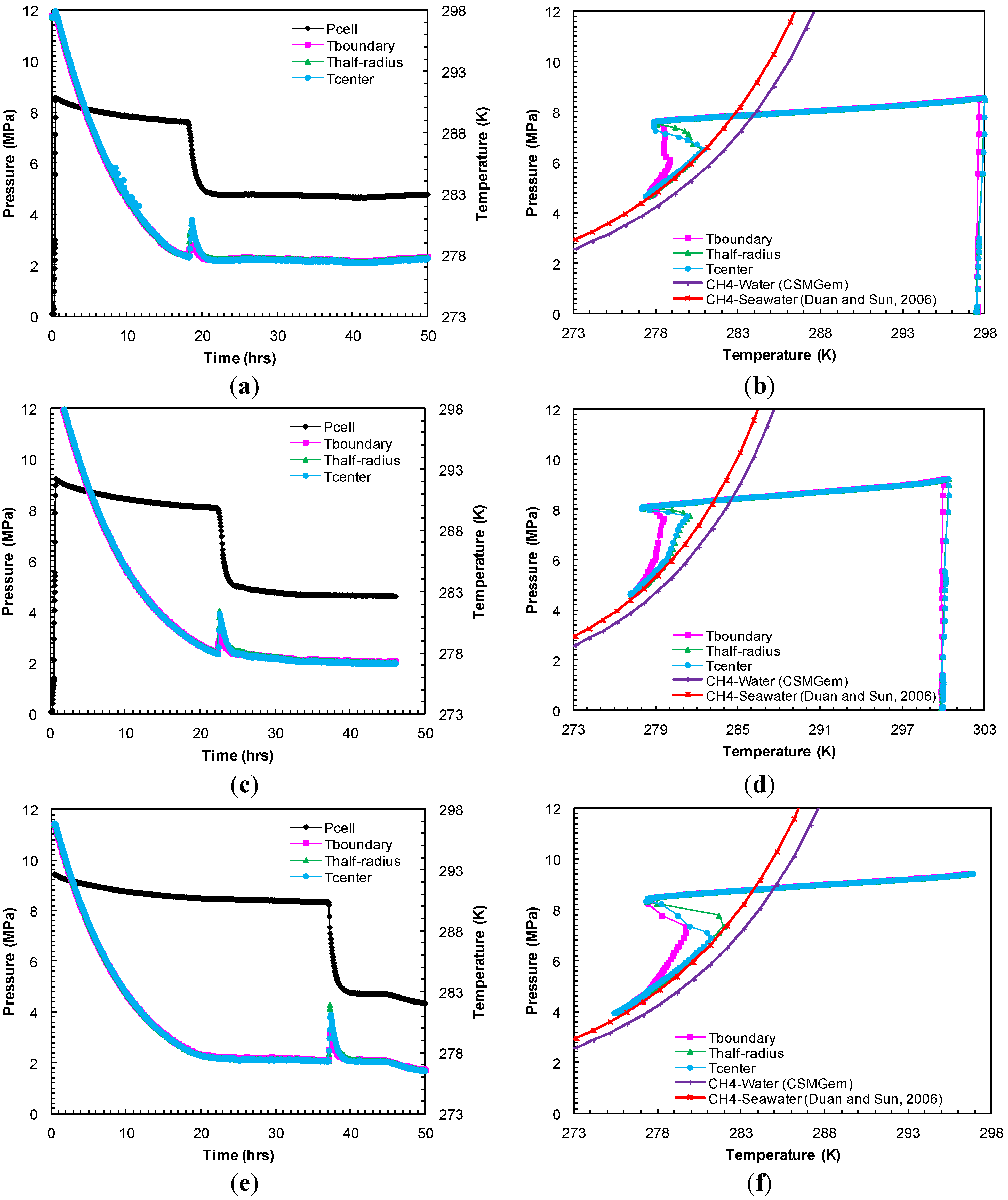
A set of experiments (Experiments 1–3) were performed under a constant confining pressure of 10.4 MPa and a sediment temperature of 277.2 K. However, the methane charging pressure (pore pressure) was varied to study hydrate formation kinetics at different effective pressures that are defined as the difference between the confining pressure and pore pressure. In Experiment 1, under an effective pressure of 1.9 MPa, the sediment cooling lowered the system pressure gradually (Figure 2a). After 8.8 h of cooling, the P-T values of the system entered the hydrate stability region (Figure 2b). However, hydrate formation was observed after 18.2 h of cooling i.e., 9.4 h after the system entered into the hydrate stability region. Hydrate formation was initially accompanied by a temperature spike in all thermocouple readings due to the exothermic nature of hydrate formation and a pressure drop due to methane consumption. Subsequently, the pore pressure reached a constant value, an equilibrium pressure of 4.8 MPa at a temperature of 277.6 K after 22 h (Figure 2a). This can also be discerned from Figure 2b where the system P-T conditions followed the methane-seawater (33%) equilibrium curve from Duan and Sun [18]. In Experiment 2, with methane charging pressure set at 9.2 MPa, the system P-T conditions entered the hydrate stability region after 10.5 h of cooling (Figure 2c). However, the hydrate formation initiated at 22.4 h, i.e., 11.9 h after the system P-T conditions entered the hydrate stability region. Consequently, the system P-T reached equilibrium conditions: 4.7 MPa at 277.5 K, for the methane-seawater system as shown in Figure 2d. For the 9.5 MPa charging (Experiment 3), the hydrate formation began to appear at 37.1 h, i.e., 29.3 h after the system entered into the hydrate stability region at 7.9 h in Figure 2e. Figure 2f shows the system P-T conditions which follow the theoretical methane-seawater equilibrium values: 4.7 MPa at 277.4 K at the end of the formation event in Experiment 3.

Figure 2. (a,c,e) Cell pressure/temperatures against time during methane charging and subsequent hydrate formation in Experiments 1–3; (b,d,f) Comparison of cell pressure against temperature within sand-pack during hydrate formation in Experiments 1–3 with the seawater-bulk methane hydrate stability curve.

Figure 2. (a,c,e) Cell pressure/temperatures against time during methane charging and subsequent hydrate formation in Experiments 1–3; (b,d,f) Comparison of cell pressure against temperature within sand-pack during hydrate formation in Experiments 1–3 with the seawater-bulk methane hydrate stability curve.

Table 3 compares hydrate formation time measured after the system P-T conditions entered the methane hydrate-seawater stability regions for Experiments 1–3. The effective stress is inversely related to the coefficient of compression (compression index) [19]. Hence, as the effective stress decreases, the coefficient of compression increases with the degree of consolidation. Table 3 shows that the hydrate formation event was delayed with increasing pore pressure or consolidation in Experiments 1–3. This is consistent with Kleinberg et al. [20] who studied the hydrate formation kinetics under sub-seafloor conditions mimicked in the 5.1 cm diameter and 30 cm long Berea sandstone. Yousif and Sloan [21] also performed similar experiments with lower permeability (8.388 × 10⁻² μm²). Berea sandstone with mean pore radius of 3.5 µm at effective pressure of 1 MPa where long formation time (40 h) was observed, followed by slow growth of hydrates in the pore space. In the most permeable Berea sandstone core, no hydrate formation was seen until the first hour and a slow accumulation thereafter over the next 5 h.

Table 3. Summary of the effect of pore-pressure/consolidation on the kinetics of methane hydrate formation Experiments 1–3 at a constant confining pressure and cooling rate. Note: Time for hydrate formation is reported after system pressure-temperature entered into hydrate stability region.

Experiment	Pore pressure (MPa)	Confining pressure (MPa)	Effective pressure (MPa)	Time for hydrate formation (h)
1	8.59	10.44	1.95	9.39
2	9.25	10.44	1.29	11.86
3	9.54	10.44	1.01	29.27

Table 3. Summary of the effect of pore-pressure/consolidation on the kinetics of methane hydrate formation Experiments 1–3 at a constant confining pressure and cooling rate. Note: Time for hydrate formation is reported after system pressure-temperature entered into hydrate stability region.

Experiment	Pore pressure (MPa)	Confining pressure (MPa)	Effective pressure (MPa)	Time for hydrate formation (h)
1	8.59	10.44	1.95	9.39
2	9.25	10.44	1.29	11.86
3	9.54	10.44	1.01	29.27

3.2. Kinetics of Dissociation of Methane Hydrates by Step-wise Depressurization at a Constant Temperature

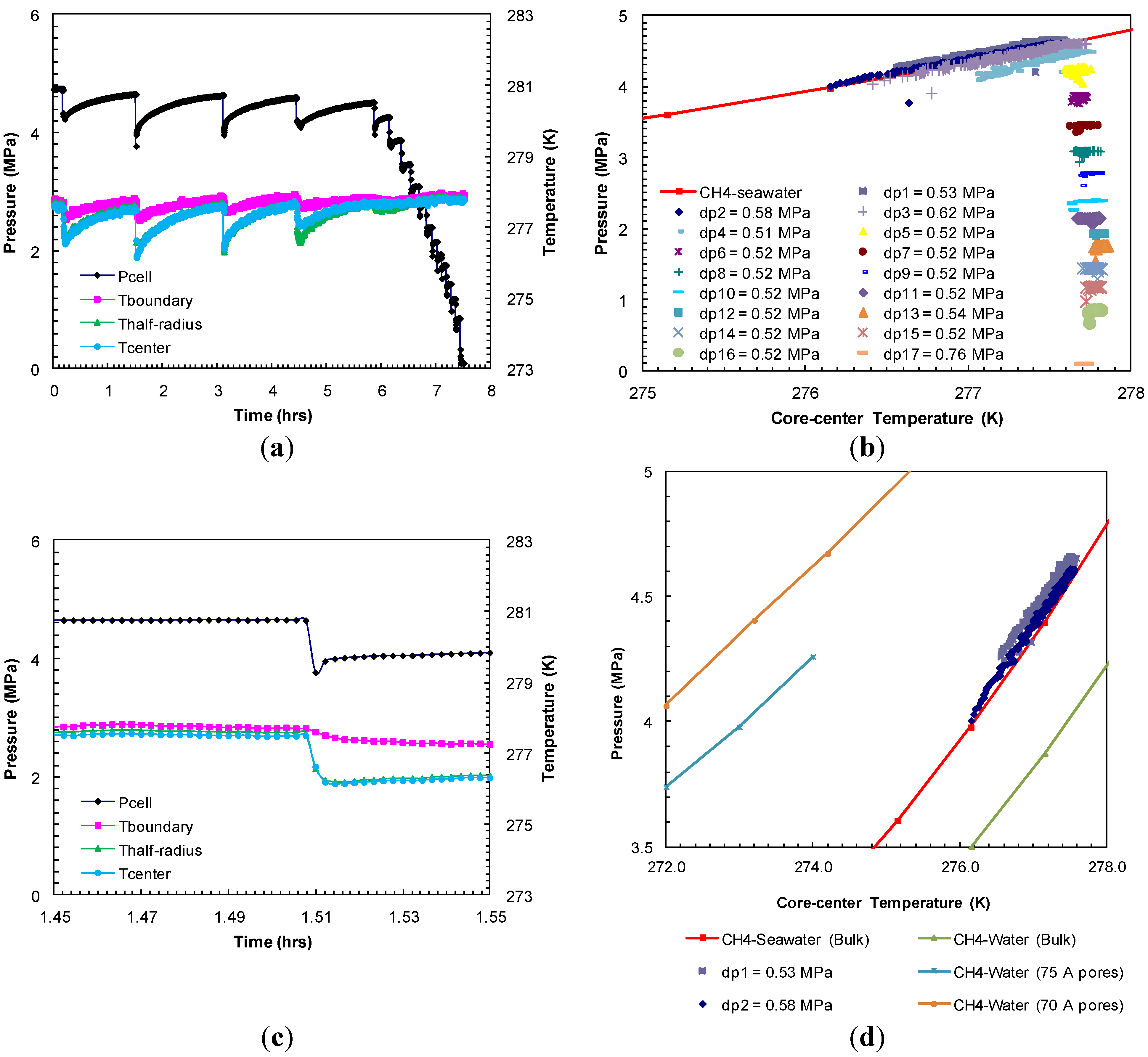
The dissociation of formed methane hydrates was achieved through a step-wise depressurization from the hydrate equilibrium pressure at the set bath temperature. The entire dissociation event from Experiment 1 is shown in Figure 3a. The dissociation at each depressurization step was short lived. As the gas evolved due to depressurization, the sediment temperature dropped due to endothermic hydrate dissociation that accompanies gas expansion. As the gas evolution ceased (in 8–10 s), the cell outlet valve was closed after which the sediments were allowed to warm up to the bath temperature. This allowed for studying the subsequent dissociation at a constant (bath) temperature. The second pressure drop (dp2) of 0.96 MPa resulted in the sediment cooling as low as 276.2 K (Figure 3c). It is evident that the greater the pressure drop during dissociation, higher the degree of cooling and longer time period was observed for sediments to reach the bath temperature. Figure 3b shows each post-depressurization event (dps1–17) P-T conditions during sediment warm-up to the bath temperature. These post-depressurization P-T conditions representing hydrate equilibrium during thermally induced dissociation follow the theoretical pure methane hydrate-seawater P-T stability curve [18] until hydrates were present within the sediments. After the fourth pressure drop (dp4) of 0.5 MPa, all hydrates dissociated completely and the subsequent post-depressurization curves represent methane gas warm-up. Figure 3d compares observed post-depressurization curves for initial pressure drops (dps1 and 2) with P-T stability curves for theoretical pure methane hydrate-seawater (33%) [18], theoretical pure methane hydrate-water [22] and laboratory observations of methane hydrate-water system in 75 Å [1] and 70 Å pores [9]. Clearly, salinity and pore size of the host media significantly affect hydrate stability conditions. The post-depressurization curves for initial pressure drops (dps1 and 2) are slightly shifted towards a higher pressure from the theoretical pure methane hydrate-seawater. This slight shift could be due to the minimal excess pore pressure (≈0.1 MPa) generated as a result of confined and well-connected Ottawa sand pores (pore diameter: 46–58 µm) and lower rate of gas hydrate dissociation at hydrate equilibrium P-T conditions. These observations are consistent with theoretical study by Xu and Germanovich [23] where the magnitude of excess pore pressure was found to depend on the sediments pore network and the rate of gas hydrate dissociation.

Figure 3. (a) Cell pressure/temperatures against time during dissociation with sequences of pressure drop and thermally induced dissociation in Experiment 1; (b) Post-depressurization equilibrium pressure against temperature measured at the center of the sand-pack in Experiment 1. Each dataset corresponds to pressure-temperature (P-T) conditions during thermally induced dissociations. Equilibrium conditions of methane hydrates-seawater were obtained from Duan and Sun [18]; (c) Cell pressure/temperatures against time during dissociation at 1.51 h from (a); (d) Post-depressurization (dps1–5) equilibrium pressure against temperature measured at the center of the sand-pack from (b).

Figure 3. (a) Cell pressure/temperatures against time during dissociation with sequences of pressure drop and thermally induced dissociation in Experiment 1; (b) Post-depressurization equilibrium pressure against temperature measured at the center of the sand-pack in Experiment 1. Each dataset corresponds to pressure-temperature (P-T) conditions during thermally induced dissociations. Equilibrium conditions of methane hydrates-seawater were obtained from Duan and Sun [18]; (c) Cell pressure/temperatures against time during dissociation at 1.51 h from (a); (d) Post-depressurization (dps1–5) equilibrium pressure against temperature measured at the center of the sand-pack from (b).

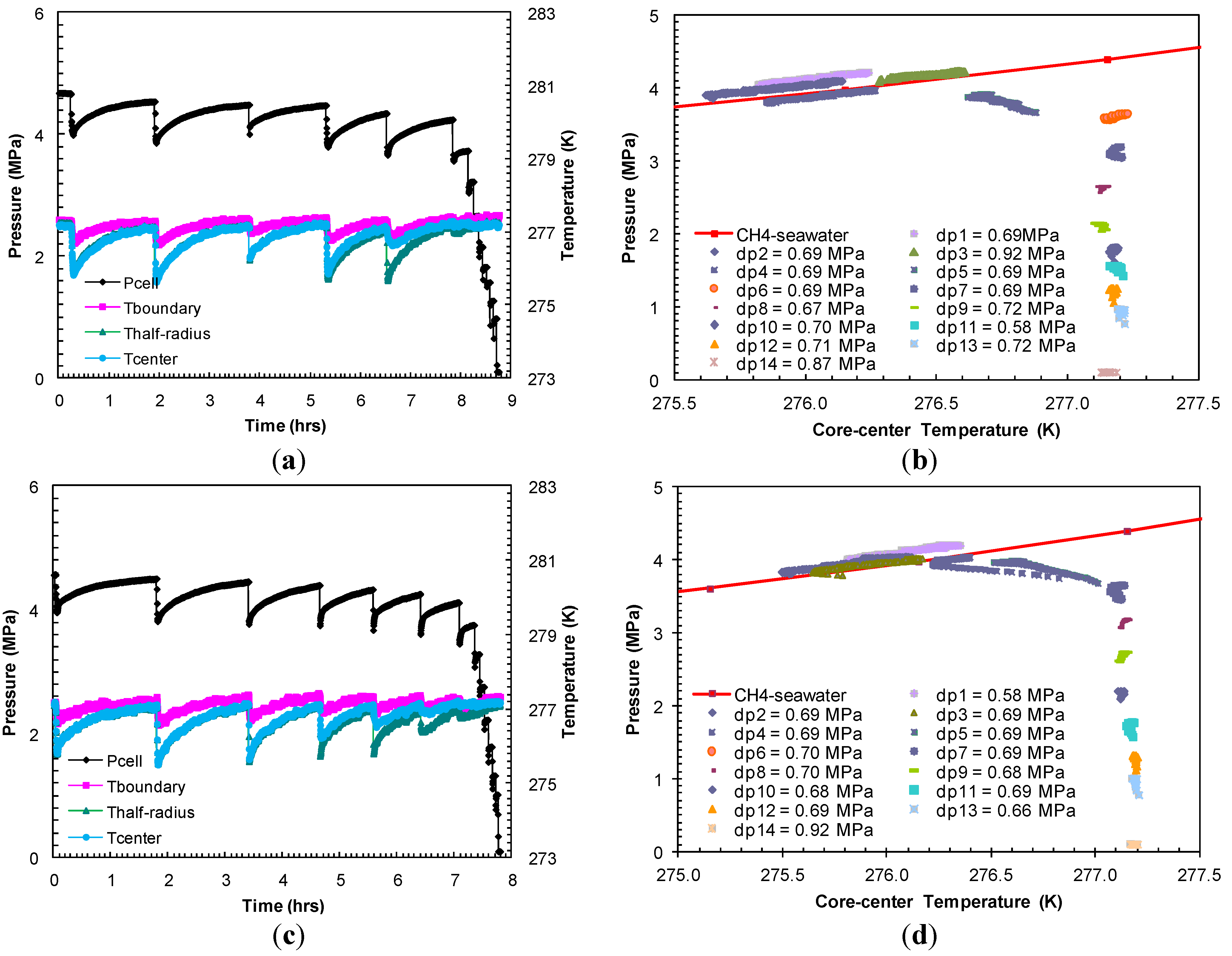
The hydrates formed in Experiment 2 were dissociated with pressure drops (dps1–5) ranging between 0.69 MPa and 0.92 MPa from the equilibrium pressure at a bath temperature of 277.2 K (Figure 4a). The dissociation events shown in Figure 4b indicated that the P-T equilibrium after the first five pressure drops (dps1–5) followed the theoretical P-T stability curve for bulk methane hydrates from seawater with a minimal excess pore pressure. The pressure drops following the first five gas releases did not affect sediment temperature, which confirmed complete hydrate dissociation.

Figure 4. (a,c) Cell pressure/temperatures against time during dissociation with sequences of pressure drop and thermally induced dissociation in Experiments 2 and 3; (b,d) Post-depressurization equilibrium pressure against temperature measured at the center of the sand-pack in Experiments 2 and 3. Each dataset corresponds to P-T conditions during thermally induced dissociations. Equilibrium conditions of methane hydrates-seawater were obtained from Duan and Sun [18].

Figure 4. (a,c) Cell pressure/temperatures against time during dissociation with sequences of pressure drop and thermally induced dissociation in Experiments 2 and 3; (b,d) Post-depressurization equilibrium pressure against temperature measured at the center of the sand-pack in Experiments 2 and 3. Each dataset corresponds to P-T conditions during thermally induced dissociations. Equilibrium conditions of methane hydrates-seawater were obtained from Duan and Sun [18].

In Experiment 3, the dissociation was carried out with a series of pressure drops (dps1–7) 0.61–0.69 MPa from the hydrate equilibrium pressure at the bath temperature (277.2 K) (Figure 4c) attained at the end of the formation event. The post-depressurization P-T equilibrium (Figure 4d) confirms complete hydrate dissociation after the seventh pressure drop (dp7) of 0.70 MPa. With an individual pressure drop of similar order in Experiment 2 (Figure 4b) and Experiment 3 (Figure 4d), the number of pressure drops to dissociate hydrates in Experiment 3 is higher than that required in Experiment 2. This may be due to the higher hydrate saturation in Experiment 3 as a result of an elevated methane charging pressure.

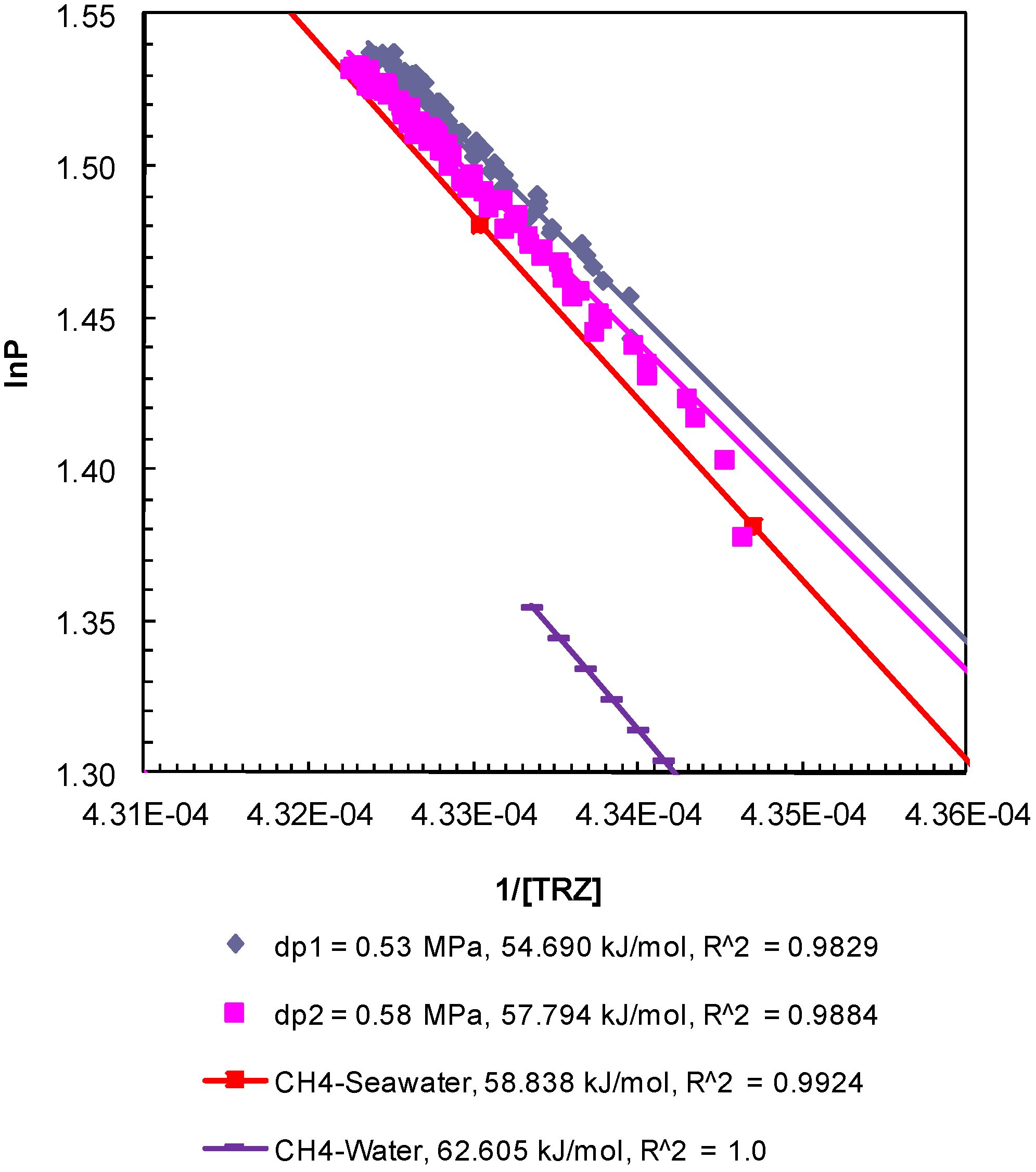
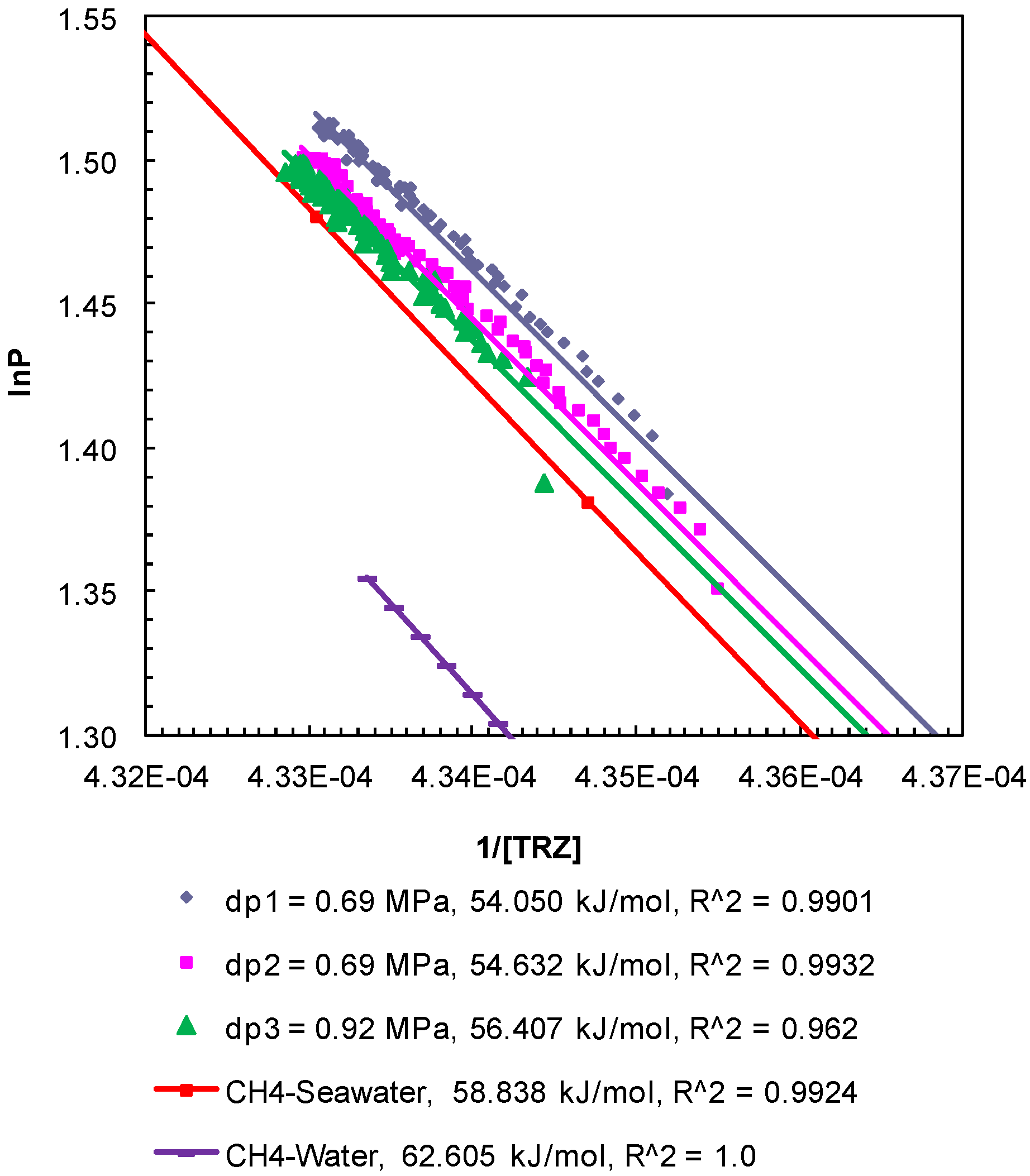
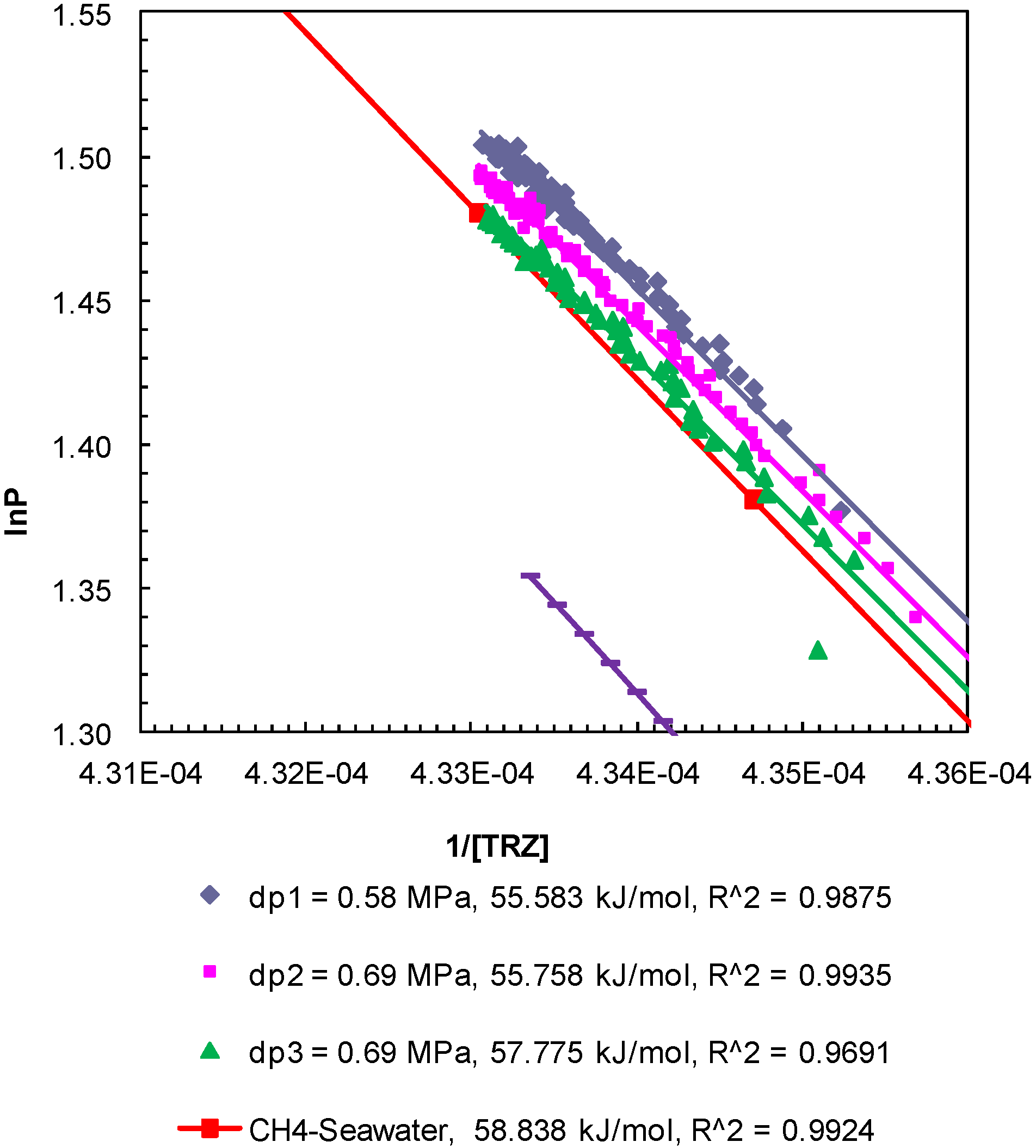
The enthalpy of hydrate dissociation was computed using the Clausius-Clapeyron equation [24] applied to the post-depressurization P-T data from Experiment 1 (Figure 5), Experiment 2 (Figure 6), and Experiment 3 (Figure 7). The slopes of lnP plotted against 1/[TRZ], where P (MPa) is pore pressure; T (K) is sediment temperature; R (8.314 J/mol-K) is universal gas constant; and Z is methane compressibility at P-T conditions, yield values of the enthalpy of dissociation of methane hydrates between 54.50 kJ/mol and 57.79 kJ/mol. The computed values are consistent but lower than those computed from theoretical P-T data for bulk hydrates obtained from CSMGem (Center for Hydrate Research Colorado School of Mines, Golden, Colorado, USA) [22] (62.61 kJ/mol) and that from methane-seawater equilibrium data (58.84 kJ/mol) obtained from Duan and Sun [18]. The enthalpies of dissociation reported from experimental investigations of bulk methane hydrates [25] and carbon dioxide hydrates [26] are 54.44 ± 1.45 and 63.6 ± 1.8 kJ/mol, respectively. The values obtained from the post-depressurization data in this study exhibit conditions such as seawater and excess pore pressure developed during thermally induced dissociation of methane hydrates from Ottawa sand-pack (pore diameter: 46–58 µm) under a confining pressure of 10.44 MPa.

Figure 5. Post-depressurization (dps1 and 2) P-T conditions from Experiment 1 plotted as lnP against 1/[TRZ]. The Clausius-Clapeyron equation was used to calculate the enthalpy of dissociation (∆H_hyd in kJ/mol) of methane hydrates from seawater in porous media at a confining pressure of 10.44 MPa. Equilibrium conditions of bulk methane hydrates-water obtained from CSMGem and those for bulk methane hydrates-seawater obtained from Duan and Sun [18] were used to calculate the theoretical ∆H_hyd. The R² values indicate the correlation coefficient for linear regression performed to compute the slope as ∆H_hyd.

Figure 5. Post-depressurization (dps1 and 2) P-T conditions from Experiment 1 plotted as lnP against 1/[TRZ]. The Clausius-Clapeyron equation was used to calculate the enthalpy of dissociation (∆H_hyd in kJ/mol) of methane hydrates from seawater in porous media at a confining pressure of 10.44 MPa. Equilibrium conditions of bulk methane hydrates-water obtained from CSMGem and those for bulk methane hydrates-seawater obtained from Duan and Sun [18] were used to calculate the theoretical ∆H_hyd. The R² values indicate the correlation coefficient for linear regression performed to compute the slope as ∆H_hyd.

Figure 6. Post-depressurization (dps1–3) P-T conditions from Experiment 2 plotted as lnP against 1/[TRZ]. The Clausius-Clapeyron equation was used to calculate enthalpy of dissociation (∆H_hyd in kJ/mol) of methane hydrates from seawater in porous media at a confining pressure of 10.44 MPa. The R² values indicate the correlation coefficient for linear regression performed to compute the slope as ∆H_hyd.

Figure 6. Post-depressurization (dps1–3) P-T conditions from Experiment 2 plotted as lnP against 1/[TRZ]. The Clausius-Clapeyron equation was used to calculate enthalpy of dissociation (∆H_hyd in kJ/mol) of methane hydrates from seawater in porous media at a confining pressure of 10.44 MPa. The R² values indicate the correlation coefficient for linear regression performed to compute the slope as ∆H_hyd.

Figure 7. Post-depressurization (dps1–3) P-T conditions from Experiment 3 plotted as lnP against 1/[TRZ]. The Clausius-Clapeyron equation was used to calculate enthalpy of dissociation (∆H_hyd in kJ/mol) of methane hydrates from seawater in porous media at a confining pressure of 10.44 MPa. The R² values indicate the correlation coefficient for linear regression performed to compute the slope as ∆H_hyd.

Figure 7. Post-depressurization (dps1–3) P-T conditions from Experiment 3 plotted as lnP against 1/[TRZ]. The Clausius-Clapeyron equation was used to calculate enthalpy of dissociation (∆H_hyd in kJ/mol) of methane hydrates from seawater in porous media at a confining pressure of 10.44 MPa. The R² values indicate the correlation coefficient for linear regression performed to compute the slope as ∆H_hyd.

3.3. Effect of Sediment Temperature on the Kinetics of Dissociation of Methane Hydrates by Step-Wise Depressurization

Experiments 4–6 were also performed with a method similar to the one that was utilized in Experiments 1–3, i.e., the hydrate formation was achieved by a single gradual charging of methane (9.1 MPa) through a completely seawater saturated sand-pack under a confining pressure of 10.4 MPa. However, the cell was cooled down to experimental temperatures of 275.2, 279.2 and 281.2 K in Experiments 4–6, respectively, to investigate the effect of sediment temperature on: (a) the degree of sub-cooling during each depressurization step; (b) the time scale for sediments to warm-up to the bath temperature after each depressurization; and (c) to establish methane hydrate P-T equilibrium in porous media at temperatures even lower and higher than previous Experiments 1–3.

In Experiments 4–6, the dissociation of hydrates was achieved with pressure drops of about 0.69 MPa from the equilibrium pressure for the methane hydrates-seawater system governed by the experimental temperature. In Experiment 4, the endothermic cooling responses observed at all thermocouples reading for the first nine pressure drops (dps1–9) at cell temperature (275.2 K) confirmed complete hydrate dissociation in the system (Figure 8a). The presence of hydrates until the ninth pressure drop of 0.68 MPa is also confirmed by the post-depressurization P-T shown in Figure 8b where the plots for dps1–9 follow the theoretical methane-seawater P-T curve [18].

In Experiment 5, the dissociating pressure drops were on the order of about 0.69 MPa from the equilibrium pressure (5.55 MPa) at a cell temperature of 279.2 K. After about ten pressure drops (dps1–10), all hydrates appear to have dissociated since the cell pressure did not come back to the hydrate equilibrium pressure and no endothermic cooling was observed within the sand-pack (Figure 9c,d).

Experiment 6 involved methane charging pressure of 9.27 MPa and an experimental temperature of 281.2 K. The system attained P-T conditions of 8.66 MPa and 283.6 K after 8.7 h of cooling to enter the hydrate-seawater stability region. However no apparent signs of hydrate formation (sudden pressure drop or exothermic temperature profiles) were observed at the end of 140 h with the system P-T conditions of 7.48 MPa and 281.2 K. Subsequently, the dissociation was achieved with a series of pressure drops of 0.69 MPa. Figure 8e shows system the P-T data against time during the entire event of dissociation. Figure 8f compares the recorded system P-T with a methane-seawater equilibrium curve data. Figure 8e shows that no endothermic cooling was recorded by any of the system thermocouples during the entire dissociation event, which confirms negligible hydrate formation in the system.

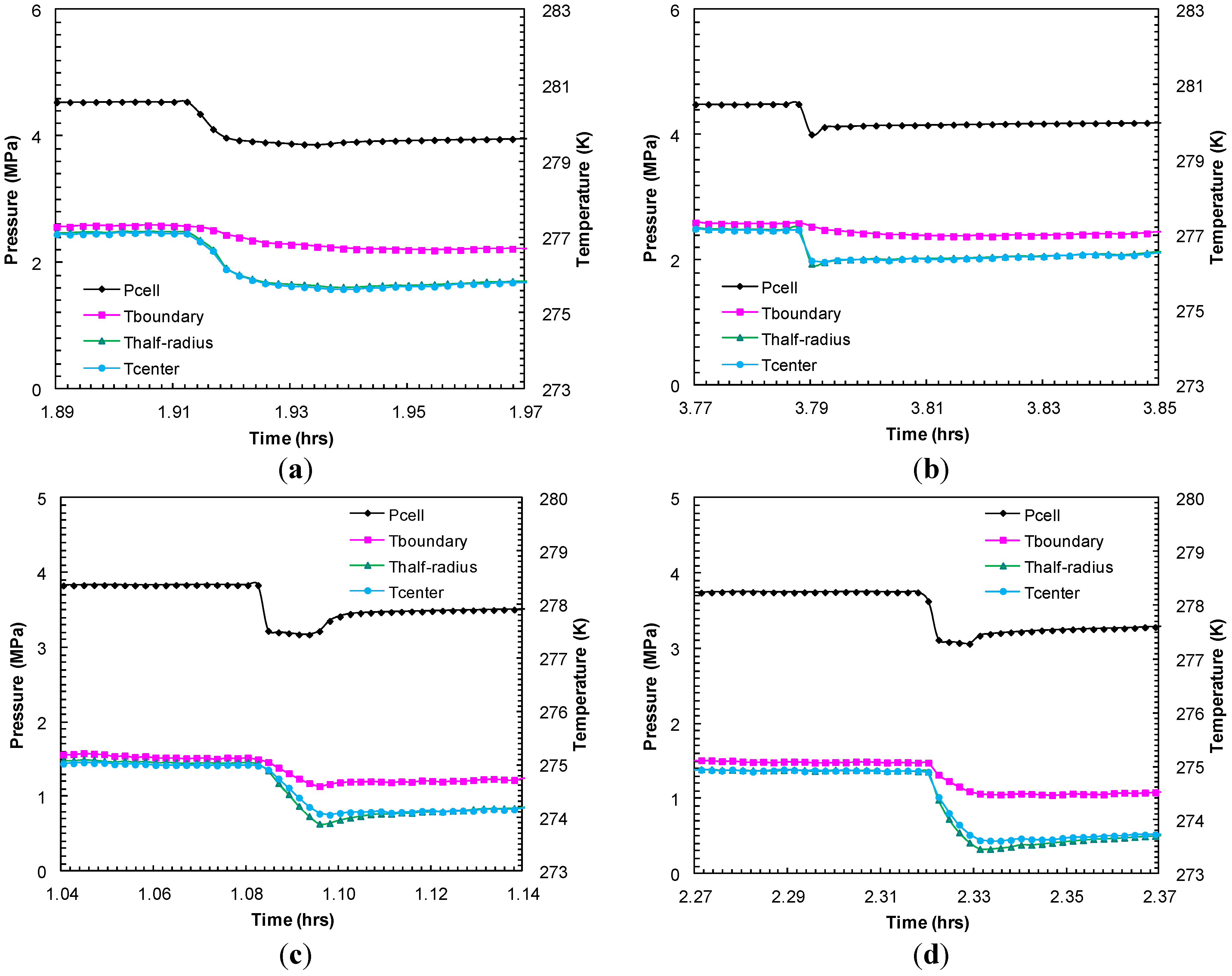
Figure 9 compares the thermocouple responses during short-lived dissociations at similar pressure drops from Experiments 2 and 4 in order to examine the preferential hydrate dissociation due to depressurization. The endothermic effect due to hydrate dissociation was recorded with a higher degree of cooling at the center than at the half-radius and the boundary of the sand-pack. Although the degree of cooling at the sand-pack boundary could be controlled by heat transfer between the core holder and the surrounding water bath maintained at a constant temperature, a higher degree of cooling observed at the center of the sand-pack may be due to hydrates predominantly formed within/dissociated from the interior part of the sand-pack. However, as expected, during thermally induced dissociation, the sand-pack boundary warmed at a faster rate than the sand-pack interior.

Figure 8. (a,c,e) Cell P-T against time during dissociation with sequences of pressure drop and thermally induced dissociation in Experiments 4–6; (b,d,f) Post-depressurization equilibrium pressure against temperature measured at the center of the sand-pack in Experiments 4–6. Each dataset corresponds to P-T conditions during thermally induced dissociations. Equilibrium conditions of methane hydrates-seawater were obtained from Duan and Sun [18].

Figure 8. (a,c,e) Cell P-T against time during dissociation with sequences of pressure drop and thermally induced dissociation in Experiments 4–6; (b,d,f) Post-depressurization equilibrium pressure against temperature measured at the center of the sand-pack in Experiments 4–6. Each dataset corresponds to P-T conditions during thermally induced dissociations. Equilibrium conditions of methane hydrates-seawater were obtained from Duan and Sun [18].

Figure 9. Thermocouple responses at various locations within sand-pack (center, half radius, sand-pack boundary) during dissociation with successive pressure drops: (a) dp2 = 0.69 MPa; and (b) dp3 = 0.92 MPa from Experiment 2; (c) dp2 = 0.66 MPa; and (d) dp3 = 0.68 MPa from Experiment 4.

Figure 9. Thermocouple responses at various locations within sand-pack (center, half radius, sand-pack boundary) during dissociation with successive pressure drops: (a) dp2 = 0.69 MPa; and (b) dp3 = 0.92 MPa from Experiment 2; (c) dp2 = 0.66 MPa; and (d) dp3 = 0.68 MPa from Experiment 4.

The data from Experiments 1–3 show that higher pressure drops during the dissociation of hydrates at a constant sediment temperature (277.2 K) caused a larger degree of sediment-cooling. The higher degree of sediment cooling obviously requires a longer time for sediments to reach to the bath temperature. However, the degree of cooling of the sediment was also found to be dependent upon the sediment temperature (Experiments 3–5) for a constant pressure drop. 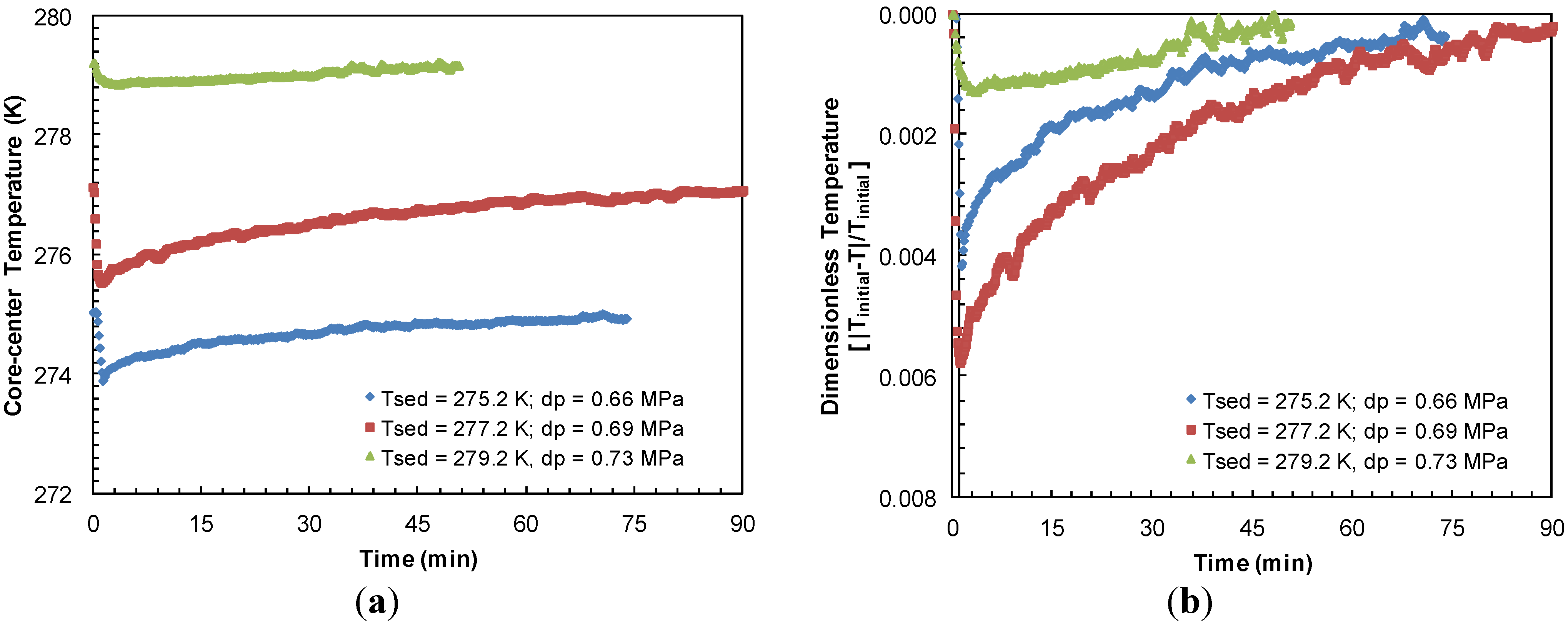Figure 10a compares the sediment cooling and subsequent time for warm-up to the bath temperature from Experiments 3–5 at similar pressure drops. The highest endothermic effect due to hydrate dissociation was observed when sediment temperature dropped to a low of 273.9 K at the center of sand-pack due to a pressure drop of 0.66 MPa below the equilibrium pressure at 275.2 K. Figure 10b depicts the sediment sub-cooling data from Figure 10a on a relative dimensionless scale against time. It appears that a lower sediment temperature causes a higher degree of cooling upon hydrate dissociation and in turn, it takes longer for the system to warm-up to its initial value.

Figure 10. (a) Thermocouple response at half-radius of the sand-pack during dissociation with similar pressure drops below hydrate equilibrium pressure at sediment temperatures of 275.2, 277.2 and 279.2 K in Experiments 4, 3 and 5, respectively; (b) Dimensionless sediment temperature change [|I_nitial-T|/I_nitial] against time for similar pressure drops for dissociation from sediments at 275.2, 277.2, and 279.2 K. Experiments 3–5 were performed at a constant confining pressure of 10.44 MPa.

Figure 10. (a) Thermocouple response at half-radius of the sand-pack during dissociation with similar pressure drops below hydrate equilibrium pressure at sediment temperatures of 275.2, 277.2 and 279.2 K in Experiments 4, 3 and 5, respectively; (b) Dimensionless sediment temperature change [|I_nitial-T|/I_nitial] against time for similar pressure drops for dissociation from sediments at 275.2, 277.2, and 279.2 K. Experiments 3–5 were performed at a constant confining pressure of 10.44 MPa.

4. Conclusions

In the reported methane hydrate formation and dissociation studies, the hydrates were formed in water saturated Ottawa sand-pack by varying pore pressure and sediment temperature, while the confining pressure was kept constant throughout all experiments. The hydrate formation was found to be delayed with increasing pore pressure or consolidation. The reported hydrate formation time was measured after the system P-T entered the hydrate stability region. The formation times observed for a seawater-consolidated Ottawa sand system were 9.39, 11.86, and 29.27 h at effective pressures of 1.85, 1.19, and 0.90 MPa, respectively. The observed longer time is likely due to a combination of hydrate inhibition caused by salts in the seawater used and an increased consolidation.

Hydrate dissociation, induced by depressurization, was short-lived and caused sediment cooling due to its endothermic nature. The endothermic effect was seen as a higher degree of cooling measured at the center and the half-radius thermocouples than that at the sand-pack boundary. This may be due to predominant hydrate formation within, as well as dissociation from the sand-pack interior. A higher pressure drop during dissociation at a constant sediment temperature caused a higher degree of sediment-cooling. The lower sediment temperature showed a higher degree of cooling upon hydrate dissociation with a constant pressure drop.

The post-depressurization sediment warm-up to the initial cell temperature represented a thermally induced dissociation during which the system P-T conditions followed theoretical P-T equilibrium for a methane hydrate-seawater system on the higher pressure side due to the excess pore pressure generated within a confined sand-pack (pore diameter: 46–58 µm). The enthalpy of hydrate dissociation computed from the post-depressurization P-T equilibrium is 55.83 ± 1.41 kJ/mol for the seawater and Ottawa sand-pack system. These values are lower than those computed from the theoretical P-T data for bulk hydrates from pure water (62.61 kJ/mol) and bulk hydrates from seawater (58.84 kJ/mol) due to the effect of salt and the porous media under confining pressure respectively. These observations could have significant implications for hydrate dissociation in a subseafloor environment where dissociation due to depressurization could result in instantaneous methane release followed by thermally induced dissociation. The excess pore pressure generated during hydrate dissociation could be higher within fine-grained sediments with faults and barriers which could cause geological sliding.