Short-Term Load Forecasting for Microgrids Based on Artificial Neural Networks

Abstract

Electricity is indispensable and of strategic importance to national economies. Consequently, electric utilities make an effort to balance power generation and demand in order to offer a good service at a competitive price. For this purpose, these utilities need electric load forecasts to be as accurate as possible. However, electric load depends on many factors (day of the week, month of the year, etc.), which makes load forecasting quite a complex process requiring something other than statistical methods. This study presents an electric load forecast architectural model based on an Artificial Neural Network (ANN) that performs Short-Term Load Forecasting (STLF). In this study, we present the excellent results obtained, and highlight the simplicity of the proposed model. Load forecasting was performed in a geographic location of the size of a potential microgrid, as microgrids appear to be the future of electric power supply.

1. Introduction

One of the most remarkable characteristics of the traditional energy production and distribution system is that most power is generated at large plants located far from the end-use points. This causes losses during transport and hinders the possibility of decentralizing power generation, resulting in a high dependence on large generation plants. In recent times, a conceptual change has been proposed so as to make the current supply system more sustainable in economic and environmental terms, as reflected for instance in the Lisbon Treaty [1].

According to these new concepts, and in order to increase sustainability and optimize resource consumption, electric utilities are constantly trying to adjust power supply to the demand. Taking into account that it is extremely difficult to store energy at a large scale, power generation has to be adjusted to demand in real time. Accordingly, it is important that electric load forecasting be as accurate as possible.

However, electric power demand depends on many factors, as the day of the week, the month of the year, etc., which makes electric load forecasting quite a complex process that involves more than only statistical methods. In recent years, electric load forecasting is being performed using several prediction algorithms, and among them, Artificial Neural Networks (ANNs) are one of the most popular options due to their ability to automatically learn from experience and adapt themselves [2].

On the other hand, the need for achieving a balance between electric power generation and demand has added to the emergence of smaller electric power generation and demand environments called microgrids, in which adaptation of production to load can be performed much more dynamically due to their distributed smaller elements and the geographical proximity of all elements (which in addition helps reduce transport loses). The load curve for a microgrid disaggregates electric power consumption data, making traditional methods (designed for nation- or region-wide forecasting) unsuitable for its direct application because of two main reasons. In microgrids, not only the aggregated consumption figure is several times smaller than in region-wide areas, but the load curve presents a much higher variability and does not always conform to the same shape. Some examples of typical load curves for different environments are presented in Figure 1 in order to illustrate the differences. It is easy to realize that the typical load curve is noisier and presents abrupter changes as the environment is more disaggregated.

This paper presents an ANN-based architectural model for Short-Term Load Forecasting (STLF) in small microgrid scenarios. After this introduction, Section 2 briefly presents the global concept of Smart Grid (SG) and microgrid (which represents an evolution of traditional grids into more localized power generation systems) and new distributed-intelligence technologies, which are expected to be incorporated into different components of the grid. Section 3 reviews the state of the art of the application of ANNs in load forecasting. Section 4 describes a new proposal for an ANN-based architectural model for STLF in microgrid environments. Section 5 presents the validation of the model with real world data. Section 6 analyzes the results obtained and, finally, Section 7 summarizes the conclusions of this study.

Figure 1. (a) Country; (b) substation (potential microgrid); (c) industrial park (potential microgrid); (d) home consumption.

Figure 1. (a) Country; (b) substation (potential microgrid); (c) industrial park (potential microgrid); (d) home consumption.

2. Evolution of Power Supply Systems: Smart Grids and Microgrids

2.1. Smart Grids and Microgrids

In recent years, national administrations and international institutions are adopting strategic plans to accelerate the development and deployment of low carbon technologies, putting in place several initiatives to concentrate, promote and reinforce efforts aimed at reducing carbon emissions in Europe. Some examples are the European Strategic Energy Technology Plan (SET-PLAN) [3], the Spanish platform FutuRed [4], or the European technological platform Smartgrids [5]. Public and private efforts are leading to a transition from the traditional grid to new electric power supply models based on SG. The term SG is used to describe a “smart” electric power supply system that uses Information and Communications Technologies (ICT) to optimize electric power generation and distribution, and achieve a balance between electric power generation and demand. SGs are based on the usage of Smart Meters (SM) to retrieve real time data from users and elements of the grid and the application of intelligent algorithms to adapt the behavior of the nodes so as to improve the performance of the network at various levels.

On the other hand, a microgrid is a localized physical space consisting of distributed power generation, storage and consumption. According to the Consortium for Electric Reliability Technology Solutions (CERTS), a microgrid is an “aggregation of loads and micro-power units jointly operating as a single system to provide both electric power and heat, includes power units, energy storage and interconnected loads that can operate both connected to the bulk power system and in isolation from the grid in case disturbances may arise”. Therefore, microgrids have the potential to become autonomous and independent energy systems capable, while they are still connected to the global network to allow higher level interactions.

When ICTs are incorporated into a microgrid, it becomes a SG of a specific size. In this case, in order to adjust electric power production of its generation elements, disaggregated load forecasting is required within the microgrid.

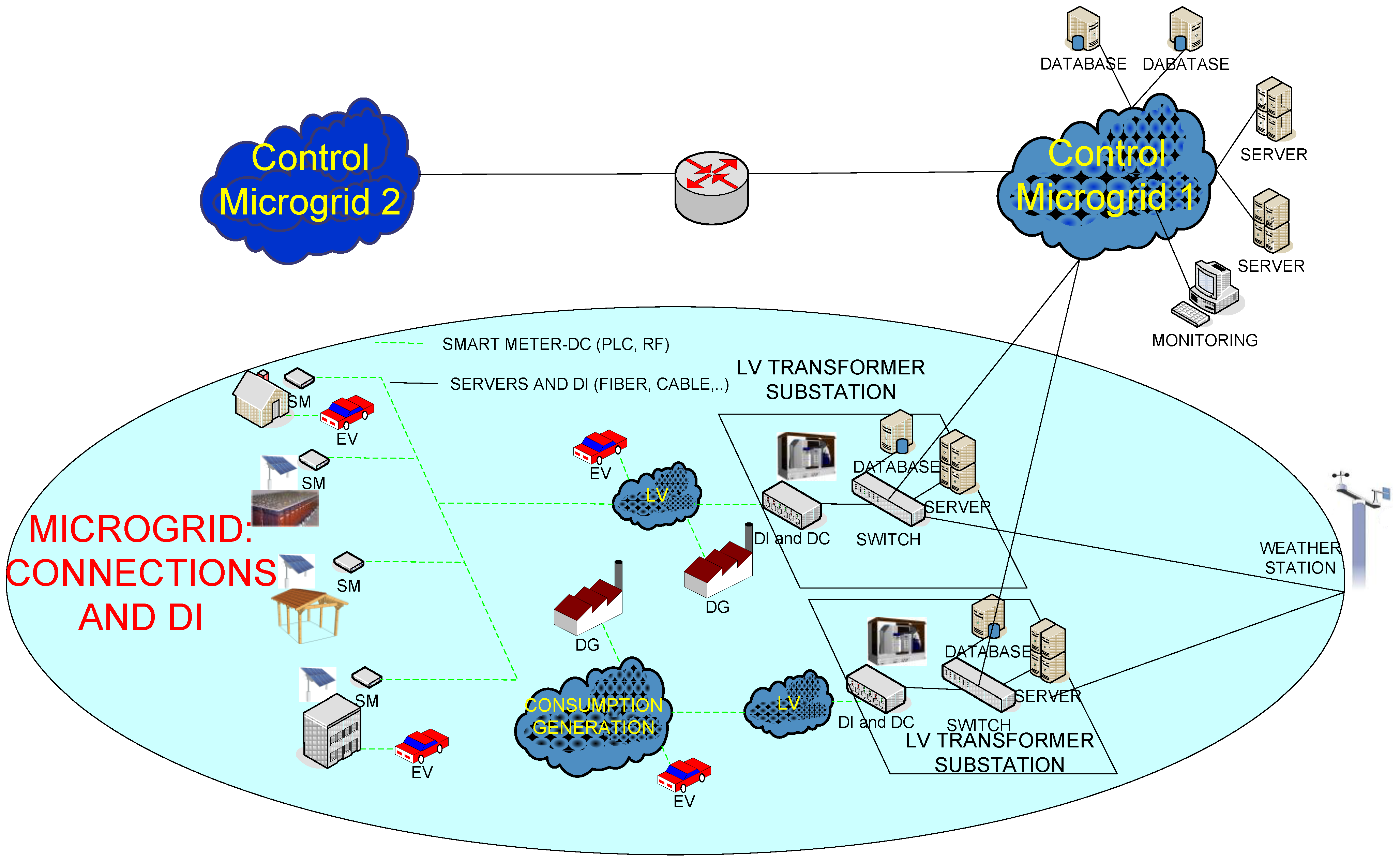
2.2. New Distributed Intelligence Elements in the Grid

The imminent deployment of SM at end-points will enable utilities to accurately identify demand patterns. Microgrid operators will get more reliable values from disaggregated profiles, which will enable them, for example, to perform more reliable Demand Response (DR) and make more accurate aggregated forecasts based on disaggregated data.

The new concept and physical distribution of SG and microgrids will require the deployment of Distributed Intelligence (DI) in traditional sites where to date there were no distributed electronics. This intelligence will control the behavior of the different smart elements of the grid. Figure 2 shows a hypothetical microgrid including DI, Distributed Generation (DG), end-point and storage elements. One of the most important inputs to this DI scenario is the disaggregated load forecasting, which allows smart elements in the grid to react in advance to the demand. Microgrids use techniques with Multi-Agent Systems for island mode operation [6,7] and for strategic control [8]. Similarly, [9] present a new nonintrusive energy monitoring method using ANN.

Figure 2. Microgrid example.

Figure 2. Microgrid example.

3. Artificial Neural Networks for Electric Power Load Forecasting in Microgrids

3.1. Background

Load forecasting is a challenging task, as there are a large number of influential relevant variables that must be considered, and several strategies have been used to deal with this complex problem. Forecasting models can be classified according to the factors considered as time series models (univariate) and causal models. The former methods model energy load on the basis of past data [10,11,12,13,14], while the latter model electric load on the basis of exogenous and social factors [15,16,17,18,19,20,21,22]. Intelligence-based forecasting techniques have also been employed as those based on expert systems [23,24], fuzzy inference [25] and fuzzy-neural [26,27].

However, one of the most popular methods for load forecasting are ANNs, in all their different flavors. There are ANNs based on the MultiLayer Perceptron (MLP) developed by Rumelhart [28]; others employ Radial Basis Functions Networks (RBF), proposed by Bromhead and Lowe [29]; recurrent networks, such as those proposed by Elman [30,31], and other models are based on Self-Organizing Maps (SOM), which were introduced by Kohonen [32]. Cascade combinations of some of the models above and others have also been employed for a wide array of tasks related to data analysis, prediction, estimation, etc. [33,34].

In the work reported by Park et al. [35], an ANN system with one output neuron is employed for hourly, total and peak load forecast. Ho et al. [36] perform a peak load forecast 24 h ahead; the same forecast is used by Ho et al. [23], as input to an expert system that performs 24-hour ahead load forecasting. ANNs with one output can be repeatedly used to forecast load curves, as in [37,38] or by using a 24-hour parallel system, as shown McMenamin et al. [39]. Lee et al. [40] present a day divided into three periods having one ANN forecasting the load for each period. Lu et al. [41] conducted an experiment with three ANN models of two utilities, and conclude that systems are dependent and must be adjusted to each of the utilities. With Papalexopoulos et al. [42], temperature is represented by non-linear functions, which are used as input, and suggests a set of measures to improve load performance in public holidays. Barkitzis et al. [43] present an improved model that considers public holidays.

Some publications present systems where a set of ANNs work together to compute a forecasting. Alfuhaid et al. [44] use a small ANN that pre-processes a data set and produces peak, valley and total load forecasts; these forecasts, in combination with other data, are used as input to a larger ANN to obtain next-day load forecast. Lamedica et al. [45] present 12 ANNs—one for each month of the year—where load curves are classified using Kohonen’s Self-Organized Map.

Artificial intelligence techniques as fuzzy logic have been combined with ANNs. With Srinivasan et al. [46], quantitative and qualitative data are presented to a “front-end processor”, which assigns four fuzzy numbers measuring the expected load change to each of the four periods of the day. Each number together with temperature data are presented to the ANN, which produces a load forecasting. In the work of Kim et al. [47], an ANN produces a provisional load forecast, then, a fuzzy expert system is used to modify the provisional load forecast on the basis of temperature data and day type (workday/holiday). Daneshdoost et al. [48] classify data into 48 fuzzy subsets by temperature and humidity, then each subset is modeled by its own ANN. Senjyu et al. [49] present a hybrid correction method where fuzzy logic, based on “similar days”, corrects the neural network output to obtain next-day load forecast.

Basically, [35,36,37,38,39,49,50] present peak load or aggregated daily predictions, which is a very useful parameter for instance for plant operations planning, but not detailed enough to perform other precise activities such as DR. For these, more detailed approaches calculating several predictions a day are required, in order to identify the nuances of the predicted load.

References [51,52,53] describe complex models capable of hourly prediction 24-hour in advance, but they use between 40 and 50 input variables and a hidden layer with a number of neurons ranging from 24 to 50. A similar case is presented in [44], where 30-minute predictions are provided 24 h in advance, but using more than 50 input variables. These works are prone to the curse of dimensionality effect as reported in [54]: the number of training patterns required to properly train the network increases exponentially with the dimension of the input space. This means that the high dimensional input of these solutions will take more measures to be properly trained, and as such, when installed in a new environment, a solution with a smaller number of inputs will start to output better results sooner.

3.2. Geographical Area in Load Forecasting

There is a variety of experiments reported which apply load forecasting methods to very different geographical areas: nations, regions and big metropolitan areas. In the work by Hsu et al. [50], peak and valley loads are forecasted for the city of Taiwan, which presents 5500–9000 MW loads. Taylor et al. [55] present load forecasts for England and Wales, with 30,000–45,000 MW consumption. In Chu et al. [56], the Taiwan Power Company (Taipower)—through Heat Index (HI)—perform peak load forecasting with values over 33,000 MW. In [51,57,58], the chosen areas for load forecasting are large provinces, which present high electric power consumption. Rejc et al. [52] apply a novel short-term active-power-loss forecast method for Slovenia, which has a consumption of 950–1550 MW. Nose-Filho et al. [59] analyzed a New Zealand distribution subsystem and performed forecasting using data from several nodes in an electrical network system; consumption data, however, are still high: 150–300 MW. Kebriaei et al. [53] present a forecasting method based on fuzzy logic and an ANN, and proposes a modified RBF, which uses genetic algorithms to estimate the weights for the network in a Mazandaran area in Iran, with consumption ranging 800–1550 MW.

However, all the publications examined so far [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]—regardless of the forecast model and target—have in common that the prediction is calculated for a large geographical area where the electric power load is aggregated and very high.

However, as shown in Figure 1, the features of the aggregated load curve of a large (metropolitan, regional or national) area are much different from the aggregated load curve of a microgrid, and therefore, their results cannot be directly extrapolated to microgrid environments. While the solutions studied in the literature [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,55,56,57,58,59] present sometimes good prediction efficiency figures (normally their MAPEs are around 2%), they deal almost exclusively with big areas, and mainly entire countries, and they are never applied to smaller environments of the size of small cities or microgrids. Therefore, they do not give any evidence of how will they behave when applied to highly variable load curves.

Works regarding load curve data processing in microgrids have started to appear only recently, such as clustering of load curves in [60], which helps extracting meaningful information by finding groups of similar patterns. Strictly speaking about load forecasting, [61] presents a STLF model for a microgrid based on Multiple Classifier Systems (MCS), using data from a similar microgrid-sized environment with a similar load curve. MCSs are systems combining a set of basic classifiers offering a better performance when operating together than on their own. The base classifiers can include different classification approaches or be trained differently, with different algorithms and data sets, and then combined with a fusion method. This specific work employs four base classifiers (MLP or RBF are used due to its good generalization ability), dividing the training set into several parts: 24 h, 3 days, 1 week and 1 month before the predicting hours. Dynamic weighting is selected as the fusion method. With a dataset collected from the aggregated load in the city of Hong Kong from September 2008 to August 2010, the MAPE found for this model is 15.66% with a Generalized Regression Neural Network (GRNN-MLP) and 15.12%, with a Radial Basis Function Neural Network (RBFNN). These errors are sensibly higher than those reported in works applied to national/regional environments.

4. An Architectural Model for Load Forecasting in Microgrids

A microgrid is capable of controlling electric power loads that will range between thousands of kW to hundreds of MW. Consequently, while traditional grids supply electric power to a whole country, microgrids supply electric power to small cities and villages. Disaggregated data are known to produce load peaks and valleys that are more difficult to forecast, and thus traditional methods are not directly applicable if accurate results are required. This section presents not only a prediction algorithm, but a complete ANN-based system for forecasting electric load in microgrids. For implementation and testing of this system, real world electric load data from Soria, a small Spanish city with a size that could be considered similar to that of a microgrid, has been employed.

4.1. Dataset

The real data used in this study were provided by the Spanish electric power utility company Iberdrola (Bilbao, Spain). The historical record provided spans from 1 January 2008 to 31 December 2010 (for a total of 1096 daily records sliced in 15-minute reports) corresponding to a substation located in Soria, Spain, that supplied electricity to this small city. The data provided included information about day of the month, month, year and hourly electric loads making up the daily load curve. This dataset has been enriched with calendar information (day of the week, day type—workday/public holiday) and daily aggregated load. Loads ranged between 7 and 39 MW, which is a load similar to that of a microgrid, rather than to a large area or country. A total of 70% of the data available were employed for ANN training, and the remaining 30% were used for the validation/testing phase.

4.2. Top Level Architecture of the Forecasting System

The aim of the system is to operate in real time within a microgrid environment, receiving data from data concentrators connected to smart meters and other smart data sources present in the grid. The architecture of the predictor is shown in Figure 3.

Figure 3. System architecture.

Figure 3. System architecture.

The different components are:

• Historical Data: a database containing all the data handled by the system. This includes raw and filtered load data (processed by modules 2 and 3) in periods of 15-minute and 1 h, and the forecasting reports produced by the ANN.
• Data Processing: this module implements three algorithms carrying out the following operations: a) to detect missing data produced by faults in the data retrieval system, completing them via interpolation when possible; and b) to cluster 15-minute samples so as to get hourly and daily loads.
• Outlier Detection: this module tries to identify faulty data (potentially caused by malfunctions in sensors or communications) and remove them from the database. To complete this task, the outlier detector searches for abnormal data (meaning data which is outside the typical values of a given magnitude). Therefore, it is necessary to distinguish between abnormal values that are correct—as in the case of low electric power demand in a public holiday as compared to the demand in a workday—and errors that might be caused by a technical failure, which are the ones that must be identified and removed. For the detection of outliers, the Principal Component Analysis (PCA) is employed [62], which is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. Figure 4 shows the results yielded by PCA with components (components are the eigenvectors of the correlation matrix and are different from the covariance matrix) 8 and 9. Out of the 1096 daily patterns available in the dataset, a total of 53 patterns were marked as outliers.
• ANN: the ANN receives data from 1 and, once forecast is performed, the information obtained is sent to 5 to be distributed among the different elements of the grid and to 1 to be stored for future use.
• Output: this module is called after forecast in 4 is completed. Its main task is to send data to different devices where it is displayed, as an operator’s screen, a mobile device, etc.

Figure 5 shows the on-line operation scheme of the predictor. Internal processes are distinguished from external processes. Internal processes are those performed by a predictor during operation. External processes are those dependent on external events or on interaction with external devices. In this figure we can see that in order to perform a forecast for day d, the information stored in the Historical Data are presented to the trained ANN, which produces an hourly forecast for day d.

Figure 4. (a) PCA Analysis of the dataset showing components 8 and 9; (b) Example of identified outlier daily consumption patterns: Blue and red are faulty data; Green is a correct (but abnormal) pattern.

Figure 4. (a) PCA Analysis of the dataset showing components 8 and 9; (b) Example of identified outlier daily consumption patterns: Blue and red are faulty data; Green is a correct (but abnormal) pattern.

Figure 5. On-line operation of the predictor.

Figure 5. On-line operation of the predictor.

4.3. Artificial Neural Network Design

The ANN-based system presented works over the hypothesis that the daily electric load pattern is related to the pattern of the previous day and other calendar data. More specifically:

▪

Electric consumption highly depends on the hour of the day, and the load curve of the previous day. This previous day load curve actually packs a lot of information about other conditions (season and weather, as shown by Hernández et al. [63]) that are not explicitly fed into the system in this work.

▪

There are many next-day total-load forecasting models, the 24 h-ahead forecast of the aggregated total load for the day. This is a very valuable input data for the ANN which packs a lot of information.

▪

Therefore, load forecasting is performed on the basis of previous-day hourly load curve, aggregated daily load forecast, and calendar variables (day of the week, month, etc.)

▪

Periodic variables are supplied to the network in the form of values of sines and cosines, as it has been demonstrated that this transformation significantly improves the performance of the ANN, as shown Drezga et al. [64]. Day of the week and month, which are essential for the ANN to detect weekly, monthly and seasonal patterns, are entered as sine and cosine, because the cyclical variables are best understood by ANN, as shown in [65,66].

▪

While previous studies on load patterns—as the Red Eléctrica de España (REE) study [67]—have demonstrated that the type of day—workday or public holiday—has a clear effect on electric load, during the testing phase it was found that the accuracy of the forecast did not improve with the information provided by the type of day. The reason for this could be that the input variables used for the load curve of the previous day and the aggregated load forecast for the forecast day are enough for the network to understand the type of forecast day.

▪

Electric load highly varies between workdays and weekends; electric demand in a public holiday is similar to that on Sundays.

▪

The seasonality of electric demand is evident, as it significantly varies throughout the year.

The architecture employed in this study follows the next model: to perform a load forecasting for day d, when day d − 1 ends and the data for that day are available, the system can perform the load forecast for day d. The architecture implemented is shown in Figure 6, a three-layer MLP: an input layer, a hidden layer, and an output layer.

Figure 6. MLP architecture. The Figure shows the variables of the input and output layers.

Figure 6. MLP architecture. The Figure shows the variables of the input and output layers.

Input:

▪

L_(d−1)1, L_(d−1)2, L_(d−1)3,…, L_(d−1)24: represent the 24 values for the load curve of the previous day.

▪

Day of the week d − 1: this variable is presented as two variables expressed as sine and cosine by sin[(2·π·day)/7]_(d−1) and cos[(2·π·day)/7]_(d−1), with day from 0 to 6 (Sunday = 0, Monday = 1, Tuesday = 2, Wednesday = 3,…, Saturday = 6).

▪

Month d − 1: this variable is presented as two variables expressed as sine and cosine by sin[(2·π·day)/12]_(d−1) and cos[(2·π·day)/12]_(d−1), month from 1 to 12 (January = 1, February = 2,…, November = 11, December = 12).

▪

NDTL_d: Next Day’s Total Load, which can be easily estimated with an error ranging ±2% using for instance the model proposed by Hsu et al. [68].

Output:

▪

L_d1, L_d2, L_d3,…, L_d24 represent the 24 values of the load curve for the forecast day.

Hidden:

▪

The neurons of the hidden layer are fully connected with input and output layer neurons.

▪

There are 16 neurons in the hidden layer.

Prior to operation, the ANN has to be trained. During this training stage, the ANN network is confronted with a series of inputs coupled with the real expected output, that is, a set of inputs is associated to the real load curve that the system would have had to forecast. During this training, the internal weights of the ANN are adjusted to produce the appropriate outputs.

ANN optimization—both to determine the number of neurons in the hidden layer and to establish the best training algorithm—is usually performed by a heuristic method. In our case, we decided to use an automated script where all parameters were modified (number of neurons in the hidden layer, training function, network performance function during training, etc.), calculating the estimation error for several test runs for each combination of parameter values. The best results were obtained with a total of 16 neurons in the hidden layer, the Bayesian Regulation Backpropagation training function and the Sum Squared Error network performance function.

4.4. Error Calculation

Models and forecast accuracy were validated by MAPE, which is widely recommended in the field of research and is expressed as:

$$MAPE=100\times \frac{{\displaystyle \sum _{i=1}^n\left|\frac{L(i)-\widehat{L}(i)}{L(i)}\right|}}{n}$$

(1)

where L(i) represents the measured value for t = i, $\widehat{L}(i)$ represents the estimated value and n represents the test sample size.

Once the MAPE_d for each of the days of the testing set is obtained, the mean error for all days is estimated by means of:

$$ERRO{R}_{OP}=\frac{{\displaystyle \sum _{i=1}^{k}MAP{E}_d}}{k}$$

(2)

To examine how the prediction error is reflected on the load curve, error is displayed on a graphic including all forecasted days in the testing set; using this method, the forecast mean error for each of the 24 h is obtained by means of:

$$MAPE\_h_i=100\times \frac{{\displaystyle \sum _{k=1}^{n}MAP{E}_{i,k}}}{n}$$

(3)

with i = 1, 2,…, 24; n stands for the sample size in the testing set and MAPE_i,k the hourly error i for the day k.

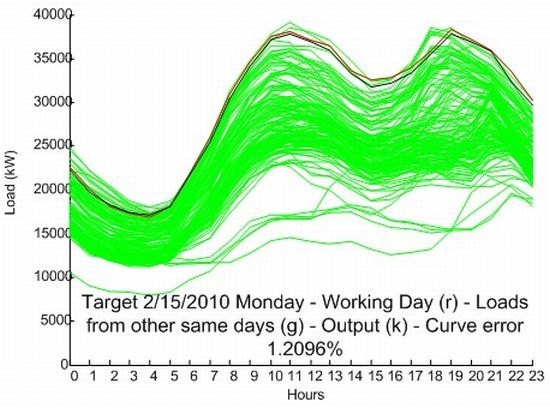
5. Results

This section provides the errors per day, Probability Density Function (PDF) curve errors, errors per hour, PDF curve errors per hour, and the forecasts of several days with low mean error, when our system is running.

5.1. Results

Once the network is trained, a forecast is performed for the testing set; a forecast load curve is generated for each datum and the daily average error is estimated; average errors are displayed in Figure 7 together with the mean value, mean ± standard deviation and mean ± 2× standard deviation. The mean error of the whole testing phase yielded a value of 2.4037%. The figure uses a specific nomenclature with the format “A B/C – D E”. A represents the day type of the previous day (2: workday, 1: holiday); B is the month number; C is the day of the month; D is the day of the week (Monday, Thursday), and E the day type (workday/holiday).

Figure 7. Errors per day (without bad measures). In the x-axis are the days. In the y-axis are the errors by Equation (1).

Figure 7. Errors per day (without bad measures). In the x-axis are the days. In the y-axis are the errors by Equation (1).

In Figure 8 errors are expressed as PDF, where the intervals between the mean and mean ± standard deviation, and mean and mean ± 2× standard deviation are displayed. As the figure shows, most errors (72%) correspond to the first interval, as shown in the percentages displayed in Table 1. Over and below that interval, errors have a similar distribution.

Figure 8. Curve errors data. In the x-axis are the errors by Equation (1). In the y-axis are the probability densities.

Figure 8. Curve errors data. In the x-axis are the errors by Equation (1). In the y-axis are the probability densities.

Table 1. Error distribution per day.

Variable	Value	Percentage
Mean	0.024	2.40%
Standard deviation (Std.)	0.0095	0.95%
No. of errors above ×1 Std.	42	14.73
No. of errors between ×1 Std.	206	72.28%
No. of errors below ×1 Std.	37	12.99%
No. of errors above ×2 Std.	12	4.21%
No. of errors between ×2 Std.	273	95.79%
No. of errors below ×2 Std.	0	0.00%

Table 1. Error distribution per day.

Variable	Value	Percentage
Mean	0.024	2.40%
Standard deviation (Std.)	0.0095	0.95%
No. of errors above ×1 Std.	42	14.73
No. of errors between ×1 Std.	206	72.28%
No. of errors below ×1 Std.	37	12.99%
No. of errors above ×2 Std.	12	4.21%
No. of errors between ×2 Std.	273	95.79%
No. of errors below ×2 Std.	0	0.00%

Figure 9 displays errors per hour occurred during the testing phase. Most errors occur in specific parts of the load curve, which normally follows the same topology: from hour 4 to hour 7, the curve starts rising from the first valley; from hour 10 to hour 15, the curve rises until reaching the first peak; the curve starts to drop into the second valley; from hour 18 to hour 21, the curve starts rising again towards the second peak; at the end of the day the curve starts to drop.

Figure 10 displays errors per hour expressed as PDF and shows the intervals between the mean and mean ± standard deviation; and mean and mean ± 2× standard deviation. Most errors are concentrated in the first interval—62%—as evidenced by the percentages shown in Table 2. A total of 21% and 17% of errors are above and below the first interval respectively.

Figure 9. Errors per hour (without bad measures). In the x-axis are the 24 h. In the y-axis are the errors by Equation (3).

Figure 9. Errors per hour (without bad measures). In the x-axis are the 24 h. In the y-axis are the errors by Equation (3).

Figure 10. Curve errors per hours. In the x-axis are the errors by Equation (3). In the y-axis are the probability densities.

Figure 10. Curve errors per hours. In the x-axis are the errors by Equation (3). In the y-axis are the probability densities.

Table 2. Error distribution per hour.

Variable	Value	Percentage
Mean	0.024	2.40%
Standard deviation (Std.)	0.0030	0.30%
No. of errors above ×1 Std.	5	20.83%
No. of errors between ×1 Std.	15	62.50%
No. of errors below ×1 Std.	4	16.67%
No. of errors above ×2 Std.	0	0.00%
No. of errors between ×2 Std.	23	95.83%
No. of errors below ×2 Std.	1	4.17%

Table 2. Error distribution per hour.

Variable	Value	Percentage
Mean	0.024	2.40%
Standard deviation (Std.)	0.0030	0.30%
No. of errors above ×1 Std.	5	20.83%
No. of errors between ×1 Std.	15	62.50%
No. of errors below ×1 Std.	4	16.67%
No. of errors above ×2 Std.	0	0.00%
No. of errors between ×2 Std.	23	95.83%
No. of errors below ×2 Std.	1	4.17%

Figure 11 shows load curve forecasts for three days with a low daily mean error, where (a) represents the forecast for 2/15/2010 with a mean error of 1.20%; (b) represents the forecast for 5/18/2010 with a mean error of 1.10%; and (c) represents 12/21/2010 with a mean error of 1.13%. As we can see, the forecast load curve coincides almost completely with the real load curve.

Figure 11. Forecasts with low mean error: (a) 2/15/2010; (b) 5/18/2010; (c) 12/21/2010.

Figure 11. Forecasts with low mean error: (a) 2/15/2010; (b) 5/18/2010; (c) 12/21/2010.

5.2. Computational Cost

As indicated above, MatLab was employed to implement the ANN and the rest of scripts developed for additional tasks (error estimation, figures, etc.). We used a desktop computer with an Intel Core2 vPro 3.4GHz 2GB RAM processor.

The computation method is as follows: the training set is imported to the Historical Data database, as shown in Figure 3; then ANN training is initiated. For this work, the computer used 70% of all data available and took 16 min and 43 s to train the ANN model.

When the network is trained as shown in Figure 5, then the data obtained are used to predict the load curve for the forecast day. The computer took 2 min and 49 s to process the testing set (outliers excluded), display the load curves and complete the database. Therefore, approximately, the computer needs 0.59 s to produce a forecast for one day.

6. Result Analysis

6.1. Error Distribution

As shown in Figure 7, and as supported by the results displayed in Figure 8 and Table 1, the daily mean error is within the mean ± standard deviation range, which means that errors ranged between 1.45% and 3.35%, which are fairly good results. Figure 7 also shows that the days with high daily mean errors (above 4%) were special days; further details on this regard are provided below.

By observing the hourly mean error shown in Figure 9, the data displayed in Figure 10 and Table 2, we can see that the most significant errors occur at the turning points of the forecast load curve. This coincidence may suggest that additional information on the form of the curve should be used to improve forecasts and prevent the most serious errors.

6.2. Errors per Day of the Week and Month

Figure 12 represents the evolution of the daily mean error per day of the week. The reason why the highest mean errors occur on Fridays, Saturdays and Sundays is that the training set (load curve) is more scattered; as a result, data uncertainty is higher in weight adjustment after training, and errors increase. In addition, as regards Saturdays and Sundays, their load curves significantly differ—both in demand and form—from those of other days of the week. Fridays are also a special day, as it marks the beginning of the weekend and electric power demand is lower than in the rest of the days.

Figure 13 shows the evolution of daily mean errors by month. October and November include fewer days because of the removed outliers; the mean error per month approximately ranges between 2% and 3%, which evidences the accuracy of forecasts.

6.3. Error Analysis

The purpose of this Section is to present the most significant forecast errors and analyze the reason underlying such errors; finally, this Section summarizes the conclusions drawn from this experience.

The forecast for 4/2/2010, with a mean error of 4.34%. 2 April 2010 is Good Friday (Holy Week) and the previous day is also a public holiday; consequently, a small number of pattern pairs with the same characteristics had been previously fed to the network in the training phase.

The forecast for 5/1/2010, with a mean error of 4.77%. The load in this holiday Saturday is similar to that in the working Saturdays of the same month; as compared with the previous day, the Friday before the holiday Saturday presents half the load; the shape of the curve is irregular, especially at the origin of the curve; however, towards the end, the load is similar to other Fridays of the same month.

Figure 12. Errors per day. The y-axis represents the forecast error by Equation (1). The x-axis represents each of the forecast days.

Figure 12. Errors per day. The y-axis represents the forecast error by Equation (1). The x-axis represents each of the forecast days.

Figure 13. Errors per month. The y-axis represents the forecast error by Equation (1). The x-axis represents the days of the month.

Figure 13. Errors per month. The y-axis represents the forecast error by Equation (1). The x-axis represents the days of the month.

The forecast for 6/24/2010, with a mean error of 3.92%. That Thursday is a local holiday called Jueves la Saca, and the load is clearly lower than in other holiday Thursdays; in addition, though the Wednesday before Jueves la Saca is not a local holiday, it is included in the holidays and the load is clearly atypical.

The prediction for the 12/8/2010 with a mean error of 4.73%. That day is a holiday Wednesday where the load is lower than in working Wednesdays of the same month; there was only one similar Wednesday in 2008; nevertheless, the ANN model predicts a demand rise and the curve starts to rise before the real curve, causing an error. The Tuesday before the holiday Wednesday is lower than that for other Tuesdays of the same month; for this reason, the forecast curve starts low to prematurely drop; the end of the curve is atypical, and is much lower than the real load curve.

The forecast for 12/25/2010, with a mean error of 8.04%. That day is a Christmas Saturday, the load is lower than in other Saturdays of the same month, and the first peak occurs later than usual. The previous day is Christmas Eve, which is a working day; consequently, the load curve is lower than the average load curve for the whole month and than previous years. Although Christmas Eve is not a public holiday, demand is much lower than in normal working days, which leads to significant forecast errors.

The forecast for the 12/31/2010 with a mean error of 4.78%. That day is New Year’s Eve, and it was a working Friday; that year, there were only two working Fridays with a similar load curve; that Friday’s curve is lower than that of other working Fridays and slightly higher than that of Sundays of the same month. The day before New Year’s Eve is a low-profile day as compared to other Thursdays of the same month, and it presents an atypical shape between 11 and 16 h; all these factors together caused the forecast error.

6.4. Association between Errors and Availability of Training Patterns

The association between the mean error obtained during the testing phase, and the number of patterns fed to the ANN during the training phase has been analyzed. For such purpose, different numbers of patterns were presented to the same model during the training phase: initially, 150 patterns were fed to the model, then the number of patterns was gradually increased (in steps of 50) until reaching 700 patterns. A forecast was produced for each of the days in the testing set; the optimum architecture for each network was achieved by the following method: firstly, a script was used to test all training and performance functions of a network with three neurons; then, the number of neurons in the hidden layer was increased to four and the network’s training and performance functions were tested again; then, the number of neurons was increased to five and so forth, until the network had 9 neurons. The reason for using this method is that the model’s architecture is entirely dependent on the number of input patterns, as shown in Table 3.

The data above were entered in MatLab, which yielded a cubic polynomial, as follows:

$$Y=-1e^{-0.08}\times X^3+2.2e^{-0.05}\times X^2-0.017\times X+6.8$$

(4)

where Y is the mean error of the Testing phase, and X is the number of patterns used in the training phase. The association between mean error and the number of patterns is evidenced in Figure 14. Red dots stand for the real error value of the ANN, while green dots represent error values according to the polynomial function for a specific number of patterns. Figure 13 evidences that, at some point, the architecture cannot further improve the mean error by increasing the number of training patterns. The ANN presented reached its maturity phase, as additional patterns did not appear to improve the mean error. It is worth noting that the mean error for the 730 days in the testing set was 2.40%. The improvement with respect to the results of the test including 700 training patterns is irrelevant. By means of Equation (4), we can estimate that by using 750 and 800 patterns we would obtain a mean error of 2.38% and 2.33% respectively; this improvement is far from being as significant as the improvement achieved between the beginning and middle of the test, as shown in Table 4. To assess how error was improved by increasing the number of neurons, we used Equation (5):

$$\mathrm{\Delta }erro{r}_{networks\_patterns}=\frac{\left|erro{r}_i-erro{r}_j\right|}{pattern{s}_i-pattern{s}_j}$$

(5)

where i = 2,…, 12; j = 1,…,11; with data in Table 4 error_i, error_j, pattern_i and patterns_j. High values obtained by Equation (5) suggest a significant error improvement against the number of patterns.

Table 3. Correlation between errors and the number of training patterns.

Network number	Patterns	Neurons	Error
1	150	3	4.78%
2	200	4	4.18%
3	250	4	3.94%
4	300	4	3.48%
5	350	6	3.26%
6	400	6	3.04%
7	450	12	2.82%
8	500	12	2.65%
9	550	13	2.62%
10	600	13	2.58%
11	650	15	2.48%
12	700	16	2.41%

Table 3. Correlation between errors and the number of training patterns.

Network number	Patterns	Neurons	Error
1	150	3	4.78%
2	200	4	4.18%
3	250	4	3.94%
4	300	4	3.48%
5	350	6	3.26%
6	400	6	3.04%
7	450	12	2.82%
8	500	12	2.65%
9	550	13	2.62%
10	600	13	2.58%
11	650	15	2.48%
12	700	16	2.41%

Figure 14. Evolution of mean error in the testing phase with respect to the number of patterns employed in the training phase. Fitting curve is red line and real curve is blue line.

Figure 14. Evolution of mean error in the testing phase with respect to the number of patterns employed in the training phase. Fitting curve is red line and real curve is blue line.

Table 4. Error variation between networks with respect to the number of patterns.

Networks i–j	Patterns added	Indicator given by Equation (5)
2–1	50	0.01199
3–2	50	0.00478
4–3	50	0.00428
5–4	50	0.00428
6–5	50	0.00455
7–6	50	0.00440
8–7	50	0.00340
9–8	50	0.00060
10–9	50	0.00080
11–10	50	0.00200
12–11	50	0.00140

Table 4. Error variation between networks with respect to the number of patterns.

Networks i–j	Patterns added	Indicator given by Equation (5)
2–1	50	0.01199
3–2	50	0.00478
4–3	50	0.00428
5–4	50	0.00428
6–5	50	0.00455
7–6	50	0.00440
8–7	50	0.00340
9–8	50	0.00060
10–9	50	0.00080
11–10	50	0.00200
12–11	50	0.00140

6.5. Comparison with Other Solutions

In principle, the results of this work can be only compared directly to other load curve forecasting methods also validated in microgrid-sized environments. Like [61], this work also presents a MLP-based prediction model. The approach followed in this work employs load curves from day d − 1 as an input to predict load curves for day d in the output, which allows a more intimate input-output relationship and a more efficient internal weight adjustment than the models in [61], which use as inputs groups of curves up to three days before the day to forecast. This could explain the better MAPE results obtained by the solution employed in this work: 2%–5% against figures around 15%.

When compared to the large-area load forecasting methods studied in Section 3, several differences can be extracted. References [35,36,37,38,39] and [49,50] offer generally short prediction horizons, normally forecasting values in the next hour. While this work employs 29 input variables and 16 neurons in the hidden layer, [44,51,52,53] use high dimensional input spaces (with a number of input variables ranging from 40 and 50 and neurons in the hidden layer between 24 and 50) and therefore require a bigger training database to reach similar results.

Finally it is worth mentioning that most of the works in the literature only study daily MAPEs. In this paper, however, a detailed hour-by-hour MAPE is presented which allows hourly error studies as presented in Section 5.

7. Conclusions and Future Studies

This paper proposes an ANN-based model for short-term load forecasting in disaggregated, microgrid-sized environments using a simple MLP-based architecture. For such purpose, relevant input variables were selected in order to minimize forecast errors. As remarked above, forecasting is more complex in a microgrid due to the increased variability of disaggregated load curves. An accurate forecasting in a microgrid will depend on the variables employed and the way they are presented to the ANN. This study also shows numerically that there is a close relationship between forecast errors and the number of training patterns used, so it is necessary to carefully select the training data to be employed with the system. Finally, this work demonstrates that the concept of load forecasting and the ANN tools employed are also applicable to the microgrid domain with very good results, showing that small errors around 3% are achievable. This demonstration is backed up by a detailed database containing real information of load curves disaggregated up to city/microgrid level running for three entire years.