Feasibility of a Simple Small Wind Turbine with Variable-Speed Regulation Made of Commercial Components

Abstract

The aim of this study was to propose and evaluate a very small wind turbine (VSWT) that competes with commercial grid-connected VSWTs in terms of simplicity, robustness and price. Its main components are a squirrel-cage induction generator (SCIG) driven by a frequency converter. The system has a direct-drive shaft, and may be constructed with commercial equipment. Simulation of the wind turbine effect is done with a motor. A control program regulates the variable-speed of rotation through three operational modes: (i) to drive the turbine to its optimum operation point; (ii) to limit its maximum rotational speed; and (iii) to limit the maximum power it generates. Two tests were performed, in order to evaluate the dynamic response of this system under variable wind speeds. The tests demonstrate that the system operates at the optimum operational point of the turbine, and within the set limits of maximum rotational speed and maximum generated power. The drop in performance in relation to its nominal value is about 75%, when operating at 50% of the nominal power. In summary, this VSWT with its proposed control program is feasible and reliable for operating direct-shaft grid-connected VSWTs.

1. Introduction

Wind energy, as a renewable energy source to generate electricity, has rapidly developed and assumed more importance [1], as awareness of global warming due to fossil-fuel energy consumption and environmental pollution has risen. Nevertheless, wind generator designs must be optimized to lower the cost of energy, which remains a primary factor for the inclusion of wind technology in the energy mix. Favourable incentives in many countries impact straightforwardly on the commercial acceptance of grid-connected wind turbines.

Wind energy conversion systems can be up to several MW of power. Even though there is no strict definition of a small wind turbine (SWT) in the literature, these turbines are generally considered to have a size of up to 30–50 kW and very small wind turbines (VSWT), or micro wind turbines (MWT), of less than 3–7 kW [2]. A wind generator consists of a wind turbine coupled to a generator. In the majority of large turbines, a gearbox is coupled to a low speed wind turbine rotor to increase speed. The use of direct shaft coupling is more common in SWTs due to their higher wind turbine speeds. The generator feeds power to utility grids or autonomous loads. Large wind turbines usual form a wind farm and are connected to the grid. The most important applications for SWTs are in stand-alone systems, from which electricity is fed into a battery bank or into a direct application, in places that do not have access to a power grid. However, the trend is to connect SWTs to the public grid, thanks to government incentives such as net metering or tax credits.

The maximum conversion efficiency in wind turbines occurs at an optimal ratio between turbine angular speed and wind speed [3]. As wind velocity varies over time, variation of the angular speed of the turbine is used to optimize conversion efficiency. Modification of turbine shape, by varying the blade pitch angle, is used to limit generated power in case of high wind speeds. Both control methods are used at simultaneously in large wind turbines. In grid-connected alternating current (AC) wind turbines with variable full-span pitch control, rotational speed of the turbine has to be constant to control the AC grid frequency of the wind turbine. In this type of turbine, the blades rotate around their longitudinal axis which optimizes their aerodynamics for any given rotational speed.

In small and medium-size wind turbines, fixed-pitch and pitch-controlled horizontal-axis wind turbines are the two common topologies. For fixed-pitch wind turbines, the rotor speed control strategies are fixed speed and variable speed [4]. The rotational speed of the generator in a variable-speed wind turbine varies in proportion to wind speed, in order to maintain its operational point at an optimum. Some variable-speed VSWTs are often fixed-pitch, which reduces maintenance costs and increases the working life of a wind turbine. Power electronic devices, called frequency converters, are often used to regulate the rotor speed while the grid frequency is constant. There are other methods for operating at variable-speed, such as mechanical variable-speed devices coupled between the turbine and the generator, but these methods are not commonly used. Compared with constant speed operation, variable-speed wind turbines provide substantially higher energy output, lower mechanical stress and less power fluctuation [5]. A variable-speed controlled wind turbine is proposed in this work.

In variable-speed wind turbines with a grid connection, the rotor speed has to be changed while the grid frequency remains constant [6]. Variable-speed has mainly been implemented in three ways: (i) conventional commutator-type direct current (DC) generators, typically used for SWTs that deliver DC current directly from the generator; (ii) direct AC-to-AC frequency converters, such as cycloconverters, rarely used in actual turbines; and (iii) modern frequency converters (AC–DC–AC), that convert variable-frequency and variable-voltage power from a generator into constant grid-frequency and grid-voltage. The following generators and frequency-converter components are commonly used in wind turbines [7]:

• DC generators: these generators consist of a spinning armature and a surrounding stationary and constant field, generated by a winding or permanent magnet. The output of the turning armature is continuously mechanically switched, so that the output current flows in the same direction. The addition of commutators and brushes makes DC designs more expensive and less reliable than comparable AC generators. It is for this reason that AC generators are used more often than DC ones.
• AC synchronous generators (alternators): the rotor in these generators has magnetic poles that create the field. There are two types of synchronous generators:

  ○

  Synchronous Generators with a wound rotor. Slip rings on the rotor feed DC into wire-wound magnetic pole pieces, which provide the magnetic field for generator action, and reactive power (kVAs) supplied by the machine to the grid [8]. They are common in the largest machines, and require maintenance of the slip ring contacts [9].

  ○

  Permanent Magnet Synchronous Generators (PMSG). The magnetic field is provided by permanent magnetic poles in place in the rotor. They require no external excitation current to create the magnetic field, nor the use of slip rings. The flux density of high performance permanent magnets is limited, and there is no way to control the strength of the magnetic field. Large high-performance permanent magnets are costly, and PMSG are commonly used for smaller wind turbines. In PMSG, a diode bridge rectifier may be used at the generator terminals as no external excitation current is needed. Much research has been performed using a diode rectifier. Using a thyristor-based grid-side inverter allows continuous control of the inverter firing angle, regulating turbine speed through the DC-link voltage [10,11].

• Induction Generators (AC asynchronous generators): the current in the rotor is induced by the differential speed of the spinning rotor coils with respect to the spinning stator magnetic field. The induction generators have the disadvantage of requiring external reactive power, and depend on an external voltage source to produce a magnetic field [12]. The induction generator has two main constructive forms:

  ○

  Doubly Fed Induction Generators (DFIG) have the rotor wound in copper or aluminium. Their advantage is that the torque can be maintained at its rated value well above the synchronous speed. It is able to produce, not only below, but even above rated power, and to transfer maximum power over a wide speed range [13,14,15]. DFIG are externally accessible through slip rings and brushes and can be controlled in the following two ways [16]: (i) the electrical torque and the slip percentage can be controlled by inserting a variable resistor in the wound rotors; (ii) the injection of currents of appropriate frequency into the rotor windings with a power converter can control both the torque and the slip [17]. Then, the converter power rating is reduced while most of the power flows through the stator, directly connected to the grid [14]. This makes the DFIG excellent for high power applications.

  ○

  Squirrel-Cage Induction Generators (SCIG) are the simplest form of induction generators. They have a rotor formed from welded copper bars, rods or copper castings embedded in a soft iron cylindrical rotor. They are relatively inexpensive, robust, and have maintenance-free operation. The speed of the SCIG may be regulated by means of a rectifier and an inverter interposed between the cage induction generator stator and the grid [12,18]. The power converter has to be rated at total system power. The supply side PWM inverter allows for control of real and reactive power transferred to the grid, which is the configuration studied in this paper.

An algorithm programmed into the turbine control system determines the operational speed of variable-speed wind turbines [12]. There are several methods to determine the maximum power point (MPP) [5]:

• Using a maximum power point tracking (MPPT) algorithm that searches for the turbine rotating speed that will generate maximum power [19,20,21,22,23]. If the dynamics of the speed controller are very fast, large transients in generator torque may occur.
• Measuring wind velocity and adjusting the turbine rotating speed to the maximum power coefficient.
• Measuring the shaft speed and turbine output power, and then estimating the wind speed. Rotor speed can be measured with an encoder, however encoders are expensive. Modern frequency converters can measure both shaft speed and output power [24,25]. This is the approach used in our study.

Wind turbines also need to limit the maximum rotational speed and the power generated at high wind speeds, in order to limit the angular velocity of the turbine and generator power extraction [26,27]. There are several methods for limiting the speed and peak power output of a wind turbine. In the passive stall control, the design of the rotor aerodynamics causes the rotor to stall at high wind speeds, losing extracted power. The yawing control uses a mechanical device to turn the rotor out of alignment, when a given wind speed is exceeded. In the aerodynamic control, elements such as flaps or full-span pitch control are implemented as an emergency control method that only feathers the blades in an over-speed condition. Finally, in active methods, the power output is controlled over a wide range of wind speeds. An active method is implemented in this work.

The SCIG has been operated as a wind generator [28], but it does not implement a dynamic control for the optimum operation point, and speed and power limitations. A variable-speed control has been presented for a lineal wind profile [29]. A SCIG with a double-sided pulse width modulated converter has been operated at its optimum operational point [30], but without imposing speed and power limits. DFIG has been used with power converters for wind turbines [13,16]. In [31], an adaptation of a control board based on a floating point digital signal processor (DSP) is developed and the programmed algorithms perform a vector control over the torque on the generator that also eliminates the need for position and shaft-speed sensors.

In this study, the dynamic operation of a wind turbine is tested that incorporates a SCIG with a commercial frequency converter, which is controlled to operate at its optimum operational point and which limits the maximum rotational speed and power limit. The aim of this study is to propose and evaluate a VSWT that competes with commercial grid-connected VSWTs in terms of simplicity, robustness and price. Its main components are a SCIG driven by a frequency converter. The system is devised for grid connection, has a direct-drive shaft, and may be constructed with commercial equipment. To do so, a motor bench was fitted with two asynchronous motors: one acting as a motor wind turbine and the other as the generator. Realistic wind speed profiles, representative of real conditions, are applied to the system in order to study its non-steady state behaviour. The wind turbine adjusts its angular speed to maintain the turbine at the optimum operational point, within the speed and power limits. Finally, the energy produced, and the performance of the system is analysed and discussed.

2. Method

2.1. System Description

The system constructed for this work has two parts, the turbine side and the generator side. Each one is independently operated, and they have a direct mechanical coupling. They are represented in Figure 1.

Figure 1. Schematic diagram representing the motor-turbine and generator systems.

Figure 1. Schematic diagram representing the motor-turbine and generator systems.

The motor that simulates the wind turbine is a 1400 rpm three-phase asynchronous SCIG with a nominal power of 3 kW (AEG AM100LT4). It has the function of acting like a real wind turbine. The motor turbine is independently driven by a frequency converter with vector control (Schneider ATV 71 5.5 kW).

The generator is a 710 rpm three-phase asynchronous machine with a nominal power of 1.1 kW (AC 100LM). It is driven by a frequency converter at a set speed (Schneider ATV 71 2.2 kW). The frequency converter has a built-in chopper connected to a dissipative resistance bank. It consumes the energy produced by the generator.

The control has been developed with a PC user control interface programmed using LabView software (National Instruments, Austin, TX, USA). The motor-turbine and the generator are independently driven. The control assigns a reference torque to the motor-turbine, and a reference angular speed to the generator. The references are assigned through a data acquisition module to the frequency converters (NI cDAQ 9172; National Instruments, Austin, TX, USA).

Frequency converters use vector control in order to ensure that the machines are at the point of operation referenced by the program. Field-oriented control (FOC), more generally known as vector control is the most sophisticated and modern speed control method for asynchronous motors. The method consists of controlling the magnitude and phase of the magnetic flux, so that its behaviour is similar to the DC motors. Frequency converters used in this paper have vector control as one of their properties and have been used without sensors (sensorless). Sensorless means that the shaft speed and position are estimated by measuring voltages and currents consumed by the machine and using a previously calculated mathematical model, so no additional sensor or encoder is required to know the speed and torque of the machine. A general block diagram of the sensorless vector control can be seen in Figure 2.

Figure 2. Block diagram representing sensorless vector control in a frequency converter.

Figure 2. Block diagram representing sensorless vector control in a frequency converter.

2.2. Wind Turbine Model

The power generated by a wind turbine ($P_T$) is dependent on the wind speed, which may be expressed as [3,32,33]:

$$P_T=\frac{1}{2}·\rho ·\pi R^2·v^3·C_P\left(\lambda ,\beta \right)$$

(1)

where ρ is the air density; R is the radius of the turbine; v is the wind speed; and $C_P\left(\lambda ,\beta \right)$ is the power coefficient. The power coefficient $C_P\left(\lambda ,\beta \right)$ depends on the type of turbine and operating conditions. In this study, the control is accomplished by adjusting the rotor angular speed. Therefore the pitch angle is constant equally to zero. λ is the tip-speed ratio, defined as:

$$\lambda =\frac{{\omega }_T·R}{v}$$

(2)

where ${\omega }_T$ is the angular speed of the rotor; and β is the pitch angle of the blades, the angle at which the rotor blades are rotated along its long axis. A generic model for a three-blade turbine is used to model the power coefficient $C_P\left(\lambda ,\beta \right)$, as shown in [34]:

$$C_P(\lambda ,\beta )=\frac{1}{2}\left(\frac{98}{{\lambda }_i}–0.4\beta –5\right)·e^{\left(\frac{–16.5}{{\lambda }_i}\right)}$$

(3)

where β is the pitch angle of the blades, and ${\lambda }_i$ is defined as:

$${\lambda }_i={\left[\frac{1}{\left(\lambda +0.089\right)}–\frac{0.035}{\left({\beta }^3+1\right)}\right]}^{–1}$$

(4)

The present study is for a fixed pitch angle turbine ($\beta =0$), so the power coefficient is only dependent on the tip-speed ratio. $C_P\left(\lambda \right)$ is presented in Figure 3a. As seen in the figure, peak power occurs at the point where $C_P$ is at a maximum.

Figure 3. (a) Power coefficient $C_P$ as a function of tip speed ratio λ; (b) Torque coefficient $C_M$ as a function of λ.

Figure 3. (a) Power coefficient $C_P$ as a function of tip speed ratio λ; (b) Torque coefficient $C_M$ as a function of λ.

The torque produced by the turbine $M_T$ is:

$$M_T=\frac{P_T}{{\omega }_T}$$

(5)

From Equations (2) and (5) the angular speed of the rotor ${\omega }_T$ can be expressed as:

$${\omega }_T=\frac{\lambda ·v}{R}$$

(6)

Substituting Equations (1) and (6) in Equation (5), turbine toque $M_T$ can be expressed as:

$$M_T=\frac{1}{2}·\rho ·\pi R^3·v^2·C_M\left(\lambda \right)$$

(7)

where $C_M\left(\lambda \right)$ is the torque coefficient related to the power coefficient as:

$$C_M\left(\lambda \right)=\frac{C_P\left(\lambda \right)}{\lambda }$$

(8)

Figure 3b shows the torque coefficient derived from Equations (3) and (8). It is marked ${\lambda }_{opt}$ and $C_{Mopt}$, which correspond to the maximum power coefficient $C_{Pmax}$. According to Equation (8):

$$C_{Mopt}=\frac{C_{Pmax}}{{\lambda }_{opt}}$$

(9)

Substituting Equation (6) in Equation (7), turbine torque $M_T$ is expressed as:

$$M_T=\frac{1}{2}·\rho ·\pi R^5·\frac{{\omega }_T^2}{{\lambda }^2}·C_M\left(\lambda \right)$$

(10)

The optimal angular speed of the turbine ${\omega }_{Tópt}^2$ is calculated from Equation (10), for which the power coefficient is maximum $C_{Pmax}$:

$${\omega }_{Topt}=\sqrt{\frac{2·M_T·{\lambda }_{opt}^2}{\rho ·\pi R^5·C_{Mopt}}}$$

(11)

Figure 4 plots the curve of the optimum rotational speed as a function of the turbine torque. It indicates the optimum operational point for each wind velocity.

Figure 4. Turbine torque as function of the rotational speed for several wind speeds, and the optimum operation curve.

Figure 4. Turbine torque as function of the rotational speed for several wind speeds, and the optimum operation curve.

The performance of the generator decreases as the power that is generated decreases. In this study, the relative performance is defined as the performance of the generator in relation to a reference operation value. The relative performance value is therefore 1 when operating at the reference power, which is calculated as:

$$relative performance=\frac{\raisebox{1ex}{$P_G$}\!\left/ \!\raisebox{-1ex}{$P_T$}\right.}{\raisebox{1ex}{$P_{G_{ref}}$}\!\left/ \!\raisebox{-1ex}{$P_{T_{ref}}$}\right.}$$

(12)

where $P_G$ and $P_T$ are the power that is generated and the power supplied by the motor-turbine, respectively. $P_{G_{ref}}$ and $P_{T_{ref}}$ represent the power that is generated and the power supplied by the motor-turbine at the reference value for power generation.

2.3. Wind Turbine Control

The motor turbine is independently driven by the frequency converter at the torque calculated by Equation (7), which depends on the instant wind velocity and rotational speed. Rotational speed is directly measured by the power converter. The wind velocity sample is given from a real measurement [35]. Air density and wind turbine radius are considered as constants, and presented in Table 1.

Table 1. Main characteristics of the wind turbine.

Maximum power coefficient	0.482
Optimum λ	6.75
Radius	1.0 m
Air density $\left({\rho }_{air}\right)$	1.1 Kg/m3

Table 1. Main characteristics of the wind turbine.

Maximum power coefficient	0.482
Optimum λ	6.75
Radius	1.0 m
Air density $\left({\rho }_{air}\right)$	1.1 Kg/m3

The generator control has three functions. First, it optimizes the power generation, operating the turbine at its optimum angular speed. Second, the control limits the maximum angular speed for the generator, and third, it limits the power generation. Therefore, the control has three operational modes: optimum point operation, maximum rotational speed operation, and maximum power operation.

Optimum point operation means that the angular speed of the wind turbine is set to the point at which power generation is at a maximum, given by Equation (11). It depends on the torque generated by the turbine, which is measured directly by the power converter.

Maximum rotational speed operation occurs when the generator rotational speed reaches the maximum limit and the power generated is below the power limit. A constant rotational speed is then set at that maximum. The turbine control unit checks that the rotational speed given by Equation (11) is below the maximum limit.

The maximum power operation runs when the maximum admissible power is reached by the generator. The system reduces the rotational speed, the turbine operates below its optimum, and the production of power is adjusted the maximum admissible. This causes a transient period where the power generated is above the maximum limit. The angular speed is calculated using Equations (5) and (10).

Figure 5 presents the control algorithm, with the numbered steps. In step 1, the calculations are completed to obtain the optimum operational point, as a function of the actual rotational speed and torque of the turbine, measured by the power converter, and aware of the turbine characteristic curve $C_P$. The calculation is made in correspondence with Equations (1), (2), (7)–(9). In step 2, the rotational speed for optimum operation is calculated using Equation (11).

Figure 5. Control algorithm and meaning of the symbols.

Figure 5. Control algorithm and meaning of the symbols.

P_t = Maximum power of the turbine; v = Wind speed (generated wave); n = Actual rpm meas. by the converter; C_P = Actual power coefficient; C_M = Torque coefficient; ${\lambda }_o$ = Optimum lambda; $C_{Po}$ = Optimum power coefficient; $C_{Mo}$ = Optimum torque coefficient; $M_{to}$ = Optimum torque; $M_l$ = Actual torque measured by the converter; ${\omega }_{máx}$ = Maximum rotat.speed limit; $P_{máx}$ = Maximum power limit

In steps 3 and 4, the control decides whether the optimal rotational speed of the generator exceeds the maximum that is admissible for the generator. If below the limit, the optimum rotational speed is selected using Equation (11), operating in the optimum point operation mode. Otherwise the rotational speed of the generator is set in this step to the maximum admissible speed.

In step 5, the power that would be generated at the previous angular speed of the generator is calculated and compared in step 6 with the maximum power limit of the generator. If the generator output is above the generator limit, the angular speed of the generator is reduced in step 7, until the power that is produced is equal to the maximum admissible, using Equations (5) and (10). In this situation, the control is working in the maximum power operation mode. Otherwise, if the power generation is below the generator limit, and the rotational speed is set to the maximum admissible, the generator is operating at its maximum rotational speed. Finally, in step 8, the angular rotational speed selected in the previous steps is consigned to the power converter.

3. Results

This section presents the results of two tests representative of the simulated operation of a small direct-drive wind generator. In the first test, both the optimum operational point and maximum generated power are controlled. In the second test, the maximum rpm of the generator is controlled, as well as the optimum point of operation and the maximum power that is generated. Table 1 shows the main turbine characteristics for both tests and Figure 3a shows the power coefficient given by Equation (3).

3.1. First Test—Power Limit Control

In the first test, the wind speed waveform presented in Figure 6a is applied to the turbine model, which is between 5.8 and 11.0 m/s. This waveform is obtained from real measurements presented in [35], using a 140 s time span. A maximum generated power limit of 600 W is set, which corresponds, according to Equation (1), to a wind speed of 9.18 m/s. There are therefore two operational regions:

• Below this wind speed, the control unit maintains the optimal operational point of the turbine according to torque Equation (11).
• Above this wind speed, the control unit maintains power generation at a constant operation of 600 W.

Figure 6a presents the values for the torque and generated power. Figure 6b presents the theoretical and the real rotational speed of the generator. The theoretical rotational speed is calculated by applying Equation (11) in the optimum operational mode.

Figure 6. (a) Wind speed sample, turbine torque and generated power; (b) Theoretical and real rotational speed of the turbine.

Figure 6. (a) Wind speed sample, turbine torque and generated power; (b) Theoretical and real rotational speed of the turbine.

Figure 7a,b presents the operational points for the torque and generated power. They also plot the theoretical lines followed by the generator control unit. The plot of the generated power has two parts. In the first part, the power increases with respect to rotational speed operating in the maximum power point, given by the Equation (11). In the second part, the power remains constant, reducing the rotational speed as the wind speed increases.

Generator performance decreases as generated power decreases. Figure 8 shows the relative performance as a function of generated power according to Equation (12). The relative performance is 1 when operating at a reference power of 600 W.

Table 2 summarizes the information from the first test, averaging the data for the two intervals of operational modes: the optimal operational mode and the power limitation mode.

Figure 7. (a) Turbine torque as a function of the rotational speed; (b) Generated power as a function of the rotational speed of the turbine.

Figure 7. (a) Turbine torque as a function of the rotational speed; (b) Generated power as a function of the rotational speed of the turbine.

Figure 8. Relative performance of the turbine as a function of generated power and its linear regression.

Figure 8. Relative performance of the turbine as a function of generated power and its linear regression.

Table 2. First test averaged values for the two operational modes, and globally.

Magnitudes	Optimum	Maximum power	Global
Wind speed interval (m/s)	5.8–9.18	9.18–11	5.8–11
Time (s)	77	63	140
Avg. wind speed (m/s)	7.56	9.91	8.60
Avg. torque (Nm)	5.1	9.5	7.0
Avg. speed (rpm)	447	563	498
Avg. generated power (W)	253	559	388
Avg. relative performance (%)	71.8	93.2	84.2

Table 2. First test averaged values for the two operational modes, and globally.

Magnitudes	Optimum	Maximum power	Global
Wind speed interval (m/s)	5.8–9.18	9.18–11	5.8–11
Time (s)	77	63	140
Avg. wind speed (m/s)	7.56	9.91	8.60
Avg. torque (Nm)	5.1	9.5	7.0
Avg. speed (rpm)	447	563	498
Avg. generated power (W)	253	559	388
Avg. relative performance (%)	71.8	93.2	84.2

3.2. Second Test—Speed and Power Limit Control

The second test involved a wind waveform with the same profile as the first test, and with a 600 s time length (10 min), which is presented in Figure 9a. In this test, two limits are imposed:

• A speed limit of 600 rpm is set, which corresponds to a wind speed of 8.98 m/s.
• A limit is set for power generation at 700 W. It corresponds, to a wind speed of 9.66 m/s.

There are therefore three operational modes:

• Below a wind speed of 8.98 m/s, the control unit maintains operation at the optimal point of the turbine according to torque Equation (11).
• Between a wind speed of 8.98 and 9.66 m/s, the control unit maintains a constant rotational speed of 600 rpm.
• Above a wind speed of 9.66 m/s, the control unit maintains a constant power generating operation of 700 W.

Figure 9a presents the values for the torque and generated power. Figure 9b presents the theoretical and the real rotational speed of the generator. The theoretical rotational speed is calculated by applying Equation (11) in the optimum operational mode.

Figure 9. (a) Wind speed sample, turbine torque and generated power; (b) Theoretical and real rotational speed of the turbine.

Figure 9. (a) Wind speed sample, turbine torque and generated power; (b) Theoretical and real rotational speed of the turbine.

Figure 10a,b present the operational points of the torque and generated power. They also plot the theoretical lines followed by the generator control unit. The plot of the generated power has three parts. In the first part, the power increases with respect to rotational speed when operating at the maximum power point, given by the Equation (11), until the rotational speed limit is reached at a wind speed of 8.98 m/s. In the second part, the rotational speed is maintained at its maximum limit until the power limit is reached at a wind speed of 9.66 m/s. In the third part, the power remains constant, reducing the rotational speed as wind speed increases.

As generated power decreases, performance also decreases. Figure 11 shows the relative performance as a function of generated power according to Equation (12). The relative performance is 1 when operating at a reference power of 700 W.

Figure 10. (a) Turbine torque as a function of the rotational speed; (b) Generated power as a function of the rotational speed of the turbine.

Figure 10. (a) Turbine torque as a function of the rotational speed; (b) Generated power as a function of the rotational speed of the turbine.

Figure 11. Relative performance of the turbine as a function of generated power and its linear regression.

Figure 11. Relative performance of the turbine as a function of generated power and its linear regression.

Table 3 summarizes the information from the second test. It averages the data for the three intervals of operation: optimum operational mode, the rotational speed limit mode, and the maximum power limit mode.

Table 3. Second test averaged values for the three operational modes, and globally.

Magnitudes	Optimum	Maximum rpm	Maximum power	Global
Wind speed interval (m/s)	5.8–8.98	8.98–9.66	9.66–11	5.8–11
Time (s)	292	161	147	600
Avg. wind speed (m/s)	7.33	9.35	10.27	8.60
Avg. torque (Nm)	4.8	8.5	10.7	7.2
Avg. speed (rpm)	434	582	587	511
Avg. generated power (W)	226	517	658	410
Avg. relative performance (%)	71.3	81.4	94.0	82.7

Table 3. Second test averaged values for the three operational modes, and globally.

Magnitudes	Optimum	Maximum rpm	Maximum power	Global
Wind speed interval (m/s)	5.8–8.98	8.98–9.66	9.66–11	5.8–11
Time (s)	292	161	147	600
Avg. wind speed (m/s)	7.33	9.35	10.27	8.60
Avg. torque (Nm)	4.8	8.5	10.7	7.2
Avg. speed (rpm)	434	582	587	511
Avg. generated power (W)	226	517	658	410
Avg. relative performance (%)	71.3	81.4	94.0	82.7

4. Discussion

This paper presents the operation of a squirrel-cage induction generator (SCIG) controlled by a frequency converter for small wind turbines (SWT). This system, devised for grid connection, with variable-speed regulation, and a direct-drive shaft, may be built with commercial equipment. It has been demonstrated that: (i) the system may be operated at variable-speeds in a satisfactory way, as it maintains both speed and power limits simultaneously and ensures optimal system performance within the set limits; and that (ii) the drop in the performance relative to its nominal value is about 75%, when operating at 50% of the nominal power, which is a reasonable value. Therefore, its simplicity, robustness and cost make it a feasible implementation that can compete in the VSWT market segment.

4.1. Variable-Speed Operation

The tests presented demonstrate that the system operates satisfactorily at variable-speeds, showing good dynamic control both at the operating point and at the working limits. The system accurately tracks the set speed, as can be seen in Figure 6b and Figure 9b. It has three operational modes: optimum operational point, maximum rotational speed operation, and maximum power operation.

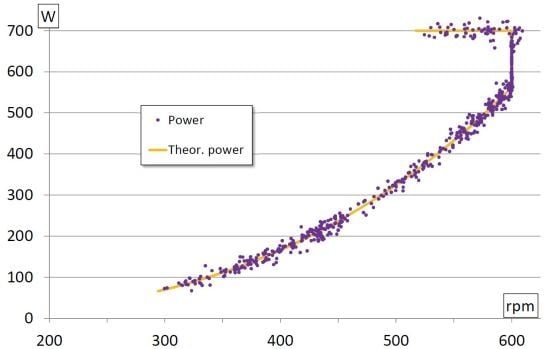
• The control operates the turbine at its optimum point speed, when the maximum rotational speed and the maximum power limit are not reached. The turbine speed, given by Equation (11), is set to generate maximum power, which may be seen from Figure 7b and Figure 10b. The most distant points of the theoretical lines are due to data readings of transient periods.
• When the maximum rotational speed is reached, the control maintains turbine operation at its maximum, as seen in Figure 10b. The use of a frequency converter means that the speed limit control is very accurate.
• The control unit maintains the maximum admissible power generated by the turbine at high winds, by reducing its rotational speed, as seen in Figure 7b and Figure 10b. This causes a transient period where the power generated is above the maximum limit, because the torque increases, and because of wind turbine and generator inertia. For the sake of simplicity, wind turbine inertia is not considered in this study, because of its small influence on SWTs. The system surpasses the maximum power limit by less than 10% and only for a short time during the transient periods. This can be seen in Figure 7b and Figure 10b. These transient periods are not dangerous for the generator, as there is no significant overheating.

4.2. Relative Performance

The test results also demonstrate that the drop in the relative performance of the system with respect to the nominal operational conditions in low power regimes is reasonable. Maximum performance of the generator and the frequency converter are achieved when operating near the maximum nominal values. In this study, the drop in performance at low power regimes is presented, assuming the systems operate at 100% of the nominal value of generated power. This makes the results less-dependent on the absolute performance values of the chosen generator and frequency converter.

Relative performance at the nominal maximum power (600 W for first test and 700 W for second test) is set to 1, as shown in Figure 7a and Figure 10a. When the generated power decreases to 75% of the nominal, the relative performance is about 85%. When generated power is at 50% of the nominal power, the relative performance is at about 75%. For power generated at 25% of nominal power, the relative performance is at about 65%. The points of the relative performance have a dispersion rate due to the variable wind speed transient periods. Table 2 and Table 3 present the average values of relative performance for the three operational modes. As the aggregated values are strongly dependent on the chosen wind profile, they are presented as examples of the average operation of the proposed generator system.

4.3. Advantages and Disadvantages of the Proposed Wind Turbine

First, the proposed system with an asynchronous generator is reliable, robust and simple. Very small wind turbines (VSWT) frequently use permanent magnet synchronous generators (PMSG). PMSG are, in general, bulky and expensive in comparison with SCIG. The SCIG is very rugged, its operational reliability is better than a PMSG machine, it requires little maintenance, is widely used and inexpensive. Second, commercial frequency converters are versatile and have the capacity to be configured for different generators and turbines. Once the turbine power curve [$C_P\left(\lambda \right)$] is known, wind turbine operation may be controlled without measuring the wind speed. Frequency converters have a very fast transient response. They can run the generator as a motor for start-up, and can quickly stop the turbine. Continuous power generation from zero to the highest turbine speed is possible. The line side power factor is unity with no harmonic current injection, and the inverter may be operated as a VAR/harmonic compensator when spare capacity is available [36,37]. As the generator is running at light loads most of the time, the machine rotor flux can be reduced from the rated value to reduce the core loss and thereby increase machine-converter system efficiency. Modern frequency converters have the option of inserting a built-in controller, to program the control strategies for optimal operation and maximum power and speed limits. The built-in programmable control unit could be also used to implement start-up techniques, or fine tune the optimum operational point tracking of the turbine, due to the variables such as air density, or changes in the turbine curve due to dirt or other factors. Finally, the generated energy can be supplied to the grid directly using a double-side frequency converter or a commercial regenerative braking unit connected to the converter DC link. The generated energy may either be consumed as DC, connecting the loads to the DC converter link, or may be stored in a battery bank.

The main disadvantage of the proposed wind turbine configuration is that the asynchronous generator requires an initial excitation to begin to generate electricity, which means it is more appropriate for grid connection. Nevertheless, autonomous operation is also possible either with a start-up capacitor [28] or with a battery connected to the DC link. Secondly, the converter rating has to be similar to the rated power of the generator, because it converts the total energy that is generated. Finally, it requires standby power consumption, due to the control circuit of the converter, which could be significant at low winds.

Overall, considering the above advantages, and with the present trend of decreasing converter and control unit costs, this type of conversion system has the potential to be widely accepted in the future.

4.4. Limitations and Strengths of This Study

The first limitation is that this study used a motor to simulate a wind turbine. This allowed us to carry out the tests in a controlled environment, without reliance on natural wind resources and actual wind turbines. Second, for the sake of simplicity, neither motor rotor inertia nor turbine inertia have been taken into account. Nevertheless, as the study is for SWTs, turbine inertia has little influence on operation, making the regime transitions smoother. Detailed explanations of the wind turbine model taking in account the turbine inertia is given in [5]. Third, the energy generated in the test has been consumed in dissipative resistances. Nevertheless, the energy that is generated can be supplied to the grid directly through a double-sided frequency converter. Moreover, the control program has been implemented in a PC and a data acquisition unit. Nevertheless, modern frequency converters have the option of a built-in controller.

To our knowledge, no other study has dynamically tested the operation of a wind turbine based on SCIG with a frequency converter, which is controlled to operate at its optimum point and that limits the maximum rotational speed and power limit. A further strong point is that the results are from real tests rather than computer simulations. Finally, the experimental success of the prototype considered in this paper can be replicated in the field with real SWTs. The proposed control can be used for a given turbine, substituting the power coefficient curve C_P used in this study, defined in Equations (3) and (4) and presented in Figure 3a, by its own power coefficient curve.

5. Conclusions

This paper has presented the variable-speed operation of a VSWT that is built with a SCIG and a frequency converter. Devised for grid connections, this system has a direct-drive shaft, and may be built with commercial equipment. The study has demonstrated that, under test conditions, the system operates at variable-speeds in a satisfactory way, maintaining both speed and power limits simultaneously and ensuring optimal system performance within the set limits. The drop in performance relative to its nominal value when operating at low regimes, is reasonable. Therefore, its simplicity, robustness and cost make it a feasible implementation that has the potential to gain wide acceptance in the VSWT market segment.