A Vector-Controlled Distributed Generator Model for a Power Flow Based on a Three-Phase Current Injection Method
Abstract
:1. Introduction
2. Power Flow Model for a DG
2.1. DG Overview

2.2. Steady-State Phase Current Output Models
| Property | Type 1 DG | Type 2 DG | Type 3 DG |
|---|---|---|---|
| Output filter | L, LC, LCL | LC | LCL |
| Controlled current | IDG | IVSC | IVSC |
| Equivalent circuit | 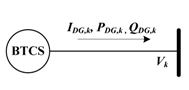 |  | 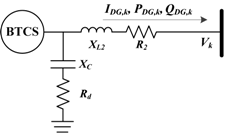 |
3. Implementation of the TCIM Power Flow
3.1. Basic Equations
- ,
- real and imaginary parts of current mismatch;
- ,
- real and imaginary parts of bus admittance matrix;
- ,
- real and imaginary parts of phase voltage;
- ,
- active and reactive power injections of load;
- ,
- real and imaginary parts of output current of the DG.
3.2. Structure of the Jacobian Matrix

3.3. Calculation of the Jacobian Matrix
3.4. Representation of the Reactive Power Limit


3.5. Power Flow Procedure
- Step 1:
- Determine the bus model for the voltage-control-mode DG-connected buses, based on the rules shown in Figure 4;
- Step 2:
- Calculate the three-phase reactive power outputs of the bounded PQ buses, using Equation (53);
- Step 3:
- Calculate the current and voltage mismatches, using Equations (14), (15) and (25);
- Step 4:
- Test the convergence: if the absolute values of all mismatches are within the convergence tolerance, terminate the power flow; otherwise, go to Step 5;
- Step 5:
- Calculate the Jacobian matrix;
- Step 6:
- Update the state variable vector using Equation (31), and go to Step 1.
3.6. Modifications for Type 1 DG
- (1)
- The second terms of Equations (16)–(21) are eliminated;
- (2)
- γk in Equationa (16)−(21) and Equations (37)–(42) is set equal to zero;
- (3)
- The last two matrices of Equation (36) are eliminated; and
- (4)
- Equation (53) is modified to
4. Case Studies and Results
4.1. Verification of Accuracy

| Property | Value | Unit |
|---|---|---|
| Maximum q-axis current, iq,max | 650 | A |
| Minimum q-axis current, iq,min | −650 | A |
| System frequency, fsys | 60 | Hz |
| Switching frequency, fsw | 10 | kHz |
| Converter side inductance, L1 | 0.25 | mH |
| Grid side inductance, L2 | 0.11 | mH |
| Capacitance, C | 279 | μF |
| Damping resistance, Rd | 0.17 | Ω |
4.1.1. Reactive Power Control-Mode DG




4.1.2. Voltage Control-Mode DG

4.2. Application to a Large Distribution System
- Case 1:
- Each DG operates in reactive power control mode. The reactive power reference value is set at 0 kVar. The DG-connected buses are modeled as PQ buses;
- Case 2:
- Each DG operates in voltage control mode. The reference voltage is 1.03 pu. A q-axis current limit is not imposed (i.e., the current is not bounded). Therefore, the DG-connected buses are always modeled as PV buses;
- Case 3:
- The operating mode and reference voltage are the same as in Case 2, but a q-axis current limit is included. The DG-connected buses can be modeled as either PV buses or bounded PQ buses, depending on the q-axis current and voltage mismatch.
| Property | Value | Unit |
|---|---|---|
| AC voltage, Vac | 690 | V |
| Maximum q-axis current, iq,max | 100 | A |
| Minimum q-axis current, iq,min | −100 | A |
| Grid side inductance, L2 | 0.3 | mH |
| Capacitance, C | 27.8 | μF |
| Damping resistance, Rd | 0.9 | Ω |


5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Deshmukh, S.; Natarajan, B. Voltage/VAR control in distribution networks via reactive power injection through distributed generators. IEEE Trans. Smart Grid 2012, 3, 1226–1234. [Google Scholar] [CrossRef]
- Kim, Y.J.; Ahn, S.J.; Hwang, P.I.; Pyo, G.C.; Moon, S.I. Coordinated control of a DG and voltage control devices using a dynamic programming algorithm. IEEE Trans. Power Syst. 2013, 28, 42–51. [Google Scholar] [CrossRef]
- Hen-Geul, Y.; Gayme, D.F.; Low, S.H. Adaptive VAR control for distribution circuits with photovoltaic generators. IEEE Trans. Power Syst. 2012, 27, 1656–1663. [Google Scholar]
- Saadat, H. Power System Analysis; McGraw Hill: Singapore, 1999. [Google Scholar]
- Zhu, Y.; Tomsovic, K. Adaptive power flow method for distribution systems with dispersed generation. IEEE Trans. Power Deliv. 2002, 13, 822–827. [Google Scholar] [CrossRef]
- Jan-E-Alam, M.; Muttaqi, K.M.; Sutanto, D. Assessment of Distributed Generation Impacts on Distribution Networks Using Unbalanced Three-Phase Power Flow Analysis. In Proceedings of 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8.
- Khushalani, S.; Solanki, J.M.; Schulz, N.N. Development of three-phase unbalanced power flow using PV and PQ models for distributed generation and study of the impact of DG models. IEEE Trans. Power Syst. 2007, 22, 1019–1025. [Google Scholar] [CrossRef]
- Farag, H.E.; El-Saadany, E.F.; El Shatshat, R.; Zidan, A. A generalized power flow analysis for distribution systems with high penetration of distributed generation. Electr. Power Syst. Res. 2011, 81, 1499–1506. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Mashhour, E. Distributed generation modeling for power flow studies and a three-phase unbalanced power flow solution for radial distribution systems considering distributed generation. Electr. Power Syst. Res. 2009, 79, 680–686. [Google Scholar] [CrossRef]
- Li, F.; Broadwater, R.; Thompson, J.; Goodman, F. Analysis of Distributed Resources Operating in Unbalanced Distribution Circuits. In Proceedings of 2000 IEEE Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000; pp. 2315–2319.
- Nor, K.M.; Abdel-Akher, M. Analysis of Three Phase Distribution Networks with Distributed Generation. In Proceedings of IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; pp. 1563–1568.
- Kamh, M.Z.; Iravani, R. Unbalanced model and power flow analysis of microgrids and active distribution systems. IEEE Trans. Power Deliv. 2010, 25, 2851–2858. [Google Scholar] [CrossRef]
- Kamh, M.Z.; Iravani, R. Unified model of three-phase electronically coupled distributed energy resources for power-flow analysis. IEEE Trans. Power Deliv. 2011, 26, 899–909. [Google Scholar] [CrossRef]
- Abdel-Akher, M.; Mahmoud, K. Unbalanced distribution power-flow model and analysis of wind turbine generating systems. Int. Trans. Electr. Energy Syst. 2012, 23, 689–700. [Google Scholar] [CrossRef]
- Abdel-Galil, T.K.; Abu-Elanien, A.E.B.; El-Saadany, E.F.; Girgis, A.; Mohamed, Y.A.-R.I.; Salama, M.M.A.; Zeineldin, H.H. Final Report: Protection Coordination Planning with Distributed Generation; Natural Resources Canada (NRCan), CETC Varennes—Energy Technology and Programs Sector: Québec, Canada, 2007. [Google Scholar]
- Garcia, P.A.N.; Pereira, J.L.R.; Carneiro, S., Jr.; da Costa, V.M.; Martins, N. Three-phase power flow calculations using the current injection method. IEEE Trans. Power Syst. 2000, 15, 508–514. [Google Scholar] [CrossRef]
- Garcia, P.A.N.; Pereira, J.L.R.; Carneiro, S., Jr. Voltage control devices models for distribution power flow analysis. IEEE Trans. Power Syst. 2001, 16, 586–594. [Google Scholar] [CrossRef]
- Da Costa, V.M.; Oliveira, M.L.; Guedes, M.R. Developments in the analysis of unbalanced three-phase power flow solutions. Int. J. Electr. Power Energy Syst. 2007, 29, 175–182. [Google Scholar] [CrossRef]
- De Araujo, L.R.; Penido, D.R.R.; Carneiro, S., Jr.; Pereira, J.L.R.; Garcia, P.A.N. Comparisons between the three-phase current injection method and the forward/backward sweep method. Int. J. Electr. Power Energy Syst. 2010, 32, 825–833. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltatic and Wind Power Systems; Wiley-IEEE Press: Singapore, 2011. [Google Scholar]
- Ahmed, K.H.; Finney, S.J.; Williams, B.W. Passive Filter Design for Three-Phase Inverter Interfacing in Distributed Generation. In Proceedings of 2007 Compatibility in Power Electronics, Gdansk, Poland, 29 May–1 June 2007; pp. 1–9.
- Twining, E.; Holmes, D.G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter. IEEE Trans. Power Electron. 2003, 18, 888–895. [Google Scholar] [CrossRef]
- Shen, G.; Xu, D.; Xi, D.; Yuan, X. An improved control strategy for grid-connected voltage source inverters with a LCL filter. IEEE Trans. Power Electron. 2008, 23, 1899–1906. [Google Scholar] [CrossRef]
- Garcia, P.A.N.; Pereira, J.L.R.; Carneiro, S.; Vinagre, M.P.; Gomes, F.V. Improvements in the representation of PV buses on three-phase distribution power flow. IEEE Trans. Power Deliv. 2004, 19, 894–896. [Google Scholar] [CrossRef]
- Prusty, B.K.; Ali, S.M.; Sahoo, D.K. Modeling and control of grid-connected hybrid photovoltaic/battery distributed generation system. Int. J. Eng. Res. Technol. 2012, 1, 1–10. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, E.S. PSCAD/EMTDC-based modeling and analysis of a gearless variable speed wind turbine. IEEE Trans. Energy Convers. 2007, 22, 421–430. [Google Scholar] [CrossRef]
- Distribution Test Feeders. Available online: http://ewh.ieee.org/soc/pes/dsacom/testfeeders/index.html (accessed on 17 May 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hwang, P.-I.; Moon, S.-I.; Ahn, S.-J. A Vector-Controlled Distributed Generator Model for a Power Flow Based on a Three-Phase Current Injection Method. Energies 2013, 6, 4269-4287. https://doi.org/10.3390/en6084269
Hwang P-I, Moon S-I, Ahn S-J. A Vector-Controlled Distributed Generator Model for a Power Flow Based on a Three-Phase Current Injection Method. Energies. 2013; 6(8):4269-4287. https://doi.org/10.3390/en6084269
Chicago/Turabian StyleHwang, Pyeong-Ik, Seung-Il Moon, and Seon-Ju Ahn. 2013. "A Vector-Controlled Distributed Generator Model for a Power Flow Based on a Three-Phase Current Injection Method" Energies 6, no. 8: 4269-4287. https://doi.org/10.3390/en6084269
APA StyleHwang, P.-I., Moon, S.-I., & Ahn, S.-J. (2013). A Vector-Controlled Distributed Generator Model for a Power Flow Based on a Three-Phase Current Injection Method. Energies, 6(8), 4269-4287. https://doi.org/10.3390/en6084269





