Prognostics of Lithium-Ion Batteries Based on Battery Performance Analysis and Flexible Support Vector Regression
Abstract
:1. Introduction
2. Analysis of Lithium-Ion Battery Capacity Degradation
2.1. Experimental Equipment and Data Sources
2.2. Capacity Degradation
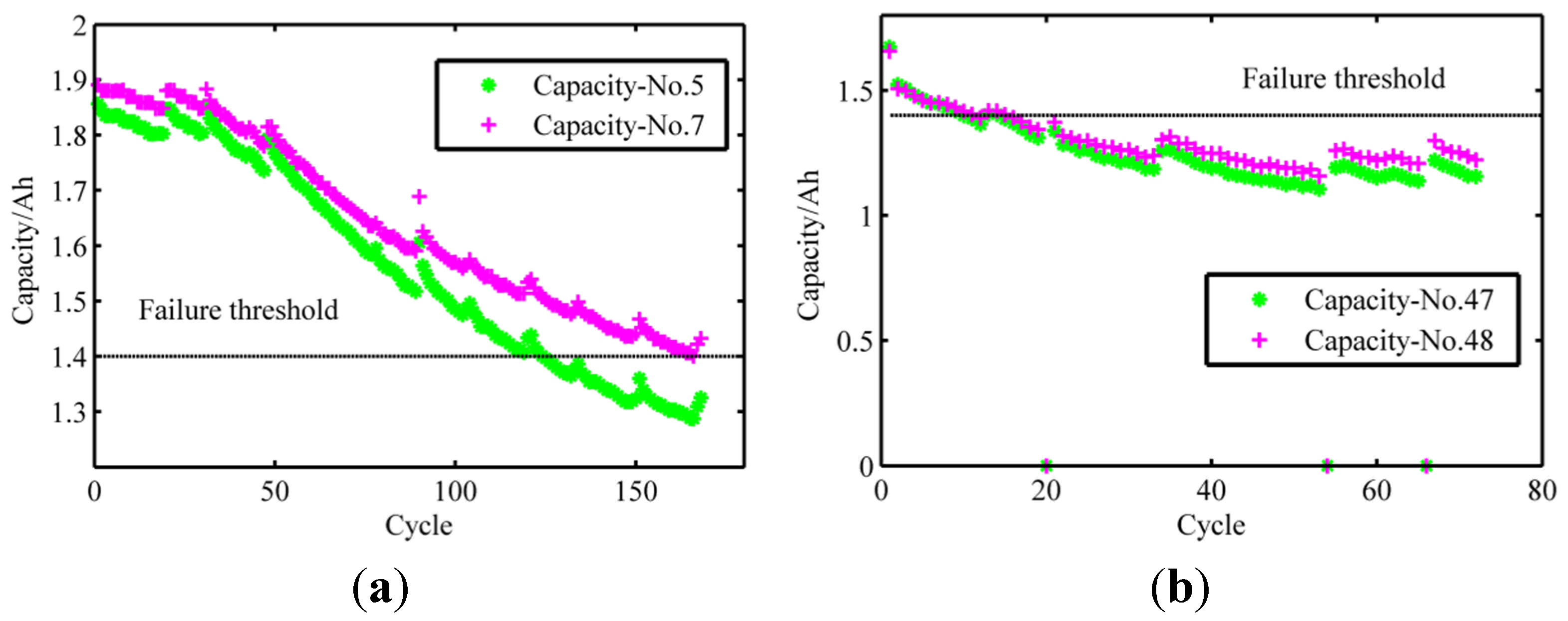
3. Energy Efficiency and Working Temperature
| Symbols | Description | Symbols | Description |
|---|---|---|---|
| ICi | Charge current in the ith cycle | WCi | Charge power in the ith cycle |
| IDi | Discharge current in the ith cycle | WDi | Discharge power in the ith cycle |
| UCi | Charge voltage in the ith cycle | ηi | Energy efficiency in the ith cycle |
| UDi | Discharge voltage in the ith cycle | Ci | The capacity in the ith cycle |
| tCi | Charge time in the ith cycle | i | Cycle |
| tDi | Discharge time in the ith cycle | RUL | Remaining useful life |
| wti | Temperature in the ith cycle | SVR | Support vector regression |
| T | Ambient temperature | F-SVR | Flexible support vector regression |
| bti | Working temperature in the ith cycle | SSE | Sum of squared errors |
| W | Power of the battery | RMSE | Root mean square error |

3.1. Energy Efficiency
3.2. Working Temperature
4. Prediction of the Remaining Useful Life for Lithium-Ion Batteries

4.1. Support Vector Regression
4.2. Flexible Support Vector Regression

4.3. Non-Iterative Prediction Model
4.4. Iterative Multi-Step Prediction Model
5. Prognostic Results and Discussion

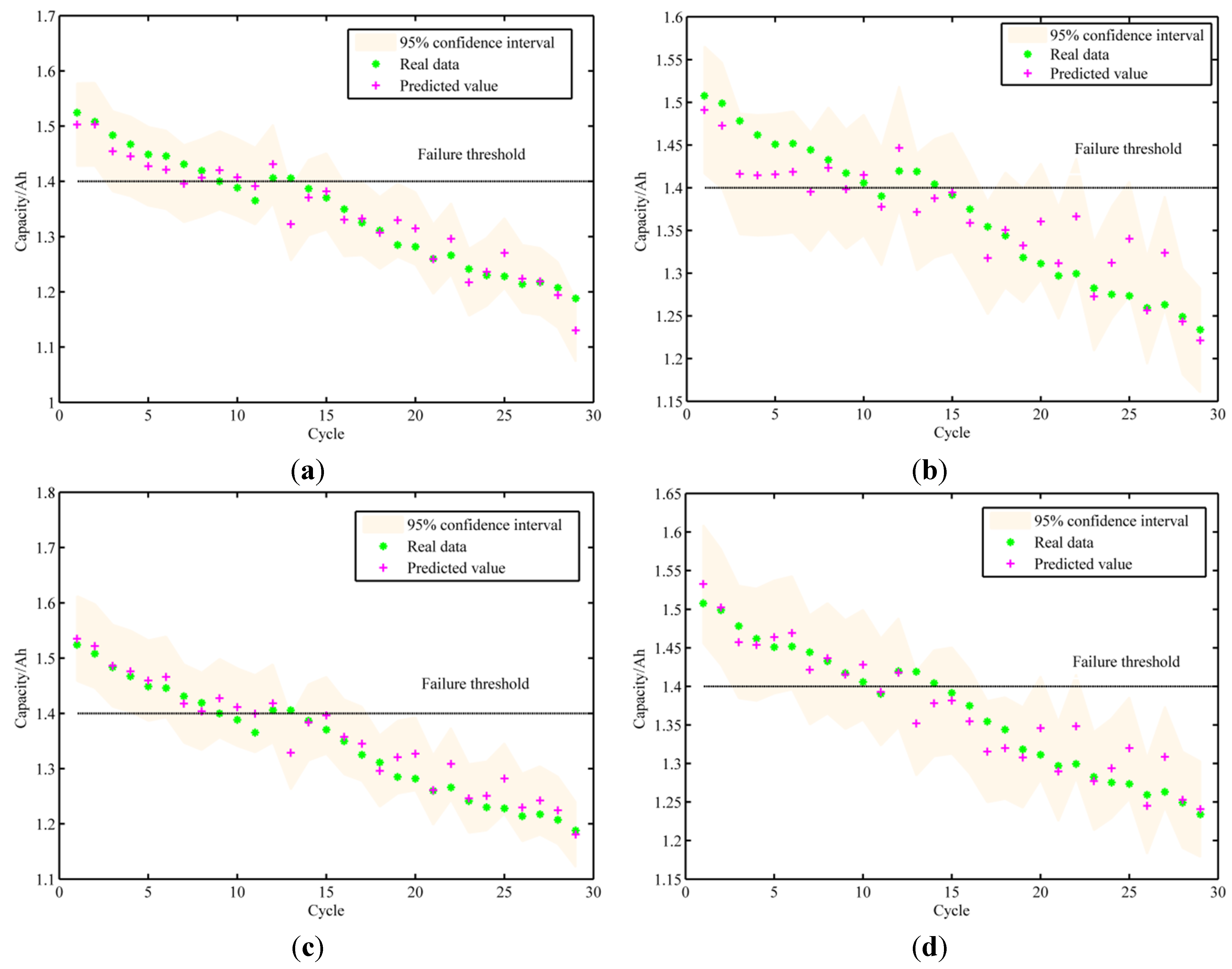
| Battery | Method | SSE | RMSE | Real cycle | Predictive cycle | ERUL |
|---|---|---|---|---|---|---|
| No. 5’s odd-number cycle | SVR | 0.6378 | 0.0394 | 62 | 60 | 2 |
| F-SVR | 0.1250 | 0.0231 | 62 | 61 | 1 | |
| No. 7 | SVR | 0.6216 | 0.0202 | 168 | 168 | 0 |
| F-SVR | 0.8642 | 0.0407 | 168 | 150 | 18 | |
| No. 47 | SVR | 0.0369 | 0.0097 | 10 | 7 | 3 |
| F-SVR | 0.0337 | 0.0099 | 10 | 11 | 1 | |
| No. 48 | SVR | 0.0473 | 0.0050 | 11 | 9 | 2 |
| F-SVR | 0.0318 | 0.0069 | 11 | 11 | 0 |
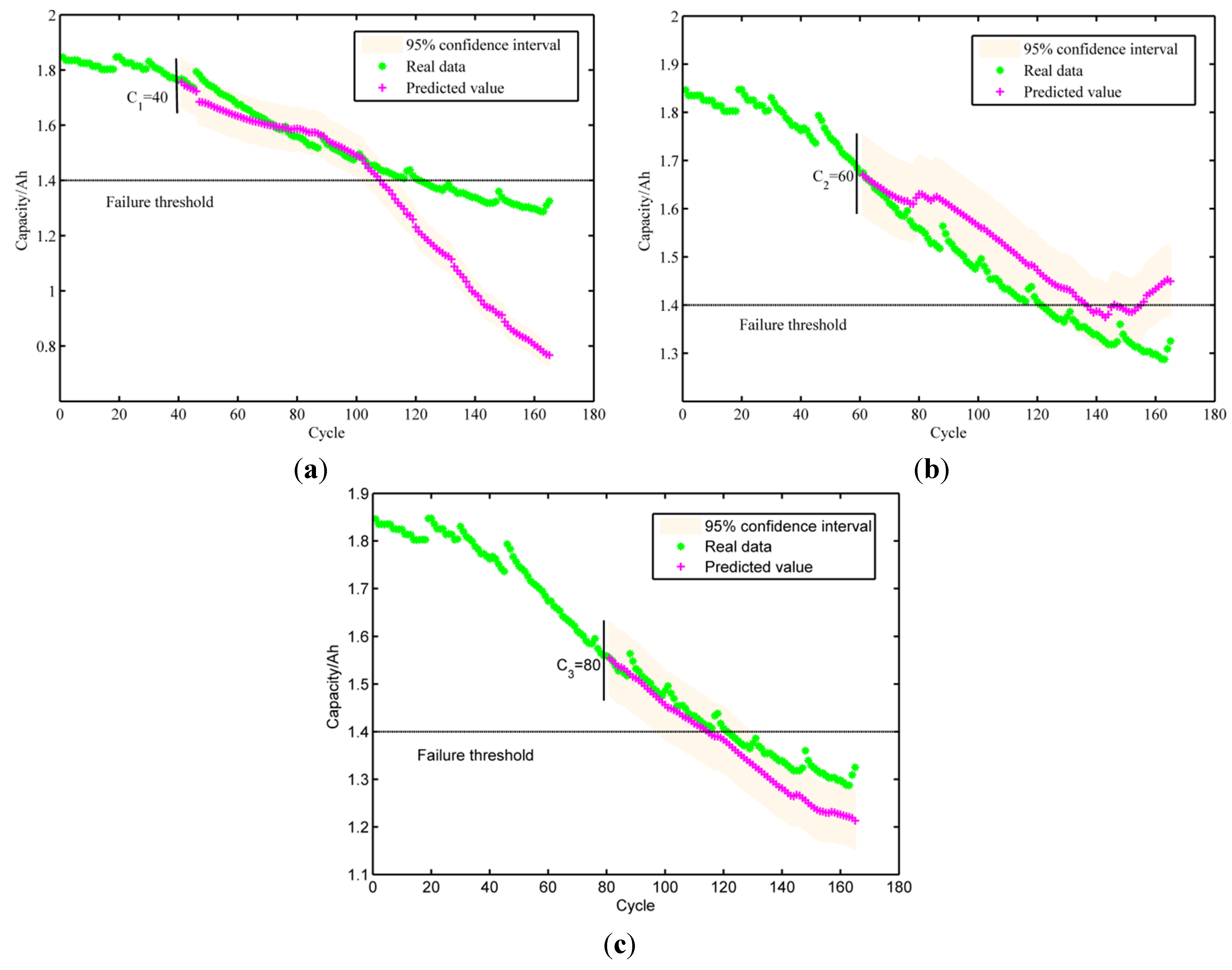
| ith cycle | SSE | RMSE | Real Cycle | Predictive Cycle | ERUL |
|---|---|---|---|---|---|
| 40th cycle | 6.7649 | 0.1150 | 124 | 112 | 12 |
| 60th cycle | 0.6719 | 0.0210 | 124 | 140 | 16 |
| 80th cycle | 0.2807 | 0.0300 | 124 | 118 | 6 |
6. Conclusions
- (1)
- the energy efficiency and the battery working temperature are used as input physical characteristics of the two proposed models;
- (2)
- the energy efficiency is found to be closely related to the capacity of the lithium-ion battery;
- (3)
- a non-iterative prediction model based on the F-SVR method is proposed;
- (4)
- an iterative multi-step prediction model based on the SVR method is proposed.
Acknowledgments
Conflicts of Interest
References
- He, Z.; Gao, M.; Wang, C.; Wang, L.; Liu, Y. Adaptive state of charge estimation for Li-ion batteries based on an unscented Kalman filter with an enhanced battery model. Energies 2013, 6, 4134–4151. [Google Scholar] [CrossRef]
- Liu, D.; Wang, H.; Peng, Y.; Xie, W.; Liao, H. Satellite lithium-ion battery remaining cycle life prediction with novel indirect health indicator extraction. Energies 2013, 6, 3654–3668. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Source 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Jungst, R.G.; Nagasubramanian, G.; Case, H.L.; Doughty, D.H. Modeling capacity fade in lithium-ion cells. J. Power Source 2005, 140, 157–161. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons learned from the 787 Dreamliner issue on lithium-ion battery reliability. Energies 2013, 6, 4682–4695. [Google Scholar] [CrossRef]
- Chen, Y.; Miao, Q.; Zheng, B.; Wu, S.; Pecht, M. Quantitative analysis of lithium-ion battery capacity prediction via adaptive bathtub-shaped function. Energies 2013, 6, 3082–3096. [Google Scholar] [CrossRef]
- Jin, G.; Matthews, D.E.; Zhou, Z. A Bayesian framework for online degradation asseeement and residual life prediction of secondary batteries inspacecraft. Reliab. Eng. Syst. Saf. 2013, 113, 7–20. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Wang, X.X.; Ma, L.Y. A compact K nearest neighbor classification for power plant fault diagnosis. J. Inf. Hiding Multimed. Signal Process. 2014, 5, 508–517. [Google Scholar]
- Zhang, Q.; White, R.E. Capacity fade analysis of a lithium ion cell. J. Power Source 2008, 179, 793–798. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Groot, J. State-of-Health Estimation of Li-Ion Batteries: Cycle Life Test Methods; Chalmers University of Technology: Göteborg, Sweden, 2012. [Google Scholar]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Source 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Le, D.; Tang, X. Lithium-ion battery state of health estimation using Ah-V characterization. In Proceedings of the Annual Conference of Prognostics and Health Management (PHM) Society, Montreal, QC, Canada, 25–29 September 2011; pp. 367–373.
- Tang, S.; Yu, C.; Wang, X.; Guo, X.; Si, X. Remaining useful life prediction of lithium-ion batteries based on the wiener process with measurement error. Energies 2014, 7, 520–547. [Google Scholar] [CrossRef]
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectron. Reliab. 2013, 53, 805–810. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Chen, C.; Pecht, M. Prognostics of lithium-ion batteries using model-based and data-driven methods. In Proceedings of the 2012 IEEE Conference on Prognostics and System Health Management (PHM), Beijing, China, 23–25 May 2012; pp. 1–6.
- Fan, Z.; Liu, G.; Si, X.; Zhang, Q. Degradation datadriven approach for remaining useful life estimation. J. Syst. Eng. Electron. 2013, 24, 173–182. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Source 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Fleischer, C.; Wang, W.; Bai, Z.; Sauer, D.U. On-line self-learning time forward voltage prognosis for lithium-ion batteries using adaptive neuro-fuzzy inference system. J. Power Source 2013, 243, 728–749. [Google Scholar] [CrossRef]
- Chang, W.Y. Estimation of the state of charge for a LFP battery using a hybrid method that combines a RBF neural network, an OLS algorithm and AGA. Int. J. Electr. Power Energy Syst. 2013, 53, 603–611. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L. On-line equalization for lithium-ion battery packs based on charging cell voltages: Part 2. Fuzzy logic equalization. J. Power Source 2014, 247, 460–466. [Google Scholar] [CrossRef]
- Álvarez Antón, J.; García Nieto, P.; Blanco Viejo, C.; Vilán Vilán, J. Support vector machines used to estimate the battery state-of-charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Source 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tusi, K.T. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Yi, H.; Song, X.F.; Jiang, B.; Liu, Y.F.; Zhou, Z.H. Flexible support vector regression and its application to fault detection. Acta Autom. Sin. 2013, 39, 272–284. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery Data Set; National Aeronautics and Space Administration (NASA) Ames Prognostics Data Repository: Moffett Field, CA, USA, 2007. [Google Scholar]
- Xue, X.; Wang, S.; Guo, W.; Zhang, Y.; Wang, Z.L. Hybridizing energy conversion and storage in a mechanical-to-electrochemical process for self-charging power cell. Nano Lett. 2012, 12, 5048–5054. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.S.; Perkins, P.; Schneider, M.E. Pulse Charge Technique to Trickle Charge a Rechargeable Battery. U.S. Patent 5,539,298, 23 July 1996. [Google Scholar]
- Zhang, W.; Duan, D.; Yang, L. Relay selection from a battery energy efficiency perspective. In Proceedings of the IEEE MILCOM 2009 on Military Communications Conference, Boston, MA, USA, 18–21 October 2009; pp. 1–7.
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer-Verlag: Berlin, Germany, 1995. [Google Scholar]
- Hao, P.Y. New support vector algorithms with parametric insensitive/margin model. Neural Netw. 2010, 23, 60–73. [Google Scholar] [CrossRef] [PubMed]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhao, L.; Su, X.; Ma, P. Prognostics of Lithium-Ion Batteries Based on Battery Performance Analysis and Flexible Support Vector Regression. Energies 2014, 7, 6492-6508. https://doi.org/10.3390/en7106492
Wang S, Zhao L, Su X, Ma P. Prognostics of Lithium-Ion Batteries Based on Battery Performance Analysis and Flexible Support Vector Regression. Energies. 2014; 7(10):6492-6508. https://doi.org/10.3390/en7106492
Chicago/Turabian StyleWang, Shuai, Lingling Zhao, Xiaohong Su, and Peijun Ma. 2014. "Prognostics of Lithium-Ion Batteries Based on Battery Performance Analysis and Flexible Support Vector Regression" Energies 7, no. 10: 6492-6508. https://doi.org/10.3390/en7106492
APA StyleWang, S., Zhao, L., Su, X., & Ma, P. (2014). Prognostics of Lithium-Ion Batteries Based on Battery Performance Analysis and Flexible Support Vector Regression. Energies, 7(10), 6492-6508. https://doi.org/10.3390/en7106492




