A Zero Input Current Ripple ZVS/ZCS Boost Converter with Boundary-Mode Control

Abstract

In this paper, in order to achieve zero ripple conditions, the use of a ripple mirror (RM) circuit for the boost converter is proposed. The operation modes are studied and steady-state analyses performed to show the merits of the proposed converter. It is found that the proposed RM circuit technique can provide much better flexibility than the two-phase interleaved boost converter for locating the zero ripple operating point in the design stage. In addition, the choice of using a boundary-mode control is mainly based on the consideration of achieving both ZVS (zero voltage switching)/ZCS (zero current switching) soft-switching and constant on-time control for the converter. To verify the performance of the proposed converter, a 48 V input and 200 W/200 V output prototype is constructed. Experimental results verify the effectiveness of the proposed converter.

1. Introduction

Given Earth’s limited stores of fossil fuels and the consequences of their usage in the environment, various alternative energy sources have now been explored and developed. Unfortunately, multiple complications exist with such energy sources: for example, fuel cells and photovoltaic modules cannot accept currents in the reverse direction, do not perform well with current ripples, and have low voltage characteristics [1,2,3,4,5,6,7,8,9,10,11]. For these reasons, normally a boost converter is required to step-up and regulate the input voltage to a higher value [3,4,6,7,8,9,10,11]. However, the inherent inductor current ripple of the boost converter causes a high frequency input in the current ripple [6,7,9].

Various essays have been presented to solve the problems caused by the high frequency current ripple [5,6,7,8,9,10,11]. Generally speaking, a large electrolytic capacitor can be used in a converter DC (direct current) link to absorb harmonics. However, an electrolytic capacitor has poor reliability, limited temperature rating, poor shelf life, higher equivalent series resistance (ESR), and is large in size. In [5], a high frequency active filter is adopted as a solution to eliminate the DC link electrolytic capacitor. This solution has been verified by simulation studies on a three-phase pulse-width modulation (PWM) inverter system.

One common method is to adopt interleaved boost converters to minimize the high frequency input ripples [8,9,10,11]. Nevertheless, the interleaved control still suffers from several disadvantages. First, as a single converter module, it is not possible to implement the corresponding interleaved control strategy. Second, there is no guarantee that the various inductors have identical characteristics, so harmonic current elimination may not be optimal and current balancing issues should be considered [8,10,11].

In [7], a mirror of the boost converter called “Ripple Mirror (RM) Circuit” is introduced and this structure presents the other drawback to be only efficient in steady-state and continuous conduction mode (CCM) operation. In addition, experimental results are lacking in this essay and the estimated conversion efficiency is relatively low due to hard switching.

In this paper, a ZVS (zero voltage switching)/ZCS (zero current switching) boost converter with RM circuit and boundary-mode control to achieve the zero input current ripple is presented. It is found that the proposed RM circuit technique can provide a much better flexibility than the two-phase interleaved boost converter for locating the zero ripple operating point in the design stage. In addition, the choice of using a boundary-mode control is mainly due to taking in the consideration the achieving of both ZVS/ZCS soft-switching and constant on-time control for the converter. An experimental 200 W power rating prototype is constructed, and the measured results indeed verify the effectiveness of the proposed converter.

2. Circuit Topology and Operation Principle

2.1. Configuration of the Proposed Converter

The RM circuit configuration is dependent upon the concerned converter configuration. As the illustration shows, the commonly used simple boost converter will be considered for applying the proposed RM circuit principle. Figure 1 shows the complete configuration of the proposed zero input ripple boost converter, which could also be integrated into a local distributed generation (DG) system [4,8,9]. This architecture makes it easier to distribute the DC power generated by the renewable energy sources or energy storage devices [4]. From Figure 1, it can be seen that the RM circuit is composed of two power MOSFETs, S_RM and S'_RM, a RM inductor L_RM, and a blocking capacitor C_B.

As observed from Figure 1, the input current i_s is the sum of inductor current i_L and the RM inductor current i_RM. Also, due to the mirror control signals, when switches S and S_RM are turned on i_L will be increased generating a linearly increasing ripple current as shown in Figure 2a for 0 < t <dT_s. At the same time, switch S'_RM is turned off, and current i_RM will decrease generating a linearly decreasing ripple current as shown in Figure 2b for 0 < t < dT_s. Hence, with proper design a zero input ripple effect can be achieved as shown in Figure 2c for 0 < t < dT_s. Similarly, the same ripple canceling effect can be achieved for distinct.

Figure 1. Configuration of the zero input current ripple ZVS/ZCS boost converter.

Figure 1. Configuration of the zero input current ripple ZVS/ZCS boost converter.

Figure 2. Steady-state current waveforms of the proposed converter (a) inductor current i_L; (b) RM (Ripple Mirror) inductor current i_LRM and (c) input current i_s.

Figure 2. Steady-state current waveforms of the proposed converter (a) inductor current i_L; (b) RM (Ripple Mirror) inductor current i_LRM and (c) input current i_s.

2.2. Operation Principle of the Proposed Converter with Boundary-Mode Control Strategy

For simplicity, the equivalent circuit of the proposed converter can be depicted as shown in Figure 3a, where R_L and R_C, R_RM and R_CB are ESRs of the corresponding inductors and capacitors. In addition, assuming that the power flow is unidirectional, one can replace MOSFET S' with a simple diode while the corresponding control circuit can be ignored. The gating signals as well as the voltage and current waveforms of the key components are shown in Figure 3b. From it, one can see that the gate signals of the ripple mirror circuit are the same as that of the conventional boost converter. The operation principle of the proposed converter can be analyzed and described mode by mode under assumptions: (1) all components are assumed to be ideal components except capacitors and inductors; (2) the proposed converter is operated under boundary-mode control, and is in the steady-state.

Figure 3. (a) The equivalent circuit of the corresponding power circuit, and (b) the gate signals and key voltage and current waveforms of the proposed converter.

Figure 3. (a) The equivalent circuit of the corresponding power circuit, and (b) the gate signals and key voltage and current waveforms of the proposed converter.

2.2.1. Mode 1: t₀ ≤ t ≤ t₁ = dT_s

Figure 4 shows the equivalent circuit of the proposed converter in Mode 1. At t₀, the main switch S and the ripple mirror switch S_RM are turned on and the complementary ripple mirror switch S'_RM is turned off. In this mode, source energy of the ideal voltage source V_s is stored in the main inductor L and the energy stored in the capacitor C is discharged to the output resistor R. In the time interval [t₀, t₁], the ripple mirror inductor is reversed biased by the voltage V_CB + V_o − V_s. Hence, one can see from Figure 3b that i_RM decreases from a positive value to a negative value. In other words, the loop current flow directions for intervals [t₀, t₁'] and [t₁', t₁] are different. This explains why the proposed ripple mirror circuit requires an active switch S_RM to achieve bidirectional current flow capability. Also from Figure 4, one can see clearly that the ripple mirror current i_RM can be designed to cancel the ripple of the main inductor current i_L to achieve constant input current i_s. Mode 1 ends when t = dT_s = t₁ and the main switch S as well as the ripple mirror switch S_RM is turned off.

Figure 4. The equivalent circuit of the proposed converter in Mode 1.

Figure 4. The equivalent circuit of the proposed converter in Mode 1.

By using Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL), the corresponding circuit equations in Mode 1 can be obtained as shown in Equations (1)–(6):

(1)

(2)

(3)

(4)

i_S (t) = i_L (t) + i_RM (t)

(5)

(6)

2.2.2. Mode 2: t₁ ≤ t ≤ t₂ = T_s

The equivalent circuit of the proposed converter which contains current loops in Mode 2 is shown in Figure 5. At t₁, the complementary ripple mirror switch S'_RM is turned on, and the main switch S and the ripple mirror switch S_RM are turned off. The energy of the main inductor L is discharged to the output resistor R and the capacitor C in this mode. In the time interval between t₁ and t₂, the ripple mirror inductor is forward biased by the input voltage. Hence, one can see from Figure 3b that i_RM increases from a negative value to a positive value. In other words, the loop current flow directions for intervals [t₁, t₂'] and [t₂', t₂] are different. Similarly, one can observe from Figure 3b that the ripple mirror current i_LRM can be designed to cancel the ripple of the main inductor current i_L to achieve constant input current i_s which is the sum of inductor current i_L and ripple mirror inductor current i_RM. Mode 2 ends when t = T_s = t₂ and the main inductor current i_L reaches zero. The complementary ripple mirror switch S'_RM is turned off and the main switch S as well as the ripple mirror switch S_RM is turned on at the end of Mode 2.

Figure 5. The equivalent circuit of the proposed converter in Mode 2.

Figure 5. The equivalent circuit of the proposed converter in Mode 2.

The corresponding circuit equations in Mode 2 can be obtained by KVL and KCL as shown in Equations (7)–(12):

(7)

(8)

(9)

(10)

i_s (t) = i_L (t) + i_RM (t)

(11)

(12)

2.3. Steady-State Analysis the Proposed Converter

The state-space averaging technique is used to derive the corresponding DC model of the proposed converter following Equations (13)–(18):

(13)

(14)

(15)

0 = DI_RM

(16)

I_s = I_L + I_RM

(17)

(18)

Since the main capacitor ESR R_C is much smaller than the load resistance R (R >> R_C), Equations (13)–(18) can be simplified further as shown in Equations (19)–(24), and the equivalent circuit of the DC model can be expressed as shown in Figure 6. It can be observed that the blocking capacitor C_B blocks the DC current from the primary side of the upper DC transformer. Therefore, the ripple mirror circuit does not process real power, and the RM circuit does not induce much power dissipation:

V_s = R_LI_L + (1 − D)V_C

(19)

V_s = DV_C + DV_CB

(20)

(21)

0 = I_RM

(22)

I_s = I_L

(23)

V_o = V_C

(24)

From the DC model of the proposed converter derived in Equations (19)–(24), it is straightforward to achieve the voltage gain as follows:

(25)

By neglecting the ESR of the main capacitor R_C, Equation (25) can be simplified further as shown in Equation (26):

(26)

Also, substituting V_C into Equation (14), the voltage across the blocking capacitor V_CB, can be expressed in terms of V_s as follows:

(27)

If the ESR of the main inductor R_L is too small to be neglected, with the same approximation, Equation (27) can be simplified further as:

(28)

Furthermore, steady-state input current I_s can be derived from Equation (15) by substituting V_o with Equation (25) as follows:

(29)

Similarly, by neglecting the ESR of the main capacitor R_C, Equation (29) can be simplified further as shown in Equation (30):

(30)

Figure 6. The equivalent circuit of the DC model of the proposed converter.

Figure 6. The equivalent circuit of the DC model of the proposed converter.

3. Analysis, Design and Control Strategy of Proposed Topology

3.1. Analysis of the Boost Converter

From Figure 3b, one can see that the input current i_s can be regarded as a pure DC value. The steady-state main inductor current I_L equals the sum of the inductor current i_L and the ripple mirror inductor current i_RM. Thus, one can derive the relationship between the main inductor L and the ripple mirror inductor L_RM by the sum of di_L/dt and di_RM/dt from the circuit Equations (1) and (2), allow the result to be zero to achieve the following equation:

(31)

From Equation (31), it can be easily found that the inductance of the ripple mirror inductor L_RM is dependent upon the voltage across ESRs of the inductors, namely R_L and R_RM, and the designed duty ratio D_dr. Furthermore, if the designed duty ratio D_dr is over than 0.5, the inductance of the ripple mirror inductor L_RM will be smaller than that of the main inductor L. The input current ripple, Δi_s of the proposed converter can be derived as follows:

(32)

In Equation (32), the magnitude of the peak to peak input current ripple is dependent upon the designed duty ratio D_dr. When D_dr equals d and when assuming R_L × I_L equals zero, the peak to peak input current ripple equals zero. Hence, one can design the zero input current ripple operating point at the desired point. To further understand, a converter prototype with 48 V input, 200 V/200 W output, and switching frequency of 20 kHz specifications, is used to illustrate it, where the resistance of ESR of the is equal to 0.3 Ω and resistance of the output resistor R is equal to 200 Ω. The dissipation term R_LI_L/V_s of the system is about 0.025. Substituting the per unit values of the input current ripple Δi_s, the input voltage V_s, the operation period T_s, and the inductance of the main inductor L into Equation (32) and let the design operating point D_dr be 0.75, one can obtain the following result:

|Δi_s| = |Δi_L + Δi_RM| = |−2.925 + 3.925d|

(33)

Figure 7a shows the absolute value of the peak to peak input current ripple, |Δi_s|, versus duty ratio d with three different techniques. The proposed converter has a smaller input current ripple as compared with the two-phase interleaving control and the conventional boost converter when the duty ratio d is over 0.67. A better view of the ripple canceling capability around the duty ratio d of 0.75 is shown in Figure 7b. It can be seen that the proposed ripple mirror circuit technique possesses a much better ripple canceling capability than others around the designed operating point. Furthermore, unlike the fixed ripple canceling capability curve of the two-phase interleaving control, the proposed ripple mirror circuit shows a much better flexibility of being able to locate the zero input current ripple operating point dependent upon different designs. That means the |Δi_s| curve of the entire converter can be moved to the left or to the right side depending on the design.

Figure 7. The absolute value of the input current ripple, |Δi_s|, versus the duty ratio d with different techniques. (a) With full range of duty ratio d and (b) around the duty ratio d = 0.75.

Figure 7. The absolute value of the input current ripple, |Δi_s|, versus the duty ratio d with different techniques. (a) With full range of duty ratio d and (b) around the duty ratio d = 0.75.

3.2. Design Considerations of Main Components for the Boost Converter

The duty ratio D is determined by the voltage gain of the proposed converter as shown in Equation (25). Considering the voltage drop on ESR of the main inductor, the duty ratio is D = 0.76. Thus, the inductance of the main inductor can be derived as follows:

(34)

The minimum capacitance of the main capacitor C can be found from the equation of the output voltage ripple of the boost converter as follows:

(35)

However, because the ESR of the main capacitor C will enlarge the output voltage ripple, which may also influence the performance of the feedback control loop, the minimum capacitance may not be applied. Hence, one can select a much larger capacitance C = 330 μF of the main capacitor to have a better output voltage ripple and a better feedback control loop performance. For the power MOSFET S and diode D_b, to avoid overheating of the component, the product of the current stress and the on-resistance of the power MOSFET should be about 50% lower than the power dissipation limit for the power MOSFET S and the current stress of the power diode should be 50% lower than the forward current limit for the diode D_b.

3.3. Design Considerations of Main Components for the Ripple Mirror Circuit

The inductance of the ripple mirror inductor L_RM can be found from Equation (31) as follows:

(36)

Likewise, the voltage stress of the blocking capacitor C_B can be found from Equation (27) as follows:

(37)

We select a capacitor with over 200 V rated voltage and about 10 μF. This is enough to clamp a smooth voltage in switching cycles and lessen the LC resonance effect caused by the blocking capacitor C_B and ripple mirror inductor L_RM. For the power MOSFETs of the ripple mirror circuit, namely S_RM and S'_RM, the current stress and the voltage stress are about a half times large than the boost converter power MOSFET S. However, because of the switching loss caused by the hard switching, the avalanche capability is much more important to these power MOSFETs. Thus, one can apply smaller gate resistor and a high speed MOSFET to lessen the crossover region of the drain to source voltage and current, which may also have better synchronization with the power MOSFET S of the boost converter.

3.4. Control Strategy Realization of the Proposed Converter

As illustrated, the adopted boundary-mode control strategy is shown in Figure 8, as well as the corresponding control signals in Figure 9. From Figure 9, one can see that the turn-on of the MOSFETs is coincidental with the zero crossing detection signal generated by the current transformer L_CT. In other words, the MOSFETs turns on when the voltage across the inductor V_CT crosses the zero from negative to positive. However, the turn-off of the MOSFETs is similar to that of an average current mode control. Note that the starter will be bypassed either after the boost converter is starting up or when the switching frequency f_sw is over 15 kHz.

Figure 8. Realization diagram of the proposed boundary-mode control strategy.

Figure 8. Realization diagram of the proposed boundary-mode control strategy.

Figure 9. Control signals of the adopted boundary-mode control strategy.

Figure 9. Control signals of the adopted boundary-mode control strategy.

By applying the boundary-mode control, the turn-on of all MOSFETs in every switching cycle can be maintained unchanged. This means that the ripple canceling capability of the RM circuit will remain effective under all load conditions. It is worth mentioning some other features as well. First, the control circuit does not need an external compensation signal when the duty ratio d of the proposed converter is over 50% because the current error of the main inductor L, generated by disturbance, will reset every switching cycle; therefore the problem of stability is nonexistent. Second, both zero voltage switching (ZVS) turn-on of the power MOSFETs and zero current switching (ZCS) turn-off of the diode D_b of the proposed converter can be achieved naturally. The soft-switching capability can enhance the conversion efficiency by lessening both the switching loss and the reverse recovery loss. Third, the size of the main inductor L can be made smaller than that of the CCM control and contribute to the reducing of conduction loss as well. Hence, it is seen that the boundary-mode control is especially suitable for the proposed converter where not only the on-time can be fixed but also many additional advantages mentioned above can be fully utilized.

4. Experimental Results

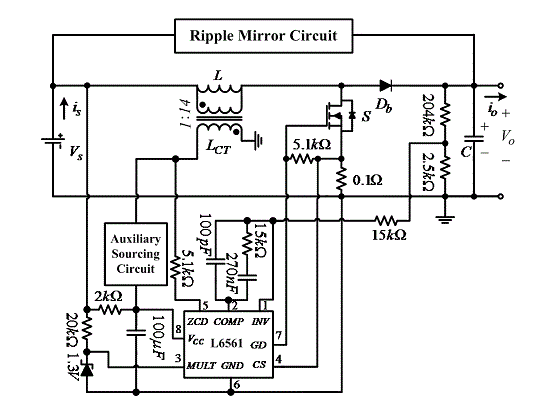
Table 1 shows the specification of experimental prototype of the proposed converter. The main control circuit is implemented by the L6561 controller of STMicroelectronics (Geneva, Switzerland) which is wildly used for controlling boost converter under boundary-mode conditions. The circuit schematic of proposed converter prototype is implemented as shown in Figure 10a.

Table 1. Specifications of the proposed converter.

Specifications	Values
Input Voltage	48 V
Output Voltage	200 V
Output Voltage Ripple	≤0.1%
Rated Output Power	200 W
Rated Switching Frequency	20 kHz

Table 1. Specifications of the proposed converter.

Specifications	Values
Input Voltage	48 V
Output Voltage	200 V
Output Voltage Ripple	≤0.1%
Rated Output Power	200 W
Rated Switching Frequency	20 kHz

Figure 10. Experimental prototype of the proposed converter: (a) the circuit schematic; (b) top side view and (c) bottom side view.

Figure 10. Experimental prototype of the proposed converter: (a) the circuit schematic; (b) top side view and (c) bottom side view.

The power circuit which contains the main inductor L and the main capacitor C is on the top side of the printed circuit board (PCB) with through-hole components for well thermal management as shown in Figure 10b. The control circuit of the proposed converter is on the bottom side of the PCB with surface-mount components to lessen the parasitic effect and noise which may occur in the control circuit as shown in Figure 10c. From Figure 11, one can see that with a resistive voltage sensor and voltage feedback control, the output voltage experimental waveform of the proposed converter is about 200 V. Also, less than 1% output voltage ripple fits in with the specification showed in Table 1.

The experimental gate signal v_GS waveforms of the MOSFETs, among the main switch S, the RM switch S_RM, and the complementary RM switch S'_RM, are shown in Figure 12. From Figure 12a and Figure 12b, it can be found that the switching frequency f_sw, under a full load condition, is merely half of the under half load condition. Also, with the cursor tools of the LeCroy wave runner, one can obtain the on-time delay of the MOSFETs of the RM circuit as about 562 ns and the off-time delay of the MOSFETs of the RM circuit as about 166ns compared with the v_GS waveform of the main switch S.

Figure 11. The output voltage waveform of the proposed converter under full load condition (50 ms/div).

Figure 11. The output voltage waveform of the proposed converter under full load condition (50 ms/div).

Figure 13 shows the current waveforms under half load and full load conditions. The proposed converter has an excellent ripple canceling capability under half load and full load conditions because of the constant on-time of the MOSFETs which is invariant to any load conditions by applying a boundary-mode control strategy.

Figure 12. Gate signal waveforms of the proposed converter under (a) half, and (b) full load conditions (50 ms/div).

Figure 12. Gate signal waveforms of the proposed converter under (a) half, and (b) full load conditions (50 ms/div).

Figure 13. Current waveforms of the proposed converter under (a) half, and (b) full load conditions (50 ms/div).

Figure 13. Current waveforms of the proposed converter under (a) half, and (b) full load conditions (50 ms/div).

Figure 14 shows the measured waveforms of an output voltage and output current, an input current and inductor current of the proposed converter under the dynamic load change between half load and full load conditions. From the same figure, it can be seen that the output voltage almost remains a constant value which only has a slight disturbance when the load is changed.

Figure 15 shows the peak to peak input current ripple under several load conditions. Comparing the results of the ripple canceling capability which contains boost converters with two phase interleaving control, the proposed converters are shown in the same table and the same figure with the same power capacity. The peak to peak input current ripple of the proposed converter is much lower than that of the boost converters with two phase interleaving control strategy, even under the worst scenario which is under 25% load condition.

Figure 14. The measured waveforms of the proposed converter under dynamic load change (100 ms/div).

Figure 14. The measured waveforms of the proposed converter under dynamic load change (100 ms/div).

Figure 15. Peak to peak input current ripple under different loads.

Figure 15. Peak to peak input current ripple under different loads.

By applying the boundary-mode control strategy, the main switch S can be turned on with zero voltage switching naturally as shown in Figure 16. As well as the power diode D_b being turned off naturally with zero current switching as shown in Figure 17. Both the soft switching on the main switch S and the power diode D_b may lessen the switching loss of the proposed converter. Hence, the proposed converter can have better efficiency.

Figure 16. The turn-on ZVS waveform of the main switch S under full load conditions (20 ms/div).

Figure 16. The turn-on ZVS waveform of the main switch S under full load conditions (20 ms/div).

Figure 17. The turn-off ZCS waveform of the power diode D_b under full load conditions (20 ms/div).

Figure 17. The turn-off ZCS waveform of the power diode D_b under full load conditions (20 ms/div).

Table 2 shows the measured efficiency records of the proposed converter. For comparison, the experimental results of a conventional converter without RM circuit are also shown in the same table. In Table 2, one can see that the proposed converter has best efficiency of 95.57% under a half load condition. The worst efficiency which is 93.9%, is obtained under full load condition. The contents of Table 2 can be expressed as shown in Figure 18. The efficiency curve of the proposed converter is very close to that without a RM circuit. The largest difference between the two curves occurs in a 25% load condition which is about 0.11%. One can see that the proposed low power ripple mirror circuit only processes ripple power, so the entire efficiency is just slightly influenced.

Table 2. Efficiency records under different load conditions.

Load Conditions	Without RM	With RM
25% load	95.00%	94.89%
50% load	95.67%	95.57%
60% load	95.42%	95.39%
70% load	95.07%	95.05%
80% load	94.76%	94.72%
90% load	94.50%	94.43%
Rated load	93.94%	93.90%

Table 2. Efficiency records under different load conditions.

Load Conditions	Without RM	With RM
25% load	95.00%	94.89%
50% load	95.67%	95.57%
60% load	95.42%	95.39%
70% load	95.07%	95.05%
80% load	94.76%	94.72%
90% load	94.50%	94.43%
Rated load	93.94%	93.90%

Figure 18. Efficiency comparison for the constructed experiment prototype with and without the proposed RM circuit.

Figure 18. Efficiency comparison for the constructed experiment prototype with and without the proposed RM circuit.

5. Conclusions

A ZVS/ZCS boost converter with RM circuit and boundary-mode control to achieve a zero ripple condition is presented. It was found that the proposed RM circuit technique can provide much better flexibility than the two-phased interleaved boost converter for locating the zero ripple operating point in the design stage. Operation modes, steady-state analyses as well as the control circuit realization of the proposed topology are also described for design reference. To verify the performance of the proposed converter, a 48 V input and 200 W/200 V output prototype is constructed. Experimental results indeed verify the effectiveness of the proposed converter. It is of great interest that this converter can be an alternative filtering solution for applications where low-voltage high-power sources should have current ripples of low amplitude and for applications for which the use of a passive filter (such simple capacitive filter) can lead to a non-optimal solution in terms of cost, weight, size, and bandwidth. The presented filtering system has been tested on a simple boost converter, which allows verifying its main abilities. Additional studies must be done to compare this solution to a passive one in terms of size, weight, and price, in the case of medium power applications.