PID Controller Design for UPS Three-Phase Inverters Considering Magnetic Coupling

Abstract

In three-phase inverters used in uninterruptible power supplies (UPSs), three-limb inductors and three-limb transformers are commonly used in consideration of cost and size. However, magnetic coupling exists between the three phases of the inverter, which can result in complex models. When instantaneous feedback control strategies are introduced to achieve high quality output waveforms, the transient analysis of the closed-loop inverters becomes difficult. In this paper, the phenomenon of magnetic coupling in three-phase inverters due to three-limb inductors and three-limb transformers is analyzed. A decoupled dynamic model is derived based on the instantaneous symmetrical components transformation, which comprises three decoupled equivalent circuits of instantaneous symmetrical components. Analyses based on this model indicate that magnetic coupling may have a significant impact on the performance of three-phase inverters under unbalanced load conditions and transient responses. For three-phase inverters in UPSs with Proportional-Integral-Differential (PID) closed-loop control strategies, the interactive influence between instantaneous closed-loop regulation and magnetic coupling is researched. Finally, a method of reliability analysis and PID controller design for inverters with magnetic coupling is derived. Simulation and experiment results validate the model and conclusions.

1. Introduction

In consideration of cost and size, the three-phase transformers and three-phase inductors of three-phase inverters used in uninterruptible power supplies (UPS) normally have magnet cores with a three-limb structure, also known as a core-type structure [1,2,3]. Hence, coupling exists between the three phases of the inverter because the main flux of each limb must pass through the other two limbs. In addition, a pulse width modulation (PWM) inverter in a UPS must introduce various instantaneous feedback control strategies, such as PID, multiple feedback controls, etc. to adapt for diverse, unpredictable nonlinear loads [4,5]. However, in the design of instantaneous control strategies, the appropriate dynamic models become complex when magnetic coupling is considered. Typically this coupling has been ignored, in other words, a three-limb transformer is treated as the combination of three single-phase transformers and a three-limb inductor is treated as the combination of three single-phase inductors [2,3]. For many practical problems, this approximation is acceptable; however, its applicability is not fully understood.

While magnetic coupling is not considered for three-phase inverters, dynamic models in the d-q rotation frame or in the α-β stationary frame are simpler than in the a-b-c frame. Two sets of regulators, for positive and negative sequence components, can be introduced for unbalanced load conditions [6,7,8,9,10,11]. Unfortunately, even ignoring magnetic coupling, transient analysis is complex due to strong coupling between axes [12,13,14].

In three-phase inverters, an unbalanced condition would occur when unbalanced loads or unbalanced bridge voltages are present. Such conditions can also appear during transient responses such as a sudden change of load, though even in steady state analyses based on symmetrical components (SC), it has been concluded that ignoring magnetic coupling in three-limb transformers and three-limb inductors is not correct under unbalanced conditions [15]. During transient responses, magnetic coupling cannot be ignored either.

SCs have been used for analyzing three-limb transformers and three-limb inductors under unbalanced conditions for many years, especially for fault situations of power systems [15,16,17]. Normally, periodic three-phase variables in each circle are assumed. They are analyzed by their fundamental and harmonic SCs separately [18]. For three-limb transformers, a duality derived model [19] and an equivalent circuit model in the a-b-c stationary frame have been proposed [20]. However, such models based on SCs in the frequency domain are more suitable for analyzing slow transient responses in a power system. In inverters where transient responses are fast, the three-phase variables can no longer be treated as periodic waves. Hence they cannot be expressed by SCs.

For inverters with a three-limb transformer and three-limb inductor, to obtain optimal instantaneous closed-loop control, magnetic coupling should be considered in the dynamic models so that transient performance can be properly considered. To the authors’ knowledge, transient models in the design of instantaneous closed-loop controllers while considering the magnetic coupling has been seldom reported in literature.

A transformation known as the instantaneous symmetrical components transformation (ISCT) has been proposed that can be used in the analysis of transient responses in AC motors [21,22]. Its transformation matrix is similar to the symmetrical components transformation (SCT), but is performed on three-phase instantaneous variables. The transformation results in instantaneous symmetrical components (ISC), which have also been used for extracting instantaneous values or disturbances in three-phase power systems [9,23,24,25]. Because ISC-based dynamic models for three-limb transformers and three-limb inductors are simpler in formulation [26,27], it may also be a useful tool when magnetic coupling is taken into account in transient responses of inverters. However, it has been seldom reported in the literature.

In this paper, magnetic coupling is studied using ISCs, and we proceed as follows: First, in Section 2, the instantaneous symmetrical component transformation is reviewed. Next, in Section 3, a transient model for a three-phase PWM inverter is derived based on ISCs which considers magnetic coupling due to a three-limb inductor and three-limb transformer. Based on this model, in Section 4, the transient performance of three-phase inverters is evaluated, especially considering the influence of magnetic coupling. Furthermore, for inverters with PID closed-loop control strategies, the influence between instantaneous closed-loop control and magnetic coupling is analyzed. Then, a performance analysis and controller design for a three-phase inverter with magnetic coupling is derived. Finally, in Section 5, the results of the simulations are presented and validated with experiments and Section 6 concludes the paper.

2. The Instantaneous Symmetrical Components Transformation

Main text paragraph. In this section, the instantaneous symmetrical components transformation will be reviewed. The instantaneous symmetrical components transformation (ISCT), introduced by Lyon, W.V. [21,28], is expressed as:

$$\left[\begin{array}{c}{x}^{+}(t)\\ x^{-}(t)\\ x^0(t)\end{array}\right]=\frac{1}{\sqrt{3}}\left[\begin{array}{ccc}\text{1}& \text{α}& {\text{α}}^{\text{2}}\\ \text{1}& {\text{α}}^{\text{2}}& \text{α}\\ \text{1}& \text{1}& \text{1}\end{array}\right]\cdot \left[\begin{array}{c}{x}_a(t)\\ x_b(t)\\ x_c(t)\end{array}\right]$$

(1)

where α = e^j2π/3, the x_a, x_b, x_c are three-phase instantaneous variables, and x⁺, x⁻, x⁰ are the resulting ISCs, including the instantaneous positive-sequence component (IPSC), the instantaneous negative-sequence component (INSC) and the instantaneous zero-sequence component (IZSC), respectively. The inverse transformation is expressed as:

$$\left[\begin{array}{c}{x}_a(t)\\ x_b(t)\\ x_c(t)\end{array}\right]=\frac{1}{\sqrt{3}}\left[\begin{array}{ccc}\text{1}& \text{1}& \text{1}\\ {\text{α}}^{\text{2}}& \text{α}& \text{1}\\ \text{α}& {\text{α}}^{\text{2}}& \text{1}\end{array}\right]\cdot \left[\begin{array}{c}{x}^{+}(t)\\ x^{-}(t)\\ x^0(t)\end{array}\right]$$

(2)

According to Equation (1), the IZSC is a real variable and the IPSC and INSC are complex variables and are complex conjugates.

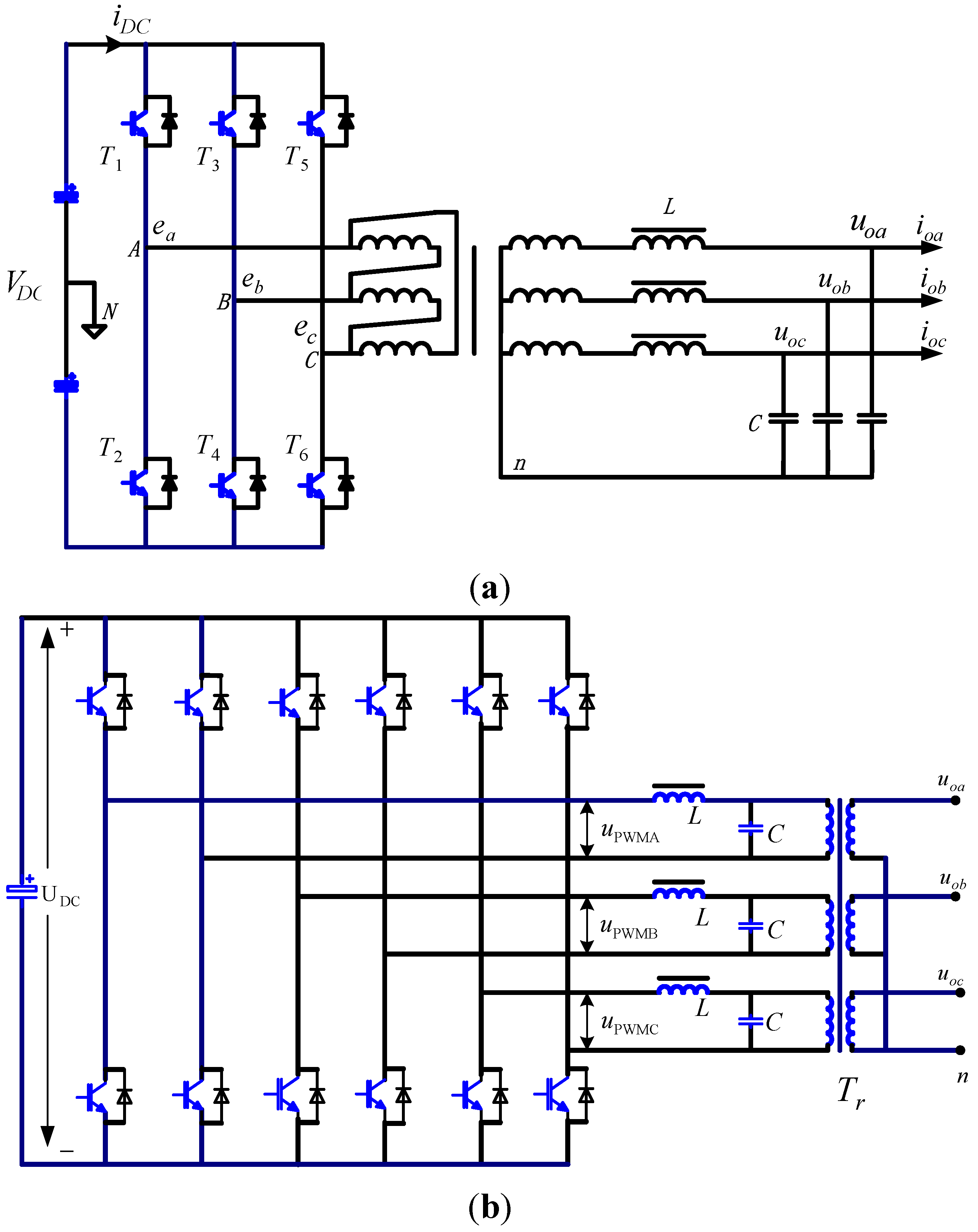
Typically, for normal three-phase, three-bridge inverters shown in Figure 1a, no current flows in the IZSC. In contrast, we consider the three-phase full-bridge inverter shown in Figure 1b, because the IZSC current output from the inverter bridges can flow in the three-limb inductor and three-limb transformer. Hence, the IZSC will influence the inverter and should be included in the dynamic model.

Figure 1. (a) Three-phase three bridge inverter; (b) Three-phase full bridge inverter.

Figure 1. (a) Three-phase three bridge inverter; (b) Three-phase full bridge inverter.

3. ISC Model for Three-Phase Inverters

In this section, an ISC model for a three-phase inverter is presented, including a model for a three-limb transformer, a model for a three-limb inductor, a model for a three-phase load, and finally a complete model combining the three.

3.1. ISC Model for Three-Limb Transformer

The defining variables of the transformer are shown in Figure 2, where u_A, u_B, u_C and i_A, i_B, i_C are three-phase voltages and currents in the primary windings and u_a, u_b, u_c and i_a, i_b, i_c are three-phase voltages and currents in the secondary windings. In addition, the number of turns of the primary and secondary windings are given by N₁ and N₂, respectively, φ_A, φ_B, φ_C are the flux linkages in the three primary windings, and φ_a, φ_b, φ_c are the flux linkages in the three secondary windings.

Figure 2. Variables of the six windings in a three-limb transformer.

Figure 2. Variables of the six windings in a three-limb transformer.

In each winding, ignoring any nonlinearity, the flux linkage is determined by the currents linearly as:

$$\left[\begin{array}{c}{\phi }_A(t)\\ {\phi }_B(t)\\ {\phi }_C(t)\\ {\phi }_a(t)\\ {\phi }_b(t)\\ {\phi }_c(t)\end{array}\right]=\left[\begin{array}{cccccc}{L}_{AA}& M_{AB}& M_{AC}& M_{Aa}& M_{Ab}& M_{Ac}\\ M_{BA}& L_{BB}& M_{BC}& M_{Ba}& M_{Bb}& M_{Bc}\\ M_{CA}& M_{CB}& L_{CC}& M_{Ca}& M_{Cb}& M_{Cc}\\ M_{aA}& M_{aB}& M_{aC}& L_{aa}& M_{ab}& M_{ac}\\ M_{bA}& M_{bB}& M_{bC}& M_{ba}& L_{bb}& M_{bc}\\ M_{cA}& M_{cB}& M_{cC}& M_{ca}& M_{cb}& L_{cc}\end{array}\right]\times \left[\begin{array}{c}{i}_A(t)\\ i_B(t)\\ i_C(t)\\ i_a(t)\\ i_b(t)\\ i_c(t)\end{array}\right]$$

(3)

and the voltage is determined by the flux linkages and currents [29], as:

$$\left[\begin{array}{c}{u}_A(t)\\ u_B(t)\\ u_C(t)\\ u_a(t)\\ u_b(t)\\ u_c(t)\end{array}\right]=\left[\begin{array}{cccccc}{r}_1& 0& 0& 0& 0& 0\\ 0& r_1& 0& 0& 0& 0\\ 0& 0& r_1& 0& 0& 0\\ 0& 0& 0& r_2& 0& 0\\ 0& 0& 0& 0& r_2& 0\\ 0& 0& 0& 0& 0& r_2\end{array}\right]\cdot \left[\begin{array}{c}{i}_A(t)\\ i_B(t)\\ i_C(t)\\ i_a(t)\\ i_b(t)\\ i_c(t)\end{array}\right]+\frac{d}{dt}\left[\begin{array}{c}{\phi }_A(t)\\ {\phi }_B(t)\\ {\phi }_C(t)\\ {\phi }_a(t)\\ {\phi }_b(t)\\ {\phi }_c(t)\end{array}\right]$$

(4)

In Equation (3), L_xx (with x = A, B, C, a, b, or c) is the self-inductance of winding x and M_xy is the mutual inductance between winding x and winding y. In Equation (4), r₁ is the resistance of the primary windings and r₂ is the resistance of the secondary windings.

Now, assuming that the three-phase windings are symmetrical and that the three limbs of the core have the same permeance λ, then L_xx and M_xy can be expressed as [29]:

$$L_{AA}=L_{BB}=L_{CC}=L_{1m}+L_{1l}$$

(5)

$$L_{aa}=L_{bb}=L_{cc}=L_{2m}+L_{2l}$$

(6)

$$M_{AB}=M_{BA}=M_{BC}=M_{CB}=M_{AC}=M_{CA}=-\frac{1}{2}{L}_{1m}$$

(7)

$$M_{ab}=M_{ba}=M_{bc}=M_{cb}=M_{ac}=M_{ca}=-\frac{1}{2}{L}_{2m}$$

(8)

$$M_{Aa}=M_{aA}=M_{Bb}=M_{bB}=M_{Cc}=M_{cC}=M_{12}$$

(9)

$$M_{Ab}=M_{Ac}=M_{Ba}=M_{Bc}=M_{Ca}=M_{Cb}=M_{aB}=M_{aC}=M_{bA}=M_{bC}=M_{cA}=M_{cB}=-\frac{1}{2}{M}_{12}$$

(10)

In the above equations, L_1l is leakage inductance of each primary winding and L_2l is leakage inductance of each secondary winding. In addition, L_1m and L_2m are the inductances due to the main fluxes that flow through the limbs of the primary and secondary windings respectively, and M₁₂ is mutual inductance between the primary and secondary winding due to the main fluxes in the limbs, which are given as:

$$L_{1m}=N_1\cdot (i_A\cdot N_1)\cdot \lambda /i_A=\lambda N_1^2$$

(11)

$$L_{2m}=N_2\cdot (i_a\cdot N_2)\cdot \lambda /i_a=\lambda N_2^2$$

(12)

$$M_{12}=N_1\cdot (i_a\cdot N_2)\cdot \lambda /i_a=\lambda N_1{N}_2$$

(13)

All parameters of the secondary windings can be given in terms of those on the primary side, so that:

$${L^{\prime }}_{2m}=L_{2m}\cdot {(N_1/N_2)}^2={M^{\prime }}_{12}=M_{12}\cdot (N_1/N_2)=L_{1m}$$

(14)

and L_2l and r₂ of the secondary windings become:

$${L^{\prime }}_{2l}=L_{2l}\cdot {(N_1/N_2)}^2$$

(15)

$${r^{\prime }}_2=r_2\cdot {(N_1/N_2)}^2$$

(16)

For convenience, the prime symbol is omitted in the remainder of this paper. Given the above, Equation (3) becomes:

$$\left[\begin{array}{c}{\phi }_A(t)\\ {\phi }_B(t)\\ {\phi }_C(t)\\ {\phi }_a(t)\\ {\phi }_b(t)\\ {\phi }_c(t)\end{array}\right]=\left[\begin{array}{cccccc}{L}_{1m}+L_{1l}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}\\ -\frac{1}{2}{L}_{1m}& L_{1m}+L_{1l}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}& -\frac{1}{2}{L}_{1m}\\ -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}+L_{1l}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}\\ L_{1m}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{\text{1}m}+L_{2l}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}\\ -\frac{1}{2}{L}_{1m}& L_{1m}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}+L_{2l}& -\frac{1}{2}{L}_{1m}\\ -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}& -\frac{1}{2}{L}_{1m}& -\frac{1}{2}{L}_{1m}& L_{1m}+L_{2l}\end{array}\right]\times \left[\begin{array}{c}{i}_A(t)\\ i_B(t)\\ i_C(t)\\ i_a(t)\\ i_b(t)\\ i_c(t)\end{array}\right]$$

(17)

Next, using ISCT, the decoupled ISC equations can be derived from Equations (4) and (17), and are given as:

$$\{\begin{array}{l}{\phi }_1^{+}(t)=L_1\cdot i_1^{+}(t)+L_m\cdot i_2^{+}(t)\\ {\phi }_1^{-}(t)=L_1\cdot i_1^{-}(t)+L_m\cdot i_2^{-}(t)\\ {\phi }_1^0(t)=L_{1l}\cdot i_1^0(t)\\ {\phi }_2^{+}(t)=L_2\cdot i_2^{+}(t)+L_m\cdot i_1^{+}(t)\\ {\phi }_2^{-}(t)=L_2\cdot i_2^{-}(t)+L_m\cdot i_1^{-}(t)\\ {\phi }_2^0(t)=L_{2l}\cdot i_2^0(t)\end{array}$$

(18)

$$\{\begin{array}{l}{u}_1^{+}(t)=r_1\cdot i_1^{+}(t)+L_1\cdot \frac{d}{dt}[i_{\text{1}}^{+}(t)]+L_m\cdot \frac{d}{dt}[i_2^{+}(t)]\\ u_1^{-}(t)=r_1\cdot i_1^{-}(t)+L_1\cdot \frac{d}{dt}[i_1^{-}(t)]+L_m\cdot \frac{d}{dt}[i_2^{-}(t)]\\ u_1^0(t)=r_1\cdot i_1^0(t)+L_{1l}\cdot \frac{d}{dt}[i_1^0(t)]\\ u_2^{+}(t)=r_2\cdot i_2^{+}(t)+L_2\cdot \frac{d}{dt}[i_2^{+}(t)]+L_m\cdot \frac{d}{dt}[i_1^{+}(t)]\\ u_2^{-}(t)=r_2\cdot i_2^{-}(t)+L_2\cdot \frac{d}{dt}[i_2^{-}(t)]+L_m\cdot \frac{d}{dt}[i_1^{-}(t)]\\ u_2^0(t)=r_2\cdot i_2^0(t)+L_{2l}\cdot \frac{d}{dt}[i_2^0(t)]\end{array}$$

(19)

where $L_m=\frac{3}{2}{L}_{1m}$, $L_1=L_{1l}+L_m$ and $L_2=L_{2l}+L_m$ . Also, the ${\phi }_1^{+}$ , ${\phi }_1^{-}$ , ${\phi }_1^0$ and ${\phi }_2^{+}$ , ${\phi }_2^{-}$ , ${\phi }_2^0$ are ISCs of ${\phi }_A$ , ${\phi }_B$ , ${\phi }_C$ and ${\phi }_a$ , ${\phi }_b$ , ${\phi }_c$ , the $u_1^{+}$ , $u_1^{-}$ , $u_1^0$ and $u_2^{+}$ , $u_2^{-}$ , $u_2^0$ are ISCs of μ_A, μ_B, μ_C and u_a, u_b, u_c and the $i_1^{+}$ , $i_1^{-}$ , $i_1^0$ and $i_2^{+}$ , $i_2^{-}$ , $i_2^0$ are ISCs of i_A, i_B, i_C and i_a, i_b, i_c. Here, a subscript “1” of an ISC denotes the ISC in the primary windings, and a subscript “2” denotes the ISC in the secondary windings. Using Equation (19), ISC equivalent circuits can be derived and are shown in Figure 3. It is observed that the equivalent circuits of the IPSC and INSC have the same form, which is different from that of IZSC, as indicated by the dash line in Figure 3c.

Figure 3. The ISC equivalent circuits for the three-limb transformer: (a) IPSC; (b) INSC; (c) IZSC.

Figure 3. The ISC equivalent circuits for the three-limb transformer: (a) IPSC; (b) INSC; (c) IZSC.

Selecting $i_1^{+}$ , $i_2^{+}$ as state variables, from Equation (19), IPSC state equations are given as:

$$\frac{d}{dt}\left[\begin{array}{c}{i}_1^{+}\\ i_2^{+}\end{array}\right]=\left[\begin{array}{cc}-\frac{r_1{L}_2}{K_m{L}_m}& \frac{r_2}{K_m}\\ \frac{r_1}{K_m}& -\frac{r_2{L}_1}{K_m{L}_m}\end{array}\right]\cdot \left[\begin{array}{c}{i}_1^{+}\\ i_2^{+}\end{array}\right]+\left[\begin{array}{cc}\frac{L_2}{K_m{L}_m}& -\frac{1}{K_m}\\ -\frac{1}{K_m}& \frac{L_1}{K_m{L}_m}\end{array}\right]\cdot \left[\begin{array}{c}{u}_1^{+}\\ u_2^{+}\end{array}\right]$$

(20)

where $K_m=\frac{L_1\cdot L_2}{L_m}-L_m$ . The INSC has the same state equation form as the IPSC. Finally, the IZSC state equations are given as:

$$\frac{d}{dt}\left[\begin{array}{c}{i}_1^0\\ i_2^0\end{array}\right]=\left[\begin{array}{cc}-\frac{r_1}{L_{1l}}& 0\\ 0& -\frac{r_2}{L_{2l}}\end{array}\right]\cdot \left[\begin{array}{c}{i}_1^0\\ i_2^0\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L_{1l}}& 0\\ 0& \frac{1}{L_{2l}}\end{array}\right]\cdot \left[\begin{array}{c}{u}_1^0\\ u_2^0\end{array}\right]$$

(21)

3.2. ISC Model for Three-Limb Inductor

The three-limb inductor has the same magnet core as the three-limb transformer, but with only three windings. Variables r_L and L_l are the resistance and leakage inductance for each winding. Their flux linkages are defined as ${\phi }_{LA}$ , ${\phi }_{LB}$ , ${\phi }_{LC}$ , and their voltages and currents are $u_{LA}$ , $u_{LB}$ , $u_{LC}$ and $i_{LA}$ , $i_{LB}$ , $i_{LC}$ , respectively, with all variables related through:

$$\left[\begin{array}{c}{\phi }_{LA}(t)\\ {\phi }_{LB}(t)\\ {\phi }_{LC}(t)\end{array}\right]=\left[\begin{array}{ccc}L& -\frac{1}{2}{L}_m& -\frac{1}{2}{L}_m\\ -\frac{1}{2}{L}_m& L& -\frac{1}{2}{L}_m\\ -\frac{1}{2}{L}_m& -\frac{1}{2}{L}_m& L\end{array}\right]\cdot \left[\begin{array}{c}{i}_{LA}(t)\\ i_{LB}(t)\\ i_{LC}(t)\end{array}\right]$$

(22)

where $L=L_l+L_m$ . Next, ISC equations are derived from Equation (22), as:

$$\{\begin{array}{c}{\phi }_L^{+}(t)=L\cdot i_L^{+}(t)\\ {\phi }_L^{-}(t)=L\cdot i_L^{-}(t)\\ {\phi }_L^0(t)=L_l\cdot i_L^0(t)\end{array}$$

(23)

where ${\phi }_L^{+}$ , ${\phi }_L^{-}$ , ${\phi }_L^0$ are the ISCs of ${\phi }_{LA}$ , ${\phi }_{LB}$ , ${\phi }_{LC}$ , $i_L^{+}$ , $i_L^{-}$ , $i_L^0$ are the ISCs of $i_{LA}$ , $i_{LB}$ , $i_{LC}$ . The equations of three-phase voltages in the inductors can also be simplified using Equation (4). The ISCs of $u_{LA}$ , $u_{LB}$ , $u_{LC}$ are $u_L^{+}$ , $u_L^{-}$ , $u_L^0$ , which can be expressed by:

$$\{\begin{array}{c}{u}_L^{+}(t)=r_L\cdot i_L^{+}(t)+L\cdot \frac{d}{dt}[i_L^{+}(t)]\\ u_L^{-}(t)=r_L\cdot i_L^{-}(t)+L\cdot \frac{d}{dt}[i_L^{-}(t)]\\ u_L^0(t)=r_L\cdot i_L^0(t)+L_l\cdot \frac{d}{dt}[i_L^0(t)]\end{array}$$

(24)

are given as the equivalent circuits of the ISCs as shown in Figure 4.

Figure 4. The ISC equivalent circuits for the three-limb inductor: (a) IPSC; (b) INSC; (c) IZSC.

Figure 4. The ISC equivalent circuits for the three-limb inductor: (a) IPSC; (b) INSC; (c) IZSC.

It can be observed from Figure 4 that the equivalent circuit of the IPSC has the same form as that of the INSC, but different from that of the IZSC. Importantly, the impedance seen by $i_L^0$ is $r_L+j\omega L_l$ , not $r_L+j\omega L$ .

Finally, if $i_L^{+}$ and $i_L^0$ are selected as state variables, from Equation (24), IPSC and IZSC state equations are derived as:

$$\frac{d}{dt}[i_L^{+}]=-\frac{r_L}{L}\cdot [i_L^{+}]+\frac{1}{L}\cdot [u_L^{+}]$$

(25)

$$\frac{d}{dt}[i_L^0]=-\frac{r_L}{L_l}\cdot [i_L^0]+\frac{1}{L_l}\cdot [u_L^0]$$

(26)

and the INSC has the same state equation form as that of the IPSC.

3.3. ISC Model for Three-Phase Load

For a three-phase load with voltages $u_{za}$ , $u_{zb}$ , $u_{zc}$ and currents $i_{za}$ , $i_{zb}$ , $i_{zc}$ , in the Laplace domain, they are related by:

$$\left[\begin{array}{c}{u}_{za}(s)\\ u_{zb}(s)\\ u_{zc}(s)\end{array}\right]=\left[\begin{array}{ccc}{z}_a& 0& 0\\ 0& z_b& 0\\ 0& 0& z_c\end{array}\right]\cdot \left[\begin{array}{c}{i}_{za}(s)\\ i_{zb}(s)\\ i_{zc}(s)\end{array}\right]$$

(27)

where $z_a=r_a+s{L}_a$ , $z_b=r_b+s{L}_b$ and $z_c=r_c+s{L}_c$ . Applying the ISCT to Equation (27), the ISC equation is given as:

$$\left[\begin{array}{c}{u}_z^{+}(s)\\ u_z^{-}(s)\\ u_z^0(s)\end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc}{z}^0& z^{-}& z^{+}\\ z^{-}& z^0& z^{-}\\ z^{+}& z^{-}& z^0\end{array}\right]\cdot \left[\begin{array}{c}{i}_z^{+}(s)\\ i_z^{-}(s)\\ i_z^0(s)\end{array}\right]$$

(28)

where $\left[\begin{array}{c}{z}^{+}\\ z^{-}\\ z^0\end{array}\right]\text{=}\left[\begin{array}{ccc}1& \alpha & {\alpha }^2\\ 1& {\alpha }^2& \alpha \\ 1& 1& 1\end{array}\right]\cdot \left[\begin{array}{c}{z}_a\\ z_b\\ z_c\end{array}\right]$ .

For unbalanced loads, $z_a\ne z_b\ne z_c$ , thus $z^{+}$ and $z^{-}$ are not zero, while for balanced loads, $z_a=z_b=z_c=r_z+s{L}_z$ , and Equation (28) becomes:

$$\left[\begin{array}{c}{u}_z^{+}(s)\\ u_z^{-}(s)\\ u_z^{\text{0}}(s)\end{array}\right]=\left[{\begin{array}{ccc}{r}_z+s{L}_z& 0& 0\\ 0& r_z+s{L}_z& 0\\ 0& 0& r_z+sL\end{array}}_z\right]\cdot \left[\begin{array}{c}{i}_z^{+}(s)\\ i_z^{-}(s)\\ i_z^{\text{0}}(s)\end{array}\right]$$

(29)

3.4. ISC Model for Whole Inverter

For three-phase inverters as shown in Figure 1, combining the ISC equivalent circuits of the three-limb inductor and three-limb transformer, the ISC equivalent circuits can be given as shown in Figure 5, where $u_{\text{PWM}}^{+}$ , $u_{\text{PWM}}^{-}$ , $u_{\text{PWM}}^0$ are the ISCs of $u_{\text{PWMA}}$ , $u_{\text{PWMB}}$ , $u_{\text{PWMC}}$ .

Figure 5. ISC equivalent circuits for three-phase inverters: (a) IPSC; (b) INSC; (c) IZSC.

Figure 5. ISC equivalent circuits for three-phase inverters: (a) IPSC; (b) INSC; (c) IZSC.

It should be noted that, a short circuit exists in the IZSC equivalent circuit as indicated by the dashed, red line in Figure 5c, and the inductance of the inductor highlighted in red is $L_l$ , not $L$ . So, this inverter has different characteristics from three-phase inverters with three single-phase inductors and three single-phase transformers, wherein the IPSC, INSC and IZSC all have the same equation.

It is also important to note that coupling does not exist between the IPSC, INSC and IZSC equivalent circuits. Therefore, the equivalent circuits in Figure 5 give an easy way to analyze the transient responses of three-phase inverters with magnetic coupling. In this paper, the transient model for a three-phase inverter with magnetic coupling is expressed by these three ISC equivalent circuits.

4. Transient Characteristics of Three-Phase Inverters Considering Magnetic Coupling

In this section, the transient behavior of three-phase inverters will be considered including magnetic coupling. To begin, in Figure 5c, the impedance of capacitor $C$ is given as $Z_C=\frac{1}{sC}$ . If we define $Z_{Ll}=r_L+s{L}_l$ and $Z_{1l}=r_1+s{L}_{l1}$ , the parallel combination of $Z_C$ and $Z_{1l}$ results in:

$$Z_{para}=Z_{1l}\parallel Z_C=\frac{Z_{1l}{Z}_C}{Z_{1l}+Z_C}=\frac{Z_{1l}}{Z_{1l}\cdot sC+1}$$

(30)

Note that at low frequencies, $\left|sC\right|\approx 0$ , thus $Z_{para};Z_{1l}$ . The current $i_1^0$ is given as:

$$i_1^0(s)=\frac{u_{\text{PWM}}^0(s)}{Z_{Ll}+Z_{1l}}\text{=}\frac{u_{\text{PWM}}^0(s)}{(r_L+r_1)+s(L_{Ll}+L_{1l})}$$

(31)

In three-wire three-bridge inverters, $i_1^0$ does not exist; however, for inverters such as those in Figure 1b, current $i_1^0$ is an inherent, serious problem that should be evaluated. At low frequencies, the $r_L$ , $r_1$ , $\omega L_l$ , $\omega L_{1l}$ are small, and therefore a small voltage $u_{\text{PWM}}^0$ can result in a large current $i_1^0$ , which may lead to over-current in power switches and shutdown of inverters.

For inverters in UPSs, it is necessary to introduce various instantaneous control strategies, such as PID and multiple feedback controls, to adapt for diverse nonlinear loads [4,5]. Among various instantaneous control strategies, the PID control strategy has a simple form and high robustness and is thus analyzed in this paper. Figure 6 gives a diagram of a three-phase inverter with three PID controllers in which the voltages of the three-phase capacitor, $u_{\text{CA}}$ , $u_{\text{CB}}$ , $u_{\text{CC}}$ , are sampled. In Figure 6, T_r is the three-limb transformer and L is the three-limb inductor. A PID controller $R(s)$ is used for each phase, which has the form:

$$R(s)=K_P+\frac{K_I}{s}+K_{D}s$$

(32)

Based on the ISC equivalent circuits in Figure 5, the IPSC equivalent circuit of Figure 6 is shown in Figure 7, where $u_{\text{m}}^{+}$ is the IPSC of the modulation signals $u_{\text{mA}}$ , $u_{\text{mB}}$ , $u_{\text{mC}}$ ; $u_C^{+}$ is the IPSC of the capacitor voltages $u_{\text{CA}}$ , $u_{\text{CB}}$ , $u_{\text{CC}}$ ; $u_{\text{ref}}^{+}$ is the IPSC of the reference voltages $u_{\text{refA}}$ , $u_{\text{refB}}$ , $u_{\text{refC}}$ ; $u_o^{+}$ is the IPSC of the load voltages $u_{oa}$ , $u_{ob}$ , $u_{oc}$ ; and $i_o^{+}$ is the IPSC of the load currents $i_{oa}$ , $i_{ob}$ , $i_{oc}$ . For inverters in UPSs, currents $i_{oa}$ , $i_{ob}$ , $i_{oc}$ and their ISCs are treated as disturbances in the model because the diverse sets of loads for UPS are unpredictable.

Figure 6. A three-phase inverter with PID closed-loop controllers.

Figure 6. A three-phase inverter with PID closed-loop controllers.

Figure 7. IPSC equivalent circuit for three-phase inverters with a PID controller.

Figure 7. IPSC equivalent circuit for three-phase inverters with a PID controller.

Treating the transistors (see Figure 1), typically IGBTs, as ideal switches, when the DC bus voltage is constant and the switching frequency is high enough, the inverter bridges will amply low frequency modulation signals linearly and can be modeled as an amplifier with gain $K_b$ [4,5], given by

$$u_{\text{PWM}}^{+}(s)=K_b\cdot u_{\text{m}}^{\text{+}}(s)$$

(33)

Neglecting $r_1$ , $r_2$ and $L_m$ , the transfer function block diagram of the IPSC derived from Figure 7 is shown in Figure 8. The inductance $L_{leak}$ is defined as:

$$L_{leak}=L_{1l}+L_{2l}$$

(34)

Figure 8. IPSC transfer function diagram for three-phase inverters with instantaneous feedback control.

Figure 8. IPSC transfer function diagram for three-phase inverters with instantaneous feedback control.

Hence, from Figure 8, the IPSC transfer function is derived as:

$$u_o^{+}(s)=\frac{K_{b}R(s)}{P_{close}(s)}{u}_{\text{ref}}^{\text{+}}(s)-\frac{L(s)}{P_{close}(s)}{i}_o^{+}(s)-L_{leak}s\cdot i_o^{+}(s)$$

(35)

where $P_{close}(s)=LC{s}^2+r_{L}Cs+K_b{H}_f(s)R(s)+1$ and $L(s)=Ls+r_L$ .

Since the INSC is always the complex conjugate of the IPSC, its equivalent circuit and the transfer function all have the same forms as those of IPSC. The IZSC equivalent circuit is shown in Figure 9.

Figure 9. IZSC equivalent circuit for three-phase inverters with instantaneous feedback control.

Figure 9. IZSC equivalent circuit for three-phase inverters with instantaneous feedback control.

From Figure 9, the IZSC of the load voltages can be expressed as:

$$u_o^0(s)=-Z_{inv}^0(s)\cdot i_o^0(s)$$

(36)

where the impedance $Z_{inv}^0$ is:

$$Z_{inv}^0(s)=L_{2l}\cdot s$$

(37)

Next, Equation (2) can be used to solve for the three-phase voltages of the load, as:

$$u_{oa}(s)=\frac{K_{b}R(s)}{P_{close}(s)}[u_{\text{refA}}(s)-\frac{u_{\text{ref}}^{\text{0}}(s)}{\sqrt{3}}]-\frac{L(s)}{P_{close}(s)}[i_{oa}(s)-\frac{i_o^0(s)}{\sqrt{3}}]-L_{leak}s\cdot i_{oa}(s)+L_{1l}s\cdot \frac{i_o^0(s)}{\sqrt{3}}$$

(38)

$$u_{ob}(s)=\frac{K_{b}R(s)}{P_{close}(s)}[u_{\text{refB}}(s)-\frac{u_{\text{ref}}^{\text{0}}(s)}{\sqrt{3}}]-\frac{L(s)}{P_{close}(s)}[i_{ob}(s)-\frac{i_o^0(s)}{\sqrt{3}}]-L_{leak}s\cdot i_{ob}(s)+L_{1l}s\cdot \frac{i_o^0(s)}{\sqrt{3}}$$

(39)

$$u_{oc}(s)=\frac{K_{b}R(s)}{P_{close}(s)}[u_{\text{refC}}(s)-\frac{u_{\text{ref}}^{\text{0}}(s)}{\sqrt{3}}]-\frac{L(s)}{P_{close}(s)}[i_{oc}(s)-\frac{i_o^0(s)}{\sqrt{3}}]-L_{leak}s\cdot i_{oc}(s)+L_{1l}s\cdot \frac{i_o^0(s)}{\sqrt{3}}$$

(40)

The corresponding block diagram for Equations (38)–(40) is shown in Figure 10. It can be observed that the IZSC voltage $u_{\text{ref}}^{\text{0}}$ and current $i_o^0$ are added as two disturbances, which influence the three-phase inverter in unbalanced conditions.

In the design of the PID controller, stability and high performance should be guaranteed while magnetic coupling exists. In a three-phase inverter, since the three-phase variables can be described by ISCs and its dynamic model can be expressed by ISC equivalent circuits, the analysis of the three-phase variables can be decomposed into the analysis of the IPSC, INSC and IZSC. In Figure 5, the IPSC and INSC equivalent circuits are the same, and they are also the same as a single-phase inverter when magnetic coupling is neglected so that the three-phase inverter is seen as three single-phase inverters. So, at the beginning of this analysis, the three-limb transformer and three-limb inductor can be treated as three, separated single-phase transformers and single-phase inductors, and the equivalent circuits of the IPSC and INSC can be obtained naturally. Hence the analysis results for a single-phase inverter are also valid for the IPSC and INSC equivalent circuit. In contrast, the IZSC equivalent circuit is different from that of the IPSC and INSC, so it should be evaluated separately; essentially, the effect of $u_{\text{ref}}^{\text{0}}$ and $i_o^0$ must be evaluated. Based on this conclusion, the design procedure for the instantaneous controller should include two steps:

• The magnetic coupling is first neglected, and the three-phase inverter is modeled as three single-phase inverters so that the controller design can ensure the dynamic performance of the IPSC.
• The voltage $u_{\text{ref}}^{\text{0}}$ and current $i_o^0$ are then evaluated to guarantee the performance of IZSC.

For the case shown in Figure 6, $R(s)$ can be designed according to the block diagram shown in Figure 8. Next, according to Figure 9, $u_{\text{PWM}}^0$ should be kept zero, otherwise compensation is needed. In practice, however, keeping $u_{\text{ref}}^{\text{0}}=0$ is sufficient. The reference $u_{\text{ref}}^{\text{0}}$ will appear in parallel inverter systems, and the independent regulation of three phase voltages for restraining circulating current in each phase will result in considerable voltage $u_{\text{PWM}}^0$ , giving rise to serious problems. In addition, the 3rd order IZSC harmonics due to dead zones in the drive circuits of the power switches contribute to $u_{\text{PWM}}^0$ [30].

Unbalanced load currents contain $i_o^0$ , which contribute $u_o^0$ through $Z_{2l}\text{=}{r}_2+L_{2l}s$ according to Figure 9. This is indeed an advantage of a three-limb transformer when compared with three single-phase transformers, because $u_o^0$ is not significant due to small $Z_{2l}$ . However, on the other hand, $u_o^0$ can’t be regulated by instantaneous feedback controls because voltage $u_{\text{PWM}}^0$ is bypassed by the three-limb transformer.

Figure 10. Block diagram for a three-phase inverter with PID control considering magnetic coupling.

Figure 10. Block diagram for a three-phase inverter with PID control considering magnetic coupling.

5. Simulation and Experiment Results

A prototype of 50 kVA three-phase inverter was built for the following experiments, which had the structure given in Figure 1b. The three-limb transformer T_r is used as the output transformer and the three-limb inductor L is used as a filter. A PID controller is used for R(s). The parameters of the inverter and its controller are shown in Table 1.

Table 1. Parameters of Inverter and Controller.

L	C	r	L1l (per unit)	L2l (per unit)	Kb	Hf (s)	R(s)
0.6 mH	140 uF	0.12 Ω	2.5%	2.5%	53.8	0.019	$9.4+\frac{2.06\times {10}^4}{s}+1.85\times {10}^{-3}s$

Table 1. Parameters of Inverter and Controller.

L	C	r	L1l (per unit)	L2l (per unit)	Kb	Hf (s)	R(s)
0.6 mH	140 uF	0.12 Ω	2.5%	2.5%	53.8	0.019	$9.4+\frac{2.06\times {10}^4}{s}+1.85\times {10}^{-3}s$

The bode diagram of IPSC is shown in Figure 11. It can be seen that the PID controller designed for IPSC behaves good performance. Then the INSC has the same performance. However, according to Equation (36), the IZSC cannot be regulated by PID controller due to magnetic couples.

Figure 11. Bode diagram of IPSC.

Figure 11. Bode diagram of IPSC.

A simulation to analyze the effect of the IZSC is shown in Figure 12a. When $u_{\text{PWM}}^0(s)=0$ , the primary side current i_A in the transformer is negligible and is not shown. The phase-shift between $u_{\text{PWMA}}$ and $u_{\text{PWMB}}$ is changed from 120° to 122.3°. The simulation shows that the current i_A is 20A, even without load. The distortion of i_A is due to dead-times of the power switches. In the experiment, i_A is measured by an oscilloscope and is shown in Figure 12b. The experimental result is the similar to that of the simulation shown in Figure 12a.

The proposed model in Figure 10 is also validated with a simulation incorporating an unbalanced load step-up which is realized by a step up of the resistive load during phase “a”. When the magnetic couples are neglected, the waveform of the load voltages is shown in Figure 13a. It can be seen that, only phase “a” is influenced during step-up process. Next, the magnetic couples are considered and the waveform of the load voltages is shown in Figure 13b. During single-phase load step-up, due to magnetic coupling, all three phases are influenced by the IZSCs. Also, due to the superposition of $i_o^0$ , which has the same waveform as $i_a$ , the voltage magnitudes of phases “b” and “c” are changed by $i_o^0$ . They have different values as indicated by the dashed line labeled as “Line1” in Figure 13b. The largest voltage magnitude appears in phase “c” and the lowest magnitude voltage appears in the phase “a”.

Figure 12. Primary current of three-limb transformer in unbalanced condition: (a) Simulation; (b) Experiment.

Figure 12. Primary current of three-limb transformer in unbalanced condition: (a) Simulation; (b) Experiment.

Figure 13. Simulation waveforms of the three phase load voltage (single-phase load step up): (a) No magnetic couples; (b) With magnetic couples; (c) IPSC locus of load voltage with magnetic couples.

Figure 13. Simulation waveforms of the three phase load voltage (single-phase load step up): (a) No magnetic couples; (b) With magnetic couples; (c) IPSC locus of load voltage with magnetic couples.

The corresponding IPSC locus is shown in Figure 13c. The dot labeled as “A” denotes the moment of load step-up. Before load step-up, the locus is a circle as indicated by the thin, red line. However, after step-up, the locus changes to an ellipse due to the unbalance three-phase load voltages as indicated by the thick line.

A corresponding experiment was performed also by a step-up of resistive load in phase “a”, and the corresponding waveforms are shown in Figure 14. The waveform is similar to that of simulation, except for small oscillations in phases “b” and “c”, which are caused by the parasitic inductances and capacitance in the inverter. Unfortunately, these effects are difficult to include in the simulation.

In this example, simulation and experiment show that the influence of magnetic couples on the inverter system is acceptable even though the IZSCs are not compensated, because the incurred IZSC is small due to small $Z_{inv}^0$ and $u_{ref}^0=0$ . However, for many applications, such as parallel inverter system, $u_{ref}^0$ or $Z_{inv}^0$ are large, then the compensations of IZSCs should be considered.

Figure 14. Experimental waveforms of three-phase load voltages (step up of single-phase resistive load)

Figure 14. Experimental waveforms of three-phase load voltages (step up of single-phase resistive load)

6. Conclusions

For three-phase inverters used in UPSs, three-limb transformers and three-limb inductors are commonly used in their construction, which can bring about magnetic coupling. Here, we derived a dynamic model based on the instantaneous symmetrical components transformation, which considers this magnetic coupling phenomenon. The model includes IPSC, INSC and IZSC equivalent circuits. There is no coupling between these circuits even with magnetic coupling, and hence the model is simple to solve and is suitable for analyzing the transient behavior of three-phase inverters with magnetic coupling. Based on this model, analysis indicated that magnetic coupling might have a significant impact on the dynamic performance of three-phase inverters under unbalanced conditions. For inverters with instantaneous PID closed-loop control strategies, the influence between closed-loop control and magnetic coupling was studied and a corresponding method for performance analysis and controller design for three-phase inverters considering magnetic coupling was derived. Finally, simulation and experimental results validated the model and conclusions.