Study on the Characteristics of Expander Power Output Used for Offsetting Pumping Work Consumption in Organic Rankine Cycles †
Abstract
:1. Introduction
2. Basic Assumptions Adopted in Analyses
2.1. Assumptions of the Cycle

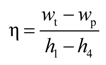
2.2. Specific Pumping Work
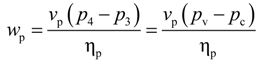
2.3. Specific Expander Power
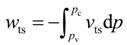

3. Analyses on Expander Power Used for Offsetting Pumping Work
3.1. The BWR

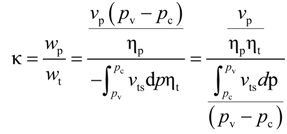
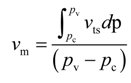
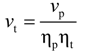
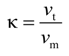
3.2. The Categories of the Expansion Process




4. Calculation Results and Analyses
4.1. Sub-Critical ORCs


| Working fluid | Critical temperature (°C) | Critical pressure (MPa) | Critical density (kg·m−3) |
|---|---|---|---|
| R245fa (CF3CH2CHF2) | 154.1 | 3.640 | 517.1 |
| R123 (CF3CHCl2) | 183.7 | 3.662 | 550.0 |
| R134a (CH2FCF3) | 101.7 | 4.059 | 511.9 |
| R143a (CH3CF3) | 72.71 | 3.761 | 431.0 |


4.2. Super-Critical ORCs

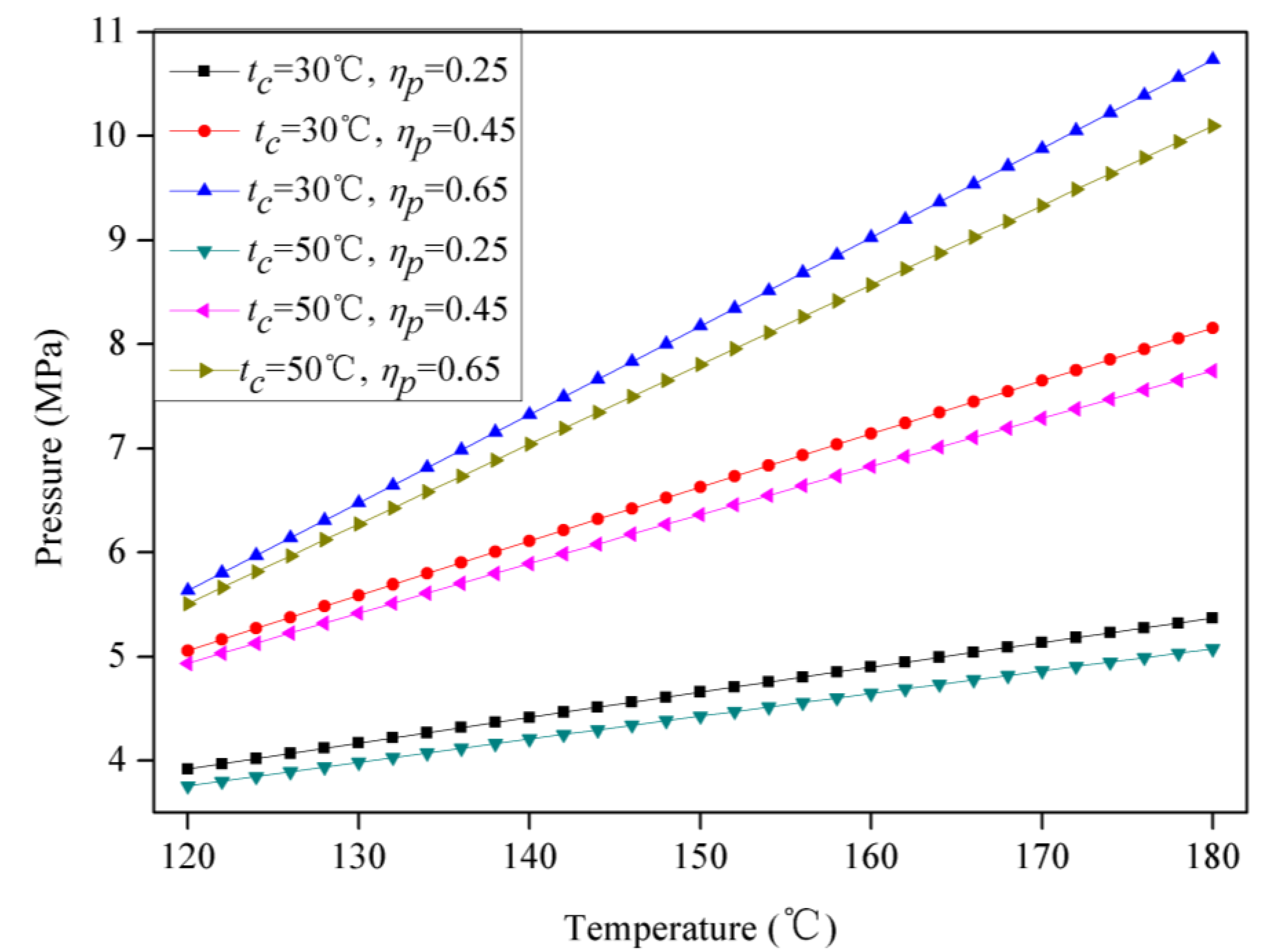
5. Conclusions
Nomenclature
| pv | evaporating pressure (Pa/MPa) |
| pc | condensing pressure (Pa/MPa) |
| p | pressure (Pa/MPa) |
| wt | expander power (J∙kg−1) |
| wp | pumping work (J∙kg−1) |
| η | efficiency (%) |
| h | enthalpy (J∙kg−1) |
| vp | specific volume of liquid working fluid delivered by the circulation pump (m3∙kg−1) |
| ηp | efficiency of the circulation pump (%) |
| vts | specific volume of working fluid in the ideal isentropic expansion process (m3∙kg−1) |
| wts | maximum of expander power (J∙kg−1) |
| ηe | efficiency of the expander |
| κ | back work ratio |
| vm | integral mean value of vts (m3∙kg−1) |
| vt | threshold value of working fluid specific volume (m3∙kg−1) |
| v2s | final value of vts (m3∙kg−1) |
| t | temperature (°C) |
| tc | condensing temperature (°C) |
Subscripts
| 1, 2, 3, 4 | state points in cycle (as shown in Figure 1) |
| p | circulation pump |
| t | expander |
| v | evaporating |
| c | condensing |
| s | isentropic |
Acronyms
| ORC | organic Rankine cycle |
| BWR | back work ratio |
| NWC | negative work cycle |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gao, H.; Liu, C.; He, C.; Xu, X.; Wu, S.; Li, Y. Performance analysis and working fluid selection of a supercritical organic Rankine cycle for low grade waste heat recovery. Energies 2012, 5, 3233–3247. [Google Scholar] [CrossRef]
- Sprouse, C.; Depcik, C. Review of organic Rankine cycles for internal combustion engine exhaust waste heat recovery. Appl. Therm. Eng. 2013, 51, 711–722. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, H.; Song, S.; Yang, F.; Liu, H.; Zhao, G.; Zhang, J.; Yao, B. Effects of degree of superheat on the running performance of an organic Rankine cycle (ORC) waste heat recovery system for diesel engines under various operating conditions. Energies 2014, 7, 2123–2145. [Google Scholar] [CrossRef]
- Pikra, G.; Salim, A.; Prawara, B.; Purwanto, A.J.; Admono, T.; Eddy, Z. Development of small scale concentrated solar power plant using organic Rankine cycle for isolated region in Indonesia. Energy Procedia 2013, 32, 122–128. [Google Scholar]
- Nusiaputra, Y.; Wiemer, H.-J.; Kuhn, D. Thermal-Economic modularization of small, organic Rankine cycle power plants for mid-enthalpy geothermal fields. Energies 2014, 7, 4221–4240. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggemann, D. Fluid selection for the organic Rankine cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar]
- Qiu, G.; Liu, H.; Riffat, S. Expanders for micro-CHP systems with organic Rankine cycle. Appl. Therm. Eng. 2011, 31, 3301–3307. [Google Scholar] [CrossRef]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of organic Rankine cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar]
- Borsukiewicz-Gozdur, A. Pumping work in the organic Rankine cycle. Appl. Therm. Eng. 2013, 51, 781–786. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar]
- Sauret, E.; Rowlands, A.S. Candidate radial-inflow turbines and high-density working fluids for geothermal power systems. Energy 2011, 36, 4460–4467. [Google Scholar] [CrossRef]
- Pei, G.; Li, J.; Li, Y.; Wang, D.; Ji, J. Construction and dynamic test of a small-scale organic Rankine cycle. Energy 2011, 36, 3215–3223. [Google Scholar]
- Quoilin, S.; Lemort, V.; Lebrun, J. Experimental study and modeling of an organic Rankine cycle using scroll expander. Appl. Energy 2010, 87, 1260–1268. [Google Scholar] [CrossRef]
- Bracco, R.; Clemente, S.; Micheli, D.; Reini, M. Experimental tests and modelization of a domestic-scale ORC (organic Rankine cycle). Energy 2013, 58, 107–116. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; He, W.; Gao, L.; Wang, B.; Ma, S.; Dai, Y. Construction and preliminary test of a low-temperature regenerative organic Rankine cycle (ORC) using R123. Renew. Energy 2013, 57, 216–222. [Google Scholar] [CrossRef]
- Zheng, N.; Zhao, L.; Wang, X.D.; Tan, Y.T. Experimental verification of a rolling-piston expander that applied for low-temperature organic Rankine cycle. Appl. Energy 2013, 112, 1265–1274. [Google Scholar] [CrossRef]
- Lei, B.; Wu, Y.T.; Lu, Y.W.; Guo, H.; Ma, C.F. Research on the Characteristics of Expander Output Power Used for Offsetting Pumping Work in Organic Rankine Cycles. In Proceedings of the International Heat Transfer Symposium (IHTS2014), Beijing, China, 6–9 May 2014.
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an organic Rankine cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, X.; Chen, Z.; Wang, Z. Experimental study on organic Rankine cycle for waste heat recovery from low-temperature flue gas. Energy 2013, 55, 216–225. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wu, Y.-T.; Lei, B.; Ma, C.-F.; Zhao, L.; Wang, J.-F.; Guo, H.; Lu, Y.-W. Study on the Characteristics of Expander Power Output Used for Offsetting Pumping Work Consumption in Organic Rankine Cycles. Energies 2014, 7, 4957-4971. https://doi.org/10.3390/en7084957
Wu Y-T, Lei B, Ma C-F, Zhao L, Wang J-F, Guo H, Lu Y-W. Study on the Characteristics of Expander Power Output Used for Offsetting Pumping Work Consumption in Organic Rankine Cycles. Energies. 2014; 7(8):4957-4971. https://doi.org/10.3390/en7084957
Chicago/Turabian StyleWu, Yu-Ting, Biao Lei, Chong-Fang Ma, Lei Zhao, Jing-Fu Wang, Hang Guo, and Yuan-Wei Lu. 2014. "Study on the Characteristics of Expander Power Output Used for Offsetting Pumping Work Consumption in Organic Rankine Cycles" Energies 7, no. 8: 4957-4971. https://doi.org/10.3390/en7084957
APA StyleWu, Y.-T., Lei, B., Ma, C.-F., Zhao, L., Wang, J.-F., Guo, H., & Lu, Y.-W. (2014). Study on the Characteristics of Expander Power Output Used for Offsetting Pumping Work Consumption in Organic Rankine Cycles. Energies, 7(8), 4957-4971. https://doi.org/10.3390/en7084957




