Finite Element Method Modeling of Sensible Heat Thermal Energy Storage with Innovative Concretes and Comparative Analysis with Literature Benchmarks
Abstract
:1. Introduction
Design of Sensible Heat Thermal Energy Storage Systems and High Performance Materials

2. Materials and Methods
2.1. Design Criteria and Simulation Approach for Sensible Heat Thermal Energy Storage Differential Elements


- (a)
- the storage materials are considered homogeneous and isotropic;
- (b)
- for the length L, the variation of temperature in axial direction can be neglected;
- (c)
- the steel pipes, due to their very high thermal conductivity, have a negligible effect on heat transfer to the solid media;
- (d)
- the operating delta T for the element is 40 K (from 623 K to 663 K), so that thermal properties are assumed to be constant;
- (e)
- the HTF is considered as an infinite power tank during a complete thermal cycle;
- (f)
- for the operating storage cycle, the charging period lasts 3600 s, and the following break period lasts 3600 s.
2.2. Storage Materials Selected From Literature Review on Sensible Heat Thermal Energy Storage
| Material | Density ρsol (kg/m3) | Specific heat capacity csol (J/(kg·K)) | Thermal conductivity ksol (W/(m·K)) | Thermal diffusivity αsol × 107 (m2/s) | Volumetric heat capacity Cvol (kW·h/(m3·K)) | Reference |
|---|---|---|---|---|---|---|
| PC | 2451 | 810 | 1.02 | 5.14 | 0.551 | [46] |
| HT | 2750 | 916 | 1.00 | 3.97 | 0.700 | [9] |
| CC | 3500 | 866 | 1.35 | 4.45 | 0.842 | [9] |
| A4 | 2680 | 950 * | 2.43 | 9.54 | 0.707 | [12] |
| FC | 2440 | 630 | 1.16 | 7.55 | 0.427 | [46] |
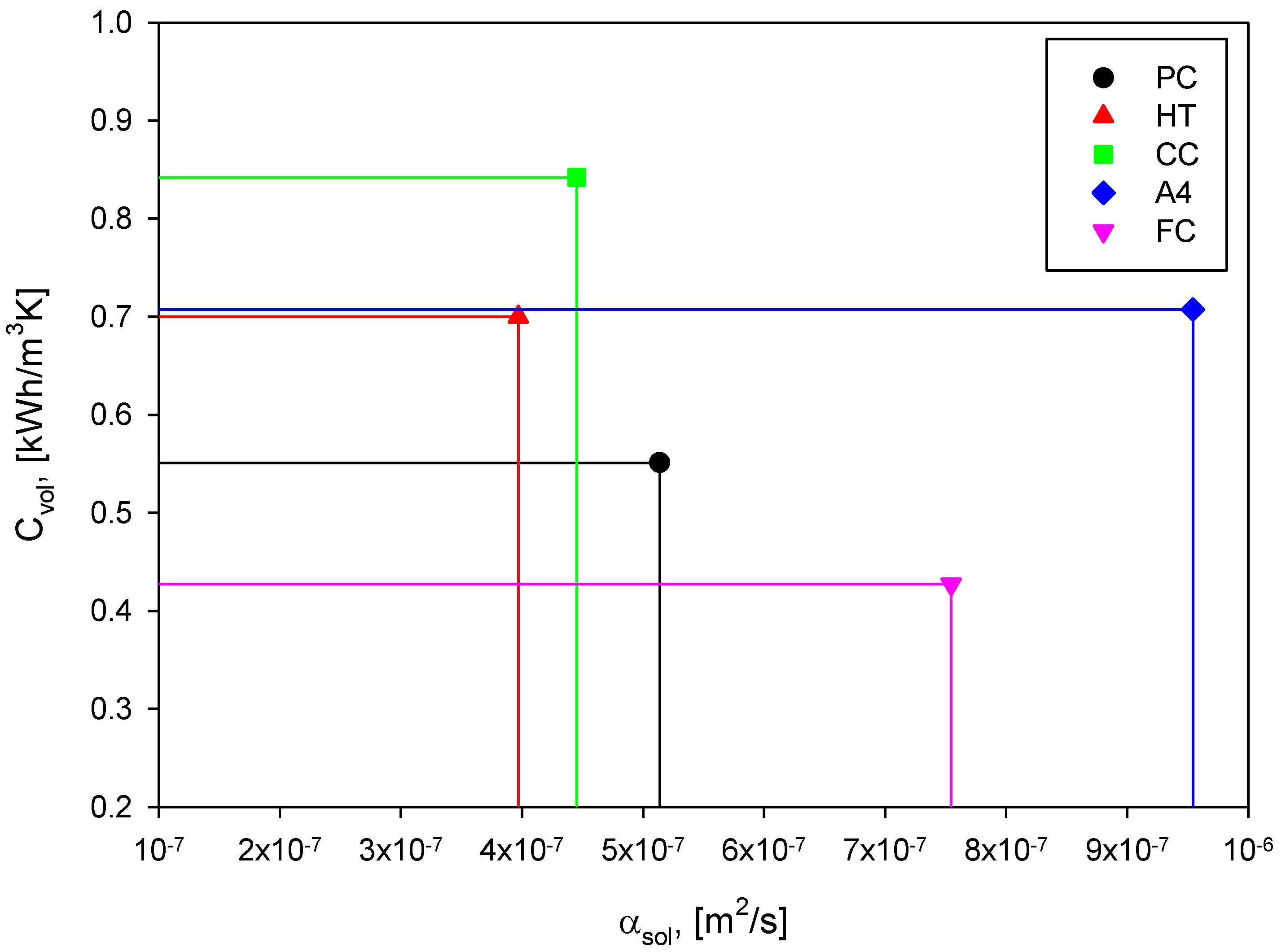
- (1)
- For a fixed value of the rectangular area, i.e., thermal conductivity, the constitutive equation for thermal properties describes a hyperbola, hence a high value of the thermal diffusivity corresponds to a low value of the volumetric heat capacity and vice versa;
- (2)
- (3)
- A proper design of storage systems must be based on the selection of a high-thermal performance storage material so that an optimum balance between capacitive and heat transport behavior is required to the solid medium;
- (4)
- Both thermal diffusivity and volumetric heat capacity must increase and, for these characteristics, mix design and aggregate selection play the most important role.
2.3. Lightweight Concretes and Geopolymeric Concrete Tested for Sensible Heat Thermal Energy Storage
| Oxides | CEM II/A-L 42.5R | Fly ash | Marble sludge |
|---|---|---|---|
| CaO | 60.84 | 4.32 | 53.76 |
| SiO2 | 20.66 | 53.75 | 2.13 |
| Al2O3 | 4.89 | 28.12 | 0.12 |
| Fe2O3 | 3.24 | 6.99 | 0.69 |
| MgO | 1.94 | 1.59 | 0.15 |
| SO3 | 2.95 | - | - |
| Na2O | 0.12 | 0.87 | - |
| K2O | 0.84 | 1.89 | - |
| Cl− | 0.94 | - | - |
| LoI * | 5.76 | 6.01 | 42.74 |
| Materials | Unit | PA0 | PA10 | PA20 | PA30 | G |
|---|---|---|---|---|---|---|
| CEM II/A-L 42.5R | kg/m3 | 300 | 300 | 300 | 300 | - |
| Marble sludge | kg/m3 | 146 | 152 | 171 | 183 | - |
| Crushed limestone | kg/m3 | 1648 | 1351 | 1227 | 1101 | 854 |
| Plastic aggregate | kg/m3 | 0 | 70 | 140 | 210 | - |
| Fly ash | kg/m3 | 90 | 90 | 90 | 90 | 208 |
| Alkaline solution | kg/m3 | - | - | - | - | 138 |
| Superplasticizer | L/m3 | 6.86 | 7.26 | 8.91 | 9.95 | - |
| w/c ratio | - | 0.5 | 0.5 | 0.5 | 0.5 | - |
3. Results and Discussion
3.1. Simulation Results for Selected Storage Materials


| Material | msol (kg) | ΔTeff (K) | Vtot × 103 (m3) | Qeff (kW·hth) | Qnom (kW·hth) | ηstorage (%) | Volume power density (kW·hth/m3) | Power density (kW·hth/ton) |
|---|---|---|---|---|---|---|---|---|
| PC | 14.92 | 33.32 | 6.40 | 0.112 | 0.134 | 83.58 | 17.50 | 7.51 |
| HT | 16.74 | 29.69 | 6.40 | 0.126 | 0.170 | 74.12 | 19.69 | 7.53 |
| CC | 21.30 | 31.39 | 6.40 | 0.161 | 0.205 | 78.54 | 25.16 | 7.56 |
| A4 | 16.31 | 38.56 | 6.40 | 0.166 | 0.172 | 96.51 | 25.94 | 10.18 |
| FC | 14.85 | 37.23 | 6.40 | 0.097 | 0.104 | 93.27 | 15.16 | 6.53 |


| Material | msol (kg) | ΔTeff (K) | Vtot × 103 (m3) | Qeff (kW·hth) | Qnom (kW·hth) | ηstorage (%) | Volume power density (kW·hth/m3) | Power density (kW·hth/ton) |
|---|---|---|---|---|---|---|---|---|
| PC | 16.11 | 31.87 | 6.88 | 0.116 | 0.145 | 80.00 | 16.86 | 7.20 |
| HT | 14.25 | 32.96 | 5.50 | 0.120 | 0.145 | 82.76 | 21.82 | 8.42 |
| CC | 15.07 | 36.93 | 4.62 | 0.134 | 0.145 | 92.41 | 29.00 | 8.89 |
| A4 | 13.74 | 39.30 | 5.44 | 0.142 | 0.145 | 97.93 | 26.10 | 10.33 |
| FC | 20.71 | 32.13 | 8.80 | 0.116 | 0.145 | 80.00 | 13.18 | 5.60 |


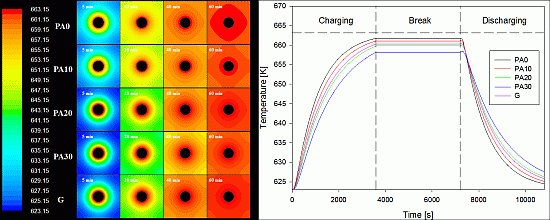
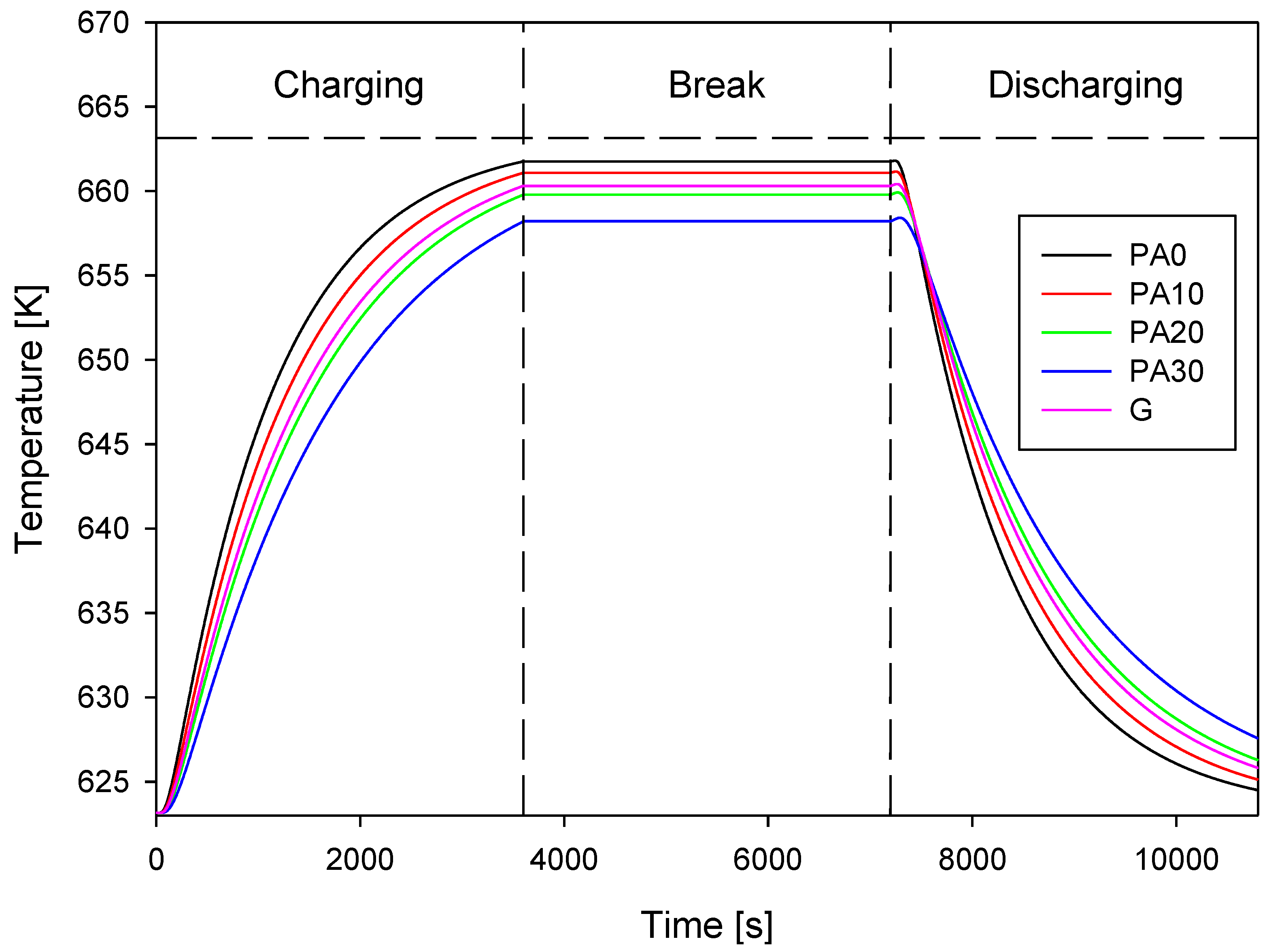
3.2. Thermal Characterization of Tested Concretes and Simulation Results
| Mixture | Thermal conductivity ksol (W/m·K) | Density ρsol (kg/m3) | Specific heat capacity csol (J/kg·K) |
|---|---|---|---|
| PA0 | 1.42 | 2094 | 722 |
| PA10 | 1.18 | 1914 | 743 |
| PA20 | 0.94 | 1762 | 766 |
| PA30 | 0.71 | 1518 | 789 |
| G | 1.01 | 1811 | 751 |




| Material | msol (kg) | ΔTeff (K) | Vtot × 103 (m3) | Qeff (kW·hth) | Qnom (kW·hth) | ηstorage (%) | Volume power density (kW·hth/m3) | Power density (kW·hth/ton) |
|---|---|---|---|---|---|---|---|---|
| PA0 | 12.74 | 38.49 | 6.40 | 0.098 | 0.102 | 95.86 | 15.31 | 7.69 |
| PA10 | 11.65 | 37.87 | 6.40 | 0.091 | 0.096 | 94.63 | 14.22 | 7.81 |
| PA20 | 10.72 | 36.58 | 6.40 | 0.083 | 0.091 | 90.94 | 12.97 | 7.74 |
| PA30 | 9.24 | 35.02 | 6.40 | 0.071 | 0.081 | 87.66 | 11.09 | 7.69 |
| G | 11.02 | 37.11 | 6.40 | 0.085 | 0.092 | 92.42 | 13.28 | 7.71 |


4. Conclusions
Nomenclature
| c | specific heat capacity (J/(kg·K)) |
| k | thermal conductivity (W/(m·K)) |
| Cvol | volumetric heat capacity (kW·h/(m3·K)) |
| PA0–30 | concrete mixture (subscript from 0 to 30 indicate the percentage of plastic aggregate) |
| G | geopolymer |
| T | temperature (K) |
| t | time (s) |
| Q | thermal energy (kW·h) |
| m | weight (kg) |
| V | volume (m3) |
| di | inner tube diameter (m) |
| da | distance between center of two parallels tube (m) |
| L | length (m) |
| W | width (m) |
| H | height (m) |
| ΔT | temperature difference (K) |
Greek Symbols
| ρ | density (kg/m3) |
| α | thermal diffusivity (m2/s) |
| η | heat storage efficiency (%) |
Subscripts
| 0 | initial |
| f | final |
| tot | total |
| nom | nominal |
| eff | effective |
| th | thermal |
| sol | solid |
Author Contributions
Conflicts of Interest
References
- Gil, A.; Medrano, M.; Martorell, I.; Làzaro, A.; Dolado, P.; Zalba, B.; Cabeza, L.F. State of the art on high temperature thermal energy storage for power generation. Part 1—Concepts, materials and modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–55. [Google Scholar]
- Medrano, M.; Gil, A.; Martorell, I.; Potau, X.; Cabeza, L.F. State of the art on high temperature thermal energy storage for power generation. Part 2—Case studies. Renew. Sustain. Energy Rev. 2010, 14, 56–72. [Google Scholar]
- Kuravi, S.; Trahan, J.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. Thermal energy storage technologies and systems for concentrating solar power plants. Prog. Energy Combust. Sci. 2013, 39, 285–319. [Google Scholar] [CrossRef]
- Tatsidjodoung, P.; Le Pierrès, N.; Luo, L. A review of potential materials for thermal energy storage in buildings applications. Renew. Sustain. Energy Rev. 2013, 18, 327–349. [Google Scholar] [CrossRef]
- Winter, C.J.; Sizmann, R.L.; Vant-Hull, L.L. Solar Power Plants; Springer-Verlag: Berlin, Germany, 1991. [Google Scholar]
- Laing, D.; Bahl, C.; Bauer, T.; Fiss, M.; Breidenbach, N.; Hempel, M. High-temperature solid-media thermal energy storage for solar thermal power plants. IEEE Proc. 2012, 100, 516–524. [Google Scholar] [CrossRef]
- Laing, D.; Bahl, C.; Bauer, T.; Lehmann, D.; Steinmann, W.D. Thermal energy storage for direct steam generation. Sol. Energy 2011, 85, 627–633. [Google Scholar] [CrossRef]
- Laing, D.; Lehmann, D.; Bahl, C. Comcrete storage for solar thermal power plants and industrial process heat. In Proceedings of the 3rd International Renewable Energy Storage Conference (IRES III 2008),, Berlin, Germany, 24–25 November 2008.
- Laing, D.; Steinmann, W.D.; Tamme, R.; Richter, C. Solid media thermal storage for parabolic trough power plants. Sol. Energy 2006, 80, 1283–1289. [Google Scholar] [CrossRef]
- Skinner, J.E.; Strasser, M.N.; Brown, B.M.; Selvam, R.P. Testing of high-performance concrete as a thermal energy storage medium at high temperatures. J. Sol. Energy Eng. 2013, 136. [Google Scholar] [CrossRef]
- John, E.E.; Hale, W.M.; Selvam, R.P. Concrete as a thermal energy storage medium for thermocline solar energy storage systems. Sol. Energy 2013, 96, 194–204. [Google Scholar] [CrossRef]
- Guo, C.; Zhu, J.; Zhou, W.; Chen, W. Fabrication and thermal properties of a new heat storage concrete material. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2010, 25, 628–630. [Google Scholar] [CrossRef]
- Yuan, H.W.; Lu, C.H.; Xu, Z.Z.; Ni, Y.R.; Lan, X.H. Mechanical and thermal properties of cement composite graphite for solar thermal storage materials. Sol. Energy 2012, 86, 3227–3233. [Google Scholar] [CrossRef]
- Bai, F.; Xu, C. Performance analysis of a two-stage thermal energy storage system using concrete and steam accumulator. Appl. Therm. Eng. 2011, 31, 2764–2771. [Google Scholar] [CrossRef]
- Steinmann, W.D.; Buschle, J. Analysis of thermal storage systems using modelica. In Proceedings of the 4th International Modelica Conference, Hamburg, Germany, 7–8 March 2005; pp. 331–337.
- Selvam, R.P.; Castro, M. 3D FEM model to improve the heat transfer in concrete for thermal energy storage in solar power generation. In Proceedings of the ASME 2010 4th International Conference on Energy Sustainability, Phoenix, AZ, USA, 17–22 May 2010; Volume 2, pp. 699–707.
- Tamme, R.; Laing, D.; Steinmann, W.D. Advanced thermal energy storage technology for parabolic trough. J. Sol. Energy Eng. 2004, 126, 794–800. [Google Scholar]
- Arpino, F.; Massarotti, N.; Mauro, A.; Muoio, R.; Vanoli, L. Modeling of thermal energy storage: A review of different systems. In Proceedings of the 3rd International Conference on Computational Methods for Thermal Problems, Lake Bled, Slovenia, 2–4 June 2014.
- Frattini, D.; Ferone, C.; Colangelo, F.; de Pertis, M.; Cioffi, C. Computational evaluation of different construction materials performance in thermal energy storage systems. In Proceedings of the 3rd International Conference on Computational Methods for Thermal Problems, Lake Bled, Slovenia, 2–4 June 2014.
- Caverzan, A.; Cadoni, E.; di Prisco, M. Tensile behavior of high performance fibre-reinforced cementitious composites at high strain rates. Int. J. Impact Eng. 2012, 45, 28–38. [Google Scholar] [CrossRef]
- Corinaldesi, V.; Moriconi, G. Durable fiber reinforced self-compacting concrete. Cem. Concr. Res. 2004, 34, 249–254. [Google Scholar] [CrossRef]
- Zhang, J.; Gong, C.; Guo, Z.; Zhang, M. Engineered cementitious composite with characteristic of low drying shrinkage. Cem. Concr. Res. 2009, 39, 303–312. [Google Scholar] [CrossRef]
- Fernandez, A.I.; Martìnez, M.; Segarra, M.; Martorell, I.; Cabeza, L.F. Selection of materials with potential in sensible thermal energy storage. Sol. Energy Mater. Sol. Cells 2010, 94, 1723–1729. [Google Scholar] [CrossRef]
- Navarro, M.E.; Martìnez, M.; Gil, A.; Fernàndez, A.I.; Cabeza, L.F.; Olives, R.; Py, X. Selection and characterization of recycled materials for sensible thermal energy storage. Sol. Energy 2012, 107, 131–135. [Google Scholar]
- Zabalza Bribián, I.; Valero Capilla, A.; Aranda Usón, A. Life cycle assessment of building materials: Comparative analysis of energy and environmental impacts and evaluation of the eco-efficiency improvement potential. Build. Environ. 2011, 46, 1133–1140. [Google Scholar]
- Flatt, R.J.; Roussel, N.; Cheeseman, C.R. Concrete: An eco material that needs to be improved. J. Eur. Ceram. Soc. 2012, 32, 2787–2798. [Google Scholar] [CrossRef]
- Bignozzi, M.C. Sustainable cements for green buildings construction. Procedia Eng. 2011, 21, 915–921. [Google Scholar] [CrossRef]
- Cioffi, R.; Colangelo, F.; Montagnaro, F.; Santoro, L. Manufacture of artificial aggregate using MSWI bottom ash. Waste Manag. 2011, 31, 281–288. [Google Scholar] [CrossRef] [PubMed]
- Colangelo, F.; Cioffi, R. Use of cement kiln dust, blast furnace slug and marble sludge in the manufacture of sustainable artificial aggregates by means of cold bonding pelletization. Materials 2013, 6, 3139–3159. [Google Scholar] [CrossRef]
- Cioffi, R.; Maffucci, L.; Martone, G.; Santoro, L. Feasibility of manufacturing building materials by recycling a waste from ion exchange process. Environ. Technol. 1998, 19, 1145–1150. [Google Scholar] [CrossRef]
- Ferone, C.; Colangelo, F.; Cioffi, R.; Montagnaro, F.; Santoro, L. Use of reservoir clay sediments as raw materials for geopolymer binders. Adv. Appl. Ceram. 2013, 112, 184–189. [Google Scholar] [CrossRef]
- Andini, S.; Cioffi, R.; Colangelo, F.; Ferone, C.; Montagnaro, F.; Santoro, L. Characterization of geopolymer materials containing MSWI fly ash and coal fly ash. Adv. Sci. Technol. 2010, 69, 123–128. [Google Scholar] [CrossRef]
- Andini, S.; Cioffi, R.; Colangelo, F.; Grieco, T.; Montagnaro, F.; Santoro, L. Coal fly ash as raw material for the manufacture of geopolymer-based products. Waste Manag. 2008, 28, 416–423. [Google Scholar] [CrossRef] [PubMed]
- Ferone, C.; Colangelo, F.; Messina, F.; Santoro, L.; Cioffi, R. Recycling of pre-washed municipal solid waste incinerator fly ash in the manufacturing of low temperature setting geopolymer materials. Materials 2013, 6, 3420–3437. [Google Scholar] [CrossRef]
- Andini, S.; Montagnaro, F.; Santoro, L.; Accardo, G.; Cioffi, R.; Colangelo, F. Mechanochemical processing of blast furnace slag for its reuse as adsorbent. Chem. Eng. Trans. 2013, 32, 2299–2304. [Google Scholar]
- Bayasi, Z.; Zeng, J. Properties of polypropylene fiber reinforced concrete. ACI Mater. J. 1993, 90, 605–610. [Google Scholar]
- Kim, S.B.; Yi, N.H.; Kim, H.Y.; Kim, J.-H.J.; Song, Y.-C. Material and structural performance evaluation of recycled PET fiber reinforced concrete. Cem. Concr. Compos. 2010, 32, 232–240. [Google Scholar] [CrossRef]
- Sakulich, A.R. Reinforced geopolymer composites for enhanced material greenness and durability. Sustain. Cities Soc. 2011, 1, 195–210. [Google Scholar] [CrossRef]
- Ferone, C.; Colangelo, F.; Cioffi, R.; Montagnaro, F.; Santoro, L. Mechanical performances of weathered coal fly ash based geopolymer bricks. Procedia Eng. 2011, 21, 745–752. [Google Scholar] [CrossRef]
- Hussain, M.; Varley, R.J.; Cheng, Y.B.; Simon, G.P. Investigation of thermal and fire performance of novel hybrid geopolymer composites. J. Mater. Sci. 2004, 39, 4721–4726. [Google Scholar] [CrossRef]
- Kong, D.L.Y.; Sanjayan, J.G. Damage behavior of geopolymer composites exposed to elevated temperatures. Cem. Concr. Compos. 2008, 30, 986–991. [Google Scholar] [CrossRef]
- Kong, D.L.Y.; Sanjayan, J.G.; Sagoe-Crentsil, K. Factors affecting the performance of metakaolin geopolymers exposed to elevated temperatures. J. Mater. Sci. 2008, 43, 824–831. [Google Scholar] [CrossRef]
- Guerrieri, M.; Sanjayan, J.G. Behavior of combined fly ash/slag-based geopolymers when exposed to high temperatures. Fire Mater. 2010, 34, 163–175. [Google Scholar]
- Shaikh, F.U.A.; Vimonsatit, V. Compressive strength of fly-ash-based geopolymer concrete at elevated temperatures. Fire Mater. 2014. [Google Scholar] [CrossRef]
- Salomoni, V.A.; Majorana, C.E.; Giannuzzi, G.M.; Miliozzi, A.; di Maggio, R.; Girardi, F.; Mele, D.; Lucentini, M. Thermal storage of sensible heat using concrete modules in solar power plants. Sol. Energy 2014, 103, 303–315. [Google Scholar] [CrossRef]
- Ozger, O.B.; Girardi, F.; Giannuzzi, G.M.; Salomoni, V.A.; Majorana, C.E.; Fambri, L.; Baldassino, N.; di Maggio, R. Effect of nylon fibres on mechanical and thermal properties of hardened concrete for energy storage systems. Mater. Des. 2013, 51, 989–997. [Google Scholar] [CrossRef]
- Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements; European Standard EN 197-1:2011; European Committee for Standardization (CEN): Brussels, Belgium, 2011.
- Aukour, F.J. Incorporation of marble sludge in industrial building eco-blocks or cement bricks formulation. Jordan J. Civ. Eng. 2009, 3, 58–65. [Google Scholar]
- Concrete—Part 1: Specification, Performance, Production and Conformity Criteria; European Standard UNI EN 206-1:2006; European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- Fernandez-Jimenez, A.; Palomo, A. Nanostructure/Microstructure of Fly Ash Geopolymers. In Geopolymers: Structure, Processing, Properties and Industrial Applications; Provis, J.L., van Deventer, J.S.J., Eds.; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2009; pp. 89–117. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ferone, C.; Colangelo, F.; Frattini, D.; Roviello, G.; Cioffi, R.; Maggio, R.D. Finite Element Method Modeling of Sensible Heat Thermal Energy Storage with Innovative Concretes and Comparative Analysis with Literature Benchmarks. Energies 2014, 7, 5291-5316. https://doi.org/10.3390/en7085291
Ferone C, Colangelo F, Frattini D, Roviello G, Cioffi R, Maggio RD. Finite Element Method Modeling of Sensible Heat Thermal Energy Storage with Innovative Concretes and Comparative Analysis with Literature Benchmarks. Energies. 2014; 7(8):5291-5316. https://doi.org/10.3390/en7085291
Chicago/Turabian StyleFerone, Claudio, Francesco Colangelo, Domenico Frattini, Giuseppina Roviello, Raffaele Cioffi, and Rosa Di Maggio. 2014. "Finite Element Method Modeling of Sensible Heat Thermal Energy Storage with Innovative Concretes and Comparative Analysis with Literature Benchmarks" Energies 7, no. 8: 5291-5316. https://doi.org/10.3390/en7085291
APA StyleFerone, C., Colangelo, F., Frattini, D., Roviello, G., Cioffi, R., & Maggio, R. D. (2014). Finite Element Method Modeling of Sensible Heat Thermal Energy Storage with Innovative Concretes and Comparative Analysis with Literature Benchmarks. Energies, 7(8), 5291-5316. https://doi.org/10.3390/en7085291