A New Energy-Absorbing Device for Motion Suppression in Deep-Sea Floating Platforms
Abstract
:1. Introduction
2. Novel S-Shaped TLCD
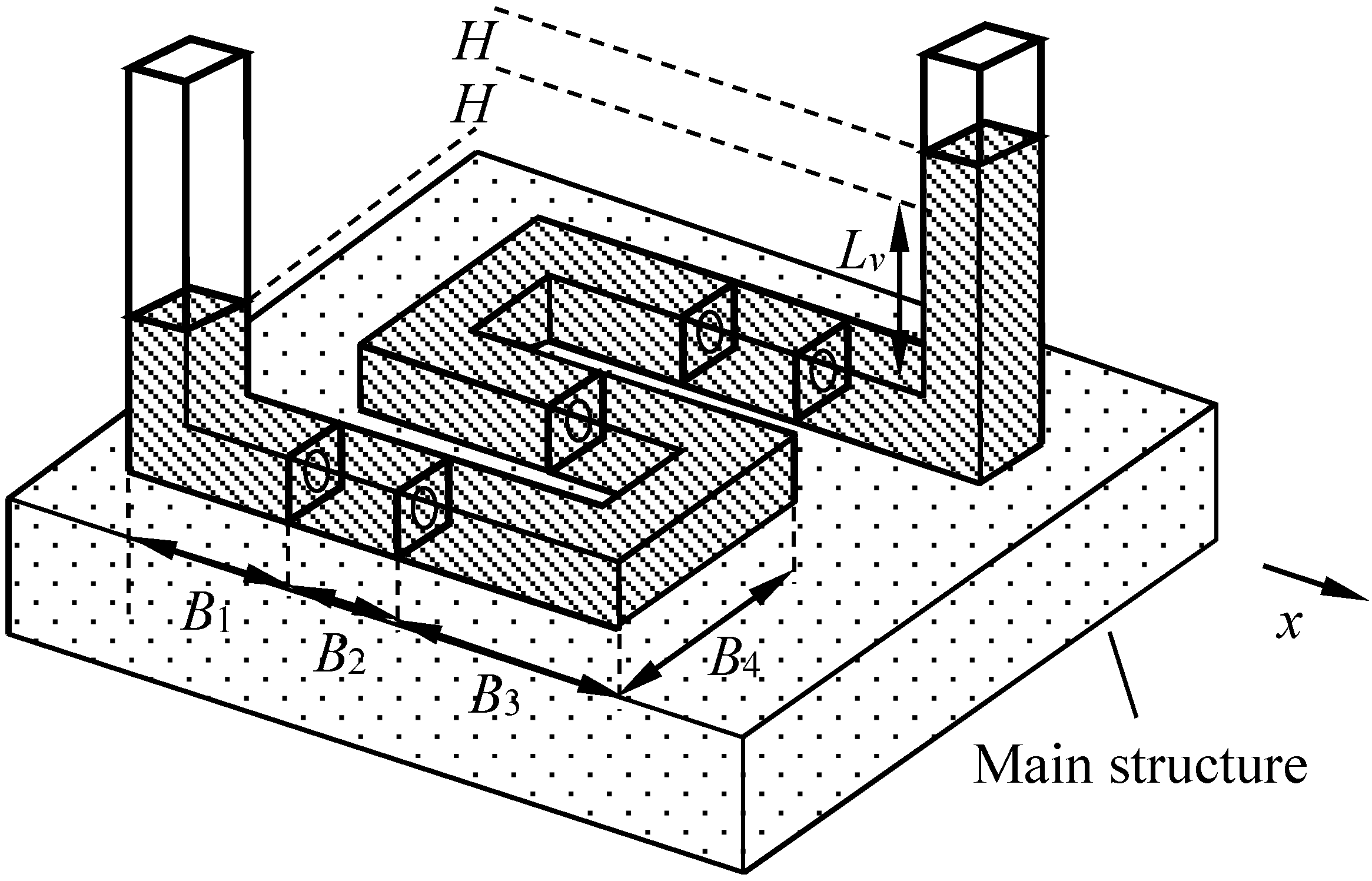
3. Theoretical Study
4. Experimental Investigation



5. Coupling Calculation Model

6. Sensitivity Analysis
| Factor | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 |
|---|---|---|---|---|---|---|---|
| x1 (°) | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| x2 | 2.0 | 2.33 | 2.67 | 3.0 | 3.33 | 3.67 | 4.0 |
| x3 | 0.52 | 0.6 | 0.68 | 0.76 | 0.84 | 0.92 | 1 |
| x4 (m) | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
| x5 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
| x6 (°) | 3.5 | 10.4 | 17.3 | 24.2 | 31.2 | 38.1 | 45 |
| x7 | 1.0 | 1.78 | 3.16 | 5.62 | 10.0 | 17.78 | 31.62 |






7. Conclusions
- The S-shaped TLCD is suitable for suppressing the horizontal motion and vertical in-plane rotation of main structures with large inherent periods by using the method of energy absorption. An S-shaped TLCD can function with a substantially shorter horizontal length compared to a conventional U-shaped TLCD. The short effective horizontal length makes the S-shaped TLCD easier to install on TLPs.
- A coupling calculation model capable of analyzing the dynamic responses of TLPs with S-shaped TLCDs is established. Various factors contributing to the improvements of TLCDs such as the inclination of the vertical liquid column, the cross-section ratio of the vertical liquid column and horizontal liquid column are considered.
- The sensitivity analysis finds:
- (a)
- The cross-section ratio of the vertical liquid column and horizontal liquid column (x5) has the biggest influence on the response of every degree of freedom among seven factors;
- (b)
- The ratio of effective horizontal length and horizontal length (x3) also has a big influence on the response of every degree of freedom;
- (c)
- The length ratio of the horizontal liquid column and vertical liquid column (x2) has some influence on the surge, sway and heave response, the same as the inclination of vertical liquid column (x1) for the heave, pitch and roll response.
- A S-shaped TLCD with uniform cross section has the best suppression effect on the surge and sway response. Selection criteria for motion suppression systems on TLPs are also proposed based on the responses of each degree of freedom.
Acknowledgments
Author Contributions
Appendix 1
Appendix 2 Orthogonal Table L49 (87) and the Numerical Results
| Case | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Wave period T = 12 s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surge (m) | Sway (m) | Heave (m) | Roll (rad) | Pitch (rad) | ||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.243 | 0.235 | 2.56 × 10−3 | 2.74 × 10−5 | 2.95 × 10−5 | ||||
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0.186 | 0.183 | 1.47 × 10−3 | 2.54 × 10−5 | 2.33 × 10−5 | ||||
| 3 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0.179 | 0.179 | 2.21 × 10−3 | 3.23 × 10−5 | 3.19 × 10−5 | ||||
| 4 | 1 | 4 | 7 | 3 | 6 | 2 | 5 | 0.166 | 0.165 | 1.63 × 10−3 | 1.10 × 10−5 | 9.20 × 10−6 | ||||
| 5 | 1 | 5 | 2 | 6 | 3 | 7 | 4 | 0.168 | 0.166 | 1.96 × 10−3 | 2.63 × 10−5 | 2.67 × 10−5 | ||||
| 6 | 1 | 6 | 4 | 2 | 7 | 5 | 3 | 0.181 | 0.177 | 1.09 × 10−3 | 2.29 × 10−5 | 2.08 × 10−5 | ||||
| 7 | 1 | 7 | 6 | 5 | 4 | 3 | 2 | 0.148 | 0.148 | 2.20 × 10−3 | 1.17 × 10−5 | 1.00 × 10−5 | ||||
| 8 | 2 | 1 | 7 | 6 | 5 | 4 | 3 | 0.172 | 0.171 | 1.70 × 10−3 | 8.75 × 10−6 | 7.86 × 10−6 | ||||
| 9 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0.131 | 0.134 | 3.12 × 10−3 | 2.63 × 10−5 | 1.81 × 10−5 | ||||
| 10 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 0.188 | 0.186 | 1.41 × 10−3 | 1.99 × 10−5 | 2.00 × 10−5 | ||||
| 11 | 2 | 4 | 6 | 1 | 3 | 5 | 7 | 0.161 | 0.161 | 2.44 × 10−3 | 1.94 × 10−5 | 1.73 × 10−5 | ||||
| 12 | 2 | 5 | 1 | 4 | 7 | 3 | 6 | 0.188 | 0.191 | 1.23 × 10−3 | 3.22 × 10−5 | 2.99 × 10−5 | ||||
| 13 | 2 | 6 | 3 | 7 | 4 | 1 | 5 | 0.163 | 0.169 | 1.93 × 10−3 | 2.34 × 10−5 | 1.93 × 10−5 | ||||
| 14 | 2 | 7 | 5 | 3 | 1 | 6 | 4 | 0.217 | 0.216 | 2.83 × 10−3 | 3.78 × 10−5 | 3.66 × 10−5 | ||||
| 15 | 3 | 1 | 6 | 4 | 2 | 7 | 5 | 0.185 | 0.185 | 2.20 × 10−3 | 3.40 × 10−5 | 3.28 × 10−5 | ||||
| 16 | 3 | 2 | 1 | 7 | 6 | 5 | 4 | 0.191 | 0.191 | 1.44 × 10−3 | 2.81 × 10−5 | 2.73 × 10−5 | ||||
| 17 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 0.158 | 0.164 | 2.14 × 10−3 | 2.52 × 10−5 | 2.32 × 10−5 | ||||
| 18 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 0.179 | 0.18 | 1.45 × 10−3 | 1.48 × 10−5 | 1.37 × 10−5 | ||||
| 19 | 3 | 5 | 7 | 2 | 4 | 6 | 1 | 0.162 | 0.162 | 2.14 × 10−3 | 1.03 × 10−5 | 9.94 × 10−6 | ||||
| 20 | 3 | 6 | 2 | 5 | 1 | 4 | 7 | 0.217 | 0.213 | 2.51 × 10−3 | 3.10 × 10−5 | 3.23 × 10−5 | ||||
| 21 | 3 | 7 | 4 | 1 | 5 | 2 | 6 | 0.173 | 0.177 | 1.98 × 10−3 | 2.17 × 10−5 | 2.09 × 10−5 | ||||
| 22 | 4 | 1 | 5 | 2 | 6 | 3 | 7 | 0.195 | 0.195 | 1.20 × 10−3 | 1.62 × 10−5 | 1.58 × 10−5 | ||||
| 23 | 4 | 2 | 7 | 5 | 3 | 1 | 6 | 0.155 | 0.155 | 2.05 × 10−3 | 1.24 × 10−5 | 1.25 × 10−5 | ||||
| 24 | 4 | 3 | 2 | 1 | 7 | 6 | 5 | 0.202 | 0.202 | 8.63 × 10−4 | 2.14 × 10−5 | 2.26 × 10−5 | ||||
| 25 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 0.171 | 0.173 | 1.89 × 10−3 | 2.14 × 10−5 | 2.07 × 10−5 | ||||
| 26 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 0.248 | 0.246 | 2.36 × 10−3 | 5.75 × 10−5 | 5.87 × 10−5 | ||||
| 27 | 4 | 6 | 1 | 3 | 5 | 7 | 2 | 0.188 | 0.188 | 1.61 × 10−3 | 2.85 × 10−5 | 3.09 × 10−5 | ||||
| 28 | 4 | 7 | 3 | 6 | 2 | 5 | 1 | 0.091 | 0.104 | 3.13 × 10−3 | 1.61 × 10−5 | 1.91 × 10−5 | ||||
| 29 | 5 | 1 | 4 | 7 | 3 | 6 | 2 | 0.174 | 0.174 | 1.78 × 10−3 | 1.76 × 10−5 | 1.83 × 10−5 | ||||
| 30 | 5 | 2 | 6 | 3 | 7 | 4 | 1 | 0.191 | 0.191 | 9.33 × 10−4 | 1.55 × 10−5 | 1.51 × 10−5 | ||||
| 31 | 5 | 3 | 1 | 6 | 4 | 2 | 7 | 0.185 | 0.189 | 1.66 × 10−3 | 3.37 × 10−5 | 3.11 × 10−5 | ||||
| 32 | 5 | 4 | 3 | 2 | 1 | 7 | 6 | 0.203 | 0.203 | 2.70 × 10−3 | 2.93 × 10−5 | 2.73 × 10−5 | ||||
| 33 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 0.175 | 0.175 | 1.64 × 10−3 | 1.83 × 10−5 | 1.83 × 10−5 | ||||
| 34 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 0.141 | 0.141 | 2.86 × 10−3 | 3.14 × 10−5 | 3.40 × 10−5 | ||||
| 35 | 5 | 7 | 2 | 4 | 6 | 1 | 3 | 0.185 | 0.19 | 1.41 × 10−3 | 3.21 × 10−5 | 2.97 × 10−5 | ||||
| 36 | 6 | 1 | 3 | 5 | 7 | 2 | 4 | 0.198 | 0.198 | 8.00 × 10−4 | 2.82 × 10−5 | 2.67 × 10−5 | ||||
| 37 | 6 | 2 | 5 | 1 | 4 | 7 | 3 | 0.189 | 0.186 | 1.49 × 10−3 | 2.00 × 10−5 | 2.00 × 10−5 | ||||
| 38 | 6 | 3 | 7 | 4 | 1 | 5 | 2 | 0.218 | 0.218 | 2.38 × 10−3 | 4.33 × 10−5 | 4.28 × 10−5 | ||||
| 39 | 6 | 4 | 2 | 7 | 5 | 3 | 1 | 0.185 | 0.187 | 1.45 × 10−3 | 3.62 × 10−5 | 3.41 × 10−5 | ||||
| 40 | 6 | 5 | 4 | 3 | 2 | 1 | 7 | 0.196 | 0.196 | 2.23 × 10−3 | 2.76 × 10−5 | 2.84 × 10−5 | ||||
| 41 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 0.178 | 0.178 | 1.41 × 10−3 | 1.65 × 10−5 | 1.60 × 10−5 | ||||
| 42 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 0.172 | 0.167 | 2.02 × 10−3 | 4.45 × 10−5 | 4.35 × 10−5 | ||||
| 43 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 0.193 | 0.19 | 1.22 × 10−3 | 3.32 × 10−5 | 3.23 × 10−5 | ||||
| 44 | 7 | 2 | 4 | 6 | 1 | 3 | 5 | 0.215 | 0.212 | 2.05 × 10−3 | 3.13 × 10−5 | 3.16 × 10−5 | ||||
| 45 | 7 | 3 | 6 | 2 | 5 | 1 | 4 | 0.182 | 0.182 | 1.05 × 10−3 | 1.96 × 10−5 | 1.92 × 10−5 | ||||
| 46 | 7 | 4 | 1 | 5 | 2 | 6 | 3 | 0.18 | 0.181 | 2.14 × 10−3 | 3.88 × 10−5 | 3.84 × 10−5 | ||||
| 47 | 7 | 5 | 3 | 1 | 6 | 4 | 2 | 0.19 | 0.187 | 7.07 × 10−4 | 2.95 × 10−5 | 2.82 × 10−5 | ||||
| 48 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0.15 | 0.153 | 1.88 × 10−3 | 2.42 × 10−5 | 2.22 × 10−5 | ||||
| 49 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 0.181 | 0.178 | 1.16 × 10−3 | 1.61 × 10−5 | 1.40 × 10−5 | ||||
| Case | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Wave period T = 16 s | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Surge (m) | Sway (m) | Heave (m) | Roll (rad) | Pitch (rad) | ||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.509 | 0.494 | 3.96 × 10−4 | 5.48 × 10−6 | 8.44 × 10−6 |
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0.391 | 0.391 | 1.19 × 10−3 | 1.08 × 10−5 | 8.38 × 10−6 |
| 3 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0.389 | 0.389 | 6.58 × 10−4 | 5.04 × 10−5 | 5.13 × 10−5 |
| 4 | 1 | 4 | 7 | 3 | 6 | 2 | 5 | 0.349 | 0.349 | 1.00 × 10−3 | 3.56 × 10−5 | 3.48 × 10−5 |
| 5 | 1 | 5 | 2 | 6 | 3 | 7 | 4 | 0.36 | 0.36 | 7.83 × 10−4 | 1.13 × 10−5 | 3.44 × 10−6 |
| 6 | 1 | 6 | 4 | 2 | 7 | 5 | 3 | 0.376 | 0.376 | 1.46 × 10−3 | 1.05 × 10−5 | 9.22 × 10−6 |
| 7 | 1 | 7 | 6 | 5 | 4 | 3 | 2 | 0.318 | 0.318 | 7.05 × 10−4 | 3.63 × 10−5 | 3.66 × 10−5 |
| 8 | 2 | 1 | 7 | 6 | 5 | 4 | 3 | 0.367 | 0.367 | 9.80 × 10−4 | 4.15 × 10−5 | 4.04 × 10−5 |
| 9 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0.292 | 0.297 | 1.84 × 10−3 | 3.38 × 10−5 | 4.76 × 10−5 |
| 10 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 0.398 | 0.395 | 1.25 × 10−3 | 1.89 × 10−5 | 1.32 × 10−5 |
| 11 | 2 | 4 | 6 | 1 | 3 | 5 | 7 | 0.352 | 0.352 | 5.48 × 10−4 | 3.09 × 10−5 | 2.78 × 10−5 |
| 12 | 2 | 5 | 1 | 4 | 7 | 3 | 6 | 0.392 | 0.401 | 1.38 × 10−3 | 3.19 × 10−6 | 2.03 × 10−6 |
| 13 | 2 | 6 | 3 | 7 | 4 | 1 | 5 | 0.347 | 0.361 | 7.68 × 10−4 | 1.42 × 10−5 | 1.92 × 10−5 |
| 14 | 2 | 7 | 5 | 3 | 1 | 6 | 4 | 0.479 | 0.479 | 2.05 × 10−4 | 1.92 × 10−5 | 2.06 × 10−5 |
| 15 | 3 | 1 | 6 | 4 | 2 | 7 | 5 | 0.4 | 0.4 | 7.44 × 10−4 | 6.52 × 10−5 | 6.15 × 10−5 |
| 16 | 3 | 2 | 1 | 7 | 6 | 5 | 4 | 0.404 | 0.409 | 1.21 × 10−3 | 6.13 × 10−5 | 4.73 × 10−5 |
| 17 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 0.335 | 0.348 | 6.68 × 10−4 | 1.52 × 10−5 | 1.73 × 10−5 |
| 18 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 0.377 | 0.383 | 1.19 × 10−3 | 2.79 × 10−5 | 2.95 × 10−5 |
| 19 | 3 | 5 | 7 | 2 | 4 | 6 | 1 | 0.348 | 0.348 | 6.94 × 10−4 | 3.76 × 10−5 | 3.41 × 10−5 |
| 20 | 3 | 6 | 2 | 5 | 1 | 4 | 7 | 0.468 | 0.46 | 3.48 × 10−4 | 5.75 × 10−5 | 9.00 × 10−6 |
| 21 | 3 | 7 | 4 | 1 | 5 | 2 | 6 | 0.361 | 0.369 | 8.33 × 10−4 | 1.28 × 10−5 | 1.33 × 10−5 |
| 22 | 4 | 1 | 5 | 2 | 6 | 3 | 7 | 0.403 | 0.403 | 1.33 × 10−3 | 2.08 × 10−5 | 2.09 × 10−5 |
| 23 | 4 | 2 | 7 | 5 | 3 | 1 | 6 | 0.336 | 0.336 | 7.17 × 10−4 | 6.69 × 10−5 | 6.69 × 10−5 |
| 24 | 4 | 3 | 2 | 1 | 7 | 6 | 5 | 0.412 | 0.412 | 1.56 × 10−3 | 7.63 × 10−5 | 2.92 × 10−5 |
| 25 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 0.364 | 0.37 | 8.31 × 10−4 | 1.89 × 10−5 | 1.81 × 10−5 |
| 26 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 0.537 | 0.537 | 4.22 × 10−4 | 5.63 × 10−5 | 5.81 × 10−5 |
| 27 | 4 | 6 | 1 | 3 | 5 | 7 | 2 | 0.399 | 0.399 | 1.04 × 10−3 | 3.00 × 10−6 | 5.74 × 10−6 |
| 28 | 4 | 7 | 3 | 6 | 2 | 5 | 1 | 0.218 | 0.243 | 2.30 × 10−3 | 8.03 × 10−5 | 8.50 × 10−5 |
| 29 | 5 | 1 | 4 | 7 | 3 | 6 | 2 | 0.374 | 0.374 | 8.12 × 10−4 | 2.75 × 10−5 | 2.17 × 10−5 |
| 30 | 5 | 2 | 6 | 3 | 7 | 4 | 1 | 0.396 | 0.396 | 1.52 × 10−3 | 2.37 × 10−5 | 2.25 × 10−5 |
| 31 | 5 | 3 | 1 | 6 | 4 | 2 | 7 | 0.392 | 0.403 | 9.90 × 10−4 | 7.80 × 10−6 | 5.65 × 10−6 |
| 32 | 5 | 4 | 3 | 2 | 1 | 7 | 6 | 0.441 | 0.441 | 3.11 × 10−4 | 2.63 × 10−6 | 2.98 × 10−6 |
| 33 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 0.376 | 0.376 | 9.90 × 10−4 | 2.28 × 10−5 | 1.99 × 10−5 |
| 34 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 0.318 | 0.318 | 9.08 × 10−4 | 1.00 × 10−4 | 1.02 × 10−4 |
| 35 | 5 | 7 | 2 | 4 | 6 | 1 | 3 | 0.385 | 0.397 | 1.20 × 10−3 | 3.38 × 10−6 | 5.37 × 10−7 |
| 36 | 6 | 1 | 3 | 5 | 7 | 2 | 4 | 0.413 | 0.413 | 1.66 × 10−3 | 4.13 × 10−6 | 5.55 × 10−6 |
| 37 | 6 | 2 | 5 | 1 | 4 | 7 | 3 | 0.397 | 0.397 | 1.09 × 10−3 | 1.54 × 10−5 | 9.99 × 10−6 |
| 38 | 6 | 3 | 7 | 4 | 1 | 5 | 2 | 0.478 | 0.478 | 4.39 × 10−4 | 2.89 × 10−5 | 3.14 × 10−5 |
| 39 | 6 | 4 | 2 | 7 | 5 | 3 | 1 | 0.393 | 0.4 | 1.17 × 10−3 | 7.58 × 10−6 | 5.97 × 10−6 |
| 40 | 6 | 5 | 4 | 3 | 2 | 1 | 7 | 0.417 | 0.417 | 5.84 × 10−4 | 1.75 × 10−5 | 2.31 × 10−5 |
| 41 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 0.38 | 0.38 | 1.21 × 10−3 | 2.55 × 10−5 | 2.19 × 10−5 |
| 42 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 0.358 | 0.369 | 7.52 × 10−4 | 2.17 × 10−5 | 2.24 × 10−5 |
| 43 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 0.405 | 0.405 | 1.28 × 10−3 | 4.85 × 10−6 | 6.35 × 10−6 |
| 44 | 7 | 2 | 4 | 6 | 1 | 3 | 5 | 0.467 | 0.461 | 6.22 × 10−4 | 6.30 × 10−6 | 7.50 × 10−6 |
| 45 | 7 | 3 | 6 | 2 | 5 | 1 | 4 | 0.38 | 0.38 | 1.38 × 10−3 | 1.62 × 10−5 | 1.69 × 10−5 |
| 46 | 7 | 4 | 1 | 5 | 2 | 6 | 3 | 0.392 | 0.395 | 1.25 × 10−3 | 1.55 × 10−5 | 2.09 × 10−5 |
| 47 | 7 | 5 | 3 | 1 | 6 | 4 | 2 | 0.392 | 0.392 | 1.61 × 10−3 | 3.44 × 10−6 | 3.73 × 10−6 |
| 48 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0.32 | 0.327 | 8.04 × 10−4 | 1.65 × 10−5 | 1.81 × 10−5 |
| 49 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 0.387 | 0.383 | 1.43 × 10−3 | 2.55 × 10−5 | 2.32 × 10−5 |
Conflicts of Interest
References
- Pecher, A.; Kofoed, J.P.; Larsen, T. Design specifications for the Hanstholm WEPTOS wave energy converter. Energies 2012, 5, 1001–1017. [Google Scholar] [CrossRef]
- Yu, J.X.; Fu, M.Y. Fatigue reliability analysis of vortex-induced vibration of submarine pipeline span. J. Tianjin Univ. 2008, 41, 1321–1325. [Google Scholar]
- Ng, K.W.; Lam, W.H.; Ng, K.C. 2002–2012: 10 years of research progress in horizontal-axis marine current turbines. Energies 2013, 6, 1497–1526. [Google Scholar] [CrossRef]
- Eatock, T.R.; Jefferys, E.R. Variability of hydrodynamic load predictions for a tension leg platform. Ocean. Eng. 1986, 13, 449–490. [Google Scholar] [CrossRef]
- Zeng, X.H.; Shen, X.P.; Wu, Y.X. Governing equations and numerical solutions of tension leg platform with finite amplitude motion. Appl. Math. Mech. 2007, 28, 37–49. [Google Scholar] [CrossRef]
- Zeng, X.H.; Li, X.W.; Liu, Y.; Wu, Y.X. Nonlinear dynamic responses of tension leg platform with slack-taut tether. China Ocean. Eng. 2009, 23, 37–48. [Google Scholar]
- Ahmad, S.K.; Ahmad, S. Active control of non-linearly coupled TLP response under wind and wave environments. Comput. Struct. 1999, 72, 735–747. [Google Scholar] [CrossRef]
- Alves, R.M.; Batista, R.C. Active/passive control of heave motion for TLP type offshore platform. In Proceedings of the Ninth (1999) international offshore and polar engineering conference, Brest, France, 30 May–4 June 1999; International Society of Offshore and Polar Engineers: Cupertino, CA, USA, 1999; pp. 332–338. [Google Scholar]
- Spillane, M.W.; Rijken, O.R.; Leverette, S.J. Vibration absorbers for deepwater TLP’s. In Proceedings of the 17th International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007; International Society of Offshore and Polar Engineers: Houston, TX, USA, 2007; pp. 210–217. [Google Scholar]
- Rijken, O.; Spillane, M.; Leverette, S.J. Vibration absorber technology and conceptual design of vibration absorber for TLP in ultradeep water. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; ASME: New York, NY, USA, 2010; pp. 629–638. [Google Scholar]
- Bian, X.S.; Leverette, S.J.; Rijken, O.R. A TLP solution for 8000 Ft water depth. In Proceedings of the ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; ASME: New York, NY, USA, 2010; pp. 255–262. [Google Scholar]
- Zhu, H.; Ou, J.; Zhai, G. Conceptual design of a deep draft semi-submersible platform with a moveable heave-plate. J. Ocean. Univ. China 2012, 11, 7–12. [Google Scholar] [CrossRef]
- Qiao, D.S.; Zhu, H.; Ou, J.P.; Fei, W. Numerical simulation for truncated model tests of deepwater semi-submersible platform with viscous damper compensated system in mooring lines. In Proceedings of the 21th (2011) International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; ISOPE: Cupertino, CA, USA, 2011; pp. 557–564. [Google Scholar]
- Taflanidis, A.A.; Angelides, D.C.; Scruggs, J.T. Simulation-based robust design of mass dampers for response mitigation of tension leg platforms. Eng. Struct. 2009, 31, 847–857. [Google Scholar] [CrossRef]
- Taflanidis, A.A.; Vetter, C.; Loukogeorgaki, E. Impact of modeling and excitation uncertainties on operational and structural reliability of tension leg platforms. Appl. Ocean. Res. 2013, 43, 131–147. [Google Scholar] [CrossRef]
- Fischer, F.J.; Liapis, S.I.; Kallinderis, Y. Mitigation of current-driven, vortex-induced vibrations of a spar platform via “SMART” thrusters. J. Offshore Mech. Arct. Eng. 2004, 126, 96–104. [Google Scholar] [CrossRef]
- Lee, H.H.; Wong, S.H.; Lee, R.S. Response mitigation on the offshore floating platform system with tuned liquid column damper. Ocean. Eng. 2006, 33, 1118–1142. [Google Scholar] [CrossRef]
- Lee, H.H.; Juang, H.H. Experimental study on the vibration mitigation of offshore tension leg platform system with UWTLCD. Smart Struct. Syst. 2012, 9, 71–104. [Google Scholar] [CrossRef]
- Bozzi, S.; Miquel, A.M.; Antonini, A. Modeling of a point absorber for energy conversion in italian seas. Energies 2013, 6, 3033–3051. [Google Scholar] [CrossRef] [Green Version]
- Huo, L.S.; Li, H.N. Torsionally coupled response control of offshore platform structures using CTLCD. In Proceedings of the Fifteenth International Offshore and Polar Engineering Conference, Seoul, Korea, 19–24 June 2005; ISOPE: Cupertino, CA, USA, 2005; pp. 296–303. [Google Scholar]
- Mousavi, S.A.; Bargi, K.; Zahrai, S.M. Optimum parameters of tuned liquid column-gas damper for mitigation of seismic-induced vibrations of offshore jacket platforms. Struct. Control. Health Monit. 2013, 20, 422–444. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Zahrai, S.M.; Bargi, K. Optimum geometry of tuned liquid column-gas damper for control of offshore jacket platform vibrations under seismic excitation. Earthq. Eng. Eng. Vib. 2012, 11, 579–592. [Google Scholar] [CrossRef]
- Christiansen, S.; Bak, T.; Knudsen, T. Damping wind and wave loads on a floating wind turbine. Energies 2013, 6, 4097–4116. [Google Scholar] [CrossRef]
- Colwell, S.; Basu, B. Tuned liquid column dampers in offshore wind turbines for structural control. Eng. Struct. 2009, 31, 358–368. [Google Scholar] [CrossRef]
- Mensah, A.F.; Dueñas-Osorio, L. Improved reliability of wind turbine towers with tuned liquid column dampers (TLCDs). Struct. Saf. 2014, 47, 78–86. [Google Scholar] [CrossRef]
- Shadman, M.; Akbarpour, A. Utilizing TLCD (tuned liquid column damper) in floating wind turbines. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; ASME: New York, NY, USA, 2012; pp. 241–247. [Google Scholar]
- Yu, J.X.; Xu, H.L. Fatigue reliability analysis of vortex induced vibration of TLP tethers in waves and current. J. Ship Mech. 2008, 12, 592–598. [Google Scholar]
- Wu, J.C.; Shih, M.H.; Lin, Y.Y.; Shen, Y.C. Design guidelines for tuned liquid column damper for structures responding to wind. Eng. Struct. 2005, 27, 1893–1905. [Google Scholar] [CrossRef]
- Hitchcock, P.A.; Kwok, K.C.S.; Watkins, R.D. Characteristics of liquid column vibration absorbers (LCVA)—I. Eng. Struct. 1997, 19, 126–134. [Google Scholar] [CrossRef]
- Hitchcock, P.A.; Kwok, K.C.S.; Watkins, R.D. Characteristics of liquid column vibration absorbers (LCVA)—II. Eng. Struct. 1997, 19, 135–144. [Google Scholar] [CrossRef]
- Gao, H.; Kwok, K.C.S.; Samali, B. Characteristics of multiple tuned liquid column dampers in suppressing structural vibration. Eng. Struct. 1999, 21, 316–331. [Google Scholar] [CrossRef]
- Hochrainer, M.J. Tuned liquid column damper for structural control. Acta. Mech. 2005, 175, 57–76. [Google Scholar] [CrossRef]
- Min, K.W.; Kim, J.; Kim, Y.W. Design and test of tuned liquid mass dampers for attenuation of the wind responses of a full scale building. Smart Mater. Struct. 2014, 23, 045020:1–045020:10. [Google Scholar]
- Gao, H.; Kwok, K.C.S.; Samali, B. Optimization of tuned liquid column dampers. Eng. Struct. 1997, 19, 476–486. [Google Scholar] [CrossRef]
- Subrat, C.; Rama, D.; Giuseppe, C.M. Performance of tuned liquid column dampers considering maximum liquid motion in seismic vibration control of structures. J. Sound Vib. 2012, 331, 1519–1531. [Google Scholar] [CrossRef]
- Matteo, D.A.; Iacono, F.L.; Navarra, G.; Pirrotta, A. Direct evaluation of the equivalent linear damping for TLCD systems in random vibration for pre-design purposes. Int. J. Non-Linear Mech. 2014, 63, 19–30. [Google Scholar] [CrossRef]
- Wu, J.C.; Chang, C.H.; Lin, Y.Y. Optimal designs for non-uniform tuned liquid column dampers in horizontal motion. J. Sound Vib. 2009, 326, 104–122. [Google Scholar] [CrossRef]
- Wu, J.C.; Wang, Y.P.; Chen, Y.H. Design tables and charts for uniform and non-uniform tuned liquid column dampers in harmonic pitching motion. Smart Struct. Systems 2012, 9, 165–188. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Yu, Y.; Zhang, L.; Liu, Q.; Wu, H. A New Energy-Absorbing Device for Motion Suppression in Deep-Sea Floating Platforms. Energies 2015, 8, 111-132. https://doi.org/10.3390/en8010111
Zeng X, Yu Y, Zhang L, Liu Q, Wu H. A New Energy-Absorbing Device for Motion Suppression in Deep-Sea Floating Platforms. Energies. 2015; 8(1):111-132. https://doi.org/10.3390/en8010111
Chicago/Turabian StyleZeng, Xiaohui, Yang Yu, Liang Zhang, Qingquan Liu, and Han Wu. 2015. "A New Energy-Absorbing Device for Motion Suppression in Deep-Sea Floating Platforms" Energies 8, no. 1: 111-132. https://doi.org/10.3390/en8010111
APA StyleZeng, X., Yu, Y., Zhang, L., Liu, Q., & Wu, H. (2015). A New Energy-Absorbing Device for Motion Suppression in Deep-Sea Floating Platforms. Energies, 8(1), 111-132. https://doi.org/10.3390/en8010111





