Hybrid Intelligent Control Method to Improve the Frequency Support Capability of Wind Energy Conversion Systems
Abstract
:1. Introduction
2. Wind Energy Conversion System (WECS) Description
2.1. Variable Speed Wind Turbine Characteristics
2.2. Modeling of Permanent Magnet Synchronous Generator (PMSG)
3. Control Method of Wind Energy Conversion System (WECS)
3.1. Design of the Converters Control Loop

3.2. DC-Link Voltage Control
3.3. Pitch Angle Control Mode

3.4. De-Loaded (DL) Operation Mode
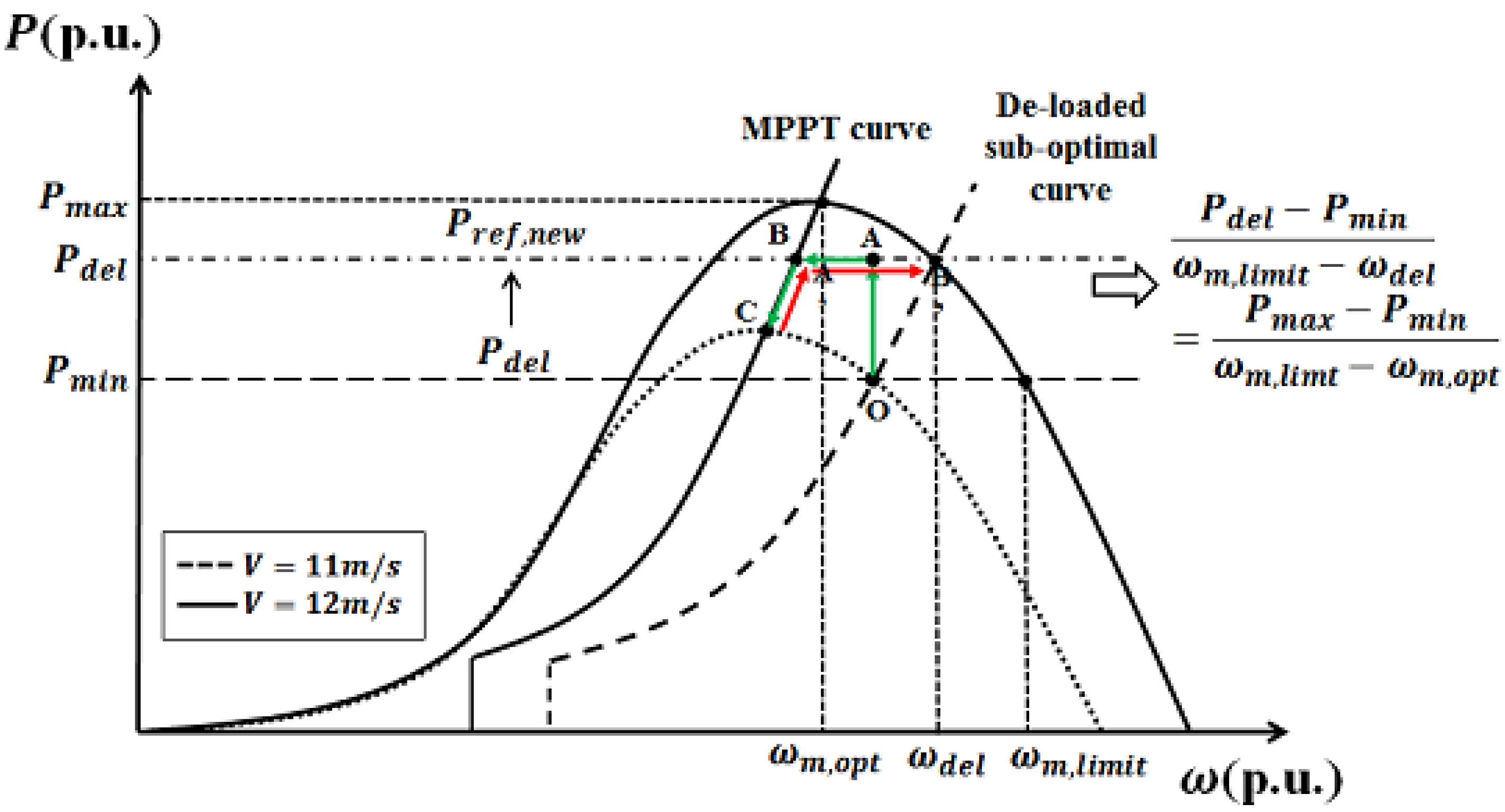

4. Hybrid Intelligent Control Method
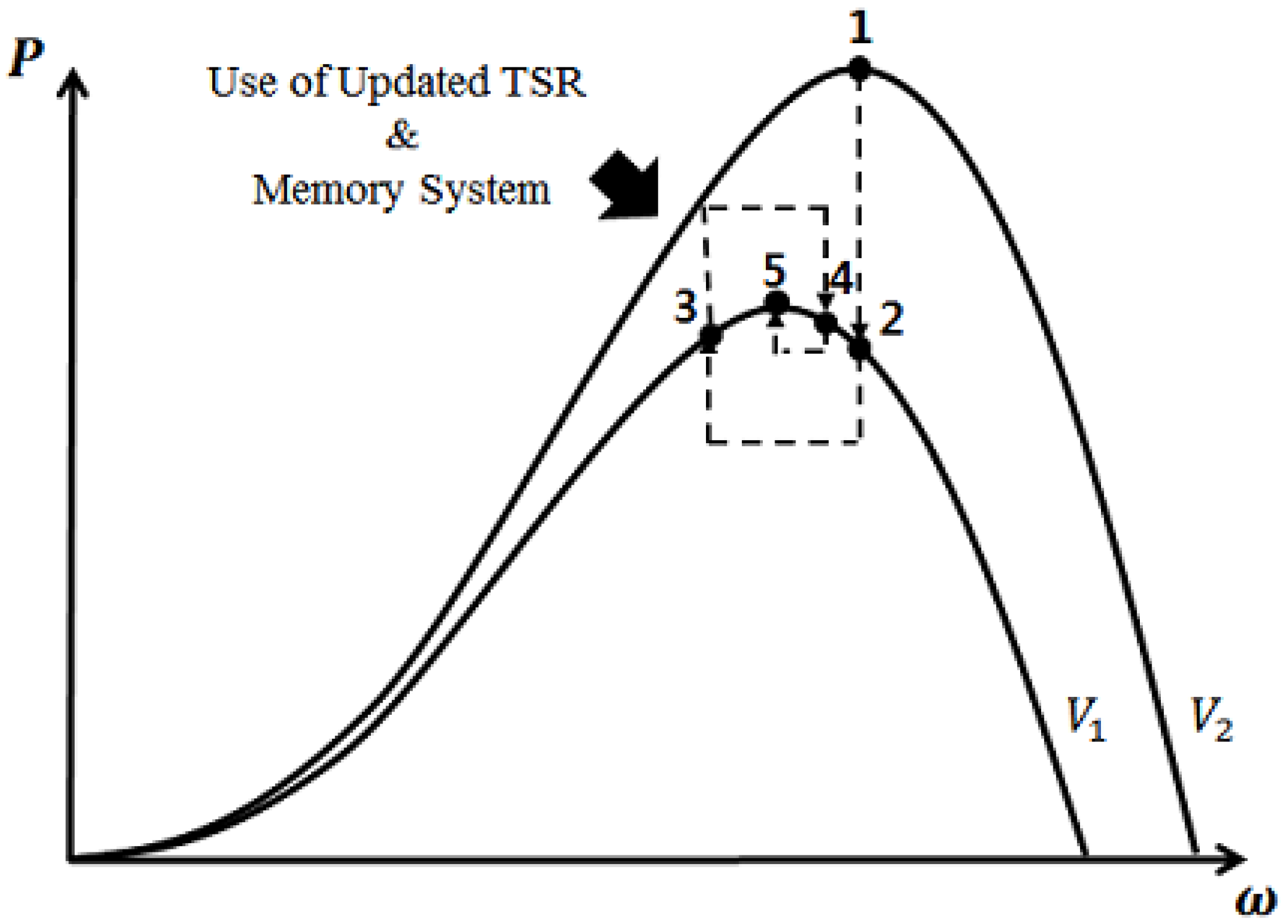
4.1. Improved Hill Climb Searching (IHCS) Algorithm

- Step 1.
- Track the MPP based on the initial TSR.
- Step 2.
- Check the MPP. If it is satisfied, go to Step 3. Otherwise, the procedure returns to Step 1 by regulating the reference rotor speed (ωref).
- Step 3.
- Save the wind speed and rotor speed in the memory system.
- Step 4.
- Calculate the optimal TSR from the rotational speed component of the stored MPP from each wind speed in the memory system.
- Step 5.
- Update the TSR and operating point. Although the wind speed suddenly changes, the IHCS algorithm can trace the MPP by going through the calculation process with the initial TSR and updated TSR in the memory.
4.2. Advanced Frequency Support Control Method



5. Case Study and Results

| Parameters | Notation | Value |
|---|---|---|
| Blade radius | R | 38 m |
| Air density | ρ | 1.205 kg/m2 |
| Maximum power coefficient | Cp,max | 0.4412 |
| Rated wind speed | Vw,rated | 12 m/s |
| Rated generator power | Pm,rated | 2 MW |
| Rated RMS line-to-line voltage | Vm,rated | 0.69 kV |
| Rated machine speed | ωm,rated | 376.99 rad/s |
| Pole pairs | P | 11 |
| Gen.+Turbine inertia const. | H | 5.7267 s |
| PM flux | Ψf | 136 Wb |
| Stator d-axis inductance | Lmd | 0.334 H |
| Stator q-axis inductance | Lmq | 0.217 H |
| Stator leakage inductance | Lsi | 0.0334 H |
| Stator resistance | Rs | 0.08 Ω |
| Parameters | Value | |
|---|---|---|
| Steam Turbine | Gas Turbine | |
| H | 5.4 s | 1.86 s |
| Xd | 1.456 p.u. | 1.94 p.u. |
| 0.206 p.u. | 0.2259 p.u. | |
| 0.147 p.u. | 0.1723 p.u. | |
| 3.735 s | 10.4 s | |
| 0.032 s | 0.03 s | |
| Xl | 0.161 p.u. | 0.15 p.u. |
| Xq | 1.405 p.u. | 1.92 p.u. |
| 0.500 p.u. | 0.402 p.u. | |
| 0.147 p.u. | 0.1723 p.u. | |
| 0.305 s | 0.83 s | |
| 0.080 s | 0.055 s | |
| Rated RMS L-N voltage | 7.976 kV | 7.976 kV |
| Rated RMS line current | 0.2008 kA | 0.2008 kA |
5.1. Dynamic Performance Test of an Individual Permanent Magnet Synchronous Generator (PMSG)



| Method | Control Characteristic | ||
|---|---|---|---|
| Average Power (MW) | Increasing Power Percentage | Efficiency | |
| Conventional HCS | 0.721955 | - | 95.59 |
| IHCS | 0.750112 | 3.754% | 99.32 |

5.2. Simulation Result of the Proposed Hybrid Intelligent Control Method

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heier, S. Wind Energy Power Plants. In Grid Integration of Wind Energy, 2nd ed.; John Wiley & Sons: London, UK, 2006. [Google Scholar]
- Ruuskanen, V.; Immonen, P.; Nerg, J.; Pyrhonen, J. Determining electrical efficiency of permanent magnet synchronous machines with different control method. Electr. Eng. 2012, 94, 97–106. [Google Scholar]
- Chinchilia, M.; Arnaltes, S.; Burgos, J.C. Control of permanent-magnet generator applied to variable-speed wind-energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]
- Datta, R.; Ranganathan, V.T. A method of tracking the peak power points for a variable speed wind energy conversion system. IEEE Trans. Energy Convers. 2003, 18, 163–168. [Google Scholar] [CrossRef]
- Barakati, S.M.; Kazerani, M.; Aplevich, J.D. Maximum power tracking control for a wind turbine system including a matrix converter. IEEE Trans. Energy Convers. 2009, 24, 705–713. [Google Scholar] [CrossRef]
- Jadhav, H.T.; Roy, R. A comprehensive review on the grid integration of doubly fed induction generator. Int. J. Electron. Power Energy Syst. 2013, 49, 8–18. [Google Scholar] [CrossRef]
- Dalala, Z.M.; Zahid, Z.U.; Yu, W.; Cho, Y.; Lai, J.S. Design and Analysis of an MPPT Technique for Small-Scale Wind Energy Conversion Systems. IEEE Trans. Energy Convers. 2013, 28, 756–767. [Google Scholar] [CrossRef]
- Gonzalez, L.G.; Figueres, E.; Carranza, O. Maximum-power-point tracking with reduced mechanical stress applied to wind-energy-conversion-systems. Appl. Energy 2010, 87, 2304–2312. [Google Scholar] [CrossRef]
- Lalouni, S.; Rekioua, D.; Idjdarene, K.; Tounzi, A. Maximum Power Point Tracking Based Hybrid Hill-climb Search Method Applied to Wind Energy Conversion System. Electric. Power Compon. Syst. 2015, 43, 1028–1038. [Google Scholar] [CrossRef]
- Lin, W.M.; Hong, C.M.; Cheng, F.S. Fuzzy neural network output maximization control for sensorless wind energy conversion system. Energy 2015, 35, 592–601. [Google Scholar] [CrossRef]
- Hafiz, F.; Abdennour, A. Optimal use of kinetic energy for the inertial support from variable speed wind turbines. Renew. Energy 2015, 80, 629–643. [Google Scholar] [CrossRef]
- Alaboudy, A.H.K.; Daoud, A.A.; Desouky, S.S.; Salem, A.A. Converter controls and flicker study of PMSG-based grid connected wind turbines. Ain Shams Eng. J. 2013, 4, 75–91. [Google Scholar] [CrossRef]
- Morimoto, S.; Nakayama, H.; Sanada, M.; Takeda, Y. Sensorless output maximization control for variable-speed wind generation system using IPMSG. IEEE Trans. Ind. Appl. 2005, 41, 60–67. [Google Scholar] [CrossRef]
- Mullance, A.; O’Malley, M. The inertial response of induction-machine-based wind turbines. IEEE Trans. Power Syst. 2005, 20, 1496–1503. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Ramtharan, G.; Ekanayake, J.B.; Jenkins, N. Frequency support from doubly fed induction generator wind turbines. Renew. Power Gener. IET 2007, 1, 3–9. [Google Scholar] [CrossRef]
- Conroy, J.F.; Watson, R. Frequency response capability of full converter wind turbine generators in comparison to conventional generation. IEEE Trans. Power Syst. 2008, 23, 649–656. [Google Scholar] [CrossRef]
- Chien, L.R.C.; Lin, W.T.; Yin, Y.C. Enhancing frequency response control by DFIGs in the high wind penetrated power systems. IEEE Trans. Power Syst. 2011, 26, 710–718. [Google Scholar] [CrossRef]
- Almeida, R.G.; Lopes, J.A.P. Participation of doubly fed induction wind generators in system frequency regulation. IEEE Trans. Power Syst. 2007, 22, 944–950. [Google Scholar] [CrossRef]
- Almeida, R.G.; Castronuovo, E.D.; Pecas, J.A. Optimum generation control in wind parks when carrying out system operator requests. IEEE Trans. Power Syst. 2006, 21, 718–725. [Google Scholar] [CrossRef]
- Kayikci, M.; Milanovic, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- Keung, P.K.; Li, P.; Banakar, H.; Ooi, B.T. Kinetic energy of wind-turbine generators for system frequency support. IEEE Trans. Power Syst. 2009, 24, 279–287. [Google Scholar] [CrossRef]
- Ganjefar, S.; Ghasemi, A.A. A novel-strategy controller design for maximum power extraction in standalone windmill systems. Energy 2014, 76, 326–335. [Google Scholar] [CrossRef]
- Zhang, S.; Tseng, K.J.; Vilathgamuwa, D.M.; Nguyen, T.D.; Wang, X.Y. Design of a robust grid interface system for PMSG-based wind turbine generators. IEEE Trans. Ind. Electron. 2011, 58, 316–328. [Google Scholar] [CrossRef]
- Fernandez, L.M.; Garcia, C.A.; Jurado, F. Operating capability as a PQ/PV node of a direct-drive wind turbine based on a permanent magnet synchronous generator. Renew. Energy 2010, 35, 1308–1318. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Takahashi, R.; Murata, T.; Tamura, J. A variable speed wind turbine control strategy to meet wind farm grid code requirements. IEEE Trans. Power Syst. 2010, 25, 331–340. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Xu, L. Conventional and novel control designs for direct driven PMSG wind turbines. Electr. Power Syst. Res. 2010, 80, 328–338. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, S.Y.; Kim, M.K.; Choi, J.W. Hybrid Intelligent Control Method to Improve the Frequency Support Capability of Wind Energy Conversion Systems. Energies 2015, 8, 11430-11451. https://doi.org/10.3390/en81011430
Heo SY, Kim MK, Choi JW. Hybrid Intelligent Control Method to Improve the Frequency Support Capability of Wind Energy Conversion Systems. Energies. 2015; 8(10):11430-11451. https://doi.org/10.3390/en81011430
Chicago/Turabian StyleHeo, Shin Young, Mun Kyeom Kim, and Jin Woo Choi. 2015. "Hybrid Intelligent Control Method to Improve the Frequency Support Capability of Wind Energy Conversion Systems" Energies 8, no. 10: 11430-11451. https://doi.org/10.3390/en81011430
APA StyleHeo, S. Y., Kim, M. K., & Choi, J. W. (2015). Hybrid Intelligent Control Method to Improve the Frequency Support Capability of Wind Energy Conversion Systems. Energies, 8(10), 11430-11451. https://doi.org/10.3390/en81011430





