Critical Clearing Time and Wind Power in Small Isolated Power Systems Considering Inertia Emulation

Abstract

The stability and security of small and isolated power systems can be compromised when large amounts of wind power enter them. Wind power integration depends on such factors as power generation capacity, conventional generation technology or grid topology. Another issue that can be considered is critical clearing time (CCT). In this paper, wind power and CCT are studied in a small isolated power system. Two types of wind turbines are considered: a squirrel cage induction generator (SCIG) and a full converter. Moreover, the full converter wind turbine’s inertia emulation capability is considered, and its impact on CCT is discussed. Voltage is taken into account because of its importance in power systems of this kind. The study focuses on the small, isolated Lanzarote-Fuerteventura power system, which is expected to be in operation by 2020.

1. Introduction

The unprecedented worldwide development of wind power over recent decades reached around 318,644 GW by the end of 2014, and it is estimated that global wind power capacity will continue to increase [1].

Integrating wind power into power systems is an increasingly common challenge. Large amounts of wind power can be introduced into continental power systems, such as the European grid managed by the members of the European Network of Transmission System Operators for Electricity (ENTSO-E). On the other hand, small, isolated power systems, such as those found on small islands, can experience problems related to stability, and this can influence wind integration [2].

One issue that deserves consideration in wind power integration is the critical clearing time (CCT), particularly in small, isolated power systems. CCT can be seen as a measure of the transient stability of a power system [3,4] and can be defined as the maximum allowed duration of a three-phase short circuit before loss of system stability. As a part of the Spanish Grid Codes, a set of protection coordination criteria and a methodology leading to CCT evaluation were developed by the Spanish Transmission System Operator (TSO) Red Eléctrica de España (REE) [5,6]. The CCT calculation methodology implies performing dynamic stability simulations by applying a short circuit in the nodes of the network and varying the fault time until a set of criteria are fulfilled [7,8]. The set of criteria to be fulfilled through this trial and the error approach specify that the following is not allowed:

(1)

loss of system stability;

(2)

an unacceptable value of load shedding;

(3)

unacceptable parameters values in the subsequent steady state.

The Spanish TSO has established 10% of load as the unacceptable value for Spanish power systems on islands and in other small systems [6].

There are other methods for CCT estimation, such as Lyapunov energy function, artificial neuronal networks or hybrid methods. However, the trial and error method using dynamic simulations provides more accuracy results. In this paper, we use the trial and error method and the above-mentioned criteria to study how using inertia emulation could impact CCT values and eventually the wind power penetration level.

A TSO uses CCT for designing protection schemes in power systems. A significant modification of the CCT values can cause problems in protection system behavior that can have an impact on the stability or security of the power system itself.

Several papers and reports have investigated wind power and system stability through CCT, and their results show that there is a relationship between them. They suggest a modification of CCT values when wind power is introduced into a power system [9,10,11].

Other papers have analyzed inertia emulation from wind turbines and have shown a positive impact of the inertia emulation on the frequency response [12,13,14,15,16,17,18,19,20].

These papers usually look at large power systems and conventional generation based on large thermal or hydro generator units. Generation unit outages or transmission tie line outages are examples of the types of disturbances studied in papers considering inertia emulation. Medium and low voltage networks or feeders are also studied, and the analysis in these papers focuses on the time evolution of frequency.

In [21], the power system of an island and wind farms with inertia emulation are considered. The integration of a hydro-pump storage system was analyzed, but short-circuit disturbance was not taken into account.

In this paper, the relationship between wind power and CCT is studied in a small, isolated power system with two types of wind turbines: the squirrel cage induction generator (SCIG) and the full converter. Furthermore, the inertia emulation capability of the full converter wind turbine is considered. A comparative analysis of the different results achieved is presented. In order to obtain CCT values, a three-phase short circuit disturbance is simulated. Therefore, inertia emulation performance was studied when a three-phase short circuit takes place. Network voltages are also considered because of their relevance in this type of power system. Thus, a more global analysis of the small and isolated power system can be undertaken. Almost all of the system’s conventional generation is based on small diesel generators.

The study has been carried out on the planned Lanzarote-Fuerteventura power system, which is expected to be in operation by 2020. Its generation power capacity, voltage level, inertia constant and grid topology are features that make it a good example of a small, isolated power system.

Modeling and analysis are performed using PSS^®E v32 software (Siemens-PTI, Schenectady, NY, USA).

2. Methodology

CCT values are obtained through a trial and error procedure [22] when using dynamic analysis for several three-phase short circuit events at some Lanzarote-Fuerteventura power system buses. Simulation results were studied to find out what determines the CCT.

These short circuit disturbances were simulated at five selected buses in order to know the overall behavior of the power system. The selected buses are: (1) Punta Grande power plant and Las Salinas power plant; (2) Haría-Teguise and Jandía as the farthest buses from power plants; and (3) Corralejo, which is a bus in between both power plants.

In order to analyze the wind power impact on CCT, three types of wind turbine were studied: SCIG, full converter and full converter with inertia emulation capability. Each wind farm in the power system is equipped with only one kind of wind turbine. Thus, their CCT values can show some differences.

In every case, wind power was increased from 0 MW to 150 MW, in steps of 10 MW. This wind power was generated by wind farms according to their rated powers.

In order to find CCT values, the CCT definition given in the Introduction section is used. In this way, the unacceptable value of load shedding is equal to or higher than 10% of the load.

Photovoltaic power plants were not modeled to avoid their effects on the results.

The model of the Lanzarote-Fuerteventura power system for steady-state analysis and dynamic simulation was created using PSS^®E v32.

3. Description of the Studied Power System

The system studied here is the Lanzarote-Fuerteventura power system 2020. Lanzarote and Fuerteventura are two of the Spanish Canary Islands.

The Lanzarote and Fuerteventura power systems are linked by a submarine cable and, therefore, constitute a single power system.

At present, each island has only one conventional power plant. On Lanzarote, Punta Grande has a capacity of 232.4 MW, and Las Salinas, on Fuerteventura, has a capacity of 187.0 MW. Both power plants have conventional diesel and gas turbine units. New power generators are not expected to be installed in the foreseeable future, because power demand has decreased over recent years [23]. The units at these power plants are listed in Table 1.

Table 1. Conventional generation units.

Punta Grande unit name	Capacity (MVA)	Las Salinas unit name	Capacity (MVA)
Diesel 1	9.4	Diesel 1	5.4
Diesel 2	9.4	Diesel 2	5.4
Diesel 3	9.4	Diesel 3	6.3
Diesel 4	20	Diesel 4	9.4
Diesel 5	20	Diesel 5	9.4
Diesel 6	30	Diesel 6	30
Diesel 7	22.5	Diesel 7	18
Diesel 8	22.5	Diesel 8	18
Diesel 9	22.5	Diesel 9	18
Diesel 10	22.5	Gas 1	32.42
Diesel 11	22.5	Gas 2	40.93
Gas 1	27.24	Gas Mobile 1	15
Gas 2	40.93	-	-

Table 1. Conventional generation units.

Punta Grande unit name	Capacity (MVA)	Las Salinas unit name	Capacity (MVA)
Diesel 1	9.4	Diesel 1	5.4
Diesel 2	9.4	Diesel 2	5.4
Diesel 3	9.4	Diesel 3	6.3
Diesel 4	20	Diesel 4	9.4
Diesel 5	20	Diesel 5	9.4
Diesel 6	30	Diesel 6	30
Diesel 7	22.5	Diesel 7	18
Diesel 8	22.5	Diesel 8	18
Diesel 9	22.5	Diesel 9	18
Diesel 10	22.5	Gas 1	32.42
Diesel 11	22.5	Gas 2	40.93
Gas 1	27.24	Gas Mobile 1	15
Gas 2	40.93	-	-

Peak power demand in 2013 was 251 MW, and it is expected to reach 384 MW by 2020.

At present, the power system is operated at 66 kV in the transmission network and at 20 kV at the distribution level. The transmission network has eight buses. The rated voltage of the submarine cable is 66 kV, with a transmission capacity of 60 MVA.

New substations and transmission lines of 132-kV rated voltage have been planned for 2020. In addition, the undersea link will be reinforced by a second submarine cable of 132-kV rated voltage and 130 MVA of capacity. The power system will then have 26 buses at two voltage levels, 66 kV and 132 kV.

Currently, the two-island system has five wind farms. Total wind power capacity is 21.86 MW. The most widely-used type of wind turbine is the SCIG with a gear box.

The installed wind power is expected to have increased by 2020. Wind power could rise to 162 MW [24]. Most of the new wind farms will be full converter wind turbines.

4. System Modeling

This section describes the model of the Lanzarote-Fuerteventura 2020 power system that was implemented in PSS^®E v32.

Conventional units in power plants, wind power energy converters, power substations and lines of the transmission network have been modeled. The distribution system and power demands are represented through loads at corresponding buses.

A single-line diagram of the Lanzarote-Fuerteventura 2020 power system is shown in Figure 1.

Transmission lines have been modeled using a π model with their conductances neglected. The power factor of loads is 0.9. A two-winding transformer model is used for transformers of generation units and for substation transformers. Resistance and reactance are considered.

Figure 1. Lanzarote-Fuerteventura power system expected by the year 2020.

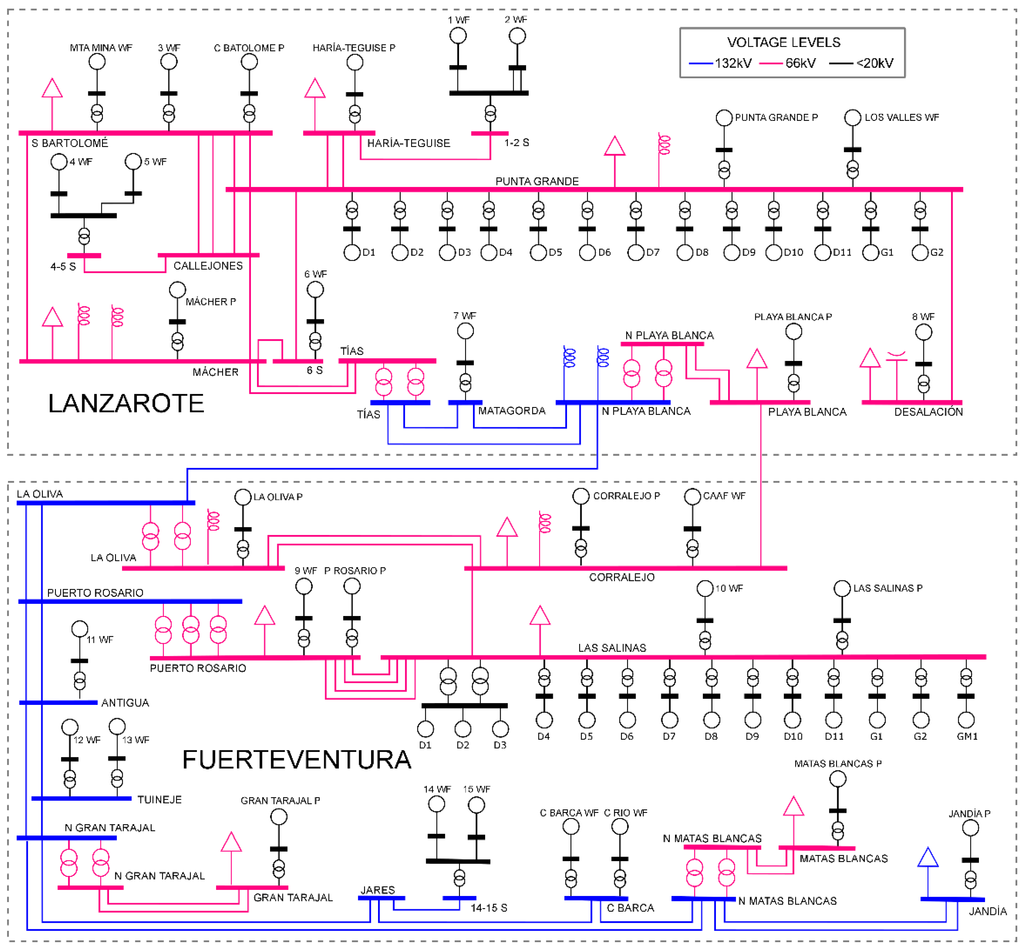
Figure 1. Lanzarote-Fuerteventura power system expected by the year 2020.

4.1. Conventional Generation

Diesel generators are represented by GENSAL models, and gas turbine generators are modeled with GENROE. Both models belong to the PSS^®E library.

The turbine governor model used for diesel units is DEGOV1 (Woodward diesel governor). The GAST2A turbine governor model is used for gas turbine units.

PSS^®E models used for excitation control in diesel units and gas turbine units are simplified excitation system (SEXS) and ESDCA1 (IEEE Type DC1A excitation system), respectively.

4.2. Wind Conversion Energy System

4.2.1. Squirrel Cage Induction Generator (SCIG) Wind Turbine

A SCIG wind turbine, or so-called Type 1, is connected to the grid through a transformer. The generator operates at a nearly fixed speed, related to the grid frequency. The wind turbine generates active power when the shaft speed is higher than the grid frequency. The generator consumes reactive power to create its magnetic field. Thereby, a capacitor bank is used for power factor correction. Normally, in this wind turbine type, there is a soft-starter to limit the higher starting currents [25]. A diagram of this wind turbine is depicted in Figure 2.

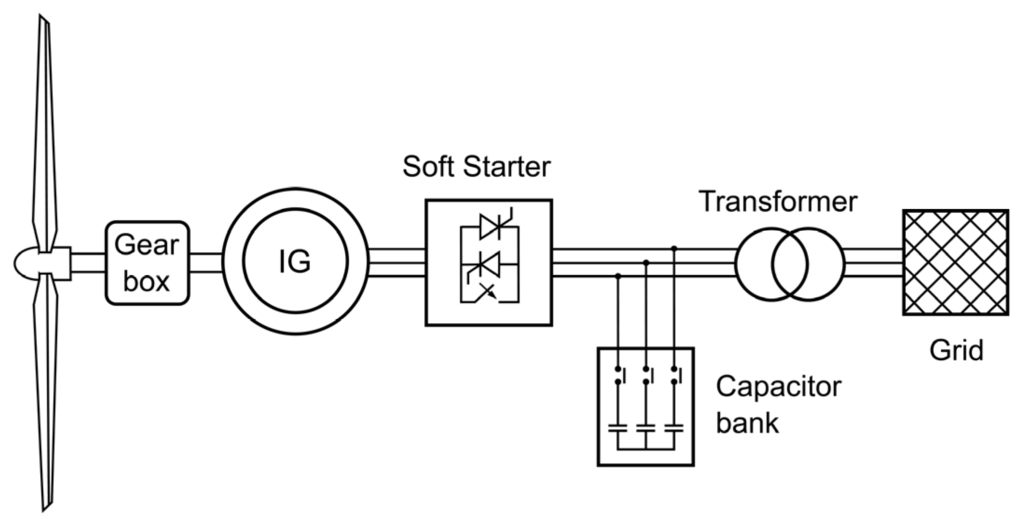
Figure 2. Diagram of the squirrel cage induction generator (SCIG) wind turbine.

Figure 2. Diagram of the squirrel cage induction generator (SCIG) wind turbine.

The model used for SCIG wind turbines is the well-known PSS^®E WT1 model [26]. This model includes the WT1G generator model, the WT12T wind turbine model and the WT12A pseudo-governor model.

The WT1G model is a modification of the standard induction machine model and considers rotor flux dynamics. The WT12T model is based on a two-mass representation of the wind turbine drive shaft. It includes rotor blades, the shaft and the machine with the gear box. This model determines speed deviation. The WT12A model calculates the mechanical torque of the blades’ shaft by processing rotor speed deviation and active power at generator terminals. A connectivity diagram of these models can be seen in [26].

4.2.2. Full Converter Wind Turbine

In a full converter wind turbine, a generator is connected to the grid through a power converter. This allows variable speed in the turbine shaft. The converter rectifies the variable-frequency AC power from the generator into DC and then inverts the DC power to AC at the grid frequency. Figure 3 shows this type of wind turbine. The generator can be a wound rotor synchronous generator (WRSG), a permanent magnet synchronous generator (PMSG) or an SCIG [25]. In this paper, the WRSG is considered.

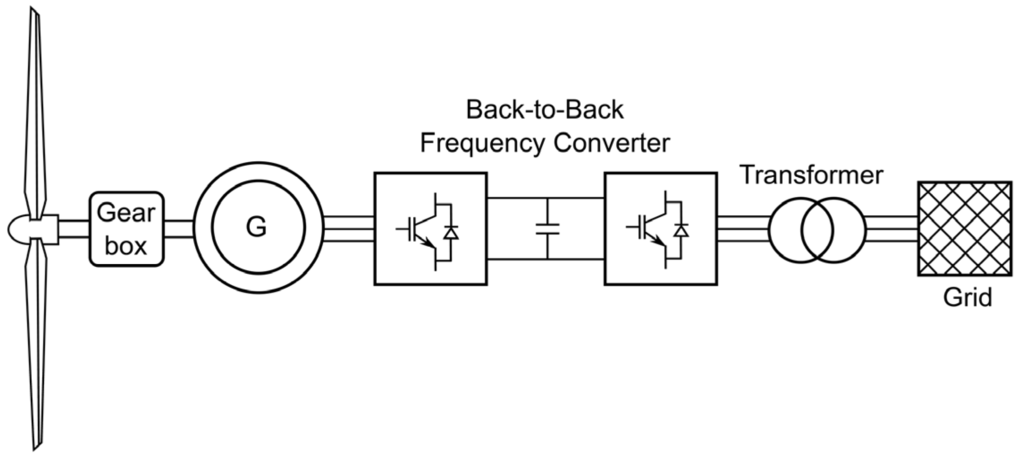
Figure 3. Diagram of a full converter wind turbine.

Figure 3. Diagram of a full converter wind turbine.

Model characteristics of the considered wind turbine are described in [27,28].

The dynamic behavior of the wind turbine is related to the converter control system for the simulation times normally used. Therefore, modeling the converter control system is enough for wind turbine representation in almost all cases. Figure 4 shows a diagram for the model of the wind turbine.

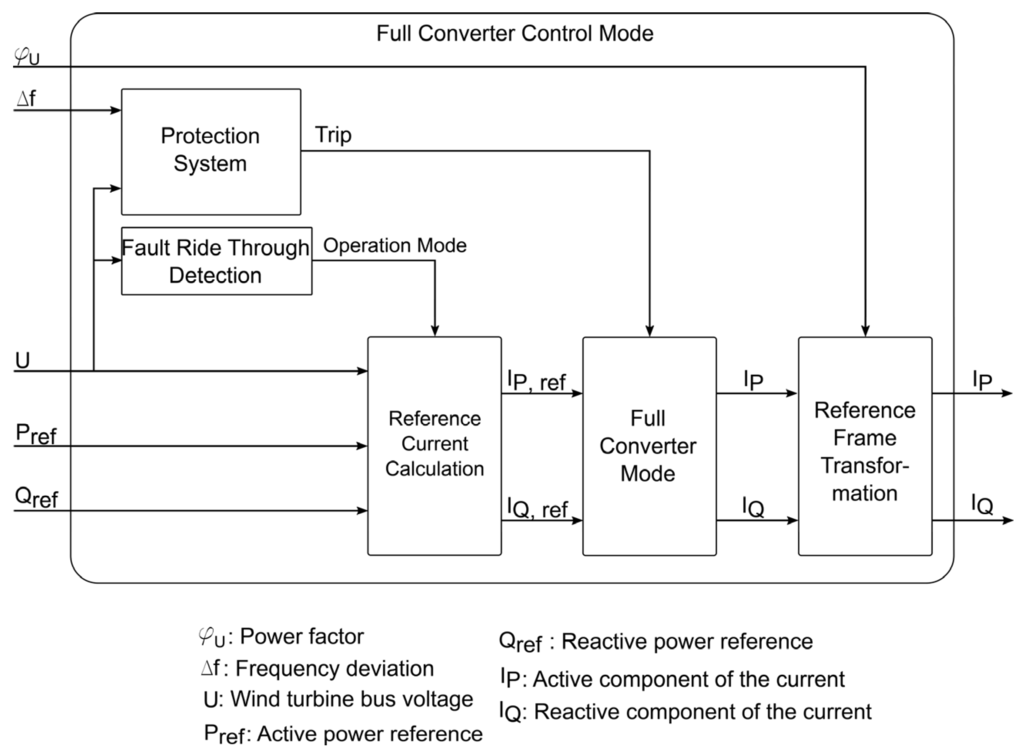
Figure 4. Simplified diagram of the full converter wind turbine model.

Figure 4. Simplified diagram of the full converter wind turbine model.

The power converter allows supporting grid voltage by generating or consuming reactive power. Reactive power control is available for all of the active power operation range. This can be seen in Figure 5.

Figure 5. P-Q characteristic of the full converter wind turbine.

Figure 5. P-Q characteristic of the full converter wind turbine.

A full converter wind turbine with fault ride-through capability can remain in operation when a voltage dip or an overvoltage occurs. The wind turbine is also able to inject or consume additional reactive power to participate in network voltage restoration.

The reference of total current related to reactive power $I_{Q,\text{ref}}$ is obtained by Equation (1):

$$I_{Q,\text{ref}}=\frac{Q_{\text{ref}}}{U}+∆I_Q$$

(1)

where $Q_{\text{ref}}$ is the generated or consumed reactive power of the wind turbine before fault, $U$ is the voltage at the wind turbine terminals and $∆I_Q$ is the additional reactive current determined as shown in Figure 6.

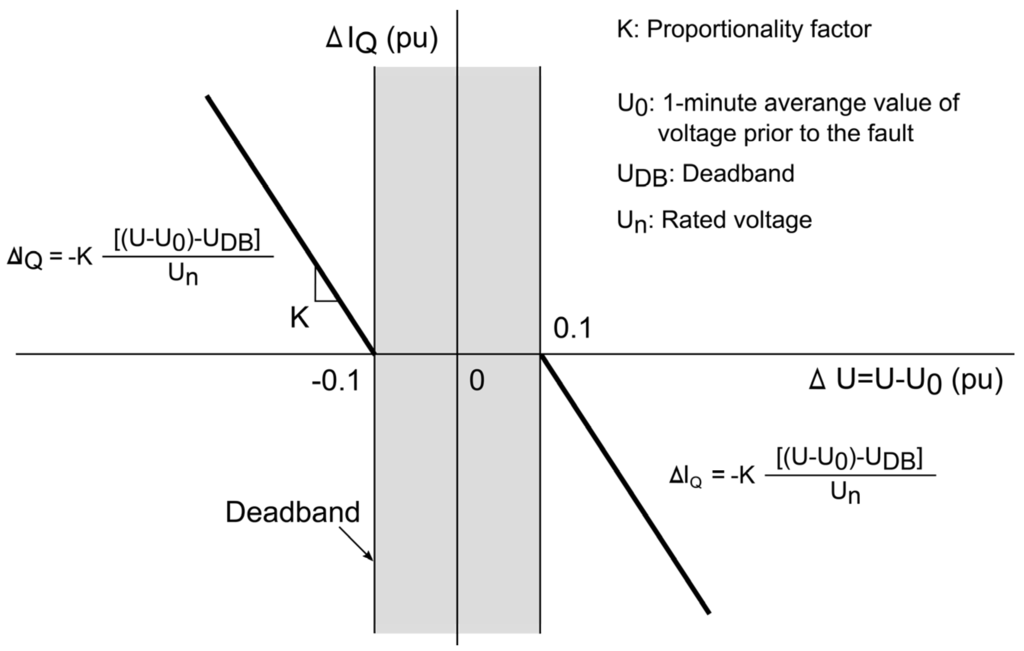
Figure 6. Additional current related to the reactive power characteristic.

Figure 6. Additional current related to the reactive power characteristic.

4.2.3. Inertia Emulation

A kind of active power control that some wind turbines can provide is inertia emulation, also called synthetic inertia or simulated inertia. A wind turbine with inertia emulation capability is able to increase the generated active power from kinetic energy stored in the rotating mass, by means of the power converter control. If there is a low system frequency value, the wind turbine injects extra active power into the network, emulating conventional synchronous generators’ inertia [12,29].

Because kinetic energy is used to increase the active power, the speed of the wind turbine decreases. In order not to reduce wind turbine speed excessively, emulation inertia can only be provided during a few seconds. According to some manufacturers, wind turbines can provide this extra active power within the first 10 s [30,31,32]. After the power increases, a period of time is needed to restore the speed to an acceptable value. This recovery period is about twice the power increase time [16,33].

Depending on the wind turbine, extra active power can vary from 4% to 10% of the wind turbine rated power [18,34]. Extra active power $P_{\text{ext}}$ can be obtained by Equation (2) used in [30].

$$P_{\text{ext}}t=\frac{1}{2}{J}_{\text{WT}}{\text{ω}}_{r0}^2-\frac{1}{2}{J}_{\text{WT}}{\text{ω}}_{rt}^2$$

(2)

where $t$ is the extra active power duration, $J_{\text{WT}}$ is the total moment of inertia of the wind turbine, ${\text{ω}}_{r0}$ is the initial rotor angular speed and ${\text{ω}}_{\text{rt}}$ is the rotor angular speed at time $t$.

In this paper, the inertia emulation control model for the full converter wind turbine considered is based on [16]. This can be seen in Figure 7. The output value $P_{\text{ext}}$ depends on the actual value of the system frequency, as shown in Figure 8.

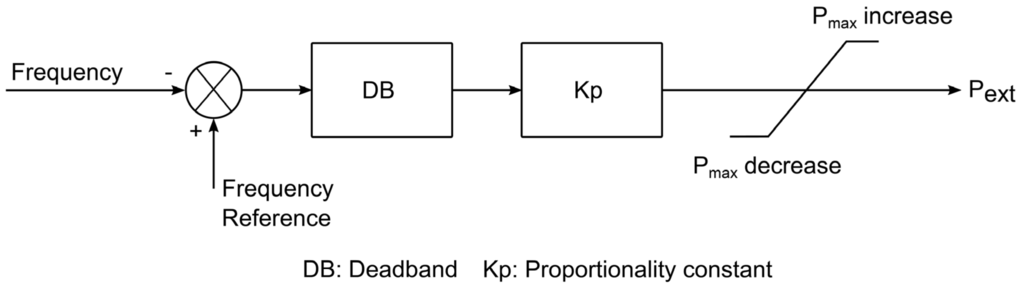
Figure 7. Basic inertia emulation model block diagram.

Figure 7. Basic inertia emulation model block diagram.

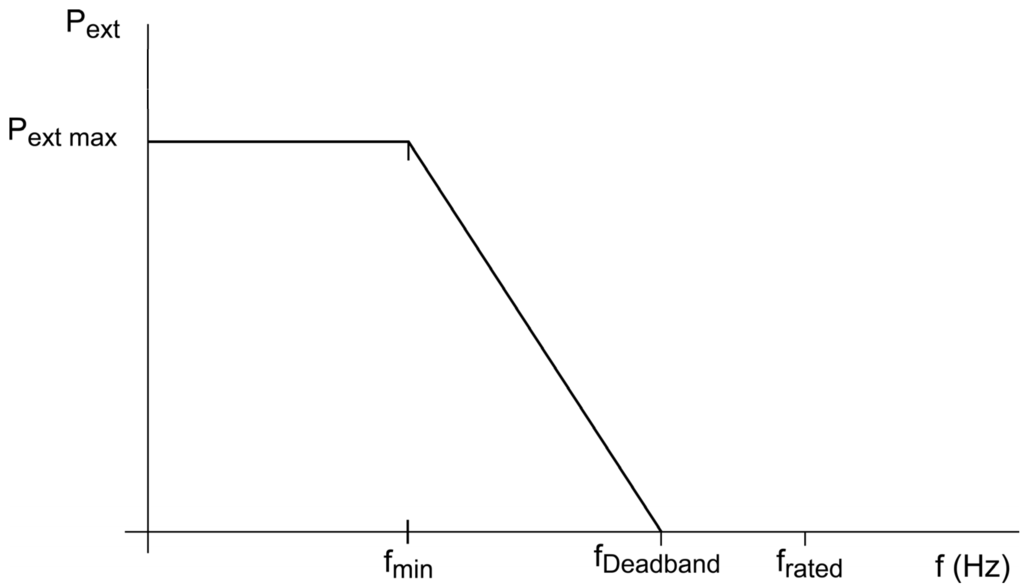
Figure 8. Graph behavior of the inertia emulation considered.

Figure 8. Graph behavior of the inertia emulation considered.

$P_{\text{ext max}}$ is 10% of rated power; f_Deadband is 49.85 Hz; and f_min is 49.25 Hz. The recovery period implemented in the model is twice the power increase time. Inertia emulation is available from 4% of rated power, and its time response is within 800 ms.

4.3. Protections Relays

Protection relays have been modeled for both the conventional units and the wind turbine generators. The protection relays considered are: under voltage and overvoltage, under frequency and over frequency, over current and over speed. Settings for these protection relays are given in Table 2.

Table 2. Protection relay settings for conventional units and wind turbines.

Generator type	Parameter	Under voltage	Overvoltage	Under frequency	Over frequency	Over current 1	Over current 2	Over speed
Conventional generator	Value	0.75 pu	1.12 pu	47 Hz	52.2 Hz	1.25 pu	3 pu	1.08 pu
	Delay (s)	0.8	1	1.25	2	6.5	0.5	Instant
Wind turbine	Value	0.8 pu	1.12 pu	47 Hz	51 Hz	1.25 pu	3 pu	1.08 pu (Only SCIG WT)
	Delay (s)	5	0.3	1.3	0.1	6.5	0.5	Instant (Only SCIG WT)

Table 2. Protection relay settings for conventional units and wind turbines.

Generator type	Parameter	Under voltage	Overvoltage	Under frequency	Over frequency	Over current 1	Over current 2	Over speed
Conventional generator	Value	0.75 pu	1.12 pu	47 Hz	52.2 Hz	1.25 pu	3 pu	1.08 pu
	Delay (s)	0.8	1	1.25	2	6.5	0.5	Instant
Wind turbine	Value	0.8 pu	1.12 pu	47 Hz	51 Hz	1.25 pu	3 pu	1.08 pu (Only SCIG WT)
	Delay (s)	5	0.3	1.3	0.1	6.5	0.5	Instant (Only SCIG WT)

4.4. Load Shedding Scheme

A load shedding scheme has been implemented in the power system model. Load shedding relays are associated with load buses. Three steps have been included in the load shedding scheme. The settings’ frequency values for first, second and third steps are 49.0, 48.9 and 48.8 Hz.

Tripping of the first and second steps causes a load shedding higher than 10%. The setting time delay for this tripping is 0.45 s.

5. Results and Discussion

Simulation results have been analyzed to investigate which of the three criteria mentioned in the Introduction section determines the CCT in the buses of the Lanzarote-Fuerteventura 2020 power system. The answer was found to be load shedding in all cases. Figure 9 presents the CCT values obtained for all of the wind turbine types: SCIG, full converter and full converter with inertia emulation capability. It can be seen that there is a progressive decrease in all of them when wind power is injected for the five buses under short circuit.

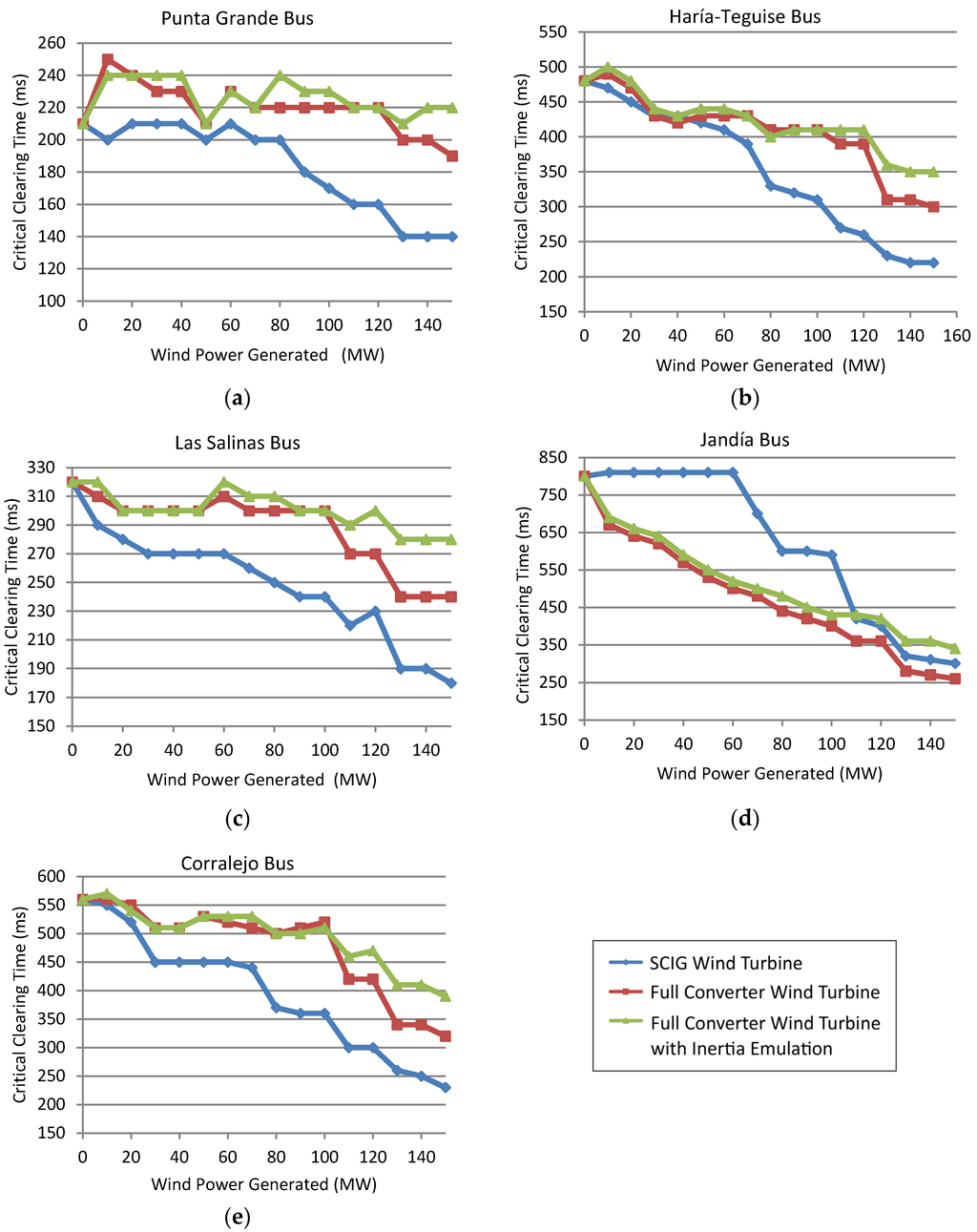
Figure 9. Critical clearing time (CCT) values obtained: (a) Punta Grande bus; (b) Haría-Teguise bus; (c) Las Salinas bus; (d) Jandía bus; (e) Corralejo bus.

Figure 9. Critical clearing time (CCT) values obtained: (a) Punta Grande bus; (b) Haría-Teguise bus; (c) Las Salinas bus; (d) Jandía bus; (e) Corralejo bus.

The decrease in the CCT values is due to the outage of wind farms. A three-phase short circuit causes a voltage dip. An overvoltage can also take place after the fault is cleared, which can be seen in others papers dealing with small isolated power systems [35]. Because of the small size of the studied power system, voltage dip and subsequent overvoltage can have an impact on the overall power system. This subsequent overvoltage causes the outage of the wind farms after the short circuit is cleared. The outages can be seen in Figure 10, which includes an example of a short circuit for every studied case.

Figure 10. Time evolution of voltage and frequency for a three-phase short circuit at: (a) Las Salinas substation, with 260 ms of clearing time and an SCIG wind turbine; (b) Punta Grande substation, with 230 ms of clearing time and a full converter wind turbine; and (c) Haría-Teguise, with 420 ms of clearing time with a full converter wind turbine and with inertia emulation capability.

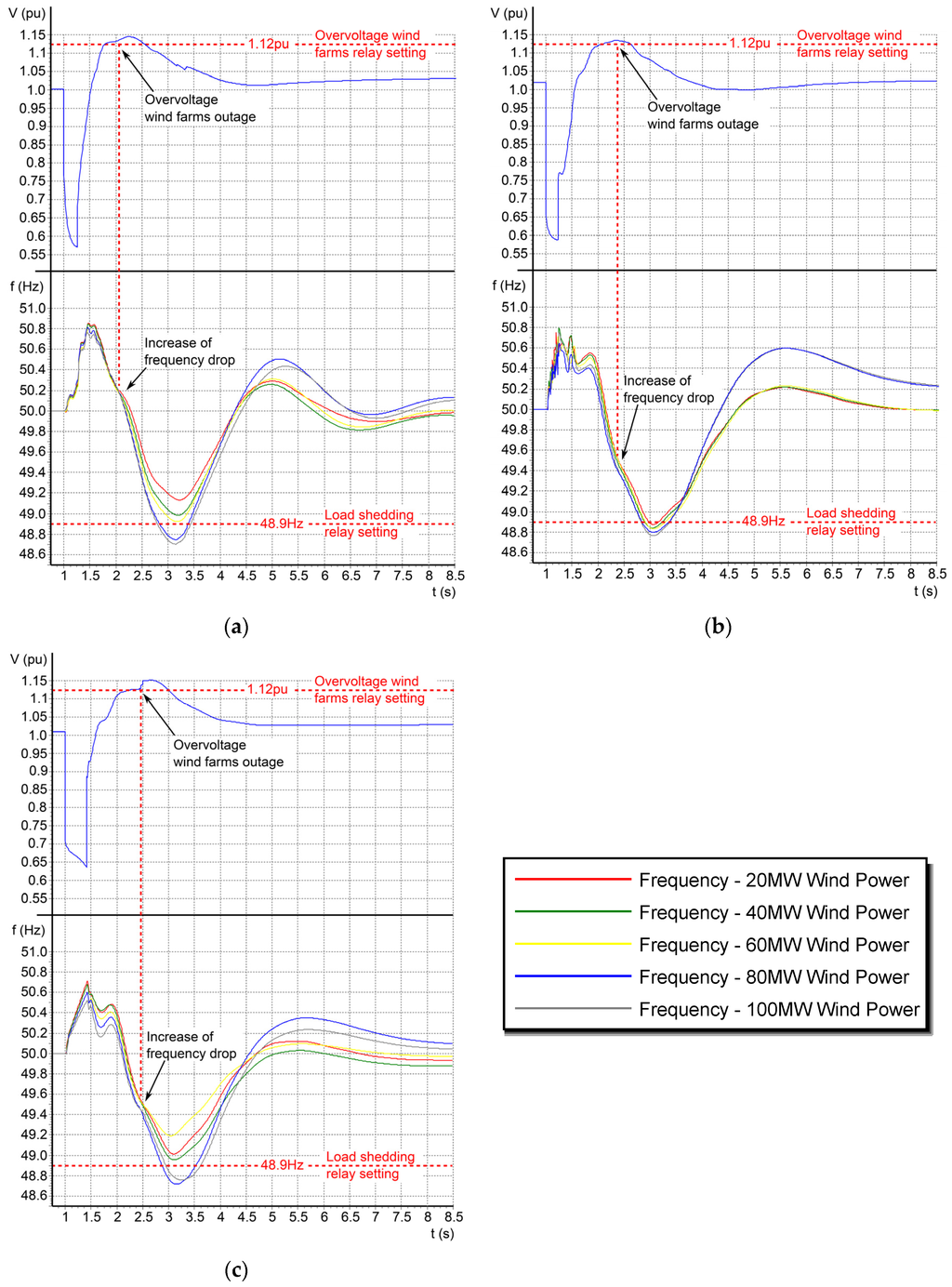
Figure 10. Time evolution of voltage and frequency for a three-phase short circuit at: (a) Las Salinas substation, with 260 ms of clearing time and an SCIG wind turbine; (b) Punta Grande substation, with 230 ms of clearing time and a full converter wind turbine; and (c) Haría-Teguise, with 420 ms of clearing time with a full converter wind turbine and with inertia emulation capability.

The swing equation of the synchronous machine (Equation (3)) is related to power system stability, and it can be used to study how wind farms have an impact on the power system.

$$\frac{\text{dω}}{\text{d}t}=\frac{1}{2H}\left(P_{\text{m}}-P_{\text{e}}\right)$$

(3)

where $\frac{\text{dω}}{\text{d}t}$ is the rotor acceleration, H is the inertia constant, $P_{\text{m}}$ is the mechanical power and $P_{\text{e}}$ is the electrical power [36].

Usually, when a short circuit occurs, electrical power at generator terminals $P_{\text{e}}$ diminishes. This causes a great acceleration in conventional generators $\frac{\text{dω}}{\text{d}t}$ and system frequency rises.

When the short circuit is cleared, electrical power starts to retrieve its previous value. Moreover, turbine governors of the generators have been actuated to reduce mechanical power $P_{\text{m}}$. Both effects cause the decrease of $\frac{\text{dω}}{\text{d}t}$, and the frequency value drops below the rated value.

Wind farm outages take place when the frequency is dropping. This leads to a greater imbalance between $P_{\text{e}}$ and $P_{\text{m}}$, followed by higher frequency deviations, as can be seen in Figure 10.

These frequency deviations can reach 48.9 Hz, causing the tripping of the first and second step of load shedding relays. The load shedding is greater than 10% of the total load and defines the CCT value. Thereby, the more the wind power is disconnected, the more CCT decreases.

Some wind farm outages caused by over frequency values can also be seen. These wind farm outages due to over frequency are about 13% of total studied short circuit cases.

The decrease in the number of running conventional generators also causes the decrease in the CCT values. In order to fulfill the Boucherot theorem, progressive introduction of wind power into the power system can require the disconnection of some conventional generators. This reduction in the number of conventional units causes a decrease in the total power system inertia. Figure 11 shows the inertia constant of the power system for the wind power amounts considered.

Figure 11. Power system inertia for different amounts of wind power.

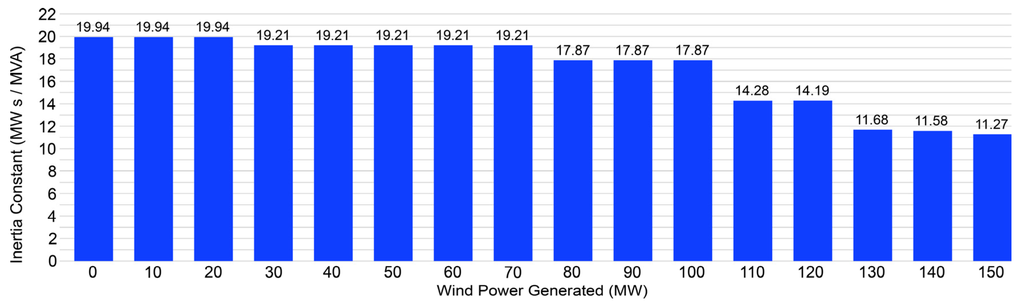
Figure 11. Power system inertia for different amounts of wind power.

Considering again the swing equation, a lower inertia constant H causes a higher frequency variation when an imbalance between $P_{\text{e}}$ and $P_{\text{m}}$ occurs.

Moreover, the reduction of active power-frequency control and of voltage control capabilities is a consequence of the decrease in the number of conventional generator units. The decrease of these capabilities also causes a CCT decrease.

Figure 9 also shows different evolutions of CCT for different wind turbines. The CCT values obtained for full converter wind turbines are higher than CCT values for SCIG wind turbines, except in the Jandía bus, which is located at the end of a long transmission line.

The Jandía bus is located far from the nearest power plant. Besides, there are wind farms connected at several buses at different points of this transmission line. This can be seen in Figure 1. When a short circuit takes place at the Jandía bus, full converter wind turbines contribute to obtaining higher voltages than in the case of SCIG. Therefore, loads at these buses are higher and cause a deeper frequency fall.

The higher CCT values with full converter wind turbines are due to the fault ride through capability of the full converter wind turbines. An example of the performance of this capability is shown in Figure 12.

Figure 12. Reactive power generated or consumed by wind farm Number 2 in both the SCIG wind turbine case and the full converter wind turbine case, for a 300-ms three-phase short circuit.

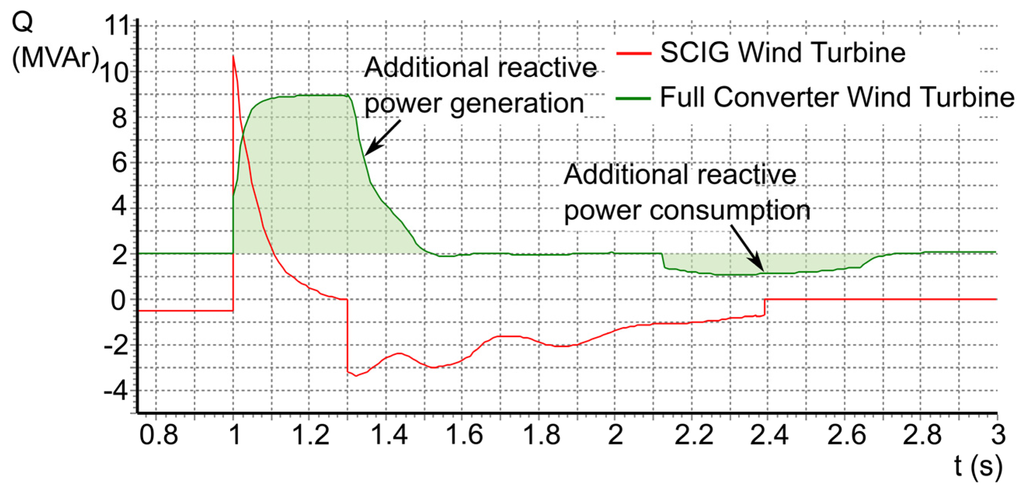
Figure 12. Reactive power generated or consumed by wind farm Number 2 in both the SCIG wind turbine case and the full converter wind turbine case, for a 300-ms three-phase short circuit.

Figure 12 shows that SCIG tripped due to an overvoltage condition at 2.4 s, causing the reactive power changes to zero at 2.4 s. In the case of the full power converter, what the figure shows is the network voltage support obtained by means of generating or consuming reactive power (Figure 5 and Figure 6). After the short circuit is cleared at 1.3 s, voltage recovery is slow, and the converter continues generating reactive power to support the bus voltage. Later, between 2.1 s and 2.7 s, wind generators with a voltage support capability absorb the reactive power to avoid a transient overvoltage condition that could take place as a part of the voltage recovery evolution. In Figure 10a, a similar transient overvoltage is shown for the SCIG case

The advantages of the voltage support capability can also be seen in Figure 13. Voltages have a higher minimum value and a lower maximum value in the case of full converter wind turbines, avoiding tripping by means of protective relay operation.

Figure 13. Time evolution of voltage and frequency for a 300-ms three-phase short circuit at the Las Salinas bus with 80 MW of total wind power.

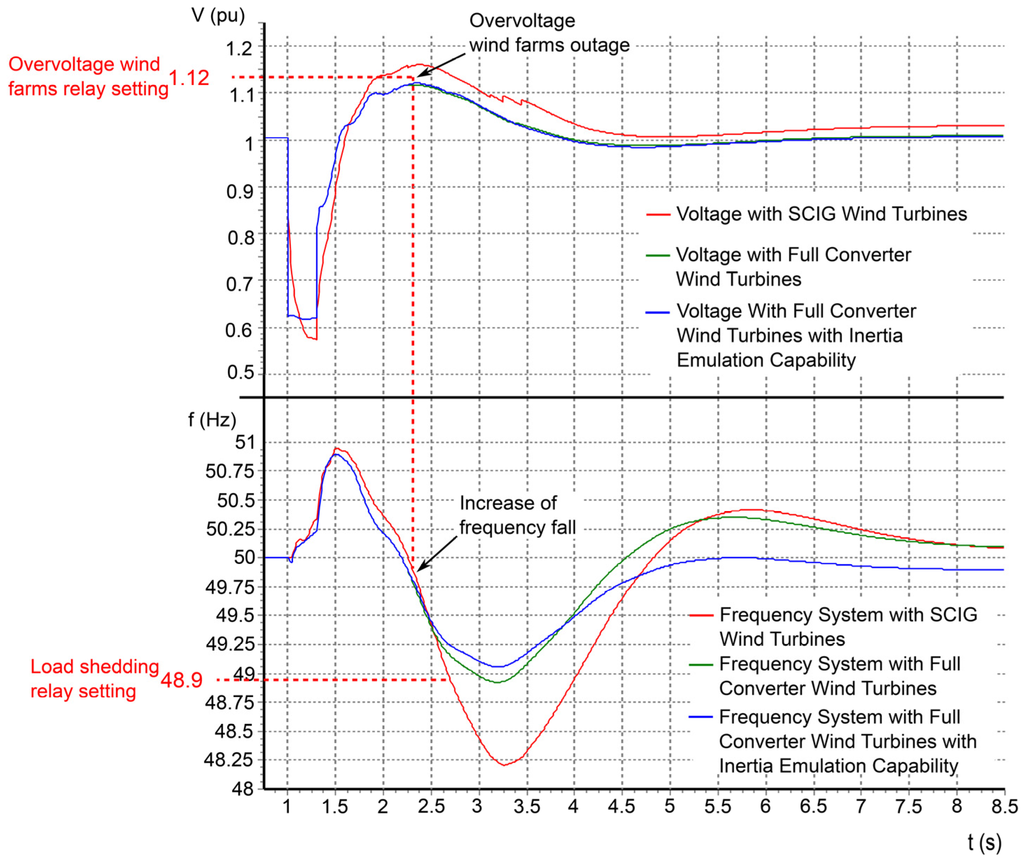
Figure 13. Time evolution of voltage and frequency for a 300-ms three-phase short circuit at the Las Salinas bus with 80 MW of total wind power.

On the contrary, SCIG tripping due to that transient overvoltage condition leads to an imbalance between generated power and load for the whole power system, causing a larger system frequency deviation and the subsequent load shedding.

Inertia emulation capability does not influence reactive power generated or consumed by full converter wind turbines when a fault takes place. Therefore, a curve for full converter wind turbines with inertia emulation capability was not included in Figure 12.

Since full converter wind turbines generate additional reactive power during a short circuit and this improves voltage values, the speed-up of the conventional generators is lower with full converter wind turbines and leads to lower frequency deviations. This can be seen in Figure 13, which shows voltage, as well as the system frequency response. This figure shows that the maximum frequency value reached is lower for full converter wind turbines as a consequence of the higher voltage values during the short circuit.

Moreover, since a full converter wind turbine consumes additional reactive power when the subsequent overvoltage takes place, this kind of wind turbine could avoid its own overvoltage outage in some short circuit cases. In these cases, such as in Figure 13, the frequency values obtained do not cause tripping of the first and second step of load shedding relays.

Figure 9 shows differences between CCT values for full converter wind turbines with and without inertia emulation capability. CCT values for full converter wind turbines with inertia emulation capability are about 3.6% higher than those obtained without inertia emulation capability.

This is due to the power increase produced by inertia emulation. When the frequency starts to fall, a wind turbine with inertia emulation capability injects extra active power, as can be seen in the example presented in Figure 14.

Figure 14. Active power generated by wind farm Number 2 for both the full converter wind turbine and the full converter with inertia emulation capability, for a 300-ms three-phase short circuit at the Las Salinas bus with 80 MW of total wind power

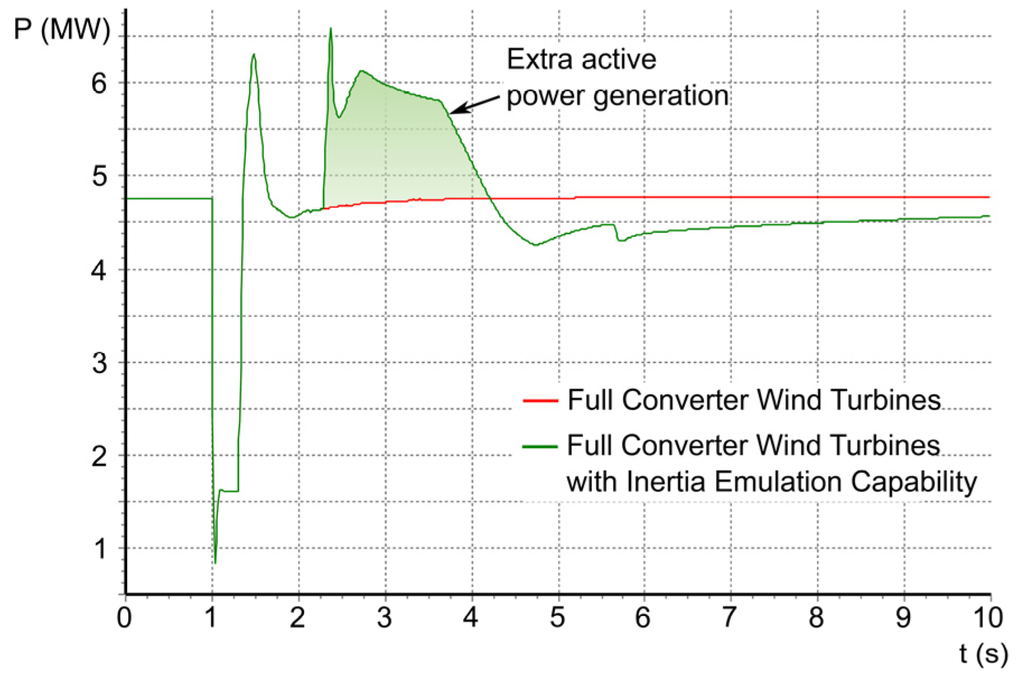
Figure 14. Active power generated by wind farm Number 2 for both the full converter wind turbine and the full converter with inertia emulation capability, for a 300-ms three-phase short circuit at the Las Salinas bus with 80 MW of total wind power

Figure 13 shows how this extra active power reduces the frequency drop. In this way, lower frequency deviation and higher frequency nadir values are produced. For instance, the frequency nadir is about 10.4% higher when a 150-ms three-phase short circuit occurs at the five analyzed buses.

If CCT values for the full converter wind turbine with inertia emulation capability are compared to corresponding values for an SCIG wind turbine, the average value is 24.3% higher, and the frequency nadir is 34.8% higher.

Thereby, inertia emulation is able to improve the CCT values in the simulations performed. However, inertia emulation could not avoid load shedding when a long short circuit caused severe frequency deviations.

6. Conclusions

This paper analyzes the effects of wind power on CCT in small and isolated power systems.

CCT is a parameter used for protection scheme design and is therefore related to power system security.

Three types of wind turbines are studied: the SCIG, the full converter and the full converter with inertia emulation capability.

The analysis shows that load shedding can be caused by large frequency deviations. This criteria determines the CCT values in the Lanzarote-Fuerteventura power system. A decrease in CCT values can be seen when wind power is increased for all types of wind turbines studied. This is due to the wind farm outages caused by overvoltage in small and isolated power systems. Thereby, voltage time evolution can have an impact on CCT values in such systems. Reduction of the inertia and power frequency control and voltage control capabilities in these power systems also causes a decrease in CCT values.

Results also show that the behavior of each particular type of wind turbine establishes differences in CCT values. CCT values for a full converter are higher than those obtained for an SCIG. When a short circuit takes place, full converter wind turbines remain in operation and generate or consume reactive power. Therefore, a full converter wind turbine could avoid its own overvoltage outage, and this leads to higher CCT values than in the case of an SCIG wind turbine.

The highest CCT values are obtained for the full converter wind turbine with inertia emulation capability. These CCT values are 3.6% higher than those for full converter wind turbines without this capability. The percentage rises to 34.8% if these results are compared with the results for SCIG wind turbines. Extra active power generated by full converter wind turbines with inertia emulation achieves lower system frequency deviation and implies the higher CCT values mentioned above. Thereby, inertia emulation can improve the CCT values in a small and isolated power system.

Therefore, these issues suggest the existence of a relationship between wind power and CCT. Hence, it is necessary to consider these aspects in studies for CCT determination or studies of wind power integration in small and isolated power systems.

A more precise estimation of CCT values can be performed, and therefore, a more effective general protection scheme can be achieved to provide security and reliability to the power system. Moreover, in order to increase wind power penetration into small and isolated power systems, some improvements can be made, such as, for example, adaptation of grid codes or enhancement of reactive power control capabilities.

Finally, as CCT values are improved by the inertia emulation capability from wind turbines, this wind power capability could increase the penetration of wind power into small and isolated power systems. Further analysis with inertia emulation capability is required in order to investigate how much wind power penetration can be introduced in each isolated power system.