Regression Models Using Fully Discharged Voltage and Internal Resistance for State of Health Estimation of Lithium-Ion Batteries

Abstract

Accurate estimation of lithium-ion battery life is essential to assure the reliable operation of the energy supply system. This study develops regression models for battery prognostics using statistical methods. The resultant regression models can not only monitor a battery’s degradation trend but also accurately predict its remaining useful life (RUL) at an early stage. Three sets of test data are employed in the training stage for regression models. Another set of data is then applied to the regression models for validation. The fully discharged voltage (V_dis) and internal resistance (R) are adopted as aging parameters in two different mathematical models, with polynomial and exponential functions. A particle swarm optimization (PSO) process is applied to search for optimal coefficients of the regression models. Simulations indicate that the regression models using V_dis and R as aging parameters can build a real state of health profile more accurately than those using cycle number, N. The Monte Carlo method is further employed to make the models adaptive. The subsequent results, however, show that this results in an insignificant improvement of the battery life prediction. A reasonable speculation is that the PSO process already yields the major model coefficients.

1. Introduction

1.1. Reliability and Life Analysis of Lithium-Ion Batteries

Research works regarding transportation systems have been focusing on the development of various types of power generators using clean energy to replace internal combustion engines (ICE), which have been recognized as significant contributors to air pollutants and greenhouse gases linked to global climate change [1,2]. The newly developed vehicle systems such as Hybrid Electric Vehicles (HEVs), Battery Electric Vehicles (BEVs) and Plug-in Hybrid Electric Vehicles (PHEVs) [3,4,5,6] all require rechargeable batteries for continuous power delivery. The lithium-ion type of battery, among numerous types, is lighter in weight, higher in power density, longer in cycle life, with a lower self-discharge rate and generates lesser pollution in use. Therefore, many researchers have been focusing their efforts on the improvement of lithium-ion batteries in the past decade, and lithium-ion batteries have become the most commonly adopted power supply for many systems [7].

The existing research on lithium-ion batteries mostly emphasizes the design of battery components such as various battery chemistries to enhance their performance [8,9,10,11,12,13]. In addition to performance, the capacity fade should be another important factor to be considered in selecting a battery. Capacity decrease is inevitable due to aging and failure processes like electrode passivation and corrosion. When the capacity drops to a certain level, the battery fails suddenly, often without any warning. Unexpected battery failures often cause serious losses and can sometimes result in catastrophes. The use of batteries is anticipated to grow rapidly, e.g., with the hybrid electric vehicle market. This demands the urgent development of battery monitoring techniques [14]. Accurate enough battery life estimation is therefore essential for the development of a reliable energy supply system.

Battery operation is a dynamic process, which is strongly influenced by the ambient environment and loading conditions [15]. As a result of that, comprehensive studies of battery ageing phenomena under various operating conditions are, if not impossible, very difficult to perform. Using test data in combination with statistical methods to build empirical relations for battery life estimation has hence become the common approach. Battery monitoring during usage has two main streams, as based on the existing researches: state of charge (SOC) and state of health (SOH) [12]. SOC provides the real information about a battery’s remaining energy, that is, the percentage of the remaining charge to the maximum capacity. SOH, which describes the physical health condition of a battery compared to a fresh one, is used to characterize the current health status and to estimate the remaining performance of a battery. To estimate SOC/SOH requires a precise capacity evaluation of a battery and the ampere-hour counting method is frequently used for this [7].

Techniques developed for SOC and SOH estimation include: fuzzy logic, electrochemical impedance spectroscopy (EIS), extended Kalman filter (EKF), and neuro-fuzzy [11,16,17,18,19,20,21,22,23,24]. Bole et al. [25,26,27] stated that the unscented Kalman filter (UKF) generally has better accuracy than the EKF [28] and derived a physics-based model for Li-ion batteries, in which an electrochemical model was constructed and a state age-dependent parameter was identified over randomized discharge profiles data via a UKF algorithm. Researches regarding battery prognosis and remaining useful life (RUL) prediction are also available. Dalal et al. [29] presented a particle filtering (PF) framework for a lithium-ion battery life prognostic system, in which a lumped parameter battery model was used to account for all the dynamic characteristics of the battery. Lately Orchard et al. [30] developed a simplified PF-based prognostic method for SOC and the estimation of discharge time. Zhang et al. [31] further implemented this technique into a mission planning to minimize failure risk. Other approaches, such as relevance vector machines (RVMs), combinations of regressions, neural networks, fuzzy logic, and distributed active learning, were developed as well for predicting battery RUL [20,32,33,34,35]. All the mentioned papers emphasized the model updating functions or the so-called adaptive modeling to account for individual batteries’ variations in addition to initial modeling. Though SOC and SOH of lithium-ion batteries have been studied for years, there is still large room for improvement in more accurate modeling and RUL prediction from test data. This is partially due to the very complicated and dynamic nature of batteries due to the environmental impact and operation profiles. The authors herein employ statistical methods, regression models and the PSO scheme to develop accurate and reliable models for the SOH estimation of lithium-ion batteries.

1.2. Aging Parameters of the Battery

A battery’s performance declines with the increase of charge/discharge process and the rate of decline is strongly related to its loading conditions and working environment. Most of the literature has adopted the fully charge/discharge cycle number N as the model parameter for battery’s SOH and RUL estimation. Micea et al. [36] employed N into a second-degree polynomial regression equation for SOH model and RUL estimation in which a least square criterion was set. He et al. [37] used N to derive an exponential growth model in terms of the sum of two exponential functions to fit the degradation curves. Xing et al. [38] compared two degradation models: one based on [37] and the other based on [36]. The comparison showed that the exponential model was superior to the polynomial one.

The cycle number N is an appropriate indicator for a battery’s aging condition. The SOH deteriorates with the increase of N as long as the operational environment does not change drastically. Nevertheless, changes of load conditions and/or working environments during a battery’s whole operation life are not uncommon. These changes may consequently result in contradictory phenomena, e.g., increasing N also increases RUL because of working temperature change. Excluding environmental changes appears to be the disadvantage of using N as the aging parameter. One way of remedying environmental changes or battery’s variations is to implement an adaptive model that updates the model coefficients after certain cycles of present operation.

This updating function nevertheless complicates the subsequent implementation and becomes less cost-effective. The thought of finding appropriate aging parameters that could truly reflect a battery’s present state hence prompted the authors to do this research. In searching for possible ageing parameters, references [39,40] discussed the internal resistance (R) increase in lithium-ion batteries and showed that a cell experienced a significant impedance rise due to power loss. The fade rate was further proved to be dependent on SOC and working temperature. Pattipati et al. [32] hence utilized the capacity decrease and power fade to describe a battery SOH. Schmidt et al. [41] developed similar methods utilizing capacity and R to estimate SOH. They presented an algorithm that distinguished the capacity fade due to cathode degradation from the impedance rise. It has been observed that the increase in internal impedance is closely related to battery capacity degradation and is suitable for battery health monitoring. R is hence selected for SOH degeneration estimation in the present study.

The open circuit voltage (OCV) is another appropriate indicator for a battery’s SOC and SOH. However, the measurement of every OCV is time-consuming because it requires a complete rest time to reach a steady state. OCV seems impractical for an on-line SOH estimation due to this limitation. The authors studied the fully discharged voltage variation with different resting time in a separate experiment and searched for any possible replacement for OCV. It is observed that taking the voltage 60 s after full discharge, denoted V_dis, to replace OCV in SOH modeling is more feasible and accurate enough to represent OCV.

2. Test Methodology

2.1. Reliability Testing

Four identical lithium cobalt oxide batteries (LiCoO₂) were used for the reliability tests in this study. The rated capacity of the tested lithium-ion batteries is 1.10 Ah. The tests were performed at room temperature, i.e., approximately 25 °C. The battery capacity was calculated as the integral of the current over the time (Coulomb counting method, [7]), i.e., Q = ∫Idt, where Q, I, and t represent the battery capacity, the current flow, and the whole discharging time, respectively.

Figure 1 shows a typical current and voltage profile of the battery for one full charge/discharge process. The current remains a constant of 1 C rate in the discharging stage till the voltage drops to a pre-designated cut-off voltage of 2.7 V. The charging process then follows the widely used constant-current/constant-voltage (CCCV) protocol, wherein, the current is held 0.55 A (0.5 C) until the voltage reaches its designated maximum value of 4.2 V, then constant voltage charging takes over till the charging current falls below 0.05 A.

Figure 1. Charge-Discharge current and voltage profiles.

Figure 1. Charge-Discharge current and voltage profiles.

The methodology for lithium battery SOH prediction is illustrated in Figure 2. Four identical batteries, labeled A, B, C and D, were tested. All these tests were 100% depth of discharge (DOD) and continuously repeated to battery failure. The parameters: fully discharged voltage (V_dis), internal resistance (R), cycle numbers (N) and charging/discharging times, were recorded at every cycle. The averages of the three batteries, A, B and C, test data are used as the training set to build up SOH model, and the test data of D is used for model validation.

Figure 2. Algorithm of SOH modeling and RUL prediction of lithium-ion batteries.

Figure 2. Algorithm of SOH modeling and RUL prediction of lithium-ion batteries.

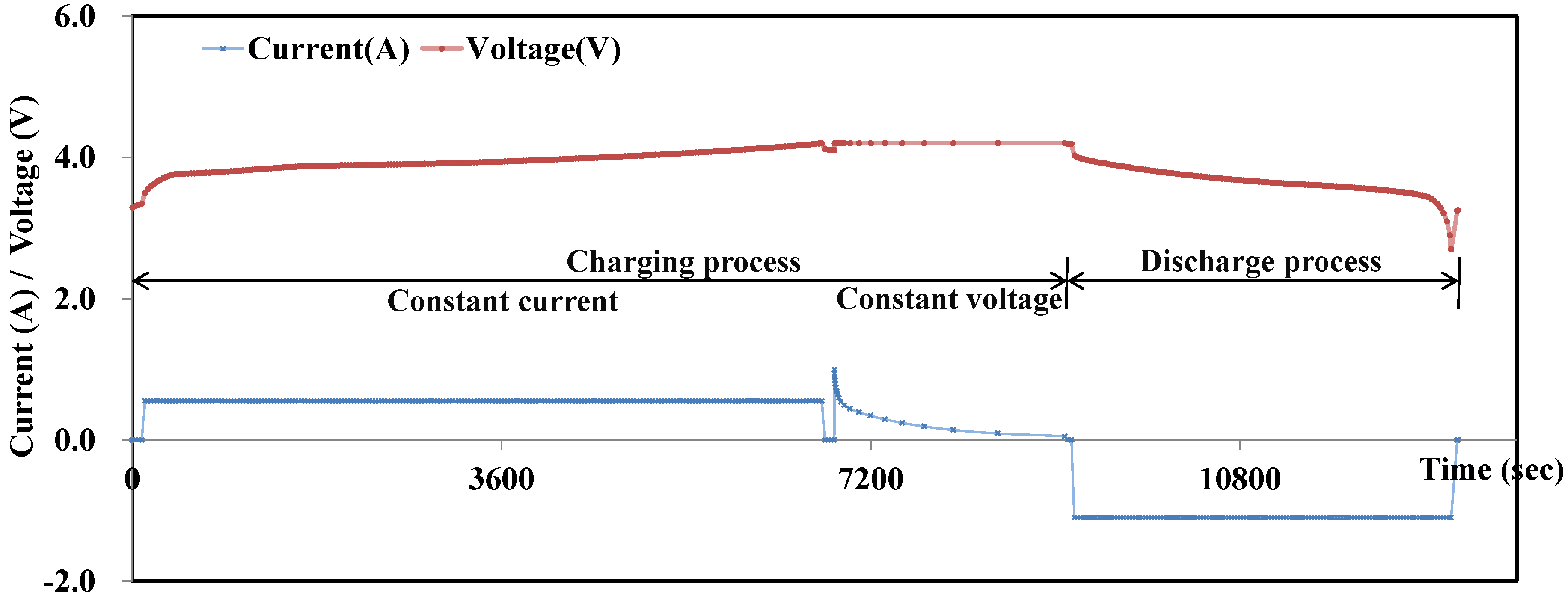
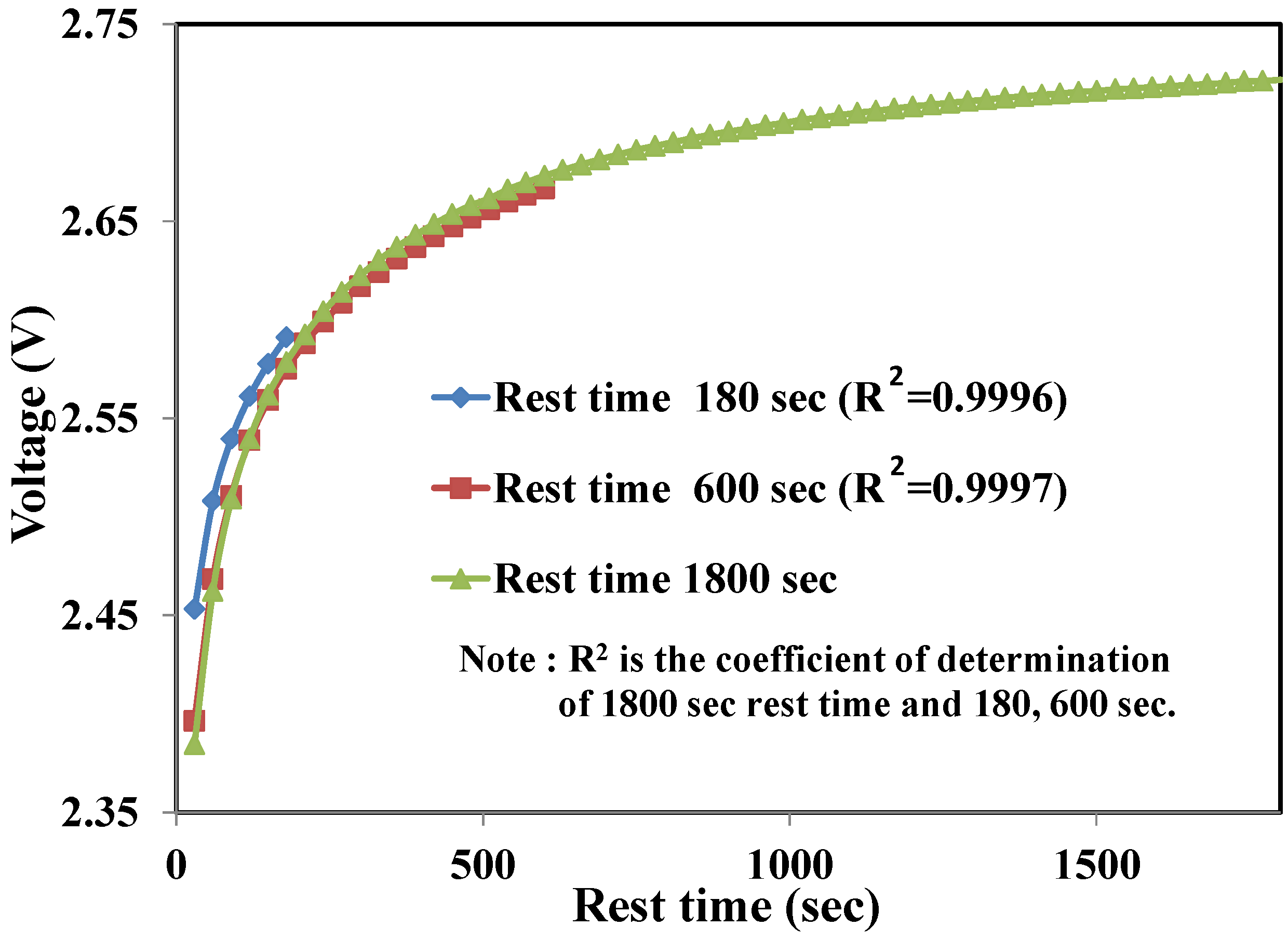
2.2. State of Health

SOH is defined as a “measure” of the health condition of a battery and its ability to deliver a specified performance compared to a fresh battery [3,4]. SOH estimation is an important factor in battery prognostics. Given the failure threshold and the SOH measurements, a battery’s RUL can be predicted through extrapolation. The SOH is commonly expressed as [42]:

$$SOH=\frac{C_i}{C_{full}}\times 100\%=f(N,OCV,R,......)$$

(1)

where C_i, the actual discharge capacity (Ah); C_full, the nominal capacity or initial discharge capacity; N, OCV, R,…, suitable parameters for reflecting battery health state.

The capacity decreases with various aging and failure processes with electrode passivation or corrosion. The failure of a lithium-ion battery occurs when the capacity degradation data drops below certain percentage of its nominal capacity [14,43]. The ISO 12405-2 standard defines a battery’s end of life when the discharge capacity drops to 80% of its original capacity and this is used in this study as the threshold of battery failure. The present study adopts V_dis and R as aging parameters. Unlike N, a monotonically increasing variable, V_dis and R are dynamic in nature so that the measures unavoidably fluctuate with many factors such as chemical reaction, ambient temperature, connector pressure, etc. Therefore, in light of standard performance test regulation of IPC, the battery is considered failed when its capacity drops below the threshold for the fifth time in the following tests.

2.3. Particle Swarm Optimizer (PSO)

The accuracy of models highly relies on the identification of model coefficients from the training data. The present study employs the particle swarm optimization (PSO) technique to search for optimal model coefficients. PSO is a stochastic population-based optimization technique that can be applied to a wide range of problems. PSO was first introduced for simulating collaborative behavior and swarming in biological populations. Unlike conventional local search optimization methods such as the least squares method and intelligent algorithms, PSO is a multi-agent parallel search technique [44,45,46]. Conceptually, each particle in PSO is equipped with a small memory comprising its previous best position. The latter includes the personal best experience and the best value so far in the group among the best positions. The “group best” is referred to as the global best particle in the entire swarm.

Hence, the potential solutions of PSO, or trial particles, basically fly through the whole problem space and settle down at an optimal position. The optimal position usually is defined by an optimization criterion which in identification problem is also referred to as fitness function or the square sum of errors between outputs obtained from real system and the identified model. Some researchers have used PSO to train neural networks and found that PSO-based adaptive neural network had a better training performance, namely faster convergence rate, as well as a better predicting ability than back propagation (BP)-based adaptive neural network.

2.4. Monte Carlo (MC) Method

Monte Carlo (MC) methods are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. Obtaining the distribution of an unknown probabilistic entity is a typical application of MC method in which one may run simulations many times over. A MC method is employed in the present study to search for optimal parameters of the adaptive regression models. The models are used to improve the RUL prediction. With the variations of battery conditions taken into account, the MC method is applied to dynamically update regression models so that the variations of the system can be accounted for.

The adaptive algorithm is configured in the following procedure: (1) Adopt the parameters obtained from the PSO approach as the mean values and use 5% of these mean values as the standard deviations. (2) Generate 10,000 sets of random parameters using normal distributions where the mean values and standard deviations are those determined in Step (1), and the range for random-number generating is centered at the mean value with a span of plus and minus one standard deviation. (3) Compute SOH values using these 10,000 sets of random parameters with 10 sets of measured input-output data, and compared each input-output data to the predicted SOH with the measured SOH. (4) Find the most accurate predicted SOH and determines the point-wise parameters that correspond to the most accurate prediction of SOH value. It will end up with 10 sets of parameters. Average out these 10 sets of parameters to obtain mean values and standard deviations which will be used in generating next 10,000 sets of random parameters. (5) Regenerate point-wise optimal solutions and the associated mean values and standard deviations. (6) Repeat steps (2)–(5) until 25 batches (each has 10 points of data) of measured data have been examined and optimal parameters have been updated. (6) Average out the optimal parameters of previous 25 batches and apply the parameters obtained to the remaining SOH prediction.

3. Test Results

3.1. The Correlations of N, V_dis, R and SOH

The SOH of a battery is often evaluated according to the battery’s internal resistance or its ability to deliver a given amount of charge. Though the tested batteries were of the same batch it is known that in the battery manufacture and assembly process there inevitably exist some uncertainties. The individual variations among them have to be in an acceptable range to assure the accuracy of regression models. The profiles of SOH versus N for the four tested batteries are illustrated in Figure 3 to show their correlations (>0.97). High correlations among them allow us to use these data in the subsequent modeling and validation. The battery aging phenomenon, from the SOH profiles, showed the degradation was non-uniform with N. SOH decreases moderately when N falls between 100 and 600. After 600 cycles, SOH descends sharply and the four SOH profiles differentiate more obviously in this stage. When the number of cycles exceeds 600, SOH values approach 80% and the batteries are expected to die soon.

Figure 3. The SOH profiles correlated to N for the four tested batteries.

Figure 3. The SOH profiles correlated to N for the four tested batteries.

The authors measured the fully discharged voltages recovered after the resting time in a separate experiment and the results are shown in Figure 4. The voltage soon after a complete discharge is usually still in transient state. It is necessary for the battery to rest for a few seconds to quench the transient oscillation. Three voltage curves, recorded every 30 s, with respect to different resting times of 3, 10, and 30 min are shown. These voltage curves are very close to each other and all consistent in trend. The voltage increases gradually and eventually reaches a steady value, presumably the OCV. This figure implies that using the OCV or some earlier measurements for SOH modeling would make less difference as long as the measurements are consistently taken at the same time instant. The OCV is hereafter replaced by an earlier measurement (60 s), denoted V_dis throughout the test because it is more feasible in real applications.

Figure 4. Fully discharged voltage recovers with rest time for three different cases.

Figure 4. Fully discharged voltage recovers with rest time for three different cases.

Figure 5 shows, separately, the correlations of SOH with the three aging parameters, N, R and V_dis for the four batteries. The results indicate SOH is strongly correlated to V_dis and R with coefficients higher than 0.95, compared to N of lower 0.9. This implies that using V_dis and R is more appropriate than using N in describing the battery aging phenomenon. The authors therefore derive new regression models of SOH using these two parameters, V_dis and R as follows.

The values of V_dis and R vary in a relatively small range throughout the battery’s useful life and appear to be sensitive to the complex chemical reactions, operating environment and measurement process, thus resulting in the significant data fluctuations shown in Figure 6. A filtering process after the raw data is collected is helpful to smooth out V_dis and R fluctuations. The raw data of V_dis and R are extracted by the first order low-pass Butterworth filter in MATLAB^®, in which the cut-off frequency is 0.1 Hz. Figure 6 illustrates cell A, B, C’s test data and their averaged (training data). The training data before and after filtering are contrasted on the figure’s upper left corners. The correlation coefficients between unfiltered and filtered data are high: 0.993 and 0.995, respectively for V_dis and R. The filtered data are apparently smoother and hence used for SOH modeling.

Figure 5. Correlations of SOH and aging parameters (N, R, and V_dis) for four batteries.

Figure 5. Correlations of SOH and aging parameters (N, R, and V_dis) for four batteries.

Figure 6. Illustrations of raw data, training data and filtered data.

Figure 6. Illustrations of raw data, training data and filtered data.

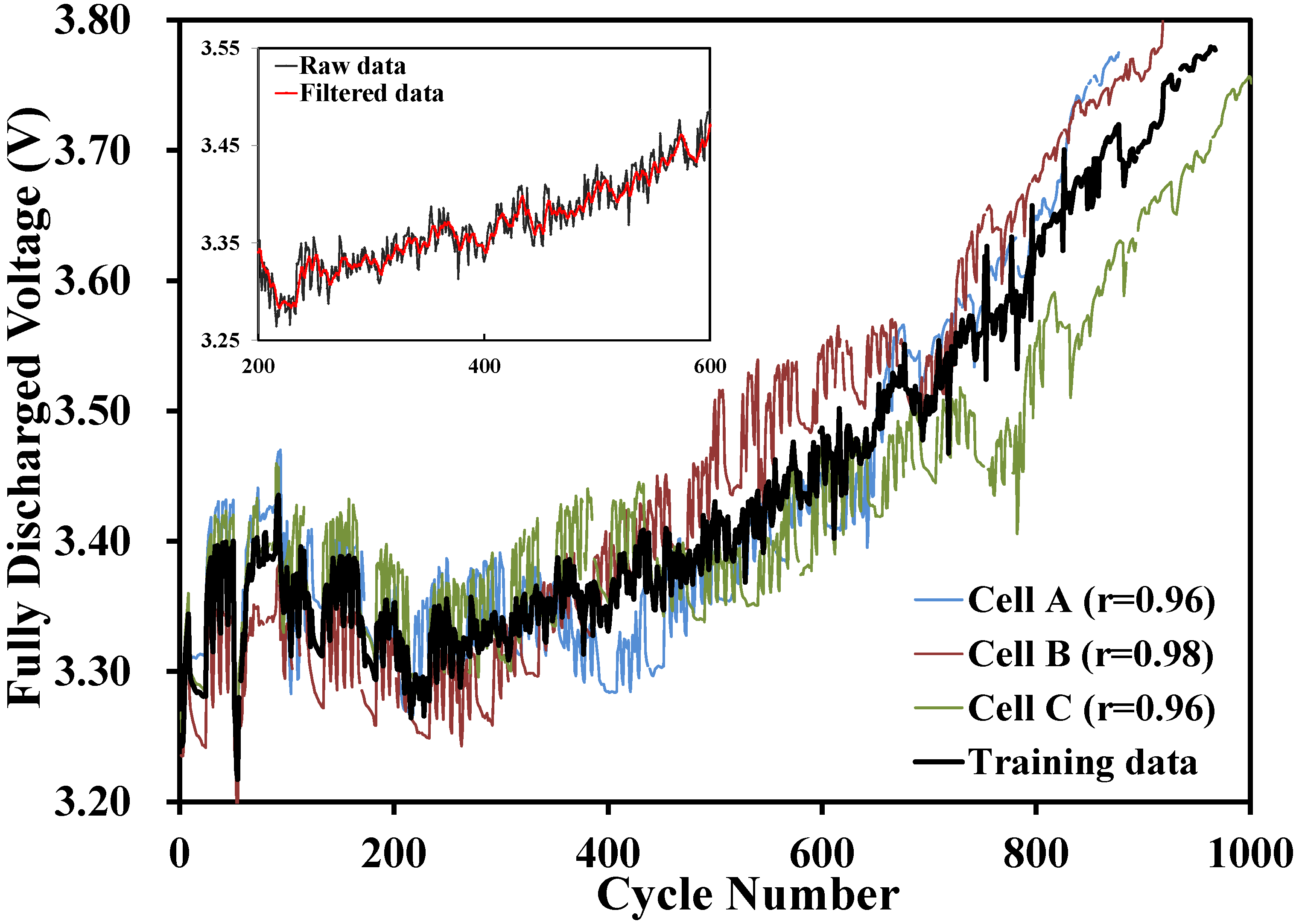
3.2. Degradation of SOH

3.2.1. (A) Cycle Number and SOH Degradation

SOH decays with the increase of charge/discharge cycle number N. Therefore, the charge/discharge cycle number N has been widely used for estimating the SOH via regression process. Micea et al. [30] used cycle number as the only variable in a second-order polynomial regression model, i.e.:

Model I (N-polynomial):

$$SO{H}_N={\gamma }_1\cdot N^2+{\gamma }_2\cdot N+{\gamma }_3$$

(2)

where the subscript N stands for cycle number and γ_i are the model coefficients. The above equation will be used as well in the present study to reconstruct SOH degeneration model in [36]. The coefficients, via the least square fitting method of MATLAB^®, are obtained as −0.000001, 0.0003 and 0.8969 for γ₁, γ₂ and γ₃, respectively. Figure 7I shows the fitted curve of Equation (2). The coefficient of determination (R²) for empirical relationship of SOH is 0.975.

3.2.2. (B) New SOH degradation model via V_dis and R

Polynomial and exponential types were frequently used for establishing SOH degradation model in the existing literature. The authors hence adopt these two types of functions to build new SOH degradation models but using V_dis and R rather than N as the aging parameters. The two models, called bi-variable polynomial (Model II) and exponential (Model III), are:

Model II (Bi-variable polynomial):

$$SO{H}_N={\alpha }_1\cdot V_{dis,N}+{\alpha }_2\cdot R_N+{\alpha }_3$$

(3)

Model III (Exponential):

$$SO{H}_N={\beta }_1\cdot e^{{\beta }_2\cdot V_{dis,N}}+{\beta }_3\cdot e^{{\beta }_4\cdot R_N}$$

(4)

α’s and β’s are the models coefficients; α₁, β₁, β₂ are related to voltage; α₂, β₃, β₄ are associated with internal impedance; α₃ is a bias constant in the bi-variable polynomial model.

We apply the training data in Equations (3) and (4) and employ the PSO method for the model coefficients. The simulations from Model II and III (red) and the original training data (black) are superimposed in Figure 7II,III. Both models closely resemble the training data with a significant correlation. Using V_dis and R in both polynomial and exponential models is inferred, from a comparison with Figure 7I, to be better than using N in polynomial model. The degrees of fitness of these two models, in model coefficients, R², average error and root mean squared error (RMSE), are given in Table 1. The R² turn out very high (>0.987) and RMSEs are very close to zero. That infers these two new SOH degradation equations are adequate to reflect a battery’s SOH. The fitness of model III is slightly better than model II if simply the model statistical parameters are compared.

Table 1. Parameters of regression model II and III.

Relationships	Model II	Model III
	$SO{H}_N={\alpha }_1\cdot V_{dis,N}+{\alpha }_2\cdot R_N+{\alpha }_3$	$SO{H}_N={\beta }_1\cdot e^{{\beta }_2\cdot V_{dis,N}}+{\beta }_3\cdot e^{{\beta }_4\cdot R_N}$
Coefficient	α1: −0.4546; α2: −13.5975 α3: 3.6551	β1: 4.7603; β2: −0.2189 β3: −0.6383; β4: 8.5675
Avg. error (%)	1.66	1.59
R2	0.987	0.988
RMSE	0.022	0.021

Table 1. Parameters of regression model II and III.

Relationships	Model II	Model III
	$SO{H}_N={\alpha }_1\cdot V_{dis,N}+{\alpha }_2\cdot R_N+{\alpha }_3$	$SO{H}_N={\beta }_1\cdot e^{{\beta }_2\cdot V_{dis,N}}+{\beta }_3\cdot e^{{\beta }_4\cdot R_N}$
Coefficient	α1: −0.4546; α2: −13.5975 α3: 3.6551	β1: 4.7603; β2: −0.2189 β3: −0.6383; β4: 8.5675
Avg. error (%)	1.66	1.59
R2	0.987	0.988
RMSE	0.022	0.021

Figure 7. SOH degradation curves of three different models.

Figure 7. SOH degradation curves of three different models.

4. Discussion

4.1. Battery Cycle Life Prediction

The R² and RMSE of the proposed models after comparison with the training data have shown excellent suitability. Experimental data of D are now applied to all three models and inspections of the cycle life predictions are examined. The results and comparisons are given in Table 2. All models’ R² are approaching 1 indicating appropriate fitness. The RMSE’s are 0.066, 0.034 and 0.032 and the estimated cycle lives are 500, 577 and 599, respectively, for Model I, II (open) and III (open). Compared to the experimental real life of 576 cycles, the errors are 76 (13.2%), 1 (0.2%), and 23 (4.0%). From these comparisons, the prediction by Model II is the most accurate, then III and I. Figure 8 overlaps the experimental data of D (black) and the calculated data of the newly derived and the existing one (red). Model I uses N as the aging parameter, which is monotonically increasing, and Equation (2) is a 2nd degree polynomials in N. The SOH curve of Model I, Figure 8I, is not surprisingly a smooth one. Models II and III use V_dis and R as aging parameters, which are fluctuating in nature, therefore the curves in Figure 8II,III oscillate. Nevertheless, the predictions by Equations (3) and (4) are apparently superior to that of Equation (2).

Figure 8. SOH calculations compared with D’s test data.

Figure 8. SOH calculations compared with D’s test data.

The verification through D’s data inferred using the bi-variables, V_dis and R, in regression models is better than using N alone. That the difference between Model II and III is not so obvious implies that a polynomial or exponential model makes less difference as far as V_dis and R are used as main parameters and employing the same PSO scheme.

4.2. Battery Cycle Life Prediction with Model Updating

The operation mechanism of a battery is an electrical-chemical reaction. This reaction is complex and relies strongly on the battery’s manufacturing process and operational environments. A regression model always needs to take each battery’s individual variations into account when implementing real applications. One of the possible ways is to provide the model with self-updating or so-called adaptive ability. Extended Kalman filter, neuro-fuzzy, and Monte Carlo are some of the feasible algorithms to achieve this purpose. He et al. [37] employed the Bayesian Monte Carlo method and obtained satisfactory results. The authors herein implemented the Monte Carlo method in the developed models to see if the life predictions could be improved. The process is described as Section 2.4. The previously obtained model coefficients from the training data are updated using every 10 cycles of D’s experimental data up to 250 cycles. After that, the models are fixed and run for cycle life predictions.

The predicted results of bi-variable polynomial and exponential model are given in Table 2 under the label “Adaptive.” It shows that the adaptive function although it enhanced the degrees of fitness, i.e., increasing R², the life prediction shows no apparent improvement.

Table 2. Predicted battery D’s cycle life from the three models.

Type	State	R2	RMSE	Cycle life prediction
				Cycle	Error (%)
Model I	Open	0.956	0.0660	500	76 (13.2)
Model II	Open	0.977	0.0342	577	1 (0.2)
	Adaptive	0.986	0.0350	577	1 (0.2)
Model III	Open	0.980	0.0322	599	23 (4.0)
	Adaptive	0.988	0.0280	599	23 (4.0)

Table 2. Predicted battery D’s cycle life from the three models.

Type	State	R2	RMSE	Cycle life prediction
				Cycle	Error (%)
Model I	Open	0.956	0.0660	500	76 (13.2)
Model II	Open	0.977	0.0342	577	1 (0.2)
	Adaptive	0.986	0.0350	577	1 (0.2)
Model III	Open	0.980	0.0322	599	23 (4.0)
	Adaptive	0.988	0.0280	599	23 (4.0)

These results imply that the derived models employing V_dis and R as aging parameters and PSO scheme for coefficients are already accurate enough and reach their limit in life prediction. Figure 9 shows D’s experimental data (black) and the predicted values with MC updating (red), respectively. After updating, R² is very close to 1 but the cycle life predictions remain unchanged.

4.3. Comparison of Models with Existing Literature

The predicted cycle lives via the derived models are now compared with those obtained from the existing models. Polynomial and exponential models have been widely cited to establish SOH degradation curves, e.g., by Xing et al. [38] and He et al. [37]. In their models, cycle number (N) was the only aging variable and both implemented an adaptive function to update the model coefficients. The comparisons with the present research are shown in Table 3 and Table 4. In Table 3, the second column is directly digested from [47] and the third column is the result of replicating their approach onto the present data of battery D. The forth column is those of bi-variable polynomial model. Using V_dis and R is apparently better than using N in life estimation as is observed from the comparisons.

Figure 9. Predictions with updating function in bi-variable polynomial and exponential model.

Figure 9. Predictions with updating function in bi-variable polynomial and exponential model.

Table 3. Comparison of the results of polynomial model.

Research	Xing et al. [38]	This study (Eq. 2)	This study (Eq. 3)
Battery type	Lithium-ion	LiCoO2	LiCoO2
Capacity (Ah)	1.35	1.1	1.1
Equation	$C_N=p_1\cdot N^2+p_2\cdot N+p_3$	$SO{H}_N={\gamma }_1\cdot N^2+{\gamma }_2\cdot N+{\gamma }_3$	$SO{H}_N={\alpha }_1\cdot V_{dis,N}+{\alpha }_2\cdot R_N+{\alpha }_3$
Condition	LSA & PF	LSA	PSO & Monte Carlo
Variable	Cycle number	Cycle number	Vdis, R
R2	0.96~0.98	0.950	0.98
Performance	102 cycles earlier	76 cycles late	1 cycle late

Table 3. Comparison of the results of polynomial model.

Research	Xing et al. [38]	This study (Eq. 2)	This study (Eq. 3)
Battery type	Lithium-ion	LiCoO2	LiCoO2
Capacity (Ah)	1.35	1.1	1.1
Equation	$C_N=p_1\cdot N^2+p_2\cdot N+p_3$	$SO{H}_N={\gamma }_1\cdot N^2+{\gamma }_2\cdot N+{\gamma }_3$	$SO{H}_N={\alpha }_1\cdot V_{dis,N}+{\alpha }_2\cdot R_N+{\alpha }_3$
Condition	LSA & PF	LSA	PSO & Monte Carlo
Variable	Cycle number	Cycle number	Vdis, R
R2	0.96~0.98	0.950	0.98
Performance	102 cycles earlier	76 cycles late	1 cycle late

Table 4. Comparison of the results of exponential model.

Research	He et al. [37]	Xing et al. [38]	This study (Eq. 4)
Battery type	Lithium-ion	Lithium-ion	LiCoO2
Capacity (Ah)	1.1	1.35	1.1
Equation	$Q_N=a\cdot {\exp }^{bN}+c\cdot {\exp }^{dN}$	$Q_N=a\cdot {\exp }^{bN}+c\cdot {\exp }^{dN}$	$SO{H}_N={\beta }_1\cdot e^{{\beta }_2\cdot V_{dis,N}}+{\beta }_3\cdot e^{{\beta }_4\cdot R_N}$
Condition	DST & Monte Carlo	LSA & PF	PSO & Monte Carlo
Variable	Cycle number	Cycle number	Vdis, R
R2	--	0.98	0.98
Performance	7 cycles	3 cycles earlier	23 cycles late

Table 4. Comparison of the results of exponential model.

Research	He et al. [37]	Xing et al. [38]	This study (Eq. 4)
Battery type	Lithium-ion	Lithium-ion	LiCoO2
Capacity (Ah)	1.1	1.35	1.1
Equation	$Q_N=a\cdot {\exp }^{bN}+c\cdot {\exp }^{dN}$	$Q_N=a\cdot {\exp }^{bN}+c\cdot {\exp }^{dN}$	$SO{H}_N={\beta }_1\cdot e^{{\beta }_2\cdot V_{dis,N}}+{\beta }_3\cdot e^{{\beta }_4\cdot R_N}$
Condition	DST & Monte Carlo	LSA & PF	PSO & Monte Carlo
Variable	Cycle number	Cycle number	Vdis, R
R2	--	0.98	0.98
Performance	7 cycles	3 cycles earlier	23 cycles late

In the cases of exponential modeling, Table 4 illustrates the results of [37], using Dempster–Shafer theory (DST), of [38], using Least Squares Approach (LSA) plus Particle Filtering (PF), and the present work. Using cycle number N as the aging parameter seems better than using V_dis and R, as seen from the table. The authors yet would remind readers that both references [37,38] employed adaptive function but the present model need not.

5. Conclusions

Lithium-ion batteries are core components in a wide variety of power source systems. Battery health monitoring, as a result of the increasing demand for lithium-ion batteries, has become more important than ever. This study combined statistical methods, regression models, and the particle swarm optimization scheme to develop new models for battery prognostics. Four identical batteries were tested and grouped into training set and validation set. N, V_dis, R were measured as aging parameters in each cycle and two different types of model, polynomial and exponential, were examined. Models employing V_dis and R as aging parameters were developed and compared to similar researches which used N was the only parameter. The authors have arrived at the following conclusions through the comparisons of SOH models and cycle predictions:

• The SOH curves decayed slowly with N in the beginning, then dropped sharply as SOH approached the failure threshold, as observed from reliability test.
• SOH is highly correlated to V_dis and R, as indicated from the test data, so that V_dis and R are suitable parameters for SOH modeling. Using V_dis and R as aging parameters rather than the commonly used N further proved to have better cycle life prediction as referred to R² and RMSE values.
• The PSO algorithm yielded optimal model coefficients and partially because of PSO was used, the selection of model type, polynomial or exponential, showed less significance. Both of the derived models accurately generated results resembling the real SOH curves of tested batteries.
• Regarding the discrimination between polynomial and exponential model, the present study showed in the polynomial model using V_dis and R as model parameters is superior to using N, but in the exponential model using N yielded better life predictions.