Discrete Fracture Modeling of 3D Heterogeneous Enhanced Coalbed Methane Recovery with Prismatic Meshing
Abstract
:1. Introduction
2. Methodology
2.1. Reservoir Characterization


2.2. Model Formulation
2.3. Numerical Discretization and Prismatic Meshing Strategies


2.4. Coupling of Coal Shrinkage and Swelling
3. Verification and Model Applications
3.1. Case 1: Model Verification


| Coal Reservoir Properties | |
| Region of interest | 1/4 of rectangular area with length 100.586 m |
| Grid system | Cartesian 11 × 11 × 1 |
| Thickness, m | 9 |
| Coal density, kg/m3 | 1434 |
| Temperature, °C | 45 |
| Initial porosity | 0.001 |
| Initial permeability (mD) | 3.4 |
| Initial water saturation | 0.592 |
| Diffusion coefficient, m2·s−1 | 7.88 × 10−11 |
| Shape factor, m−2 | 1.05 × 105 |
| Aqueous Properties | |
| Aqueous density, kg/m3 | 990 |
| Aqueous viscosity, cp | 0.607 |
| Aqueous compressibility, kPa−1 | 5.8 × 10−7 |
| Component | Sorption Constant b (kPa−1) | Langmuir Volume VL (m3/(kg Coal)) | Sorption Strain Factor εL (-) |
|---|---|---|---|
| CH4 | 2.133 × 10−4 | 0.0152 | 0.1176 |
| CO2 | 5.255 × 10−4 | 0.0310 | 0.1176 |
| N2 * | 3.671 × 10−5 | 0.0150 | 0.1176 |


3.2. Case 2: 3D Heterogeneous ECBM Simulation with Prismatic Meshing
3.2.1. Base Case






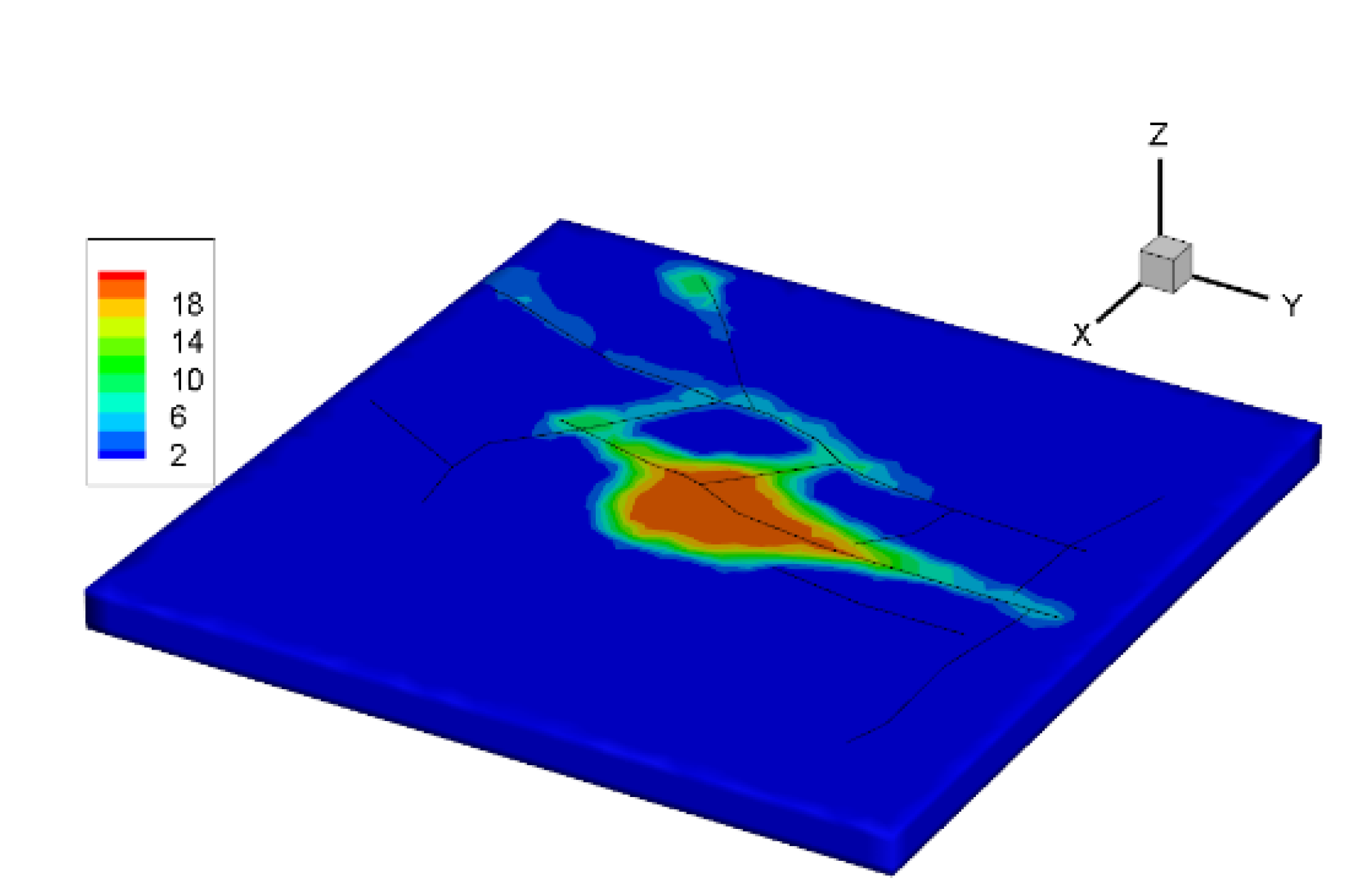




3.2.2. Ternary flooding of N2-CO2-ECBM




3.2.3. Effect of Well Patterns




3.2.4. Effect of Buoyancy


4. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gentzis, T. Subsurface sequestration of carbon dioxide—An overview from an Alberta (Canada) perspective. Int. J. Coal Geol. 2000, 43, 287–305. [Google Scholar] [CrossRef]
- Stevens, S.H.; Spector, D.; Riemer, P. Enhanced Coalbed Methane Recovery Using CO2 Injection: Worldwide Resource and CO2 Sequestration Potential. In International Oil & Gas Conference and Exhibition in China (IOGCEC); Society of Petroleum Engineers: Richardson, TX, USA, 1998. [Google Scholar]
- Gale, J.; Freund, P. Coal Bed Methane Enhancement with CO2 Sequestration Worldwide Potential. Environ. Geosci. 2001, 8, 210–217. [Google Scholar] [CrossRef]
- Puri, R.; Yee, D. Enhanced Coalbed Methane Recovery. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990; SPE-20732-MS. pp. 254–368.
- Puri, R. A micro-pilot approach to coalbed methane reservoir assessment. In Fuel and Energy Abstracts; Elsevier: Amsterdam, The Netherland, 1996; p. 419. [Google Scholar]
- Pan, Z.; Connell, L.D.; Camilleri, M.; Connelly, L. Effects of matrix moisture on gas diffusion and flow in coal. Fuel 2010, 89, 3207–3217. [Google Scholar] [CrossRef]
- Arri, L.; Yee, D.; Morgan, W.; Jeansonne, M. Modeling Coalbed Methane Production with Binary Gas Sorption. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 18–21 May 1992; SPE-24363-MS. pp. 18–21.
- Ruthven, D.M. Principles of Adsorption and Adsorption Processes; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Yang, R. Gas Separation by Adsorption Processes; Pergamon: Bergama, Turkey, 1988. [Google Scholar]
- Pan, Z.; Connell, L.D. Comparison of adsorption models in reservoir simulation of enhanced coalbed methane recovery and CO2 sequestration in coal. Int. J. Greenh. Gas Control 2009, 3, 77–89. [Google Scholar] [CrossRef]
- King, G.; Ertekin, T. A survey of mathematical models related to methane production from coal seams, Part I–Empirical and equilibrium sorption models. In International Coalbed Methane Symp; University of Alabama: Tuscaloosa, AL, USA, 1989; pp. 125–138. [Google Scholar]
- Shi, J.; Durucan, S. A bidisperse pore diffusion model for methane displacement desorption in coal by CO2 injection. Fuel 2003, 82, 1219–1229. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.; Aziz, K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators. SPE J. 2004, 9, 227–236. [Google Scholar] [CrossRef]
- Noorishad, J.; Mehran, M. An upstream finite element method for solution of transient transport equation in fractured porous media. Water Resour. Res. 1982, 18, 588–596. [Google Scholar] [CrossRef]
- Baca, R.; Arnett, R.; Langford, D. Modelling fluid flow in fractured-porous rock masses by finite-element techniques. Int. J. Numer. Methods Fluids 1984, 4, 337–348. [Google Scholar] [CrossRef]
- Kim, J.G.; Deo, M.D. Finite element, discrete-fracture model for multiphase flow in porous media. AIChE J. 2000, 46, 1120–1130. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Firoozabadi, A. Numerical simulation of water injection in fractured media using the discrete-fracture model and the Galerkin method. SPE Reserv. Eval. Eng. 2003, 6, 117–126. [Google Scholar] [CrossRef]
- Monteagudo, J.; Firoozabadi, A. Control-volume method for numerical simulation of two-phase immiscible flow in two-and three-dimensional discrete-fractured media. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Matthäi, S.; Mezentsev, A.; Belayneh, M. Control-Volume Finite-Element Two-Phase Flow Experiments with Fractured Rock Represented by Unstructured 3D Hybrid Meshes. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 31 January–2 February 2005.
- Fu, Y.; Yang, Y.; Deo, M. Three-Dimensional, Three-Phase Discrete-Fracture Reservoir Simulator Based on Control Volume Finite Element (CVFE) Formulation. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 31 January–2 February 2005.
- Durucan, S.; Edwards, J. The effects of stress and fracturing on permeability of coal. Min. Sci. Technol. 1986, 3, 205–216. [Google Scholar] [CrossRef]
- Seidle, J.; Jeansonne, M.; Erickson, D. Application of matchstick geometry to stress dependent permeability in coals. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 18–21 May 1992; SPE-24361-MS. pp. 18–21.
- Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds: A new model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996.
- Shi, J.; Durucan, S. Changes in permeability of coalbeds during primary recovery—Part 1: Model formulation and analysis. In Proceedings of the 2003 International Coalbed Methane Symposium, University of Alabama, Tuscaloosa, AL, USA, 7–8 May 2003.
- Shi, J.-Q.; Durucan, S. A model for changes in coalbed permeability during primary and enhanced methane recovery. SPE Reserv. Eval. Eng. 2005, 8, 291–299. [Google Scholar] [CrossRef]
- Robertson, E.P.; Christiansen, R.L. Modeling permeability in coal using sorption-induced strain data. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005.
- Connell, L.; Detournay, C. Coupled flow and geomechanical processes during enhanced coal seam methane recovery through CO2 sequestration. Int. J. Coal Geol. 2009, 77, 222–233. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, Z.; Liu, J.; Connell, L.D.; Elsworth, D. Effect of the effective stress coefficient and sorption-induced strain on the evolution of coal permeability: Experimental observations. Int. J. Greenh. Gas Control 2011, 5, 1284–1293. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. Int. J. Coal Geol. 2012, 92, 1–44. [Google Scholar] [CrossRef]
- Manik, J. Compositional Modeling of Enhanced Coalbed Methane Recovery; The Pennsylvania State University: University Park, PA, USA, 1999. [Google Scholar]
- Mazumder, S.; Karnik, A.A.; Wolf, K.-H. Swelling of coal in response to CO2 sequestration for ECBM and its effect on fracture permeability. SPE J. 2006, 11, 390–398. [Google Scholar] [CrossRef]
- Warren, J.; Root, P.J. The behavior of naturally fractured reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Pattison, C.; Fielding, C.; McWatters, R.; Hamilton, L. Nature and origin of fractures in Permian coals from the Bowen Basin, Queensland, Australia. Geol. Soc. Lond. Spec. Publ. 1996, 109, 133–150. [Google Scholar] [CrossRef]
- Nelson, C.R. Effects of geologic variables on cleat porosity trends in coalbed gas reservoirs. In Proceedings of the SPE/CERI Gas Technology Symposium, Calgary, AL, Canada, 3–5 April 2000.
- Odling, N.; Gillespie, P.; Bourgine, B.; Castaing, C.; Chiles, J.; Christensen, N.; Fillion, E.; Genter, A.; Olsen, C.; Thrane, L. Variations in fracture system geometry and their implications for fluid flow in fractured hydrocarbon reservoirs. Pet. Geosci. 1999, 5, 373–384. [Google Scholar] [CrossRef]
- Lohrenz, J.; Bray, B.G.; Clark, C.R. Calculating viscosities of reservoir fluids from their compositions. J. Pet. Technol. 1964, 16, 1171–1176. [Google Scholar] [CrossRef]
- Cao, H. Development of Techniques for General Purpose Simulators. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Jiang, Y. Techniques for Modeling Complex Reservoirs and Advanced Wells. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2007. [Google Scholar]
- Fan, Y. Chemical Reaction Modeling in a Subsurface Flow Simulator with Application to in situ Upgrading and CO2 Mineralization. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2010. [Google Scholar]
- Karimi-Fard, M.; Gong, B.; Durlofsky, L. Generation of coarse-scale continuum flow models from detailed fracture characterizations. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Shewchuk, J.R. Delaunay refinement algorithms for triangular mesh generation. Comput. Geom. 2002, 22, 21–74. [Google Scholar] [CrossRef]
- Belayneh, M.; Geiger, S.; Matthi, S.K. Numerical simulation of water injection into layered fractured carbonate reservoir analogs. AAPG Bull. 2006, 90, 1473–1493. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D.; Camilleri, M. Laboratory characterization of coal reservoir permeability for primary and enhanced coalbed methane recovery. Int. J. Coal Geol. 2010, 82, 252–261. [Google Scholar] [CrossRef]
- GEM Version 2012 User’s Guide; Computer Modeling Group Ltd.: Calgary, AL, USA, 2009.
- Law, D.H.-S.; van der Meer, L.; Gunter, W. Numerical Simulator Comparison Study for Enhanced Coalbed Methane Recovery Processes Part I: Pure Carbon Dioxide Injection. In Proceedings of the SPE Gas Technology Symposium, Calgary, AL, Canada, 30 April–2 May 2002.
- Shuck, E.L.; Davis, T.L.; Benson, R.D. Multicomponent 3-D characterization of a coalbed methane reservoir. Geophysics 1996, 61, 315–330. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Gong, B.; Li, J.; Li, H. Discrete Fracture Modeling of 3D Heterogeneous Enhanced Coalbed Methane Recovery with Prismatic Meshing. Energies 2015, 8, 6153-6176. https://doi.org/10.3390/en8066153
Zhang Y, Gong B, Li J, Li H. Discrete Fracture Modeling of 3D Heterogeneous Enhanced Coalbed Methane Recovery with Prismatic Meshing. Energies. 2015; 8(6):6153-6176. https://doi.org/10.3390/en8066153
Chicago/Turabian StyleZhang, Yongbin, Bin Gong, Junchao Li, and Hangyu Li. 2015. "Discrete Fracture Modeling of 3D Heterogeneous Enhanced Coalbed Methane Recovery with Prismatic Meshing" Energies 8, no. 6: 6153-6176. https://doi.org/10.3390/en8066153
APA StyleZhang, Y., Gong, B., Li, J., & Li, H. (2015). Discrete Fracture Modeling of 3D Heterogeneous Enhanced Coalbed Methane Recovery with Prismatic Meshing. Energies, 8(6), 6153-6176. https://doi.org/10.3390/en8066153





