A Four-Phase High Voltage Conversion Ratio Bidirectional DC-DC Converter for Battery Applications
Abstract
:1. Introduction



2. Coupling Mode Selection


3. Proposed Topologies and Operation Principles
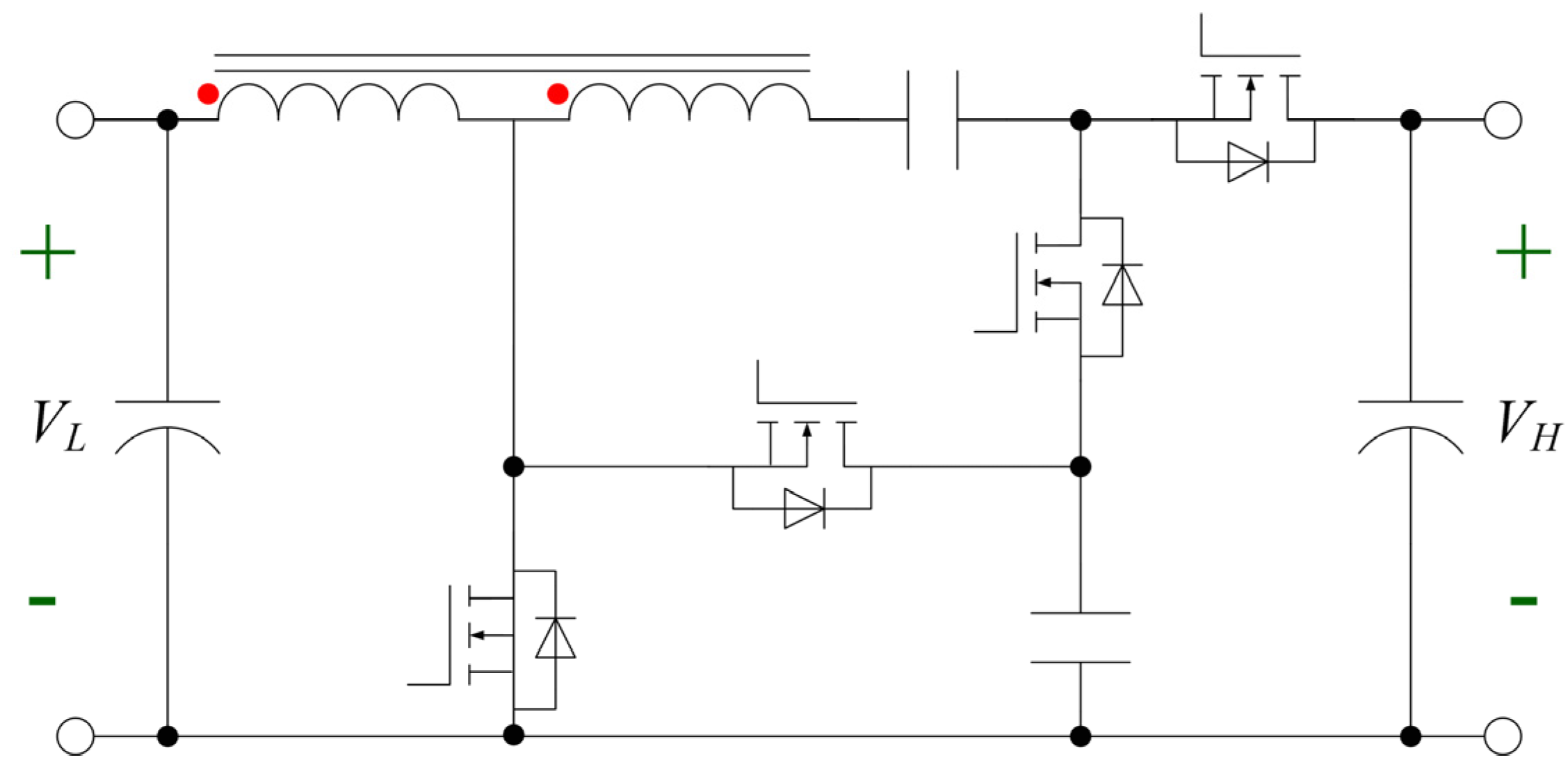
3.1. Proposed Topologies

- (1)
- All switches are treated as ideal.
- (2)
- L1 = L2 = L3 = L4 = L and C1 = C2 = C3 = C.
- (3)
- Capacitors C1, C2 and C3 are large enough that VC1, VC2 and VC3 are considered to be constant in a switching period.
- (4)
- The coupling coefficient k and the mutual inductance M of the CIs are equal, k = M/L, and the turn ratio of the CIs is equal to 1.
3.2. CCM Boost Stage


3.3. CCM Buck Stage


3.4. Discontinuous Current Mode (DCM) Boost Stage

4. Feature Analysis and Design Considerations
4.1. Voltage Gain and Duty Ratio

- (1)
- The voltage ratio of the proposed BDC is extended significantly, with duty cycle D varies from 0.5 to 0.9 (Dup) or 0.1 to 0.5 (Ddown), the voltage ratio can achieve 8 - 40 in CCM Boost operation, and 0.025 - 0.125 in CCM Buck operation.
- (2)
- Within the whole working scope, the voltage gain varies evenly when the duty cycle is changing, which is conductive to the design of the closed-loop digital controller.
4.2. Auto Current Sharing

4.3. Design Considerations
4.3.1. Optimal Design of the CIs
- (1)
- With a smaller initial channel inductance, a more tiny variation of the equivalent inductance with changing Dup/Ddown will be obtained, which indicates a smaller input ripple current in the range of any load condition;
- (2)
- The maximum equivalent inductance is related to duty cycle Dup or Ddown, for example, if rated Dup equals to 0.64 or Ddown equals to 0.36, then the optimized coupling coefficient is k = 0.3. It is obviously that the optimized k value in CCM Boost operation and CCM Buck operation is equal, when rated VL and VH are given.

4.3.2. Optimal Design of SCs
4.3.3. Selection of Power MOSFETs
4.4. Losses Distribution
4.4.1. Conduction Losses on MOSFETs
4.4.2. Switching Losses of MOSFETs
4.4.3. Capacitor ESR Losses
4.4.4. ESR Losses of CIs
4.4.5. Magnetic Losses of CIs
5. Experimental Results

| Parameters and components | Values (units) |
|---|---|
| Rated power Pn | 500 W |
| Low side input DC voltage VL | 24–48 V |
| High side input DC voltage VH | 400 V |
| Operating frequency (fS) | 200 kHz |
| Power MOSFETs | C2M0080120D |
| Switched capacitors (C1, C2, C3) | 40 μF |
| Input/Output Capacitors (CL, CH) | 80 μF |
| ESR (C1, C2, C3, CL, CH) | 5 m Ohm |
| Inductance of channel 1 (L1) | 122 μH |
| Inductance of channel 2 (L2) | 128 μH |
| Inductance of channel 3 (L3) | 124 μH |
| Inductance of channel 4 (L4) | 126 μH |
| Coupling coefficient (k) | 0.3 |
| Weight of magnetic core | 25.2 g |
| Core loss per unit weight | 20 mW/g |
| Length of magnetic path | 8.95 cm |
| Number of turns | 48 |
| ESR (L1, L2, L3, L4) | 30 m Ohm |





6. Conclusions

Acknowledgments
Author Contributions
Conflicts of Interest
References
- Long, B.; Jeong, T.W.; Lee, J.D.; Jung, Y.C.; Chong, K.T. Energy management of a hybrid AC-DC micro-grid based on a battery testing system. Energies 2015, 8, 1181–1194. [Google Scholar] [CrossRef]
- Chang, C.-H.; Wu, F.-Y.; Chen, Y.-M. Modularized bidirectional grid-connected inverter with constant-frequency asynchronous sigma-delta modulation. IEEE Trans. Ind. Electron. 2012, 11, 4088–4100. [Google Scholar] [CrossRef]
- Dong, D.; Cvetkovic, I.; Boroyevich, D.; Zhang, W.; Wang, R.; Mattavelli, P. Grid-interface bidirectional converter for residential DC distribution systems—Part one: High-density two-stage topology. IEEE Trans. Power Electron. 2013, 4, 1655–1666. [Google Scholar] [CrossRef]
- Rawn, B.G.; Lehn, P.W.; Maggiore, M. Control methodology to mitigate the grid impact of wind turbines. IEEE Trans. Energy Convers. 2007, 2, 431–438. [Google Scholar] [CrossRef]
- Carpinelli, G.; Celli, G.; Mocci, S.; Mottola, F.; Pilo, F.; Proto, D. Optimal integration of distributed energy storage devices in smart grids. IEEE Trans. Smart Grid 2013, 2, 985–995. [Google Scholar] [CrossRef]
- Wang, X.Y.; Vilathgamuwa, D.M.; Choi, S.S. Determination of battery storage capacity in energy buffer for wind farm. IEEE Trans. Energy Convers. 2008, 3, 868–878. [Google Scholar] [CrossRef]
- Wei, L.; Joos, G. Comparison of energy storage system technologies and configurations in a wind farm. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1280–1285.
- Giess, H. The operation of VRLA lead acid batteries in parallel strings of dissimilar capacity or can we now sin? In Proceedings of the 21st International Telecommunication Energy Conference, Copenhagen, Denmark, 6–9 June 1999.
- Sathyan, S.; Suryawanshi, H.M.; Ballal, M.S.; Shitole, A.B. Soft switching DC-DC converter for istributed energy sources with high step up voltage capability. IEEE Trans. Ind. Electron. 2015, 99, 1. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.H.; Sun, Y.D. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system. IEEE Trans. Power Electron. 2014, 8, 4091–4106. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.H.; Sun, Y.D. Dead-time effect of the high-frequency isolated bidirectional full-bridge DC-DC converter: Comprehensive theoretical analysis and experimental verification. IEEE Trans. Power Electron. 2014, 4, 1667–1680. [Google Scholar] [CrossRef]
- Wang, K.; Lin, C.Y.; Zhu, L.; Qu, D.; Lee, F.C.; Lai, J.S. Bidirectional dc to dc converters for fuel cell systems. In Proceedings of the Power Electronics Transportation, Dearborn, MI, USA, 22–23 October 1998; pp. 47–51.
- Jung, J.-H.; Kim, H.-S.; Ryu, M.-H.; Baek, J.-W. Design methodology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems. IEEE Trans. Power Electron. 2013, 4, 1741–1755. [Google Scholar] [CrossRef]
- Jung, J.-H.; Kim, H.-S.; Kim, J.-H.; Ryu, M.-H.; Baek, J.-W. High efficiency bidirectional LLC resonant converter for 380 V DC power distribution system using digital control scheme. In Proceedings of the 27th Annual IEEE Applied Power Electronics Conference and Exposition, 5–9 February 2012; pp. 532–538.
- Wang, Z.; Li, H. A soft switching three-phase current-fed bidirectional DC-DC converter with high efficiency over a wide input voltage range. IEEE Trans. Power Electron. 2012, 2, 669–684. [Google Scholar] [CrossRef]
- Sedaghati, F.; Hossein Hosseini, S.; Sabahi, M.; Gharehpetian, G.B. Analysis and implementation of a modular isolated zero-voltage switching bidirectional dc-dc converter. IET Power Electron. 2013, 8, 2035–2049. [Google Scholar] [CrossRef]
- Li, W.H.; Xu, C.; Yu, H.B.; Gu, Y.J.; He, X.N. Analysis, design and implementation of isolated bidirectional converter with winding-cross-coupled inductors for high step-up and high step-down conversion system. IET Power Electron. 2013, 1, 67–77. [Google Scholar] [CrossRef]
- Lin, B.-R.; Huang, C.-L.; Lee, Y.-E. Asymmetrical pulse-width modulation bidirectional DC-DC converter. IET Power Electron. 2008, 3, 336–347. [Google Scholar] [CrossRef]
- Ko, Y.-P.; Lee, Y.-S.; Liu, L.-J. Design of high efficiency multi-phase QR ZCS switched-capacitor bidirectional power converters. In Proceedings of the 8th International Conference on Power Electronics and ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 860–867.
- Zhao, Q.; Lee, F.C. High-efficiency, high step-up DC-DC converters. IEEE Trans. Power Electron. 2003, 1, 65–73. [Google Scholar] [CrossRef]
- Law, K.K.; Cheng, K.W.E.; Yeung, Y.P.B. Design and analysis of switched-capacitor-based step-up resonant converters. IEEE Trans. Circuits Syst. 2005, 5, 943–948. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Chiu, Y.-Y. Zero-current-switching switched-capacitor bidirectional DC-DC converter. IEE Proc. Electric Power Appl. 2005, 6, 1525–1530. [Google Scholar] [CrossRef]
- Hsieh, Y.-P.; Chen, J.-F.; Yang, L.-S.; Wu, C.-Y.; Liu, W.-S. High-conversion-ratio bidirectional DC-DC converter with coupled inductor. IEEE Trans. Ind. Electron. 2014, 1, 210–222. [Google Scholar] [CrossRef]
- Duan, R.-Y.; Lee, J.-D. High-efficiency bidirectional DC-DC converter with coupled inductor. IET Power Electron. 2012, 1, 115–123. [Google Scholar] [CrossRef]
- Wai, R.-J.; Duan, R.-Y.; Jheng, K.-H. High-efficiency bidirectional dc-dc converter with high-voltage gain. IET Power Electron. 2012, 2, 173–184. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Ko, Y.-P.; Cheng, M.-W.; Liu, L.-J. Multiphase zero-current switching bidirectional converters and battery energy storage application. IEEE Trans. Power Electron. 2013, 8, 3806–3815. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Chiu, Y.-Y.; Cheng, M.-W. Inverting ZCS switched-capacitor bi-directional converter. In Proceedings of the 37th Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–6.
- Kwon, M.; Choi, W. High gain soft-switching bidirectional DC-DC converter for eco-friendly vehicles. IEEE Trans. Power Electron. 2014, 4, 1659–1666. [Google Scholar] [CrossRef]
- Xue, L.K.; Wang, P.; Wang, Y.F.; Li, W. High step-up DC-DC converter with switched capacitors and interleaved inductors. In Proceedings of the 2014 International Electronics and Application Conference and Exposition, Shanghai, 5–8 November 2014; pp. 26–29.
- Wong, P.L.; Wu, Q.Q.; Xu, P.; Yang, B.; Lee, F.C. Investigating coupling inductors in the interleaving QSW VRM. In Proceedings of the 15th 2000 Annual IEEE Applied Power Electronics Conference and Exposition, New Orleans, LA, USA, 6–10 February 2000; pp. 973–978.
- Pressman, A.I.; Billings, K.; Morey, T. Swiching Power Supply Design, 3rd ed.; McGraw-Hill Education: New York, NY, USA, 2009. [Google Scholar]
- Havanur, S. Quasi-clamped inductive Switching behaviour of power Mosfets. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4349–4354.
- Ren, Y.C.; Xu, M.; Zhou, J.H.; Lee, F.C. Analytical loss model of power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- McLyman, W.T. Transformer and Inductor Design Handbook, 3rd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2004. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, L.-K.; Wang, P.; Wang, Y.-F.; Bei, T.-Z.; Yan, H.-Y. A Four-Phase High Voltage Conversion Ratio Bidirectional DC-DC Converter for Battery Applications. Energies 2015, 8, 6399-6426. https://doi.org/10.3390/en8076399
Xue L-K, Wang P, Wang Y-F, Bei T-Z, Yan H-Y. A Four-Phase High Voltage Conversion Ratio Bidirectional DC-DC Converter for Battery Applications. Energies. 2015; 8(7):6399-6426. https://doi.org/10.3390/en8076399
Chicago/Turabian StyleXue, Li-Kun, Ping Wang, Yi-Feng Wang, Tai-Zhou Bei, and Hai-Yun Yan. 2015. "A Four-Phase High Voltage Conversion Ratio Bidirectional DC-DC Converter for Battery Applications" Energies 8, no. 7: 6399-6426. https://doi.org/10.3390/en8076399
APA StyleXue, L. -K., Wang, P., Wang, Y. -F., Bei, T. -Z., & Yan, H. -Y. (2015). A Four-Phase High Voltage Conversion Ratio Bidirectional DC-DC Converter for Battery Applications. Energies, 8(7), 6399-6426. https://doi.org/10.3390/en8076399






