Autonomous Household Energy Management Based on a Double Cooperative Game Approach in the Smart Grid

Abstract

Taking advantage of two-way communication infrastructure and bidirectional energy trading between utility companies and customers in the future smart grid (SG), autonomous energy management programs become crucial to the demand-side management (DSM). Most of the existing autonomous energy management schemes are for the scenario with a single utility company or the scenario with one-way energy trading. In this paper, an autonomous household energy management system with multiple utility companies and multiple residential customers is studied by considering the bidirectional energy trading. To minimize the overall costs of both the utility companies and the residential customers, the energy management system is formulated as a double cooperative game. That is, the interaction among the residential users is formulated as a cooperative game, where the players are the customers and the strategies are the daily schedules of their household appliances; and the interaction among the utility companies is also formulated as a cooperative game, where the players are the suppliers and the strategies are the proportions of the daily total energy they provide for the customers. Without loss of generality, the bidirectional energy trading in the double cooperative game is formulated by allowing plug-in electric vehicles (PEVs) to discharge and sell energy back. Two distributed algorithms will be provided to realize the global optimal performance in terms of minimizing the energy costs, which can be guaranteed at the Nash equilibriums of the formulated cooperative games. Finally, simulation results illustrated that the proposed double cooperative game can benefit both the utility companies and residential users significantly.

1. Introduction

Demand-side management (DSM) generally refers to such activities implemented to improve energy efficiency, to reduce cost at the customer side and to control the energy consumption [1,2]. DSM was actually put forward 30 years ago [3–5], but it did not attract enough attention until the smart grid (SG) concept came. In an SG, consumers of electricity will be also producers by selling electricity energy with their distributed generators or energy storage devices, and the classic electricity consumers will be prosumers [6]. Consequently, prosumers’ electricity networks in an SG will form a bidirectional market. DSM, together with the integration of distributed generation and energy storage [7–13] are considered increasingly essential elements of the SG [14–16].

Load control and management (LCM) is one of the main categories of DSM [4,17], which is conducted by comprehensive analysis of the user’s electricity consumption from their normal patterns in response to changes in the price of electricity, such as real-time pricing and time-of-use (ToU) pricing, then determining the optimal operation and load control plan. Residents are one of the main users of DSM, and autonomous residential energy consumption scheduling (ECS) has been becoming a hot topic because a large number of residential customers have already been equipped with smart meters and plug-in electric vehicles (PEVs) [18,19]. Smart meters provide the possibility and foundation of autonomous energy management based on the two-way communication and remote control technology. PEVs, representing a significant new household load, which can also store energy and sell it back to the power grid [20–22], provide the crucial need of appropriate load-shifting control, both for the residential users and the existing distribution system. As a result, one can say that DSM programs for residential users are mainly designed to manage the electricity consumption depending on the users’ lifestyles and benefits.

Along with the fast development of SG, more and more DSM programs have been developed to manage household energy consumption. The main objective of these DSM programs is to optimize and control the energy consumption automatically by considering scenarios with different energy suppliers and different energy users. A dual decomposition-based approach was successfully taken by some researchers [6,23–26] for modeling these distributed optimization issues in an SG. Additionally, game-theoretic methods, including cooperative games, noncooperative games and evolutionary games, have been extensively employed as solution techniques for optimizing energy consumption by resolving the equilibriums of the games; because game-theoretic methods can capture the features of these interactions and study the possible outcomes and corresponding equilibriums [27]. In this paper, we focus on an autonomous household energy management in an SG system that consists of multiple utility companies and multiple residential users with PEVs, which are allowed to discharge and sell energy back. The cooperative game-theoretic method on the scenario with one single utility company developed in our previous work [18] is extended to the double cooperative game approach for multiple utility companies, in which a cooperative game is formulated for the utility companies, as well. There are two main reasons that we choose two cooperative games for both the utility companies and residential users: one is that we assume all human beings have a consensus to save energy costs cooperatively; the other is that a cooperative game can provide more benefits for both sides or at least one side in a game [28].

The rest of this paper is organized as follows. Related research work is reviewed and discussed in Section 2. The scenario with multiple utility companies and multiple residential users in an SG is described in Section 3, and the system model is studied. Section 4 formulates the double cooperative game approach and provides two distributed algorithms to realize the global optimal performance at Nash equilibriums. Simulation results are given and analyzed extensively in Section 5. Finally, conclusions are summarized in Section 6.

2. Related Work

Current game-theoretic approaches for DSM programs have been focused on the interaction between a utility company and end users, such as in [29], Yang et al. provided a game-theoretic approach to optimize the ToU pricing for utility companies with a single-user-type scenario and a scenario with multiple users. The proposed game-theoretic method can benefit both the utility company and the users by obtaining a Nash equilibrium. Another smart pricing scenario based on the Vickrey–Clarke–Groves mechanism was analyzed with the game-theoretic method in [30]. Tushar et al. [31] focused on the energy exchange between a utility company and PEVs, and a noncooperative game was developed to optimize a tradeoff between the benefit of battery charging and associated costs; while in [32], the authors focus on the interactions among the end users by formulating cooperative game-theoretic ECS for residential users. The proposed method can not only cut down the total cost of all users, as well as each users electricity payment, but also reduce the value of the peak-to-average ratio (PAR). Moreover, the authors in [2] introduced the concept of fairness into the users’ utility functions, then designed new autonomous demand response systems that can achieve both optimality and fairness with a smart electricity billing mechanism.

Most of the aforementioned research papers are about the scenario with a single utility company. However, it is possible and reachable for residential users to buy electricity from different utility providers as distributed renewable energy generation and distributed energy storage in an SG are developed. Therefore, it becomes important to study the autonomous DSM programs with multiple utility companies. Wang et al. [33] presented a game-theoretic double auction market model that allows the incorporation of power markets with multiple users and multiple suppliers, where a noncooperative game was formulated among distributed storage units in an SG. Maharjan et al. [34] established a model for multiple utility companies and multiple consumers as a Stackelberg game to maximize the revenue of each company and the payoff of each consumer. Different from only one game model being employed for the scenario with multiple utility companies in the above papers, Chai et al. [35] proposed the conception of a two-level game, in which the first-level among multiple utility companies was formulated as a non-cooperative game and the second-level among end users was formulated as a evolutionary game. The proposed two-level scheme is illustrated to be able to reduce peak load and demand variation, while the paper has not reached autonomous household appliance ECS, and also, bidirectional energy trading is not considered either.

Different from the current literature, this paper employs the double cooperative game approach for multiple utility companies and multiple residential users, and bidirectional energy trading is also considered by allowing the end users to buy and sell energy from/to the power grid with their PEVs. The main contributions of this paper include the following: (1) a double cooperative game approach is proposed for multiple utility companies and multiple end users in an SG, where strategies of the cooperative game for the residential users are the daily schedules of their household appliances and strategies of the cooperative game for the utility companies are proportions of the daily total energy they provide for the customers; (2) two distributed algorithms are provided to realize the global optimal performance in terms of minimizing the energy costs, which can be guaranteed at the Nash equilibriums of the formulated cooperative games; and (3) simulations are carried out to verify the effectiveness and efficiency of the proposed double game approach, and the results show that both the utility companies and residential users can benefit significantly.

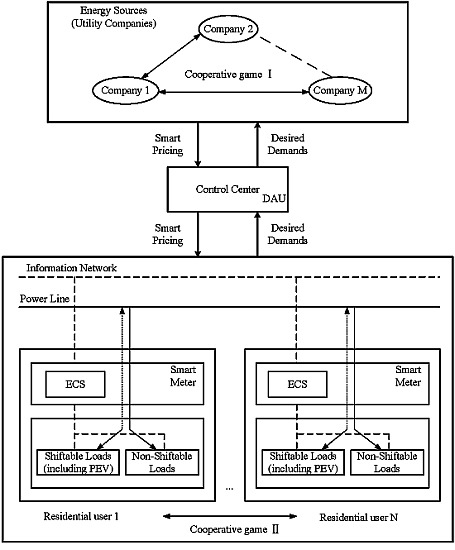
3. System Model

As shown in Figure 1, we consider a scenario that contains multiple utility companies and multiple residential users. Each user is equipped with a smart meter with an ECS unit to schedule household electricity consumption automatically. Smart meters are connected to the power line from a distribution station, which connects to the multiple utility companies [35]. All residential users and the utility companies can communicate with each other via an information network, which also contains the control center. The desired demands of all residential users will be delivered to the data aggregation unit (DAU) via the smart meters, and also, the smart pricing from different utility companies will be sent to the DAU. The control center processes and integrates the information received from utility companies and residential users; the overall power demands from the residential users will be calculated and sent to all utility companies, and an integrated price policy based on smart pricing from different utility companies will be obtained and broadcast to all residential users. According to this background in the SG, each utility company will need to decide a reasonable proportion of electricity power for the overall desired demands based on pricing information of other utility companies and residential users’ energy consumption schedules.

We suppose that there are M utility companies and N residential users in the scenario, and let $ℳ$ = {1, 2, ⋯, M}, $\mathcal{N}=\{1,2,\cdots ,N\}$. Let $l_n^h$ and $L_m^h$ represent the energy consumption of user $n\in \mathcal{N}$ and the energy provided from utility company m ∈ $ℳ$ in a daily time slot h ∈ $\mathscr{H}$ = {1, 2 ⋯ H}, respectively. One can choose each time slot as 1 h, and then, H = 24. Additionally, the total energy consumed by all of the residential users and provided by all utility companies in 1 h can be calculated as [18,32]:

$$L_h={\displaystyle \sum _{n\in \mathcal{N}}{l}_n^h}={\displaystyle \sum _{n\in ℳ}{L}_m^h}$$

(1)

which can be also called the total energy demand per hour. Therefore, the total power demands for all users in the whole day can be expressed as ${\displaystyle \sum _{h\in \mathscr{H}}{L}_h}$. Consequently, the welfare model for utility companies and the load dispatch model for residential users will be formulated.

3.1. Welfare Model for Utility Companies

The welfare model for utility companies is applied to satisfy the costs of multiple utility companies. Let $C_{m,h}(L_m^h)$ denote the energy cost function of utility company m. The energy cost model must satisfy some characteristics, such as utility companies are obliged to satisfy all of the users at any time, so the energy cost function must be continuous about the consumed energy; and the increment speed of the energy cost gets faster with the increase of $L_m^h$. Therefore, there are some assumptions for the welfare model [18,36]:

• The cost functions are strictly convex and always increasing with respect to the total demand;
• When residential users buy electricity energy from the SG, we have $C_{m,h}(L_m^h)>0$ for $L_m^h>0$; when users sell electricity energy back to the SG, we have $C_{m,h}(L_m^h)<0$ for $L_m^h<0$;
• At any given time slot h, the price at which the SG sells electricity energy to the residential users is always no less than the price at which it buys.

It should be noted that the first one of the listed three assumptions is essential to guarantee the existence of the unique Nash Equilibrium, while the remaining two are assumed to make the cost function reasonable for bidirectional energy trading. In other words, the listed first assumption will be enough for the DSM study without considering selling energy back to power grid [32].

According to the above assumptions, a simple quadratic cost function, such as $C_{m,h}(L_m^h)=a_m^h{\left(L_m^h\right)}^2$, a_h > 0 used in [32], clearly does not satisfy the condition for selling energy back. Although logarithmic cost functions can meet all of the requirements [36], the following simplified quadratic function used in [18]:

$$C_{m,h}(L_m^h)=a_m^h{\left(L_m^h\right)}^2+b_m^h{L}_m^h$$

(2)

is employed in this paper, where $b_m^h>0$. The cost function in Equation (2) is close to the logarithmic one and easier to compute.

3.2. Load Dispatch Model for Residential Users

Following the residential load models in [18,32], we define A_n as all appliances owned by residential user n. It should be noted that some of the appliances are non-shiftable (such as lights, refrigerator) and some are shiftable (especially EVs). Additionally, the appliance scheduling vector of user n is [32]:

$${\mathbf{x}}_{n,a}=[x_{n,a}^1,\dots ,x_{n,a}^h,\dots ,x_{n,a}^H]$$

(3)

where $x_{n,a}^h$ is the consumed energy of appliance $a\in {\mathcal{A}}_n$. Let E_n,a represent the total energy that is planned to finish the operation of shiftable appliance a of user n. Let [α_n,a, β_n,a] be a time slot for appliance a to be scheduled, where 1 ≤ α_n,a < β_n,a ≤ H. For example, the washer may choose α_n,a = 15 and β_n,a = 17 to finish the operation. Therefore, the following constraint has to be satisfied:

$${\displaystyle \sum _{h={\propto }_{n,a}}^{{\beta }_{n,a}}{x}_{n,a}^h}=E_{n,a}$$

(4)

Besides, $x_{n,a}^h=0$ must hold for all h ∈ $\mathscr{H}$\$\mathscr{H}$_n,a, where:

$${\mathscr{H}}_{n,a}=\{{\alpha }_{n,a},\cdots ,{\beta }_{n,a}\}\forall n\in \mathcal{N}$$

(5)

The interval $\mathscr{H}$_n,a also has some constraints. For appliance a, the interval provided by user n must be longer or at least equal to the time interval that finishes the operation. Moreover, the total energy consumed by all appliances in one day must be equal to the consumptions of the whole day. Therefore, one can have the following equation:

$${\displaystyle \sum _{h\in \mathscr{H}}{L}_h}={\displaystyle \sum _{n\in \mathcal{N}}{\displaystyle \sum _{a\in {\mathcal{A}}_n}{E}_{n,a}}}$$

(6)

On the other hand, non-shiftable appliances cannot be scheduled, and they have strict time intervals. For example, the refrigerator must operate all the time, so α_n,a = 1 and β_n,a = 24. Another constraint is that each appliance has its own power level, and the consumption of energy must be under a certain value. Therefore, the following constraint is also to be satisfied:

$${\gamma }_{n,a}^{\min }\le x_{n,a}^h\le {\gamma }_{n,a}^{\max },\forall h\in {\mathscr{H}}_{n,a}$$

(7)

where ${\gamma }_{n,a}^{\max }$ denotes the maximum power level and ${\gamma }_{n,a}^{\min }$ denotes the minimum power level.

As a result, for each user n, we can define a vector x_n, and it is formed by vectors x_n,a for all appliances $a\in {\mathcal{A}}_n$. Therefore, a feasible ECS set X_n corresponding to user n can be summarized as [18]:

$${\chi }_n=\left\{{\mathbf{x}}_n|{\displaystyle \sum _{h={\alpha }_{n,a}}^{{\beta }_{n,a}}{x}_{n,a}^h=E_{n,a},x_{n,a}^h=0\forall h\in \mathscr{H}\backslash {\mathscr{H}}_{n,a},{\gamma }_{n,a}^{\min }\le x_{n,a}^h\le {\gamma }_{n,a}^{\max }\forall h\in {\mathscr{H}}_{n,a}}\right\}$$

(8)

4. Double Cooperative Game among Utility Companies and Residential Users

In this section, we will formulate the double cooperative game among utility companies and residential users. Additionally, two distributed algorithms will be provided to realize the global optimal performance in terms of minimizing the energy costs.

4.1. Cooperative Game among Utility Companies

According to the welfare model for utility company m as given in Equation (2), all of the welfare models for utility companies can be given as follows:

$$\begin{array}{c}{C}_{1,h}=a_1^h{\left(L_1^h\right)}^2+b_1^h{L}_1^h\\ ⋮\\ C_{m,h}=a_m^h{\left(L_m^h\right)}^2+b_m^h{L}_m^h\\ ⋮\\ C_{M,h}=a_M^h{\left(L_M^h\right)}^2+b_M^h{L}_M^h\end{array}$$

(9)

where $L_m^h=u_m^h{L}_h(m=1,2,\cdots ,M)$ and $u_m^h\in {\Pi }_m^h\triangleq \{u_1^h,\cdots ,u_m^h,\cdots u_M^h\}$ denotes the proportion of energy that the utility company m chooses to sell to residential users in time slot h.

Utility companies choose to cooperate to minimize the total cost of all utility companies, so the payoff of the cooperative game for all of the utility companies is:

$$C={\displaystyle \sum _{h=1}^H{\displaystyle \sum _{m=1}^M{C}_{m,h}(u_m^h,L_h)}}$$

(10)

Because the proportion must less than one and the summation of all proportions for the utility companies is equal to one, therefore, one has the following constraints for $u_m^h$:

$$\{\begin{array}{l}{\displaystyle \sum _{m=1}^M{u}_m^h=1}\\ 0\le u_m^h\le 1\end{array}$$

(11)

The purpose of utility companies is to minimize the total cost by changing the amount of energy they sell. Therefore, the goal optimization is to find the most appropriate proportion of energy selling among all of the utility companies, which can be expressed by the following problem:

$$\underset{u_m^h\in {\Pi }_m^h,\forall h\in \mathscr{H}}{\min imize}{\displaystyle \sum _{h=1}^H{\displaystyle \sum _{m=1}^M{C}_{m,h}(u_m^h,L_h)}}$$

(12)

Based on the above analysis, the cooperative game among utility companies can be formulated as:

• Players: utility companies in the set $ℳ$;
• Strategies: each utility company m ∈ $ℳ$ selects its own energy generation proportion $u_m^h$ to minimize its cost;
• Payoffs: C_m(u_m, u_−m) for each utility company in the set $ℳ$ is defined as:

$$C_m(u_m,{\mathbf{u}}_{-m})={\displaystyle \sum _{h=1}^H{C}_{m,h}(u_m^h,L_h)}$$

where u_−m ≜ [u₁, ⋯, u_m−1, u_n+1, ⋯, u_M] denotes the provided energy proportions for all utility companies, except utility company m.

According to the payoffs, utility companies constantly change their strategies until the total cost is minimum. Once the minimum total cost is reached, no utility company wants to change its strategy, otherwise at least one utility company’s interest will be reduced and the balance will be violated. The strategies of the utility companies provided at the balance will be called the Nash equilibrium of the game. Nash equilibrium is the most important concept in game theory. Additionally, the mathematical definition of the Nash equilibrium of the game can be described as follows.

The strategy $(u_m^{*},{\mathbf{u}}_{-m}^{*})$ is a Nash equilibrium if and only if ∀m ∈ $ℳ$:

$$C(u_m^{*},{\mathbf{u}}_{-m}^{*})\ge C(u_m,{\mathbf{u}}_{-m}^{*})$$

(13)

The existence of Nash equilibrium must satisfy certain conditions, and it can be reached if the following conditions are satisfied [37]: (1) the amount of players is finite; (2) the strategy is closed, bounded and convex; and (3) the payoff functions are continuous quasi-concave in the strategy space. According to the defined continuous quasi-concave welfare models for finite utility companies and the closed, bounded and convex strategies employed by the utility companies, there exists a unique Nash equilibrium of the cooperative game for the utility companies.

Solving the Nash equilibrium of the game, as well as the minimization problem, can be programmed with the following distributed Algorithm 1:

Algorithm 1. Executed by utility company m

Execute Algorithm 2 by residential users

Randomly initialize um and u−m

Repeat

Solve problem in Equation (12)

if um,h changes compared to previous value then

Update um,h to the new solution

Broadcast um,h to all other utility companies

end if

if if a new update is received then

update u−m,h

end if

until no utility company wants to change the strategy.

Algorithm 1. Executed by utility company m

Execute Algorithm 2 by residential users

Randomly initialize um and u−m

Repeat

Solve problem in Equation (12)

if um,h changes compared to previous value then

Update um,h to the new solution

Broadcast um,h to all other utility companies

end if

if if a new update is received then

update u−m,h

end if

until no utility company wants to change the strategy.

4.2. Cooperative Game among Residential Users

Let C_h(L_h) represent the cost model for the residential users at time slot h similarly to the welfare model for utility companies. The overall energy cost of the total residential users will be related to the costs from the utility companies and the profit they want to make, which can be defined as:

$${\displaystyle \sum _{h=1}^H{C}_h(L_h)}=\lambda {\displaystyle \sum _{h=1}^H{\displaystyle \sum _{m=1}^M{C}_{m,h}}}=\lambda {\displaystyle \sum _{h=1}^H\left[\left({\displaystyle \sum _{m=1}^M{a}_m^h{\left(u_m^h\right)}^2}\right)L_h^2+\left({\displaystyle \sum _{m=1}^M{b}_m^h{u}_m^h}\right)L_h\right]}$$

(14)

where λ is the profit rate, which can be applied to regulate the profit of utility companies, and λ ≥ 1. When λ > 1, this means that the utility companies will make profits from residential users, and λ = 1 means that the utility companies are organizations not making a profit. For simplicity, λ=1 is selected in this study.

In terms of residential users, they want to reduce their energy cost, which can be expressed as the following optimization problem:

$$\underset{{\mathbf{x}}_n\in {\chi }_n,\forall n\in \mathcal{N}}{\min imize}{\displaystyle \sum _{h\in \mathscr{H}}{C}_h\left({\displaystyle \sum _{n\in \mathcal{N}}{\displaystyle \sum _{a\in A_n}{x}_{n,a}^h}}\right)}$$

(15)

It should be noted that the minimum value of Equation (15) is the total cost of the overall residential users. Since some users might be selfish and only interested in optimizing their own costs, it is crucial to define proper billing tariffs for residential users to guarantee that each residential user is willing to cooperate with others and make a profit. According to [18], the billing function for each residential user can be defined as:

$$b_n={\mathrm{\Omega }}_n{\displaystyle \sum _{h=1}^H{C}_h\left({\displaystyle \sum _{m\in \mathcal{N}}{\displaystyle \sum _{a\in {\mathcal{A}}_m}{x}_{m,a}^h}}\right)}+{\mathrm{\Phi }}_n{\displaystyle \sum _{h=1}^H{\eta }_m\left({\displaystyle \sum _{m\in \mathcal{N}}{x}_{m,\mathrm{v}2g}^h}\right)}$$

(16)

where:

$${\mathrm{\Omega }}_n=\frac{{\displaystyle {\sum }_{a\in {\mathcal{A}}_n}{E}_{n,a}}}{{\displaystyle {\sum }_{m\in \mathcal{N}}{\displaystyle {\sum }_{a\in {\mathcal{A}}_m}{E}_{m,a}}}}$$

(17)

and:

$${\mathrm{\Phi }}_n=\frac{E_{n,\mathrm{v}2g}}{{\displaystyle {\sum }_{m\in \mathcal{N}}{E}_{m,\mathrm{v}2g}}},E_{n,\mathrm{v}2g}={\displaystyle \sum _{h={\alpha }_{n,\mathrm{v}2g}}^{{\beta }_{n,\mathrm{v}2g}}{x}_{n,\mathrm{v}2g}^h,E_{m,\mathrm{v}2g}}={\displaystyle \sum _{h={\alpha }_{m,\mathrm{v}2g}}^{{\beta }_{m,\mathrm{v}2g}}{x}_{m,\mathrm{v}2g}^h}$$

(18)

The billing tariffs for each user in Equation (16) show that the electricity payment of each user depends on the overall energy cost and the portion of the energy consumed by him relative to the total energy consumption. More details about the deduction of the billing function and a discussion can be found in [18].

Consequently, the cooperative game among residential users can be defined as:

• Players: users in the set $\mathcal{N}$;
• Strategies: each user $n\in \mathcal{N}$ selects its ECS x_n to maximize its payoff;
• Payoffs: P_n(x_n; x_−n) for each user $n\in \mathcal{N}$ is defined as:

  $$P_n({\mathbf{x}}_n;{\mathbf{x}}_{-n})=-b_n=-{\mathrm{\Omega }}_n{\displaystyle \sum _{h=1}^H{C}_h\left({\displaystyle \sum _{m\in \mathcal{N}}{\displaystyle \sum _{a\in {\mathcal{A}}_m}{x}_{m,a}^h}}\right)}-{\mathrm{\Phi }}_n{\displaystyle \sum _{h=1}^H{\eta }_m\left({\displaystyle \sum _{m\in \mathcal{N}}{x}_{m,\mathrm{v}2g}^h}\right)}$$

  where x_−n ≜ [x₁, ⋯, x_n−1, x_n+1, ⋯, x_N] denotes the energy consumption schedules for all users, except user n.

According to the definition of the above cooperative game for residential users, they will try to schedule their household appliances to minimize the electricity payments until a Nash equilibrium of the game is reached:

$$P_n({\mathbf{x}}_n^{*};{\mathbf{x}}_{-n}^{*})\ge P_n({\mathbf{x}}_n;{\mathbf{x}}_{-n}^{*})$$

(19)

Once the game is at its unique Nash equilibrium, no residential user will benefit by deviating from ${\mathbf{x}}_n^{*}$, $\forall n\in \mathcal{N}$. The existence and uniqueness of Nash equilibrium for the cooperative game among residential users can be discussed similarly as above for the cooperative game for utility companies, whose proof can also be found in [32].

Given the cost model in Equation (14), according to the cooperative game, the residential user n will schedule household appliances l_n by considering the other residential users’ household load schedules l_−n = (l₁, ⋯ l_n−1, l_n+1, ⋯ l_N). The distributed algorithm to solve the cooperative game among the residential users can be explained as in

Table 2. Parameters of the cost model for each utility company based on the time-of-use (ToU) pricing policy: from 0:00 to 7:00 on the left and from 8:00 to 24:00 on the right.

Company	ai	bi	ai	bi
i=1	0.004	0.064	0.00084	0.064
i=2	0.0006	0.046	0.00078	0.063
i=3	0.0005	0.044	0.00080	0.065

.

The two distributed algorithms to realize the double cooperative games will be processed based on a smart pricing policy in a SG. The smart pricing policy is to encourage residential users to consume energy in a collaborative and profitable way in the SG, such as the real-time pricing and existing ToU pricing, which encourages electricity users to schedule their shiftable loads from peak hours to off-peak hours. Since the household loads of residential users are decided a day ahead of the double game, given a smart pricing policy and the cost model in Equation (14), according to the distributed Algorithm 2 for the cooperative game among residential users, the power consumption load of residential users at each hour L_h will be determined. Based on the determined L_h, proportions of the energy provided by different utility companies can be solved for the cooperative game by using the distributed Algorithm 1.

Algorithm 2. Executed by residential user n

Randomly initialize ln and l−n

Repeat

Solve problem in Equation (16) using inner point method.

if xn changes compared to current schedule then

Update xn to the new solution

Broadcast ln to all other users

end if

if if a new update is received then

update l−n

end if

until no residential user wants to change the strategy.

Algorithm 2. Executed by residential user n

Randomly initialize ln and l−n

Repeat

Solve problem in Equation (16) using inner point method.

if xn changes compared to current schedule then

Update xn to the new solution

Broadcast ln to all other users

end if

if if a new update is received then

update l−n

end if

until no residential user wants to change the strategy.

5. Case Study

In this section, a case study will be presented to illustrate the feasibility and advantages for the presented double cooperative game in the SG for the residential users’ energy consumption and the utility companies’ energy supplement.

In the case that there are M = 3 utility companies and N = 5 residential users, each residential user has two non-shiftable appliances (lights and refrigerator) and three shiftable appliances (dishwasher, washing machine and EV). Besides, a whole day is divided into H = 24 h, and each time slot is 1 h. Non-shiftable appliances have a strict energy consumption time: the refrigerator must operate all day, so α_n,a = 1 and β_n,a = 24 for the refrigerators; lights are used mainly at night, so we set α_n,a = 18 and β_n,a = 24 for the lights. Shiftable appliances can be scheduled in order to shift loads, but they also have time slots to operate, except EVs. For the washing machine, we assume that it works for 1 h between 20:00 and 23:00. For the dishwasher, we assume that it works 2 h a day: 1 h between 8:00 and 10:00 and 1 h between 20:00 and 22:00. EVs, different from other shiftable appliances, are not only used as transport vehicles, but also as storage batteries, which can discharge the surplus energy to the SG to make a profit. Suppose that EVs are employed to go to work or travel from 7:00 to 20:00, and during this period, they will not be connected to the SG. When users are at home, EVs can be charged or discharged from 20:00 to 24:00 and can be only charged from 0:00 to 7:00 the next day for transporting.

Normally, people will have different arrangements for their lives on workdays and holidays. Without loss of generality, we consider one week in the case study, i.e., there are five working days and two weekend days. In the week, the energy consumption of residential users could have fluctuations; for example, it is realistic for residential users that they do not use the washing machine at home everyday. Besides, residential users do not need to work on the weekend, so it is unnecessary for them to charge EVs to the full level; therefore, the energy consumption of EVs on weekend days could be less than the one on week days. In order to demonstrate that each residential user can reduce their cost in the cooperative game even if they have few shiftable appliances, we suppose residential User 5 does not have an EV. Here, we list the energy consumption for the five residential users on Friday and Saturday as an example, as shown in

Table 1. Electricity consumption of each residential load (kW h): Friday on the top and Saturday on the bottom.

Users	Refrigerator	Light	Washing machine	EV	Dishwasher
1	1.32	1.3	1.49	14.4	0
2	1.32	1.0	1.30	14.4	1.44
3	1.32	0.8	1.49	14.4	1.44
4	1.32	1.0	0	14.4	1.44
5	1.32	1.2	1.49	0	1.44
1	1.32	1.3	1.49	12.7	0
2	1.32	1.0	1.30	12.7	1.44
3	1.32	0.8	1.49	12.7	1.44
4	1.32	1.0	1.49	12.7	1.44
5	1.32	1.2	1.49	0	1.44

. According to [18,38–40], we assume that the batteries of the EVs are identical and the capacities of the EVs are the same: 20 kW h; the charging power is 8 kW; the discharging power is 4.3 kW; the discharging depth is 80%; the charging/discharging efficiency is 92%; and the depreciation coefficient is a_η = 0.03, i.e., ${\eta }_{PEV}(l_{\text{v2g}})=0.03l_{\text{v2g}}^2$.

The cost model parameters for the three utility companies are defined together with the smart pricing policy. In the case study, the ToU pricing policy is employed, and the prices are divided into daytime hours’ (from 8:00 to 24:00) pricing and nighttime hours’ (from 8:00 to 24:00) pricing. Referring to the cost function setting in [18,32], the parameters of cost models for the three utility companies are selected as shown in Table 2.

According to the above given background of the case study, the double cooperative game among multiple residential users and multiple utility companies can be implemented automatically with the two distributed algorithms. For comparison, two situations of the utility companies are considered: “with game” and “without game”, which mean identical proportions of the three utility companies and optimized proportions based on the cooperative game, respectively; three situations of the residential users are considered: “no ECS”, “ECS without discharging” and “ECS with discharging”, which mean residential users schedule their appliances at the permitted starting time α_n,a without the cooperative game and the household appliances will be scheduled based on the result of the cooperative game without/with discharging electricity energy back to the grid with their EVs, respectively.

Figure 2 shows the total cost of three utility companies in a week when there is no cooperative game among residential users. From the figure, one can see that the total cost of the three utility companies is reduced everyday when the game among the utility companies is involved. In another words, the utility companies will benefit when they are cooperating with each other regardless of whether the residential users optimize their appliances’s scheduling or not. Moreover, when the double game among utility companies and residential users is considered, the cost of utility companies should be reduced further. As shown in Figure 3, one can see that the cost of each utility company or the total cost of all three utility companies keeps decreasing when residential users take part in the cooperative game and discharge energy back with their PEVs. Therefore, the double cooperative game will benefit the utility companies more than only the cooperative game employed among themselves.

To illustrate daily energy consumption and the cost of residential users among the double cooperative game, simulation results on Friday for the five residential users are presented as shown in Figure 4. The left column of the figure shows the total energy consumption of the five residential users for the cases of no ECS, ECS without discharging and ECS with discharging, from top to bottom, respectively. One can see that when the cooperative game among users is employed, some shiftable loads have been shifted to the duration with lower electricity price, i.e., from 0:00 to 7:00, compared to the case of no cooperative game among the users. Additionally, when PEVs are allowed to store and discharge energy back to the grid, the PEVs will be charged at a lower electricity price and discharged at a high electricity price, which is from 23:00 to 24:00, as shown in the figure. The right column of Figure 4 shows the cost of each residential user on Friday for the cases of no ECS, ECS without discharging and ECS with discharging, from top to bottom, respectively. For each case of the residential user, two cases of utility companies are also considered to calculate the cost. One can see that the payments of each residential user decrease monotonically along with the combined cases: “no ECS” and “without game”, “no ECS” and “with game”, “ECS without discharging” and “without game”, “ECS without discharging” and “with game”, “ECS with discharging” and “without game” and “ECS with discharging” and “with game”.

Additionally, the total cost of each user in a week is also calculated, as shown in Figure 5. It is straightforward that the total cost of a week for each residential user is reduced when the double cooperative game is employed compared to only the cooperative game in which residential users participate only. Therefore, the double cooperative game will also benefit the residential users more than only the cooperative game employed among themselves.

As a result of the case study, the double cooperative game will benefit both residential users and utility companies more than the cooperative game employed only by one side and, furthermore, for no game employed by either side.

6. Conclusions

In this paper, we have constructed a double cooperative game with multiple utility companies and multiple residential users in the SG. The games among multiple utility companies and residential users are both selected as a cooperative game, which can provide more benefits for both sides or at least one side in a game. Moreover, we also consider that residential users can store and sell energy back to the grid with their PEVs. Simulation results show that: (1) the proposed double cooperative game approach can reduce the aggregate payments of the five residential users from 29.5 dollars to 28.9 dollars with only the cooperative game among the residential users in a week; (2) the aggregated cost of the three utility companies will decrease from 34.2 dollars with the double cooperative game approach to 28.9 dollars with only the cooperative game among the utility companies in a week; (3) once users sell energy back to the utility company by using their PEVs, the aggregated residential users’ payments in a week will reduce further to 25.3 dollars; (4) the maximum aggregated cost of the three utility companies in a week, as well as the maximum aggregated payments of the five residential users in a week would be 35.6 dollars in the case of no games on both sides. Therefore, the proposed double cooperative game will benefit both residential users and utility companies more than the cooperative game employed only by one side and, furthermore, for no game employed by either the utility companies or the residential users. Although the electricity users considered in this paper are only residents, the double game framework could be applied to different users with different games.