Switching Control of Wind Turbine Sub-Controllers Based on an Active Disturbance Rejection Technique
Abstract
:1. Introduction
- (1)
- MPPT control to achieve maximum power. When the wind speed is below the rated value, the output power is less than the rated one too. In this stage, the control target of the unit is to improve the wind energy utilization ratio, and then improve the energy conversion rate and the power generated by the turbines, so the generator speed is controlled to make the turbines operate at the best tip-speed-ratio and track the maximum power points. In [7], for example, a novel sensorless MPPT control strategy for capturing the maximum energy from fluctuating wind was used in a PMSG system. The MPPT controller was developed to function as a wind speed estimator to generate an appropriate duty cycle for controlling power MOSFET switches in the boost converters in order to capture the maximum power under variable wind speed conditions. In [8], proportional integral (PI) and fuzzy controllers were tested to extract the maximum power from the wind. Simulation results were given to show the performance of the proposed fuzzy control system in MPPT in a wind energy conversion system (WECS) under various wind conditions. In [9], a fuzzy-logic based MPPT method for a standalone wind turbine system was proposed. The hill climb searching (HCS) method was used to achieve the MPPT of the PMSG wind turbine system. A sliding mode voltage control strategy was proposed in [10] for capturing the maximum wind energy based on fuzzy logic control, which was shown to have higher overall control efficiency than the conventional proportional integral derivative (PID) control. A short technical review of WECS was given in [11], where the control strategies of controllers for both DFIG-WECS and PMSG-WECS and various MPPT technologies for efficient production of energy from the wind were discussed.
- (2)
- Variable pitch control to maintain constant power. When the wind speed is above the rated value, the output power of the system is still increasing with the wind speed. If not restricted, the output power will exceed the power limit of the connected grid, which will lead to off-net work. Therefore, the control objective of this stage is to maintain the output power of the unit in the vicinity of the rated power. When the wind speed is increasing, reducing the speed of the generator and increasing the pitch angle can both limit the increase of output power, due to the constraints of the regulating range of generator speed and the complexity of the generator control, so in this stage, variable pitch control is adopted to reduce wind energy absorption and thus maintain the stability of the output power by adjusting the pitch angle. Pitch control is the most efficient and popular power control method, especially for variable-speed wind turbines [12]. In [13], an advanced pitch angle control strategy based on fuzzy logic was proposed for variable-speed wind turbine systems. In [14], a new pitch control method that combined fuzzy adaptive PID control with fuzzy feed forward control was proposed. The fuzzy adaptive PID controller was able to ensure the unit had a better control result than a PID controller at various wind speeds. The fuzzy feed forward controller improved the responsiveness of the pitch control system. A variable pitch back stepping sliding-mode controller (BSMC) for wind turbines based on a radial basic function neural network (RBFNN) was designed in [15], which could stabilize the output power of wind turbines and effectively improve the performance of variable pitch systems. In [16], a sliding mode variable structure controller based on the analysis of the features of the variable pitch was proposed, which showed that sliding mode control could cope with the traditional chattering problems seen in variable structure systems, and had the advantages of robustness and fast response.
2. Designing of the Sub-Controllers
2.1. The Controller in Maximum Power Points Tracking Stage
2.2. The Controller in the Constant Power Stage
3. Sub-Controller Switching
4. Design of the Active Disturbance Rejection Controller
4.1. The Basic Principle of Active Disturbance Rejection Control
4.2. Design of Active Disturbance Rejection Controller
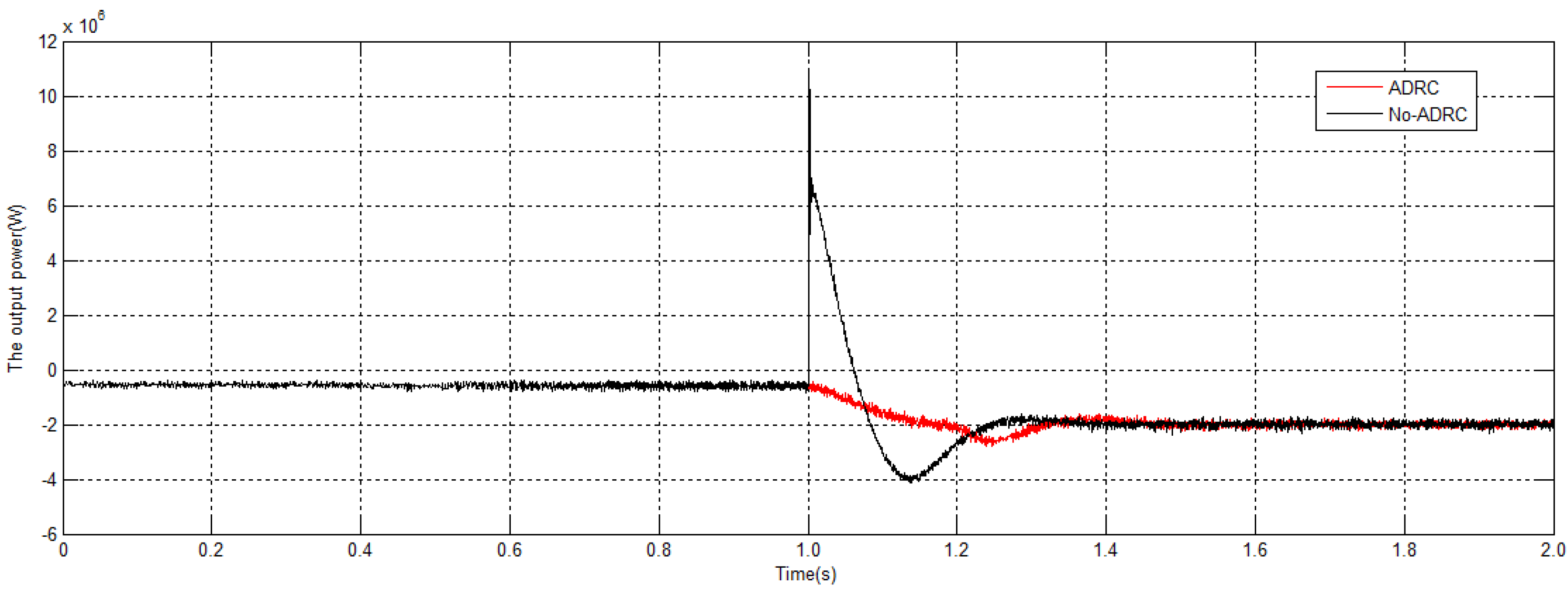
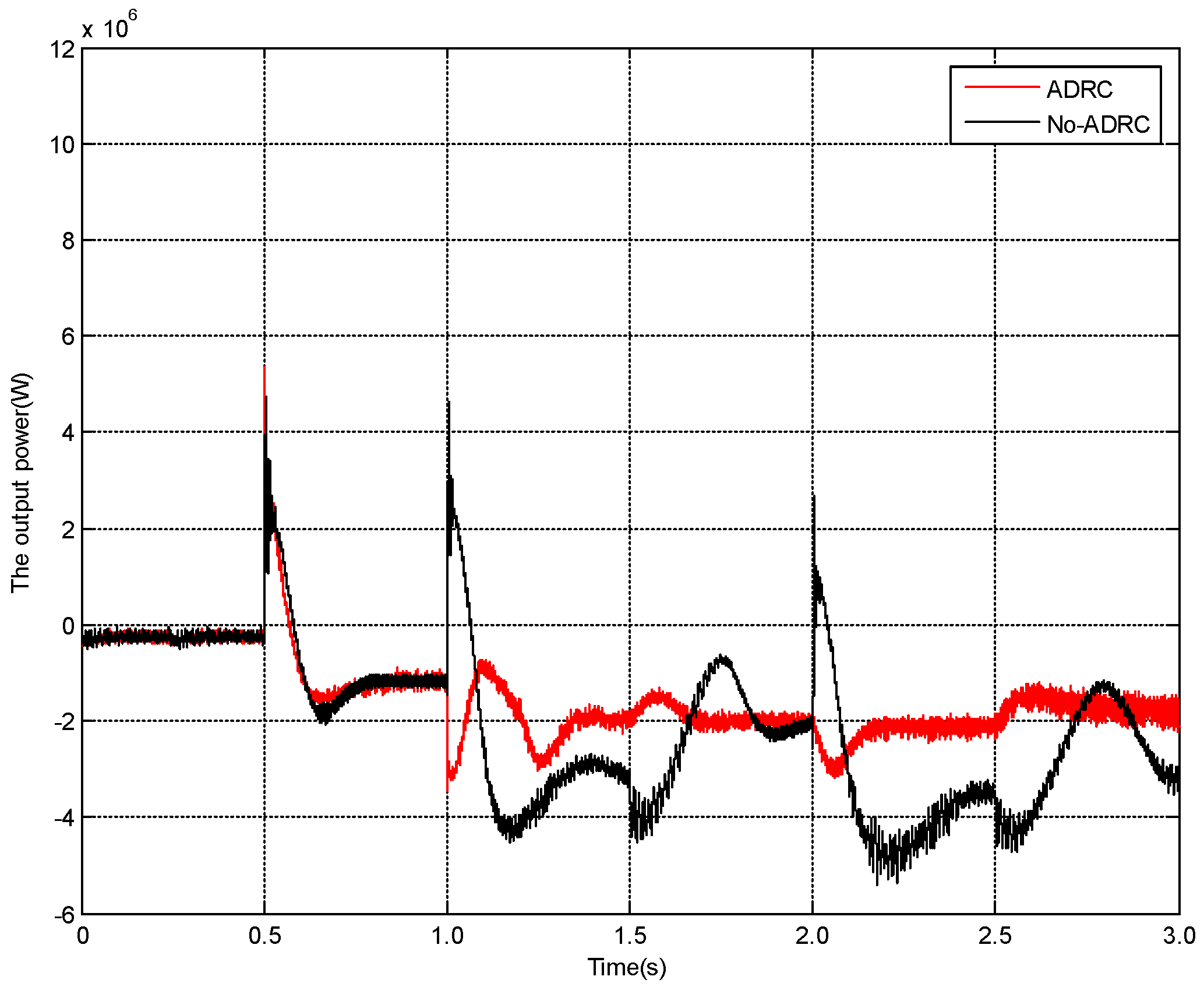
5. Simulation Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, T. Statistics on global wind power installed capacity in 2015. Wind Energy Ind. 2016, 2016, 51–56. [Google Scholar]
- European Wind Energy Association. Pure Power: Wind Energy Targets for 2020 and 2030, 2009 Update. Available online: http://www.ewea.org/fileadmin/ewea_documents/documents/publications/reports/ Pure_power_Full_Report.pdf (accessed on 31 July 2015).
- The US Department of Energy (US DoE). Chapter 4: The Wind Vision Roadmap: A Pathway Forward in Wind Vision: A New Era for Wind Power in the United States. Available online: http://www.energy.gov/ sites/prod/files/wv_chapter4_the_wind_vision_roadmap.pdf (accessed on 20 March 2016).
- China May Have 500 GW of Wind Parks in 2030—Study (21 October 2014). Available online: http://renewables.seenews.com/news/china-may-have-500-gw-of-wind-parks-in-2030-study-444069 (accessed on 20 March 2016).
- Gu, F. Power Control of Wind Farm Based on Doubly-fed Generators. Master’s Thesis, Shandong University, Jinan, China, April 2009. [Google Scholar]
- Xiao, Y.; Zhang, T.; Ding, Z.; Li, C. The Study of Fuzzy Proportional Integral Controllers Based on Improved Particle Swarm Optimization for Permanent Magnet Direct Drive Wind Turbine Converters. Energies 2016, 9, 343. [Google Scholar] [CrossRef]
- Tiang, T.L.; Ishak, D. Novel MPPT control in permanent magnet synchronous generator system for battery energy storage. In Proceedings of the 2nd International Conference on Mechanical and Aerospace Engineering, Bangkok, Thailand, 29–31 July 2011; pp. 5179–5183.
- Amine, B.M.; Souhila, Z.; Tayeb, A.; Ahmed, M. Adaptive fuzzy logic control of wind turbine emulator. Int. J. Power Electron. Drive Syst. 2014, 4, 233–240. [Google Scholar]
- Minh, H.Q.; Cuong, N.C.; Chau, T.N. A fuzzy-logic based MPPT method for stand-alone wind turbine system. Am. J. Eng. Res. 2014, 3, 177–184. [Google Scholar]
- Yin, X.X.; Lin, Y.G.; Li, W.; Gu, Y.J.; Lei, P.F.; Liu, H.W. Sliding mode voltage control strategy for capturing maximum wind energy based on fuzzy logic control. Int. J. Emerg. Electr. Power Syst. 2015, 70, 45–51. [Google Scholar] [CrossRef]
- Babu, N.R.; Arulmozhivarman, P. Wind energy conversion systems—A technical review. J. Eng. Sci. Technol. 2013, 8, 493–507. [Google Scholar]
- Salazar, J.; Tadeo, F.; Witheephanich, K.; Hayes, M.; de Prada, C. Control for a variable speed wind turbine equipped with a permanent magnet synchronous generator (PMSG). In Proceedings of the 3rd International Conference on Sustainability in Energy and Buildings (SEB’11), Marseilles, France, 1–3 June 2011; pp. 151–168.
- Van Tan, L.; Nguyen, T.H.; Lee, D.-C. Advanced Pitch Angle Control Based on Fuzzy Logic for Variable-Speed Wind Turbine Systems. IEEE Trans. Energy Convers. 2015, 30, 578–587. [Google Scholar] [CrossRef]
- Xiao, Y.; Huo, W.; Nan, G. Study of Variable Pitch Control for Direct-drive Permanent Magnet Wind Turbines Based on Fuzzy Logic Algorithm. J. Inf. Comput. Sci. 2015, 12, 2849–2856. [Google Scholar] [CrossRef]
- Liao, Q.; Qiu, X.-Y.; Jiang, R.-Z. Variable pitch control of wind turbine based on RBF neural network. In Proceedings of the 2014 International Conference on Power System Technology (POWERCON), Chengdu, China, 20–22 October 2014.
- Wang, X.; Zhu, W.; Qin, B.; Li, P. Sliding mode control of pitch angle for direct driven PM wind turbine. In Proceedings of the 26th Chinese Control and Decision Conference (CCDC), Changsha, China, 31 May–2 June 2014.
- Mansour, M.; Mansouri, M.N.; Mimouni, M.F. Study of performance of a variable-speed wind turbine with pitch control based on a permanent magnet synchronous generator. In Proceedings of the International Multi-Conference on Systems, Signals and Devices (SSD’11), Sousse, Tunisia, 22–25 March 2011. [CrossRef]
- Lee, S.-H.; Joo, Y.; Back, J.; Seo, J.-H.; Choy, I. Sliding mode controller for torque and pitch control of PMSG wind power systems. J. Power Electron. 2011, 11, 342–349. [Google Scholar] [CrossRef]
- Kim, H.W.; Kin, S.S.; Ko, H.S. Modeling and control of PMSG-based variable-speed wind turbine. Electr. Power Syst. Res. 2010, 80, 46–52. [Google Scholar] [CrossRef]
- Ren, Y.; An, Q. Flexible Grid Connected Operation and Control of Doubly Fed Wind Power Generation Unit, 1st ed.; China Machine Press: Beijing, China, 2011; pp. 120–144. [Google Scholar]
- Chi, W.; Shi, Q.; Chen, H. Control strategy study of direct-driven wind-power system with PMSG based on back-to-back PWM converter. J. Mech. Electr. Eng. 2012, 29, 434–438. [Google Scholar]
- Wang, S.; Li, Z. Adaptive PI optimization control for variable-pitch wind turbines. Acta Energiae Solaris Sin. 2013, 34, 1579–1586. [Google Scholar]
- Han, J. Auto-disturbances-rejection Controller and It’s Applications. Control Decis. 1998, 13, 1579–1586. [Google Scholar]
- Sun, K.; Zhao, Y.; Shu, Q. A position sensorless vector control system of permanent magnet synchronous motor based on active-disturbance rejection controller. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009.
- Han, J. From PID technique to active disturbances rejection control technique. Control Eng. China 2002, 9, 13–18. [Google Scholar]
- Huang, Y.; Zhang, W. Development of active disturbance rejection controller. Control Theory Appl. 2002, 19, 484–492. [Google Scholar]






















| EC | PB | PM | PS | ZE | NS | NM | NB | ||
|---|---|---|---|---|---|---|---|---|---|
| U | |||||||||
| E | |||||||||
| PB | PB | PB | PB | PB | PM | ZE | ZE | ||
| PM | PB | PB | PB | PB | PM | ZE | ZE | ||
| PS | PM | PM | PM | PM | ZE | NS | NS | ||
| PZ | PM | PM | PS | ZE | NS | NM | NM | ||
| NZ | PM | PM | PS | ZE | NS | NM | NM | ||
| NS | PS | PS | ZE | NM | NM | NM | NM | ||
| NM | ZE | ZE | NM | NB | NB | NB | NB | ||
| NB | ZE | ZE | NM | NB | NB | NB | NB | ||
| Controller | Regulating Time | Overshoot | Steady-State Error |
|---|---|---|---|
| No-ADRC | 0.33 s | 99.98% | 22.00% |
| ADRC | 0.45 s | 25.00% | 16.88% |
| Controller | Regulating Time | Overshoot | Steady-State Error |
|---|---|---|---|
| No-ADRC | 0.27 s | 152.27% | 25.42% |
| ADRC | 0.31 s | 61.82% | 11.86% |
| Controller | Regulating Time | Overshoot |
|---|---|---|
| No-ADRC | 0.33 s | 107.50% |
| ADRC | 0.46 s | 40.28% |
| Controller | Regulating Time | Overshoot |
|---|---|---|
| No-ADRC | 0.47 s | 0.66% |
| ADRC | 0.54 s | 8.31% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Hong, Y.; Chen, X.; Huo, W. Switching Control of Wind Turbine Sub-Controllers Based on an Active Disturbance Rejection Technique. Energies 2016, 9, 793. https://doi.org/10.3390/en9100793
Xiao Y, Hong Y, Chen X, Huo W. Switching Control of Wind Turbine Sub-Controllers Based on an Active Disturbance Rejection Technique. Energies. 2016; 9(10):793. https://doi.org/10.3390/en9100793
Chicago/Turabian StyleXiao, Yancai, Yi Hong, Xiuhai Chen, and Wenjian Huo. 2016. "Switching Control of Wind Turbine Sub-Controllers Based on an Active Disturbance Rejection Technique" Energies 9, no. 10: 793. https://doi.org/10.3390/en9100793
APA StyleXiao, Y., Hong, Y., Chen, X., & Huo, W. (2016). Switching Control of Wind Turbine Sub-Controllers Based on an Active Disturbance Rejection Technique. Energies, 9(10), 793. https://doi.org/10.3390/en9100793




