Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress
Abstract
:1. Introduction
2. Methods
2.1. Study Site
2.2. Observations
2.2.1. Sea Surface Height Data
2.2.2. Acoustic Doppler Current Profiler (ADCP)
2.3. Hydrodynamic Model
2.3.1. Mathematical Framework
2.3.2. Configuration and Boundary Forcing
2.3.3. Calibration
2.3.4. Parameterisation of Tidal Turbines
2.3.5. Model Output
3. Model Calibration and Evaluation
4. Results
4.1. Near-Bed Velocity Fields
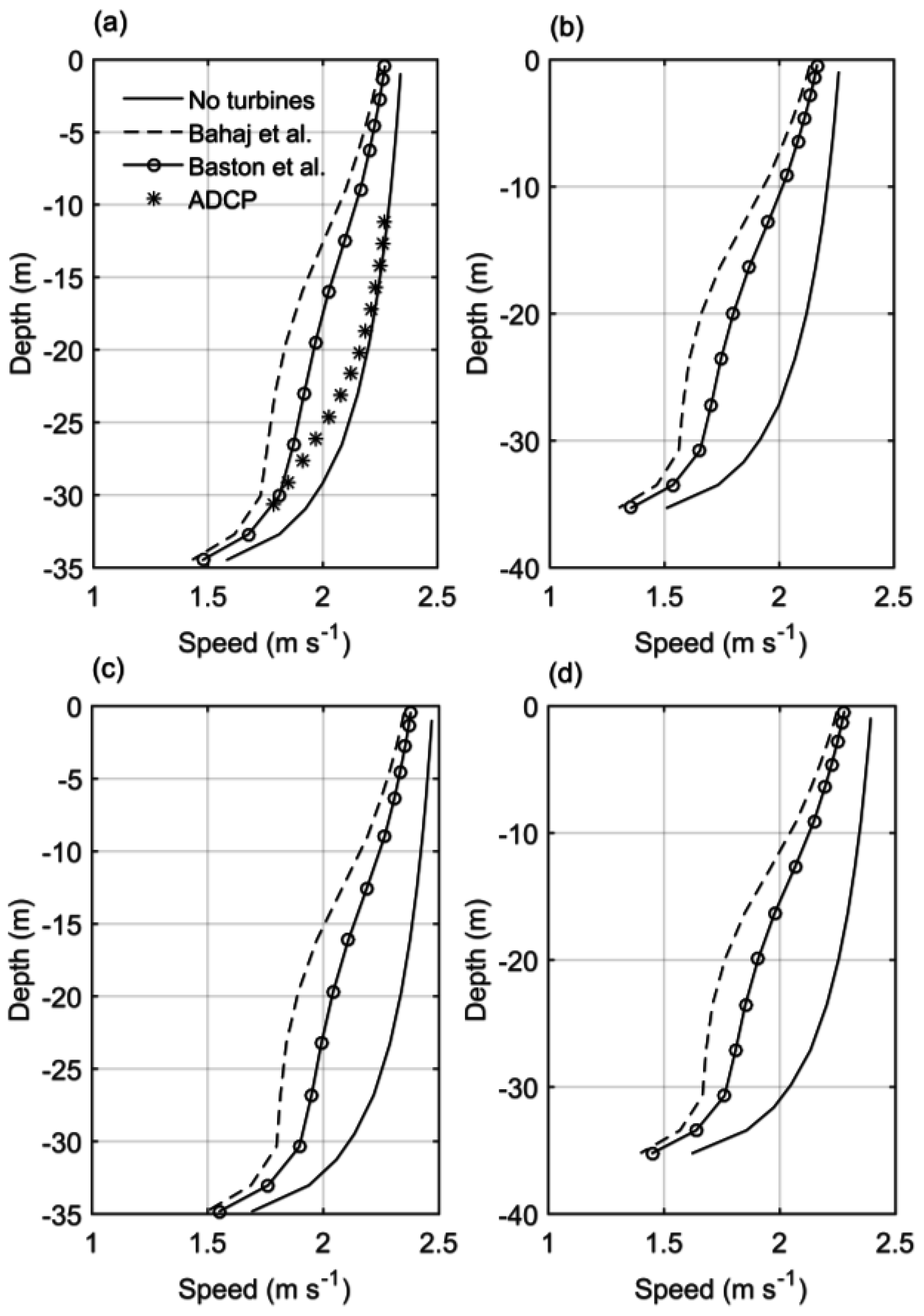
4.2. Turbine Effects on Velocity Profiles
4.3. Turbine Effects on Near-Bed Velocity Fields
4.4. Local Bed Shear Stress
4.5. Power Generation
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Draper, S.; Adcock, T.A.A.; Borthwick, A.G.L.; Houlsby, G.T. Estimate of the tidal stream power resource of the Pentland Firth. Renew. Energy 2014, 63, 650–657. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Draper, S.; Houlsby, G.T.; Borthwick, A.G.; Serhadlioglu, S. The available power from tidal stream turbines in the Pentland Firth. Proc. R. Soc. A 2013, 469, 20130072. [Google Scholar] [CrossRef]
- Meygen LTD. MeyGen Tidal Energy Project Phase 1 Environmental Statement. Available online: http://77.68.107.10/Renewables%20Licensing/MG_Sound_of_Stroma_Offshore_Tidal_Array/ES/Complete%20ES.pdf (accessed on 16 November 2015).
- Shields, M.A.; Dillon, L.J.; Woolf, D.K.; Ford, A.T. Strategic priorities for assessing ecological impacts of marine renewable energy devices in the Pentland Firth (Scotland, UK). Mar. Policy 2011, 33, 635–642. [Google Scholar] [CrossRef]
- Bonar, P.A.; Bryden, I.G.; Borthwick, A.G. Social and ecological impacts of marine energy development. Renew. Sustain. Energy Rev. 2015, 47, 486–495. [Google Scholar] [CrossRef]
- Neill, S.P.; Litt, E.J.; Couch, S.J.; Davies, A.G. The impact of tidal stream turbines on large-scale sediment dynamics. Renew. Energy 2009, 34, 2803–2812. [Google Scholar] [CrossRef]
- Neill, S.P.; Jordan, J.R.; Couch, S.J. Impact of tidal energy converter (TEC) arrays on the dynamics of headland sand banks. Renew. Energy 2012, 37, 387–397. [Google Scholar] [CrossRef]
- Martin-Short, R.; Hill, J.; Kramer, S.C.; Avdis, A.; Allison, P.A.; Piggott, M.D. Tidal resource extraction in the Pentland Firth, UK: Potential impacts on flow regime and sediment transport in the Inner Sound of Stroma. Renew. Energy 2015, 76, 596–607. [Google Scholar] [CrossRef]
- Fairley, I.; Masters, I.; Karunarathna, H. The cumulative impact of tidal stream turbine arrays on sediment transport in the Pentland Firth. Renew. Energy 2015, 80, 755–769. [Google Scholar] [CrossRef]
- Harendza, A. Benthic Habitats in a Tide-Swept Channel of the Pentland Firth and Their Potential Responses to a Tidal Energy Development. Ph.D. Thesis, University of Aberdeen, Aberdeen, UK, 2014. [Google Scholar]
- McIlvenny, J.; Tamsett, D.; Gillibrand, P.A.; Goddijn-Murphy, L. On the sediment dynamics in a tidally energetic channel: The Inner Sound, northern Scotland. J. Mar. Sci. Eng. 2016, 4, 31. [Google Scholar] [CrossRef]
- Tamsett, D.; McIlvenny, J.; Watts, A. Colour sonar: Multi-frequency sidescan sonar images of the seabed in the Inner Sound of the Pentland Firth, Scotland. J. Mar. Sci. Eng. 2016, 4, 26. [Google Scholar] [CrossRef]
- Easton, M.C.; Woolf, D.K.; Bowyer, P.A. The dynamics of an energetic tidal channel, the Pentland Firth, Scotland. Cont. Shelf Res. 2013, 48, 50–60. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Woolf, D.K.; Easton, M.C. Current Patterns in the Inner Sound (Pentland Firth) from Underway ADCP Data. J. Atmos. Ocean. Technol. 2013, 30, 96–111. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Gardline Surveys, Pentland Firth Tidal Stream Observations; Navigation Safety Branch of the Maritime and Coastguard Agency: Southampton, UK, 2001.
- Baston, S.; Harris, R.E. Modelling the hydrodynamic characteristics of tidal flow in the Pentland Firth. In Proceedings of the 9th European Wave and Tidal Energy conference, Southampton, UK, 5–9 September 2011.
- Walters, R.A.; Casulli, V. A robust, finite element model for hydrostatic surface water flows. Commun. Numer. Methods Eng. 1998, 14, 931–940. [Google Scholar] [CrossRef]
- Walters, R.A. Coastal ocean models: Two useful finite element methods. Cont. Shelf Res. 2005, 25, 775–793. [Google Scholar] [CrossRef]
- Walters, R.A. A semi-implicit finite element model for non-hydrostatic (dispersive) surface waves. Int. J. Numer. Methods Fluids 2005, 49, 721–737. [Google Scholar] [CrossRef]
- Gillibrand, P.A.; Lane, E.M.; Walters, R.A.; Gorman, R.M. Forecasting extreme sea surface height and coastal inundation from tides, surge and wave setup. Aust. J. Civ. Eng. 2011, 9, 99–112. [Google Scholar]
- Lane, E.M.; Gillibrand, P.A.; Arnold, J.R.; Walters, R.A. Tsunami inundation modeling with RiCOM. Aust. J. Civ. Eng. 2011, 9, 83–98. [Google Scholar]
- Walters, R.A.; Gillibrand, P.A.; Bell, R.; Lane, E.M. A study of tides and currents in Cook Strait, New Zealand. Ocean Dyn. 2010, 60, 1559–1580. [Google Scholar] [CrossRef]
- Plew, D.R.; Stevens, C.L. Numerical modelling of the effect of turbines on currents in a tidal channel–Tory Channel, New Zealand. Renew. Energy 2013, 57, 269–282. [Google Scholar] [CrossRef]
- Walters, R.A.; Tarbotton, M.R.; Hiles, C.E. Estimation of tidal power potential. Renew. Energy 2013, 51, 255–262. [Google Scholar] [CrossRef]
- Walters, R.A. A coastal ocean model with subgrid approximation. Ocean Model. 2016, 102, 45–54. [Google Scholar] [CrossRef]
- Casulli, V. Eulerian-lagrangian methods for hyperbolic and convection dominated parabolic problems. In Computational Methods for Non-linear Problems; Taylor, C., Owen, D., Hinton, E., Eds.; Pineridge Press: Swansea, UK, 1987; pp. 239–268. [Google Scholar]
- Walters, R.A.; Lane, E.M.; Henry, R.F. Semi-lagrangian methods for a finite element coastal ocean model. Ocean Model. 2008, 19, 112–124. [Google Scholar] [CrossRef]
- Walters, R.A.; Lane, E.M.; Hanert, E. Useful time-stepping methods for the Coriolis term in a shallow water model. Ocean Model. 2009, 28, 66–74. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modelling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Walters, R.A.; Plew, D.R. Numerical modelling of environmental flows using DAM: Some preliminary results. Acta Geophys. 2008, 56, 918–934. [Google Scholar] [CrossRef]
- Nikora, V.; McLean, S.; Coleman, S.; Pokrajac, D.; Walters, R.A. Double-averaging concept for rough-bed open-channel and overland flows: Theoretical background. J. Hydraul. Eng. ASCE 2007, 133, 873–883. [Google Scholar] [CrossRef]
- Shives, M.; Crawford, C.; Hiles, C.; Walters, R.A. Combining numerical methods for basin and turbine scales for improved modelling of in-situ turbine arrays. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013.
- Waldman, S.; Genet, G.; Bastón, S.; Side, J. Correcting for mesh size dependency in a regional models representation of tidal turbines. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- Kramer, S.C.; Piggott, M.D. A correction to the enhanced bottom drag parameterisation of tidal turbines. Renew. Energy 2016, 92, 385–396. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Molland, A.F.; Chaplin, J.R.; Batten, W.M.J. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Baston, S.; Waldman, S.; Side, J. Modelling energy extraction in tidal flows. In TeraWatt Position Papers; Marine Alliance for Science and Technology for Scotland (MASTS): St Andrews, UK, 2015; pp. 75–107. Available online: http://www.masts.ac.uk/media/35656/position_papers_terawatt_e-book.pdf (accessed on 23 March 2016).
- Daly, T.; Myers, L.E.; Bahaj, A.S. Modelling of the flow field surrounding tidal turbine arrays for varying positions in a channel. Philos. Trans. R. Soc. A 2013, 371, 20120246. [Google Scholar] [CrossRef] [PubMed]
- Vennell, R.; Funke, S.W.; Draper, S.; Stevens, C.; Divett, T. Designing large arrays of tidal turbines: A synthesis and review. Renew. Sustain. Energy Rev. 2015, 41, 454–472. [Google Scholar] [CrossRef]
- Funke, S.W.; Farrell, P.E.; Piggott, M.D. Tidal turbine array optimization using the adjoint approach. Renew. Energy 2014, 63, 658–673. [Google Scholar] [CrossRef]









| Site | Period | Latitude | Longitude | Sample Interval (min) |
|---|---|---|---|---|
| Scrabster | 11/11/2012–17/09/2013 | 58.6103 | −3.5439 | 10 |
| ADCP | 18/02/2013–24/03/2013 | 58.6598 | −3.1287 | 10 |
| Stroma | 15/01/2013–14/03/2013 | 58.6691 | −3.1175 | 10 |
| John O’Groats | 14/10/2011–17/09/2013 | 58.6486 | −3.0639 | 10 |
| Wick | 01/01/2011–31/12/2011 | 58.5742 | −3.0604 | 15 |
| Site | Period | Latitude | Longitude | Water Depth (m) |
|---|---|---|---|---|
| C1 | 14/09/2001–18/10/2001 | 58.7261 | −3.2364 | 82 |
| C2 | 14/09/2001–18/10/2001 | 58.7169 | −3.0858 | 80 |
| C3 | 14/09/2001–18/10/2001 | 58.6703 | −2.9764 | 72 |
| ADCP (East) | 18/02/2013–24/03/2013 | 58.6598 | −3.1287 | 36 |
| Run | Period | Number of Tidal Turbines | Rated Power (MW) | Total Power (MW) | CT and CP |
|---|---|---|---|---|---|
| 1 | 18/02/2013–24/03/2013 | 0 | N/A | 0 | N/A |
| 2 | 18/02/2013–24/03/2013 | 1 | 1.5 | 1.5 | Constant |
| 3 | 18/02/2013–24/03/2013 | 1 | 1.5 | 1.5 | Variable |
| 4 | 18/02/2013–24/03/2013 | 4 | 1.5 | 6 | Constant |
| 5 | 18/02/2013–24/03/2013 | 4 | 1.5 | 6 | Variable |
| 6 | 18/02/2013–24/03/2013 | 57 | 1.5 | 85.5 | Constant |
| 7 | 18/02/2013–24/03/2013 | 57 | 1.5 | 85.5 | Variable |
| Site | M2 | S2 | N2 | O1 | K1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | G | A | G | A | G | A | G | A | G | ||
| Scrabster | Obs | 1.36 | 244 | 0.51 | 277 | 0.29 | 219 | 0.10 | 351 | 0.14 | 142 |
| Model | 1.37 | 246 | 0.51 | 281 | 0.30 | 222 | 0.09 | 8 | 0.13 | 143 | |
| ADCP (East) | Obs | 0.94 | 279 | 0.43 | 317 | 0.16 | 250 | 0.11 | 7 | 0.09 | 170 |
| Model | 0.96 | 278 | 0.33 | 315 | 0.20 | 255 | 0.10 | 16 | 0.13 | 157 | |
| Stroma | Obs | 0.89 | 282 | 0.36 | 325 | 0.17 | 249 | 0.11 | 1 | 0.13 | 176 |
| Model | 0.93 | 281 | 0.32 | 318 | 0.19 | 259 | 0.10 | 15 | 0.13 | 157 | |
| John O’Groats | Obs | 0.83 | 284 | 0.28 | 320 | 0.18 | 257 | 0.10 | 8 | 0.11 | 161 |
| Model | 0.93 | 287 | 0.31 | 325 | 0.18 | 265 | 0.10 | 21 | 0.12 | 161 | |
| Wick | Obs | 0.96 | 322 | 0.32 | 1 | 0.18 | 298 | 0.11 | 29 | 0.10 | 176 |
| Model | 1.00 | 319 | 0.34 | 351 | 0.20 | 292 | 0.10 | 32 | 0.12 | 172 | |
| Site | Z (m) | East | North | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AO | AM | GO | GM | AO | AM | GO | GM | ||
| C1 | 11 | 1.80 | 2.38 | 249 | 252 | 0.12 | 0.22 | 165 | 229 |
| 43 | 1.78 | 2.17 | 248 | 251 | 0.07 | 0.25 | 229 | 264 | |
| 75 | 1.31 | 1.80 | 249 | 249 | 0.14 | 0.25 | 267 | 267 | |
| C2 | 9 | 2.64 | 2.74 | 243 | 245 | 1.06 | 1.44 | 70 | 69 |
| 41 | 2.50 | 2.61 | 243 | 245 | 1.00 | 1.35 | 68 | 67 | |
| 73 | 1.54 | 2.18 | 244 | 244 | 0.56 | 1.09 | 66 | 65 | |
| C3 | 9 | 1.85 | 1.86 | 248 | 253 | 1.86 | 2.03 | 74 | 92 |
| 37 | 1.50 | 1.74 | 248 | 252 | 1.49 | 1.93 | 73 | 91 | |
| 65 | 1.09 | 1.41 | 248 | 252 | 1.01 | 1.49 | 73 | 74 | |
| ADCP (East) | 11 | 3.16 | 3.18 | 236 | 230 | 0.27 | 0.19 | 222 | 168 |
| 22 | 2.97 | 3.06 | 236 | 230 | 0.42 | 0.24 | 225 | 190 | |
| 31 | 2.47 | 2.63 | 236 | 230 | 0.58 | 0.30 | 226 | 205 | |
| Mean Difference | 0.22 (13%) | 4 | 0.27 (66%) | 21 | |||||
| Site | Z (m) | East | North | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AO | AM | GO | GM | AO | AM | GO | GM | ||
| C1 | 11 | 0.63 | 0.90 | 268 | 282 | 0.07 | 0.08 | 221 | 266 |
| 43 | 0.59 | 0.81 | 268 | 282 | 0.07 | 0.09 | 220 | 271 | |
| 75 | 0.41 | 0.67 | 267 | 281 | 0.06 | 0.08 | 236 | 274 | |
| C2 | 9 | 0.90 | 0.99 | 269 | 274 | 0.36 | 0.52 | 94 | 96 |
| 41 | 0.84 | 0.94 | 269 | 273 | 0.35 | 0.49 | 93 | 95 | |
| 73 | 0.51 | 0.79 | 269 | 273 | 0.20 | 0.40 | 93 | 94 | |
| C3 | 9 | 0.64 | 0.67 | 272 | 281 | 0.62 | 0.73 | 99 | 119 |
| 37 | 0.51 | 0.62 | 271 | 281 | 0.46 | 0.70 | 99 | 119 | |
| 65 | 0.40 | 0.51 | 271 | 280 | 0.31 | 0.54 | 97 | 102 | |
| ADCP (East) | 11 | 1.28 | 1.07 | 271 | 262 | 0.15 | 0.07 | 255 | 212 |
| 22 | 1.18 | 1.02 | 272 | 262 | 0.20 | 0.09 | 259 | 227 | |
| 31 | 0.97 | 0.88 | 271 | 262 | 0.25 | 0.11 | 261 | 240 | |
| Mean Difference | 0.16 (26%) | 9 | 0.12 (47%) | 23 | |||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillibrand, P.A.; Walters, R.A.; McIlvenny, J. Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress. Energies 2016, 9, 852. https://doi.org/10.3390/en9100852
Gillibrand PA, Walters RA, McIlvenny J. Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress. Energies. 2016; 9(10):852. https://doi.org/10.3390/en9100852
Chicago/Turabian StyleGillibrand, Philip A., Roy A. Walters, and Jason McIlvenny. 2016. "Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress" Energies 9, no. 10: 852. https://doi.org/10.3390/en9100852
APA StyleGillibrand, P. A., Walters, R. A., & McIlvenny, J. (2016). Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress. Energies, 9(10), 852. https://doi.org/10.3390/en9100852





