Project Management for a Wind Turbine Construction by Applying Fuzzy Multiple Objective Linear Programming Models

Abstract

Meeting the demand of energy is a challenge for many countries these days, and generating electricity from renewable resources has become a main trend for future economic development. The construction of a renewable energy plant is costly and timely; therefore, a good project management model is essential. In this paper, a fuzzy multiple objective linear programming (FMOLP) model is constructed based on program evaluation and review technique (PERT) first. With the consideration of the different degrees of importance of the multiple objectives, a fuzzy multiple weighted-objective linear programming (FMWOLP) model is constructed next. Through each proposed model, a compromise solution can be devised to maximize the total degree of satisfaction while considering multiple objectives. The results can provide references for the management on what activities and how long these activities should be crashed, how much the total project cost should be, and how long the total project duration time should be. Finally, the proposed models are applied to a case study of a wind turbine construction in Taiwan.

1. Introduction

Many countries are facing the challenge of the escalating demand for energy as a result of an increase in world population, depletion of fossil fuels, and intensification of global warming. At the 2015 United Nations Climate Change Conference (COP 21), world leaders gathered in Paris to tackle the issue of carbon dioxide (CO₂) reduction to stop global warming. How to reduce CO₂ emissions in each country without limiting its economic growth, while making life better for citizens, is a difficult task, and the key to CO₂ reduction strategy is the use of renewable energy. Renewable energy can eliminate or reduce harmful emissions and can convert infinite renewable resources into energy [1]. More and more countries have acknowledged that the development of renewable energy sources is essential for the environment and the economy in the long run [2]. The development of a renewable energy plant needs a tremendous amount of time and capital, and the implementation of such a project is a difficult task [3].

Project management techniques, such as program evaluation and review technique (PERT) and critical path method (CPM), have been applied abundantly in various project management fields. However, these techniques have been proclaimed to have some drawbacks [4,5,6]. For example, Wayne and Cottrell [4] listed five drawbacks of PERT, such as the difficulty for project engineers to accurately estimate the optimistic, most likely, and pessimistic duration of an activity; the lengthy duration to perform multiple time estimates; and the consideration of only the critical path, but not near-critical path, in computing project completion time probabilities. In a real-world project management environment, the input data and relevant factors—such as unit operating cost, unit required time, and available resources—are often imprecise because of incomplete and unavailable information over the planning horizon and the imprecision of decision makers’ judgments [5]. Thus, many scholars have tried to improve these techniques, and one of the directions is the incorporation of the fuzzy set theory [5,6].

In this study, two project management models are proposed. The first is a model that applies fuzzy multiple objective linear programming (FMOLP) based on PERT is developed. The model considers multiple objectives—including minimizing total project cost, minimizing total project duration time, and maximizing total crash time—under an uncertain project management environment. In the second model, the weights of the multiple objectives are considered, and a fuzzy multiple weighted-objective linear programming (FMWOLP) model is developed. The rest of this paper is organized as follows. In Section 2, some recent works in project management are reviewed. In Section 3, two project management models are constructed. In Section 4, a case study of a wind turbine construction in Taiwan is examined. Some final remarks are made in the last section.

2. Recent Works in Project Management

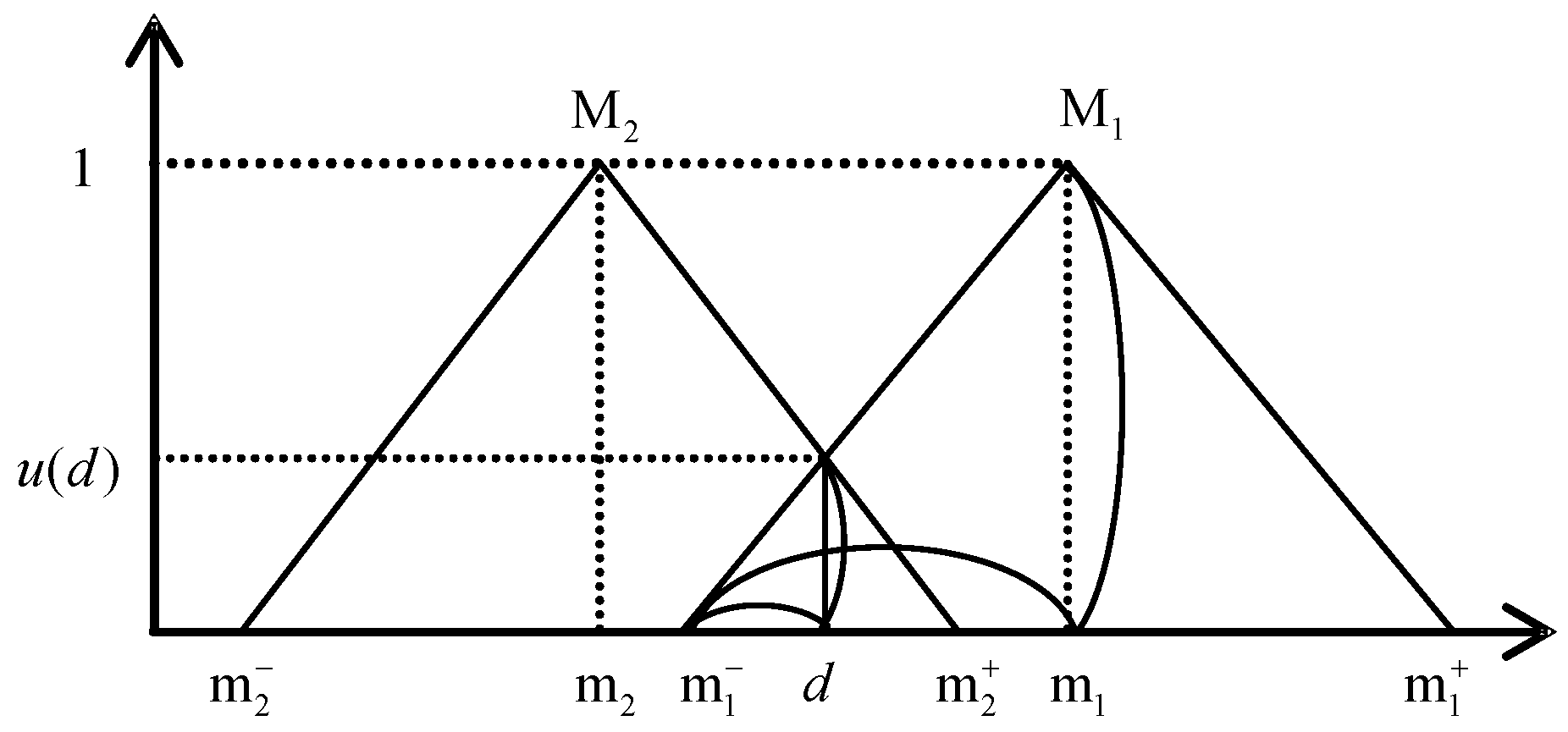
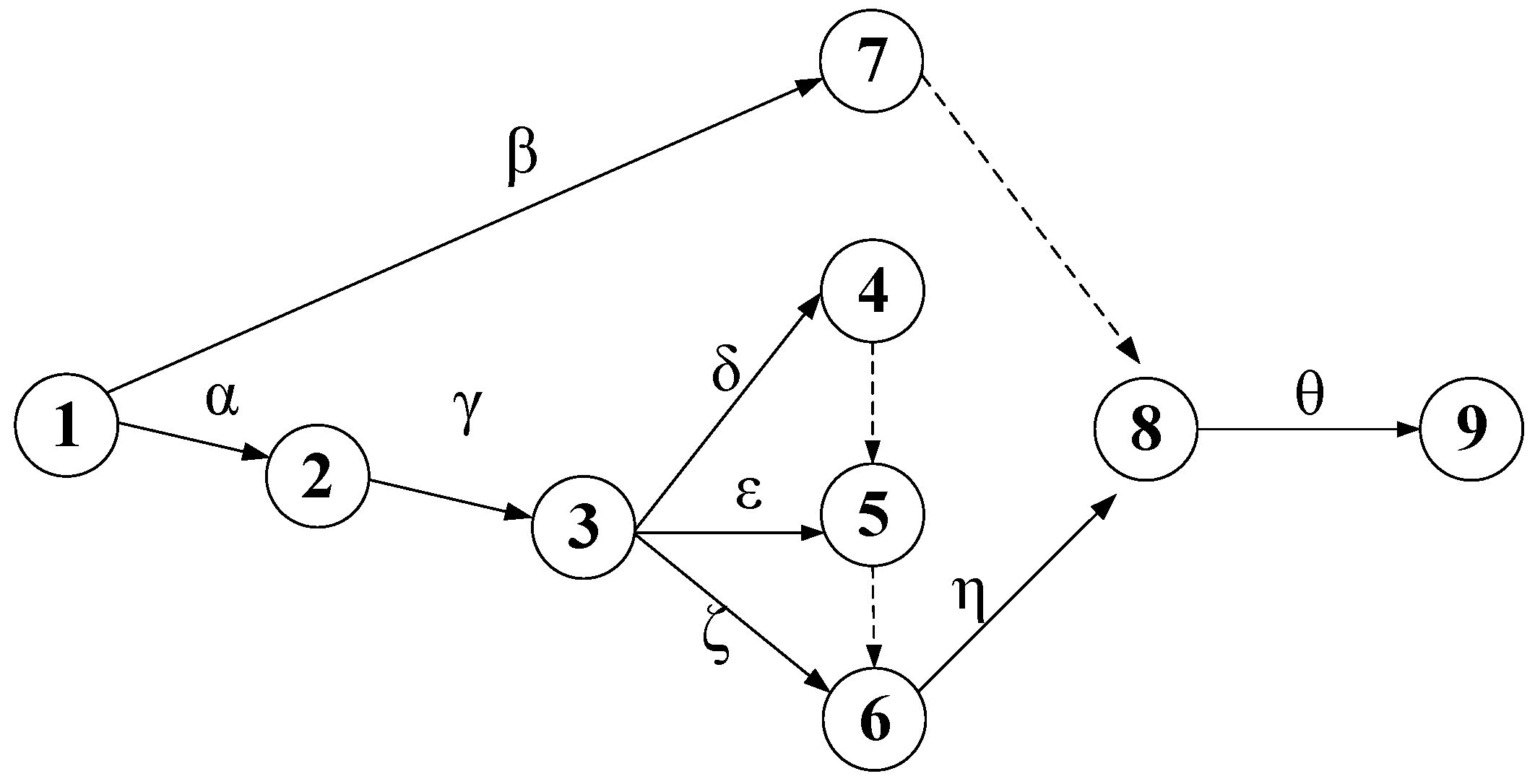
In recent years, project management methods, such as CPM and PERT, have evolved to better tackle real-world problems. Fuzzy set theory is often applied to deal with the incompleteness or unavailability of information needed to approach problems. Chanas and Zieliński [7] performed a critical path analysis in the network when activity times are fuzzy in nature. Two methods were proposed to calculate the path degree of criticality. The first one was for activity times with fuzziness in general form, and the second one was for activity times with fuzzy numbers of the L-L type. Chen and Chang [8] constructed a fuzzy PERT algorithm, where a fuzzy number was used to represent the duration time of each activity. The proposed algorithm could find multiple possible critical paths in a fuzzy project network. Dubois et al. [9] performed an extensive overview of fuzzy set-based approaches to scheduling. They studied fuzzy PERT, which considers incomplete information, and changes the probability distributions of activity durations into possibility distributions. Chen and Huang [10] studied the cycle-time management problem in a supply-chain system and proposed the use of fuzzy PERT to calculate the total fuzzy cycle time of the supply-chain system. Chen and Huang [11] proposed a fuzzy PERT approach to measure the critical degree of each activity and to find the critical path in a project network. Fuzzy activity time of each activity was considered and was represented by a triangular fuzzy number, and the fuzzy set theory and the PERT technique were incorporated to develop the model. Chen and Hsueh [12] presented an approach for solving the CPM problem with fuzzy activity times. The problem was formulated as a linear programming model with fuzzy coefficients of the objective function. Yager’s ranking method was then used to transform the fuzzy CPM problem into a crisp problem, which was subsequently solved by conventional streamlined solution methods. Liang [13] applied the fuzzy set theory and proposed a possibilistic linear programming (PLP) approach to solve multiple objective project management decision problems. The multiple imprecise goals were assumed to have triangular possibility distribution, and the approach was claimed to minimize the total project costs and the completion time simultaneously. Liang [14] further solved the fuzzy multi-objective project management problem using a two-phase fuzzy goal programming method. Phase I solved the fuzzy multi-objective linear programming problem by applying fuzzy decision-making concepts proposed by previous scholars. Phase II improved the solution by using the satisfaction degree from Phase I as a constraint, and used a compensatory weighted average operator to obtain an overall satisfaction degree. Yakhchali and Ghodsypour [15] presented a polynomial algorithm to compute latest starting times of activities in interval-valued networks. The algorithm considered fuzzy durations and attempted to minimize time lags. Liang [16] further solved the project management problems with multiple goals in uncertain environments by proposing a two-phase fuzzy goal programming method. The first phase used the minimum operator method, and the second phase used the weighted average operator method. The method aimed to minimize total project costs, total completion time, and total crashing costs, simultaneously. Chen and Tsai [17] performed a time–cost tradeoff analysis of project networks under fuzzy environments when the duration times and costs were uncertain. The proposed approach formulated a pair of parametric mathematical programs to find the membership function of the fuzzy minimum total crash cost. Liang et al. [5] proposed a fuzzy mathematical programming approach for solving the imprecise project management decision problems. Triangular fuzzy number was used to represent the imprecise goal and costs, and the proposed model aimed to minimize the total project costs. Maravas and Pantouvakis [18] proposed a project cash flow analysis approach when the activity durations and costs were uncertain. Chrysafis and Papadopoulos [6] proposed an approach for estimating some important factors, such as activity times, float, criticality degree for each activity and for each path, project duration, and probability for project completion time. The approach was based on fuzzy statistics and fuzzy probabilities and could be used when the statistical data for the project activity duration existed. Jeang [19] first applied response surface methodology (RSM), a statistical analysis method, to solve the time–cost tradeoff problem for project management with a single objective. A multi-objective optimization in project scheduling was then presented to consider multiple objectives—including project budget, completion time, total cost probability, and completion time probability—and compromise programming was used to solve the problem. Creemers et al. [20] considered the risk of activity failure and the possible pursuit of alternative technologies in the project scheduling problem. A generic model was proposed first to incorporate stochastic durations, non-zero failure probabilities, and modular completion subject to precedence constraints. A dynamic-programming model was constructed next to devise an execution policy to maximize the expected net present value of the project. Yaghoubi et al. [21] studied the resource allocation in multiclass dynamic PERT networks with finite capacity as Markov processes and proposed a multi-objective model. A simulated annealing (SA) algorithm, which used the goal attainment formulation, was applied to solve the multi-objective problem.

3. Proposed Models

3.1. Fuzzy Multiple Objective Linear Programming (FMOLP)

For the project management problem, a fuzzy multiple objective linear programming (FMOLP) model is proposed. The steps are as follows:

Step 1: Construct a mathematical model. By balancing the time and cost, a compromise project implementation plan is found. Three objectives are considered: least total project cost, shortest total project duration time, and longest total crash time.

(1)

Objective function 1: Minimize the total project cost TC.

$$\mathrm{Min}TC={\displaystyle \sum _i{\displaystyle \sum _j{K}_{D_{ij}}}}+{\displaystyle \sum _i{\displaystyle \sum _j{Y}_{ij}{s}_{ij}+l\times \mathrm{Max}\left\{0,\left(E_N-TP\right)\right\}}}$$

(1)

where ${\displaystyle \sum _i{\displaystyle \sum _j{K}_{D_{ij}}}}$ is the direct cost, including operating personnel cost, equipment cost, outsourcing cost, and overtime cost; ${\displaystyle \sum _i{\displaystyle \sum _j{Y}_{ij}{s}_{ij}}}$ is the crashing cost; and $l\times \mathrm{Max}\left\{0,\left(E_N-TP\right)\right\}$ is the penalty cost, including supervision cost, contractual penalties, administration cost, and interests.

(2)

Objective function 2: Minimize the total project duration time TP.

$$\mathrm{Min}TP=E_N-E_1$$

(2)

(3)

Objective function 3: Maximize the total crash time TR.

$$\mathrm{Max}TR={\displaystyle \sum _i{\displaystyle \sum _j{Y}_{ij}}}$$

(3)

The constraints are:

$$E_i+T_{ij}-E_j\le 0,foralli,j$$

(4)

$$T_{ij}=D_{ij}-Y_{ij},foralli,j$$

(5)

$$Y_{ij}\le D_{ij}-d_{ij},foralli,j$$

(6)

$$E_N\le \zeta$$

(7)

and all variables are nonnegative.

Equation (4) is a constraint for the precedence of activities in the network. Equations (5) and (6) are the constraints for the crash time in each activity. Equation (7) ensures that the last activity is completed before or on the required project completion time, F.

Step 2: Calculate the positive ideal solution (PIS) and the negative ideal solution (NIS) of the three objective functions.

$${TC}^{PIS}=\mathrm{Min}TC,{TC}^{NIS}=\mathrm{Max}TC$$

(8)

$${TP}^{PIS}=\begin{array}{cc}\mathrm{Min}& TP\end{array},T{TP}^{NIS}=\begin{array}{cc}\mathrm{Max}& TP\end{array}$$

(9)

$${TR}^{PIS}=\begin{array}{cc}\mathrm{Max}& TR\end{array},T{TR}^{NIS}=\begin{array}{cc}\mathrm{Min}& TR\end{array}$$

(10)

Based on the values of the PIS and the NIS, the membership function for each of the three objective functions is established as follows:

$${\lambda }_{TC}=\{\begin{array}{cc}1,& TC\le {TC}^{PIS}\\ \frac{{TC}^{NIS}-TC}{{TC}^{NIS}-T{C}^{PIS}},& T{C}^{PIS}<TC\le T{C}^{NIS}\\ 0,& TC>T{C}^{NIS}\end{array}$$

(11)

$${\lambda }_{TP}=\{\begin{array}{cc}1,& TP\le T{P}^{PIS}\\ \frac{T{P}^{NIS}-TP}{T{P}^{NIS}-T{P}^{PIS}},& T{P}^{PIS}<TP\le T{P}^{NIS}\\ 0,& TP>T{P}^{NIS}\end{array}$$

(12)

$${\lambda }_{TR}=\{\begin{array}{cc}1,& TR\ge T{R}^{PIS}\\ \frac{TR-T{R}^{PIS}}{T{R}^{NIS}-T{R}^{PIS}}-,& T{R}^{NIS}\le TR<T{R}^{PIS}\\ 0,& TR<T{R}^{NIS}\end{array}$$

(13)

Step 3: After the membership function values are obtained, apply the fuzzy programming method proposed by Zimmermann [22] to add auxiliary variable $\lambda$, which can consider the three objective functions simultaneously. The original fuzzy multiple objective linear programming problem can be transformed into a crisp single-goal linear programming problem. By maximizing $\lambda$, a compromise solution can be obtained.

$$\mathrm{Max}\lambda$$

(14)

$$\mathrm{s}.\mathrm{t}.\lambda \le {\lambda }_{TC}$$

(15)

$$\lambda \le {\lambda }_{TP}$$

(16)

$$\lambda \le {\lambda }_{TR}$$

(17)

Constraints (4)–(7) and all variables are nonnegative.

Step 4: Analyze the results. After solving the model, a compromise solution can be obtained. The results include the total project cost, the total project duration time, and the total crash time, and the solution can best satisfy the three objectives in the model.

3.2. Fuzzy Multiple Weighted-Objective Linear Programming (FMWOLP)

The management may consider that the importance of each objective is different. That is, some objectives are more important than others. As a result, the weights of the objectives should be determined by the management first. In this section, a fuzzy multiple weighted-objective linear programming (FMWOLP) model for project management is constructed. The relative weights of the multiple objectives are calculated by the fuzzy analytic hierarchy process (FAHP) and extent analysis method (EAM) first [23,24,25]. The FMOLP can be constructed based on the obtained weights. The procedure of the FMWOLP model is as follows:

Step 1: Form a committee for the wind turbine construction project to determine the importance of the objectives.

Step 2: Prepare a questionnaire to compare objectives pairwisely in their contribution toward achieving the maximum satisfaction of the wind turbine construction project. The pairwise comparison value between every two objectives is represented by a fuzzy number, $\tilde{1},\tilde{3},\tilde{5},\tilde{7},\tilde{9}$, as shown in

Table 1. Characteristic function of the fuzzy numbers [26].

Fuzzy Number	Characteristic Function
$\tilde{1}$	(1, 1, 3)
$\tilde{x}$	(x − 2, x, x + 2) for x = 3, 5, 7
$\tilde{9}$	(7, 9, 9)

. The opinions of each committee member are collected, and a fuzzy pairwise comparison matrix ${\tilde{B}}^f$ for expert f is as follows:

$${\tilde{B}}^f=\left[{\tilde{b}}_{pq}^f\right]==\left[\begin{array}{cccc}{\tilde{b}}_{11}^f& {\tilde{b}}_{12}^f& \cdots & {\tilde{b}}_{1G}^f\\ {\tilde{b}}_{21}^f& {\tilde{b}}_{22}^f& \cdots & {\tilde{b}}_{2G}^f\\ ⋮& ⋮& \cdots & ⋮\\ {\tilde{b}}_{G1}^f& {\tilde{b}}_{G2}^f& \cdots & {\tilde{b}}_{GG}^f\end{array}\right]=\left[\begin{array}{cccc}1& {\tilde{b}}_{12}^f& \cdots & {\tilde{b}}_{1G}^f\\ {\tilde{b}}_{21}^f& 1& \cdots & {\tilde{b}}_{2G}^f\\ ⋮& ⋮& 1& ⋮\\ {\tilde{b}}_{G1}^f& {\tilde{b}}_{G2}^f& \cdots & 1\end{array}\right] ,$$

(18)

$$\mathrm{for}p=1,2,\mathrm{...},G,q=1,2,\mathrm{...},G\mathrm{and}f=1,2,\mathrm{...},F$$

where ${\tilde{b}}_{pq}^f=\left(x^{-},x,x^{+}\right)$ and $b_{pq}^f\cdot b_{pq}^f\approx 1$.

Step 3. Combine fuzzy pairwise comparison matrices of committee members into an integrated fuzzy pairwise comparison matrix. Check the consistency of the integrated fuzzy pairwise comparison matrix.

$$\tilde{C}=\left[{\tilde{c}}_{pq}\right]=\left[\begin{array}{cccc}{\tilde{c}}_{11}& {\tilde{c}}_{12}& \cdots & {\tilde{c}}_{1G}\\ {\tilde{c}}_{21}& {\tilde{c}}_{22}& \cdots & {\tilde{c}}_{2G}\\ ⋮& ⋮& \cdots & ⋮\\ {\tilde{c}}_{G1}& {\tilde{c}}_{G2}& \cdots & {\tilde{c}}_{GG}\end{array}\right]=\left[\begin{array}{cccc}1& {\tilde{c}}_{12}& \cdots & {\tilde{c}}_{1G}\\ {\tilde{c}}_{21}& 1& \cdots & {\tilde{c}}_{2G}\\ ⋮& ⋮& 1& ⋮\\ {\tilde{c}}_{G1}& {\tilde{c}}_{G2}& \cdots & 1\end{array}\right],forp,q=1,2,\mathrm{...},G$$

(19)

where $\tilde{c}pq=\left({\tilde{b}}_{pq}^1\oplus \cdots \oplus {\tilde{b}}_{pq}^F\right)/F=\left(m_{pq}^{-},m_{pq},m_{pq}^{+}\right)$ and $cpq\cdot cqp\approx 1$, $m_{pq}^{-}$: arithmetic average of the smallest assigned value among the members, $m_{pq}^{+}$: arithmetic average of the largest assigned value among the members, and $m_{pq}$: arithmetic average of the middle values among the members.

Based on Buckley [27] and Csutora and Buckley [28], let $C=(cpq)$ be a positive reciprocal matrix, and $\tilde{C}=(\tilde{c}pq)$ be a fuzzy positive reciprocal matrix. The consistency test is performed based on Saaty [29]. If $C$ is consistent, then $\tilde{C}$ is also consistent. If $\tilde{C}$ is not consistent, the questionnaire must be modified by the members, and the consistency test must be carried out again.

Step 4. Calculate the importance weights for the multiple objectives using the EAM [23]. By Equations (20)–(27), the weight vector, w_g’, of the objectives are calculated. With two triangular fuzzy numbers, as shown in Figure 1, the degree of possibility is $V\left(M_1\ge M_2\right)=1$ when $m_1^{-}\ge m_2^{-}$, $m_1\ge m_2$, and $m_1^{+}\ge m_2^{+}$. Otherwise, the ordinate of the highest intersection point is:

$$V\left(M_2\ge M_1\right)=hgt\left(M_1\cap M_2\right)=u\left(d\right)=\frac{m_1^{-}-m_2^{+}}{(m_2-m_2^{+})-(m_1-m_1^{-})}$$

(20)

The value of fuzzy synthetic extent with respect to objective p is:

$$F_p={\displaystyle \sum _{q=1}^G{M}_{pq}}\otimes {\left[{\displaystyle \sum _{p=1}^G{\displaystyle \sum _{q=1}^G{M}_{pq}}}\right]}^{-1},p=1,2,\mathrm{...},G$$

(21)

$${\displaystyle \sum _{q=1}^G{M}_{pq}}=\left({\displaystyle \sum _{q=1}^G{m_{pq}}^{-}\begin{array}{c},\end{array}}{\displaystyle \sum _{q=1}^G{m}_{pq}\begin{array}{c},\end{array}}{\displaystyle \sum _{q=1}^G{m_{pq}}^{+}}\right),p=1,2,\mathrm{...},G$$

(22)

$${\left[{\displaystyle \sum _{p=1}^G{\displaystyle \sum _{q=1}^G{M}_{pq}}}\right]}^{-1}=\left(\begin{array}{ccccc}1/{\displaystyle \sum _{p=1}^G{\displaystyle \sum _{q=1}^G{m}_{pq}^{+}}}& ,& 1/{\displaystyle \sum _{p=1}^G{\displaystyle \sum _{q=1}^G{m}_{pq}}}& ,& 1/{\displaystyle \sum _{p=1}^G{\displaystyle \sum _{q=1}^G{m}_{pq}^{-}}}\end{array}\right)$$

(23)

A convex fuzzy number is:

$$V\left(F\ge F_1,F_2,\mathrm{...},F_G\right)=\min V\left(F\ge F_q\right),q=1,2,\mathrm{...},G$$

(24)

$$d\left(F_p\right)=\min V\left(F_p\ge F_q\right)=w_p^{\text{'}},p=1,2,\mathrm{...},G,q=1,2,\mathrm{...},G$$

(25)

The weights of the objectives are:

$$W^{\text{'}}={\left(w_1^{\text{'}},w_2^{\text{'}},\mathrm{...},w_G^{\text{'}}\right)}^T$$

(26)

After normalization, the weights of the objectives are:

$$W={\left(w_1,w_2,\mathrm{...},w_G\right)}^T$$

(27)

Step 5. Formulate the FMWOLP model for the project management of wind turbine construction. The overall objective is to maximize the satisfaction of the model, and the degrees of satisfaction for the objectives are ${\lambda }_1$,${\lambda }_2$,…${\lambda }_g$,…${\lambda }_G$. The weights of the objectives are W, obtained from Step 4. The basic model is as follows:

$$Max\lambda =w_1\times {\lambda }_1+w_2\times {\lambda }_2+\mathrm{....}+w_g\times {\lambda }_g+\mathrm{....}+w_G\times {\lambda }_G$$

(28)

$$\mathrm{subject}\mathrm{to}{\lambda }_g\le {\mu }_g(x),forallg$$

(29)

$${\lambda }_g\in \left[0,1\right],forallg$$

(30)

$$\mathrm{Additional}\mathrm{constraints}$$

where ${\lambda }_g$, ${\mu }_g(x)$, and $w_g$ represent the degree of satisfaction, the membership function, and the weight for objective g.

With the objectives of minimizing the total project cost, minimizing the total project duration time, and maximizing the total crash time, the wind turbine construction problem is formulated as follows:

$$Max\lambda =w_{TC}\times {\lambda }_{TC}+w_{TP}\times {\lambda }_{TP}+w_{TR}\times {\lambda }_{TR}$$

(31)

subject to Constraints (4)–(7) and Constraints (15)–(17) and all variables are nonnegative.

where $w_{TC}$, $w_{TP}$, and $w_{TR}$ are the normalized importance weights for the total project cost, the total project duration time, and the total crash time, respectively; ${\lambda }_{TC}$, ${\lambda }_{TP}$, and ${\lambda }_{TR}$ are the degrees of satisfaction for the total project cost, the total project duration time, and the total crash time, respectively.

4. Case Study

Because of continuous industrial development, depletion of fossil fuels, and emerging environmental consciousness, Taiwan government has acknowledged the increasing need for energy independence. Generating electricity from alternative resources has become a main trend for future economic development. Alternative energy sources (including nuclear, hydraulic, wind, wave, and solar energy) are options for meeting energy demands and maintaining a healthy environment in the future [30]. Although nuclear energy may have provided good opportunities and less pollution emissions, many people are against the operation of nuclear power plants in Taiwan after the Fukushima accident in March 2011. In addition, the government has passed relevant acts and regulations to promote renewable energy. At the same time, the transition to renewable-based energy systems continues as the costs of power systems, such as solar and wind power systems, have dropped substantially in the past 30 years. The government hopes to raise renewable energy generation capacity from 8% in 2010 to 16% by 2025 [31]. Thus, it is expected that generating electricity from renewable energy in Taiwan will become the main trend in upcoming years.

In this section, the construction project of a wind turbine is used as an example to examine the practicality of the proposed models. The activities of the project are shown in

Table 2. Activities for wind turbine project.

Activity Code	Activity	Description
α	Foundation	The construction of a wind turbine foundation using concrete and reinforcing steel.
β	Transformer and cable network	The setup of equipment external of the wind turbine, such as step-up transformer, grounding transformer and substation. Other activities include the digging of cable trenches and the layout of cables.
γ	Control equipment	The setup of cabinets and equipment for control, communication and power connection at the basement of the tower.
δ	Tower	The installation of the tower sections onto the foundation. Several individual tower sections need to be connected on site.
ε	Nacelle	The installation of the Nacelle, which comprises generating components such as a generator, gearbox, shafts, and brakes to the tower.
ζ	Rotor blade set	The fixing of rotor blades to a hub on the ground.
η	Wind turbine completion	The installation of the rotor blade set to the Nacelle to complete the wind turbine.
θ	Trial operation	The connection of the generator system with the wind turbine and the final test of the wind turbine operation.

. The basic construction data for wind turbine are shown in

Table 3. Basic construction data for a wind turbine.

Activity Code	Activity	Duration Time (Day)	Activity Cost (,000)	Crashing Cost per Day (,000)	Possible Crashed Time (Day)
α	Foundation	85	$2122.4	$4.85	25
β	Transformer and cable network	43	$1857.4	$8.17	13
γ	Control equipment	39	$944.4	$5.15	11
δ	Tower	31	$2448.0	$14.84	11
ε	Nacelle	57	$2559.2	$8.61	17
ζ	Rotor blade set	83	$2188.8	$5.44	23
η	Wind turbine completion	8	$2407.2	$45.85	3
θ	Trial operation	31	$400.0	$2.43	11

. Under a normal condition, the completion time is 246 days. The network for the project is as depicted in Figure 2.

4.1. Fuzzy Multiple Objective Linear Programming

The procedure for the fuzzy multiple objective linear programming model in the case study is as follows:

Step 1. Construct a mathematical model. Based on Equations (1)–(7), the original multiple objective linear programming model for the project implementation plan is constructed.

$$\begin{gathered} \mathrm{Min}TC=(2122.4+4.85Y_{12})+(1857.4+8.17Y_{17})+(944.4+5.15Y_{23}) \\ +(2448+14.84Y_{34})+(2559.2+8.61Y_{35})+(2188.8+5.44Y_{36}) \\ +(2407.2+45.85Y_{68})+(400+2.43Y_{89})+2000\times \mathrm{Max}\left\{0,\left(E_9-246\right)\right\} \end{gathered}$$

$$\mathrm{Min}TP=E_9-E_1$$

$$\mathrm{Max}TR=Y_{12}+Y_{17}+Y_{23}+Y_{34}+Y_{35}+Y_{36}+Y_{68}+Y_{89}$$

Subject to

$$E_1+t_{12}-E_2=0$$

$$E_1+t_{17}-E_7=0$$

$$E_2+t_{23}-E_3\le 0$$

$$E_3+t_{34}-E_4\le 0$$

$$E_3+t_{35}-E_5\le 0$$

$$E_3+t_{36}-E_6\le 0$$

$$E_6+t_{68}-E_8\le 0$$

$$E_8+t_{89}-E_9\le 0$$

$$T_{12}=85-Y_{12}$$

$$T_{17}=43-Y_{17}$$

$$T_{23}=39-Y_{23}$$

$$T_{34}=31-Y_{34}$$

$$T_{35}=57-Y_{35}$$

$$T_{36}=83-Y_{36}$$

$$T_{68}=8-Y_{68}$$

$$T_{89}=31-Y_{89}$$

$$Y_{12}\le 25$$

$$Y_{17}\le 13$$

$$Y_{23}\le 11$$

$$Y_{34}\le 11$$

$$Y_{35}\le 17$$

$$Y_{36}\le 23$$

$$Y_{68}\le 3$$

$$Y_{89}\le 11$$

$$E_9\le 246$$

and all variables are nonnegative.

Step 2: Calculate the PIS and the NIS of the three objectives for the problem by applying Equations (8)–(10). The results are shown in

Table 4. The positive ideal solution (PIS) and negative ideal solution (NIS) under each objective function. TC: total cost for the project; TP: total duration time for the project; TR: total crash time for the project.

Objective Function	Min TC	Min TP	Max TR	($\mathit{P}\mathit{I}\mathit{S}$,$\mathit{N}\mathit{I}\mathit{S}$)
TC	14,927.4	15,394.7	15,810.52	(14,927.4, 15,810.52)
TP	246	173	173.25	(173, 246)
TR	0	73	114	(114, 0)

. For example, by minimizing TC, we can obtain TP = 246 and TR = 0, thus TC = 14,927.4. The same procedure is carried out for minimizing TP and maximizing TR. Among the values of TC (with smaller being better) in Table 4, the PIS is 14,927.4, and the NIS is 15,810.52.

(1)

Based on the values of the PIS and the NIS, the membership function for each of the three objective functions is established using Equations (11)–(13). They are as follows.

$${\lambda }_{TC}=\{\begin{array}{cc}1,& TC\le 14,927.4\\ \frac{\mathrm{15,810.52}-TC}{\mathrm{15,810.52}-\mathrm{14,927.4}},& 14,927.4<TC\le 15,810.52\\ 0,& TC>15,810.52\end{array}$$

$${\lambda }_{TP}=\{\begin{array}{cc}1,& TP\le 173\\ \frac{246-TP}{246-173},& 173<TP\le 246\\ 0,& TP>246\end{array}$$

$${\lambda }_{TR}=\{\begin{array}{cc}1,& TR\ge 114\\ \frac{TR-0}{114-0},& 0\le TR<114\\ 0,& TR<0\end{array}$$

Step 3: With the membership function values, the auxiliary variable $\lambda$ is added to consider the three objective functions simultaneously. By applying Equations (15)–(17), the original fuzzy multiple objective linear programming problem is transformed into a crisp, single-goal linear programming problem. A compromise solution is calculated by maximizing $\lambda$ as follows:

$$Max\lambda$$

Subject to

$$\lambda \le \frac{\mathrm{15,810.52}-TC}{\mathrm{15,810.52}-\mathrm{14,927.4}}$$

$$\lambda \le \frac{246-TP}{246-173}$$

$$\lambda \le \frac{TR-0}{114-0}$$

$$\begin{gathered} TC=(2122.4+4.85Y_{12})+(1857.4+8.17Y_{17})+(944.4+5.15Y_{23}) \\ +(2448+14.84Y_{34})+(2559.2+8.61Y_{35})+(2188.8+5.44Y_{36}) \\ +(2407.2+45.85Y_{68})+(400+2.43Y_{89})+2000\times \mathrm{Max}\left\{0,\left(E_9-246\right)\right\} \end{gathered}$$

$$TP=E_9-E_1$$

$$TR=Y_{12}+Y_{17}+Y_{23}+Y_{34}+Y_{35}+Y_{36}+Y_{68}+Y_{89}$$

$$E_1+t_{12}-E_2=0$$

$$E_1+t_{17}-E_7=0$$

$$E_2+t_{23}-E_3\le 0$$

$$E_3+t_{34}-E_4\le 0$$

$$E_3+t_{35}-E_5\le 0$$

$$E_3+t_{36}-E_6\le 0$$

$$E_6+t_{68}-E_8\le 0$$

$$E_8+t_{89}-E_9\le 0$$

$$T_{12}=85-Y_{12}$$

$$T_{17}=43-Y_{17}$$

$$T_{23}=39-Y_{23}$$

$$T_{34}=31-Y_{34}$$

$$T_{35}=57-Y_{35}$$

$$T_{36}=83-Y_{36}$$

$$T_{68}=8-Y_{68}$$

$$T_{89}=31-Y_{89}$$

$$Y_{12}\le 25$$

$$Y_{17}\le 13$$

$$Y_{23}\le 11$$

$$Y_{34}\le 11$$

$$Y_{35}\le 17$$

$$Y_{36}\le 23$$

$$Y_{68}\le 3$$

$$Y_{89}\le 11$$

$$E_9\le 246$$

and all variables are nonnegative.

Step 4: Analyze the results. The results show that ${\lambda }_{TC}$ = 0.6174, ${\lambda }_{TP}$ = 0.9589, and ${\lambda }_{TR}$ = 0.6228. Other relevant results are shown in

Table 5. Results of the fuzzy multiple objective linear programming (FMOLP).

Activity Code	Duration Time (Day)	Crashing Cost (,000)	Crash Time (Day)
α	60	121.25	25
β	42	8.17	1
γ	28	56.65	11
δ	31
ε	57
ζ	60	125.12	23
η	8
θ	20	26.73	11

. Activities α, β, γ, ζ, and θ should be crashed. For example, activities α should be crashed. The crashing cost for the activity is $121,250, and the crash time is 25 days. Thus, the duration time for the activity will reduce from the original 85 days, as shown in Table 3, to 60 days. The compromise solution shows that the total project cost (TC) is $15,265.32 thousand, the total project duration time (TP) is 176 days, and the total crash time (TR) is 71 days. The overall satisfaction degree of the problem is 0.6174.

4.2. Fuzzy Multiple Weighted-Objective Linear Programming (FMWOLP)

The same case is performed using the proposed FMWOLP. The major difference in the two models is that the weights of the objectives are considered in the FMWOLP. The committee consists of five members, and they are invited to complete the pairwise comparison questionnaire. Based on the questionnaire results, a fuzzy pairwise comparison matrix is prepared for each member. For example, the fuzzy matrix for the first member is:

$${\tilde{B}}^1=\left[\begin{array}{ccc}(1,1,1)& (3,5,7)& (1,3,5)\\ (1/7,1/5,1/3)& (1,1,1)& (1,1,3)\\ (1/5,1/3,1)& (1/3,1,1)& (1,1,1)\end{array}\right]$$

An integrated fuzzy pairwise comparison matrix is prepared the next by combining the fuzzy pairwise comparison matrices of the five members. It is:

$$\tilde{C}=\left[\begin{array}{ccc}(1,1,1)& (3.32,5.35,7.36)& (1.55,3.68,5.72)\\ ({7.36}^{-1},{5.35}^{-1},{3.32}^{-1})& (1,1,1)& (1.25,1.72,3.94)\\ ({5.72}^{-1},{3.68}^{-1},{1.55}^{-1})& ({3.94}^{-1},{1.72}^{-1},{1.25}^{-1})& (1,1,1)\end{array}\right]$$

After the consistency test is performed, the importance weights for the multiple objectives are calculated by the EAM. The weights for minimizing the total project cost, minimizing the total project duration time, and maximizing the total crash time are:

$$W={\left(0.7183,0.2586,0.0231\right)}^T$$

By applying Equation (31), the FMWOLP model for the project management of the wind turbine construction is formulated as follows:

$$\mathrm{Max}\lambda =0.7183{\lambda }_{TC}+0.2586{\lambda }_{TP}+0.0231{\lambda }_{TR}$$

subject to Constraints (4)–(7) and Constraints (15)–(17). and all variables are nonnegative.

The results show that ${\lambda }_{TC}$ = 0.9697, ${\lambda }_{TP}$ = 0.1507, and ${\lambda }_{TR}$ = 0.0965, and some relevant results are shown in

Table 6. Results of the fuzzy multiple weighted-objective linear programming (FMWOLP).

Activity Code	Duration Time (Day)	Crashing Cost (,000)	Crash Time (Day)
α	85
β	43
γ	39
δ	31
ε	57
ζ	83
η	8
θ	20	26.73	11

. Under the FMWOLP, only activity θ should be crashed. The crashing cost for the activity is $26,730, and the crash time is 11 days. Thus, the duration time of activity θ will reduce from the original 31 days, as shown in Table 3, to 20 days. The compromise solution shows that the total project cost (TC) is $14,954.13 thousand, the total project duration time (TP) is 235 days, and the total crash time (TR) is 11 days. The overall satisfaction degree of the problem is 0.7378.

The results from the FMOLP and from the FMWOLP are rather different. This is due to the fact that the FMWOLP incorporates different weights to the multiple objectives. The committee members in this case study put a much higher importance on one objective (minimizing the total project cost) than on the other two objectives. Therefore, only activity θ, which has the lowest crashing cost per day, is crashed. If the committee members stress different degrees of importance on the objectives, then the project implementation plan may be different.

5. Conclusions

Due to world population growth and industrial development, fossil fuels are being increasingly consumed. As a result, global warming is becoming an inevitable problem. Generating electricity from renewable resources is a popular trend for future economic development. With a tremendous investment in capital, time, and effort, the selection of the most appropriate type of renewable energy and the development of a renewable energy plant are very complicated tasks.

This research integrates the program evaluation and review technique (PERT) and the fuzzy multiple objective linear programming to find the critical path when constructing a power plant under an uncertain environment. In the first model, a fuzzy multiple objective linear programming (FMOLP) model is proposed. Multiple objectives, including minimizing the total project cost, minimizing the total project duration time, and maximizing the total crash time, are considered. In the second model, the importance of different objectives is considered, and a fuzzy multiple weighted-objective linear programming (FMWOLP) model is constructed. By maximizing the total degree of satisfaction through optimizing the three objectives, we can obtain a compromise solution from each proposed model. When the importance of each objective is different, the FMWOLP model is suggested to be used so that the weights of the objectives can be considered in devising the project implementation plan. A case study of a wind turbine construction in Taiwan shows that the proposed models can help managers in implementing the project efficiently and effectively.