Modeling and Simulation of the Thermal Runaway Behavior of Cylindrical Li-Ion Cells—Computing of Critical Parameters
Abstract
:1. Introduction
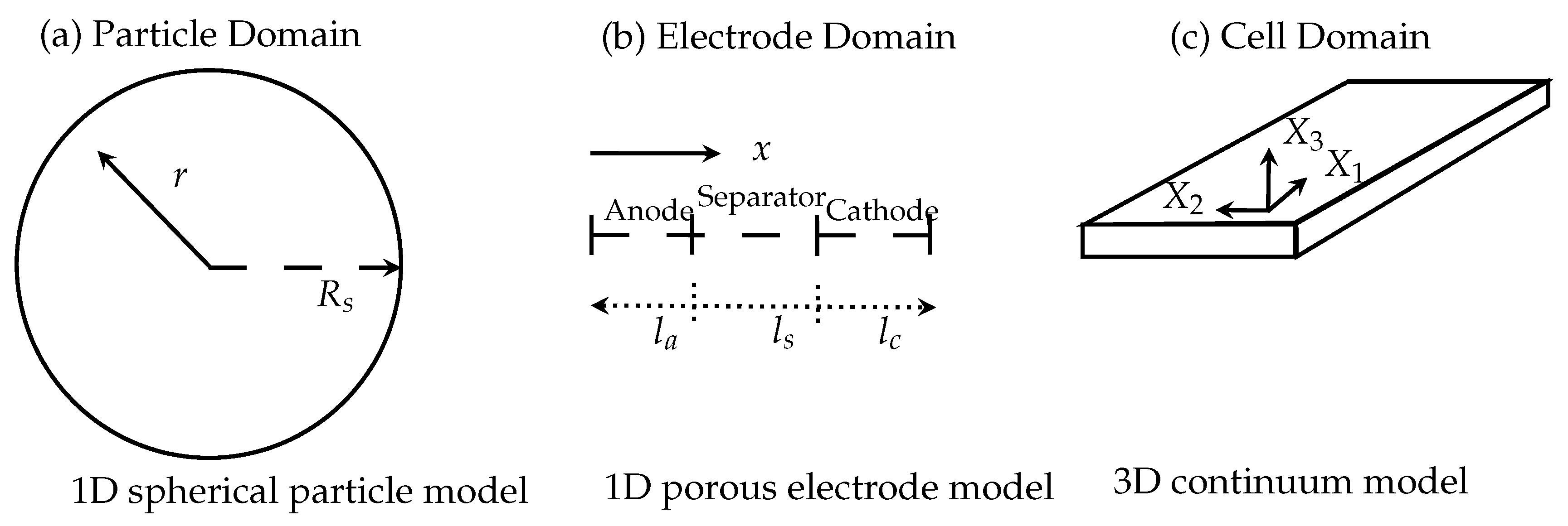
2. Modeling the Thermal Behavior of a Lithium-Ion Battery
- (1)
- In a certain (infinitesimal) time interval the cell is under constant charge, discharge or in relaxation.
- (2)
- The cell geometry resp. volume is constant, i.e., elastic processes and gas generation inside the cell are not considered.
- (3)
- Without loss of generality (W.l.o.g.) the emissivity , heat transfer coefficient h, the density , heat capacity and thermal conductivity are assumed to be constant in space and time.
2.1. The Energy Conservation
2.2. Identifying Heat Sources From Exothermic Reaction Kinetics Inside the Lithium-Ion Batteries
- (1)
- SEI decomposition reaction: At , in an exothermic reaction, the solid-electrolyte interface (SEI) decomposes.
- (2)
- Negative solvent reaction: At an exothermic reaction between the intercalated Li-ions and the electrolyte starts (NE).
- (3)
- Positive solvent reaction: For an exothermic reaction between the positive material and the electrolyte takes place under the evolution of oxygen inside the cell (PE).
- (4)
- Electrolyte decomposition: In a final exothermic reaction the electrolyte decomposes at (ELE).
2.3. Simplification of Combustion Model: The Constant Fuel Model
2.4. The Electrochemical Heat Source of a LIB and the Electrochemical Model
3. Simulations
3.1. Model Comparison
- (1)
- : In this case the LIB is unable to dissipate any generated heat to the environment. Therefore, a thermal runaway will always occur after a sufficiently large time.
- (2)
- h positive and a thermal runaway occurs after a sufficiently large time: In this case, more heat is generated inside the LIB, as can be dissipated to the environment.
- (3)
- h positive and no thermal runaway occurs after a sufficiently large time: In this case the generated heat can be dissipated completely to the environment.
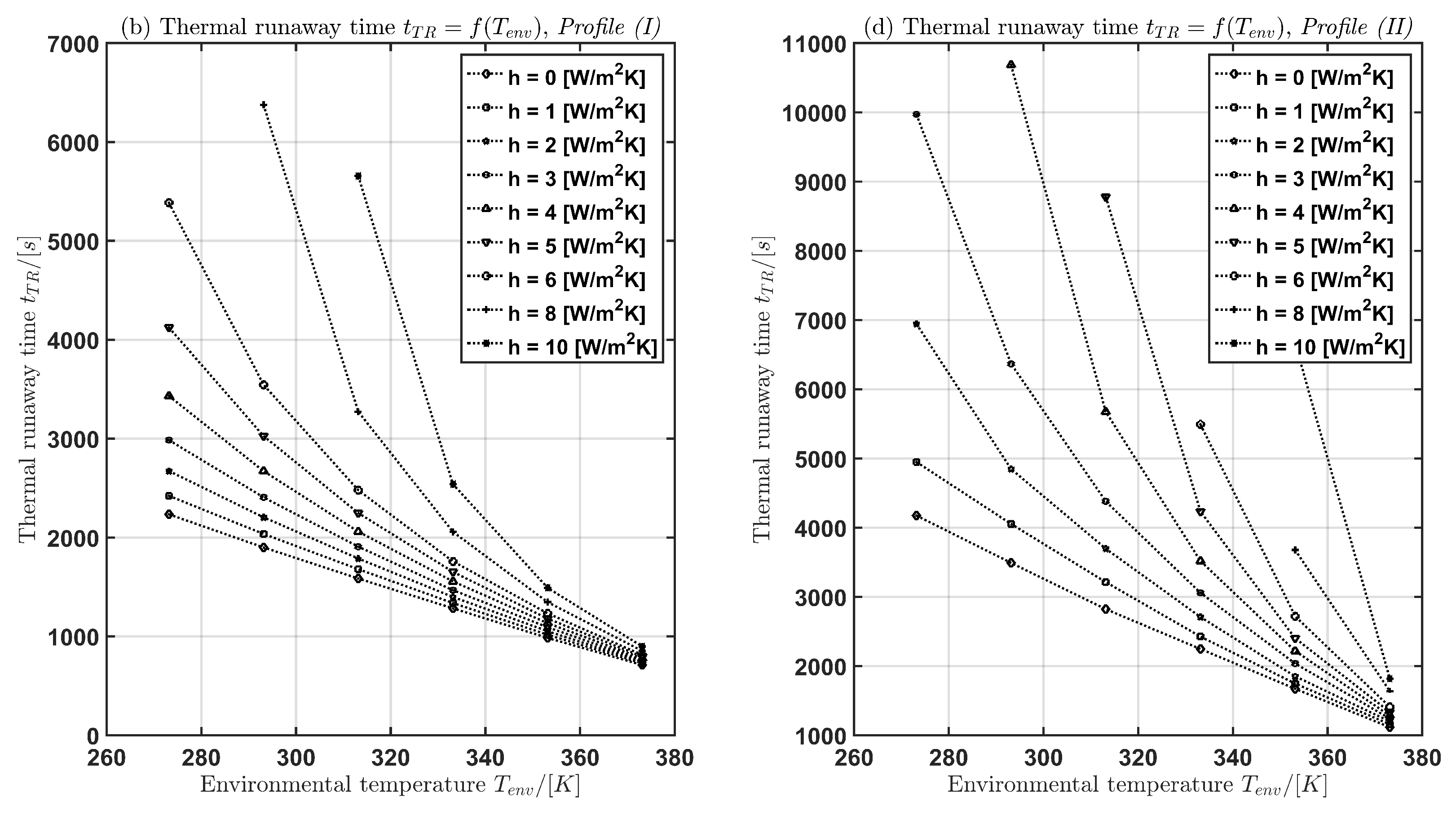
3.2. Computing the Thermal Runaway Time
3.3. Critical parameter intervals
- (a) If the environmental temperature is constant and fixed and the convective heat transfer coefficient h is allowed to vary, then with:
- -
- -
- (b) If the convective heat transfer coefficient h is constant and fixed and the environmental temperature is allowed to vary, then with:
- -
- -
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix: Simulation Parameters
| Initial values | |||
|---|---|---|---|
| Li-concentration neg. solid phase | Li-concentration pos. solid phase | ||
| Initial temperature | Li-concentration liquid phase | ||
| Li-diffusivity | |||
| Neg. solid phase | Pos. solid phase | ||
| Volume frcation | |||
| Neg. solid phase | Pos. solid phase | ||
| Neg. liquid phase | Pos. liquid phase | ||
| Maximal concentration | |||
| Neg. solid phase | Pos. solid phase | ||
| Thermal conductivity | |||
| Neg. electrode | Pos. electrode | ||
| Neg. current collector | Pos. current collector | ||
| Density | |||
| Neg. electrode | Pos. electrode | ||
| Neg. current collector | Pos. current collector | ||
| Particle radius | |||
| Neg. particle | Pos. particle | ||
| Reaction rate coefficient | |||
| Neg. electrode | Pos. electrode | ||
| Neg. electrode | Pos. electrode | ||
| Neg. current collector | Pos. current collector | ||
| Separator | |||
| Density | Thermal conductivity | ||
| Heat capacity | |||
| Battery geometry | |||
| Radius | Height | ||
| Mandrel radius | |||
| Cell thickness | Thickness battery canister | ||
| Thickness neg. current collector | Thickness pos. current collector | ||
| Length pos./neg. electrode | Length separator | ||
| Reaction Heat | Frequency | Activation Energy | Volume Content | |
|---|---|---|---|---|
| factor | ||||
| SEI reaction | ||||
| Neg. solvent reaction | ||||
| Pos. solvent reaction | ||||
| Electrolyte decomp. |
References
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling Galvanostatic Charge and Discharge of the Lithium/Polymer/ Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. Comparison of the Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Porous-Electrode Theory with Battery Applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Temperature Rise in a Battery Module with Constant Heat Generation. J. Electrochem. Soc. 1995, 142, 1054–1057. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal modeling of Lithium/Polymer Battery, I. Discharge Behavior of a Single Cell. J. Electrochem. Soc. 1995, 142, 3274–3281. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal modeling of Lithium/Polymer Battery, II. Temperature Profiles in a Cell Stack. J. Electrochem. Soc. 1995, 142, 3282–3288. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Maleki, H.; Hong, J.S.; Selman, J.R. Thermal modeling and design considerations of lithium-ion batteries. J. Power Sour. 1999, 83, 1–8. [Google Scholar] [CrossRef]
- Chen, S.C.; Wan, C.C.; Wang, Y.Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]
- Inui, Y.; Kobayashi, Y.; Watanabe, Y.; Watase, Y.; Kitamura, Y. Simulation of temperature distribution in cylindrical and prismatic lithium ion secondary batteries. Energy Convers. Manag. 2007, 48, 2103–2109. [Google Scholar] [CrossRef]
- Zhu, C.; Li, X.; Song, L.; Xiang, L. Development of the theoretically based thermal model for lithium ion battery pack. J. Power Sources 2013, 223, 155–164. [Google Scholar] [CrossRef]
- Hu, J.; Tao, L.; Jing, L. Temperature Field Analysis and Thermal Dissipation Structure Optimization of Lithium-ion Battery Pack in PEVs. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 62–71. [Google Scholar]
- Wang, C.Y.; Gu, W.B.; Liaw, B.Y. Micro-Macroscopic Coupled Modeling of Batteries and Fuel Cells. I. Model Development. J. Electrochem. Soc. 1998, 145, 3407–3417. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, C.Y.; Liaw, B.Y. Micro-Macroscopic Coupled Modeling of Batteries and Fuel Cells. II.Application to Nickel Cadmium and Nickel-Metal Hybride Cells. J. Electrochem. Soc. 1998, 145, 3418–3427. [Google Scholar] [CrossRef]
- Howes, F.A.; Whitaker, S. The Spatial Averaging Theorem Revisited. Chem. Eng. Sci. 1985, 40, 1387–1392. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J.; Iliev, O. Modeling of Species and Charge Transport in Li-Ion Batteries Based on Non-equilibrium Thermodynamics; Dimov, I., Dimova, S., Kolkovska, N., Eds.; NMA 2010, LNCS 6046; Springer: Berlin, Germany, 2011; pp. 329–337. [Google Scholar]
- Richardson, G.; Denault, G.; Please, C.P. Multiscale modeling and analysis of lithium-ion battery charge and discharge. J. Eng. Math. 2012, 72, 41–72. [Google Scholar] [CrossRef]
- Landstorfer, M.; Jacob, T. Mathematical modeling of intercalation batteries at the cell level and beyond. Chem. Soc. Rev. 2013, 42, 3234–3252. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.B.; Wang, C.Y. Thermal-Electrochemical Modeling of Battery Systems. J. Electrochem. Soc. 2000, 147, 2910–2922. [Google Scholar] [CrossRef]
- Wang, C.Y.; Srinivasan, V. Computational battery dynamics (CBD)-electrochemical/thermal coupled modeling and multi-scale modeling. J. Power Sources 2002, 110, 364–376. [Google Scholar] [CrossRef]
- Kumaresan, K.; Sikha, G.; White, R.E. Thermal Model for Lion-Ion Cell. J. Electrochem. Soc. 2008, 155, A164–A171. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Mathematical modeling of lithium ion battery with thermal effects in COMSOL Inc. Multiphysics (MP) software. J. Power Sources 2011, 196, 5985–5989. [Google Scholar] [CrossRef]
- Kim, G.H.; Smith, K.; Lee, K.J.; Santhanagopalan, A.P. Multi-Domain Modeling of Lithium-Ion Batteries Encompassing Multi-Phyiscs in Varied Length Scales. J. Electrochem. Soc. 2011, 158, A955–A969. [Google Scholar] [CrossRef]
- Guo, M.; Kim, G.H.; White, R.E. A three-dimensional multi-physics model for a Li-ion battery. J. Power Sources 2013, 240, 80–94. [Google Scholar] [CrossRef]
- Lee, K.J.; Smith, K.; Pesaran, A.; Kim, G.H. Three dimensional thermal-, electrical, and electrochemical-coupled model for cylindrical wound large format lithium-ion batteries. J. Power Sources 2013, 241, 20–32. [Google Scholar] [CrossRef]
- Abraham, D.P.; Roth, E.P.; Kostecki, R.; McCarthy, K.; MacLaren, S.; Doughty, D.H. Diagnostic examination of thermally abused high-power lithium-ion cells. J. Power Sources 2006, 161, 648–657. [Google Scholar]
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J.R. Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells. J. Electrochem. Soc. 2001, 148, A755–A761. [Google Scholar] [CrossRef]
- Spotnitz, R.; Franklin, J. Abuse behavior of high-power, lithium-ion cells. J. Power Sources 2003, 113, 81–100. [Google Scholar] [CrossRef]
- Spotnitz, R.M.; Weaver, J.; Yeduvaka, G.; Doughty, D.H.; Roth, E.P. Simulation of abuse tolerance of lithium-ion battery packs. J. Power Sources 2007, 163, 1080–1086. [Google Scholar] [CrossRef]
- Kim, G.H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Thermal analyses of LiCoO2 lithium-ion battery during oven tests. Heat Mass Transf. 2014, 50, 1405–1416. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Numerical simulations and thermal behavior analysis for oven thermal abusing of LiCoOO2 lithium-ion battery. CIESC J. 2014, 65, 647–657. [Google Scholar]
- Lopez, C.F.; Jeervarajan, J.A.; Mukherjee, P.P. Characterizarion of Lithium-Ion Battery Thermal Abuse Behavior Using Experimental and Computational Analysis. J. Electrochem. Soc. 2015, 162, A2163–A2173. [Google Scholar] [CrossRef]
- Chen, M.; Sun, Q.; Wu, K.; Liu, B.; Peng, P.; Wang, Q. A Thermal Runaway Simulation on a Lithium Titanate Battery and Battery Module. Energies 2015, 8, 490–500. [Google Scholar] [CrossRef]
- Tanaka, N. Modeling and Simulation of Thermo-Electrochemistry of Thermal Runaway in Lithium-Ion Batteries. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2015. [Google Scholar]
- Bebernes, J.; Eberly, D. Mathematical Problems from Combustion Theory; Applied Mathematical Sciences Volume 83, Springer: Berlin, Germany, 1989. [Google Scholar]
- Volpert, V. Elliptic Partial Differential Equations, Volume 2: Reactions-Diffusion Equations; Birkhäuser: Basel, Switzerland, 2014. [Google Scholar]
- Frank-Kamentstskij, D.A. Diffusion And Heat Transfer in Chemical Kinetics; Plenum Press: New York, NY, USA, 1969. [Google Scholar]
- Guo, G.; Long, B.; Cheng, B.; Zhou, S.; Cao, B. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application. J. Power Sources 2010, 195, 2393–2398. [Google Scholar]
- Chiu, K.-Ch.; Lin, C.-H.; Yeh, S.-F.; Lin, Y.-H.; Chen, K.-C. An electrochemical modeling of lithium-ion battery nail penetration. J. Power Sources 2014, 251, 254–263. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Sun, J. Catastrophe analysis of cylindrical lithium ion battery. Nonlinear Dyn. 2010, 61, 763–772. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Lisbona, D.; Snee, T. A review of hazards associated with lithium and lithium-ion batteries. Process Saf. Environ. Protect. 2011, 89, 434–442. [Google Scholar] [CrossRef]
- Veluchamy, A.; Doh, C.-H.; Kim, D.-H.; Lee, J.-H.; Shin, H.-M.; Jin, B.-S.; Kim, H.-S.; Moon, S.-I. Thermal analysis of LixCoO2 cathode material of lithium ion battery. J. Power Sources 2009, 189, 855–858. [Google Scholar] [CrossRef]
- Dahn, J.R.; Fuller, E.W.; Obrovac, M.; Von Sacken, U. Thermal stability of LixCoO2,LixNiO2 and λ-MnO2 and consequences for the safety of Li-ion cells. Solid State Ion. 1994, 69, 265–270. [Google Scholar] [CrossRef]
- Melcher, A.; Ziebert, C.; Lei, B.; Zhao, W.; Rohde, M.; Seifert, H.J. Modellierung und Simulation des thermischen Runaways in zylindrischen Li-Ionen Batterien. In Workshop ASIM/GI-Fachgruppen “Simulation technischer Systeme inklusive der Grundlagen und Methoden in Modellbildung und Simulation”; Tikhomiriv, D., Mammen, H.-T., Pawletta, T., Eds.; ARGESIM Report 51, ASIM Mittelung AM 158, ISBN 978-3-901608-48-3, Hochschule Hamm-Lippstadt, 10./11.03.2016; ARGESIM Verlag: Vienna, Austria.
- Roetzel, W.; Spang, B. VDI Heat Atlas, C3 Typical Values of Overall Heat Transfer Coefficients, Springer Materials; Springer-Verlag: Berlin, Germany, 2010. [Google Scholar]
- Gomadam, P.M.; White, R.E.; Weidner, J.W. Modeling Heat Conduction in Spiral Geometries. J. Electrochem. Soc. 2003, 150, A1339–A1345. [Google Scholar] [CrossRef]
- Chen, S.-C.; Wang, Y.-Y.; Wan, C.-C. Thermal Analysis of Spirally Wound Lithium Batteries. J. Electrochem. Soc. 2006, 153, A637–A648. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, B.; Huang, J. Simultaneous estimation of thermal parameter for large-format laminated lithium-ion batteries. J. Power Sources 2014, 259, 106–116. [Google Scholar] [CrossRef]
- Drake, S.J.; Wetz, D.A.; Ostanek, J.K.; Miller, S.P.; Heinzel, J.M.; Jain, A. Measurment of anisotropic thermophysical properties of cylindrical Li-ion cells. J. Power Sources 2014, 252, 298–304. [Google Scholar] [CrossRef]
- Semenoff, N.N. Zur Theorie des Verbrennungsprozesses. Z. Phys. Hadron. Nucl. 1928, 48, 571–582. [Google Scholar] [CrossRef]






| Parameter | Zhang [50] | Drake [51] | Simulation |
|---|---|---|---|
| Initial: | |||
| Optimized: | |||
| Initial: | |||
| Optimized: | |||
| Initial: | |||
| Optimized: | |||
| - | - |
| Zone | Abraham [26] | Peng [32] | Simulation |
|---|---|---|---|
| (I) | |||
| (II) | for | ||
| for | |||
| (III) | for | ||
| for | |||
| Chemistry |
| (a) : | 0 | 2 | 4 | 6 | 8 | 10 | (b) : | 0 | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2234 | 2672 | 3431 | 5385 | - | - | 4173 | 6943 | - | - | - | - | ||
| 1899 | 2204 | 2671 | 3544 | 6376 | - | 3490 | 4847 | 10684 | - | - | - | ||
| 1585 | 1787 | 2059 | 2478 | 3272 | 5656 | 2821 | 3695 | 5673 | - | - | - | ||
| 1283 | 1398 | 1556 | 1758 | 2057 | 2539 | 2246 | 2708 | 3517 | 5491 | - | - | ||
| 984 | 1052 | 1133 | 1232 | 1346 | 1490 | 1671 | 1850 | 2217 | 2719 | 3677 | 6664 | ||
| 1116 | 1199 | 1282 | 1408 | 1636 | 1818 | 710 | 741 | 777 | 812 | 852 | 897 |
| Profile (I) | () | () | Profile (II) | () | () |
|---|---|---|---|---|---|
| Profile (I) | () | () | Profile (II) | () | () |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melcher, A.; Ziebert, C.; Rohde, M.; Seifert, H.J. Modeling and Simulation of the Thermal Runaway Behavior of Cylindrical Li-Ion Cells—Computing of Critical Parameters. Energies 2016, 9, 292. https://doi.org/10.3390/en9040292
Melcher A, Ziebert C, Rohde M, Seifert HJ. Modeling and Simulation of the Thermal Runaway Behavior of Cylindrical Li-Ion Cells—Computing of Critical Parameters. Energies. 2016; 9(4):292. https://doi.org/10.3390/en9040292
Chicago/Turabian StyleMelcher, Andreas, Carlos Ziebert, Magnus Rohde, and Hans Jürgen Seifert. 2016. "Modeling and Simulation of the Thermal Runaway Behavior of Cylindrical Li-Ion Cells—Computing of Critical Parameters" Energies 9, no. 4: 292. https://doi.org/10.3390/en9040292
APA StyleMelcher, A., Ziebert, C., Rohde, M., & Seifert, H. J. (2016). Modeling and Simulation of the Thermal Runaway Behavior of Cylindrical Li-Ion Cells—Computing of Critical Parameters. Energies, 9(4), 292. https://doi.org/10.3390/en9040292






