Energy Transformations in a Self-Excited Switched Reluctance Generator

Abstract

Wind generation systems require mechanisms that allow optimal adaptation of the generator to varying wind speed and to extract maximum energy from the wind. Robust and affordable high-performance methods are also needed for isolated sites. This paper takes this approach, in which an AC switched reluctance generator is used as a generator with a variable rotor speed. Although the voltage obtained is of insufficient quality to connect the generator directly to the power grid, this kind of generator can be used in isolated sites to charge a battery bank with a simple bridge rectifier. Due to the nonlinear behavior of the machine with the position and current, along with the alternating nature of the current that circulates through its phases, the machine experiences cyclical energy transformations of a mechanical, electrical and magnetic nature. This paper analyzes these transformations for the purpose of providing guidelines for machine design and optimization as a wind turbine in isolated sites.

1. Introduction

The switched reluctance motor (SRM) plays a key role in systems that require rugged electrical operating mechanisms [1,2,3,4,5]. To power this equipment, a Miller asymmetric bridge inverter is used [6]. Use of this motor as a generator is limited to regenerative braking processes. The phase inductance profile according to the rotor position is used to define the value and sign of the motor torque [6,7]. The torque is proportional to the slope of the inductance and, therefore, in order to function as a generator, phase current is needed in the negative slope area of the inductance. This negative torque is used to brake the motor, transforming its mechanical inertial energy into electrical power. The Miller bridge does not allow the motor to run in generator mode with constant current and only functions with current in pulse mode to prevent excessive current amplitudes [7].

Another way to use the machine is with alternating current. In this case, an oscillating circuit is formed with the phase inductance and an external capacitor. The resulting system is self-excited due to the residual remnant magnetism, starting to oscillate when the rotor speed stimulates the circuit with a frequency close to the resonance frequency. Self-excitation has been widely used with induction machines, and the use of this machine has been proposed for wind generation, particularly in areas at some distance from the power grid [8,9,10,11]. The machine saturation is used as a voltage control component. If generation is performed using constant power, as in the case of hydropower turbines, electronically-controlled loads are used as a voltage-stabilizing element [12,13]. These generators are based on a fourth-degree model, whereas a switching reluctance machine (SRM) has a second-degree model for each phase [14,15]. Since the phase-to-phase coupling is lower, the model is less complex. This, added to the simple construction of the stator and the absence of conductors in the rotor, provides a more robust, more affordable solution than the induction machine.

In the switched reluctance generator (SRG), the AC voltage generated can be used to power a load connected in parallel with the capacitor [16]. The voltage waveform contains harmonics that prevent it from being used as an alternative generator to the power grid, unless the load accepts a lower quality level, but can be used to charge a battery bank in isolated sites. In this case, the complexity or control of a Miller bridge is not required, and a bridge rectifier with diodes is sufficient [17].

Due to the nonlinear behavior of the SRM with the position and current, along with the alternating nature of the current that circulates through its phases, the machine experiences cyclical energy transformations of a mechanical, electrical, and magnetic nature. To describe this behavior, a plot of the flux linkage per phase with respect to the phase current is used. As a result, the transformed mechanical energy is represented by the area in a closed flux-current path [15,16,17].

This work analyzes these transformations for the purpose of providing guidelines for machine design and optimization of a wind turbine in isolated sites.

The rest of the paper is organized as follows: the equations for the resulting circuit are obtained first. The basic representative paths are then analyzed and the energy transformation that takes place is associated with them. For greater understanding, a linear system is first used; then the effect of nonlinearity is subsequently highlighted. Finally, numerical results are shown for a path, such as the one analyzed and completed, with experimental results.

2. Circuit Model of a Phase

Figure 1 shows the structure of an 8/6 four-phase switched reluctance motor, which is the same as the generator that will work in self-excited mode and with alternating current. Two opposite coils, A and A’, are series-connected to form a phase a. The same applies to phases b, c, and d.

A basic phase circuit model is formed by the winding resistance R_F and inductance L_F (θ, i_F). Figure 2 shows these components, along with the resonance capacitor, C, and the load resistance, R_L. The inductance depends on the angular position of the rotor and stator, reaching its peak value when a rotor tooth is aligned with a stator tooth.

The circuit equations are as follows:

$${\mathrm{v}}_{\mathrm{C}}-{\mathrm{R}}_{\mathrm{F}}\cdot {\mathrm{i}}_{\mathrm{F}}=\frac{\mathrm{d}\mathsf{\lambda }\left(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}}\right)}{\mathrm{d}\mathrm{t}}$$

(1)

$$\mathsf{\lambda }\left(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}}\right)={\mathrm{L}}_{\mathrm{F}}\left(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}}\right)\cdot {\mathrm{i}}_{\mathrm{F}}$$

(2)

$$\mathrm{C}\frac{\mathrm{d}{\mathrm{v}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}=-\left({\mathrm{i}}_{\mathrm{F}}+{\mathrm{i}}_{\mathrm{L}\mathrm{O}\mathrm{A}\mathrm{D}}\right)$$

(3)

The RLC circuit formed is self-excited with the remnant magnetism and behaves as a parametric oscillator [18]. The drive action is handled by the variable reluctance with a periodic frequency pattern close to resonance [19]. Its use as a self-excited autonomous AC generator was published comparing the star connection with the delta connection [20].

Nevertheless, the load is connected in series with the circuit, which limits its applicability. In our case, the parallel connection is used because it is more fitting for the need to connect and disconnect loads and is more flexible if it is necessary to modify the capacity and, therefore, the resonance frequency, in order to adapt to variable rotor speeds.

The AC voltage frequency is given by:

$$\mathrm{f}=\frac{\mathrm{n}}{60}\frac{\mathrm{N}\mathrm{r}}{2}$$

(4)

where n is the rotor speed in rpm and Nr is the number of rotor teeth.

Figure 3 shows the coil factor L_F/N² according to the position for different phase current values, where N is the number of turns per coil. The current is given as a percentage of the rated current, In. The rated current is the result of using a current density of 5 A/mm² in the area available for the conductor. The function is periodic with the rotor position having a period equal to the rotor pitch.

The data have been obtained numerically by finite element analysis (FEA) for a machine with the specifications shown in

Table 1. Geometric and electric machine data.

Magnitude	Value
Rotor diameter (mm)	60
Stack length (mm)	30
Stator diameter (mm)	120
Gap (mm)	0.2
Rated speed (rpm)	500
Current density (A/mm2)	5
Coil Cu-area (mm2)	119
# of ampere-turns per phase (NI)	467
# of turns per coil	234
Per-phase rated current (A)	2
Steel sheet	M600-50A
Torque (N·m)	1.5

. Formally, the B-H curve of the steel sheet M600-50A has been experimentally characterized and used by the FEA simulation program. Each point in Figure 4 represents a finite element simulation which provides information of the stored linear and nonlinear energy. By processing these information, as is described in [21], the flux linkage λ(θ, i_F) is obtained. Finally, the dependency of the inductance L_F on the angle θ and the current i_F is derived from Equation (2).

3. Unit Paths in the Flux-Current Diagram and Energy Transformations

The work areas through which the machine passes along a cycle are obtained from the paths followed in the flux-current diagram of a phase. The linear case is simulated first, followed by the nonlinear case.

Multiplying Equation (1) by the phase current, i_F, an energy equation is obtained that allows us to conclude that the machine supplies electrical energy power if:

$$\mathrm{d}{\mathrm{W}}_{\mathrm{E}}={\mathrm{i}}_{\mathrm{F}}\cdot \mathrm{d}\mathsf{\lambda }\left(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}}\right)<0$$

(5)

In other words, the sign of the current must have the opposite sign as the flux variation. To determine the source of this energy, the variation of magnetic energy must be analyzed.

3.1. Linear Case

In this case, there is a linear relationship between linked flux and current, i.e., L_F (θ, i_F) = L_F (θ). The operating modes are obtained by performing an energy balance over path A-B between the next two points, as shown in Figure 4. If the machinery does not move, the position θ is maintained, the start and end points of the path are on the same current flux curve. The condition L_F(θ_A)·di_F − dλ₁= 0 shown in the middle column of

Table 2. Flux of energy associated to paths.

Electrical energy $\mathrm{d}\mathsf{\lambda }(\mathsf{\omega }\mathrm{t},{\mathrm{i}}_{\mathrm{F}})\cdot {\mathrm{i}}_{\mathrm{F}}$	${\mathrm{L}}_{\mathrm{F}}(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}})\cdot \mathrm{d}{\mathrm{i}}_{\mathrm{F}}-\mathrm{d}\mathsf{\lambda }(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}})$
	>0	=0	<0
>0
=0
<0

is met. Any energy exchange is performed as a transformation between electrical and magnetic energy. Path A-B stores electrical energy supplied to the machine as magnetic energy (area DABC). Path AB’ implies a rotor movement from position θ_A to θ_B, which means that L_F(θ_A)·di_F − dλ₁ > 0. Area OAB’ is the mechanical energy supplied to the machine and area DAB’C’ is the electrical energy supplied to the machine, both of them stored in the machine as magnetic energy. In general, the condition that indicates that the machine takes mechanical energy is:

$${\mathrm{L}}_{\mathrm{F}}({\mathsf{\theta }}_{\mathrm{A}})\cdot \mathrm{d}{\mathrm{i}}_{\mathrm{F}}-\mathrm{d}\mathsf{\lambda }\left({\mathsf{\theta }}_{\mathrm{A}}\right)>0$$

(6)

This situation is shown in the first column of Table 2. The sign change of Equation (5) is shown in the right column of the same table.

The generator mode can be interpreted graphically as shown in Figure 5. The machine is generating when the magnetic curve λ(θ_B, i_F) that passes through point A is above the characteristic λ(θ_B, i_F) that contains the final point B. Along path A-B, the swept and enclosed area between both curves represents the magnetic energy transformed into electrical power [1]. The generator mode means that the area is swept clockwise. When returning to A from point B, the area is swept in the counterclockwise direction and the machine is in motor mode. Among the possible paths, there are six representative paths in which the energy transformation is not mixed. Figure 6 shows these paths. Along paths 3 and 6, the rotor does not move and there is no mechanical energy. Along path 3 the electrical energy is stored as magnetic energy. On path 6, the opposite to path 3 occurs. Paths 5 and 2 do not involve electrical power exchange. The mechanical energy is transformed and stored as magnetic energy along path 2. On path 5, the opposite to path 2 occurs. On paths 4 and 1, there is no exchange of magnetic energy. The mechanical energy is transformed into electrical power along path 1. On path 4, the opposite to path 1 occurs. Table 2 shows the energy fluxes associated with the path shown in Figure 6. These have been ordered by taking Equations (4) and (5) as criteria. Between these representative paths, there may be many others that involve mixed energy transformations.

Figure 7 contains a plot of the simple and mixed energy transformations: simple transformations take place along the main paths and mixed transformations take place when the path described is between two main paths. The mixed transformations obtained outside the main paths are obtained as superimposition of the adjacent transformations.

3.2. Nonlinear Case

In the nonlinear case, the condition for the generator mode is expressed by the following equation:

$${\mathrm{L}}_{\mathrm{F}}(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}})\cdot \mathrm{d}{\mathrm{i}}_{\mathrm{F}}-\mathrm{d}\mathsf{\lambda }\left(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}}\right)<0$$

(7)

where L_F (θ, i_F) is the local derivative at the point considered according to the expression:

$${\mathrm{L}}_{\mathrm{F}}(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}})={\frac{\partial \mathsf{\lambda }\left(\mathsf{\theta },{\mathrm{i}}_{\mathrm{F}}\right)}{\partial {\mathrm{i}}_{\mathrm{F}}}|}_{\mathsf{\theta }=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}}$$

(8)

Consequently, both Table 2 and Figure 7 basically represent the linear and nonlinear cases at the same time. Nevertheless, in the nonlinear case, line 6-3 of Figure 7 would not pertain entirely to the magnetic characteristic as in the linear case. Only the center of Figure 7 belongs to the nonlinear magnetic curve. Line 6-3 is tangent to the curve at the origin of the paths.

4. Working Areas in a Cyclical Path

The working areas through which a self-excited switched reluctance machine running as an AC generator are demonstrated with an example. A nonlinear case has been considered directly. The inductance profile is obtained from the coil factor of Figure 3 by multiplying by the square of the number of turns and placing the two coils in series. The results are shown in Figure 8.

The nonlinear path obtained when the machine turns at 500 rpm has been superimposed on this figure. This same path is shown in Figure 9, although now the flux of the magnetic core is shown as a function of the current during a cycle. The area enclosed by the two loops represents the mechanical energy generated by turn and by cycle transformed into electrical power. Each loop corresponds to a half-cycle of alternating voltage. This energy is given by the following:

$${\mathrm{E}}_{\mathrm{E}}=2\cdot \mathrm{N}\cdot {\displaystyle \oint {\mathrm{i}}_{\mathrm{F}}}\cdot \mathrm{d}\mathsf{\lambda }$$

(9)

It has been assumed that each phase has two coils in series. Considering only the upper loop or half-cycle, both the current and the flux are null at point O. At point A, the rotor and the stator are aligned, whereas point B represents the state of greatest flux in the machine; at point D, the rotor and stator are in the position of maximum misalignment. In generator mode, the path takes a clockwise direction. In Figure 9 are also superimposed the phase linked flux line corresponding to aligned position which is tangent to the loop in point and the phase linked flux line corresponding to unaligned position which is tangent to the loop in point D. A half-cycle is divided into the following paths:

4.1. Path OA

From O to A, the machine takes electrical power from the capacitor. The energy supplied by the capacitor is represented by the following:

$${\mathrm{E}}_{\mathrm{E}\_\mathrm{O}\mathrm{A}}=\mathrm{N}\cdot {\displaystyle {\int }_{\mathrm{O}}^{\mathrm{A}}{\mathrm{i}}_{\mathrm{F}}\cdot \mathrm{d}\mathsf{\lambda }}$$

(10)

As the magnetic curve sweeps in the counterclockwise direction, electrical energy is also transformed into mechanical energy. In total, the electrical power represented by Equation (9) can be expressed as:

$${\mathrm{E}}_{\mathrm{E}\_\mathrm{O}\mathrm{A}}={\mathrm{N}\cdot {\displaystyle {\int }_{\mathrm{O}}^{\mathrm{A}}{\mathrm{i}}_{\mathrm{F}}\cdot \mathrm{d}\mathsf{\lambda }}|}_{\mathsf{\theta }=0}+{\mathrm{E}}_{\mathrm{M}\mathrm{E}\mathrm{C}\mathrm{H}\_\mathrm{O}\mathrm{A}}$$

(11)

The first term on the right side is the magnetic energy at A and the second, the mechanical energy that exits the machine toward the primary motor. Therefore, it works as a motor attempting to accelerate the machine.

The path followed is between directions 4 and 3 of Figure 7. Point A coincides exactly with direction 3.

4.2. Path AB

In path AB, the flux state continues to increase until it peaks at point B. At point A, the rotor is aligned with the stator and separates in path AB. The machine receives electrical energy; however, because the magnetic curve moves clockwise, mechanical energy from the primary motor is transformed into magnetic energy. The path is located between directions 3 and 2 of Figure 7. Point B coincides exactly with direction 2 in which electrical power changes its sign.

4.3. Path BC

Between B and C, the machine provides electrical power that charges the capacitor. Likewise, the magnetic curve for the rotor position sweeps clockwise, which means that the mechanical energy from the primary motor is being transformed, part of which goes to the load and part is stored in the magnetic circuit. The path followed is between directions 2 and 1 of Figure 7. Point C corresponds exactly to direction 1, which has no magnetic energy variations.

4.4. Path CD

The magnetic curve for the rotor position sweeps in the clockwise direction, which means that that the mechanical energy from the primary motor is being transformed. The magnetic energy is also diminishing. Both types of energy are transformed into electrical power that charges the capacitor and feeds the charge. The path followed is between directions 1 and 6 of Figure 7. Point D corresponds exactly to direction 6 in which the rotor and stator are in the position of maximum misalignment.

4.5. Path DO

The magnetic curve corresponding to the rotor position sweeps counterclockwise which means that the primary motor receives mechanical energy. Since electrical power is also being produced, magnetic energy is the source of both. The path followed is between directions 6 and 5 of Figure 7. The sign change of the electrical energy takes place right at point O. This point is represented by direction 5 in Figure 7. By this point, the other half-cycle starts, following the same steps as the first half-cycle.

The sign change of the electrical work takes place at the origin, a characteristic associated with direction 5 of Figure 7. The sign change of the magnetic energy also takes place, a characteristic associated with direction 4 of Figure 7. This means that the path between directions 5 and 4 takes place entirely at the origin and, therefore, has no physical existence.

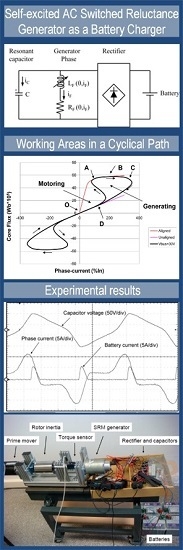
5. Experimental Results

In order to test the form of a path experimentally, one of the phases of an 8/6 motor was used. A test set-up following the scheme in Figure 10 is used for experiments. A 495 μF capacitor is used. The battery bank is composed of five batteries of 12 V connected in series. The machine rotates at 710 rpm. The prime mover is a torque controlled synchronous motor. Rotor inertia is driven by the motor to smooth speed oscillations due to the pulsed torque. A 20 N·m torque sensor is placed between the inertia and the 8/6 switched reluctance generator [22].

Figure 11 shows a photograph of the text setup, and Figure 12 shows the measurement of the time trend of the capacitor voltage, phase current, and charging current. The alternating voltage can be seen to have harmonic content that prevents it from being used as a substitute for grid voltage, except for non-critical loads such as occurs when heating or powering rectifiers.

Figure 13 shows the relative trends of these state variables in the flux linkage vs. phase diagram according to capacitor voltage. Two operating cases are shown: (a) non-duty with the battery bank disconnected and (b) with the battery bank connected. In both cases, the rotor speed is 710 rpm. During non-duty operation, the system is nonlinear and of second order following (1) and (3) with i_LOAD = 0. The phase diagram corresponds to a limit cycle. The cycle size increases with rotor speed. When the battery bank is connected, the figure size is reduced because the amplitude of the capacitor voltage is limited by the bank voltage.

In Figure 14 are shown the cyclical paths for the two cases in Figure 13. The increase in the linked area is due to the incorporation of energy demand when the battery bank is connected. The decrease in flux amplitude is due to the decrease in the voltage amplitude of the capacitor. The shapes of the curves have the form obtained numerically in Figure 9. The unloaded area represents losses. It would reduce with proper machine design with less phase resistance.

6. Conclusions

The various operating zones of an AC self-excited switched reluctance generator and its respective energy transformations have been described systematically, all analyzed for the linear and nonlinear cases. An understanding of these transformations allows the design procedure and the properties of the limit cycle to be undertaken. A phase has been seen to function as a motor part of the time, which results in sign inversion of the torque of the motor shaft. This inversion is neutralized when all of the motor phases are used because the energy transfers are performed internally between the machine phases. This situation neutralizes potential noise production with the primary generator couplings. This noise is present in the case of only one phase. The qualitative results obtained with the linear magnetic characteristic are maintained with the nonlinear magnetic characteristic. The third voltage harmonic that appears in the load prevents it from being used as a substitute for grid power except when allowed by the load. The ruggedness of this generator means it may be suitable for isolated sites with low maintenance. Another potential use is to power a direct current bus through a rectifier and use it for battery charging in isolated sites. The capability to maintain oscillation at different rotor speeds, plus the possibility to vary the resonance frequency by changing the capacitor capacity, would allow the rotor to be used with a small variable-speed wind turbine.