Super-Twisting Differentiator-Based High Order Sliding Mode Voltage Control Design for DC-DC Buck Converters
Abstract
:1. Introduction
- A robust HOSM controller based on PCL is designed for DC-DC buck converters, the corresponding systematic and detailed design procedure is presented in detail through theoretical analysis and simulation studies.
- By adding a super-twisting differentiator (STD) into the controller design, the current sensor is no longer needed for the converter control. The proposed HOSM + STD controller only uses the measurement of output voltage as control input. Thus the control system is simplified and the robustness of HOSM can also be preserved.
2. Super-Twisting Differentiator Design
2.1. DC-DC Buck Power Converter Model
2.2. Differentiator Design Based on Super-Twisting Algorithm
2.3. Gains of the STD
3. Sliding Mode Controller Design
3.1. Traditional Sliding Mode Control
3.2. Second Order Sliding Mode Control
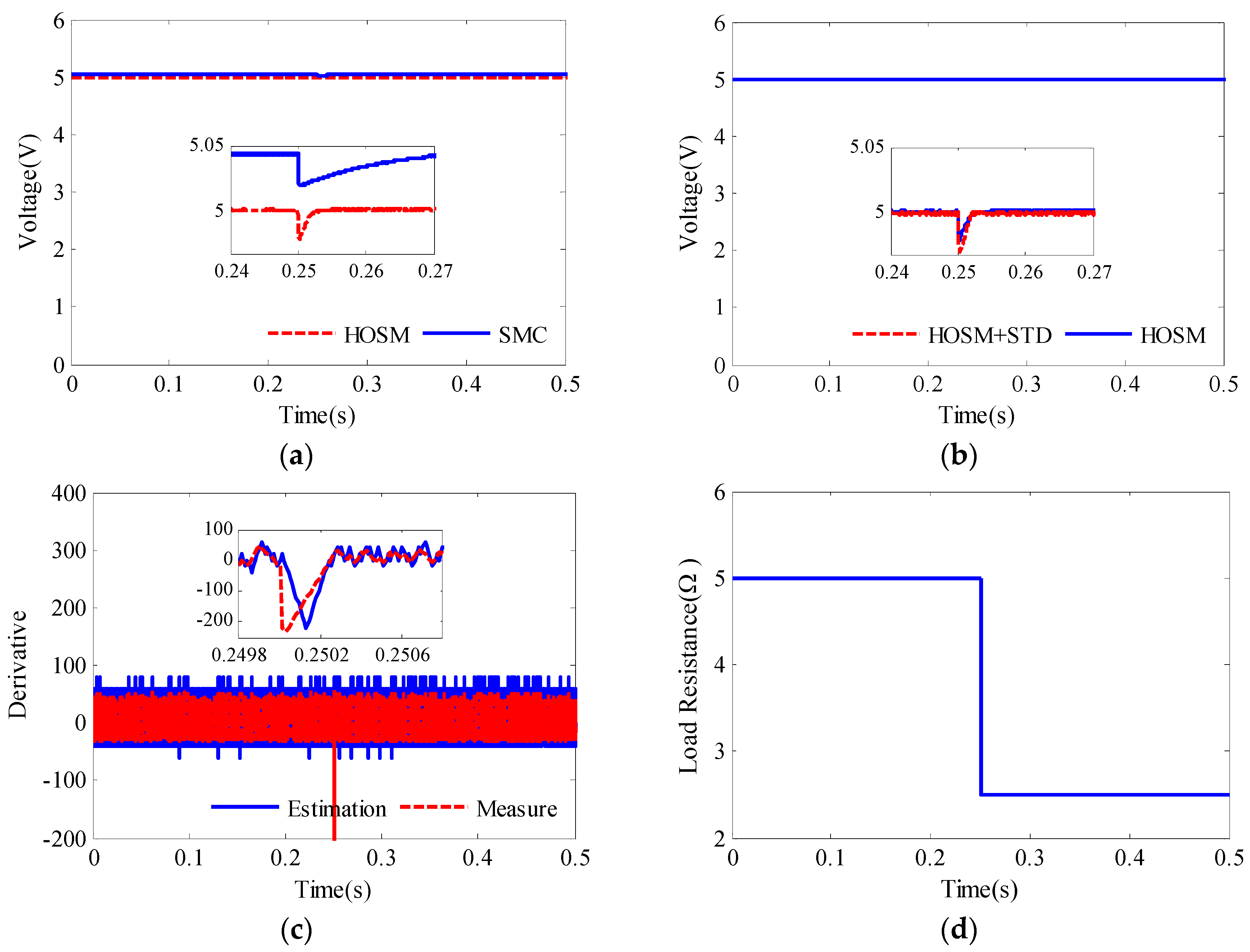
4. Simulation Results
4.1. Controller Performance with Different Design Parameters
4.2. Disturbance in Input Voltage
4.3. Disturbance in Output Load Resistance
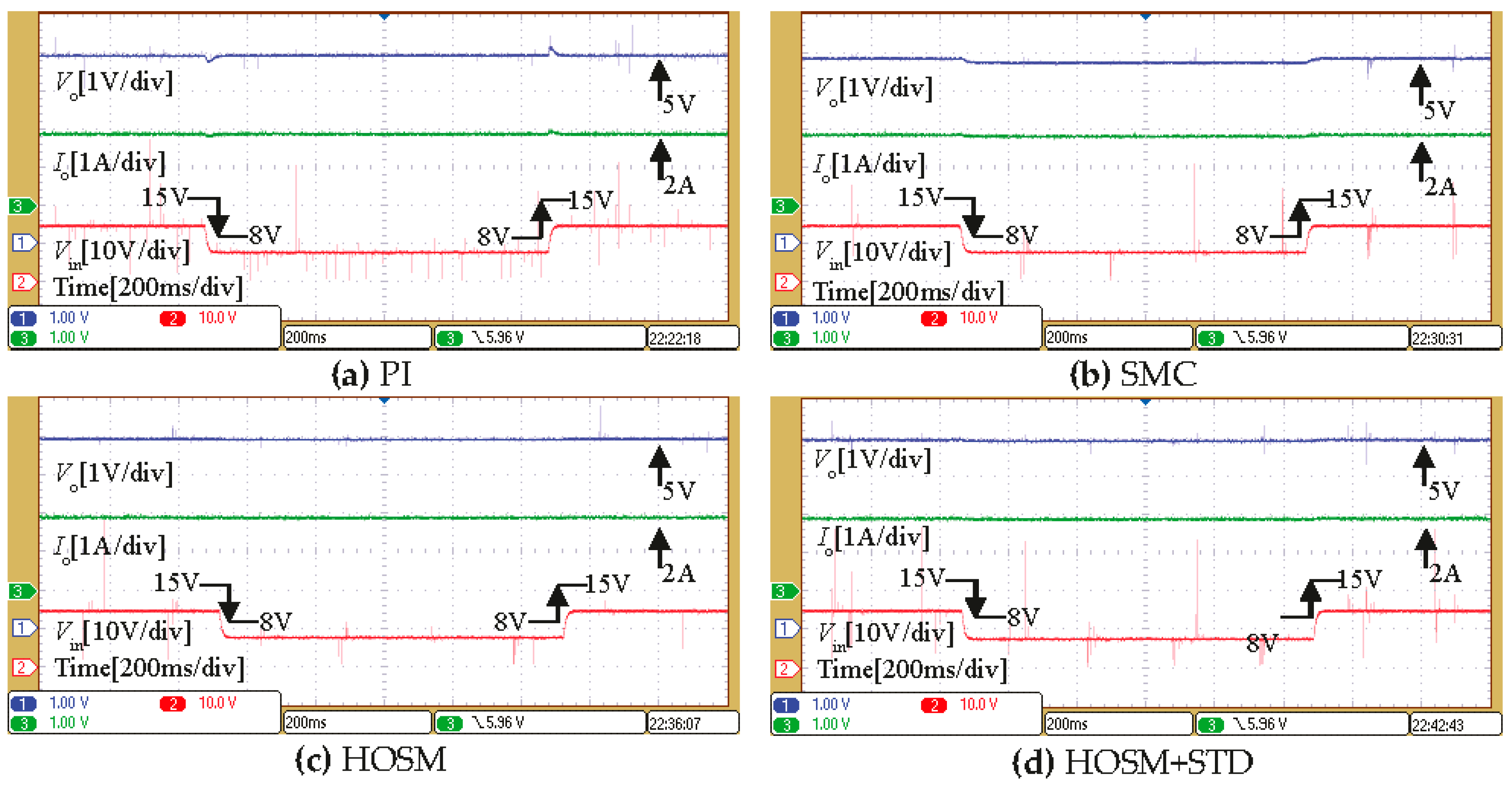
5. Experimental Results
6. Conclusions
- The proposed HOSM controller can achieve stronger robustness, less steady state error, faster convergence, better voltage regulation and load regulation than SMC.
- By adding a super-twisting differentiator (STD) into the HOSM controller design, the current sensor is no longer needed for the converter control. The proposed HOSM + STD controller only uses the measurement of output voltage as control input. The performance of HOSM + STD controller in terms of robustness, steady state error, voltage regulation is similar to HOSM controller.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Niyato, D.; Wang, P.; Kim, D.I.; Han, Z. Wireless charger networking for mobile devices: Fundamentals, standards, and applications. IEEE Wirel. Commun. 2015, 22, 126–135. [Google Scholar] [CrossRef]
- Olvitz, L.; Vinko, D.; Švedek, T. Wireless power transfer for mobile phone charging device. In Proceedings of the 35th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2012; pp. 141–145.
- Musavi, F.; Edington, M.; Eberle, W. Wireless power transfer: A survey of EV battery charging technologies. In Proceedings of the 4th Annual IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1804–1810.
- Zhang, F.; Liu, X.; Hackworth, S.A.; Sclabassi, R.J.; Sun, M. In vitro and in vivo studies on wireless powering of medical sensors and implantable devices. In Proceedings of the 2009 IEEE Life Science Systems and Applications Workshop, Bethesda, MD, USA, 9–10 April 2009; pp. 84–87.
- Wang, J.; Li, J.; Ho, S.; Fu, W.; Li, Y.; Yu, H.; Sun, M. Lateral and angular misalignments analysis of a new PCB circular spiral resonant wireless charger. IEEE Trans. Magn. 2012, 48, 4522–4525. [Google Scholar] [CrossRef]
- Prasad, P.; Thakur, N. Wireless resonant power transmission. In Proceedings of the International Conference on ICT for Sustainable Development (ICT4SD), Ahmedabad, India, 3–4 July 2015; pp. 417–425.
- Ottman, G.K.; Hofmann, H.F.; Bhatt, A.C.; Lesieutre, G.A. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron. 2002, 17, 669–676. [Google Scholar] [CrossRef]
- Villa, J.L.; Sallán, J.; Llombart, A.; Sanz, J.F. Design of a high frequency inductively coupled power transfer system for electric vehicle battery charge. Appl. Energy 2009, 86, 355–363. [Google Scholar] [CrossRef]
- Vadim, I.U. Survey paper variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar]
- Venkataramanan, R. Sliding Mode Control of Power Converters. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 6 May 1986. [Google Scholar]
- Utkin, V. Sliding mode control of DC/DC converters. J. Frankl. Inst. 2013, 350, 2146–2165. [Google Scholar] [CrossRef]
- Tan, S.-C.; Lai, Y.-M.; Cheung, M.K.-H.; Tse, C.K. On the practical design of a sliding mode voltage controlled buck converter. IEEE Trans. Power Electron. 2005, 20, 425–437. [Google Scholar] [CrossRef]
- Tan, S.-C.; Lai, Y.; Tse, C.K. A unified approach to the design of PWM-based sliding-mode voltage controllers for basic DC-DC converters in continuous conduction mode. IEEE Trans. Circuits Syst. Regul. 2006, 53, 1816–1827. [Google Scholar]
- Tan, S.-C.; Lai, Y.-M.; Tse, C.K. General design issues of sliding-mode controllers in DC-DC converters. IEEE Trans. Ind. Electron. 2008, 55, 1160–1174. [Google Scholar]
- Wai, R.-J.; Shih, L.-C. Design of voltage tracking control for DC-DC boost converter via total sliding-mode technique. IEEE Trans. Ind. Electron. 2011, 58, 2502–2511. [Google Scholar] [CrossRef]
- Chen, Z. PI and sliding mode control of a Cuk converter. IEEE Trans. Power Electron. 2012, 27, 3695–3703. [Google Scholar] [CrossRef]
- Mamarelis, E.; Petrone, G.; Spagnuolo, G. Design of a sliding-mode-controlled SEPIC for PV MPPT applications. IEEE Trans. Ind. Electron. 2014, 61, 3387–3398. [Google Scholar] [CrossRef]
- Lopez Santos, O.; Martinez-Salamero, L.; Garcia, G.; Valderrama-Blavi, H.; Sierra-Polanco, T. Robust sliding-mode control design for a voltage regulated quadratic boost converter. IEEE Trans. Power Electron. 2015, 30, 2313–2327. [Google Scholar] [CrossRef]
- Oucheriah, S.; Guo, L. PWM-based adaptive sliding-mode control for boost DC-DC converters. IEEE Trans. Ind. Electron. 2013, 60, 3291–3294. [Google Scholar] [CrossRef]
- Cavallo, A.; Guida, B. Sliding mode control for DC/DC converters. In Proceedings of the 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 7088–7094.
- Agostinelli, M.; Priewasser, R.; Marsili, S.; Huemer, M. Fixed-frequency Pseudo Sliding Mode control for a Buck-Boost DC-DC converter in mobile applications: A comparison with a linear PID controller. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1604–1607.
- Ahmed, M.; Kuisma, M.; Tolsa, K.; Silventoinen, P. Implementing sliding mode control for buck converter. In Proceeding of the 34th IEEE Power Electronics Specialist Conference (PESC), Acapulco, Mexico, 15–19 June 2003; Volume 2, pp. 634–637.
- Lin, S.-C.; Tsai, C.-C. Adaptive voltage regulation of PWM buck DC-DC converters using backstepping sliding mode control. In Proceedings of the 2004 IEEE International Conference on Control Applications, Taipei, Taiwan, 2–4 September 2004; Volume 2, pp. 1382–1387.
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Sahraoui, H.; Drid, S.; Chrifi-Alaoui, L.; Hamzaoui, M. Voltage control of DC-DC buck converter using second order sliding mode control. In Proceedings of the 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015; pp. 1–5.
- Huangfu, Y.; Wu, Y. A robust flyback converter based on high order sliding mode control for fuel cell. In Proceedings of the 40th Annual Conference of the IEEE Industrial Electronics Society (IECON), Dallas, TX, USA, 29 October–1 November 2014; pp. 3936–3940.
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Levant, A. Principles of 2-sliding mode design. Automatica 2007, 43, 576–586. [Google Scholar] [CrossRef]
- Komurcugil, H. Adaptive terminal sliding-mode control strategy for DC-DC buck converters. ISA Trans. 2012, 51, 673–681. [Google Scholar] [CrossRef] [PubMed]
- Komurcugil, H. Non-singular terminal sliding-mode control of DC-DC buck converters. Control Eng. Pract. 2013, 21, 321–332. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Harmouche, M.; Wack, M. Adaptive-gain second-order sliding mode observer design for switching power converters. Control Eng. Pract. 2014, 30, 124–131. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Davila, J.; Fridman, L.; Levant, A. Second-order sliding-mode observer for mechanical systems. IEEE Trans. Autom. Control 2005, 50, 1785–1789. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Li, S.; Wu, B.; Qian, C. Robust control for PWM-based DC-DC buck power converters with uncertainty via sampled-data output feedback. IEEE Trans. Power Electron. 2015, 30, 504–515. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Yang, J.; Wu, B.; Li, Q. Extended state observer-based sliding mode control for PWM-based DC-DC buck power converter systems with mismatched disturbances. IET Control Theory Appl. 2015, 9, 579–586. [Google Scholar] [CrossRef]
- Seshagiri, S.; Block, E.; Larrea, I.; Soares, L. Optimal PID design for voltage mode control of DC-DC buck converters. In Proceedings of the IEEE Indian Control Conference (ICC), Hyderabad, India, 4–6 January 2016; pp. 99–104.
- Zhuo, S.; Huangfu, Y. Robust buck converter design with a high-order sliding mode differentiator. In Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society (IECON), Yokohama, Japan, 9–12 November 2015; pp. 162–167.
- Atassi, A.; Khalil, H. Separation results for the stabilization of nonlinear systems using different high-gain observer designs. Syst. Control Lett. 2000, 39, 183–191. [Google Scholar] [CrossRef]
- Raviraj, V.; Sen, P.C. Comparative study of proportional-integral, sliding mode, and fuzzy logic controllers for power converters. IEEE Trans. Ind. Appl. 1997, 33, 518–524. [Google Scholar] [CrossRef]
- Tan, S.-C.; Lai, Y.; Tse, C.K. Indirect sliding mode control of power converters via double integral sliding surface. IEEE Trans. Power Electron. 2008, 23, 600–611. [Google Scholar]






| Item | Value |
|---|---|
| Input Voltage, Vin | 8–15 V |
| Reference Voltage, Vref | 5 V |
| Inductance, L | 2 mH |
| Capacitance, C | 4700 μF |
| Load Resistance, R | 2.5–10 Ω |
| Parameter | Value |
|---|---|
| λ0 | 2 × 106 |
| λ1 | 2 × 103 |
| k | 85 |
| β | 70.2 |
| Controller | Output Voltage | |
|---|---|---|
| Rising Time | Steady State Error | |
| SMC | 57.5 ms | 48.2 mV, 0.96% |
| HOSM | 57.5 ms | 2.6 mV, 0.05% |
| HOSM + STD | 54.9 ms | 0.7 mV, 0.01% |
| Controller | Output Voltage | |
|---|---|---|
| Voltage Drop | Recovery Time | |
| SMC | 67.9 mV, 1.36% | 73.8 ms |
| HOSM | 3.2 mV, 0.06% | 1.3 ms |
| HOSM + STD | 1.4 mV, 0.03% | 0.1 ms |
| Controller | Output Voltage | |
|---|---|---|
| Transient Voltage Drop | Recovery Time | |
| SMC | 23.6 mV, 0.47% | 30.6 ms |
| HOSM | 21.3 mV, 0.43% | 5.1 ms |
| HOSM + STD | 29.2 mV, 0.58% | 2.1 ms |
| Type | Controller | Output Voltage | |
|---|---|---|---|
| Voltage Drop/Raise | Recovery Time | ||
| 15 V→8 V→15 V | PI | 240 mV | 42 ms |
| HOSM + STD | 24 mV | 10 ms | |
| 10 Ω→2.5 Ω→10 Ω | PI | 360 mV | 12.5 ms |
| HOSM + STD | 40 mV | 2.5 ms | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huangfu, Y.; Zhuo, S.; Rathore, A.K.; Breaz, E.; Nahid-Mobarakeh, B.; Gao, F. Super-Twisting Differentiator-Based High Order Sliding Mode Voltage Control Design for DC-DC Buck Converters. Energies 2016, 9, 494. https://doi.org/10.3390/en9070494
Huangfu Y, Zhuo S, Rathore AK, Breaz E, Nahid-Mobarakeh B, Gao F. Super-Twisting Differentiator-Based High Order Sliding Mode Voltage Control Design for DC-DC Buck Converters. Energies. 2016; 9(7):494. https://doi.org/10.3390/en9070494
Chicago/Turabian StyleHuangfu, Yigeng, Shengrong Zhuo, Akshay Kumar Rathore, Elena Breaz, Babak Nahid-Mobarakeh, and Fei Gao. 2016. "Super-Twisting Differentiator-Based High Order Sliding Mode Voltage Control Design for DC-DC Buck Converters" Energies 9, no. 7: 494. https://doi.org/10.3390/en9070494
APA StyleHuangfu, Y., Zhuo, S., Rathore, A. K., Breaz, E., Nahid-Mobarakeh, B., & Gao, F. (2016). Super-Twisting Differentiator-Based High Order Sliding Mode Voltage Control Design for DC-DC Buck Converters. Energies, 9(7), 494. https://doi.org/10.3390/en9070494









