Electric Vehicle to Power Grid Integration Using Three-Phase Three-Level AC/DC Converter and PI-Fuzzy Controller

Abstract

This paper presents the control and simulation of an electric vehicle (EV) charging station using a three-level converter on the grid-side as well as on the EV-side. The charging station control schemes with three-level AC/DC power conversion and a bidirectional DC/DC charging regulator are described. The integration of EVs to the power grid provides an improvement of the grid reliability and stability. EVs are considered an asset to the smart grid to optimize effective performance economically and environmentally under various operation conditions, and more significantly to sustain the resiliency of the grid in the case of emergency conditions and disturbance events. The three-level grid side converter (GSC) can participate in the reactive power support or grid voltage control at the grid interfacing point or the common coupling point (PCC). A fuzzy logic proportional integral (FL-PI) controller is proposed to control the GSC converter. The controllers used are verified and tested by simulation to evaluate their performance using MATLAB/SIMULINK. The comparison of a PI-controller and a PI-Fuzzy controller for the EV charging station shows the effectiveness of the proposed FL-PI controller over conventional PI controller for same circuit operating conditions. A good performance for PI-Fuzzy in terms of settling time and peak overshoot can observed from the simulation results.

1. Introduction

Recently, Electric vehicles (EV) became popular, and thus building EV charging stations is important in order to fulfill the electrical energy demand of the vast number of electric vehicles. Nowadays, due to the widespread accessibility of electrical grids, parking lots, fast EV charger stations, and residential areas can offer the electrical energy required to charge EVs. An energy management control strategy is required for the charging stations in order to design and select an optimum contracted capacity to improve operation performance [1,2,3]. Efficient battery chargers can play a vital role in the development of recent EVs. The battery charger characteristics affect the charging time and battery life, as well as the charging efficiency. EV battery chargers should have the advantages of higher efficiency and reliability, with higher power density, light weight, smaller size, and lower cost. The charger circuit operation depends mainly on circuit topology, circuit components, control strategy, and soft switching techniques [4]. Generally, the EV-Charger control algorithms can be implemented by using analog/digital controllers, microcontrollers, digital signal processors, and some specific integrated circuits. However, this depends on upon the complexity of the power circuit, cost, and the rating of power converters. From a power quality point of view, an EV charger must guarantee that current drawn from the utility has lower harmonic distortion to minimize power quality impact. Furthermore, it should have a high power factor to maximize the available real power drawn from the utility grid.

The batteries of plug-in EVs can be charged from a standard outlet at home or a special outlet at a charging booth. However, an extra charging load will result in an imbalance in power demand and supply, which consequently may lead to under-frequency or under-voltage instability. In contrast, a sudden discharge of electrical energy from the EVs may result in a voltage swell at the involved distribution point. For this reason, in order to ensure grid stability, this bi-directional energy flow between the power grid and the EVs must be controlled carefully [5]. The integration of EVs is important to support a resilient grid and to overcome extreme events and fault conditions. For the flexible operation of distribution systems under uncertain and changing conditions, EV integration is considered a potential solution for improving resiliency in distribution systems [6,7,8,9]. EVs with onboard batteries are qualified for supporting the electricity grid by absorbing the excessive amount of electrical energy and returning the power back to the grid when necessary. EVs control scheme controls the power flow based on certain preset limits of the DC bus voltage. The energy flow control between the utility grid and EVs has been made mainly for voltage support and peak reduction [6]. The fuzzy control techniques are in popular use due to the linguistic representation of rules without needing to develop a system mathematical model. Thus, a control technique can be easily designed for charge and discharge, even with the connection of a large number of EVs.

Various power circuit topologies and control schemes have been developed for either single-phase or three-phase EV chargers [10,11]. These EV chargers can be either half-bridge or full-bridge converter topologies. The half-bridge power converter has fewer circuit components, low cost, and higher efficiency, but suffers from high component stresses. In contrast, the full-bridge converter has more components and lower device stresses, with higher cost. Moreover, this circuit topology needs more inputs with pulse-width modulation (PWM) that add to the complication and cost of the control circuit. However, in a wide battery side voltage range, the efficiency of the half-bridge converter drops quickly with lower battery pack voltage. This problem can be mitigated by using a three-level bi-directional DC–DC converter, which is considered suitable for charge station application. In addition, a much smaller inductor is required, and there is no audible noise in the three-level converter compared with a variable frequency PWM half-bridge converter, either. Due to all of the advantages mentioned previously, the bi-directional three-level DC–DC converter is recommended for municipal parking deck EV charger stations. Multilevel converters can minimize the size and reduce the devices stress, which makes them more suitable for three-level EV chargers, allowing a smaller size and lower cost of filter components. Multilevel PWM converters are attractive for high-power and bidirectional power flow applications, such as EV battery and energy storage systems [10,11]. Three-phase bidirectional multilevel converters are recommended for high-power charger systems in spite of the added complexity of control circuitry and additional components, which can increase the total cost [12]. These converters are characterized by a high level of power quality at AC input mains with reduced total harmonic distortion (THD), higher power factor, reduced electromagnetic interference (EMI) noise, and provide a ripple-free, regulated DC output voltage insensitive to both supply and load disturbances [13,14,15,16,17,18]. Additional advantages of these converters are lower switch voltage stress and the utilization of smaller passive devices, such as capacitors and inductors [19,20,21,22]. These advantages make the three-level bidirectional AC–DC converters more suitable for EV charger station application. The control strategy for the two-level converter topology cannot be directly used for the three-level PWM converter because of its special requirements, such as the evasion of excessive ΔV in line-to-line and phase voltages of the converter and the balance control for neutral-point potential. Several low-cost bi-directional DC–DC converters are suitable for the application of EV charger stations, which have been introduced and compared [18].

Generally, the typical control strategies utilized for the three-level PWM power converter were presented in [23]. These strategies include direct power control, voltage oriented control, and space vector modulation-based direct power control. Similarly, in the two-level converter, the control system for the three-level converter also aims to keep the DC-bus voltage level at the required value and forces the grid current to be approximately sinusoidal and in phase with the grid voltage. Therefore, this means unity-power-factor condition. A power controller was developed for optimization of the fuel economy for parallel hybrid vehicles (PHVs) [24]. The energy management control scheme is implemented by a power controller that controls the flow of energy between the grid and other system components.

This paper presents the simulation and controller design of an EV charger station using a three-level converter on the grid-side as well as on the EV-side. The control strategy is demonstrated using proportional integral controllers (PI) and fuzzy-logic-PI. This controller will coordinate both the charging and discharging of EVs. The proposed algorithm has the advantages of simplicity and robustness that make this algorithm solution promising for applications in the future smart energy grid. The presented work mainly focuses on the control architecture for using the EVs’ batteries for grid support as distributed energy storage systems. A simulation-based analysis of the charging station for multiple Electric Vehicles is done to test the charging units’ capability to handle different scenarios. The charging station performance is improved when controlled with the addition of a fuzzy logic controller (FLC) to the PI controller instead of just proportional-integral-derivative (PID) controller. Such improvements to the charging and discharging operation has been observed.

2. Studied EV Charging Station

As shown in Figure 1, the grid-connected EV-charger station was composed of three main parts: a number of EV chargers, a power converter for grid interface, and a controller for system integration. Each EV charge regulator consists of a PWM DC/DC voltage source converter, which is referred to as the EV-side converter in this paper. The three-phase grid voltage is rectified to a DC voltage by utilizing a three-phase three-level rectifier/inverter (see Figure 1). Electric vehicles are connected to the DC-bus through an EV charger and in parallel with each other. The charging station control system consists of the EV-side controller, the grid-side interface controller, and the centralized charging controller level [25,26]. At the EV-side controller, each EV is charged/discharged through the DC/DC power converter to perform the charge and discharge process of EV batteries. At the grid-side controller, the three-level AC/DC inverter/converter is controlled by keeping a constant DC-bus voltage and regulating reactive power supplied to/ delivered from the grid by the three-phase three-level (TPTL) rectifier.

In the integrated charging station controller, the central control system delivers the power reference signals to each individual EV-side charge regulator by taking into account the utility grid dynamic conditions, the EV state of charge (SOC), and charge/discharge requirements, while the local EV-side controller ensures that the power reference signal sent by the centralized control system is satisfied [27]. Depending on the system conditions, the direction of the power flow can be determined to perform the grid to vehicle (G2V), and vehicle to grid (V2G) power management control functions.

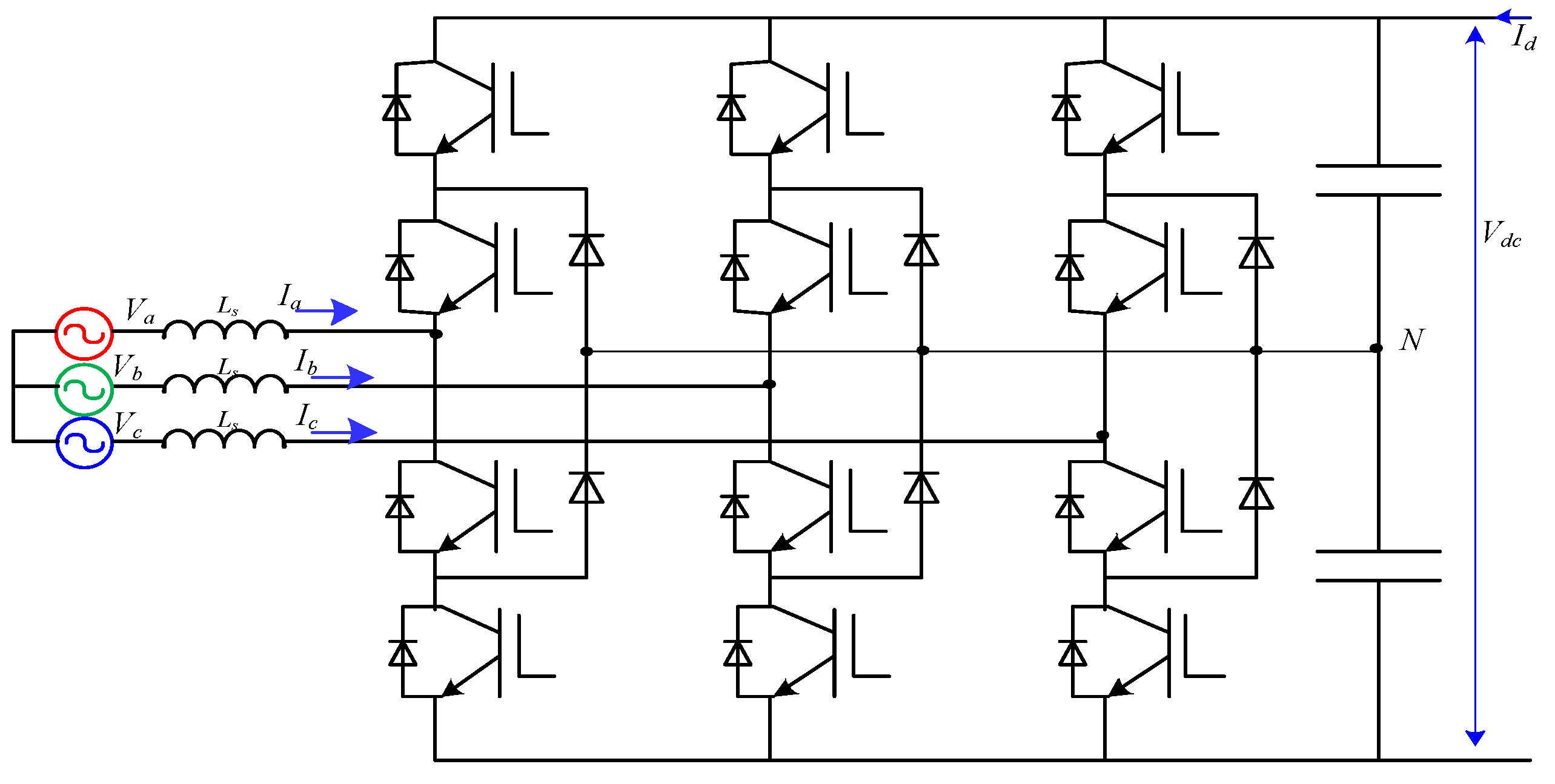
2.1. Three-Level PWM bidirectional Rectifier/Inverter

The bidirectional AC–DC power converter is the main link between the grid and the EVs. In EV charge mode, this converter acts as a rectifier that converts the AC voltage from the utility into a DC bus voltage. In the case of V2G mode, it acts as an inverter that inverts the DC voltage to an AC voltage to supply power back to the grid. The Three-phase three-level (TPTL) voltage source inverter (VSI) based on a diode clamped scheme is utilized in order to reduce the total harmonic distortion of the inverter-mode/mains voltages, as shown in Figure 2. The current harmonics resulting from the switching frequency can be suppressed by a grid-side filter of relatively small volume. In TPTL, the neutral point potential is also useful for voltage formation beside the positive and negative DC-bus voltages. For this reason, all power semiconductors switching devices face only half of the line voltage; this results in a reduction of the power switching losses by a factor of approximately two. Consequently, this results in an increase of the system efficiency, a reduction of the heat sink, and a further increase in the converter power density.

2.2. EV-Side Converter

The charging station studied here works in both G2V and V2G for charging/discharging the EV energy storage devices which should utilize a bi-directional converter. Some charging stations work only in the G2V mode for charging the EV batteries, which could utilize unidirectional converter. Although the V2G scheme is expected to be widespread in EVs and hybrid electric vehicles (HEVs) in the future smart grid, it is not probable that people will accept feeding back energy at a wayside charger station. The voltage stress of active switches and diodes in the three-level converter is half of that in half-bridge power converter [20]. Additionally, the current stress of power active and passive devices is similar to those of the three-level and half-bridge converter. In order to ensure the same ripple-current-ratio of inductor (e.g., 30%), the switching frequency in the TPTL converter can be much lower than that of half-bridge power converter. Hence, inductor size in the TPTL converter is much lower than the one used for the half-bridge converter—e.g., 1/3 [20]. The proposed bi-directional PWM DC/DC converter will be utilized to charge/discharge the EV battery, and the voltage level of V_d in Figure 2 will be large. In the case where V_d is low, the performance of that power converter will worsen. In this case, the current ripple in the inductor will increase because the duty cycle is small, and the converter efficiency will be lower because the output power is decreased while the power losses are not proportionally decreasing. To overcome this problem, a variable frequency control scheme is introduced [18]. It is obvious that the TPTL converter has a higher performance efficiency in both buck and boost operation mode. However, by considering all the comparisons of these two converters, the three-level DC/DC converter has better performance on nearly all issues. Therefore, it will be chosen as the EV charge/discharge. One clear disadvantage of the TPTL power converter is that it requires four switches, while the half-bridge power converter only needs two switches. However, the voltage stress on the active switches used in the half-bridge topology is twice that in the TPTL converter.

3. Charging Station Control Strategy

3.1. Battery Charging/Discharging Requirements

The battery is considered a vital device in EVs. Batteries can store the electrical energy in the form of chemical energy through charging and release the stored energy by internal chemical reactions through the discharge process [28,29]. The charging and discharging process of a battery bank could be influenced by many factors, such as reactant concentration, temperature, and range of reaction [30]. Thus, a corresponding energy management strategy of charging or discharging should be pursued and developed to extend the lifecycle of the EV battery and maintain the battery working with a higher performance. Typical recommended guidelines that should be followed for discharging regulation of an EV battery include maximum continuous discharging current and maximum 30 s discharging pulse current. Those two limits are usually specified by the battery manufacturer to protect the battery from excessive discharging rates that could damage the battery or decrease its capacity. However, the first specification suggests the maximum desired current at which the battery can be continuously charged or discharged. It determines the maximum continuous power that the EV battery can deliver to the grid in the case of V2G mode. The second specification defines the maximum current the battery can withstand during discharging for pulses of up to 30 s.

For charge regulation of a battery, three basic schemes are usually used for charging control of an EV's battery. These schemes are constant current, constant voltage, and taper-current charging [31]. The Constant-current (CC) charging merely means that the charger supplies current with a relatively uniform rate, regardless of the battery temperature or state of charge. This charging algorithm assists in the elimination of imbalances between cells and series-connected batteries. However, defining the battery charging current rate can be challenging. Generally, a charging current that is too low cannot satisfy the charging time speed requirement, and a high-rate charging current could readily stimulate excessive damage during the charging process by gasification of the battery electrolyte. The Constant-voltage (CV) charging ensures almost the same input voltage to the battery throughout the charging process, regardless of its state of charge. The CV chargers normally cause a high initial current to the EV battery because of the higher voltage difference between the battery and the EV charger. In a taper-current charging scheme, the charging current decreases proportionally to the terminal voltage rise of the EV battery [30]. Normally, CC and CV charging methods are integrated together during the battery charging process. Generally, the charging schemes consist of CC charging until the EV battery voltage reaches the charge voltage level, then CV charging is applied, allowing the charge current to taper until it becomes a very small value. It is recommended to follow the charging current during the charging process, which represents the ideal current at which the battery should be charged initially (to roughly 70% of state-of-charge) under the CC charging scheme before transitioning into CV charging scheme [32,33].

3.2. Control of EV-Side Converter

The EV-side DC–DC converter (ESC) controller is shown in Figure 3. A control algorithm for the battery charger is proposed in [29]. These ESC chargers can be integrated within each EV so as to enable specific charging schemes, depending on the EV requirement. In this paper, the CC and CV control strategies have been utilized and then combined together to achieve the requirements of the EV battery charge and discharge process. The ESC controller consists of two control loops—the first is an inner fast current loop (PI_c) and the second is an outer slow voltage loop (PI_v). This nested-loop charge control structure is required only for the CV control algorithm, assuming that the current flowing into the EV battery is positive. The battery voltage Vbat is compared with the battery voltage reference Vbat* then the result of comparison passed to the voltage loop controller PIv. Then, if I_batt > 0, the battery is charging; otherwise, I_batt < 0, then it is discharged. In Figure 3, the switch pointer moves through the top or bottom based on the control input. This input depends on of the SOC current reference I_ref(soc) and CC mode current reference I_ref(sat) in the middle. However, the system operates in the following three modes depending on the SOC and sign (I_ref):

• Case 1: In the case of I_ref < 0, the switch is in the bottom position, and the circuit is controlled to operate in the CC discharge mode. The energy is supplied by the battery to the utility grid or to another EV. This can be done by regulating and adjusting the current reference. To prevent the DC–DC converter from operation at a non-linear modulation state, the voltage signal is generated by the current control loop, which is maintained between −V_tri and +V_tri through a saturation block, where V_tri refers to the magnitude of the triangle carrier PWM waveform.
• Case 2: If the current reference I_ref > 0 and the EV battery SOC is below 70%, the switch is in the bottom position, and the EV-side converter operates in the condition of constant current charging.
• Case 3: If the current reference I_ref > 0 and the EV battery SOC is over 70%, the switch is then moved to the top position, and the EV-side converter switches to CV charging mode. Hence, the voltage controller loop produces a reference current and passes it to the current-loop controller. In this case, the current-loop controller operates the DC/DC power converter to regulate the battery charging at the desired current reference.

To protect the EV battery, the charging current should not violate the maximum current limit. This can be done by passing the current reference through a saturation block. The saturation block forces upper and lower limits on an input current reference signal generated by the voltage-loop controller. In addition, for a seamless transition from the CC to the CV charging scheme, the initial value of the PIv controller should be specified by the same current reference value used for the PIc controller before the control transition takes place. The control scheme enables the charger to transfer the energy from/to the DC bus more effectively while maintaining the connection between the carport and vehicle. As soon as the battery charges, a smaller current is required to preserve the battery voltage. Therefore, the output voltage regulation (OVR) controller produces a current reference signal which passed to the output current regulation (OCR) controller. The limit range of the current reference signal is determined as a function of the DC bus voltage. The upper limit of current reference is set by the maximum current that the EV battery can safely withstand. Once the DC bus voltage decreases below the predetermined limits, the converter will supply energy to the DC bus, as shown in Figure 4. For this reason, the saturation limit of the current reference is reduced if the DC bus voltage continues to decrease during the operation of the converter at full power. The current limit saturation function, f(V_in), is defined as:

$$I_{ref(sat)}=f(V_{in})=\frac{I_{ref\max }}{V_2-V_1}(V_{in}-V_1)$$

(1)

where I_refmax is the maximum current permitted to pass to the EV battery; V₁ is the lower limit of DC bus voltage that is allowed before a fault or overload is detected; V₂ is the DC link voltage setpoint where the power converter reaches its maximum power limit; and V_in is the input voltage (or DC bus voltage). Therefore, the current reference is adjusted by the OVR controller, and the OCR loop regulates the duty ratio and maintains the output current within its limit values. The OCR limits the output current flow based on the energy demand from the DC bus. When the DC bus voltage is too high, the saturation upper limit is adjusted by the OCR current reference. As the DC bus voltage increases, the OCR saturation limit decreases, thus supplying less energy to the DC bus.

3.3. Reactive Power Support function

The EV charger controller studied here provides two main objectives. First, it ensures that there is a surplus active power to charge the customers EV batteries. Secondly, if the utility requested reactive power, then the controller responds immediately. Figure 1 shows the block diagram of the EV charger controller that is equipped with the reactive power support function or the V2G operation mode. As shown in Figure 1, the grid side converter (GSC) can support the grid by reactive power and injects it at the common coupling point (PCC). In the reactive power support mode, the q-axis current reference is produced by a reactive power controller. However, the voltage support to the AC system, the q-axis current reference signal is generated by the PCC voltage controller (see Figure 1). During this mode, the GSC converter should generate as much reactive power as possible, depending on how much the PCC voltage drops. To improve charging station performance, the EV-side converter and GSC should be integrated together. The GSC operates in the optimal control mode with a high amount of active power supplied from the EVs to the grid—i.e., maintaining the DC-link voltage as the first priority while ensuring the reactive power support to the grid and controlling the power demand as much as possible [24].

The EV-charger controller has two inputs, with one input being an active power setting and the other a reactive power setting. An active power command can be derived depending on the EV battery pack size, the SOC, and the user option for the EV charging style (slow, fast, or mixed charging). The reactive power control setting can be immediately requested by the utility [9]. The suggested control scheme uses direct–quadrature–zero transformation equations, low-pass filters, active and reactive power calculation, and a phase-locked loop (PLL) algorithm that achieves synchronization with the utility grid voltage. Phase currents i_a, i_b, and i_c, and utility voltages v_sa, v_sb, and v_sc are converted from a-b-c coordinates to a d-q frame using Park transformation and ωt produced by the PLL. The d-q components can be described using the following equations:

$$\left[\begin{array}{c}{v}_d\\ v_q\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc}\sin (\omega t)& \sin (\omega t-\frac{2\pi }{3})& \sin (\omega t+\frac{2\pi }{3})\\ \cos (\omega t)& \cos (\omega t-\frac{2\pi }{3})& \cos (\omega t+\frac{2\pi }{3})\end{array}\right]\times \left[\begin{array}{c}{v}_{sa}\\ v_{sb}\\ v_{sc}\end{array}\right]$$

(2)

$$\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc}\sin (\omega t)& \sin (\omega t-\frac{2\pi }{3})& \sin (\omega t+\frac{2\pi }{3})\\ \cos (\omega t)& \cos (\omega t-\frac{2\pi }{3})& \cos (\omega t+\frac{2\pi }{3})\end{array}\right]\times \left[\begin{array}{c}{i}_{sa}\\ i_{sb}\\ i_{sc}\end{array}\right]$$

(3)

After applying the above transformation, the three-phase grid voltages and currents in the d-q frame are used to calculate the three-phase instantaneous active power and reactive power shown, respectively, as follows:

$$P=\frac{3}{2}\left(v_d\times i_d+v_q\times i_q\right)$$

(4)

$$Q=\frac{3}{2}\left(v_q\times i_d-v_d\times i_q\right)$$

(5)

The computed instantaneous active and reactive power include oscillation and average components. However, to acquire the average components, two low-pass filters are utilized to the outputs of the active power and the reactive power. The two outer PI control loops are applied to track active and reactive power reference commands. These PI controllers generate active current reference i^*_d and reactive current reference i^*_q, as shown in the following equations:

$$i_d^{*}=k_{pp}(P_{ref}-P)+k_{ip}{\displaystyle \int (P_{ref}-P)dt}$$

(6)

$$i_q^{*}=k_{pq}(Q_{ref}-Q)+k_{iq}{\displaystyle \int (Q_{ref}-Q)dt}$$

(7)

where k_pp and k_pq are proportional constants, and k_ip and k_iq are integral constants for the used PI controllers. P_ref is the reference of the charging power, and Q_ref is the reference value of the reactive power required by the AC grid.

The control of the GSC converter is designed by integrating inner loop current and outer voltage loop (DC bus voltage). Comparing the voltage reference with the actual voltage in the outer loop results in the current reference, which is used for the inner loop control. Hence, the inner PI loops are established by comparing actual measured line currents obtained by utilizing the Park transformation matrix with the current reference (obtained using Equations (6) and (7)). The results (e_d and e_q) are first summed with the decoupling terms and are then normalized by the DC-link voltage (the battery voltage) to get the duty ratios in the d–q coordinate. These calculations are summarized as follows:

$$\left[\begin{array}{c}{d}_d\\ d_q\end{array}\right]=\frac{1}{V_{dc}}\left[\begin{array}{c}{e}_d+v_d+3\omega L\times i_q\\ e_q+v_q-3\omega L\times i_d\end{array}\right]$$

(8)

To obtain the duty ratios in the a–b–c frame coordinates, one can use the inverse matrix transformation, which can be expressed as the following:

$$\left[\begin{array}{c}{D}_a\\ D_b\\ D_c\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{cc}\sin (\omega t)& \cos (\omega t)\\ \sin (\omega t-\frac{2\pi }{3})& \cos (\omega t-\frac{2\pi }{3})\\ \sin (\omega t+\frac{2\pi }{3})& \cos (\omega t+\frac{2\pi }{3})\end{array}\right]\times \left[\begin{array}{c}{d}_d\\ d_q\end{array}\right]$$

(9)

4. Simulation of EV Charger Station

Figure 4 shows the EV charger station simulation model built in Matlab/Simulink. The model consists of a grid model connected to a charging station through a three-level converter and EV battery chargers. Two controllers are used; the first is the charging controller and the second is the GSC controller. The grid model composed of a three-phase voltage source in series with an inductive (RL) branch and connected to a three-phase 600/240 V isolating transformer. The three-phase short-circuit level at base voltage is 30 MVA. The battery model represents a dynamic generic model parameterized to simulate most popular types of EV batteries.

4.1. Charging Controller

The charging currents and voltages of EV batteries are measured. The EV-battery charging current reference and the corresponding duty ratio for each PWM converter are determined in the Simulink model. The controller model can also decide the turn-on or turn-off intervals of the power switch connecting each EV battery. The major functions of the charge controller blocks are the regulation scheme of charging current, the voltage regulation, and the termination decision of the charging process. The charging current scheme is developed based on constant charge current. The charging reference current for each EV battery is calculated at this stage. The traditional PI approach is used to regulate the charging currents and voltages according to the reference currents from the charging current strategy and the reference voltages. The current and voltage regulation laws are formulated in Equations (10) and (11), respectively.

$$d=d_{old}+k_{pi}(I_{ref}-I)+k_{ii}{\displaystyle \int (I_{ref}-I)dt}$$

(10)

$$d=d_{old}+k_{pv}(V_{ref}-V)+k_{iv}{\displaystyle \int (V_{ref}-V)dt}$$

(11)

where V and I are the measured voltage and current of the EV battery, d and d_old are the recent and previous duty ratios used to control the EV-side converter, V_ref and I_ref are the reference voltage and charging current of each EV battery, and k_pi, k_ii, and k_pv, k_iv are the proportional and integral gains for charging current and voltage regulations, respectively. The termination of the charging process can be determined when the charging process stops and outputs a turn-off signal to the corresponding EV-side converter as the charging termination happens.

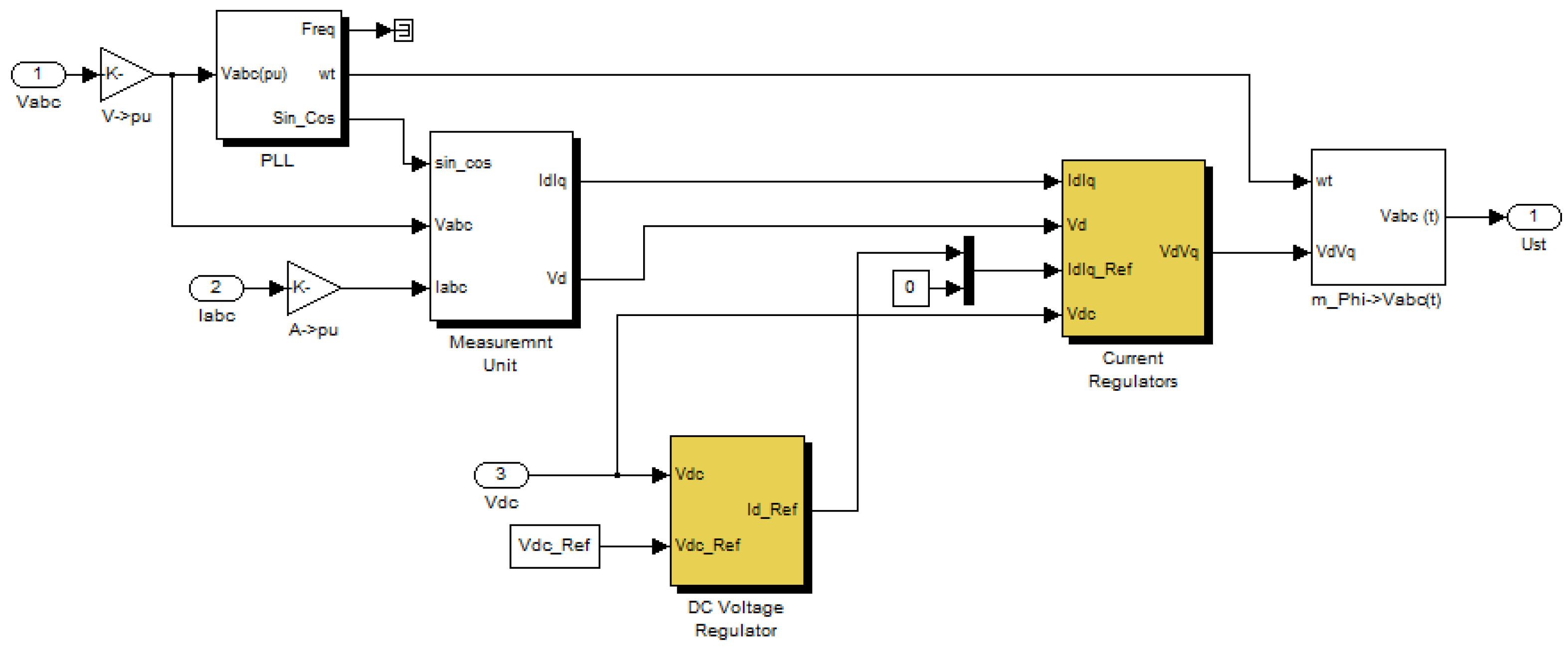
4.2. GSC Controller

The block diagram of the GSC controller in the developed Simulink model is shown in Figure 5. The controller includes a current Regulator, V_DC Regulator, and PLL & measurements. The regulator calculates the required reference voltages for the inverter according to the current references I_d and I_q (reactive current). The PI-fuzzy logic is used for current regulation (Figure 6). The I_q reference is set to zero in the case of G2V and has a specified value in the case of V2G mode. The required active current I_d reference is determined for the current regulator. The PLL & measurements block is required for synchronization with grid and current/voltage measurements, respectively. The PWM Generator produces the gate signals to the active switches according to the required reference voltages. The carrier frequency in this model is set to 1980 Hz (33 × 60 Hz).

4.3. Proposed Fuzzy PI Controller

Due to the non-linear characteristics of EV chargers and distribution networks, a traditional control technique must be substituted by utilizing efficient intelligent fuzzy logic controllers (FLC). This type of controller plays a vital role in distribution networks, supplying EV chargers with efficient, reliable operation and higher power quality. Usually, an FLC controller is composed of three main components: a fuzzification unit, a base rule unit, and a defuzzification unit. More details of those combinations can be found in [6]. The charge and discharge rates are controlled by using FLC. In this case, the input factors to the charging controller, such as the SOC of each EV and the voltage condition at the node on which the charging station is connected. If SOC is low and the node voltage is high, the EV battery will charge, while for a higher SOC and lower node voltage, the EV battery will discharge. However, there are some cases where both the node voltages and SOC are high or both are low. In such conditions, a specific charging/discharging rate is employed. Consequently, the FLC must be adjusted to take care of critical situations as well, so as to maintain the voltage fluctuations at the distribution node within the standard limits.

The fuzzy logic variables may have truth values extending in various degrees between 0 and 1, renowned as their membership grade. Fuzzy logic can treat with the uncertainties in the EV charging system through a straightforward IF-THEN rule-based approach, thus eliminating the requirement of a mathematical model of the controlled system. This is useful, particularly in complex systems that are difficult to model mathematically. However, the complexity of fuzzy logic-based systems increases quickly with the number of inputs and outputs. Figure 7 shows a Mamdani type FLC [34], which has been discussed in this paper. The studied system control scheme has been arranged at two levels. The first level is the charger station, while the second level is the distribution node level. The charger station controller (CSC) will determine the individual involvement of the EVs for charging or discharging. Each EV battery’s SOC and the node voltage are the input parameters to the CSC.

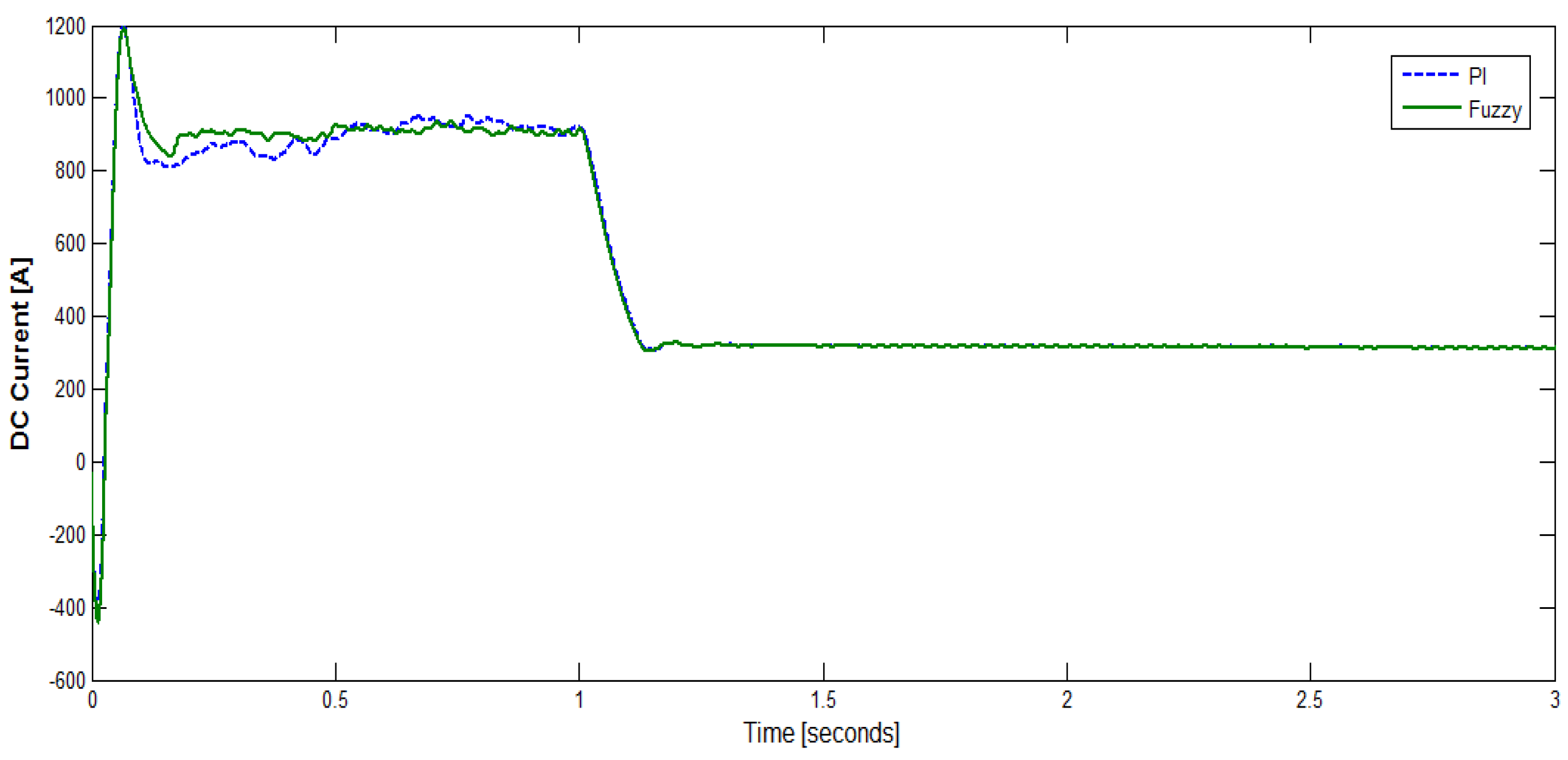
5. Results and Discussion

In this study, the simulation has been carried out for 5 s so as to verify the transient behavior of the system using a fuzzy logic-proportional integral (FL-PI) controller. The charging and discharging scenarios of EVs are presented separately. The grid support is verified by injecting reactive power to the AC distribution grid. In order to verify the effectiveness of the given controllers, the performances are tested by using Matlab/Simulink for the EV charger station in comparison with the proportional integral controllers. Simulation of EV charger station is implemented to monitor the impacts of EV technology on the present grid. The data generated from this model will allow utilities to forecast the impact of the charging stations on the grid. The schematic of the modeled system is shown in Figure 4. The model parameters are listed in

Table 1. System parameters.

Parameters	Rating
AC Input Voltage	600 V
System frequency	50 Hz
Source Inductance	26.5 mH
Transformer power rating	15 kVA
Transformer primary voltage	600 V
Transformer secondary voltage	60 V
AC filter rating	2 kVA
converter bridge rating	15 KVA
DC current rating	20 A
DC output voltage	48 V

. The model consists of a three-phase grid connection bus at 600 V·rms. The DC voltage from the rectifier is fed to a controlled DC–DC converter to supply DC power to the vehicle battery at a constant current. A control loop is used to vary the firing pulses to the bidirectional power converter that switches and controls the output voltage, which is matched to the battery voltage level. Two types of control circuits were employed to control the charging current. The current in the line and the current fed to the converter are shown in Figure 8. The current drawn from the AC system is sinusoidal due to the AC filters employed. The lack of such AC filters will directly feed the harmonics into the grid source.

The impact of a few charging stations is unlikely to impact the grid in a dramatic way. However, if a large number of such charging stations are deployed in the future, then there is going to be an impact on the grid. The anticipated impact will be a result of the relative short circuit ratio of the grid presented at the PCC point. Figure 9 shows the rectified DC voltage, while Figure 10 shows the rectified DC current.

The active and reactive powers fed to the charging station are shown in Figure 11. From a quick inspection of Figure 11, it represents G2V mode to charge the connected EVs. The charging station works on such a mode, in which energy flows from the utility grid to the EV chargers station, depending on number of electric vehicles required to be charged and the battery capacity of each vehicle. The energy absorbed/released can be seen from active and reactive power waveforms at both ends of the GSC and EV-side converters. The control schemes for reactive power in steady state are described in Figure 1; all control the q-axis current reference by multiplying the d-axis current-reference by the output from the reactive power regulator. In no-load, the d-axis current reference is zero, so the reactive power controller has no effect in no-load. In practice, it is necessary to work in unity power factor to improve the efficiency of the system. This is acceptable at a certain level; if the system is pure resistive or capacitive, it may cause some problems in the electrical system. The electrical AC power system supplies or consumes both real and reactive powers. The real power achieves useful work, while reactive power improves the voltage that should be regulated for system reliability, and it is useful to maintain System voltage healthily. In other words, the reactive power has a deep effect on the stability of power systems because it has an impact on voltages throughout the system. Figure 12 shows the active and reactive power waveforms in the case of V2G mode, where the reactive power is injected to grid.

The simulation results are also tabulated as a comparative performance in view of settling time and peak overshoot, as shown in

Table 2. Comparative performance of the used controllers.

Parameter	Controller	Settling Time	Peak Overshot
DC Voltage	PI	0.75 s	24%
	Fuzzy-PI	0.25 s	24%
DC current	PI	0.85 s	33%
	Fuzzy-PI	0.25 s	33%
Active power	PI	0.76 s	30%
	Fuzzy-PI	0.5 s	40%
Reactive power	PI	1.2 s	450%
	Fuzzy-PI	0.6 s	300%

. The output of the conventional proportional-integral-derivative controller (PID) system has a quite high overshoot and settling time.

The rectified DC voltage reached a stable value of 500 V at time 0.25 s using the fuzzy PI controller, while it reaches the steady state value at time 0.75 s. The DC current reached a steady state value of 850 A at time 0.25 s using the fuzzy PI controller, while it reaches the steady state value at 0.85 s when using the PI controller. The active power reaches a steady state value of 500 KVA at time 0.5 s using the fuzzy PI, while reaching the same value at 0.76 s using the PI controller. From these figures, it is clear that the fuzzy PI controller performed more efficiently than the PI controller. In V2G mode, energy flows from EVs to the grid according to the discharging capacity of each EV. As shown Figure 12, the GSC can supply the reactive power or support the voltage at the PCC coupling point. In the reactive power injection mode, the q-axis current reference i^*_q is produced by using a reactive power controller. While in the utility AC system voltage support control mode, the q-axis current reference is produced by the PCC voltage controller, during which the GSC should supply reactive power as much as possible, depending on the PCC voltage drop level. From Figure 9, Figure 10, Figure 11 and Figure 12 it is clear that responses gained verifies that the PI-fuzzy controller provides better settling time performance than the conventional PI controller. Hence, the control approach using the PI-fuzzy concept is more accurate, intelligent, and faster than the traditional PI control strategy. From inspection of Figure 12, it represents a case study of reactive power support to grid. The charging station works in V2G mode, in which power flows from the EV charging station to the utility grid, depending on how many connected electric vehicles and the charging capacity of each vehicle and grid condition.

6. Conclusions

In this paper, the use of electric vehicles (EVs) is proposed as a temporary power supply to support critical infrastructure during emergencies. The use of EVs and a community-level storage unit further enhances the resilience of the microgrid, by utilizing the available the electric vehicles, and by investing its storage unit. The charging reference current for each EV battery and the correspondent duty ratio for each power converter are determined in the Simulink model. The developed Simulink model of the controller also regulates the turn-on or turn-off periods of the switch connected to each EV battery. Hence, the charging controller can generate a turn-off signal when the charging stops or a fault is detected. Typical control strategy for three-level PWM rectifier/inverter was presented. The PI controller and PI-FLC controller are evaluated to verify the suitable controller for the EV charging station. A comparison between PI controller and Fuzzy controller demonstrate the superiority of proposed PI-Fuzzy over conventional PI for the same conditions. The simulation results show that the PI-FLC controller has better operation performance.