Abstract
Demand Side Management (DSM) is a popular approach for grid-aware peak-shaving. The most commonly used DSM methods either have no look ahead feature and risk deploying flexibility too early, or they plan ahead using predictions, which are in general not very reliable. To counter this, a DSM approach is presented that does not rely on detailed power predictions, but only uses a few easy to predict characteristics. By using these characteristics alone, near optimal results can be achieved for electric vehicle (EV) charging, and a bound on the maximal relative deviation is given. This result is extended to an algorithm that controls a group of EVs such that a transformer peak is avoided, while simultaneously keeping the individual house profiles as flat as possible to avoid cable overloading and for improved power quality. This approach is evaluated using different data sets to compare the results with the state-of-the-art research. The evaluation shows that the presented approach is capable of peak-shaving at the transformer level, while keeping the voltages well within legal bounds, keeping the cable load low and obtaining low losses. Further advantages of the methodology are a low communication overhead, low computational requirements and ease of implementation.
1. Introduction
In the future, we expect an increasing penetration of electric vehicles, photovoltaic panels, heat pumps and wind turbines. As especially heat pumps and electric vehicles create relatively large and synchronized peaks, often at times when there is little renewable energy available, the balance between production and consumption of electricity becomes more and more an urgent issue.
To counter the problems that arise due to this trend (for a survey, see [1]), Demand Side Management (DSM) techniques can be deployed to prevent peaks. Here, DSM is the collective term for a set of techniques that control the production or consumption within the customers’ premises. A central entity (e.g., the network operator) requests customers, via a steering signal, to adapt their production or consumption in order to shape the load profile of a certain subgroup of the grid (e.g., a group of houses). These customers can either adapt their behavior manually, or install a device that is referred to as a Home Energy Management System (HEMS), which makes such decisions on their behalf. In the latter situation, the HEMS should start appliances (referred to as smart appliances) when the consumption should be increased, or should advance or delay the use of such an appliance when the consumption should be decreased. In addition, energy storage (e.g., batteries) can be used to mitigate a surplus of renewable energy by charging, and a peak in the consumption by discharging. In this article, we focus on electric vehicles as they introduce both a significant load, and provide a lot of flexibility.
There are several types of DSM approaches described in the literature. In this article, we consider two important classes of such approaches. The first class, called control-based DSM, makes control decisions for appliances for the next time period based on available data at the given time such as consumption, flexibility, priorities, etc. The second class, called planning-based DSM, plans control decisions for a longer period in the future (e.g., one day ahead). Because control-based DSM does not plan ahead, it risks using the available flexibility too early, such that no flexibility is left when later on, e.g., a large peak occurs. Planning-based DSM does take this into account, but requires predictions of future production/consumption. For example, the planning-based DSM approaches in [2,3] require such predictions at a house level. In Section 2, we discuss control and planning-based DSM in more detail, and argue that both approaches have serious disadvantages.
In Section 3, we describe how a HEMS can be used to control the charging of a single electric vehicle (EV) at the house level to follow some desired load profile. In contrast to the related work (e.g., [4]), no prediction of a load profile is required. We show that a prediction of a single parameter characterizing the optimal solution and a prediction of the load for the upcoming interval is sufficient to make a near-optimal planning of an electric vehicle. We provide an analysis that studies how the results of our online approach approximates the optimal solution, and give a bound on the maximal relative deviation. This bound shows that, under reasonable circumstances, the costs for the achieved solution are only a few percent more than that of the optimal solution.
Section 4 generalizes these results to the case of a neighborhood with multiple EVs. The presented solution is a peak-shaving approach that keeps the overall load of the neighborhood below a certain level, and simultaneously keeps the load profiles of each individual house as flat as possible. By this, also the risk that the voltage exceeds the legal bounds (e.g., 207 V–253 V in The Netherlands [5]) is minimized, the cable load is kept low and thereby unnecessary losses are avoided. Note, that a DSM approach that does not take these aspects into account may cause more problems than it solves, as was shown by Hoogsteen et al. [6].
Since Section 3 and Section 4 depend on predictions of a few characterizing values, we study how these predictions are obtained. Section 5 uses measured data and discusses how the required predictions of the characteristics can be easily obtained.
The potential of our approach is evaluated in Section 6 and compared to the state-of-the-art research. We show that the few parameters we need can be predicted accurately and are sufficient for near optimal operation of a group of houses. Section 7 concludes this article.
Summarizing, the contribution of this article is a demand side management methodology with the following properties:
- It only uses a prediction of a single parameter that characterizes the optimal solution, together with a power prediction of the house for the upcoming interval to plan the charging of an electric vehicle in a house.
- A peak at the transformer can be counteracted with low communication overhead using a decision making process that also requires predictions of characteristics that aid at making trade-offs at the neighborhood level.
- A prediction scheme for the required parameters, combined with a sensitivity study that shows that the results do not suffer much from prediction errors.
2. Related Work
There are several classes of DSM approaches in the literature. In Section 2.1, we discuss control-based DSM approaches, and in Section 2.2 planning-based DSM approaches. As we use electric vehicles as a proof of concept, we treat DSM applied for a group of electric vehicles specifically in Section 2.3.
2.1. Control-Based DSM
The first class of approaches is control-based DSM. These approaches use an estimation of the current state of the system, and make online control decisions based on this state. As these approaches do not take future decisions into account, they may deploy flexibility at an early stage, while this flexibility might be of more use at a later time. As a result, it can occur that a large peak cannot be prevented because the system has already used most of its flexibility.
Example 1.
A typical example for this is the control of a battery in combination with photovoltaic (PV) panels in a house. A control-based DSM approach would charge the battery starting at the time more energy is produced by the PV than is consumed inside the house. On a sunny summer day, this generally leads to a full battery before noon. As a consequence, the high PV peak cannot be reduced by the battery and the local distribution grid may get capacity problems. In Germany, this is nowadays already a serious problem (see, e.g., [7]).
An example of control-based DSM is the PowerMatcher (see, e.g., [8,9]). Recently, some of these control-based approaches have been adapted to incorporate some form of predictions to mitigate to some extent the mentioned disadvantages (see, e.g., [10]).
2.2. Planning-Based DSM
The second class of approaches, planning-based DSM, makes a more detailed prediction of the future power production/consumption (e.g., one day ahead in time) and uses this information to plan the control decisions for smart appliances (a planning) to attain a given goal (e.g., peak-shaving). The strength of this approach, compared to control-based DSM, is that flexibility can be preserved for when it is required the most. A disadvantage may be that to make the needed plannings, specialized algorithms are required at device level (e.g., [4]) and/or for groups of appliances or houses (e.g., [2]).
In the approaches described in [2,3], each house makes a prediction of its average power consumption for each 15 min interval within the upcoming day (i.e., 96 intervals). These predictions are sent to a neighborhood controller, and summed up to obtain the predicted neighborhood profile. This predicted neighborhood profile indicates when peaks occur, and gives also hints on how the house profiles could be adopted to counter these peaks. Based on this, the neighborhood controller requests some or all houses to follow a new desired (or difference) profile [2], or it sends incentives to houses to adapt their profile [3]. Each house on its turn uses both the information sent by the neighborhood controller and its previous predictions and planning to make a new planning for all its controllable appliances. This procedure is repeated iteratively until the neighborhood controller is satisfied with the resulting planned neighborhood profile.
The drawback of these type of approaches is that they are sensitive to poor predictions. When the predictions are not accurate, the derived planning may be of a low quality or even not valid. Although some information is relatively easy to predict at the neighborhood level [11,12], it is often hard to predict the same information at the household level [11]. Furthermore, the error made due to poor predictions at the household level may accumulate at the neighborhood level. This effect can be explained the best by a simple artificial example:
Example 2.
Household power prediction problem. Consider a group of 100 houses, where each house contains a television and where each of the television is used with a 90% probability at 8 p.m. When a house controller has to decide if it incorporates the TV within its planning at 8 p.m., it should do this since the probability is close to 1. Within the planning at the neighborhood level, this implies that all 100 televisions are likely to be switched on at 8 p.m. However, when one would estimate, on a neighborhood level, how many televisions are turned on at 8 p.m., the best estimator is the expected value, which is 90 TVs. This shows that if predictions are based on probabilities, prediction errors may accumulate at the neighborhood level.
The example indicates that summing up local predictions of events may cause prediction errors that would not have been made at a more global level. Furthermore, predictions based on statistics alone work in general only for large groups, e.g., for neighborhoods instead of houses [11]. When this observation is used as a work-around in the planning-based DSM approach, details about user behavior and measurements are accumulated at the neighborhood controller level such that decisions may be made there based on probabilities over large groups (instead of within the house). However, such an approach would no longer be (decentralized) DSM, but is, e.g., closer to demand response [1] and no longer distributed. Furthermore, it would require sharing of privacy sensitive information. The goal of this article is to avoid the mentioned restrictions. Summarizing, we may state that robust demand side management should only rely on house level predictions if this methodology is robust against prediction errors.
2.3. Groups of Electric Vehicles
For the application of EV charging, the state-of-the-art research on DSM (see, e.g., [13,14,15,16,17]) requires EV owners to share information (e.g., EV arrival) with a centralized controller. The approach presented in this article does not require such sharing of privacy sensitive information and has a low communication footprint.
The approach ORCHARD presented in [14] also flattens the load profile for a group of EVs without requiring knowledge of future EV arrivals. It has a time complexity of for N EVs and is similar to our work in the sense that we also do not know about EV arrivals beforehand. Contrary to [14], our work requires time (for M time intervals) when an EV arrives (within each house). Furthermore, our research flattens the load both at the house level and at the neighborhood level.
3. Online Electric Vehicle Planning
This section describes for the case of charging an Electric Vehicle (EV) how a house can follow some profile, for example to make the load profile as flat as possible, by using proper charging settings. Section 3.1 introduces the corresponding EV planning problem. Section 3.2 presents our approach, which is inspired by online optimization, rolling horizon planning, and model predictive control: at the start of every time interval, we use a prediction of the power for this interval together with a prediction of a single value that characterizes the requirements for the future intervals to determine the charging power for the next time interval.
By delaying the decision for the amount of charging done in an interval until the very start of this interval, we can hope that more accurate predictions are possible. Furthermore, we can compensate for errors made in previous time intervals. Finally, Section 3.3 discusses the influence of prediction errors on this algorithm.
3.1. The EV Charging Problem
We first introduce some notation before we give a formal definition of the EV planning problem. Let be the time interval at which the electric vehicle arrives at house and is ready to be charged, let be the the interval at which the charging has to be completed, and let be the energy that needs to be charged in the intervals . The EV charging decisions can be described by a vector , where is the amount of electricity charged for vehicle n during time interval m. The maximum charging power is given by (in watts), and the vector is feasible if for and , in the remaining intervals, and , where τ is the length of a time interval. To ease the notation, we use .
Let the desired power profile for the house and EV load together be . The goal is to determine a charging vector such that the uncontrollable house power consumption () together with the charging matches this desired power profile as well as possible. More precisely, we look for a vector that minimizes the Euclidean distance between the vectors and . To express the difference between the actual and desired load, we define , . Note that the aim of the objective is to bring the values of as close as possible to zero, where large values are addressed first in order to minimize the Euclidean distance (i.e., due to quadratic terms).
To ease the discussion and notation further, we omit the index n (we consider a single house), and we may assume w.l.o.g. that and . This leads to the following optimization problem:
Problem 1.
One commonly considered objective is to create a power profile that is as flat as possible, i.e., to set all elements of the vector to a constant (e.g., the average of the loads). A well-known property of Problem 1 is that all constant vectors lead to the same optimal result , hence, we may use (and thus , which is the total load) to ease the notation.
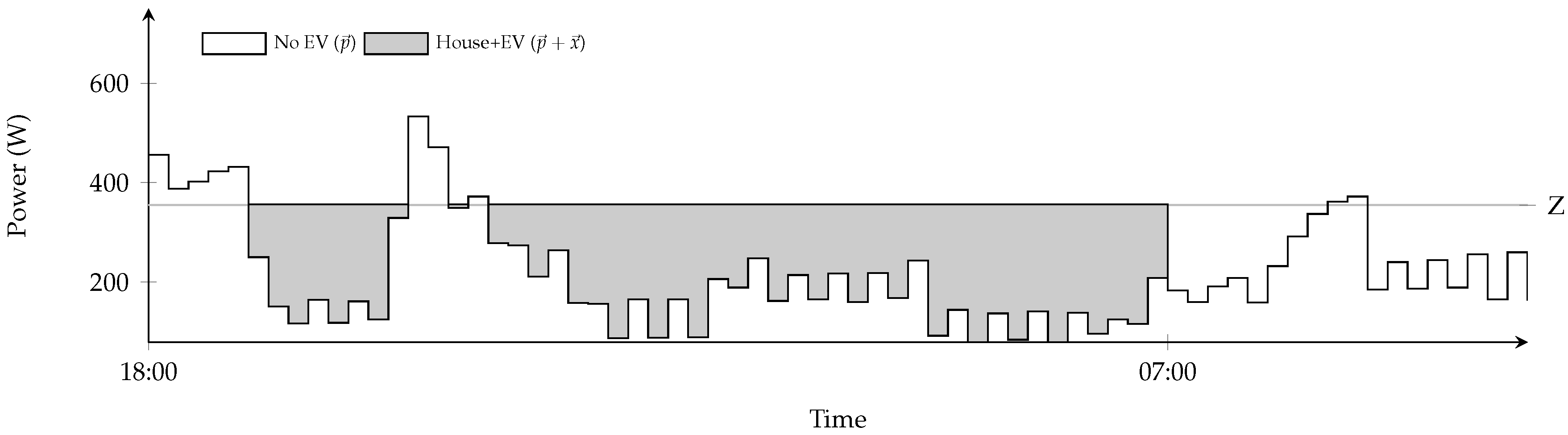
Several papers study algorithms that can solve this problem optimally. An intuitive approach is the so-called valley filling approach [16]. This approach is demonstrated graphically in Figure 1, wherein an EV (arriving at 18:00, to be fully charged at 07:00) is charged with the goal to obtain a flat profile (i.e., as mentioned before). The optimal solution flattens the total house profile by charging in such a way that the “valleys” are filled up to a certain fill level Z. This optimal fill level Z depends on the shapes of the “valleys” and the amount C to be charged. In Figure 1, C corresponds to the gray area. Note that Z can also be interpreted as the optimal minimal mismatch between the obtained and desired profile that we have to accept. If we have a lower mismatch in some other interval ℓ (i.e., ), this needs to be compensated in some other interval ℓ by a mismatch even greater than Z (i.e., ), which is, in terms of Problem 1, less flat and thus suboptimal. Charging up to the level Z (i.e., ) makes sure that the EV battery is fully charged exactly at the deadline without introducing peaks.
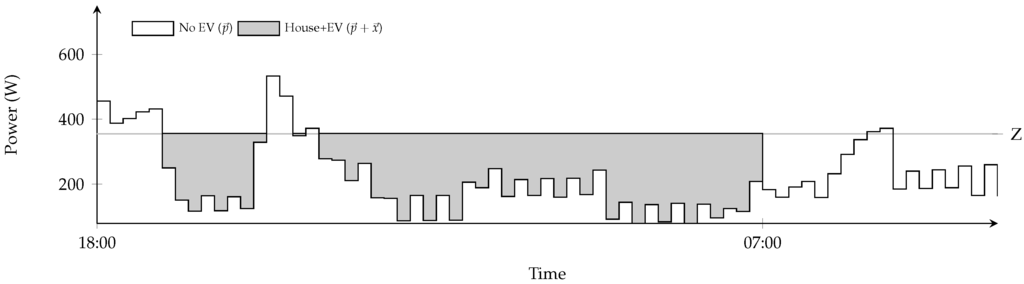
Figure 1.
Optimal EV planning.
In [16], a line search to find the value Z is proposed. A different approach is taken by van der Klauw et al. [4]. They determine the intervals in which no charging should take place, after which they can straightforwardly calculate Z. Their algorithm finds the optimal planning in time.
The EV charging problem falls in a more general class of problems that are referred to as “resource allocation problems” [18]. Hochbaum and Hong [19] study several resource allocation problems, and they present an algorithm for a generalized version of Problem 1, which also can take into account integer restrictions for the values of and has an asymptotic time complexity of . However, this algorithm has a large constant since it relies on median finding [20]. Therefore, the algorithm is in practice only fast for a relatively large M.
3.2. Online Optimization
When the power consumption in future intervals is known beforehand, the aforementioned algorithms can be used to calculate the optimal charging power for each future interval. However, in most cases, these future values are not known and must be predicted. Obviously, prediction errors may lead to non-optimal decisions, and the impact of such errors at a house level is rarely considered in the literature. Furthermore, it is in general difficult to predict the power consumption for all future charging intervals at the beginning of the planning. Therefore, we take a different approach that does not need this detailed information.
Central in our approach is the observation that for the aforementioned algorithms, a single value Z uniquely characterizes the optimal solution. For all feasible instances of Problem 1, there exists a Z such that the optimal solution can be constructed by setting
Note that this calculation, for time interval m, can be delayed until the beginning of the time interval, and, thus we can delay the prediction of to this time.
The sketched approach is in principle interval based; however, it can easily be adapted to an event based approach that recalculates the charging power whenever the power consumption of the household changes and all results in this section are also valid for the event based approach.
As a consequence of the above, the main challenge of our approach is that we do not know Z and, therefore, this value must be predicted. However, compared to approaches that predicts power for each interval, this approach has two advantages, namely, that only a single value Z is predicted (instead of the complete vector ), and that the resulting error due to an incorrect prediction can be bounded as we discuss in the next section.
3.3. Predictions
As we, in general, do not know Z, we use a prediction of Z, which we denote by . When , Equation (5) chooses charging powers that are not sufficient to charge the car up to the desired level. This can be resolved by charging at the maximum power (or some other pre-set charging power) starting from the interval where this becomes the minimum charging power that is needed to charge the EV within the remaining intervals. Note that this may result in large peaks and high costs (i.e., high objective values) at the end of the charging period, as we discuss later on. On the contrary, in the situation where , the algorithm charges faster than required resulting in some time intervals at the end of the planning period with low or zero charging power values.
Algorithm 1 takes these two cases into account and guarantees that the SoC target is reached in both situations. Note that Algorithm 1 produces the same (optimal) solution as Equation (5) when . Before the first invocation of the algorithm, the variable T, which expresses the amount of energy already charged, is initialized to zero. Then, iteratively before each interval m, this algorithm is used to calculate the charging power for this interval. Hence, at the beginning of the m-th interval, expresses the amount already charged up to this interval of the total C to be charged.
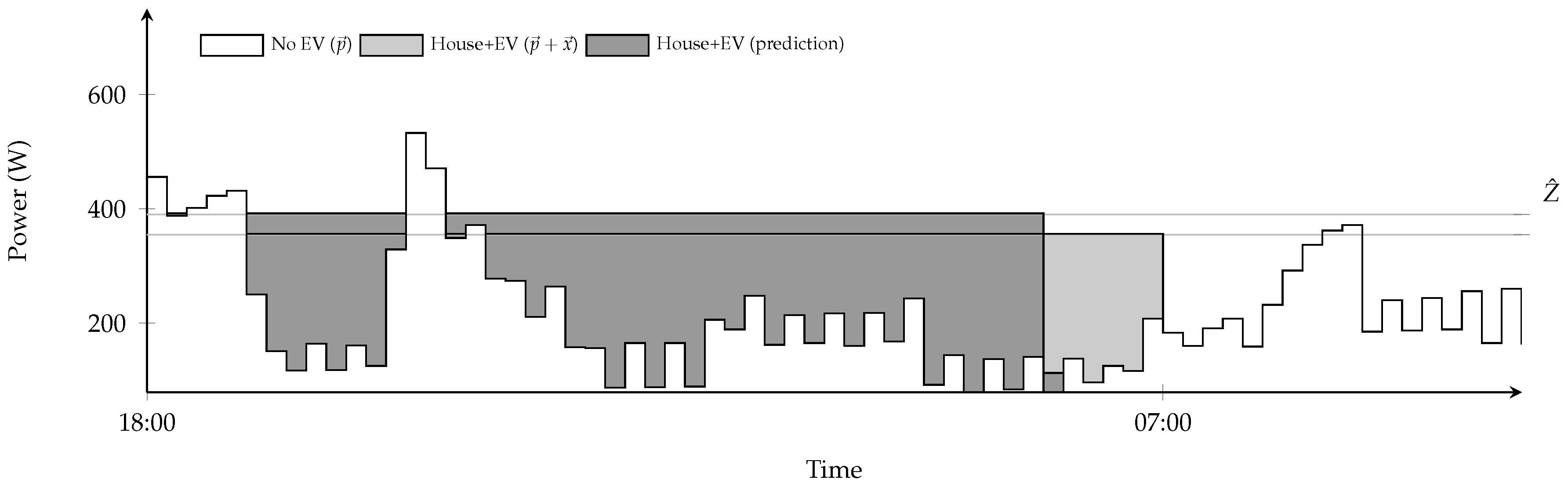
Figure 2 illustrates an instance with and , which shows that the prediction error is spread out evenly over all intervals where charging takes place, but the charging stops before the deadline. The ratio between the objective value of the optimal solution and of the online algorithm using is in this example. On the website [21], an interactive demonstration of Algorithm 1 can be found.
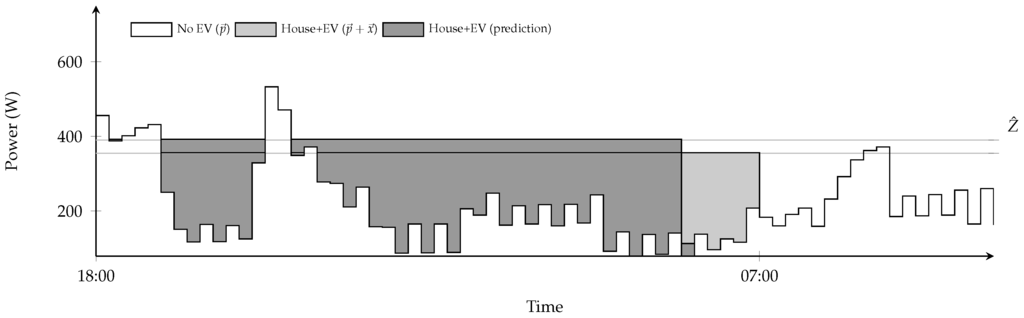
Figure 2.
Optimal EV planning and EV planning using the prediction .
| Algorithm 1 Online EV planning for time interval m. |
| {needed for } |
| if then {needed for } |
| end if |
In the following, we consider the case that . For this case, we derive a bound on the ratio between the objective value of the optimal solution and the objective value of the solution that uses the prediction , which only depends on Z and .
To ease the discussion, we use and to denote the objective value of the optimal solution and the objective value of the solution that uses the prediction , respectively. To derive bounds on the ratio , we need the following lemma.
Lemma 1.
Let be an optimal solution to an instance where (for all m), and let . Then, we have:
Proof.
Assume that in the optimal solution we have a for some m. This implies that and the algorithm tried to fill this interval up to Z, but did not succeed. The only reason for this is that the maximum amount of charging was not sufficient to reach Z. As a consequence, the algorithm will charge in this interval, which is a contradiction to for all m.
Hence, we have
☐
This lemma is used to derive a bound on the ratio between the objective value of the optimal solution, and the objective value of the solution based on the prediction .
Theorem 1.
When , the ratio between the objective value of the optimal solution and that based on the prediction is given by
Proof.
Note that when for an interval m, we have because , i.e., both solutions are the same for such intervals m. As a consequence, if the instance has an interval m with , replacing this instance by an instance with leads to an increase of the ratio as , and both and decrease by the same amount; i.e., we may assume for this proof w.l.o.g. that for all intervals m. Similarly, we may assume w.l.o.g. that , since otherwise and the ratio only improves. Because of this latter assumption, the instance meets the requirements for Lemma 1.
Let . First, we show that . For this, consider a solution of Algorithm 1, which is characterized by . Since the obtained result is feasible, we have
Now, we have
Combining this inequality with (due to Lemma 1), we get:
which proves the theorem. ☐
This theorem gives a bound on the relative deviation of the objective value of the solution of Algorithm 1 compared to the objective value of the optimal solution. Note that this bound depends only on the relative deviation of the used estimate for the fill level compared to the optimal fill level, and that this dependency on this relative deviation is dampened by the square root function.
4. Fleet Planning
This section extends the results from the previous section to charging multiple EVs. In a domestic situation, cars are typically charged when their owners arrive at home, which commonly is in the evening and coincides with a domestic consumption peak. Especially when multiple EVs are charging simultaneously within a neighborhood, there is a risk of high peaks and therefore of overloading the transformer. As we argued in the previous sections, predicting a load profile is difficult, while controlling an individual EV with only few predictions can be done. We extend this approach to multiple EVs by adding another method that shaves load peaks at the neighborhood level at the moment they are noticed (e.g., in an online setting). For this, we propose the following solution:
- The charging of EVs is planned locally within the houses such that the total household consumption power profile (including the EV) becomes as flat as possible.
- When the total power P of a group of houses is above a given threshold of X watts, the EVs are requested to decrease their total charging in the next time interval by in a way that keeps the individual local power profiles as flat as possible for their remaining charging window.
- When the total power P of a group of houses is below a given threshold of Y watts (e.g., PV production peak), the EVs are requested to increase their total charging in the next time interval by in a way that keeps the individual local power profiles as flat as possible for their remaining charging window.
This approach, which is detailed below, has several important advantages. By starting with flat profiles on house level in the first step, the individual peak loads, and with it the probability of overloading the network, decreases. Furthermore, flattening the house load increases self-consumption of locally generated electricity (e.g., PV), has a positive impact on the voltage, avoids overloading the grid, and decreases losses (as is demonstrated in Section 6).
When there is still a peak consumption for the group of houses (e.g., in the evening), the second step of the proposed approach coordinates the charging while avoiding new local peaks. To quantify these local peaks, we use a cost function that expresses how much changing the power for the upcoming interval from to influences the flatness of the entire power profile for house n (i.e., also considering impact on the future). This function aids us with finding the EVs that can contribute to obtaining a total power difference with minimal impact to the local flatness, and thus preventing problems in the future. More specifically, our objective is to obtain a total power difference Δ for the group of houses in the next time interval, while retaining the flatness of the power profiles of individual houses as much as possible. This is expressed mathematically as:
Problem 2.
where f and g are introduced for reference in the later results. To ease the presentation, maximal charging powers are not considered in this formulation. However, to solve Problem 2 with additional maximal charging power constraints, we just can solve Problem 2 (without these constraints) and fix any violations using a Pegging Method; see [22] for a discussion of such methods.
Before we can solve this problem, we first need a formal description of . These costs depend on the charging level to be attained in the charging intervals (i.e., the fill level ), and the uncontrollable loads in the other intervals. The subset of intervals where charging up to Z takes place is denoted by , i.e., contains the intervals where . Let denote the number of such intervals (excluding the first interval). Using this notation, the costs for house n can be determined as function of (note that now received a subscript to indicate the house):
Intuitively, this means that the incurred costs are the costs of charging up to in the active intervals (first term), and the costs of the intervals where no charging takes place (second term). We notice that, for practical data, (see the discussion in the next section) rarely changes with δ and may be estimated to be constant, and therefore the last term of the equation above does not have to be considered for optimization. This means that we can approximate by:
where the first term gives the costs of changing the first interval and the second term expresses the costs of the other active charging intervals. To study the influence of on the costs, we need the derivative of , given by
The following lemma provides a sufficient condition of optimality for Problem 2, which is later used to find an optimal solution.
Lemma 2.
Let be given by (6). If we have a solution to Problem 2 that satisfies
and
this solution is optimal.
Proof.
The intuition behind this lemma is that when , the costs can be decreased by slightly increasing and decreasing by the same amount.
Using this lemma, we can derive the following theorem that provides the optimal values .
Theorem 2.
Let be given by (6). Then, the optimal solution to Problem 2 is for all n:
where
Proof.
A consequence of this theorem is that only the number of charging intervals determines the change in charging power.
5. Predictions
The methods presented in the previous two sections are based on proper predictions of the fill level and the number of active charging intervals for each house n. To validate that these values are relatively easy to predict, we analyzed these values using 90 consecutive days of measurements from a Dutch house, and used this to calculate the optimal charging profile for each of the days between 18:00 and 24:00, subdivided into 24 intervals of 15 min.
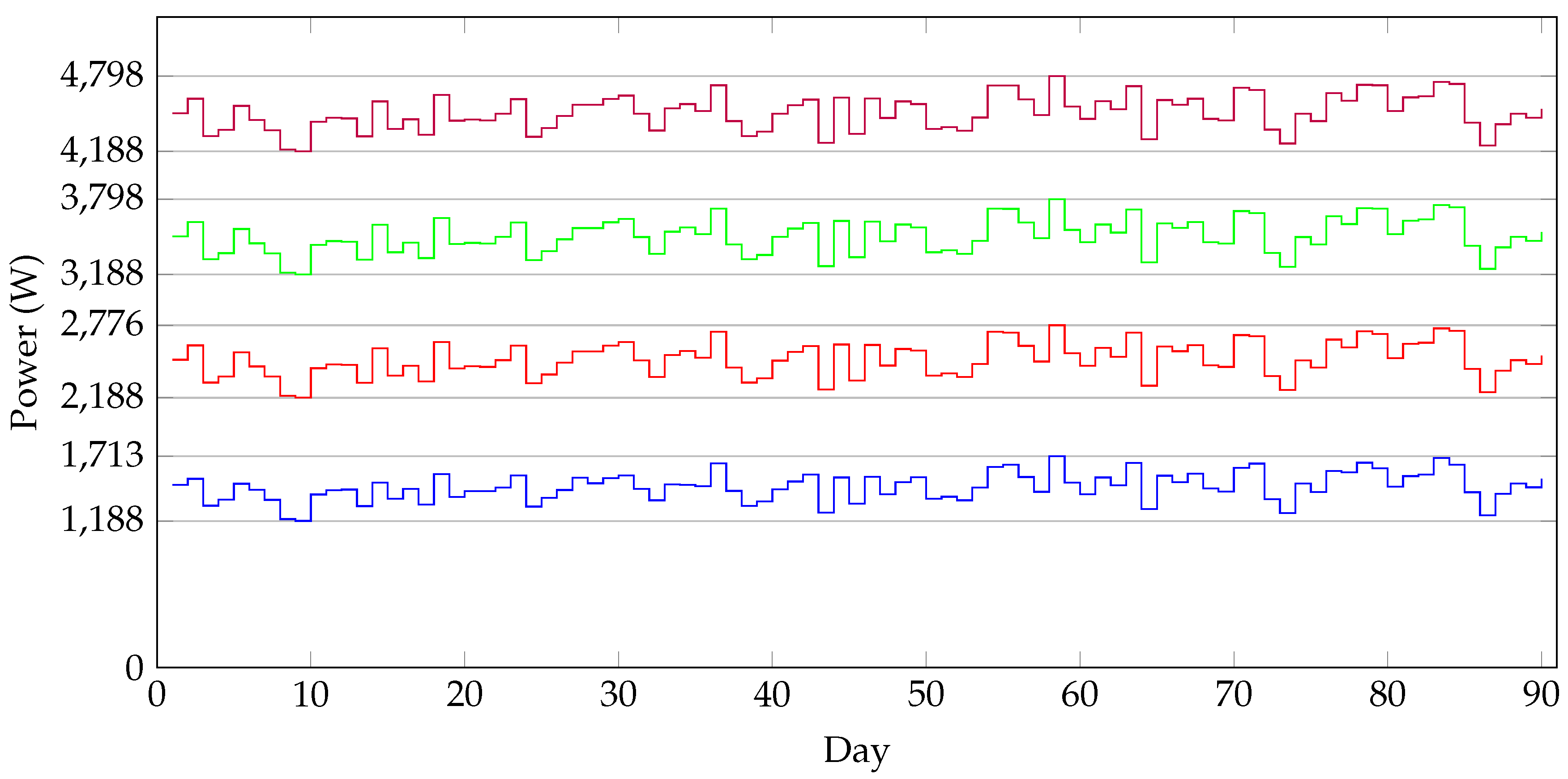
The results for different charging amounts (in kWh) are presented in Table 1. This table shows that the values for are in a small band for all 90 days. See also Figure 3, where the four graphs correspond to the different values from this table are given. When we take the maximum encountered as prediction and use this prediction for all 90 days, the last column shows that highest realized costs increase by at most 16%, although the median is significantly lower (7% additional costs). The column gives the bound of the costs as estimated by Theorem 1 and shows that this theorem provides a reasonable bound of the costs.

Table 1.
Analysis of and for 90 days for charging between 18:00 and 24:00.
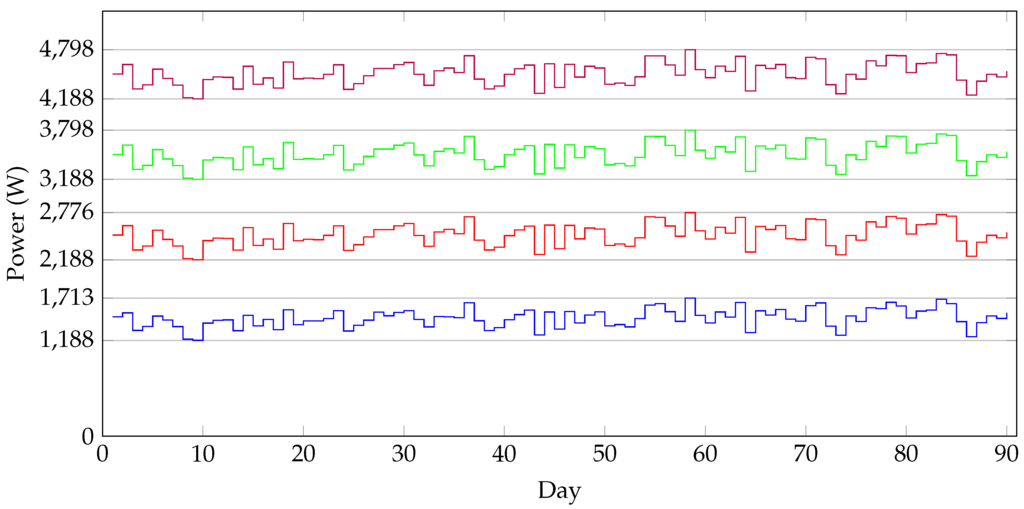
Figure 3.
Fill levels corresponding to Table 1.
These results suggest an efficient way of predicting : use measurements from the previous days to calculate the for each of these days, and use the highest encountered value as . To calculate , the deterministic EV planning algorithm from [4] can be used, and, as indicated in this paper, this algorithm can calculate the result in order of milliseconds and has a time complexity of . Since we use this approach for each EV that arrives, our approach has a complexity of , for K EVs.
Charging the EV within a relatively short interval, such as the interval between 18:00 and 24:00 above, results in a relatively high charging power, especially if the charging amount is also relatively high. This results in a profile wherein most intervals are used for charging (i.e., is close to the total number of intervals) and the profile itself is flat (i.e., it precisely reaches ). When a longer charging interval is taken with multiple higher peaks (e.g., during the day and/or evening), the charging is spread out and done at lower power. To illustrate this, we repeat the experiment with a charging between 14:00 and 24:00 (when consumption is highest). The achieved results are as presented in Table 2. Note that, in this table, the values are more diverse since the house consumption plays a larger role. Note that can be interpreted as the number of intervals with low house consumption compared to the fill level . Since even with a long charging horizon, the variation in is small, this is an additional indication that our assumption from the last section that is (almost) constant is reasonable. The results also indicate that is easy to predict, and this can be done similar to (and simultaneously with) obtaining , as was described above.

Table 2.
Analysis of and for 90 days for charging between 14:00 and 24:00.
6. Evaluation
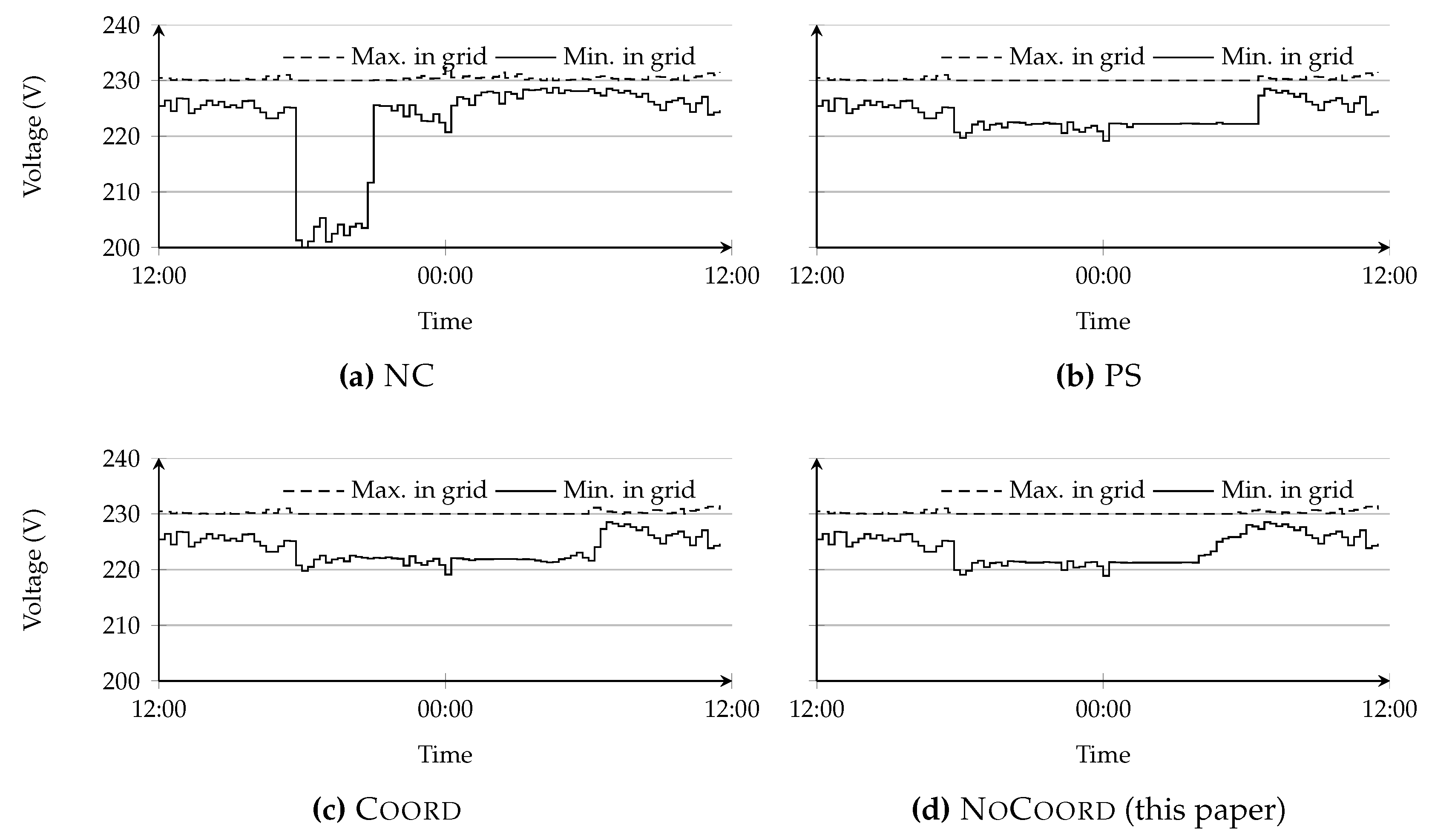
In this section, we compare our work with the state-of-the-art research and several other charging strategies. The basic variant of our approach aims to make the house load as flat as possible without coordination between the houses and is denoted by NoCoord. The extension of this technique that shaves the neighborhood peak by adding coordination is referred to by Coord. For both of our approaches, we make predictions upon arrival of the EVs using the approach from the previous section with ten days of historical data as input. We compare our approaches with the state-of-the-art research on Profile Steering (PS) from [2]. The profile steering algorithm is a heuristic that predicts the load of each house, makes a plan that is as flat as possible, and coordinates between houses to further flatten the load peak. In order to compare with the best possible behavior of PS, we assume perfect predictions for profile steering, which gives this approach a significant advantage. For completeness, we also compare to no control (NC), where EVs charge at full power at arrival, and with a grid unaware peak-shaving (PeakS), which is a simple approach that iteratively selects EVs and decreases their charging as much as possible until the desired load at the transformer is accomplished.
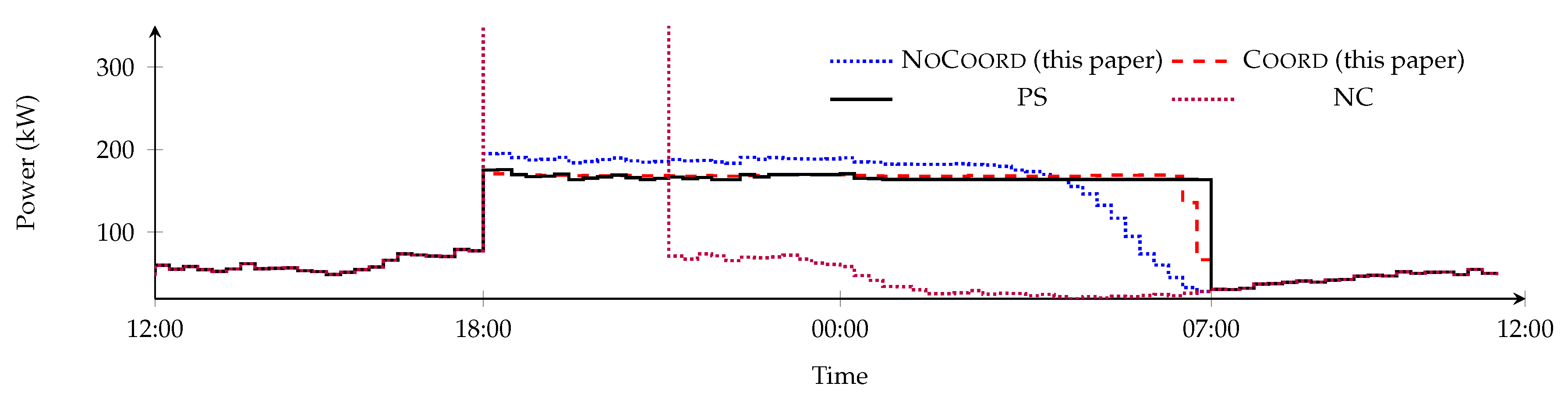
To effectively compare all approaches with the state-of-the-art research, we reproduce the case used in [2]. It considers 121 houses, all equipped with identical electric vehicles that charge 12 kWh between 18:00 and 07:00 and have a maximum charging power of 3.8 kW. We used the same data set and network files as used in [2] to calculate the load flows to obtain the active power at the transformer (incl. losses), the lowest observed voltage in the grid and the highest observed voltage in the grid. For Coord and PeakS, we need to set a limit for the peak-shaving by the neighborhood controller, and we set this limit to kW. The results are summarized in Table 3 and further detailed in Figure 4 (power) and Figure 5.

Table 3.
Comparison between DSM approaches and no control.
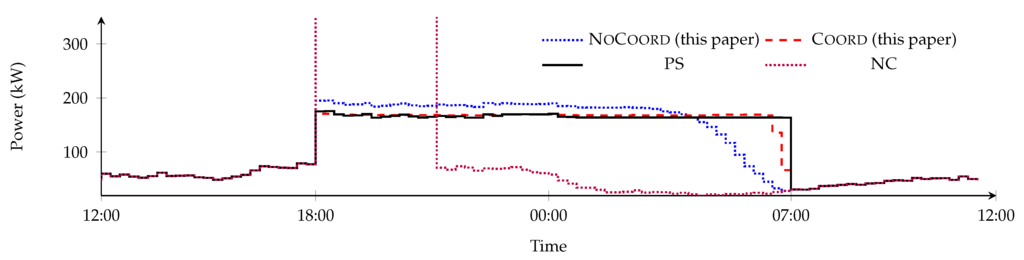
Figure 4.
Power at transformer (incl. losses).
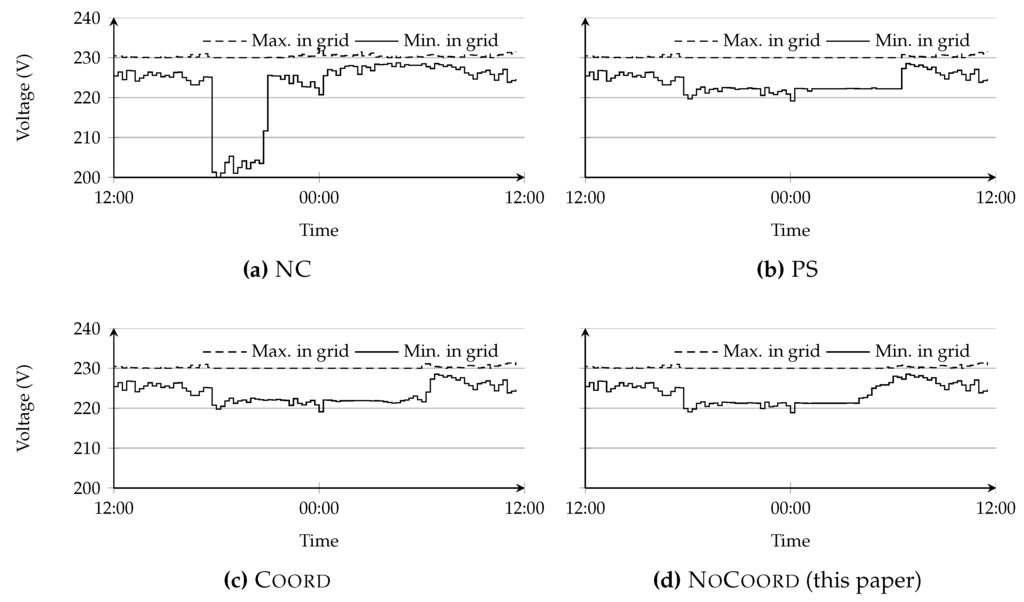
Figure 5.
Lowest and highest observed voltages.
When no control would be applied, a large peak occurs at the transformer (see Figure 4), cables are overloaded and the voltage does not stay within the legal bounds that are required in the Netherlands (i.e., NEN-EN 50160:2010 [5], 207 V–253 V). The transformer load is reduced with PeakS; however, Table 3 shows that this approach still overloads cables.
In contrast to NC and PeakS, PS reduces the load peak significantly and keeps the voltage within legal bounds (Figure 5b). Although it performs well, this algorithm depends on hard to make predictions (namely, a power value for each interval, for each house) and requires a lot of communication due to exchanging power profiles.
When no coordination controller is used (NoCoord), the resulting profile is already rather flat (Figure 4) and the voltages are well within legal bounds, and, at the end of the charging intervals, this approach is on par with PS (Figure 5d). By using the coordination controller (Coord), the profile is further flattened and the voltages are similar to the no coordination controller for this specific case.
Table 3 gives the exact losses, voltage bounds, maximum peak load and the highest overloading of a cable within the grid. Note that several scenarios share the maximum cable load of %, and the reason for this is that this cable load occurs before the EVs arrive and cannot be influenced. The table shows that the developed approaches perform similar to profile steering, while, for profile steering, knowledge about the future was used (in the real world, profile steering has to predict these values, whereas, in our experiments, we used the actual values).
7. Conclusions
Existing demand side management approaches either do not plan ahead, and thereby often may not deploy the flexibility of smart appliances when it is needed the most, or they do make a plan but this planning is based on often hard to predict (inaccurate) household power consumption.
To plan the appliances within a house, we propose using online planning. As a proof of concept, we presented an online electric vehicle planning algorithm that only requires a prediction of the fill level characteristic and a prediction of load in the next time interval as an input. The algorithm distributes the prediction error evenly over all charging intervals. This makes the algorithm very robust against incorrect predictions, especially if the predictions are higher than the actual realization. Furthermore, we presented a bound that quantifies the sensitivity of our approach to prediction errors.
We extended the house control mechanism by a neighborhood control mechanism, which initially asks the houses to make a flat profile. When the load exceeds a certain threshold, this coordination controller requests less charging from houses for the next time period in such a way that the house profiles remain as flat as possible. This method only requires a prediction of the number of active charging intervals within a house to make the required trade-off.
Both the house and neighborhood approaches require only few predictions, and we showed that these predictions are easy to obtain. In the evaluation, we studied the combination of predictions with our approach, and demonstrated that it works effectively for peak-shaving. The evaluation furthermore shows that this approach is very robust against prediction errors, and performs adequately even when the predictions are very imprecise. Compared to a naive approach, it leads to lower transportation losses, keeps the voltage within required bounds and keeps cable loads low. Furthermore, it is on par with the state-of-the-art research, which—in contrast to our work—requires predictions of flexibility and predictions of a load profile (24 hours ahead) for each house.
In future work, we aim to extend the online planning within a house to cope with appliances other than electric vehicles.
Acknowledgments
This research was conducted within the DREAM project supported by STW (#11842) and the e-balance project that has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement [609132].
Author Contributions
The concepts, ideas and theory described in this article are joint work by both authors. The simulations were conducted by Marco E. T. Gerards.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Siano, P. Demand response and smart grids–A survey. Renew. Sustain. Energy Rev. 2014, 30, 416–478. [Google Scholar] [CrossRef]
- Gerards, M.E.T.; Toersche, H.A.; Hoogsteen, G.; van der Klauw, T.; Hurink, J.L.; Smit, G.J.M. Demand side management using profile steering. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6.
- Molderink, A.; Bakker, V.; Bosman, M.G.C.; Hurink, J.L.; Smit, G.J.M. Management and Control of Domestic Smart Grid Technology. IEEE Trans. Smart Grid 2010, 1, 109–119. [Google Scholar] [CrossRef]
- van der Klauw, T.; Gerards, M.E.T.; Smit, G.J.M.; Hurink, J.L. Optimal scheduling of electrical vehicle charging under two types of steering signals. In Proceedings of the Europe IEEE PES Innovative Smart Grid Technologies Conference (ISGT-Europe), Istanbul, Turkey, 12–15 October 2014; IEEE Power & Energy Society: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- NEN-EN 50160:2010. Voltage characteristics of electricity supplied by public distribution network. August 2010. [Google Scholar]
- Hoogsteen, G.; Molderink, A.; Hurink, J.L.; Smit, G.J.M. Managing energy in time and space in smart grids using TRIANA. In Proceedings of the Europe IEEE PES Innovative Smart Grid Technologies Conference, ISGT-Europe 2014, Istanbul, Turkey, 12–15 October 2014; IEEE Power & Energy Society: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Nykamp, S.; Rott, T.; Dettke, N.; Kueppers, S. The project “ElChe” Wettringen: Storage as an alternative to grid reinforcements—Experiences, benefits and challenges from a DSO point of view. In Proceedings of the International ETG Congress 2015; Die Energiewende - Blueprints for the New Energy Age, Bonn, Germany, 17–18 November 2015.
- Kok, K. Dynamic pricing as control mechanism. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8.
- Kok, K. The PowerMatcher: Smart Coordination for the Smart Electricity Grid. Ph.D. Thesis, Vrije Universiteit Amsterdam and TNO, Amsterdam, The Netherlands, 2013. [Google Scholar]
- Wijbenga, J.; MacDougall, P.; Kamphuis, R.; Sanberg, T.; van den Noort, A.; Klaassen, E. Multi-goal optimization in PowerMatching city: A smart living lab. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe, ISGT-Europe 2014, Istanbul, Turkey, 12–15 October 2014; pp. 1–5.
- Javed, F.; Arshad, N.; Wallin, F.; Vassileva, I.; Dahlquist, E. Forecasting for demand response in smart grids: An analysis on use of anthropologic and structural data and short term multiple loads forecasting. Appl. Energy 2012, 96, 150–160. [Google Scholar] [CrossRef]
- Alfares, H.K.; Nazeeruddin, M. Electric load forecasting: Literature survey and classification of methods. Int. J. Syst. Sci. 2002, 33, 23–34. [Google Scholar] [CrossRef]
- Ruelens, F.; Vandael, S.; Leterme, W.; Claessens, B.; Hommelberg, M.; Holvoet, T.; Belmans, R. Demand side management of electric vehicles with uncertainty on arrival and departure times. In Proceedings of the 2012 3rd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8.
- Tang, W.; Bi, S.; Zhang, Y. Online coordinated charging decision algorithm for electric vehicles without future information. IEEE Trans. Smart Grid 2014, 5, 2810–2824. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S. Optimal decentralized protocol for electric vehicle charging. IEEE Trans. Power Syst. 2013, 28, 940–951. [Google Scholar] [CrossRef]
- Mou, Y.; Xing, H.; Lin, Z.; Fu, M. Decentralized optimal demand-side management for PHEV charging in a smart grid. IEEE Trans. Smart Grid 2015, 6, 726–736. [Google Scholar] [CrossRef]
- Del Razo, V.; Goebel, C.; Jacobsen, H. Vehicle-originating-signals for real-time charging control of electric vehicle fleets. IEEE Trans. Transp. Electrification 2015, 1, 150–167. [Google Scholar] [CrossRef]
- Patriksson, M. A survey on the continuous nonlinear resource allocation problem. Eur. J. Oper. Res. 2008, 185, 1–46. [Google Scholar] [CrossRef]
- Hochbaum, D.; Hong, S.P. About strongly polynomial time algorithms for quadratic optimization over submodular constraints. Math. Progr. 1995, 69, 269–309. [Google Scholar] [CrossRef]
- Blum, M.; Floyd, R.W.; Pratt, V.; Rivest, R.L.; Tarjan, R.E. Time bounds for selection. J. Comput. Syst. Sci. 1973, 7, 448–461. [Google Scholar] [CrossRef]
- Gerards, M.E.T. Online EV Planning. Available online: http://wwwhome.ewi.utwente.nl/~gerardsmet/vis/oev/ (accessed on 29 April 2016).
- Patriksson, M.; Strömberg, C. Algorithms for the continuous nonlinear resource allocation problem—New implementations and numerical studies. Eur. J. Oper. Res. 2015, 243, 703–722. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).