Discrete Element Method Simulations of the Inter-Particle Contact Parameters for the Mono-Sized Iron Ore Particles
Abstract
:1. Introduction
2. DEM Model
3. Methodology
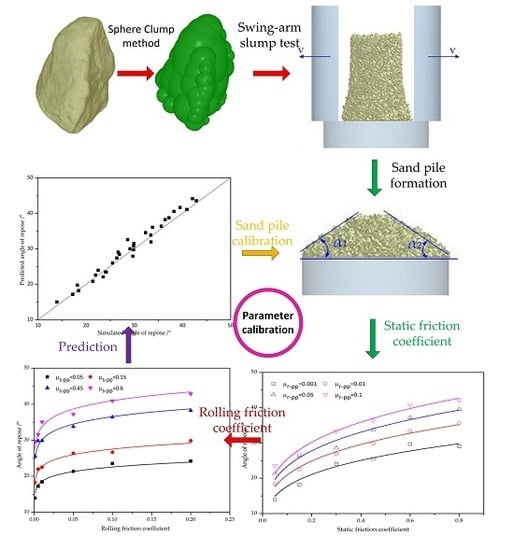
3.1. Sphere Clump Method
3.2. Simulation Conditions and Input Parameters
4. Results and Discussion
4.1. Particle Shape Estimation
4.2. Effect of Inter-Particle Contact Parameters
4.3. Formulation of A Predictive Equation
5. Conclusions
Acknowledgements
Author contributions
Conflicts of Interest
References
- Guo, Y.; Curtis, J.S. Discrete element method simulations for complex granular flows. Ann. Rev. Fluid Mech. 2015, 47, 21–46. [Google Scholar] [CrossRef]
- Bhargava, K.C.; Thompson, B.; Malmstadt, N. Discrete elements for 3D microfluidics. Proc. Natl. Acad. Sci. USA 2014, 111, 15013–15018. [Google Scholar] [CrossRef] [PubMed]
- Majidi, B.; Taghavi, S.M.; Fafard, M.; Ziegler, D.P.; Alamdari, H. Discrete element method modeling of the rheological properties of coke/pitch mixtures. Materials 2016, 9, 334. [Google Scholar] [CrossRef]
- Lee, J.; Yun, T.S.; Choi, S.U. The effect of particle size on thermal conduction in granular mixtures. Materials 2015, 8, 3975–3991. [Google Scholar] [CrossRef]
- Pennec, F.; Alzina, A.; Tessier-Doyen, N.; Nait-Ali, B.; Mati-Baouche, N.; De Baynast, H.; Smith, D.S. A combined finite-discrete element method for calculating the effective thermal conductivity of bio-aggregates based materials. Int. J. Heat Mass Transf. 2013, 60, 274–283. [Google Scholar] [CrossRef]
- Hare, C.; Ghadiri, M.; Guillard, N.; Bosworth, T.; Egan, G. Analysis of milling of dry compacted ribbons by distinct element method. Chem. Eng. Sci. 2016, 149, 204–214. [Google Scholar] [CrossRef]
- Chen, Y.; Munkholm, L.J.; Nyord, T.A. Discrete element model for soil–sweep interaction in three different soils. Soil Tillage Res. 2013, 126, 34–41. [Google Scholar] [CrossRef]
- Ghodki, B.M.; Goswami, T.K. DEM simulation of flow of black pepper seeds in cryogenic grinding system. J. Food Eng. 2017, 196, 36–51. [Google Scholar] [CrossRef]
- Müller, P.; Tomas, J. Simulation and calibration of granules using the discrete element method. Particuology 2014, 12, 40–43. [Google Scholar] [CrossRef]
- Bracey, R.J.; Weerasekara, N.S.; Powell, M.S. Performance evaluation of the novel multi-shaft mill using DEM modeling. Miner. Eng. 2016, 98, 251–260. [Google Scholar] [CrossRef]
- Cleary, P.W. A multiscale method for including fine particle effects in DEM models of grinding mills. Miner. Eng. 2015, 84, 88–99. [Google Scholar] [CrossRef]
- Cleary, P.W.; Owen, P.J. Using DEM to understand scale-up for a HICOM® mill. Miner. Eng. 2016, 92, 86–109. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Xu, B.H.; Yu, A.B.; Zulli, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technol. 2002, 125, 45–54. [Google Scholar] [CrossRef]
- Grima, A.P.; Wypych, P.W. Investigation into calibration of discrete element model parameters for scale-up and validation of particle-structure interactions under impact conditions. Powder Technol. 2011, 212, 198–209. [Google Scholar] [CrossRef]
- Ng, T.T. Input parameters of discrete element methods. J. Eng. Mech. 2006, 132, 723–729. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comput. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef]
- Wilkinson, S.K.; Turnbull, S.A.; Yan, Z.; Stitt, E.H.; Marigo, M. A parametric evaluation of powder flowability using a Freeman rheometer through statistical and sensitivity analysis: A discrete element method (DEM) study. Comput. Chem. Eng. 2016, 97, 161–174. [Google Scholar] [CrossRef]
- Coetzee, C.J. Calibration of the discrete element method and the effect of particle shape. Powder Technol. 2016, 297, 50–70. [Google Scholar] [CrossRef]
- Cleary, P.W. Charge behaviour and power consumption in ball mills: Sensitivity to mill operating conditions, liner geometry and charge composition. Int. J. Miner. Process. 2001, 63, 79–114. [Google Scholar] [CrossRef]
- Franke, J.; Cleary, P.W.; Sinnott, M.D. How to account for operating condition variability when predicting liner operating life with DEM–A case study. Miner. Eng. 2015, 73, 53–68. [Google Scholar] [CrossRef]
- Delaney, G.W.; Cleary, P.W.; Morrison, R.D.; Cummins, S.; Loveday, B. Predicting breakage and the evolution of rock size and shape distributions in AG and SAG mills using DEM. Miner. Eng. 2013, 50, 132–139. [Google Scholar] [CrossRef]
- Lommen, S.; Schott, D.; Lodewijks, G. DEM speedup: Stiffness effects on behavior of bulk material. Particuology 2014, 12, 107–112. [Google Scholar] [CrossRef]
- Malone, K.F.; Xu, B.H. Determination of contact parameters for discrete element method simulations of granular systems. Particuology 2008, 6, 521–528. [Google Scholar] [CrossRef]
- Barrios, G.K.P.; de Carvalho, R.M.; Kwade, A.; Tavares, M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technol. 2013, 248, 84–93. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Yang, S.; Zhang, H.; Yang, H.; Yue, G.G. Experimental study on the angle of repose of pulverized coal. Particuology 2010, 8, 482–485. [Google Scholar] [CrossRef]
- Just, S.; Toschkoff, G.; Funke, A.; Djuric, D.; Scharrer, G.; Khinast, J.; Knop, K.; Kleinebudde, P. Experimental analysis of tablet properties for discrete element modeling of an active coating process. AAPS PharmSciTech 2013, 14, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Ostanin, I.; Ballarini, R.; Potyondy, D.; Dumitrica, T. A Distinct Element Method for Large Scale Simulations of Carbon Nanotube Assemblies. J. Mech. Phys. Solids 2013, 61, 762–782. [Google Scholar] [CrossRef]
- Ostanin, I.; Ballarini, R.; Dumitrica, T. Distinct Element Method Modeling of Carbon Nanotube Bundles with Intertube Sliding and Dissipation. J. Appl. Mech. 2014, 81, 061004. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Thornton, C. A comparison of discrete element simulations and experiments for ‘sandpiles’ composed of spherical particles. Powder Technol. 2005, 160, 219–228. [Google Scholar] [CrossRef]
- Nakashima, H.; Shioji, Y.; Kobayashi, T.; Aoki, S.; Shimizu, H.; Miyasaka, J.; Ohdoi, K. Determining the angle of repose of sand under low-gravity conditions using discrete element method. J. Terramech. 2011, 48, 17–26. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y.L.; Zhao, X.Q. Numerical investigation on angle of repose and force network from granular pile in variable gravitational environments. Powder Technol. 2015, 283, 607–617. [Google Scholar] [CrossRef]
- Bourcier, D.; Féraud, J.P.; Colson, D.; Mandrick, K.; Ode, D.; Brackx, E.; Puel, F. Influence of particle size and shape properties on cake resistance and compressibility during pressure filtration. Chem. Eng. Sci. 2016, 144, 176–187. [Google Scholar] [CrossRef]
- Barua, S.; Yoo, J.W.; Kolhar, P.; Mitragotri, S. Particle shape enhances specificity of antibody-displaying nanoparticles. Proc. Natl. Acad. Sci. USA 2013, 110, 3270–3275. [Google Scholar] [CrossRef] [PubMed]
- Ileleji, K.E.; Zhou, B. The angle of repose of bulk corn stover particles. Powder Technol. 2008, 187, 110–118. [Google Scholar] [CrossRef]
- Cleary, P.W. The effect of particle shape on simple shear flows. Powder Technol. 2008, 179, 144–163. [Google Scholar] [CrossRef]
- Majidi, B.; Azari, K.; Alamdari, H.; Ziegler, D. Simulation of vibrated bulk density of anode-grade coke particles using discrete element method. Powder Technol. 2014, 261, 154–160. [Google Scholar] [CrossRef]
- Majidi, B.; Melo, J.; Fafard, M.; Alamdari, H. Packing density of irregular shape particles: DEM simulations applied to anode-grade coke aggregates. Adv. Powder Technol. 2015, 26, 1256–1262. [Google Scholar] [CrossRef]
- Caulkin, R.; Tian, W.; Pasha, M.; Jia, X. Impact of shape representation schemes used in discrete element modelling of particle packing. Comput. Chem. Eng. 2015, 76, 160–169. [Google Scholar] [CrossRef]
- Ketterhagen, W.R. Modeling the motion and orientation of various pharmaceutical tablet shapes in a film coating pan using DEM. Int. J. Pharm. 2011, 409, 137–149. [Google Scholar] [CrossRef] [PubMed]
- O’Sullivan, C.; Bray, J.D. Selecting a suitable time step for discrete element simulations that use the central difference time integration scheme. Eng. Comput. 2004, 21, 278–303. [Google Scholar] [CrossRef]
- Chung, Y.C.; Ooi, J.Y. Influence of discrete element model parameters on bulk behavior of a granular solid under confined compression. Part. Sci. Technol. 2008, 26, 83–96. [Google Scholar] [CrossRef]
- Mora, C.F.; Kwan, A.K.H. Sphericity, shape factor, and convexity measurement of coarse aggregate for concrete using digital image processing. Cem. Concr. Res. 2000, 30, 351–358. [Google Scholar] [CrossRef]
- Geldart, D.; Abdullah, E.C.; Hassanpour, A.; Nwoke, L.C.; Wouters, I. Characterization of powder flowability using measurement of angle of repose. China Part. 2006, 4, 104–107. [Google Scholar] [CrossRef]
- Grima, A.P.; Wypych, P.W. Development and validation of calibration methods for discrete element modeling. Granul. Matter 2011, 13, 127–132. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Xu, B.H.; Yu, A.B.; Zulli, P. Numerical investigation of the angle of repose of monosized spheres. Phys. Rev. E 2001, 64, 1–8. [Google Scholar] [CrossRef] [PubMed]











| No | x (mm) | y (mm) | z (mm) | SArp (mm2) | V (mm3) | SAes (mm2) | Ψ |
|---|---|---|---|---|---|---|---|
| 1 | 12.00 | 10.13 | 9.04 | 306.59 | 371.26 | 249.76 | 0.815 |
| 2 | 17.28 | 10.96 | 9.32 | 384.21 | 450.97 | 284.34 | 0.740 |
| 3 | 16.33 | 8.81 | 10.56 | 362.99 | 417.46 | 270.08 | 0.744 |
| 4 | 17.08 | 7.66 | 10.56 | 356.01 | 396.36 | 260.90 | 0.733 |
| 5 | 11.99 | 11.10 | 9.00 | 315.12 | 386.53 | 256.56 | 0.814 |
| 6 | 8.90 | 7.80 | 6.57 | 177.12 | 140.36 | 130.59 | 0.737 |
| 7 | 9.06 | 10.32 | 8.40 | 207.58 | 184.78 | 156.86 | 0.756 |
| 8 | 7.27 | 6.81 | 7.92 | 157.98 | 132.59 | 125.72 | 0.796 |
| 9 | 9.87 | 6.98 | 6.58 | 190.06 | 172.74 | 149.97 | 0.789 |
| 10 | 7.68 | 8.26 | 7.16 | 164.40 | 138.55 | 129.47 | 0.787 |
| 11 | 10.87 | 9.99 | 5.76 | 216.31 | 198.35 | 164.45 | 0.760 |
| 12 | 8.66 | 4.68 | 9.18 | 196.37 | 179.84 | 154.05 | 0.785 |
| 13 | 10.06 | 7.24 | 7.52 | 188.76 | 165.99 | 146.04 | 0.77 |
| 14 | 6.90 | 6.68 | 5.60 | 138.72 | 124.48 | 120.54 | 0.87 |
| 15 | 9.78 | 5.50 | 8.02 | 177.04 | 145.33 | 133.65 | 0.75 |
| 16 | 7.25 | 13.93 | 10.87 | 330.06 | 358.60 | 244.05 | 0.74 |
| 17 | 7.73 | 15.17 | 9.13 | 335.25 | 350.82 | 240.511 | 0.72 |
| 18 | 14.14 | 7.09 | 8.76 | 272.36 | 283.56 | 208.69 | 0.77 |
| 19 | 13.98 | 8.13 | 8.80 | 319.42 | 409.57 | 266.66 | 0.83 |
| 20 | 10.51 | 8.15 | 8.50 | 246.43 | 265.3 | 199.65 | 0.81 |
| 21 | 14.23 | 8.60 | 9.19 | 340.58 | 383.07 | 255.03 | 0.749 |
| 22 | 14.40 | 10.72 | 5.92 | 289.56 | 272.20 | 203.08 | 0.701 |
| 23 | 11.70 | 13.77 | 6.36 | 328.38 | 343.20 | 237.02 | 0.722 |
| 24 | 10.23 | 8.57 | 10.07 | 272.33 | 328.38 | 230.14 | 0.845 |
| 25 | 9.44 | 11.33 | 5.86 | 254.76 | 284.11 | 208.96 | 0.820 |
| 26 | 14.01 | 7.77 | 7.67 | 258.21 | 239.39 | 186.41 | 0.722 |
| 27 | 10.33 | 6.63 | 10.22 | 237.68 | 236.24 | 184.78 | 0.777 |
| 28 | 12.54 | 6.90 | 7.06 | 230.27 | 217.36 | 174.80 | 0.759 |
| 29 | 10.26 | 7.30 | 9.09 | 209.29 | 203.88 | 167.49 | 0.800 |
| 30 | 9.04 | 8.21 | 7.40 | 207.62 | 211.68 | 171.73 | 0.827 |
| 31 | 10.84 | 6.59 | 6.823 | 190.17 | 150.06 | 136.54 | 0.718 |
| 32 | 9.02 | 7.13 | 6.232 | 167.01 | 144.34 | 133.05 | 0.797 |
| 33 | 7.10 | 8.25 | 7.374 | 171.66 | 141.85 | 131.51 | 0.766 |
| 34 | 6.94 | 8.27 | 8.773 | 178.29 | 163.69 | 144.69 | 0.812 |
| 35 | 8.66 | 6.82 | 7.359 | 167.92 | 148.69 | 135.71 | 0.808 |
| 36 | 8.11 | 7.29 | 6.48 | 146.37 | 120.78 | 118.14 | 0.807 |
| Material Parameters | Symbols | Value |
|---|---|---|
| Particle density (kg m−3) | ρp | 3886 |
| Particle shear modulus (Gpa) | Gp | 2.587 |
| Particle Poisson’s ratio | νp | 0.283 |
| Wall density (kg m−3) | ρw | 1200 |
| Wall shear modulus (Gpa) | Gw | 1.05 |
| Wall Poisson’s ratio | νw | 0.41 |
| Particle-wall restitution coefficient | epw | 0.5 |
| Particle-wall static friction coefficient | μs-pw | 0.6 |
| Particle-wall rolling friction coefficient | μr-pw | 0.05 |
| Particle-particle restitution coefficient | epp | 0–0.6 |
| Particle-particle static friction coefficient | μs-pp | 0–0.8 |
| Particle-particle rolling friction coefficient | μr-pp | 0–0.2 |
| Volume Intervals (mm3) | Percent |
|---|---|
| 100–200 | 44.44% |
| 200–300 | 25% |
| 300–400 | 22.22% |
| 400–500 | 8.33% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Peng, Y.; Zhu, Z.; Zou, S.; Yin, Z. Discrete Element Method Simulations of the Inter-Particle Contact Parameters for the Mono-Sized Iron Ore Particles. Materials 2017, 10, 520. https://doi.org/10.3390/ma10050520
Li T, Peng Y, Zhu Z, Zou S, Yin Z. Discrete Element Method Simulations of the Inter-Particle Contact Parameters for the Mono-Sized Iron Ore Particles. Materials. 2017; 10(5):520. https://doi.org/10.3390/ma10050520
Chicago/Turabian StyleLi, Tongqing, Yuxing Peng, Zhencai Zhu, Shengyong Zou, and Zixin Yin. 2017. "Discrete Element Method Simulations of the Inter-Particle Contact Parameters for the Mono-Sized Iron Ore Particles" Materials 10, no. 5: 520. https://doi.org/10.3390/ma10050520
APA StyleLi, T., Peng, Y., Zhu, Z., Zou, S., & Yin, Z. (2017). Discrete Element Method Simulations of the Inter-Particle Contact Parameters for the Mono-Sized Iron Ore Particles. Materials, 10(5), 520. https://doi.org/10.3390/ma10050520