Mechanism of Magnesium Oxide Hydration Based on the Multi-Rate Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Hydration Procedure
2.3. Characterizations
3. Chemical Kinetics Model
3.1. Multi-Rate Kinetics Model
3.2. First-Order Kinetics Model
4. Results and Discussion
4.1. The Model of Hydration under Unforced Condition
4.2. The Model of Hydration under Ultrasound Condition
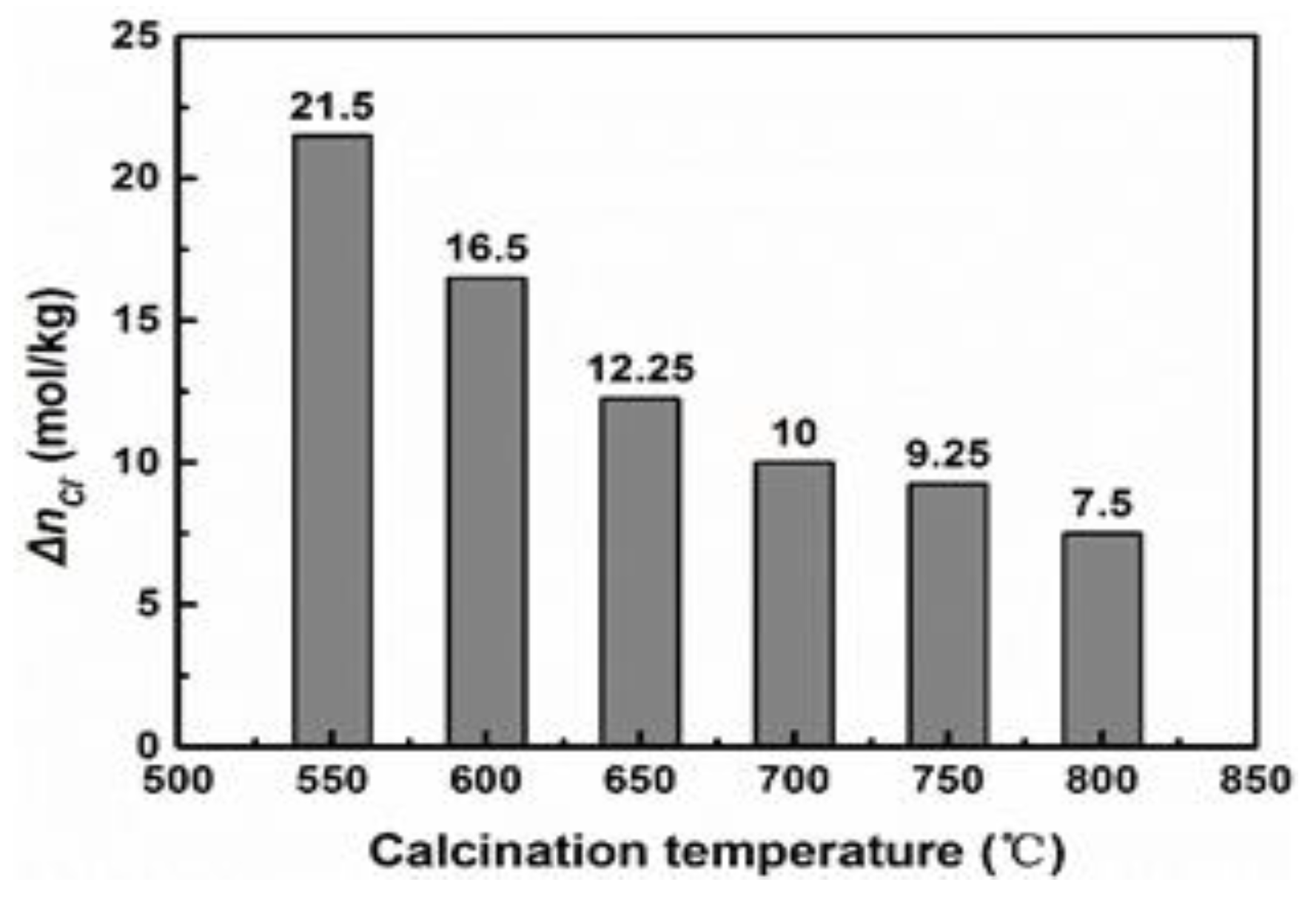
4.3. Mechanism of MgO Hydration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Taglieri, G.; Felice, B.; Daniele, V.; Ferrante, F. Mg(OH)2 nanoparticles produced at room temperature by aninnovative, facile, and scalable synthesis route. J. Nanopart. Res. 2015, 17, 411. [Google Scholar] [CrossRef]
- Gary, W.B.; El-Shazly, M.D.; El-Tantawy, F.; Al-Hazmi, F.; Ahmed, A.A. Rapid fabrication of nanostructured magnesium hydroxide and hydromagnesite via microwave-assisted technique. Powder Technol. 2013, 234, 26–31. [Google Scholar] [CrossRef]
- An, D.; Wang, L.; Zheng, Y.; Guan, S.; Gao, X.; Tian, Y.; Zhang, H.; Wang, Z.; Liu, Y. In situ preparation and surface modification of magnesium hydroxide nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2009, 348, 9–13. [Google Scholar] [CrossRef]
- Wu, J.; Yan, H.; Zhang, X.; Wei, L.; Liu, X.; Xu, B. Magnesium hydroxide nanoparticles synthesized in water-in-oil microemulsions. J. Colloid Interface Sci. 2008, 324, 167–171. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Deng, X. Preparation and properties of superfine Mg(OH)2 flame retardant. Trans. Nonferr. Met. Soc. China 2006, 16, 488–492. [Google Scholar] [CrossRef]
- Clifford, Y.T.; Tai, C.-T.; Chang, M.-H.; Liu, H.-S. Synthesis of magnesium hydroxide and oxide nanoparticles using a spinning disk reactor. Ind. Eng. Chem. Res. 2007, 46, 5536–5541. [Google Scholar] [CrossRef]
- Sierra-Fernandez, A.; Gomez-Villalba, L.S.; Milosevic, O.; Fort, R.; Rabanal, M.E. Synthesis and morpho-structural characterization of nanostructured magnesium hydroxide obtained by a hydrothermal method. Ceram. Int. 2014, 40, 12285–12292. [Google Scholar] [CrossRef]
- Liu, H.; Zong, R.; Lo, S.; Hu, Y.; Zhi, Y. Fire extinguishing efficiency of magnesium hydroxide powders under different particle size. Procedia Eng. 2018, 211, 447–455. [Google Scholar] [CrossRef]
- Nagai, N.; Ogata, F.; Otake, H.; Kawasaki, N.; Nakazawa, Y.; Kanai, K.; Okamoto, N.; Shimomura, Y. Co-instillation of nano-solid magnesium hydroxide enhances corneal permeability of dissolved timolol. Exp. Eye Res. 2017, 165, 118–124. [Google Scholar] [CrossRef] [PubMed]
- Baidukova, O.; Ekaterina, V.S. Ultrasound-assisted synthesis of magnesium hydroxide nanoparticles from magnesium. Ultrason. Sonochem. 2016, 31, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Pilarska, A.A.; Klapiszewski, Ł.; Jesionowsk, T. Recent development in the synthesis, modification and application of Mg(OH)2 and MgO: A review. Powder Technol. 2017, 319, 373–407. [Google Scholar] [CrossRef]
- Song, X.; Sun, S.; Zhang, D.; Wang, J.; Yu, J. Synthesis and characterization of magnesium hydroxide by batch reaction crystallization. Front. Chem. Sci. Eng. 2011, 5, 416–421. [Google Scholar] [CrossRef]
- Li, X.; Ma, C.; Zhao, J.; Li, Z.; Xu, S.; Liu, Y. Preparation of magnesium hydroxide nanoplates using a bubbling setup. Powder Technol. 2010, 198, 292–297. [Google Scholar] [CrossRef]
- Filippou, D.; Katiforis, N.; Papassiopi, N.; Adam, K. On the kinetics of magnesia hydration in magnesium acetate solutions. J. Chem. Technol. Biotechnol. 1999, 74, 322–328. [Google Scholar] [CrossRef]
- Tang, X.; Nie, Y.; Jin, Q.; Guo, L.; Zhao, J.; Li, T.; Zhu, Y. Kinetics and mechanism of ultrasonic-assisted magnesium oxide hydration. Ultrason. Sonochem. 2018, 40, 995–1002. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Lu, Z.; Zhang, P.; Luo, X.; Ren, X.; Teresa, D.G. Study of the synthesis and crystallization kinetics of magnesium hydroxide. Mater. Chem. Phys. 2015, 162, 734–742. [Google Scholar] [CrossRef]
- Liu, J.P.; Wang, Y.J.; Tian, Q.; Zhang, S.Z. Modeling hydration process of magnesia based on nucleation and growth theory: The isothermal calorimetry study. Thermochim. Acta 2012, 550, 27–32. [Google Scholar] [CrossRef]
- Amaral, L.F.; Oliveira, I.R.; Salomão, R.; Frollini, E.; Pandolfelli, V.C. Temperature and common-ion effect on magnesium oxide (MgO) hydration. Ceram. Int. 2010, 36, 1047–1054. [Google Scholar] [CrossRef]
- Salomão, R.; Victor, C. Magnesia sinter hydration-dehydration behavior in refractory castables. Ceram. Int. 2008, 34, 1829–1834. [Google Scholar] [CrossRef]
- Smithson, G.L.; Bakhshi, N.N. The kinetics and mechanism of the hydration of magnesium oxide in a batch reactor. Can. J. Chem. Eng. 1969, 47, 508–513. [Google Scholar] [CrossRef]
- Lidong, W.; Shuai, C.; Qiangwei, L.; Juan, W.; Shuang, L. Kinetics and mechanism of magnesium sulphite oxidation promoted by a novel cobalt-based molecular sieve catalyst. Appl. Catal. A Gen. 2016, 511, 16–22. [Google Scholar] [CrossRef]
- Li, Q.; Yang, Y.; Wang, L.; Xu, P.; Han, Y. Mechanism and kinetics of magnesium sulfite oxidation catalyzed by multiwalled carbon nanotube. Appl. Catal. B Environ. 2017, 203, 851–858. [Google Scholar] [CrossRef]
- Jia, L.; Fan, B.; Huo, R.; Li, B.; Yao, Y.; Han, F.; Qiao, X.; Jin, Y. Study on quenching hydration reaction kinetics and desulfurization characteristics of magnesium slag. J. Clean. Prod. 2018, 190, 12–23. [Google Scholar] [CrossRef]
- Rocha, S.D.F.; Mansur, M.B.; Ciminelli, V.S.T. Kinetics and mechanistic analysis of caustic magnesia hydration. J. Chem. Technol. Biotechnol. 2004, 79, 816–821. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Carey, B.; Tao, W.-Q. Pore-scale study of diffusion-reaction processes involving dissolution and precipitation using the lattice Boltzmann method. Int. J. Heat Mass Transf. 2014, 75, 483–496. [Google Scholar] [CrossRef]
- Wang, X.Y.; Yan, C.; Zheng, Y.K.; Li, E.L. Assessment of chemical kinetic models on hypersonic flow heat transfer. Int. J. Heat Mass Transf. 2017, 111, 356–366. [Google Scholar] [CrossRef]
- Qian, H.; Deng, M.; Zhang, S.; Xu, L. Synthesis of superfine Mg(OH)2 particles by magnesite. Mater. Sci. Eng. A 2007, 445–446, 600–603. [Google Scholar] [CrossRef]
- Limei, B.; Yufen, D.; Yuexin, H.; Wenqing, Z. Thermal decompositon process and kinetics of microfine magnesite. J. Northeast. Univ. (Nat. Sci.) 2018, 39, 398–403. [Google Scholar] [CrossRef]
- Bai, L.; Ma, Y.; Zhao, W.; Deng, Y.; Li, S. Optimization and mechanism in preparing active magnesium oxide from magnesite. J. Therm. Anal. Calorim. 2017, 129, 1103–1109. [Google Scholar] [CrossRef]
- Tang, X.; Guo, L.; Chen, C.; Liu, Q.; Li, T.; Zhu, Y. The analysis of magnesium oxide hydration in three-phase reaction system. J. Solid State Chem. 2014, 213, 32–37. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Physical Chemistry, 22nd ed.; Oxford University Press: New York, NY, USA, 2006; pp. 798–803. ISBN 9780198700722. [Google Scholar]
- Birchal, V.S.S.; Rocha, S.D.F.; Ciminelli, V.S.T. The effect of magnesite calcination conditions on magnesia hydration. Miner. Eng. 2000, 13, 1629–1633. [Google Scholar] [CrossRef]
- Amaral, L.F.; Oliveira, I.R.; Bonadia, P.; Salomão, R.; Pandolfelli, V.C. Chelants to inhibit magnesia (MgO) hydration. Ceram. Int. 2011, 37, 1537–1542. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Bai, L.; Ma, Y.; Wang, D.; Li, M. Mechanism of Magnesium Oxide Hydration Based on the Multi-Rate Model. Materials 2018, 11, 1835. https://doi.org/10.3390/ma11101835
Xing Z, Bai L, Ma Y, Wang D, Li M. Mechanism of Magnesium Oxide Hydration Based on the Multi-Rate Model. Materials. 2018; 11(10):1835. https://doi.org/10.3390/ma11101835
Chicago/Turabian StyleXing, Zhibo, Limei Bai, Yuxin Ma, Dong Wang, and Meng Li. 2018. "Mechanism of Magnesium Oxide Hydration Based on the Multi-Rate Model" Materials 11, no. 10: 1835. https://doi.org/10.3390/ma11101835
APA StyleXing, Z., Bai, L., Ma, Y., Wang, D., & Li, M. (2018). Mechanism of Magnesium Oxide Hydration Based on the Multi-Rate Model. Materials, 11(10), 1835. https://doi.org/10.3390/ma11101835




