Cellular Automaton Simulation of the Growth of Anomalous Eutectic during Laser Remelting Process
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Anomalous Eutectic Morphologies
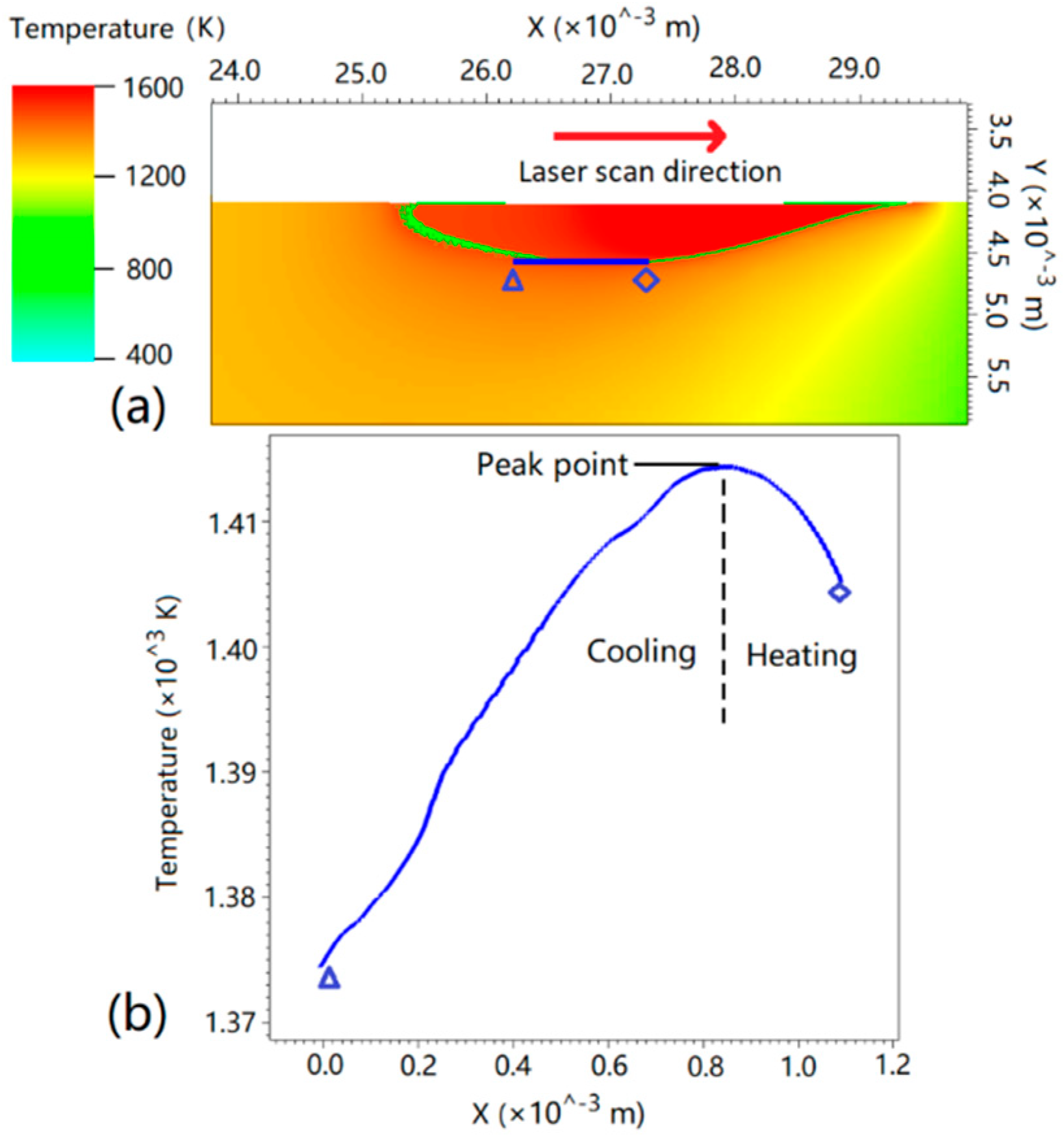
3.2. Temperature Filed at the Bottom of Melt Pool
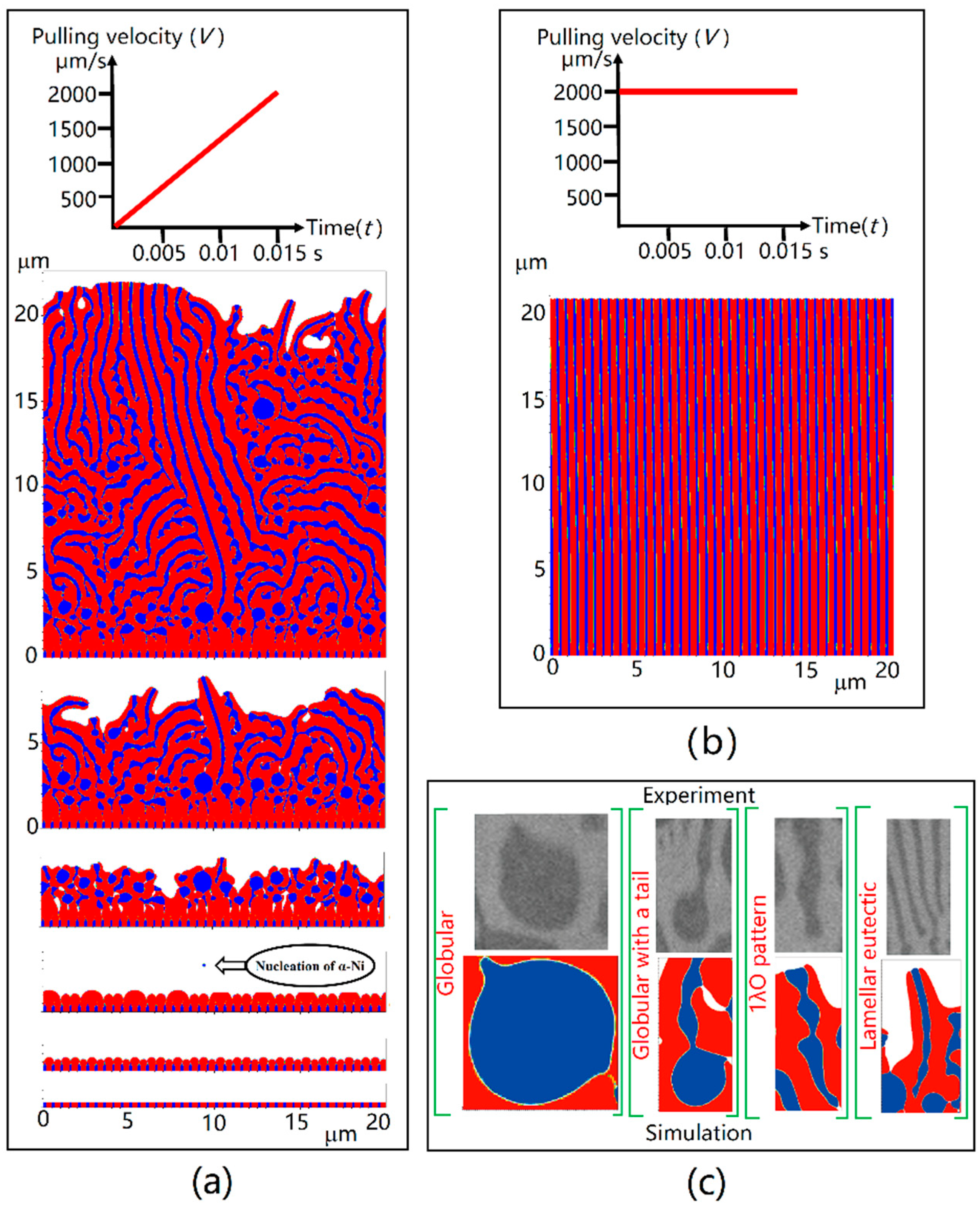
3.3. CA Simulation of Anomalous Eutectic Growth
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification; Trans Tech Publications: Aedermannsdorf, Switzerland, 1986; Volume 1. [Google Scholar]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851. [Google Scholar] [CrossRef]
- Akamatsu, S.; Plapp, M. Eutectic and peritectic solidification patterns. Curr. Opin. Solid State Mater. Sci. 2016, 20, 46–54. [Google Scholar] [CrossRef]
- Hunt, J.; Jackson, K. Binary eutectic solidification. Trans. Met. Soc. AIME 1966, 236, 843. [Google Scholar]
- Karma, A. Beyond steady-state lamellar eutectic growth. Phys. Rev. Lett. 1987, 59, 71. [Google Scholar] [CrossRef] [PubMed]
- Karma, A.; Sarkissian, A. Morphological instabilities of lamellar eutectics. Met. Mater. Trans. A 1996, 27, 635–656. [Google Scholar] [CrossRef]
- Ginibre, M.; Akamatsu, S.; Faivre, G. Experimental determination of the stability diagram of a lamellar eutectic growth front. Phys. Rev. E 1997, 56, 780. [Google Scholar] [CrossRef]
- Akamatsu, S.; Bottin-Rousseau, S.; Faivre, G. Experimental evidence for a zigzag bifurcation in bulk lamellar eutectic growth. Phys. Rev. Lett. 2004, 93, 175701. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Plapp, M. Stability of lamellar eutectic growth. Acta Mater. 2008, 56, 1348–1357. [Google Scholar] [CrossRef]
- Akamatsu, S.; Faivre, G. Traveling waves, two-phase fingers, and eutectic colonies in thin-sample directional solidification of a ternary eutectic alloy. Phys. Rev. E 2000, 61, 3757. [Google Scholar] [CrossRef]
- Akamatsu, S.; Perrut, M.; Bottin-Rousseau, S.; Faivre, G. Spiral two-phase dendrites. Phys. Rev. Lett. 2010, 104, 056101. [Google Scholar] [CrossRef] [PubMed]
- Hecht, U.; Gránásy, L.; Pusztai, T.; Böttger, B.; Apel, M.; Witusiewicz, V.; Ratke, L.; De Wilde, J.; Froyen, L.; Camel, D.; et al. Multiphase solidification in multicomponent alloys. Mater. Sci. Eng. R Rep. 2004, 46, 1–49. [Google Scholar] [CrossRef]
- Powell, G.; Hogan, L. Undercooling in silver-copper eutectic alloys. Inst. Met. J. 1965, 93, 505–512. [Google Scholar]
- Kattamis, T.; Flemings, M. Structure of undercooled Ni-Sn eutectic. Met. Mater. Trans. B 1970, 1, 1449–1451. [Google Scholar] [CrossRef]
- Wei, B.; Herlach, D.; Feuerbacher, B.; Sommer, F. Dendritic and eutectic solidification of undercooled Co-Sb alloys. Acta Met. Mater. 1993, 41, 1801–1809. [Google Scholar] [CrossRef]
- Wei, X.X.; Lin, X.; Xu, W.; Huang, Q.S.; Ferry, M.; Li, J.F.; Zhou, Y.H. Remelting-induced anomalous eutectic formation during solidification of deeply undercooled eutectic alloy melts. Acta Mater. 2015, 95, 44–56. [Google Scholar] [CrossRef]
- Mullis, A.M.; Clopet, C.R. On the origin of anomalous eutectic growth from undercooled melts: Why re-melting is not a plausible explanation. Acta Mater. 2018, 145, 186–195. [Google Scholar] [CrossRef]
- Gyoon Kim, S.; Tae Kim, W.; Suzuki, T.; Ode, M. Phase-field modeling of eutectic solidification. J. Cryst. Growth 2004, 261, 135–158. [Google Scholar] [CrossRef]
- Zhu, M.F.; Hong, C.P. Modeling of microstructure evolution in regular eutectic growth. Phys. Rev. B 2002, 66, 155428. [Google Scholar] [CrossRef]
- Qin, R.; Wallach, E.R. Computer simulations of the aluminium-silicon anomalous eutectic growth based on multiphase field method. Mater. Trans. 2003, 44, 968–972. [Google Scholar] [CrossRef]
- Lin, X.; Cao, Y.Q.; Wang, Z.T.; Cao, J.; Wang, L.L.; Huang, W.D. Regular eutectic and anomalous eutectic growth behavior in laser remelting of Ni-30wt%Sn alloys. Acta Mater. 2017, 126, 210–220. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.; Cao, Y.; Huang, W. Microstructure evolution in laser surface remelting of Ni–33wt.%Sn alloy. J. Alloys Compd. 2013, 577, 309–314. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W. Low artificial anisotropy cellular automaton model and its applications to the cell-to-dendrite transition in directional solidification. Mater. Discov. 2016, 3, 17–28. [Google Scholar] [CrossRef]
- Cummins, S.J.; Francois, M.M.; Kothe, D.B. Estimating curvature from volume fractions. Comput. Struct. 2005, 83, 425–434. [Google Scholar] [CrossRef]
- Fallah, V.; Amoorezaei, M.; Provatas, N.; Corbin, S.F.; Khajepour, A. Phase-field simulation of solidification morphology in laser powder deposition of Ti–Nb alloys. Acta Mater. 2012, 60, 1633–1646. [Google Scholar] [CrossRef]
- Li, J.; Jie, W.; Zhao, S.; Zhou, Y. Structural evidence for the transition from coupled to decoupled growth in the solidification of undercooled Ni-Sn eutectic melt. Met. Mater. Trans. A 2007, 38, 1806–1816. [Google Scholar] [CrossRef]
- Wu, Y.; Piccone, T.J.; Shiohara, Y.; Flemings, M.C. Dendritic growth of undercooled nickel-tin: Part II. Met. Mater. Trans. A 1987, 18, 925–932. [Google Scholar] [CrossRef]
- Aziz, M. Model for solute redistribution during rapid solidification. J. Appl. Phys. 1982, 53, 1158–1168. [Google Scholar] [CrossRef]
- Zhao, S.; Li, J.F.; Liu, L.; Zhou, Y.H. Cellular growth of lamellar eutectics in undercooled Ag–Cu alloy. Mater. Charact. 2009, 60, 519–524. [Google Scholar] [CrossRef]
- Hogan, L. The coupled region concept in eutectic solidification. J. Aust. Inst. Met. 1964, 9, 228–239. [Google Scholar]

| Constant | Value |
|---|---|
| Eutectic temperature (TE) | 1403 K |
| Eutectic concentration (CE) | 18.7 at.% |
| α liquidus slope at TE (mα) | −21 K/at.% |
| β liquidus slope at TE (mβ) | 37 K/at.% |
| α partition coefficient (kα) | 0.57 |
| β partition coefficient (kβ) | 1.21 |
| Diffusion coefficient of solute (Dl) | 5.0 × 10−9 m2/s |
| α Gibbs-Thomson coefficient (Гα) | 2.98 × 10−7 mK |
| β Gibbs-Thomson coefficient (Гβ) | 2.1 × 10−7 mK |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Cao, Y.; Lin, X.; Huang, W. Cellular Automaton Simulation of the Growth of Anomalous Eutectic during Laser Remelting Process. Materials 2018, 11, 1844. https://doi.org/10.3390/ma11101844
Wei L, Cao Y, Lin X, Huang W. Cellular Automaton Simulation of the Growth of Anomalous Eutectic during Laser Remelting Process. Materials. 2018; 11(10):1844. https://doi.org/10.3390/ma11101844
Chicago/Turabian StyleWei, Lei, Yongqing Cao, Xin Lin, and Weidong Huang. 2018. "Cellular Automaton Simulation of the Growth of Anomalous Eutectic during Laser Remelting Process" Materials 11, no. 10: 1844. https://doi.org/10.3390/ma11101844
APA StyleWei, L., Cao, Y., Lin, X., & Huang, W. (2018). Cellular Automaton Simulation of the Growth of Anomalous Eutectic during Laser Remelting Process. Materials, 11(10), 1844. https://doi.org/10.3390/ma11101844





