Filling of Irregular Channels with Round Cross-Section: Modeling Aspects to Study the Properties of Porous Materials
Abstract
:1. Introduction
2. Channel Shape Modeling
2.1. Channels with a Round Cross Section in Studies of Porous Materials
2.2. Channel Shape Patterns
3. Packing of Spheres into a Channel of an Irregular Shape
3.1. Review of Algorithms
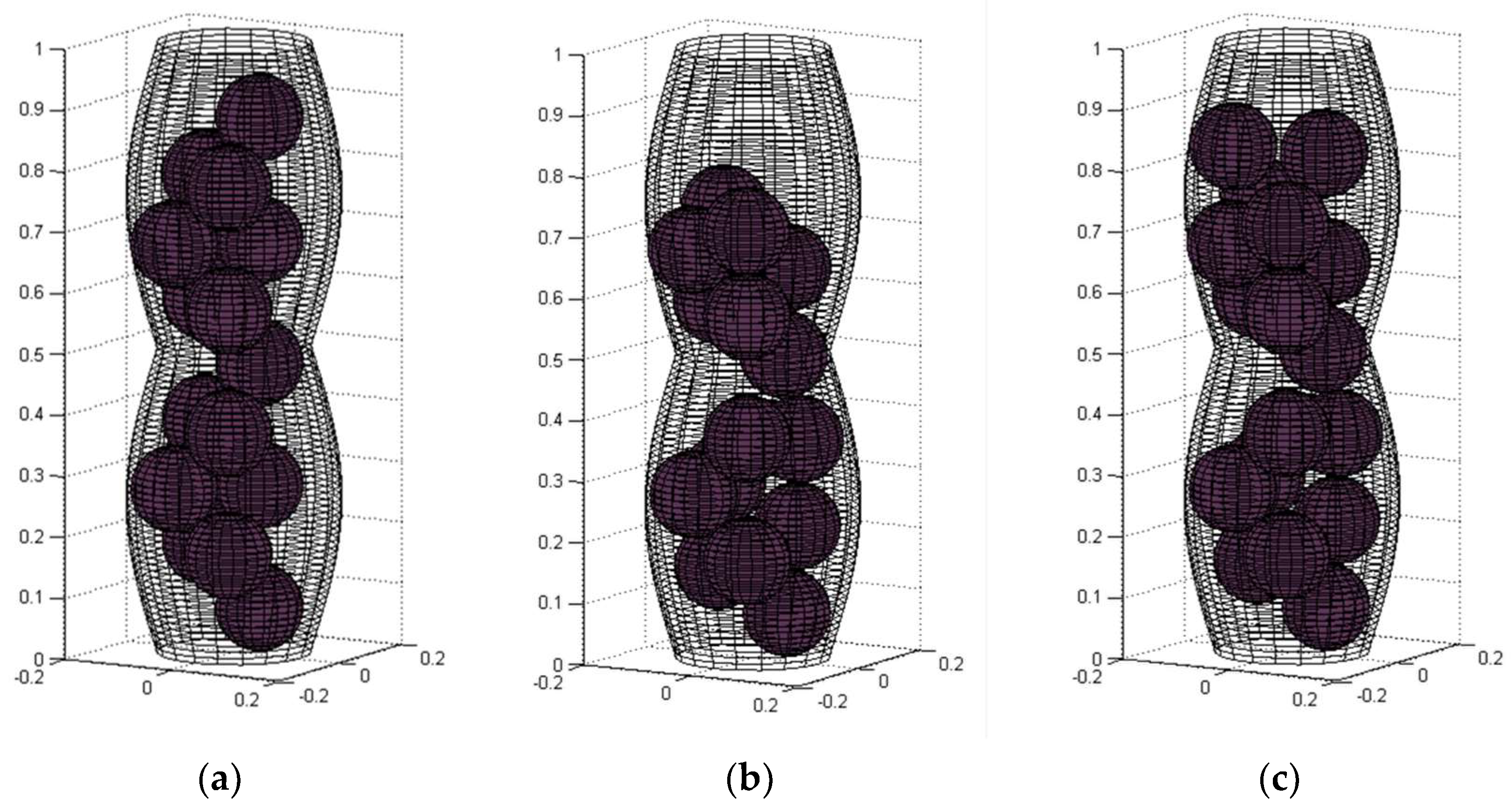
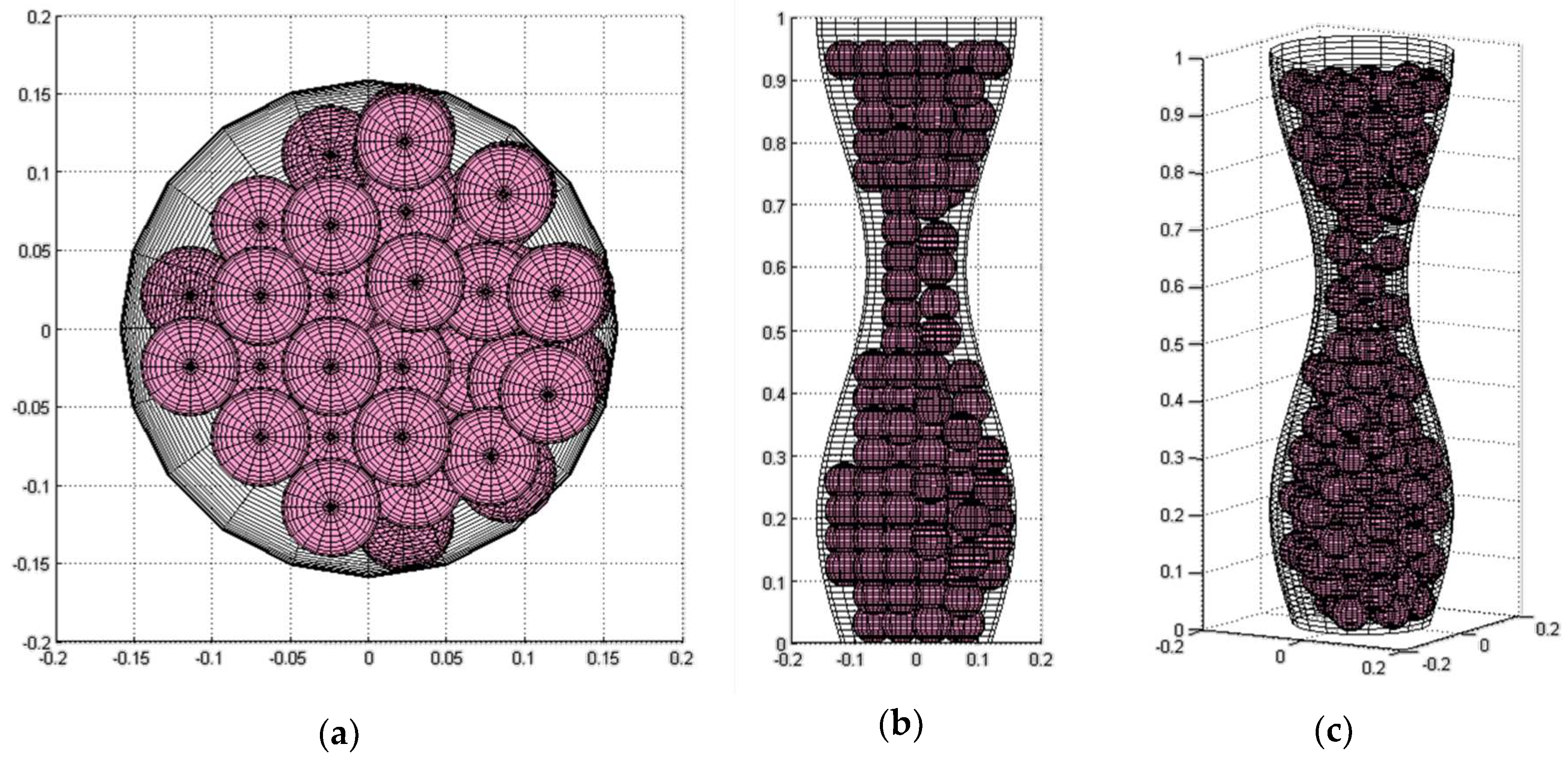
3.2. FCC-Based Algorithm
- The radius of the cross section varies in a function of f(z), according to the channel geometry: cylinder, frustum, truncated sphere, sinusoidal channel, etc.
- The x-y coordinates of each sphere are selected inside the circle described by the equation x2 + y2 = [f(z)]2.
- The values of the z coordinate must belong to the region r ≤ z ≤ L − r.
- Randomize the structure to the re-accommodation of the spheres in a more natural manner and make advantage of the free space inside of the channel.
- Make the space in the upper part of the channel free and add new spheres to increase the packing fraction if it is possible.
- The initial arrangement of the spheres results in a denser filling of the channel in its center, however, in the immediate vicinity of the wall there are plenty of empty spaces. The proposed shaking procedure allows us to designate new values of the x-y coordinates to each sphere which result from the movement of the spheres through these gaps, generating cavities into which they can be moved later. The movements are simulated along a horizontal radial line passing through the center of the cross section and a point containing the actual x-y coordinates of the sphere; the distance b between the center of the sphere and the channel wall is determined, and a random number p is obtained under the condition 0< p < b − r. Then, the sphere is moved by the distance p from its previous position over the radial line, receiving the new values of the x-y coordinates.
- Analogously, in the gravity procedure, random vertical descending movements are performed in order to assign new values to the z coordinate. The distance between the center of the sphere and the bottom of the container is determined, i.e., the old z coordinate of the sphere zold; then, a random number is generated, which will be the new z coordinate znew, under the condition r < znew < zold. The sphere will move vertically downwards; while the coordinates (x, y) remain the same.
- where zmax is the z coordinate of the sphere that is the highest up in the channel.
- the assignment of the x-y coordinates is repeated until a new sphere is deposited inside the circle of the cross section.
- The container volume is calculated depending on the channel symmetry. If the container is an axisymmetric channel, the volume is obtained from the integralTo calculate the volume of the tortuous channels or the channels with a distorted axis, the volume is given according to Cavalieri’s Principle (see e.g., Reference [76])
- Once the volume value has been calculated, the APF of the packing for the N spheres is given by
- Finally, the porosity or void fraction φ, which is the complement of the APF since this represents the size of the empty space in the container, is obtained:
4. FCC Sphere Packing in a Sinusoidal Axisymmetric Channel
- Height L = 5π;
- Maximal diameter of the cylinder Dmax = 5 units;
- Cross section period l = 2π;
- The minimal diameter of cylinder Dmin was obtained from the Dmin/Dmax ratio;
- The diameter of the spheres was considered for different percentages of Dmin (from 5 to 95%).
5. Conclusions and Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
Notations
| a | Unit cell edge |
| A | Inclination of a tube with sinusoidal non-varying radius |
| APF | Atomic packing factor |
| d | Distance between a sphere and the center of the cross section |
| D | Cross-section diameter |
| Dmax | Maximal diameter of the channel |
| Dmin | Minimal diameter of the channel |
| f(z) | z-function that defines the channel walls |
| l | Cross section period |
| L | Height of the channel |
| N | Number of spheres in the packing |
| n | Number of applied shaking and gravity procedures |
| r | Sphere radius |
| R | Cross-section radius |
| Rmax | Maximal radius of the channel |
| Rmin | Minimal radius of the channel |
| V | Volume of the channel |
| Vsphere | Volume of the sphere |
| Vvoid | Empty volume in the channel |
| ϴ | Inclination of a tilted cylinder |
| φ | Porosity or void fraction |
References
- Sloane, N.J.A. The Sphere Packing Problem. Documenta Mathematica 1998, 3, 387–396. [Google Scholar]
- Tóth, F.G. Über einen geometrischen Satz. Math. Z. 1940, 46, 78–83. [Google Scholar]
- Hales, T.C. A proof of the Kepler conjecture. Ann. Math. 2005, 162, 1065–1185. [Google Scholar] [CrossRef] [Green Version]
- Berryman, J.G. Random close packing of hard spheres and disks. Phys. Rev. A 1983, 27, 1053–1061. [Google Scholar] [CrossRef]
- Van Brakel, J. Pore Space Models for Transport Phenomena in Porous Media. Review and Evaluation with Special Emphasis on Capillary Liquid Transport. Powder Technol. 1975, 11, 205–236. [Google Scholar] [CrossRef]
- Feng, J.; Liao, Q.; Zhu, X.; Wu, R.; Wang, H.; Ding, Y.; Yashiro, K. Molecular dynamics simulation of injection of polyethylene fluid in a variable cross-section nano-channel. Sci. Bull. 2011, 56, 1848–1856. [Google Scholar] [CrossRef] [Green Version]
- Jerier, J.; Richefeu, V.; Imbault, D.; Donzé, F. Packing spherical discrete elements for large scale simulations. Comput. Methods Appl. Mech. Eng. 2010, 199, 1668–1676. [Google Scholar] [CrossRef]
- Yakub, I.; Plappally, A.; Leftwich, M.; Malatesta, K.; Friedman, K.C.; Obwoya, S.; Nyongesa, F.; Maiga, A.H.; Soboyejo, A.B.O.; Logothetis, S.; et al. Porosity, Flow, and Filtration Characteristics of Frustum-Shaped Ceramic Water Filters. J. Environ. Eng. 2013, 139, 986–994. [Google Scholar] [CrossRef]
- Tang, D.; Kim, D. Study on the transport of water molecules under the geometry confinement of aquaporin-like nanopores. Appl. Therm. Eng. 2014, 72, 120–125. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Zheng, X.; Dong, Z.; Yan, Y.; Zhang, J. Molecular dynamics simulations of water flow enhancement in carbon nanochannels. Comput. Mater. Sci. 2017, 136, 60–66. [Google Scholar] [CrossRef]
- Razmkhah, M.; Ahmadpour, A.; Mosavian, M.T.H.; Moosavi, F. What is the effect of carbon nanotube shape on desalination process? A simulation approach. Desalination 2017, 407, 103–115. [Google Scholar] [CrossRef]
- Jin, R.; Zeng, C.; Zhou, M.; Chen, Y. Atomically Precise Colloidal Metal Nanoclusters and Nanoparticles: Fundamentals and Opportunities. Chem. Rev. 2016, 116, 10346–10413. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Zhang, J.; Tang, X.; Chao, Y.; Chen, Q.; Man, X.; Dang, W. Micro-pore Structure and Gas Accumulation Characteristics of Shale in the Longmaxi Formation, Northwest Guizhou. Petroleum Res. 2016, 2, 191–204. [Google Scholar] [CrossRef]
- Centi, G.; Perathoner, S. Creating and mastering nano-objects to design advanced catalytic materials. Coord. Chem. Rev. 2011, 255, 1480–1498. [Google Scholar] [CrossRef]
- Bolton, K.; Ding, F.; Rosén, A. Atomistic Simulations of Catalyzed Carbon Nanotube Growth. J. Nanosci. Nanotechnol. 2006, 6, 1211–1224. [Google Scholar] [CrossRef] [PubMed]
- ALOthman, Z.A. A Review: Fundamental Aspects of Silicate Mesoporous Materials. Materials 2012, 5, 2874–2902. [Google Scholar] [CrossRef] [Green Version]
- Gounder, R.; Iglesia, E. The catalytic diversity of zeolites: Confinement and solvation effects within voids of molecular dimensions. Chem. Commun. 2013, 49, 3491–3509. [Google Scholar] [CrossRef] [PubMed]
- Mangeat, M.; Guérin, T.; Dean, D.S. Geometry controlled dispersion in periodic corrugated channels. EPL 2017, 118, 40004. [Google Scholar] [CrossRef] [Green Version]
- Plappally, A.K.; Yakub, I.; Brown, L.C.; Soboyejo, W.O.; Soboyejo, A.B.O. Physical Properties of Porous Clay Ceramic-Ware. J. Eng. Mater. Tech. 2011, 133, 031004. [Google Scholar] [CrossRef]
- Thommes, M.; Cychosz, K.A. Physical adsorption characterization of nanoporous materials: Progress and challenges. Adsorption 2014, 20, 233–250. [Google Scholar] [CrossRef]
- Haywood, D.G.; Saha-Shah, A.; Baker, L.A.; Jacobson, S.C. Fundamental Studies of Nanofluidics: Nanopores, Nanochannels, and Nanopipets. Anal. Chem. 2015, 87, 172–187. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Huang, J. Control water molecules across carbon-based nanochannels. Chin. Phys. B 2018, 27, 013101. [Google Scholar] [CrossRef]
- Roozbahani, M.M.; Huat, B.B.K.; Asadi, A. The effect of different random number distributions on the porosity of spherical particles. Adv. Powder Technol. 2013, 24, 26–35. [Google Scholar] [CrossRef]
- Burtseva, L.; Valdez Salas, B.; Werner, F.; Petranovskii, V. Packing of Monosized Spheres in a Cylindrical Container: Models and Approaches. Rev. Mex. Fis. E 2015, 61, 20–27. [Google Scholar] [CrossRef]
- Kosztin, I.; Schulten, K. Fluctuation-Driven Molecular Transport through an Asymmetric Membrane Channel. Phys. Rev. Lett. 2004, 93, 238102. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Yu, S.; Harrell, C.; Martin, R. Conical Nanopore Membranes. Preparation and Transport Properties. Anal. Chem. 2004, 76, 2025–2030. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, G.F.; Marshall, J.S. Particle focusing in a suspension flow through a corrugated tube. J. Fluid Mech. 2010, 660, 258–281. [Google Scholar] [CrossRef]
- Richmond, M.C.; Perkins, W.A.; Scheibe, T.D.; Lambert, A.; Wood, B.D. Flow and axial dispersion in a sinusoidal-walled tube: Effects of inertial and unsteady flows. Adv. Water Resour. 2013, 62, 215–226. [Google Scholar] [CrossRef]
- Han, C.; Tang, D.; Kim, D. Molecular dynamics simulation on the effect of pore hydrophobicity on water transport through aquaporin-mimic nanopores. Colloids Surf. A 2015, 481, 38–42. [Google Scholar] [CrossRef]
- Tang, D.; Li, L.; Shahbabaei, M.; Yoo, Y.E.; Kim, D. Molecular Dynamics Simulation of the Effect of Angle Variation on Water Permeability through Hourglass-Shaped Nanopores. Materials 2015, 8, 7257–7268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tseng, S.; Li, Y.; Lin, C.; Hsu, J. Salinity gradient power: Influences of temperature and nanopore size. Nanoscale 2016, 8, 2350–2357. [Google Scholar] [CrossRef] [PubMed]
- Adzumi, H. On the flow of gases through a porous wall. Bul. Chem. Soc. Jpn. 1937, 12, 304–312. [Google Scholar] [CrossRef]
- Wang, J.; Chen, L.; Kang, Q.; Rahman, S.S. The lattice Boltzmann method for isothermal micro-gaseous flow and its application in shale gas flow: A review. Int. J. Heat Mass Transf. 2016, 95, 94–108. [Google Scholar] [CrossRef] [Green Version]
- Experton, J.; Wu, X.; Martin, C.R. From Ion Current to Electroosmotic Flow Rectification in Asymmetric Nanopore Membranes. Nanomaterials 2017, 7, 445. [Google Scholar] [CrossRef] [PubMed]
- Yeganegi, S.; Gholampour, F. Simulation of methane adsorption and diffusion in a carbon nanotube channel. Chem. Eng. Sci. 2016, 140, 62–70. [Google Scholar] [CrossRef]
- Smith, W.O.; Foote, P.D.; Busang, P.F. Capillary rise in sands of uniform spherical grains. J. Appl. Phys. 1931, 1, 18–26. [Google Scholar] [CrossRef]
- Islam, N.; Bradshaw-Hajek, B.H.; Miklavcic, S.J.; White, L.R. The onset of recirculation flow in periodic capillaries: Geometric effects. Eur. J. Mech. B/Fluids 2015, 53, 119–128. [Google Scholar] [CrossRef]
- Berli, C.L.A.; Mercuri, M.; Bellino, M.G. Modeling the abnormally slow infiltration rate in mesoporous films. Phys. Chem. Chem. Phys. 2017, 19, 1731–1734. [Google Scholar] [CrossRef] [PubMed]
- Kou, X.Y.; Tan, S.T. A simple and effective geometric representation for irregular porous structure modeling. Comput. Aided Des. 2010, 42, 930–941. [Google Scholar] [CrossRef] [Green Version]
- Ejim, L.N.; Yerdelen, S.; McGlone, T.; Onyemelukwe, I.; Johnston, B.; Florence, A.J.; Reis, N.M. A factorial approach to understanding the effect of inner geometry of baffled meso-scale tubes on solids suspension and axial dispersion in continuous, oscillatory liquid–solid plug flows. Chem. Eng. J. 2017, 308, 669–682. [Google Scholar] [CrossRef] [Green Version]
- Rothfeld, L.B. Gaseous counterdiffusion in catalyst pellets. AIChE J. 1963, 9, 19–24. [Google Scholar] [CrossRef]
- Burada, P.S.; Hänggi, P.; Marchesoni, F.; Schmid, G.; Talkner, P. Diffusion in confined geometries. ChemPhysChem 2008, 10, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.; Mani, M.S.; Layek, G.C. Analysis of Flow Fields in a Flexible Tube with Periodic Constriction. Appl. Appl. Math. 2011, 6, 2045–2063. [Google Scholar]
- Herzig, J.P.; Leclerc, D.M.; Goff, P.L. Flow of suspensions through porous media—Application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- Gravelle, S.; Joly, L.; Detcheverry, F.; Ybert, C.; Cottin-Bizonne, C.; Bocquet, L. Optimizing water permeability through the hourglass shape of aquaporins. Proc. Natl. Acad. Sci. USA 2013, 110, 16367–16372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chu, C.F.; Ng, K.M. Flow in Packed Tubes with a Small Tube to Particle Diameter Ratio. AIChE J. 1989, 35, 148–158. [Google Scholar] [CrossRef]
- Zhao, X.; Meng, G.; Han, F.; Li, X.; Chen, B.; Xu, Q.; Zhu, X.; Chu, Z.; Kong, M.; Huang, Q. Nanocontainers made of Various Materials with Tunable Shape and Size. Sci. Rep. 2013, 2238, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, W.; Li, Z.; Li, L.; Gu, H.; Fu, J. Emerging microengineered tools for functional analysis and phenotyping of blood cells. Trends Biotechnol. 2014, 32, 586–594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Hu, M.; Guo, J.; Ou, X.; Cai, T.; Liu, Z. Pore architecture of TRIC channels and insights into their gating mechanism. Nature 2016, 538, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Labani, M.M.; Rezaee, R.; Saeedi, A.; Hinai, A.A. Evaluation of pore size spectrum of gas shale reservoirs using low pressure nitrogen adsorption, gas expansion and mercury porosimetry: A case study from the Perth and Canning Basins, Western Australia. J. Pet. Sci. Eng. 2013, 112, 7–16. [Google Scholar] [CrossRef]
- Dubey, G.P.; Malli Mohan, G.B.; Dubrovsky, A.; Amen, T.; Tsipshtein, S.; Rouvinski, A.; Rosenberg, A.; Kaganovich, D.; Sherman, E.; Medalia, O.; et al. Architecture and Characteristics of Bacterial Nanotubes. Dev. Cell 2016, 36, 453–461. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.M.; Zhang, Y.Y.; Xiang, Y.; Reddy, J.N. Recent Studies on Buckling of Carbon Nanotubes. Appl. Mech. Rev. 2010, 63, 030804. [Google Scholar] [CrossRef]
- Yuan, J.; Sundén, B. On mechanisms and models of multi-component gas diffusion in porous structures of fuel cell electrodes. Int. J. Heat Mass Transf. 2014, 69, 358–374. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, T.; Wang, J. Biomimetic phosphate assay based on nanopores. Microchim. Acta 2015, 182, 1387–1393. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, X.; Liu, Z.; Lu, S.; Xue, Q. Effect of interfacial layer on water flow in nanochannels: Lattice Boltzmann simulations. Phys. B 2016, 487, 18–24. [Google Scholar] [CrossRef]
- Ceratti, D.R.; Faustini, M.; Sinturel, C.; Vayer, M.; Dahirel, V.; Jardat, M.; Grosso, D. Critical effect of pore characteristics on capillary infiltration in mesoporous films. Nanoscale 2015, 7, 5371–5382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tu, Y.; Xiu, P.; Wan, R.; Hu, J.; Zhou, R.; Fang, H. Water-mediated signal multiplication with Y-shaped carbon nanotubes. Proc. Natl. Acad. Sci. USA 2009, 106, 18120–18124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, L.; Zhou, X.; Lu, H.; Liang, Q.; Kou, J.; Wu, F.; Fan, J. A controllable water signal transistor. Phys. Chem. Chem. Phys. 2017, 14, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Jodrey, W.S.; Tory, E.M. Simulation of random packing of spheres. Simulation 1979, 32, 1–12. [Google Scholar] [CrossRef]
- Jodrey, W.S.; Tory, E.M. Computer simulation of isotropic, homogeneous dense random packing of equal spheres. Powder Technol. 1981, 30, 111–118. [Google Scholar] [CrossRef]
- Jodrey, W.S.; Tory, E.M. Computer simulation of close random packing of equal spheres. Phys. Rev. A 1985, 32, 2347–2351. [Google Scholar] [CrossRef]
- Soontrapa, K.; Chen, Y. Mono-sized sphere packing algorithm development using optimized Monte Carlo technique. Adv. Powder Technol. 2013, 24, 955–961. [Google Scholar] [CrossRef]
- Roozbahani, M.M.; Huat, B.B.K.; Asadi, A. Effect of rectangular container’s sides on porosity for equal-sized sphere packing. Powder Technol. 2012, 224, 46–50. [Google Scholar] [CrossRef]
- Treacy, M.M.J.; Foster, M.D. Packing sticky hard spheres into rigid zeolite frameworks. Microporous Mesoporous Mater. 2009, 118, 106–114. [Google Scholar] [CrossRef]
- Lanfrey, P.; Kuzeljevic, Z.V.; Dudukovic, M.P. Tortuosity model for fixed beds randomly packed with identical particles. Chem. Eng. Sci. 2010, 65, 1891–1896. [Google Scholar] [CrossRef]
- Zhao, J.; Li, S.; Lu, P.; Meng, L.; Li, T.; Zhu, H. Shape influences on the packing density of frustums. Powder Technol. 2011, 214, 500–505. [Google Scholar] [CrossRef]
- Mościński, J.; Bargiel, M.; Rycerz, Z.A.; Jacobs, P.W.M. The Force-Biased Algorithm for the Irregular Close Packing of Equal Hard Spheres. Mol. Simul. 1989, 3, 201–212. [Google Scholar] [CrossRef]
- Smith, W.; Forester, T.R. DL_POLY_2.0: A general purpose parallel molecular dynamics simulation package. J. Mol. Graph. 1996, 14, 136–141. [Google Scholar] [CrossRef]
- Daneyko, A.; Khirevich, S.; Hötzel, A.; Seidel-Morgenstern, A.; Tallarek, U. From random sphere packings to regular pillar arrays: Effect of the macroscopic confinement on hydrodynamic dispersion. J. Chromatogr. A 2011, 1218, 8231–8248. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Tao, Y.B.; He, Y.L.; Huang, J.; Wu, Z.G.; Tao, W.Q. Three-dimensional numerical study of wavy fin-and-tube heat exchangers and field synergy principle analysis. Int. J. Heat Mass Transf. 2007, 50, 1163–1175. [Google Scholar] [CrossRef]
- Schaefer, D.W.; Keefer, K.D. Structure of random porous materials: Silica aerogel. Phys. Rev. Lett. 1986, 56, 2199–2202. [Google Scholar] [CrossRef] [PubMed]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann Equation to Simulate Lattice-Gas Automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef] [PubMed]
- Haile, J.M. Molecular Dynamics Simulation: Elementary Methods; John Wiley & Sons, Inc.: New York, NY, USA, 1992; ISBN 0-471-81966-2. [Google Scholar]
- Lee, K.O.; Holmes, T.W.; Calderon, A.F.; Gardner, R.P. Molecular Dynamics simulation for PBR pebble tracking simulation via a random walk approach using Monte Carlo simulation. Appl. Radiat. Isot. 2012, 70, 827–830. [Google Scholar] [CrossRef] [PubMed]
- Eves, H. Two Surprising Theorems on Cavalieri Congruence. Coll. Math. J. 1991, 22, 118–124. [Google Scholar] [CrossRef]
- Birgin, E.G.; Lobato, R.D. A matheuristic approach with nonlinear subproblems for large-scale packing of ellipsoids. Eur. J. Oper. Res. 2018, 272, 447–464. [Google Scholar] [CrossRef]
- Donev, A.; Torquato, S.; Stillinger, F. Neighbor list collision-driven molecular dynamics simulation for nonspherical hard particles. II. Applications to ellipses and ellipsoids. J. Comput. Phys. 2005, 202, 765–793. [Google Scholar] [CrossRef]
- Jameson, C.J.; Jameson, A.K.; Lim, H. Competitive adsorption of xenon and argon in zeolite NaA. 129Xe nuclear magnetic resonance studies and grand canonical Monte Carlo simulations. J. Chem. Phys. 1996, 104, 1709–1728. [Google Scholar] [CrossRef]






| No. | Shape Description | Studied Subject |
|---|---|---|
| 1 | Cylindrical tubes in series | Influence of temperature and nanopore size on the salinity gradient power [31]; Water flow enhancement in CNTs (Carbon Nanotubes) [10]; Diffusion of gaseous mixtures through capillaries [32]; Capillary infiltration in mesoporous silica films [38]; Modeling of bacterial components [51]; Water permeability [22]. |
| 2 | Wave axisymmetric tubes | Buckling modes of CNTs [52]; Deformability of blood cells [48]; Flow through sinusoidal tubes [46]; Dispersion in periodic corrugated axisymmetric sinusoidal channels [18]. |
| 3 | Sinusoidal tubes symmetric to the tube axis | Diffusion process of ideal gasses in capillaries and porous solids [41]; Void structure in zeolites [17]; Tortuosity factor in heterogeneous porous structures [53]. |
| 4 | Conus-like channels | Pore shape and transport properties of conical nanopore membranes [26]; Rectification of the ionic current in membranes [34]. |
| 5 | Frustum-like channels | Hysteresis curves [50]; Biomimetic ion-responsive single nanopore sensor construction [54]; Water flow enhancement in CNTs [10]; Ceramic water filters [8,19]; Water desalination [11]; Nano-injection systems [6]; Rectification of the ionic current in membranes [34]. |
| 6 | Funnel-like channels | Preparation and transport properties of conical nanopore membranes [26]; Nano-injection systems [6]; Ceramic water filters [8]; Targeted drug delivery [47]; Fluid transport in nanofluidic devices [21]; Intracellular signaling processes [49]; Capillarity in sands [36]. |
| 7 | Funnel-like extensions | Water permeability [22,30,45]. |
| 8 | Hourglass-like channels | Transport in aquaporin-like nanopores [9,10,29,30,45]; Intracellular signaling processes [49]; Fluid transport in nano-fluidic devices [21]. |
| 9 | Bottle-like channels | Hysteresis curves [50]; Targeted drug delivery [47]; Water permeability of nanochannel [55]. |
| 10 | Periodically constricted channels | Capillary infiltration in mesoporous silica films [38,56]; Dispersion in periodic corrugated elliptic shape channels [18]. |
| 11 | Sinusoidal axisymmetric channels | Diffusive transport of particles in micro-sized geometries [42]; Transport of a particulate suspension through a corrugated tube [27]; Viscous flows in the coronary artery [43]; Flow and axial dispersion [28]; Dispersion in periodic corrugated axisymmetric sinusoidal channels [18]. |
| 12 | Y-like channels | Signal processing at the molecular level [57,58]. |
| No. | Pattern | f(z) | d | V |
|---|---|---|---|---|
| (a) | Frustum | |||
| (b) | Truncated sphere | |||
| (c) | Tube with sinusoidal gradually-varying radius | |||
| (d) | Tilted cylinder | |||
| (e) | Tube with sinusoidal non-varying radius |
| Algorithm | Geometry | Packing | Size | MethodoLogy | Ref. |
|---|---|---|---|---|---|
| PACKS | Regular (semi infinity cube) | Y | multi | MC | [59] |
| ARSET | Regular (cube) | Y | mono | MC | [62] |
| Gravitational sphere packing | Cylinder | Y | mono | MC | [63] |
| Rigid zeolite frameworks | Irregular | Y | multi | MC, TES | [64] |
| Tortuosity model for a fixed bed | Irregular | Y | mono | MC | [65] |
| Dense sphere packing | Irregular (any shape) | Y | multi | DEM, TES | [7] |
| Assembly of non-spherical particles | Irregular (Frustum) | Y | multi | MC | [66] |
| Force-Biased algorithm | Periodic boundaries | Y | mono | MD | [67] |
| DL_POLY | Regular (none-isolated, cubic, ortho-rhombic, parallelepiped, truncated octahedral, rhombic dodecahedral, slab). | N | mono multi | MD | [68] |
| Single-phase flow | Irregular (sinusoidal shaped tube) | N | mono | MC, MD, TES | [69] |
| Study of fractal permeability | Irregular (non-uniform pores) | N | multi | CFD | [70] |
| SIMPLE | Irregular (wavy fin-and-tube) | N | multi | MD | [71] |
| PISO | Irregular (Corrugated sinusoidal axisymmetric tube) | N | multi | DEM | [27] |
| Imitation of a polymerization process | Irregular porous structures | N | multi | MC, TES | [39] |
| Numerical simulation of a viscous flow | Irregular (periodically constricted tube) | N | - | MD | [43] |
| LB method | Regular (containers of cross-sectional area with circular, rectangular or semi- circular geometry) | N | mono multi | MC, CFD | [73] |
| Irregular (pore throat nanochannel) | N | mono | CFD | [55] | |
| Irregular channels | N | - | CFD | [33] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ungson, Y.; Burtseva, L.; Garcia-Curiel, E.R.; Valdez Salas, B.; Flores-Rios, B.L.; Werner, F.; Petranovskii, V. Filling of Irregular Channels with Round Cross-Section: Modeling Aspects to Study the Properties of Porous Materials. Materials 2018, 11, 1901. https://doi.org/10.3390/ma11101901
Ungson Y, Burtseva L, Garcia-Curiel ER, Valdez Salas B, Flores-Rios BL, Werner F, Petranovskii V. Filling of Irregular Channels with Round Cross-Section: Modeling Aspects to Study the Properties of Porous Materials. Materials. 2018; 11(10):1901. https://doi.org/10.3390/ma11101901
Chicago/Turabian StyleUngson, Yamel, Larysa Burtseva, Edwin R. Garcia-Curiel, Benjamin Valdez Salas, Brenda L. Flores-Rios, Frank Werner, and Vitalii Petranovskii. 2018. "Filling of Irregular Channels with Round Cross-Section: Modeling Aspects to Study the Properties of Porous Materials" Materials 11, no. 10: 1901. https://doi.org/10.3390/ma11101901
APA StyleUngson, Y., Burtseva, L., Garcia-Curiel, E. R., Valdez Salas, B., Flores-Rios, B. L., Werner, F., & Petranovskii, V. (2018). Filling of Irregular Channels with Round Cross-Section: Modeling Aspects to Study the Properties of Porous Materials. Materials, 11(10), 1901. https://doi.org/10.3390/ma11101901







