Non-Destructive Assessment of Masonry Pillars using Ultrasonic Tomography
Abstract
:1. Introduction
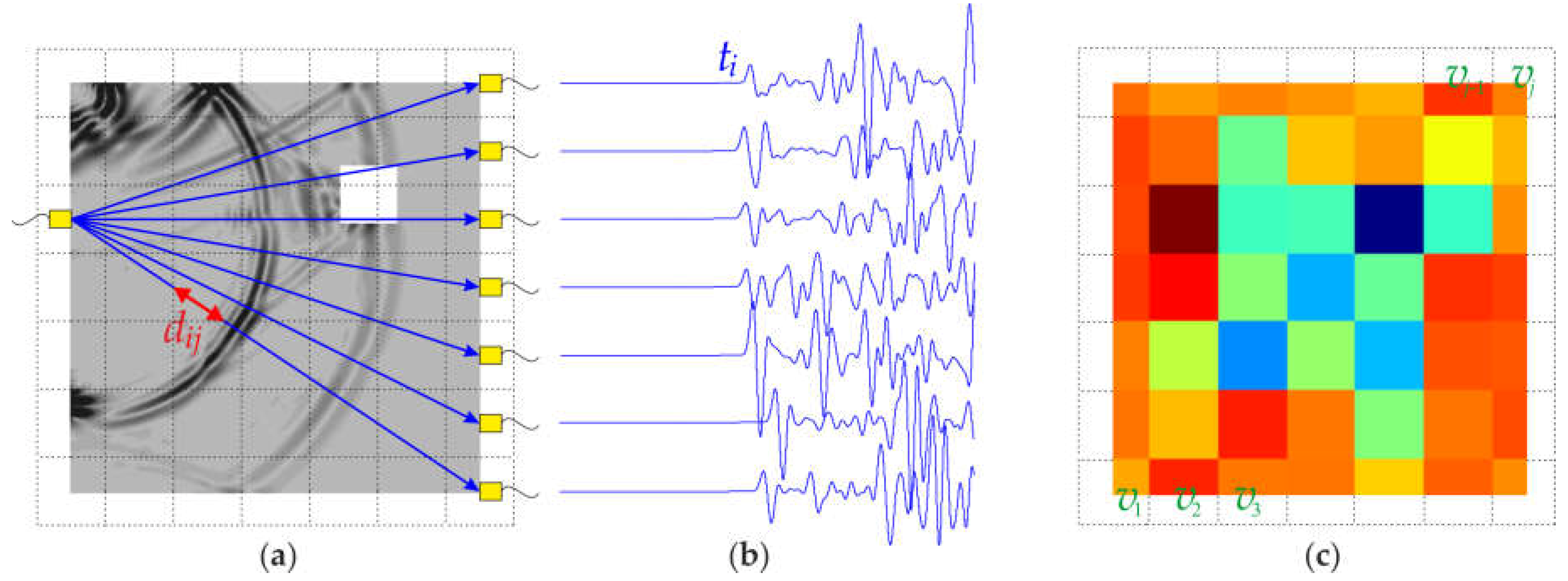
2. Theoretical Background of Ultrasonic Tomography
3. Materials and Methods
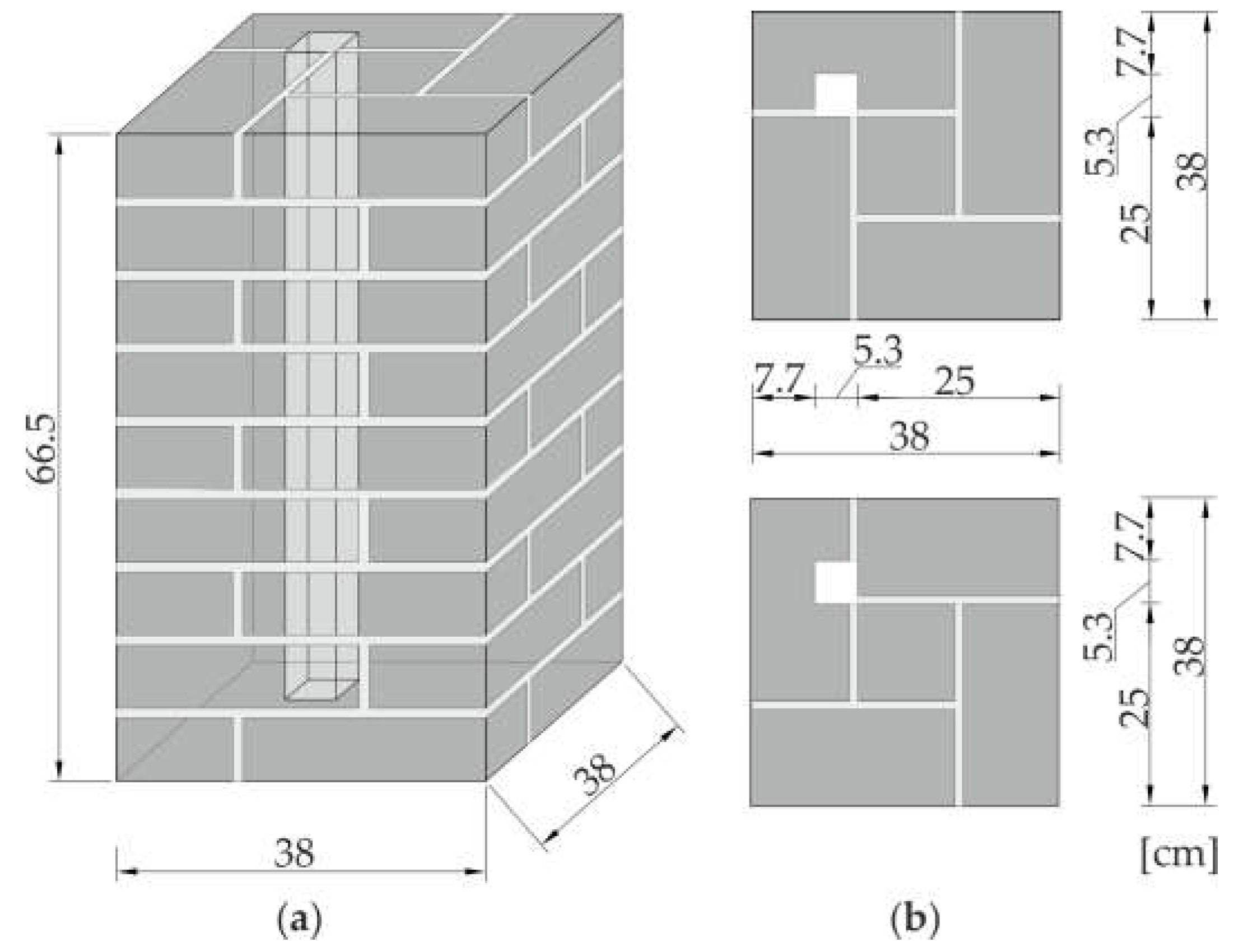
3.1. Description of Specimens
3.2. Identification of the Material Parameters
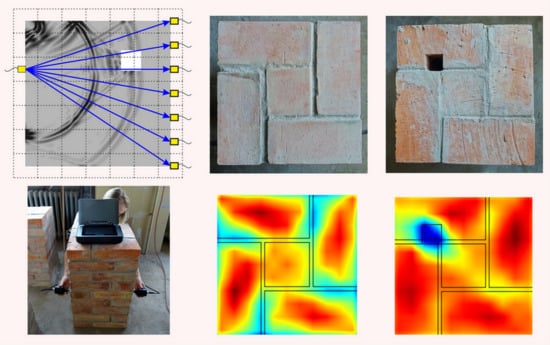
3.3. Experimental Setup
3.4. FEM Modeling
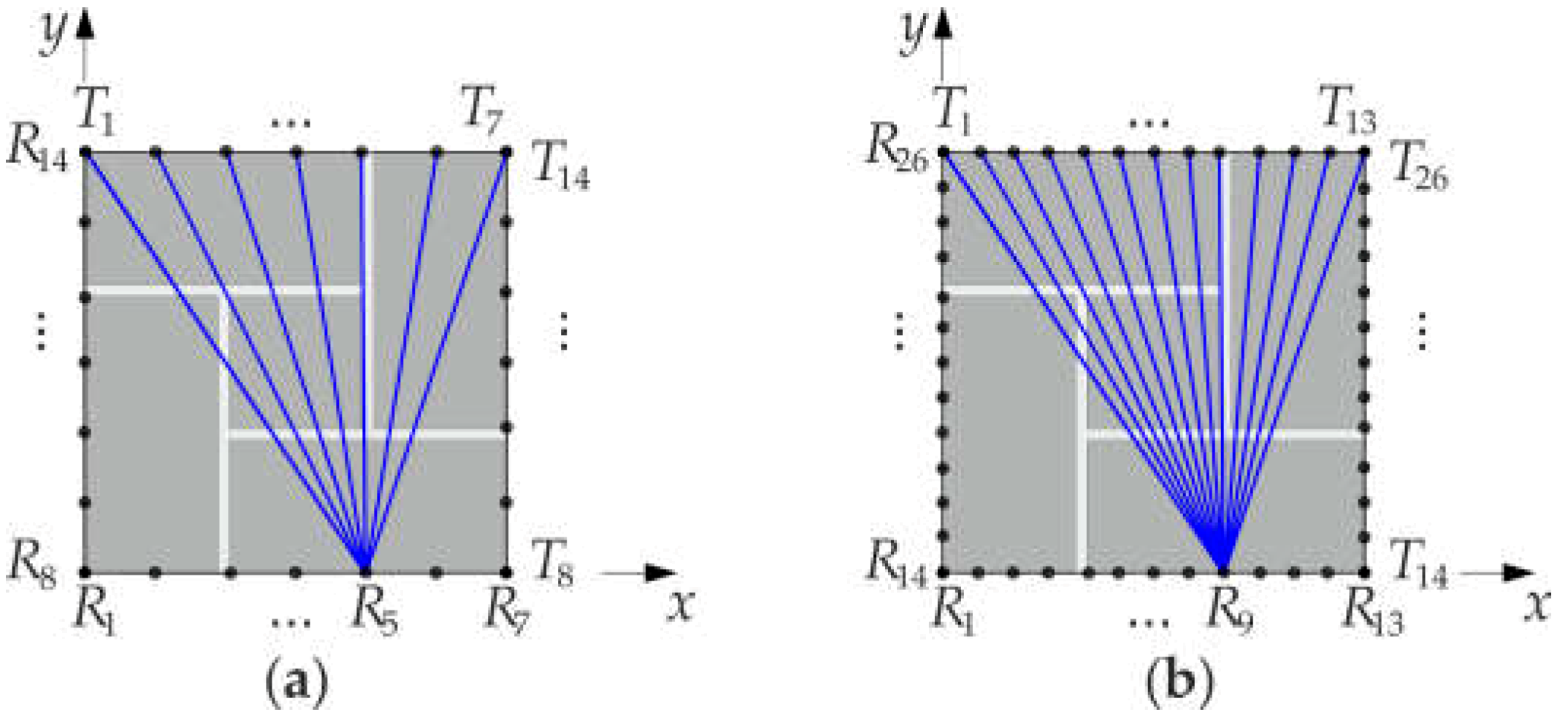
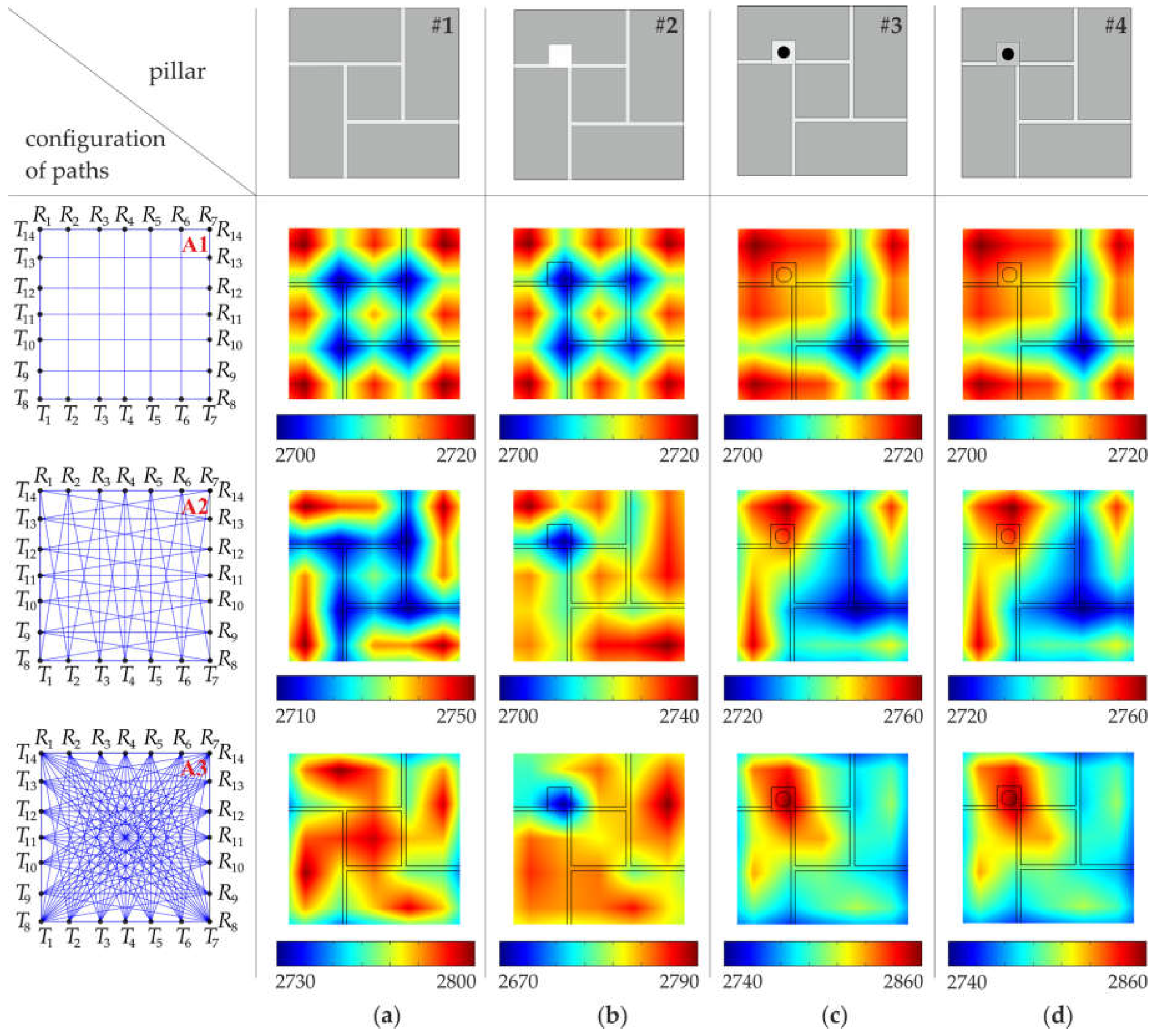
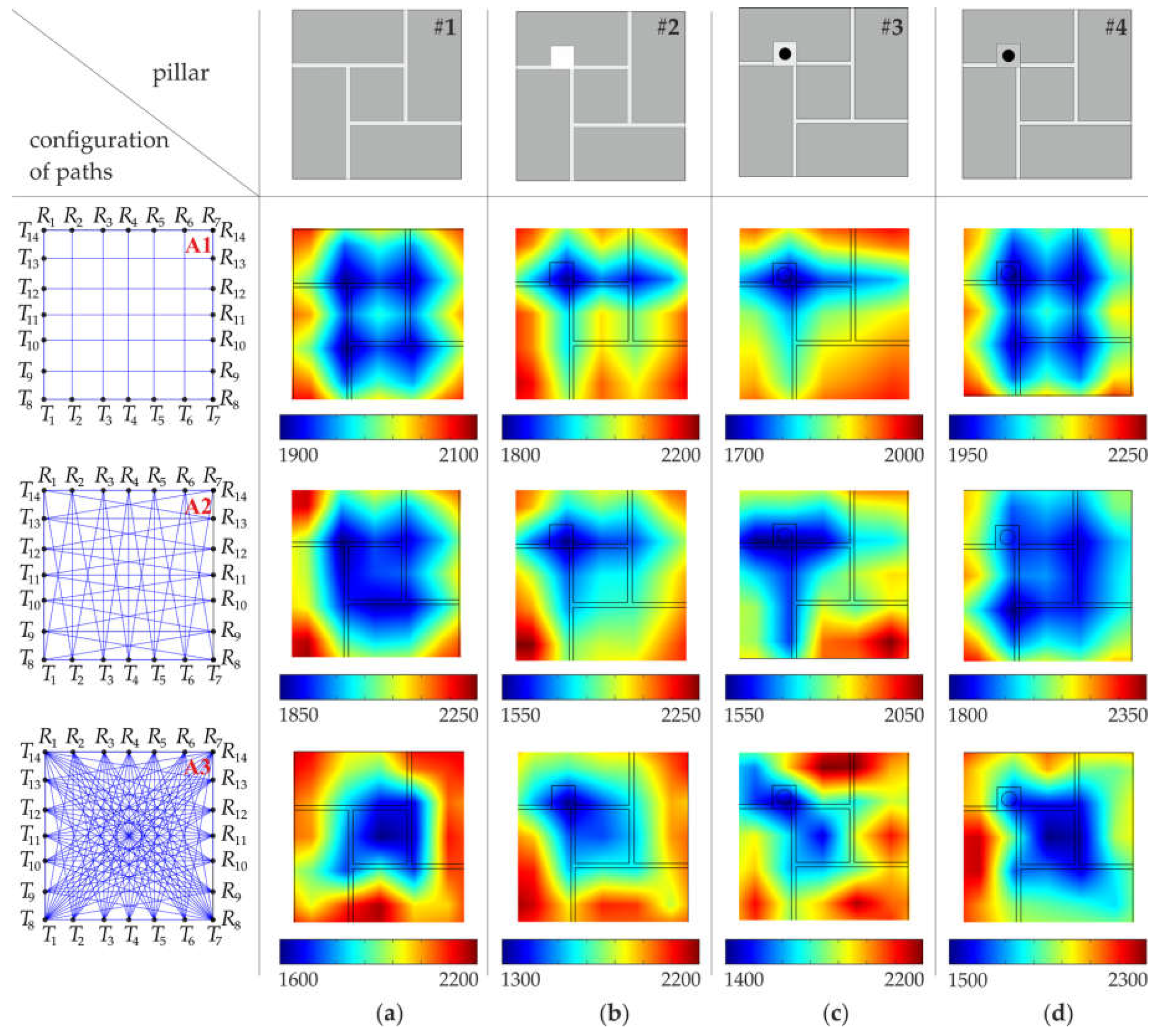
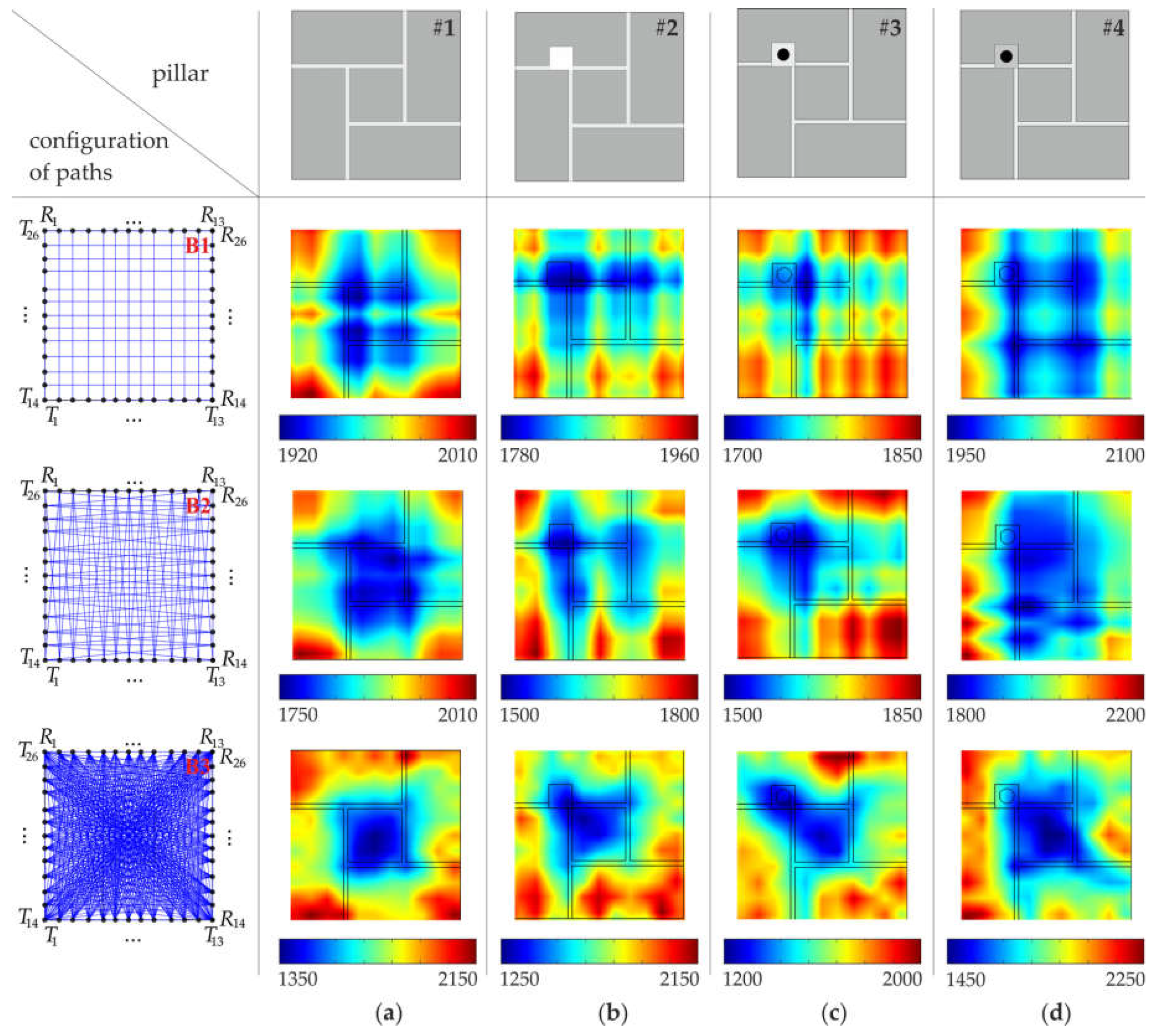
3.5. Configuration of Pixels and Paths
4. Results and Discussion
5. Conclusions
- The increase of the number of pixels and paths did not guarantee an improvement of the quality of the tomographic images. In numerical simulations made for the pillar models with idealized connections between the mortar and bricks, more accurate tomograms were obtained when a larger amount of measurement data was collected with a denser division in cells. This observation has not been confirmed in experimental tests conducted on real specimens, with connections between bricks and mortar influenced by air voids and non-ideal adhesion.
- The change in the velocity value was observed depending on the number of joints through which the wave passed. The velocity decreased with the increase of the number of joints on the wave path.
- Detection of the arrangement of joints in the cross-section was possible. The joints could be observed, based on numerical data, as line patterns with lower velocities. However, in experimental tests, the increase of the number of paths resulted in the appearance of a large zone, with lower velocity values in the central part of the pillar due to the accumulation of joints and paths crossing them.
- The inclusion in the form of a hole was identified in both the numerical and experimental tests as an area with lower velocity values.
- The inclusion in the form of an embedded bar was identified in the numerical data as an area with higher velocity values. This observation was not confirmed in experimental tests due to the existence of many factors that slowed the speed of the wave.
- The experimental tests enabled the assessment of the quality of the adhesive connection between a steel reinforcing bar embedded inside pillars, and the surrounding pillar body. The tomograms obtained for the pillar with the bar grouted by gypsum mortar revealed similar patterns as those for the pillar with the hole, which indicated poor adhesion. The maps obtained for the pillar with the bar grouted by cement mortar were similar to those obtained for the intact pillar, which indicated strong adhesion.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Binda, L.; Saisi, A.; Tiraboschi, C. Investigation procedures for the diagnosis of historic masonries. Constr. Build. Mater. 2000, 14, 199–233. [Google Scholar] [CrossRef]
- Piroglu, F.; Ozakgul, K. Site investigation of masonry buildings damaged during the 23 October and 9 November 2011 Van Earthquakes in Turkey. Nat. Hazards Earth Syst. Sci. 2013, 13, 689–708. [Google Scholar] [CrossRef] [Green Version]
- Jasiński, R.; Drobiec, Ł. Comparison Research of Bed Joints Construction and Bed Joints Reinforcement on Shear Parameters of AAC Masonry Walls. J. Civ. Eng. Archit. 2016, 10, 1329–1343. [Google Scholar] [CrossRef]
- Vasanelli, E.; Sileo, M.; Leucci, G.; Calia, A.; Aiello, M.A.; Micelli, F. Mechanical characterization of building stones through DT and NDT tests: Research of correlations for the in situ analysis of ancient masonry. Key Eng. Mater. 2015, 628, 85–89. [Google Scholar] [CrossRef]
- McCann, D.M.; Forde, M.C. Review of NDT methods in the assessment of concrete and masonry structures. NDT E Int. 2001, 34, 71–84. [Google Scholar] [CrossRef]
- Schuller, M.P. Nondestructive testing and damage assessment of masonry structures. Prog. Struct. Eng. Mater. 2003, 239–251. [Google Scholar] [CrossRef]
- Paasche, H.; Wendrich, A.; Tronicke, J.; Trela, C. Detecting voids in masonry by cooperatively inverting P-wave and georadar traveltimes. J. Geophys. Eng. 2008, 5, 256–267. [Google Scholar] [CrossRef]
- Bosiljkov, V.; Uranjek, M.; Žarnić, R.; Bokan-Bosiljkov, V. An integrated diagnostic approach for the assessment of historic masonry structures. J. Cult. Herit. 2010, 11, 239–249. [Google Scholar] [CrossRef]
- Santos-Assunçao, S.; Perez-Gracia, V.; Caselles, O.; Clapes, J.; Salinas, V. Assessment of complex masonry structures with GPR compared to other non-destructive testing studies. Remote Sens. 2014, 6, 8220–8237. [Google Scholar] [CrossRef]
- Khan, F.; Rajaram, S.; Vanniamparambil, P.A.; Bolhassani, M.; Hamid, A.; Kontsos, A.; Bartoli, I. Multi-sensing NDT for damage assessment of concrete masonry walls. Struct. Control Heal. Monit. 2015, 22, 449–462. [Google Scholar] [CrossRef]
- Micelli, F.; Cascardi, A.; Marsano, M. Seismic strengthening of a theatre masonry building by using active FRP wires. In Brick and Block Masonry: Proceedings of the 16th International Brick and Block Masonry Conference; CRC Press: Padova, Italy, 2016; pp. 753–761. [Google Scholar]
- La Mendola, L.; Lo Giudice, E.; Minafò, G. Experimental calibration of flat jacks for in-situ testing of masonry. Int. J. Archit. Herit. 2018. [Google Scholar] [CrossRef]
- Rucka, M.; Lachowicz, J.; Zielińska, M. GPR investigation of the strengthening system of a historic masonry tower. J. Appl. Geophys. 2016, 131, 94–102. [Google Scholar] [CrossRef]
- Lachowicz, J.; Rucka, M. Diagnostics of pillars in St. Mary’s Church (Gdańsk, Poland) using the GPR method. Int. J. Archit. Herit. 2018, 1–11. [Google Scholar] [CrossRef]
- Paganoni, S.; D’Ayala, D. Testing and design procedure for corner connections of masonry heritage buildings strengthened by metallic grouted anchors. Eng. Struct. 2014, 70, 278–293. [Google Scholar] [CrossRef]
- Collini, L.; Fagiani, R.; Garziera, R.; Riabova, K.; Vanali, M. Load and effectiveness of the tie-rods of an ancient Dome: Technical and historical aspects. J. Cult. Herit. 2015, 16, 597–601. [Google Scholar] [CrossRef]
- Ural, A.; Firat, F.K.; Tuğrulelçi, S.; Kara, M.E. Experimental and numerical study on effectiveness of various tie-rod systems in brick arches. Eng. Struct. 2016, 110, 209–221. [Google Scholar] [CrossRef]
- Pisani, M.A. Theoretical approach to the evaluation of the load-carrying capacity of the tie rod anchor system in a masonry wall. Eng. Struct. 2016, 124, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Ombres, L.; Verre, S. Masonry columns strengthened with Steel Fabric Reinforced Cementitious Matrix (S-FRCM) jackets: Experimental and numerical analysis. Measurement 2018, 127, 238–245. [Google Scholar] [CrossRef]
- Micelli, F.; Cascardi, A.; Aiello, M.A. A Study on FRP-Confined Concrete in Presence of Different Preload Levels. In Proceedings of the 9th International Conference on Fibre-Reinforced Polymer (FRP) Composites in Civil Engineering—CICE, Paris, France, 17–19 July 2018; pp. 493–499. [Google Scholar]
- Ferrotto, M.F.; Fischer, O.; Cavaleri, L. A strategy for the finite element modeling of FRP-confined concrete columns subjected to preload. Eng. Struct. 2018, 173, 1054–1067. [Google Scholar] [CrossRef]
- Rao, J.; Ratassepp, M.; Lisevych, D.; Hamzah Caffoor, M.; Fan, Z. On-Line Corrosion Monitoring of Plate Structures Based on Guided Wave Tomography Using Piezoelectric Sensors. Sensors 2017, 17, 2882. [Google Scholar] [CrossRef]
- Zhao, X.; Royer, R.L.; Owens, S.E.; Rose, J.L. Ultrasonic Lamb wave tomography in structural health monitoring. Smart Mater. Struct. 2011, 20, 105002. [Google Scholar] [CrossRef]
- Leonard, K.R.; Malyarenko, E.V.; Hinders, M.K. Ultrasonic Lamb wave tomography. Inverse Probl. 2002, 18, 1795–1808. [Google Scholar] [CrossRef]
- Prasad, S.M.; Balasubramaniam, K.; Krishnamurthy, C.V. Structural health monitoring of composite structures using Lamb wave tomography. Smart Mater. Struct. 2004, 13, N73–N79. [Google Scholar] [CrossRef]
- Martin, J.; Broughton, K.J.; Giannopolous, A.; Hardy, M.S.A.; Forde, M.C. Ultrasonic tomography of grouted duct post-tensioned reinforced concrete bridge beams. NDT E Int. 2001, 34, 107–113. [Google Scholar] [CrossRef]
- Chai, H.K.; Liu, K.F.; Behnia, A.; Yoshikazu, K.; Shiotani, T. Development of a tomography technique for assessment of the material condition of concrete using optimized elastic wave parameters. Materials 2016, 9, 291. [Google Scholar] [CrossRef] [PubMed]
- Chai, H.K.; Momoki, S.; Kobayashi, Y.; Aggelis, D.G.; Shiotani, T. Tomographic reconstruction for concrete using attenuation of ultrasound. NDT E Int. 2011, 44, 206–215. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Tsimpris, N.; Chai, H.K.; Shiotani, T.; Kobayashi, Y. Numerical simulation of elastic waves for visualization of defects. Constr. Build. Mater. 2011, 25, 1503–1512. [Google Scholar] [CrossRef]
- Schabowicz, K.; Suvorov, V.A. Nondestructive testing of a bottom surface and construction of its profile by ultrasonic tomography. Russ. J. Nondestruct. Test. 2014, 50, 109–119. [Google Scholar] [CrossRef]
- Schabowicz, K. Ultrasonic tomography—The latest nondestructive technique for testing concrete members—Description, test methodology, application example. Arch. Civ. Mech. Eng. 2014, 14, 295–303. [Google Scholar] [CrossRef]
- Haach, V.G.; Ramirez, F.C. Qualitative assessment of concrete by ultrasound tomography. Constr. Build. Mater. 2016, 119, 61–70. [Google Scholar] [CrossRef]
- Choi, H.; Popovics, J.S. NDE application of ultrasonic tomography to a full-scale concrete structure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1076–1085. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Ham, Y.; Popovics, J.S. Integrated visualization for reinforced concrete using ultrasonic tomography and image-based 3-D reconstruction. Constr. Build. Mater. 2016, 123, 384–393. [Google Scholar] [CrossRef] [Green Version]
- Schullerl, M.; Berra, M.; Atkinson, R.; Binda, L. Acoustic tomography for evaluation of unreinforced masonry. Constr. Build. Makrials 1997, 11, 199–204. [Google Scholar] [CrossRef]
- Binda, L.; Saisi, A.; Zanzi, L. Sonic tomography and flat-jack tests as complementary investigation procedures for the stone pillars of the temple of S. Nicolo 1’Arena (Italy). NDT E Int. 2003, 36, 215–227. [Google Scholar] [CrossRef]
- Pérez-Gracia, V.; Caselles, J.O.; Clapés, J.; Martinez, G.; Osorio, R. Non-destructive analysis in cultural heritage buildings: Evaluating the Mallorca cathedral supporting structures. NDT E Int. 2013, 59, 40–47. [Google Scholar] [CrossRef]
- Kak, A.C.; Slaney, M. Principles of Computerized Tomographic Imaging; The Institiute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Oliveira, E.F.; Dantas, C.C.; Vasconcelos, D.A.A.; Cadiz, F. Comparison Among Tomographic Reconstruction Algorithms With a Limited Data. In Proceedings of the International Nuclear Atlantic Conference-INAC 2011, Belo Horizonte, Brazil, 24–28 October 2011. [Google Scholar]
- Lu, X.; Sun, Q.; Feng, W.; Tian, J. Evaluation of dynamic modulus of elasticity of concrete using impact-echo method. Constr. Build. Mater. 2013, 47, 231–239. [Google Scholar] [CrossRef]
- Wȩglewski, W.; Bochenek, K.; Basista, M.; Schubert, T.; Jehring, U.; Litniewski, J.; Mackiewicz, S. Comparative assessment of Young’s modulus measurements of metal-ceramic composites using mechanical and non-destructive tests and micro-CT based computational modeling. Comput. Mater. Sci. 2013, 77, 19–30. [Google Scholar] [CrossRef]
- Wolfs, R.J.M.; Bos, F.P.; Salet, T.A.M. Correlation between destructive compression tests and non-destructive ultrasonic measurements on early age 3D printed concrete. Constr. Build. Mater. 2018, 181, 447–454. [Google Scholar] [CrossRef]
- Alberto, A.; Antonaci, P.; Valente, S. Damage analysis of brick-to-mortar interfaces. Procedia Eng. 2011, 10, 1151–1156. [Google Scholar] [CrossRef]




| Material | Density [kg/m3] | Young’s Modulus [GPa] | Poisson’s Ratio [-] |
|---|---|---|---|
| brick | 1642.04 | 10.55 | 0.20 |
| cement mortar | 1719.10 | 8.53 | 0.15 |
| gauged (cement lime) mortar | 1799.90 | 8.20 | 0.15 |
| gypsum mortar | 1185.70 | 3.70 | 0.15 |
| Pillar | Arrangement | vmin [m/s] | vmax [m/s] | Δv = vmax − vmin [m/s] | vavg [m/s] | SD [m/s] | CV [%] |
|---|---|---|---|---|---|---|---|
| #1 | A1 | 2699.52 | 2750.93 | 51.41 | 2732.93 | 22.0 | 0.81 |
| A2 | 2699.52 | 2765.47 | 65.95 | 2736.24 | 21.0 | 0.77 | |
| A3 | 2681.93 | 2767.02 | 85.09 | 2730.40 | 20.4 | 0.75 | |
| #2 | A1 | 2692.63 | 2751.52 | 58.89 | 2733.03 | 23.2 | 0.85 |
| A2 | 2640.62 | 2766.05 | 125.44 | 2731.99 | 27.7 | 1.02 | |
| A3 | 2640.62 | 2766.05 | 125.44 | 2721.84 | 28.8 | 1.06 | |
| #3 | A1 | 2700.46 | 2753.27 | 52.81 | 2738.87 | 17.4 | 0.64 |
| A2 | 2700.46 | 2822.93 | 122.47 | 2742.47 | 22.0 | 0.80 | |
| A3 | 2682.24 | 2825.21 | 142.97 | 2737.58 | 23.0 | 0.84 | |
| #4 | A1 | 2700.46 | 2753.27 | 52.81 | 2738.87 | 17.4 | 0.64 |
| A2 | 2700.46 | 2822.93 | 122.47 | 2742.49 | 21.9 | 0.80 | |
| A3 | 2682.24 | 2825.21 | 142.97 | 2737.58 | 23.0 | 0.84 |
| Pillar | Arrangement | vmin [m/s] | vmax [m/s] | Δv = vmax − vmin [m/s] | vavg [m/s] | SD [m/s] | CV [%] |
|---|---|---|---|---|---|---|---|
| #1 | B1 | 2699.52 | 2750.93 | 51.41 | 2737.67 | 17.4 | 0.64 |
| B2 | 2693.96 | 2756.58 | 62.62 | 2737.61 | 17.2 | 0.63 | |
| B3 | 2667.36 | 2771.10 | 103.74 | 2727.88 | 20.9 | 0.77 | |
| #2 | B1 | 2692.63 | 2751.52 | 58.89 | 2735.22 | 18.8 | 0.69 |
| B2 | 2647.13 | 2757.36 | 110.23 | 2734.08 | 22.5 | 0.82 | |
| B3 | 2618.33 | 2771.67 | 153.34 | 2719.18 | 29.0 | 1.07 | |
| #3 | B1 | 2700.46 | 2810.41 | 109.95 | 2745.15 | 21.5 | 0.78 |
| B2 | 2696.75 | 2810.41 | 113.66 | 2745.48 | 21.4 | 0.78 | |
| B3 | 2666.05 | 2825.21 | 159.15 | 2735.68 | 24.5 | 0.90 | |
| #4 | B1 | 2700.46 | 2810.41 | 109.95 | 2745.15 | 21.5 | 0.78 |
| B2 | 2696.75 | 2810.41 | 113.66 | 2745.48 | 21.4 | 0.78 | |
| B3 | 2666.05 | 2825.21 | 159.15 | 2735.68 | 24.5 | 0.90 |
| Pillar | vavg [m/s] 1 joint | vavg [m/s] 2 joints | vavg [m/s] 3 joints |
|---|---|---|---|
| #1 | 2747.70 | 2733.58 | 2726.77 |
| #2 | 2747.19 | 2734.16 | 2727.26 |
| #3 | 2747.45 | 2734.48 | 2727.47 |
| #4 | 2747.45 | 2734.48 | 2727.47 |
| Pillar | Arrangement | vmin [m/s] | vmax [m/s] | Δv = vmax − vmin [m/s] | vavg [m/s] | SD [m/s] | CV [%] |
|---|---|---|---|---|---|---|---|
| #1 | A1 | 1687.58 | 2651.26 | 963.68 | 2099.66 | 363.7 | 17.32 |
| A2 | 1687.58 | 2651.26 | 963.68 | 2104.60 | 296.1 | 14.07 | |
| A3 | 1574.48 | 2651.26 | 1076.78 | 2030.73 | 258.4 | 12.72 | |
| #2 | A1 | 1253.62 | 2908.28 | 1654.66 | 2100.92 | 463.0 | 22.04 |
| A2 | 1253.62 | 2908.28 | 1654.66 | 2042.58 | 395.5 | 19.36 | |
| A3 | 1253.62 | 2908.28 | 1654.66 | 1927.77 | 322.5 | 16.73 | |
| #3 | A1 | 1402.37 | 2615.69 | 1213.32 | 1936.08 | 304.9 | 15.75 |
| A2 | 1313.12 | 2615.69 | 1302.58 | 1876.67 | 310.2 | 16.53 | |
| A3 | 1150.91 | 2615.69 | 1464.78 | 1731.45 | 291.4 | 16.83 | |
| #4 | A1 | 1617.59 | 3068.45 | 1450.86 | 2163.11 | 465.7 | 21.53 |
| A2 | 1617.59 | 3068.45 | 1450.86 | 2107.37 | 365.2 | 17.33 | |
| A3 | 1511.52 | 3068.45 | 1556.93 | 2009.67 | 316.0 | 15.72 |
| Pillar | Arrangement | vmin [m/s] | vmax [m/s] | Δv = vmax − vmin [m/s] | vavg [m/s] | SD [m/s] | CV [%] |
|---|---|---|---|---|---|---|---|
| #1 | B1 | 1597.71 | 2651.26 | 1053.55 | 2014.90 | 330.1 | 16.38 |
| B2 | 1493.14 | 2651.26 | 1158.12 | 1969.88 | 283.3 | 14.38 | |
| B3 | 1321.90 | 2651.26 | 1329.36 | 1896.30 | 254.4 | 13.42 | |
| #2 | B1 | 1253.62 | 2908.28 | 1654.66 | 1887.48 | 422.8 | 22.40 |
| B2 | 1117.83 | 2908.28 | 1790.45 | 1807.67 | 362.3 | 20.04 | |
| B3 | 1111.81 | 2908.28 | 1796.47 | 1722.46 | 311.5 | 18.08 | |
| #3 | B1 | 1222.19 | 2615.69 | 1393.51 | 1814.67 | 314.8 | 17.35 |
| B2 | 1222.19 | 2615.69 | 1393.51 | 1748.82 | 314.9 | 18.01 | |
| B3 | 1056.88 | 2615.69 | 1558.81 | 1635.34 | 277.0 | 16.94 | |
| #4 | B1 | 1407.43 | 3068.45 | 1661.02 | 2055.87 | 424.4 | 20.64 |
| B2 | 1407.43 | 3068.45 | 1661.02 | 2001.88 | 378.7 | 18.92 | |
| B3 | 1354.30 | 3068.45 | 1714.15 | 1921.07 | 315.8 | 16.44 |
| Pillar | vavg [m/s] 1 joint | vavg [m/s] 2 joints | vavg [m/s] 3 joints |
|---|---|---|---|
| #1 | 2082.75 | 1727.25 | 1682.13 |
| #2 | 1967.77 | 1657.43 | 1638.79 |
| #3 | 1923.85 | 1578.54 | 1557.31 |
| #4 | 2002.48 | 1800.36 | 1708.91 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zielińska, M.; Rucka, M. Non-Destructive Assessment of Masonry Pillars using Ultrasonic Tomography. Materials 2018, 11, 2543. https://doi.org/10.3390/ma11122543
Zielińska M, Rucka M. Non-Destructive Assessment of Masonry Pillars using Ultrasonic Tomography. Materials. 2018; 11(12):2543. https://doi.org/10.3390/ma11122543
Chicago/Turabian StyleZielińska, Monika, and Magdalena Rucka. 2018. "Non-Destructive Assessment of Masonry Pillars using Ultrasonic Tomography" Materials 11, no. 12: 2543. https://doi.org/10.3390/ma11122543
APA StyleZielińska, M., & Rucka, M. (2018). Non-Destructive Assessment of Masonry Pillars using Ultrasonic Tomography. Materials, 11(12), 2543. https://doi.org/10.3390/ma11122543