Mechanical Behavior of Natural Fiber-Based Bi-Directional Corrugated Lattice Sandwich Structure
Abstract
:1. Introduction
2. Structure and Materials
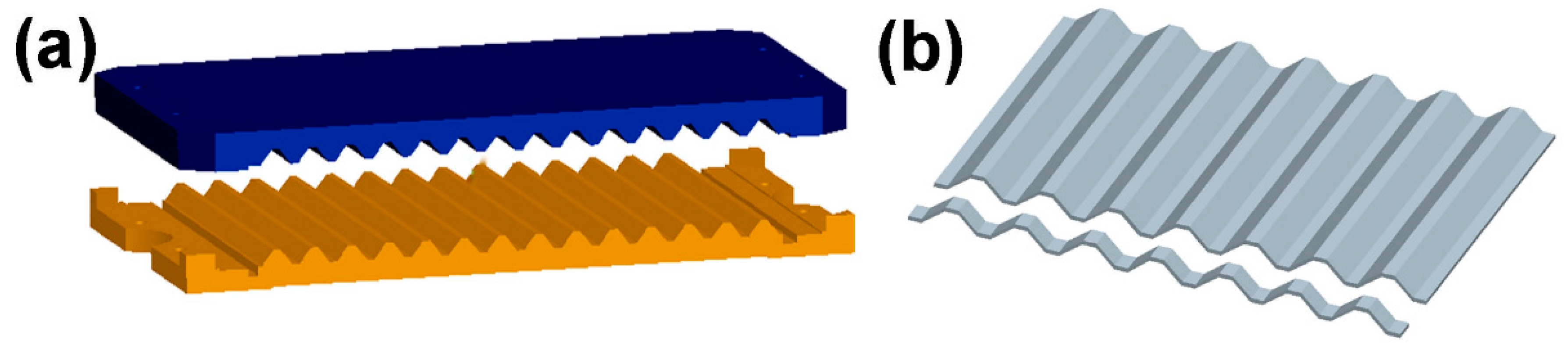
2.1. Structure and Fabrication
2.1.1. Single-Layer Structure
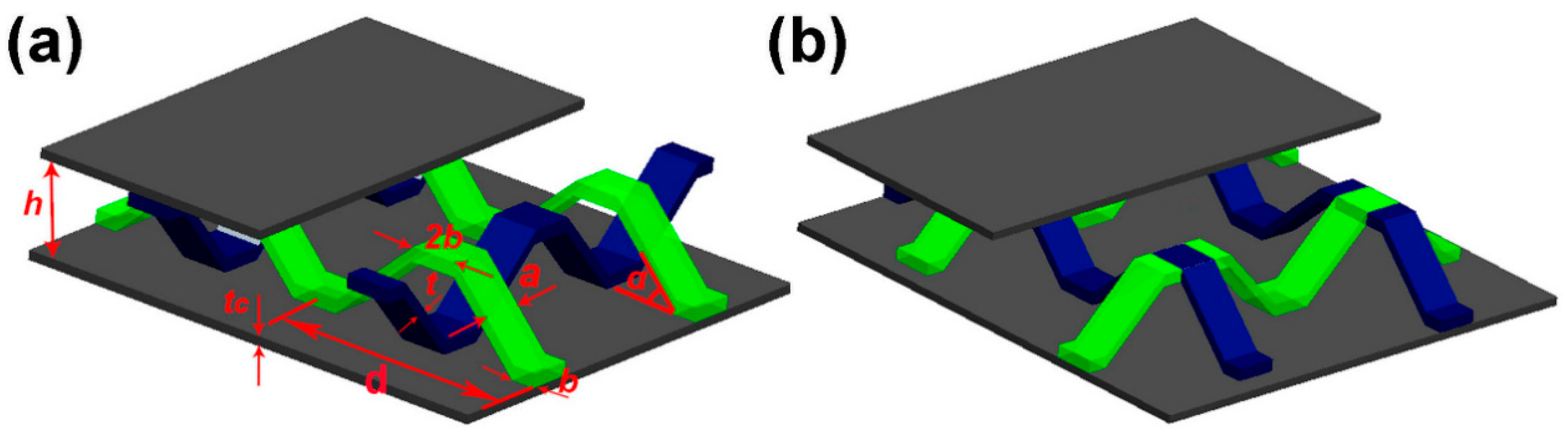
2.1.2. Double-Layer Structure
2.2. Materials
3. Experiment
3.1. Core Strut Performance
3.2. Out-Of-Plane Compression
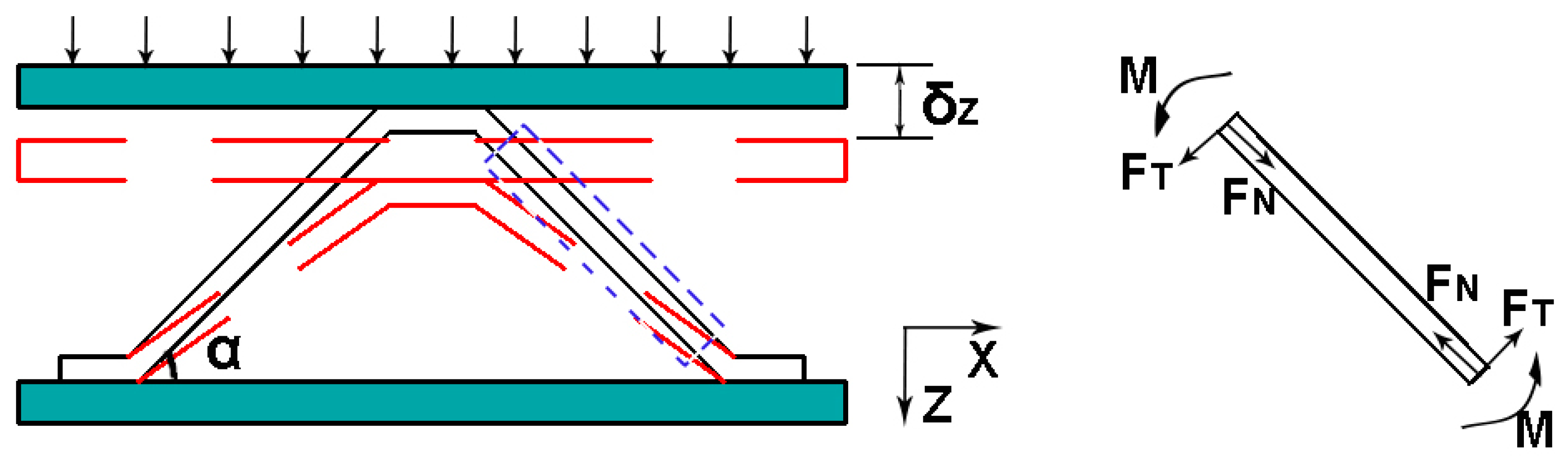
4. Theoretical Analysis
4.1. Single-Layer Structure
4.2. Double-Layer Structure
5. Results and Discussion
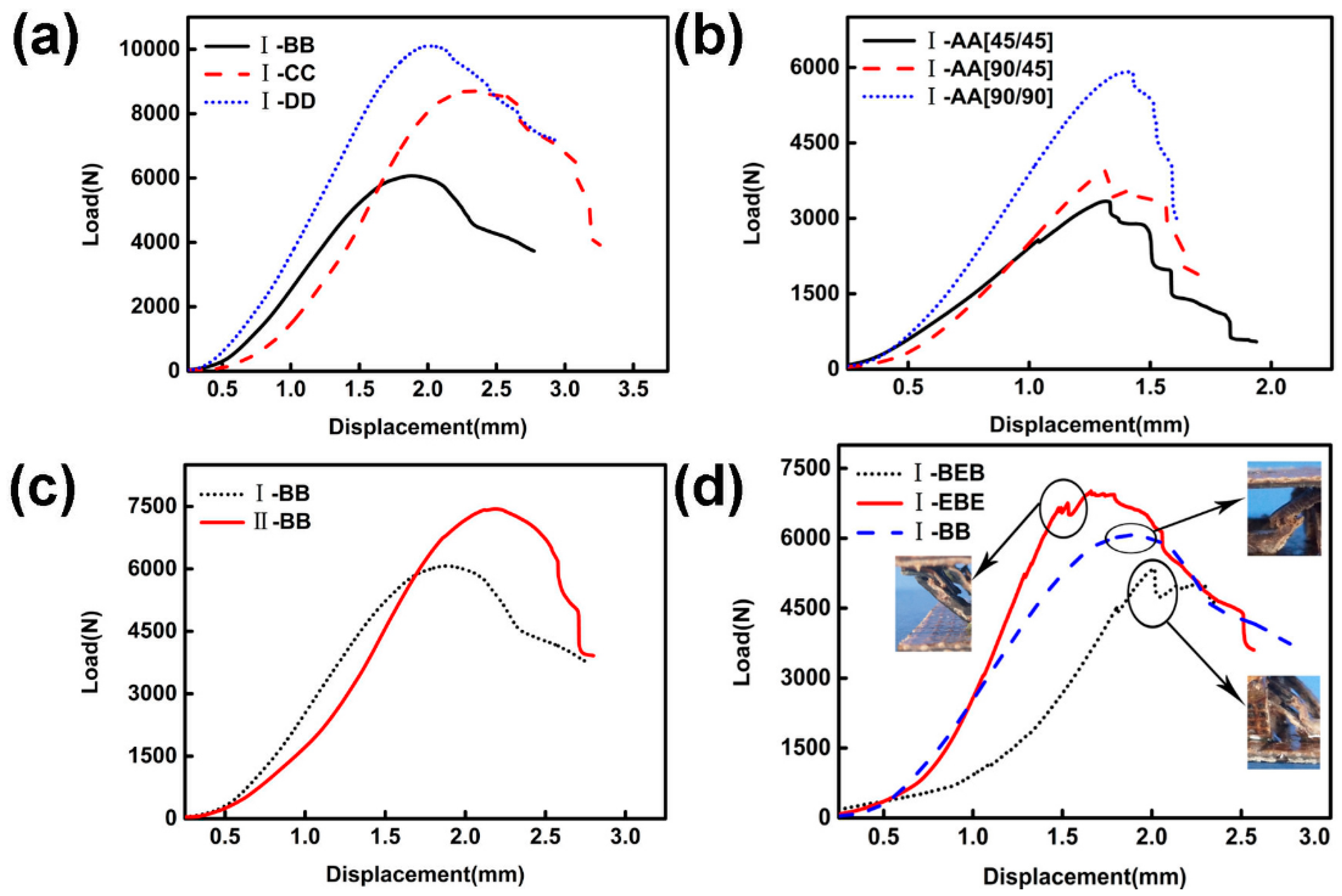
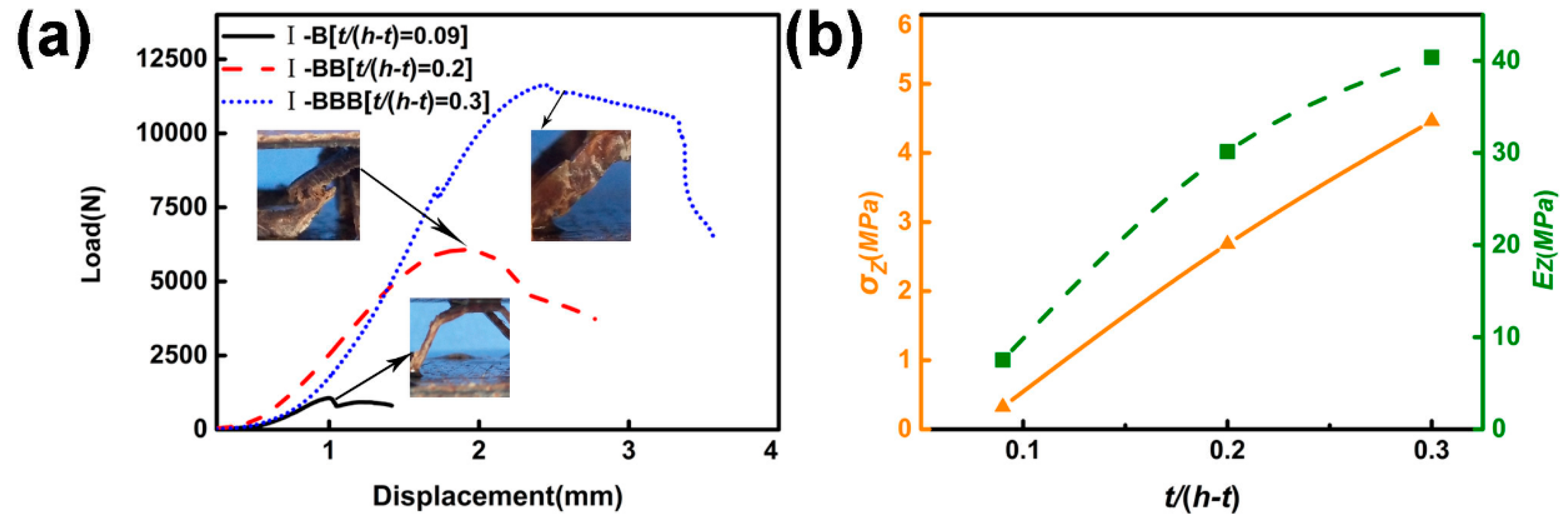
5.1. Compression of the Single-Layer Structure
5.1.1. Type of Jute Cloth
5.1.2. Fiber Angle
5.1.3. Configuration
5.1.4. Addition of Carbon Fiber Cloth
5.1.5. Volume Content
5.1.6. Length-To-Diameter Ratio of the Struts
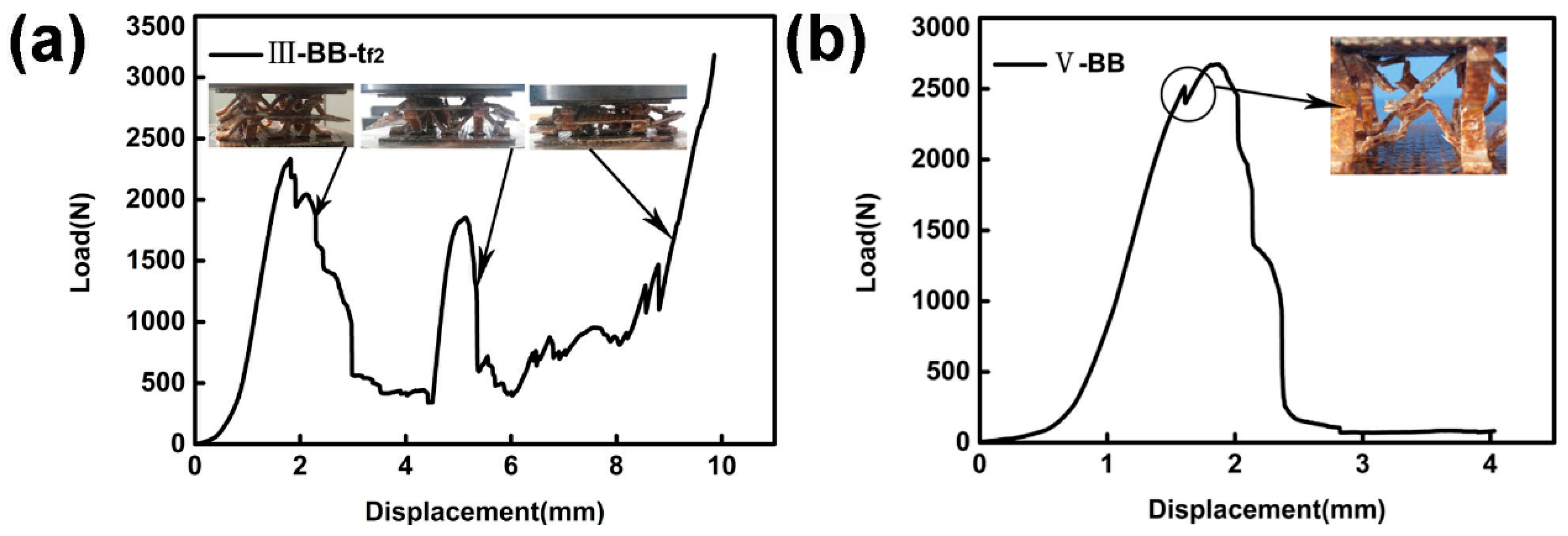
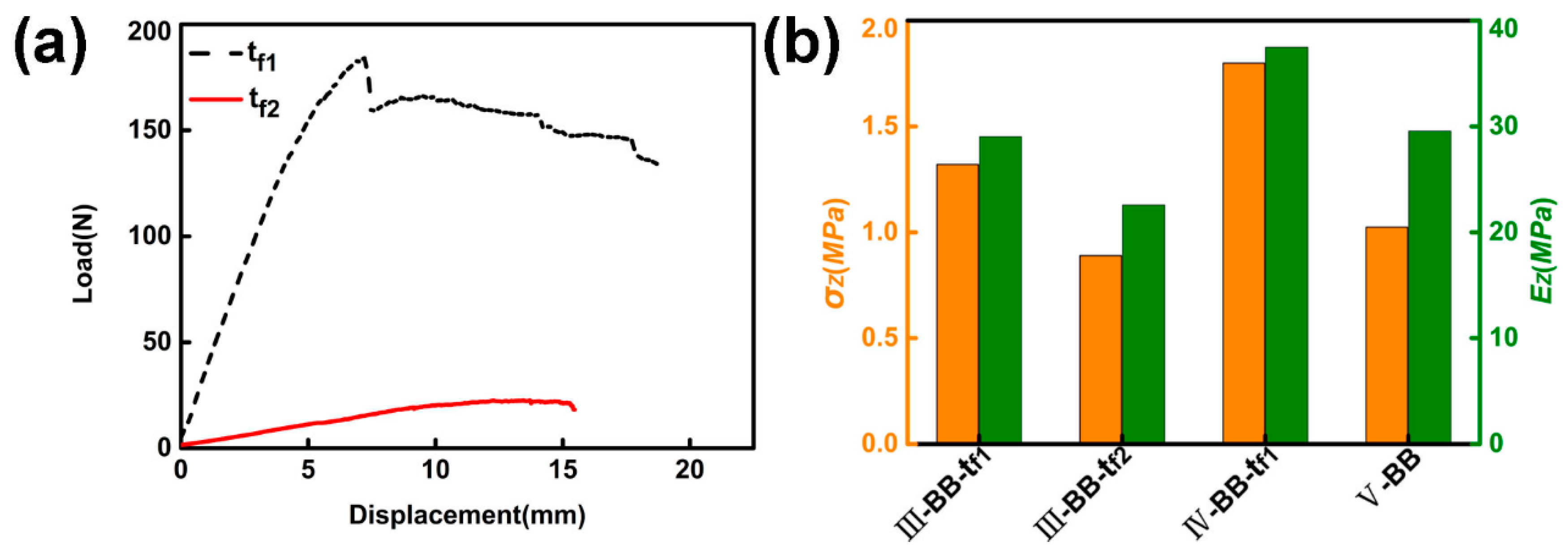
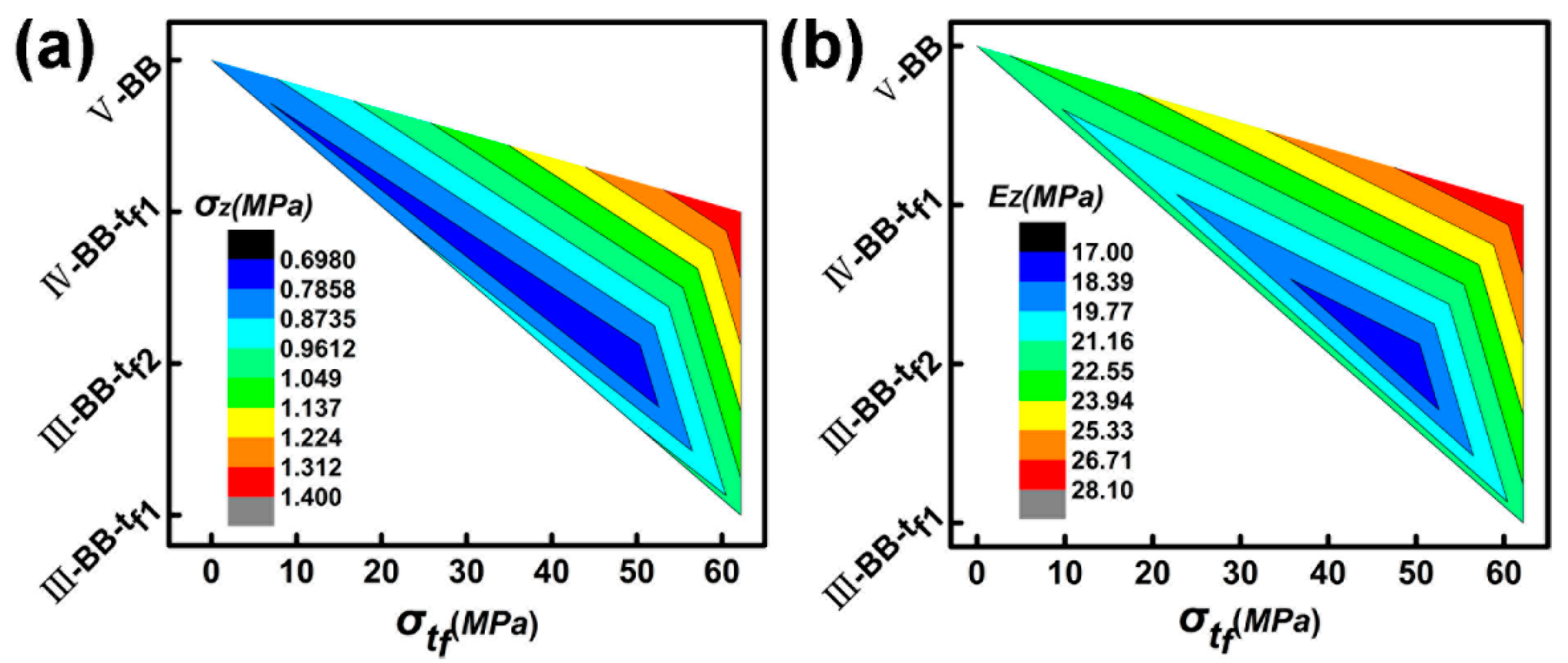
5.2. Double-Layer Structure
6. Conclusions
- In the sandwich structure prepared by jute fiber cloth and epoxy resin, the mode of core failure is mainly buckling and fracture. Damage initiation in both cases is mainly caused by the inhomogeneity of the fiber composite. The resulting sandwich structure after the addition of carbon fibers mainly fails owing to the delamination failure of the struts. Improving the hydrophilicity of the matrix material and treating the surface of the fiber can contribute to the interfacial bonding ability, thereby improving the mechanical properties.
- The effects of the fiber angle, type of fiber cloth, fiber volume content, configuration, and length-to-diameter ratio of the struts have an effect on the mechanical properties of the test piece. Optimizing the angle of the jute fiber in the strut so that the orientation of the fiber and axial forces are parallel, helps to significantly increase the compressive strength and Young’s modulus of the sample.
- In the double-layer lattice sandwich structure, the intermediate support plate acts as a stabilizer between the adjacent layers of the multilayer structure, so that each structural layer has a relatively independent structure. Increasing the strength of the intermediate support plate can effectively prevent the premature instability of the upper core layer, due to the deformation of the support plate, and contribute to the improvement of the compression performance. Optimizing the configuration can reduce the influence of the deformation of the intermediate support plate on the structure, and improve the compressive strength and Young’s modulus.
- The low-density natural fiber sandwich structure is easy to prepare, and the preparation process is reproducible, highlighting its potential for industrial use as a lattice sandwich structure. Other advantages include its low cost, environmental benignity, and biodegradability.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wang, B.; Wu, L.; Ma, L.; Sun, Y.; Du, S. Mechanical behavior of the sandwich structures with carbon fiber-reinforced pyramidal lattice truss core. Mater. Des. 2010, 31, 2659–2663. [Google Scholar] [CrossRef]
- Li, M.; Wu, L.; Ma, L.; Wang, B.; Guan, Z. Mechanical Response of All-composite Pyramidal Lattice Truss Core Sandwich Structures. Mater. Sci. Technol. 2011, 27, 570–576. [Google Scholar] [CrossRef]
- Xiong, J.; Ma, L.; Vaziri, A.; Yang, J.; Wu, L. Mechanical behavior of carbon fiber composite lattice core sandwich panels fabricated by laser cutting. Acta Mater. 2012, 60, 5322–5334. [Google Scholar] [CrossRef]
- Umer, R.; Barsoum, Z.; Jishi, H.Z.; Ushijima, K.; Cantwell, W.J. Analysis of the compression behaviour of different composite lattice designs. J. Compos. Mater. 2017, 52, 715–729. [Google Scholar] [CrossRef]
- Li, S.; Qin, J.; Li, C.; Feng, Y.; Zhao, X.; Hu, Y. Optimization and compressive behavior of composite 2-D lattice structure. Mech. Adv. Mater. Struct. 2018, 1–10. [Google Scholar] [CrossRef]
- Fan, H.; Zhou, Q.; Yang, W.; Jingjing, Z. An experiment study on the failure mechanisms of woven textile sandwich panels under quasi-static loading. Compos. Part B 2010, 41, 686–692. [Google Scholar] [CrossRef]
- Fan, H.; Yang, W.; Zhou, Q. Experimental research of compressive responses of multi-layered woven textile sandwich panels under quasi-static loading. Compos. Part B 2011, 42, 1151–1156. [Google Scholar] [CrossRef]
- Xiong, J.; Ma, L.; Wu, L.; Wang, B.; Vaziri, A. Fabrication and crushing behavior of low density carbon fiber composite pyramidal truss structures. Compos. Struct. 2010, 92, 2695–2702. [Google Scholar] [CrossRef]
- Xiong, J.; Vaziri, A.; Ma, L.; Papadopoulos, J.; Wu, L. Compression and impact testing of two-layer composite pyramidal-core sandwich panels. Compos. Struct. 2012, 94, 793–801. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; An, X.; Fan, H. Fabrication and mechanical behaviors of corrugated lattice truss composite sandwich panels. Compos. Sci. Technol. 2016, 125, 114–122. [Google Scholar] [CrossRef]
- Beharic, A.; Rodriguez Egui, R.; Yang, L. Drop-weight impact characteristics of additively manufactured sandwich structures with different cellular designs. Mater. Des. 2018, 145, 122–134. [Google Scholar] [CrossRef]
- Vitale, P.; Francucci, G.; Rapp, H.; Stocchi, A. Manufacturing and compressive response of ultra-lightweight CFRP cores. Compos. Struct. 2018, 194, 188–198. [Google Scholar] [CrossRef]
- Haldar, A.K.; Guan, Z.W.; Cantwell, W.J.; Wang, Q.Y. The compressive properties of sandwich structures based on an egg-box core design. Compos. Part B 2018, 144, 143–152. [Google Scholar] [CrossRef]
- Kooistra, G.W.; Wadley, H.N.G. Lattice truss structures from expanded metal sheet. Mater. Des. 2007, 28, 507–514. [Google Scholar] [CrossRef]
- Pflug, J.; Verpoest, I. Sandwich Materials Selection Charts. J. Sandw. Struct. Mater. 2016, 8, 407–421. [Google Scholar] [CrossRef]
- Aziz, S.H.; Ansell, M.P. The effect of alkalization and fibre alignment on the mechanical and thermal properties of kenaf and hemp bast fibre composites: Part 1—Polyester resin matrix. Compos. Sci. Technol. 2004, 64, 1219–1230. [Google Scholar] [CrossRef]
- Du, Y.; Yan, N.; Kortschot, M.T. Light-weight honeycomb core sandwich panels containing biofiber-reinforced thermoset polymer composite skins: Fabrication and evaluation. Compos. Part B 2012, 43, 2875–2882. [Google Scholar] [CrossRef]
- Malkapuram, R.; Kumar, V.; Yuvraj Singh, N. Recent Development in Natural Fiber Reinforced Polypropylene Composites. Reinf. Plast. Compos. 2008, 28, 1169–1189. [Google Scholar] [CrossRef]
- de Lemos, A.L.; Prestes Pires, P.G.; de Albuquerque, M.L.; Botaro, V.R.; de Paiva, J.M.F.; Sebasti, N.; Junior, D. Biocomposites reinforced with natural fibers:thermal, morphological and mechanical characterization. Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Petrone, G.; Rao, S.; De Rosa, S.; Mace, B.R.; Franco, F.; Bhattacharyya, D. Behaviour of fibre-reinforced honeycomb core under low velocity impact loading. Compos. Struct. 2013, 100, 356–362. [Google Scholar] [CrossRef]
- Santulli, C.; Sarasini, F.; Tirillò, J.; Valente, T.; Valente, M.; Caruso, A.P.; Infantino, M.; Nisini, E.; Minak, G. Mechanical behaviour of jute cloth/wool felts hybrid laminates. Mater. Des. 2013, 50, 309–321. [Google Scholar] [CrossRef]
- Stocchi, A.; Colabella, L.; Cisilino, A.; Álvarez, V. Manufacturing and testing of a sandwich panel honeycomb core reinforced with natural-fiber fabrics. Mater. Des. 2014, 55, 394–403. [Google Scholar] [CrossRef] [Green Version]
- Vitale, J.P.; Francucci, G.; Xiong, J.; Stocchi, A. Failure mode maps of natural and synthetic fiber reinforced composite sandwich panels. Compos. Part A 2017, 94, 217–225. [Google Scholar] [CrossRef]
- Boccarusso, L.; Durante, M.; Langella, A. Lightweight hemp/bio-epoxy grid structure manufactured by a new continuous process. Compos. Part B 2018, 146, 165–175. [Google Scholar] [CrossRef]
- Fan, H.; Fang, D.; Chen, L.; Dai, Z.; Yang, W. Manufacturing and testing of a CFRC sandwich cylinder with Kagome cores. Compos. Sci. Technol. 2009, 69, 2695–2700. [Google Scholar] [CrossRef]







| NO. | A | B | C | D | E |
|---|---|---|---|---|---|
| Surface density (g/m2) | 190 | 220 | 340 | 490 | 210 |
| NO. | t (mm) | Material | (°) | (MPa) | (MPa) | (g/cm3) |
|---|---|---|---|---|---|---|
| AA [45/45] | 1.4 | A | (45/45) | 44.1 | 1234.1 | 1.09 |
| AA [90/45] | 1.4 | A | (90/45) | 51.6 | 1496.7 | 1.09 |
| AA [90/90] | 1.4 | A | (90/90) | 56.7 | 1509.0 | 1.09 |
| B | 0.9 | B | (90) | 34.0 | 896.1 | 1.10 |
| BB [t = 1.7 mm] | 1.7 | B | (90/90) | 61.1 | 1242.9 | 1.15 |
| BB [t = 2.0 mm] | 2.0 | B | (90/90) | 54.2 | 989.0 | 1.07 |
| BBB | 3.0 | B | (90/90/90) | 79.4 | 1091.5 | 1.08 |
| CC | 2.0 | C | (90/90) | 64.1 | 1049.2 | 1.13 |
| DD | 2.0 | D | (90/90) | 63.8 | 1377.8 | 1.20 |
| BEB | 2.0 | B/E | (90/90/90) | 82.9 | 1835.6 | 1.22 |
| EBE | 2.0 | B/E | (90/90/90) | 88.0 | 2733.4 | 1.02 |
| NO. | (%) | Experimental Results (MPa) | Analytical Results (MPa) | ||
|---|---|---|---|---|---|
| I-AA [45/45] | 10.0 | 1.2 | 19.0 | 1.9 | 26.3 |
| I-AA [90/45] | 10.0 | 1.4 | 22.4 | 2.2 | 31.9 |
| I-AA [90/90] | 10.0 | 2.2 | 30.4 | 2.4 | 32.1 |
| I-B | 6.6 | 0.3 | 7.5 | 0.3 | 12.2 |
| I-BB | 13.6 | 2.6 | 30.1 | 3.3 | 30.4 |
| I0-BB | 11.8 | 2.3 | 31.9 | 3.18 | 32.3 |
| I-BBB | 18.9 | 4.5 | 40.4 | 7.5 | 51.6 |
| I-CC | 13.6 | 3.1 | 29.8 | 4.0 | 32.3 |
| I-DD | 13.6 | 3.8 | 40.1 | 3.9 | 42.4 |
| I-BEB | 13.6 | 2.3 | 27.3 | 5.1 | 56.4 |
| I-EBE | 13.6 | 2.7 | 47.3 | 5.4 | 84.1 |
| II-BB | 11.6 | 2.2 | 26.6 | 3.3 | 30.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Feng, Y.; Wang, M.; Hu, Y. Mechanical Behavior of Natural Fiber-Based Bi-Directional Corrugated Lattice Sandwich Structure. Materials 2018, 11, 2578. https://doi.org/10.3390/ma11122578
Li S, Feng Y, Wang M, Hu Y. Mechanical Behavior of Natural Fiber-Based Bi-Directional Corrugated Lattice Sandwich Structure. Materials. 2018; 11(12):2578. https://doi.org/10.3390/ma11122578
Chicago/Turabian StyleLi, Shuguang, Yanxia Feng, Mengyuan Wang, and Yingcheng Hu. 2018. "Mechanical Behavior of Natural Fiber-Based Bi-Directional Corrugated Lattice Sandwich Structure" Materials 11, no. 12: 2578. https://doi.org/10.3390/ma11122578
APA StyleLi, S., Feng, Y., Wang, M., & Hu, Y. (2018). Mechanical Behavior of Natural Fiber-Based Bi-Directional Corrugated Lattice Sandwich Structure. Materials, 11(12), 2578. https://doi.org/10.3390/ma11122578




