Next Article in Journal
Analysis of Polycyclic Aromatic Hydrocarbon (PAH) Mixtures Using Diffusion-Ordered NMR Spectroscopy and Adsorption by Powdered Activated Carbon and Biochar
Next Article in Special Issue
Active Enhancement of Slow Light Based on Plasmon-Induced Transparency with Gain Materials
Previous Article in Journal
Evaluation of Fracture Strength of Ceramics Containing Small Surface Defects Introduced by Focused Ion Beam
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 11
Issue 3
10.3390/ma11030458
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Metal-Insulator-Metal-Based Plasmonic Metamaterial Absorbers at Visible and Infrared Wavelengths: A Review

by
Shinpei Ogawa
1,* and
Masafumi Kimata
2
1
Advanced Technology R&D Center, Mitsubishi Electric Corporation, 8-1-1 Tsukaguchi-Honmachi, Amagasaki, Hyogo 661-8661, Japan
2
College of Science and Engineering, Ritsumeikan University, 1-1-1 Noji-higashi, Kusatsu, Shiga 525-8577, Japan
*
Author to whom correspondence should be addressed.
Materials 2018, 11(3), 458; https://doi.org/10.3390/ma11030458
Submission received: 23 February 2018 / Revised: 16 March 2018 / Accepted: 17 March 2018 / Published: 20 March 2018
(This article belongs to the Special Issue New Horizon of Plasmonics and Metamaterials)
Browse Figures
Versions Notes

Abstract

:
Electromagnetic wave absorbers have been investigated for many years with the aim of achieving high absorbance and tunability of both the absorption wavelength and the operation mode by geometrical control, small and thin absorber volume, and simple fabrication. There is particular interest in metal-insulator-metal-based plasmonic metamaterial absorbers (MIM-PMAs) due to their complete fulfillment of these demands. MIM-PMAs consist of top periodic micropatches, a middle dielectric layer, and a bottom reflector layer to generate strong localized surface plasmon resonance at absorption wavelengths. In particular, in the visible and infrared (IR) wavelength regions, a wide range of applications is expected, such as solar cells, refractive index sensors, optical camouflage, cloaking, optical switches, color pixels, thermal IR sensors, IR microscopy and gas sensing. The promising properties of MIM-PMAs are attributed to the simple plasmonic resonance localized at the top micropatch resonators formed by the MIMs. Here, various types of MIM-PMAs are reviewed in terms of their historical background, basic physics, operation mode design, and future challenges to clarify their underlying basic design principles and introduce various applications. The principles presented in this review paper can be applied to other wavelength regions such as the ultraviolet, terahertz, and microwave regions.

1. Introduction

Electromagnetic (EM) wave absorbers are drawing significant interest from aspects of both fundamental science and industry applications. Typical EM wave absorbers are essentially based on the intrinsic loss of the material and thus require a long optical path, which results in large volume and poor design flexibility. EM wave absorbers with absorption properties that can be efficiently controlled by their structures have thus been studied for many years. Such EM wave absorbers were first studied in the microwave range and are roughly classified into two groups, according to Reference [1], as broadband absorbers and resonant absorbers. The broadband absorbers are further categorized into two groups: geometric transition absorbers and low-density absorbers [1]. Geometric transition absorbers consist of two-dimensional (2D) periodic pyramids that cause a gradual change in the dielectric constant from the free space to the absorbers [2,3]. Low-density absorbers utilize porous materials [4,5] and the multi-reflections that occur in these pores has led to significant absorption, which was realized using thin absorbers.
The resonance absorbers are classified into three types, according to Reference [6]. Figure 1a–f shows schematic illustrations and the reflectance of the Salisbury screen, Jaumann absorber, and circuit analog (CA) absorber. All of these resonance absorbers use a quarter-wavelength gap from the top material to the bottom substrate. The Salisbury screen uses a non-periodic resistive sheet in front of a ground plate [7]. The Jaumann absorber uses two or more resistive sheets in front of each other and is a basic resonance absorber [8]. These two absorbers use purely resistive sheets. The CA absorber uses a periodic surface made of a lossy material with three layers: the top periodic metal patterns, a middle dielectric layer, and a continuous metallic bottom layer [6]. The concept of CA absorbers is the basis of recent metamaterial absorbers for a wide range of wavelength regions, from visible to microwave wavelengths.
Recent advances in plasmonics [9] and metamaterials [10] research together with the progress in nanotechnological fabrication techniques has led to novel EM absorbers at visible and infrared (IR) wavelengths. These absorbers uses localized surface plasmon polaritons (LSPPs) [11] with a metamaterial concept to achieve much smaller absorber volumes, sufficient performance, and design flexibility based on geometry rather than the materials used. SPPs are the collective oscillation of electrons between metals and dielectrics that can go beyond the diffraction limit [12]. LSPPs are key to realizing small and thin absorbers for the visible and IR wavelength regions. Therefore, much significant research has been performed on EM wave absorbers using SPPs or LSPPs at visible and IR wavelengths.
There are roughly two categories of absorbers that employ plasmonics and metamaterials: conventional periodic structures such as plasmonic crystals [13,14,15] and gratings [16,17,18,19], and metamaterial-based structures, where periodicity has less impact on the optical properties [20]. In particular, metal-insulator-metal-based plasmonic metamaterial absorbers (MIM-PMAs) are the most promising and widely studied for a wide range of wavelengths due to their high performance, such as high absorbance, incident angle, and polarization insensitivity, as well as their design flexibility and simple fabrication. Although their fundamental principles are basically the same, a wide range of applications is expected, such as solar cells [21], refractive index sensors [22], optical camouflage [23], cloaking [24], optical switches [25], color pixels [26,27], thermal IR sensors [28,29,30,31], mechanical thermal sensors [32], surface-enhanced spectroscopy [33,34], and gas sensing [35]. Therefore, this review paper aims to clarify the fundamental principle, characteristics, possibilities, and challenges of MIM-PMAs at visible and IR wavelengths to contribute to future research and the expansion of their applications.
Please note that MIM-based thermal emitters are considered as MIM-PMAs at IR wavelengths [36] because absorbance is equal to emissivity, as given by Kirchhoff’s law. To the best of our knowledge, MIM-PMAs were first demonstrated as thermal IR emitters by Puscasu and Schaich [37].

2. Structures and Materials

In this section, the fundamental structures and materials of MIM-PMAs are explained with a simple introduction of the basic optical properties. The detailed optical characteristics are discussed in a later section.
MIM-PMAs consist of three layers: a bottom metal layer, a middle dielectric layer, and a top periodic metal micropatches. Figure 2a,b shows schematic illustrations of conventional MIM-PMAs with two-dimensional (2D) and one-dimensional (1D) periodic micropatches, respectively. The absorption wavelength is fundamentally defined by the micropatch size. The 2D configuration is symmetric for two orthogonal directions, the x and y directions; therefore, the optical properties are polarization insensitive. On the other hand, the 1D configuration is asymmetric in the x and y directions, so the optical properties are polarization sensitive. Figure 2c,d shows cross-sectional views of the conventional MIM-PMAs with flat and isolated dielectric layers, respectively. The middle dielectric layers underneath the micropatches are required, so that both structures function as MIM-PMAs.
The thickness of the metal in the bottom layer and the top micropatches is required to be more than twice the depth of the operating wavelength region, e.g., 100 nm thickness is sufficient for the IR wavelength region [38]. The thickness of the middle dielectric layer can be less than the operating wavelength/50 due to the strong confinement of the waveguide mode of SPPs [39].
The possible lattice structures for 2D periodic micropatches are square, triangular, and honeycomb. However, the lattice structures have less impact on absorption properties because each micropatch acts as a single isolated resonator [40].
The shape of micropatches are roughly classified into symmetric in the two orthogonal directions, such as squares [28,41], circles [42], and crosses [38,43], and nano-particles [44,45,46], or asymmetric, such as ellipses [47], rectangles [48], wedges [49], bow-ties [50], split-ring resonators [51], and asymmetric crosses [52,53]. Nanocubes have also been used as micropatches [54,55]. The shape of the corners and the sidewall angles have an important role in defining single and multiband resonances [56]. The end shape of the micropatch produces the difference of optical modes formed in the middle dielectric layer because MIM structures can be considered as waveguides and the shape of the waveguide end defines the waveguide mode [57]. The first three micropatch shapes are symmetric in the x and y directions, and absorption occurs at a single wavelength. On the other hand, the latter four micropatch shapes are asymmetric in the x and y directions and produce two absorption wavelengths. As discussed in Section 4, the symmetry is an important parameter for polarization dependence.
It is also important to consider the temperature tolerance and compatibility of the complementary metal oxide semiconductor (CMOS) process for the choice of materials used for MIM-PMAs [43,58]. Table 1 and Table 2 show the properties of the metals and dielectrics used in MIM-PMAs [43].
The top and the bottom layers are typically based on metals such as gold (Au) [38,41], silver (Ag) [49], and aluminum (Al) [28], which are common materials for SPPs. Titanium nitride (TiN) [59,60], molybdenum (Mo) [43], and tungsten (W) [58], or highly-doped silicon (Si) [61], can be used for the bottom and top micropatches. Graphene can also be used for top micropatches in the IR wavelength region [62]. TiN or Mo have recently been used for thermal IR emitters due to requirements of high-temperature tolerance. However, absorbers require less temperature tolerance. Therefore, Al is widely employed due to its compatibility with the CMOS process and its low cost.
The middle layer is roughly classified into two groups: oxides or nitrides such as Al2O3 [41], SiO2 [40], CeO2 [63], SiN [28], and AlN [43], and semiconductors such as Si [64], germanium (Ge) [65], and ZnS [66]. Another material often used is MgF2 [33]. Phase transition materials of germanium antimony telluride [67] and VO2 [68] have been used for thermal switching. The loss is an important factor of the middle dielectric layer, as discussed in a later section. Lossless materials such as Si, Ge, ZnS, and CeO2 should be used for the IR wavelength region in the vicinity of 10 μm to maintain the linear tunability of the absorption wavelength. However, these materials are not compatible with the CMOS process. The alternative choice to avoid the influence of intrinsic loss materials is mushroom-PMAs, where small post structures connect the micropatches and the bottom layer without a continuous middle dielectric layer [69,70,71].
A perforated metal plate can be used as a top layer, which is a complementary structure of periodic micropatches [72] that provides optical properties similar to MIM-PMAs. However, there is less design flexibility due to the need for periodicity. 1D grating structures with ultra-narrow groove widths (ca. 100 nm) and high aspect ratios (>10) [16,18,73] can be classified as MIM-PMAs because such a slit is considered to be the waveguide, which is equivalent to the insulator layer in MIM structures [74,75]. However, high aspect ratios and narrow groove widths require complicated fabrication procedures. In this paper, these structures are excluded and instead focus is made on the conventional MIM-PMAs, shown as Figure 2. Other structures such as core-shell nanoparticles [76] and multi-flat-layer structures [77,78,79] can be considered to have a principle similar to that of MIM-PMAs.

3. Basic Optical Properties

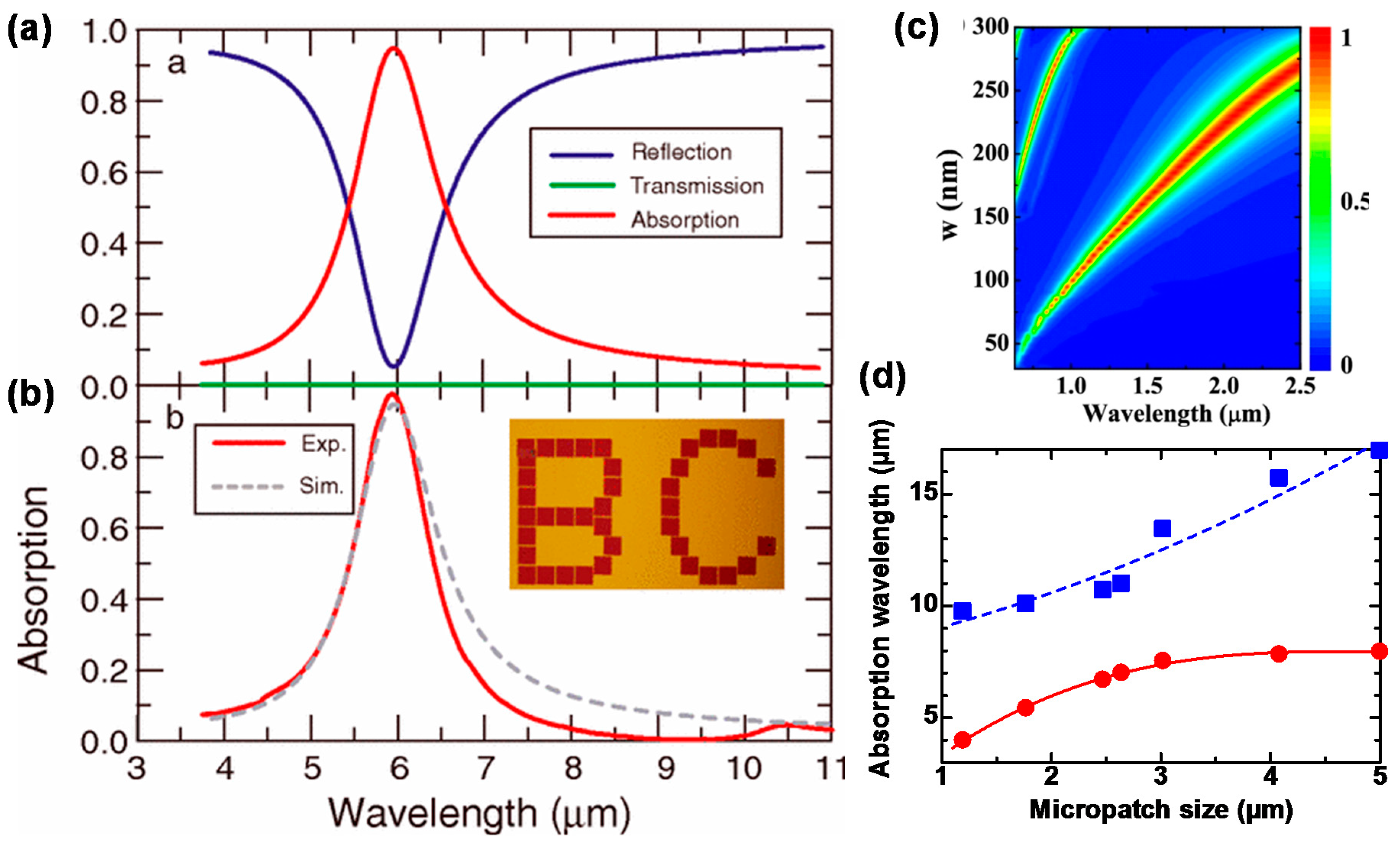
3.1. Principle

Figure 3a shows the operating principle of MIM-PMAs for incident EM waves. Figure 3b–d shows the calculated electric and magnetic fields, and the power distribution of MIM-PMAs at the absorption wavelength, respectively [41].
As shown in Figure 3a, a pair of anti-parallel oscillating currents is induced in both the bottom layer and the top micropatches, and significant magnetic resonance is produced. Dipole electric resonance is formed accordingly between the edge of the micropatches and the near bottom layer. LSPPs are induced by the incident light at the absorption wavelength. This principle is confirmed by the calculated electromagnetic field distribution, as shown in Figure 3b–d [41]. The electric displacement vectors in the bottom layer and the micropatches are opposite to each other, which generates a strong magnetic response [80] (Figure 3b). Strong electric dipole resonances are observed at the sides of the micropatches (Figure 3c). The reflectance can be completely cancelled in the far field by the interference of these two dipoles due to the π shift phase [65]. Strong absorption is thus attributed to these localized magnetic and electric dipole resonances, which provide sufficient time to consume light energy by the ohmic losses in the metals (Figure 3d).

3.2. Wavelength Selectivity

Figure 4a,b shows the calculated and measured optical properties of MIM-PMAs in IR wavelengths [38]. Wavelength selective absorption is clearly obtained at 6 μm, which is a typical wavelength-selective absorption property of MIM-PMAs. The main absorption wavelength is always longer than the period of the micropatches because wavelengths smaller than the period are diffracted. Figure 4c [41] and Figure 4d [81] show the calculated absorbance as a function of the wavelength and the micropatch size (w) in the near-IR wavelength region, as well as the measured relation between the micropatch size and the absorption wavelength in the IR wavelength region.
The absorption wavelength is almost proportional to the micropatch size in the near-IR wavelength region. In contrast, the relation between the micropatch size and the absorption wavelength is non-linear in the IR wavelength region, which is attributed to the loss of the middle dielectric layer [40]. Most oxides become lossy in the vicinity of 10 μm, where no absorption occurs, and this causes the non-linearity between the micropatch size and the absorption wavelength, as shown in Figure 4d. This is an important point for the design of MIM-PMAs for use at IR wavelengths. The thickness of the middle dielectric layer has less impact on the absorbance and the absorption wavelength, and can thus be optimized for the operating wavelength [41].

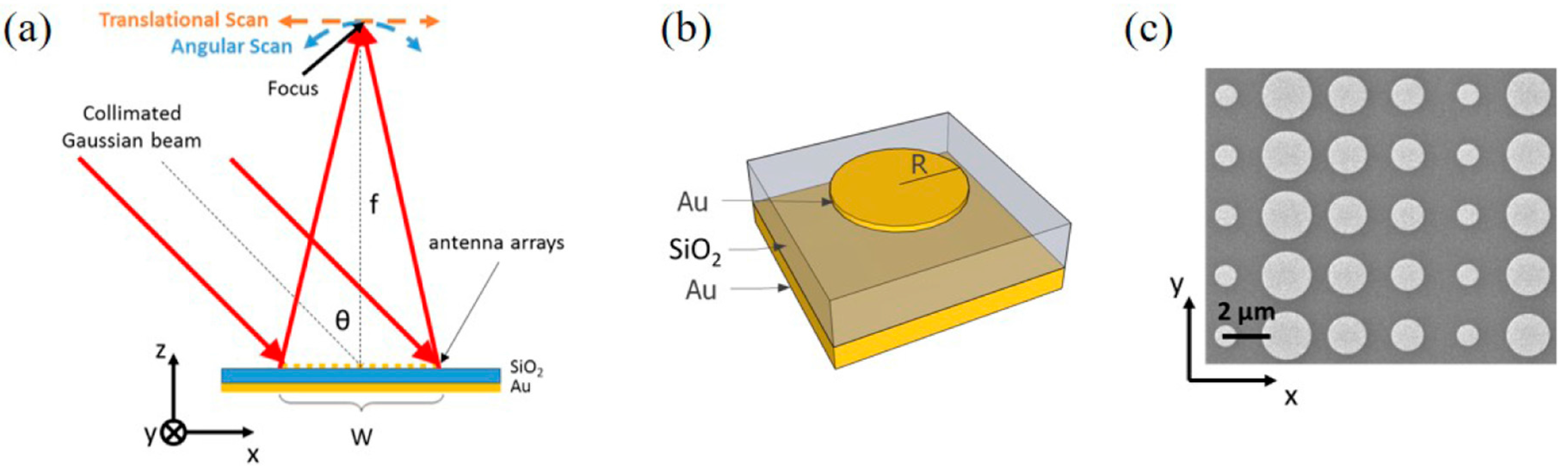
3.3. Incidence Angle Dependence

Figure 5a,b shows the calculated incident angle dependence of the absorbance as a function of the wavelength for the transverse-electric (TE) and transverse-magnetic (TM) modes, respectively [22]. The calculated model is for an MIM-PMA with 2D circle-shaped micropatches.
Figure 5 shows that the absorption can be realized at almost the same wavelength for a wide range of incidence angle up to approximately 70° for both TE and TM modes. This property is attributed to the strong LSPPs, as shown in Figure 3. The incident angle independence is an important advantage for device applications such as solar cells, IR image sensors, and biological sensors.

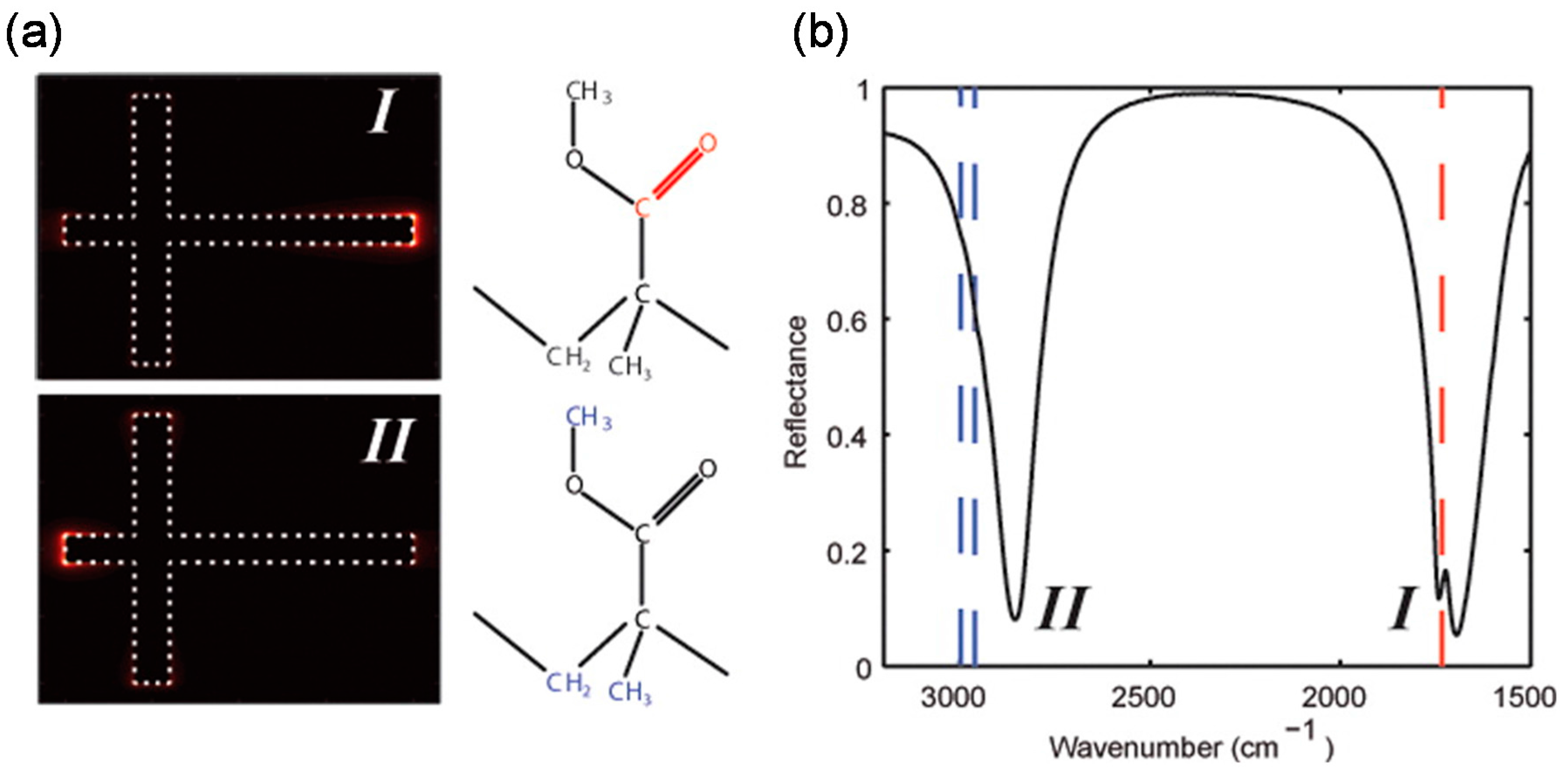
3.4. Polarization Dependence

In this section, the coordinate system is set as shown in Figure 3c,d. When the electric field of the incident light is in the x or y direction, the absorption wavelength is defined by the side-length of the micropatches in the x or y direction, respectively [39]. Each side-length of the square-shaped micropatches in the x and y direction is the same. Thus, the absorption wavelength is also the same for each polarization. MIM-PMAs with this configuration are polarization insensitive.
Different side lengths, such as ellipse [47] or asymmetric-cross-shaped [52] micropatches, produce dual band absorption, as discussed in the next section. The 1D periodic configuration shown in Figure 3b also produces two absorption modes. However, when one side-length is much longer than the other, the other absorbance is outside the operation wavelength region, which results in polarization-selective absorbers. Polarization-selective absorbers can be applied to IR polarimetric imaging [82,83] to enhance object recognition ability such as distinct human trace in a natural environment and human facial recognition [84].

3.5. Inductor-capacitor (LC) Circuit Model

The operation principle of MIM-PMAs is sometimes explained using the LC equivalent circuit model. This may be due to the influence of CA absorbers mentioned in the introduction section. Figure 6 shows a schematic illustration of the LC equivalent circuit for MIM-PMAs [40,63]. Two models are considered, with or without the loss of the insulator layer. The frequency that gives a total impedance of zero is the absorption frequency.

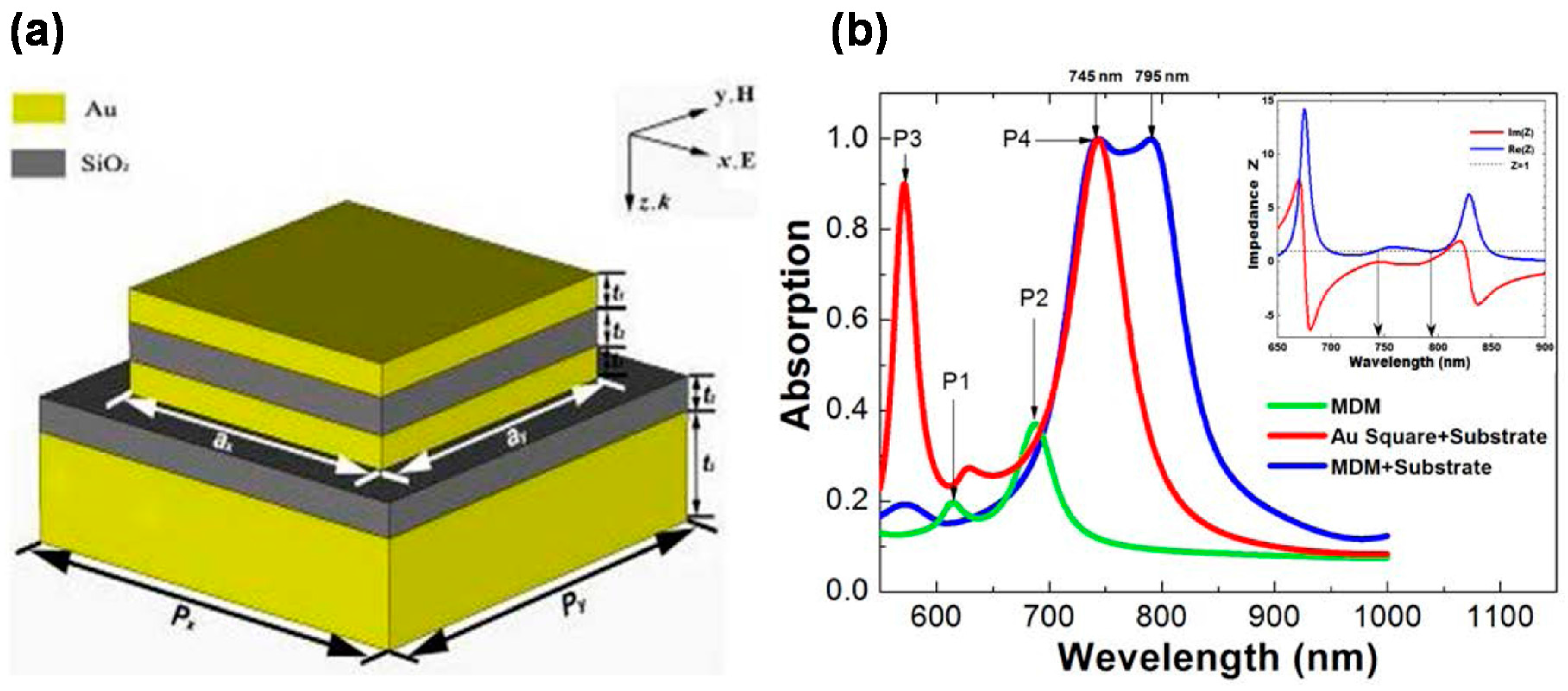
4. Multi-Band and Broadband Operation

The strategies of multi-band and broadband absorption are classified into three groups: asymmetrically-shaped [47,52,85,86,87,88,89] or multi-size [42,65,66,90,91,92,93,94] micropatches, multi-layers of MIM structure [95,96,97,98,99,100], and embedded in dielectric materials [57,101,102]. The first two are based on multi-resonance that produces multi-mode absorption. Each absorption mode becomes close, which results in broadband absorption [103]. Figure 7a–d shows MIM-PMAs with two-types of asymmetrically shaped micropatches, such as cross [52] and elliptical shapes [47], for dual-band operation. This dual-band absorption is designed in consideration of the polarization dependence for the two orthogonal directions.
Figure 8a,b shows oblique and the cross-sectional schematic illustrations of an MIM-PMA with 1D stripe-shaped multi-size-micropatches (w1 to w4), respectively [65]. Figure 8c,d shows a schematic illustration and magnetic field distribution of an MIM-PMA with 2D multi-size micropatches and the corresponding absorption spectrum, respectively [66]. The absorption spectrum is the summation of the absorption wavelengths generated by each micropatch resonator. Figure 8d shows that the distance between each resonant wavelength becomes close, which results in broadband absorption.
Figure 9a,b shows a schematic illustration of a multi-layer MIM-PMA and the calculated absorption spectrum, respectively [95]. Each MIM layer produces multi-plasmonic-resonances at different wavelengths and each resonance is coupled, so that broadband absorption occurs [103].
Broadband absorption is also achieved by MIM-PMAs with single or multi-layers embedded in lossy dielectrics such as amorphous Si [57] and SiN [101]. The resonances of MIM-PMAs can be broadened by lossy materials, which results in broad absorption. However, these structures increase the thickness and volume of the absorbers, and cause difficulties for fabrication. Care should be taken in applying them to practical devices by comparison with other convenient structures such as simple multi-flat-layer structures [77,78,79] or gold black [104,105] in terms of their thickness, ease of fabrication, and cost.

5. Advanced Structures and Applications

In this section, we briefly outline the advanced MIM-PMAs structures and applications other than absorbers to clarify the future research of MIM-PMAs. There has been growing interest in mainly three categories of advanced MIM-PMAs: flexible devices, the combination of graphene and other 2D materials, and metalenses.
One of the advanced structures is the flexible MIM-PMA [86,106,107], as shown in Figure 10 [86]. Flexible substrates such as Kapton film [86], polyethylene terephthalate (PET) [106] or polydimethylsiloxane (PDMS) [107] have enabled flexible MIM structures. MIM-PMAs coated on such flexible substrates can thus realize flexible and stretchable devices such as flexible solar cells, health care systems for the human body, and the cloaking of non-flat objects [108].
The combination of graphene [109] and other 2D atomic layer materials [110] such as MoS2 and WSe2 with MIM-PMAs [55,81,111,112,113,114,115] is also drawing significant interest because these 2D atomic layer materials can strongly interact with plasmonic resonance [116]. Figure 11 shows a schematic illustration of graphene coated on an MIM-PMA (GMIM-PMA).
MIM-PMAs serve as a platform to enhance graphene absorption and realize high-performance graphene-based photodetectors [81,111,112,114]. The Fermi level of graphene can be electrically tuned according to the applied voltage; therefore, the absorption wavelength [117], reflection angle [118], and phase [119,120] can be electrically tuned by the applied voltage for graphene.
Metalenses are a new type of flat lens based on geometrical phase control [121,122,123]. MIM-PMAs are considered as an array of optical resonators that can introduce a desired spatial profile of the optical phase and consequently mold the wavefront [123]. Figure 12 shows a schematic illustration of a metalens or reflector using MIM-PMAs [123]. The MIM-PMA structures control the reflection and their phase by phase gradient surface structures with different sized micropatches on the planar surface. Strong plasmonic resonance can change the phase of the reflection and thereby realize geometrical control of the phase. As a result, a flat metalens can be realized.
There are other rapidly growing research fields of MIM-PMAs, such as the non-linear response of second [124,125] and third [126] harmonic generation, and reflection control [127]. As discussed in this section, although MIM-PMAs are simple structures, they have significant potential for novel physics and applications.

6. Conclusions

MIM-PMAs have been reviewed here in terms of their structures, basic principles of absorption, materials used, absorption properties of incident angle and polarization dependence, and strategies of multiband or broadband operation to clarify the design strategies for visible and IR wavelengths. The same principles can be applied for a wide range of wavelength regions such as the ultraviolet [128], terahertz [129,130,131,132], and microwave [133,134,135] regions.
A single MIM structure can be considered as a single optical antenna with strong LSPPs. Therefore, MIM structures are free from the restriction of periodicity and beyond the diffraction limit, making them able to realize strong absorption and geometrical tunability of the absorption wavelength with a much thinner and smaller absorber volume than conventional EM absorbers. Such controllability opens up a new stage of EM absorber research and many novel applications are expected.
In the future research of MIM-PMAs, flexible structures are also important to expand applications, such as health care devices for human sensing. The combination of new materials such as graphene and other 2D atomic materials with MIM-PMAs gives rise to the electrical tunability of the absorption wavelength, the phase, and the reflection angle because their optical constant can be tuned according to the applied voltage. MIM-PMAs can control other wavelengths than the absorption wavelength used. Thus, MIM-PMAs can be used for flat metalenses that can go beyond the diffraction limit.
We hope that this review paper will contribute to the development of advanced MM-PMAs and the expansion of their fields of application.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ruck, G.T.; Barrick, D.E.; Stuart, W. Radar Cross Section Handbook; Peninsula Publishing: Los Altos, CA, USA, 2002; Volume 2, pp. 612–630. [Google Scholar]
  2. Keasler, C.A.; Bellotti, E. A numerical study of broadband absorbers for visible to infrared detectors. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
  3. Li, P.; Liu, B.; Ni, Y.; Liew, K.K.; Sze, J.; Chen, S.; Shen, S. Large-Scale Nanophotonic Solar Selective Absorbers for High-Efficiency Solar Thermal Energy Conversion. Adv. Mater. 2015, 27, 4585–4591. [Google Scholar] [CrossRef] [PubMed]
  4. Vorobyev, A.Y.; Topkov, A.N.; Gurin, O.V.; Svich, V.A.; Guo, C. Enhanced absorption of metals over ultrabroad electromagnetic spectrum. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
  5. Bae, K.; Kang, G.; Cho, S.K.; Park, W.; Kim, K.; Padilla, W.J. Flexible thin-film black gold membranes with ultrabroadband plasmonic nanofocusing for efficient solar vapour generation. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
  6. Munk, B.A. Frequency Selective Surfaces: Theory and Design; John Wiley & Sons: New York, NY, USA, 2000; pp. 315–325. [Google Scholar]
  7. Salisbury, W.W. Absorbent Body for Electromagnetic Waves. U.S. Patent 2599944 A, 10 June 1952. [Google Scholar]
  8. Knott, E.F.; Lunden, C.D. The two-sheet capacitive Jaumann absorber. IEEE Trans. Antennas Propag. 1995, 43, 1339–1343. [Google Scholar] [CrossRef]
  9. Kawata, S. Plasmonics: Future outlook. Jpn. J. Appl. Phys. 2013, 52. [Google Scholar] [CrossRef]
  10. Tanaka, T. Plasmonic metamaterials. IEICE Electron. Express 2012, 9, 34–50. [Google Scholar] [CrossRef]
  11. Maier, S.A.; Atwater, H.A. Plasmonics: Localization and guiding of electromagnetic energy in metal/dielectric structures. J. Appl. Phys. 2005, 98. [Google Scholar] [CrossRef]
  12. Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
  13. Ogawa, S.; Okada, K.; Fukushima, N.; Kimata, M. Wavelength selective uncooled infrared sensor by plasmonics. Appl. Phys. Lett. 2012, 100. [Google Scholar] [CrossRef]
  14. Ogawa, S.; Komoda, J.; Masuda, K.; Kimata, M. Wavelength selective wideband uncooled infrared sensor using a two-dimensional plasmonic absorber. Opt. Eng. 2013, 52. [Google Scholar] [CrossRef]
  15. Takagawa, Y.; Ogawa, S.; Kimata, M. Detection wavelength control of uncooled infrared sensors by two-dimensional lattice plasmonic absorbers. Sensors 2015, 15, 13660–13669. [Google Scholar] [CrossRef] [PubMed]
  16. Miyazaki, H.T.; Ikeda, K.; Kasaya, T.; Yamamoto, K.; Inoue, Y.; Fujimura, K.; Kanakugi, T.; Okada, M.; Hatade, K.; Kitagawa, S. Thermal emission of two-color polarized infrared waves from integrated plasmon cavities. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
  17. Ikeda, K.; Miyazaki, H.T.; Kasaya, T.; Yamamoto, K.; Inoue, Y.; Fujimura, K.; Kanakugi, T.; Okada, M.; Hatade, K.; Kitagawa, S. Controlled thermal emission of polarized infrared waves from arrayed plasmon nanocavities. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
  18. Ogawa, S.; Kimata, M. Direct fabrication and characterization of high-aspect-ratio plasmonic nanogratings using tapered-sidewall molds. Opt. Mater. Express 2017, 7, 633–640. [Google Scholar] [CrossRef]
  19. Ogawa, S.; Takagawa, Y.; Kimata, M. Broadband polarization-selective uncooled infrared sensors using tapered plasmonic micrograting absorbers. Sens. Actuators A 2018, 269, 563–568. [Google Scholar] [CrossRef]
  20. Lee, Y.P.; Rhee, J.Y.; Yoo, Y.J.; Kim, K.W. Metamaterials for Perfect Absorption; Springer: Singapore, 2016. [Google Scholar]
  21. Mann, S.A.; Garnett, E.C. Resonant Nanophotonic Spectrum Splitting for Ultrathin Multijunction Solar Cells. ACS Photonics 2015, 2, 816–821. [Google Scholar] [CrossRef] [PubMed]
  22. Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
  23. Wang, G.; Chen, X.; Liu, S.; Wong, C.; Chu, S. Mechanical Chameleon through Dynamic Real-Time Plasmonic Tuning. ACS Nano 2016, 10, 1788–1794. [Google Scholar] [CrossRef] [PubMed]
  24. Ni, X.; Wong, Z.J.; Mrejen, M.; Wang, Y.; Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 2015, 349, 1310–1314. [Google Scholar] [CrossRef] [PubMed]
  25. Qian, Z.; Kang, S.; Rajaram, V.; Cassella, C.; McGruer, N.E.; Rinaldi, M. Zero-power infrared digitizers based on plasmonically enhanced micromechanical photoswitches. Nat. Nanotechnol. 2017, 12, 969–973. [Google Scholar] [CrossRef] [PubMed]
  26. Flauraud, V.; Reyes, M.; Paniagua-Domínguez, R.; Kuznetsov, A.I.; Brugger, J. Silicon Nanostructures for Bright Field Full Color Prints. ACS Photonics 2017, 4, 1913–1919. [Google Scholar] [CrossRef]
  27. Miyata, M.; Hatada, H.; Takahara, J. Full-Color Subwavelength Printing with Gap-Plasmonic Optical Antennas. Nano Lett. 2016, 16, 3166–3172. [Google Scholar] [CrossRef] [PubMed]
  28. Maier, T.; Brueckl, H. Multispectral microbolometers for the midinfrared. Opt. Lett. 2010, 35, 3766–3768. [Google Scholar] [CrossRef] [PubMed]
  29. Chen, H.-H.; Su, Y.-C.; Huang, W.-L.; Kuo, C.-Y.; Tian, W.-C.; Chen, M.-J.; Lee, S.-C. A plasmonic infrared photodetector with narrow bandwidth absorption. Appl. Phys. Lett. 2014, 105. [Google Scholar] [CrossRef]
  30. Ogawa, S.; Kimata, M. Wavelength- or Polarization-Selective Thermal Infrared Detectors for Multi-Color or Polarimetric Imaging Using Plasmonics and Metamaterials. Materials 2017, 10, 493. [Google Scholar] [CrossRef] [PubMed]
  31. Suen, J.Y.; Fan, K.; Montoya, J.; Bingham, C.; Stenger, V.; Sriram, S.; Padilla, W.J. Multifunctional metamaterial pyroelectric infrared detectors. Optica 2017, 4, 276–279. [Google Scholar] [CrossRef]
  32. Hui, Y.; Gomez-Diaz, J.S.; Qian, Z.; Alù, A.; Rinaldi, M. Plasmonic piezoelectric nanomechanical resonator for spectrally selective infrared sensing. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef] [PubMed]
  33. Ishikawa, A.; Tanaka, T. Metamaterial Absorbers for Infrared Detection of Molecular Self-Assembled Monolayers. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Aslan, E.; Aslan, E.; Turkmen, M.; Saracoglu, O.G. Metamaterial plasmonic absorber for reducing the spectral shift between near- and far-field responses in surface-enhanced spectroscopy applications. Sens. Actuators A 2017, 267, 60–69. [Google Scholar] [CrossRef]
  35. Miyazaki, H.T.; Kasaya, T.; Iwanaga, M.; Choi, B.; Sugimoto, Y.; Sakoda, K. Dual-band infrared metasurface thermal emitter for CO2 sensing. Appl. Phys. Lett. 2014, 105. [Google Scholar] [CrossRef]
  36. Inoue, T.; De Zoysa, M.; Asano, T.; Noda, S. Realization of narrowband thermal emission with optical nanostructures. Optica 2015, 2, 27–35. [Google Scholar] [CrossRef]
  37. Puscasu, I.; Schaich, W.L. Narrow-band, tunable infrared emission from arrays of microstrip patches. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
  38. Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared spatial and frequency selective metamaterial with near-unity absorbance. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
  39. Wu, C.; Neuner, B.; Shvets, G.; John, J.; Milder, A.; Zollars, B.; Savoy, S. Large-area wide-angle spectrally selective plasmonic absorber. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
  40. Chen, Y.B.; Chiu, F.C. Trapping mid-infrared rays in a lossy film with the Berreman mode, epsilon near zero mode, and magnetic polaritons. Opt. Express 2013, 21, 20771–20785. [Google Scholar] [CrossRef] [PubMed]
  41. Hao, J.; Wang, J.; Liu, X.; Padilla, W.J.; Zhou, L.; Qiu, M. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 2010, 96. [Google Scholar] [CrossRef]
  42. Cheng, C.-W.; Abbas, M.N.; Chiu, C.-W.; Lai, K.-T.; Shih, M.-H.; Chang, Y.-C. Wide-angle polarization independent infrared broadband absorbers based on metallic multi-sized disk arrays. Opt. Express 2012, 20, 10376–10381. [Google Scholar] [CrossRef] [PubMed]
  43. Hasan, D.; Pitchappa, P.; Wang, J.; Wang, T.; Yang, B.; Ho, C.P.; Lee, C. Novel CMOS-Compatible Mo–AlN–Mo Platform for Metamaterial-Based Mid-IR Absorber. ACS Photonics 2017, 4, 302–315. [Google Scholar] [CrossRef]
  44. Monti, A.; Toscano, A.; Bilotti, F. Exploiting the surface dispersion of nanoparticles to design optical-resistive sheets and Salisbury absorbers. Opt. Lett. 2016, 41, 3383–3386. [Google Scholar] [CrossRef] [PubMed]
  45. Dereshgi, S.A.; Okyay, A.K. Large area compatible broadband superabsorber surfaces in the VIS-NIR spectrum utilizing metal-insulator-metal stack and plasmonic nanoparticles. Opt. Express 2016, 24, 17644–17653. [Google Scholar] [CrossRef] [PubMed]
  46. Monti, A.; Alù, A.; Toscano, A.; Bilotti, F. Narrowband transparent absorbers based on ellipsoidal nanoparticles. Appl. Opt. 2017, 56, 7533–7538. [Google Scholar] [CrossRef] [PubMed]
  47. Zhang, B.; Zhao, Y.; Hao, Q.; Kiraly, B.; Khoo, I.-C.; Chen, S.; Huang, T.J. Polarization-independent dual-band infrared perfect absorber based on a metal-dielectric-metal elliptical nanodisk array. Opt. Express 2011, 19, 15221–15228. [Google Scholar] [CrossRef] [PubMed]
  48. Chevalier, P.; Bouchon, P.; Jaeck, J.; Lauwick, D.; Bardou, N.; Kattnig, A.; Pardo, F.; Haïdar, R. Absorbing metasurface created by diffractionless disordered arrays of nanoantennas. Appl. Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
  49. Aydin, K.; Ferry, V.E.; Briggs, R.M.; Atwater, H.A. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2011, 2, 517. [Google Scholar] [CrossRef] [PubMed]
  50. Lin, L.; Zheng, Y. Optimizing plasmonic nanoantennas via coordinated multiple coupling. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
  51. Alici, K.B.; Turhan, A.B.; Soukoulis, C.M.; Ozbay, E. Optically thin composite resonant absorber at the near-infrared band: A polarization independent and spectrally broadband configuration. Opt. Express 2011, 19, 14260–14267. [Google Scholar] [CrossRef] [PubMed]
  52. Chen, K.; Adato, R.; Altug, H. Dual-Band Perfect Absorber for Multispectral Plasmon-Enhanced Infrared Spectroscopy. ACS Nano 2012, 6, 7998–8006. [Google Scholar] [CrossRef] [PubMed]
  53. Chen, N.; Pitchappa, P.; Ho, C.P.; Hasan, D.; Kropelnicki, P.; Alioto, M.; Lee, C. Polarization controllable multispectral symmetry-breaking absorber in mid-infrared. J. Appl. Phys. 2016, 120. [Google Scholar] [CrossRef]
  54. Akselrod, G.M.; Huang, J.; Hoang, T.B.; Bowen, P.T.; Su, L.; Smith, D.R.; Mikkelsen, M.H. Large-Area Metasurface Perfect Absorbers from Visible to Near-Infrared. Adv. Mater. 2015, 27, 8028–8034. [Google Scholar] [CrossRef] [PubMed]
  55. Huang, J.; Akselrod, G.M.; Ming, T.; Kong, J.; Mikkelsen, M.H. Tailored Emission Spectrum of 2D Semiconductors Using Plasmonic Nanocavities. ACS Photonics 2017. [Google Scholar] [CrossRef]
  56. Zhang, B.; Hendrickson, J.; Guo, J. Multispectral near-perfect metamaterial absorbers using spatially multiplexed plasmon resonance metal square structures. J. Opt. Soc. Am. B 2013, 30, 656–662. [Google Scholar] [CrossRef]
  57. Liu, T.; Takahara, J. Ultrabroadband absorber based on single-sized embedded metal-dielectric-metal structures and application of radiative cooling. Opt. Express 2017, 25, A612–A627. [Google Scholar] [CrossRef] [PubMed]
  58. Lefebvre, A.; Costantini, D.; Doyen, I.; Lévesque, Q.; Lorent, E.; Jacolin, D.; Greffet, J.J.; Boutami, S.; Benisty, H. CMOS compatible metal-insulator-metal plasmonic perfect absorbers. Opt. Mater. Express 2016, 6, 2389–2396. [Google Scholar] [CrossRef]
  59. Li, W.; Guler, U.; Kinsey, N.; Naik, G.V.; Boltasseva, A.; Guan, J.; Shalaev, V.M.; Kildishev, A.V. Refractory Plasmonics with Titanium Nitride: Broadband Metamaterial Absorber. Adv. Mater. 2014, 26, 7959–7965. [Google Scholar] [CrossRef] [PubMed]
  60. Wang, H.; Chen, Q.; Wen, L.; Song, S.; Hu, X.; Xu, G. Titanium-nitride-based integrated plasmonic absorber/emitter for solar thermophotovoltaic application. Photonics Res. 2015, 3, 329–334. [Google Scholar] [CrossRef]
  61. Gorgulu, K.; Gok, A.; Yilmaz, M.; Topalli, K.; Bıyıklı, N.; Okyay, A.K. All-Silicon Ultra-Broadband Infrared Light Absorbers. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
  62. Thongrattanasiri, S.; Koppens, F.H.L.; García de Abajo, F.J. Complete Optical Absorption in Periodically Patterned Graphene. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
  63. Matsuno, Y.; Sakurai, A. Perfect infrared absorber and emitter based on a large-area metasurface. Opt. Mater. Express 2017, 7, 618–626. [Google Scholar] [CrossRef]
  64. Du, K.; Li, Q.; Zhang, W.; Yang, Y.; Qiu, M. Wavelength and Thermal Distribution Selectable Microbolometers Based on Metamaterial Absorbers. IEEE Photonics J. 2015, 7. [Google Scholar] [CrossRef]
  65. Cui, Y.; Xu, J.; Fung, K.H.; Jin, Y.; Kumar, A.; He, S.; Fang, N.X. A thin film broadband absorber based on multi-sized nanoantennas. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
  66. Bouchon, P.; Koechlin, C.; Pardo, F.; Haïdar, R.; Pelouard, J.-L. Wideband omnidirectional infrared absorber with a patchwork of plasmonic nanoantennas. Opt. Lett. 2012, 37, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
  67. Tittl, A.; Michel, A.K.; Schaferling, M.; Yin, X.; Gholipour, B.; Cui, L.; Wuttig, M.; Taubner, T.; Neubrech, F.; Giessen, H. A Switchable Mid-Infrared Plasmonic Perfect Absorber with Multispectral Thermal Imaging Capability. Adv. Mater. 2015, 27, 4597–4603. [Google Scholar] [CrossRef] [PubMed]
  68. Wang, H.; Yang, Y.; Wang, L. Switchable wavelength-selective and diffuse metamaterial absorber/emitter with a phase transition spacer layer. Appl. Phys. Lett. 2014, 105. [Google Scholar] [CrossRef]
  69. Ogawa, S.; Fujisawa, D.; Hata, H.; Uetsuki, M.; Misaki, K.; Kimata, M. Mushroom plasmonic metamaterial infrared absorbers. Appl. Phys. Lett. 2015, 106. [Google Scholar] [CrossRef]
  70. Ogawa, S.; Fujisawa, D.; Hata, H.; Kimata, M. Absorption properties of simply fabricated all-metal mushroom plasmonic metamaterials incorporating tube-shaped posts for multi-color uncooled infrared image sensor applications. Photonics 2016, 3, 9. [Google Scholar] [CrossRef]
  71. Ogawa, S.; Fujisawa, D.; Kimata, M. Theoretical investigation of all-metal based mushroom plasmonic metamaterial absorbers at infrared wavelengths. Opt. Eng. 2015, 54. [Google Scholar] [CrossRef]
  72. Cheng, F.; Gao, J.; Luk, T.S.; Yang, X. Structural color printing based on plasmonic metasurfaces of perfect light absorption. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
  73. Bouchon, P.; Pardo, F.; Portier, B.; Ferlazzo, L.; Ghenuche, P.; Dagher, G.; Dupuis, C.; Bardou, N.; Haïdar, R.; Pelouard, J.-L. Total funneling of light in high aspect ratio plasmonic nanoresonators. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
  74. Koechlin, C.; Bouchon, P.; Pardo, F.; Pelouard, J.-L.; Haïdar, R. Analytical description of subwavelength plasmonic MIM resonators and of their combination. Opt. Express 2013, 21, 7025–7032. [Google Scholar] [CrossRef] [PubMed]
  75. Zhou, W.; Li, K.; Song, C.; Hao, P.; Chi, M.; Yu, M.; Wu, Y. Polarization-independent and omnidirectional nearly perfect absorber with ultra-thin 2D subwavelength metal grating in the visible region. Opt. Express 2015, 23, A413–A418. [Google Scholar] [CrossRef] [PubMed]
  76. Ra’di, Y.; Asadchy, V.S.; Kosulnikov, S.U.; Omelyanovich, M.M.; Morits, D.; Osipov, A.V.; Simovski, C.R.; Tretyakov, S.A. Full Light Absorption in Single Arrays of Spherical Nanoparticles. ACS Photonics 2015, 2, 653–660. [Google Scholar] [CrossRef]
  77. Li, Z.; Butun, S.; Aydin, K. Large-Area, Lithography-Free Super Absorbers and Color Filters at Visible Frequencies Using Ultrathin Metallic Films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
  78. Ding, F.; Mo, L.; Zhu, J.; He, S. Lithography-free, broadband, omnidirectional, and polarization-insensitive thin optical absorber. Appl. Phys. Lett. 2015, 106. [Google Scholar] [CrossRef]
  79. Peng, H.; Luo, Y.; Ying, X.; Pu, Y.; Jiang, Y.; Xu, J.; Liu, Z. Broadband and highly absorbing multilayer structure in mid-infrared. Appl. Opt. 2016, 55, 8833–8838. [Google Scholar] [CrossRef] [PubMed]
  80. Chettiar, U.K.; Kildishev, A.V.; Klar, T.A.; Shalaev, V.M. Negative index metamaterial combining magnetic resonators with metal films. Opt. Express 2006, 14, 7872–7877. [Google Scholar] [CrossRef] [PubMed]
  81. Ogawa, S.; Fujisawa, D.; Shimatani, M.; Matsumoto, K. Graphene on plasmonic metamaterials for infrared detection. In Infrared Technology and Applications XLII; Andresen, B.F., Fulop, G.F., Hanson, C.M., Miller, J.L., Norton, P.R., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9819, p. 98191S. [Google Scholar]
  82. Tyo, J.S.; Goldstein, D.L.; Chenault, D.B.; Shaw, J.A. Review of passive imaging polarimetry for remote sensing applications. Appl. Opt. 2006, 45, 5453–5469. [Google Scholar] [CrossRef] [PubMed]
  83. Schott, J.R. Fundamentals of Polarimetric Remote Sensing; SPIE: Bellingham, WA, USA, 2009. [Google Scholar]
  84. Gurton, K.P.; Yuffa, A.J.; Videen, G.W. Enhanced facial recognition for thermal imagery using polarimetric imaging. Opt. Lett. 2014, 39, 3857–3859. [Google Scholar] [CrossRef] [PubMed]
  85. Chen, S.; Cheng, H.; Yang, H.; Li, J.; Duan, X.; Gu, C.; Tian, J. Polarization insensitive and omnidirectional broadband near perfect planar metamaterial absorber in the near infrared regime. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
  86. Jiang, Z.H.; Yun, S.; Toor, F.; Werner, D.H.; Mayer, T.S. Conformal Dual-Band Near-Perfectly Absorbing Mid-Infrared Metamaterial Coating. ACS Nano 2011, 5, 4641–4647. [Google Scholar] [CrossRef] [PubMed]
  87. Butun, S.; Aydin, K. Structurally tunable resonant absorption bands in ultrathin broadband plasmonic absorbers. Opt. Express 2014, 22, 19457–19468. [Google Scholar] [CrossRef] [PubMed]
  88. Bai, Y.; Zhao, L.; Ju, D.; Jiang, Y.; Liu, L. Wide-angle, polarization-independent and dual-band infrared perfect absorber based on L-shaped metamaterial. Opt. Express 2015, 23, 8670–8680. [Google Scholar] [CrossRef] [PubMed]
  89. Ghobadi, A.; Hajian, H.; Gokbayrak, M.; Dereshgi, S.A.; Toprak, A.; Butun, B.; Ozbay, E. Visible light nearly perfect absorber: An optimum unit cell arrangement for near absolute polarization insensitivity. Opt. Express 2017, 25, 27624–27634. [Google Scholar] [CrossRef] [PubMed]
  90. Koechlin, C.; Bouchon, P.; Pardo, F.; Jaeck, J.; Lafosse, X.; Pelouard, J.-L.; Haïdar, R. Total routing and absorption of photons in dual color plasmonic antennas. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
  91. Bossard, J.A.; Lin, L.; Yun, S.; Liu, L.; Werner, D.H.; Mayer, T.S. Near-Ideal Optical Metamaterial Absorbers with Super-Octave Bandwidth. ACS Nano 2014, 8, 1517–1524. [Google Scholar] [CrossRef] [PubMed]
  92. Xu, J.; Zhao, Z.; Yu, H.; Yang, L.; Gou, P.; Cao, J.; Zou, Y.; Qian, J.; Shi, T.; Ren, Q.; An, Z. Design of triple-band metamaterial absorbers with refractive index sensitivity at infrared frequencies. Opt. Express 2016, 24, 25742–25751. [Google Scholar] [CrossRef] [PubMed]
  93. Khan, A.D.; Amin, M. Tunable Salisbury Screen Absorber Using Square Lattice of Plasmonic Nanodisk. Plasmonics 2016, 12, 257–262. [Google Scholar] [CrossRef]
  94. Kim, J.; Han, K.; Hahn, J.W. Selective dual-band metamaterial perfect absorber for infrared stealth technology. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
  95. Wang, J.; Fan, C.; Ding, P.; He, J.; Cheng, Y.; Hu, W.; Cai, G.; Liang, E.; Xue, Q. Tunable broad-band perfect absorber by exciting of multiple plasmon resonances at optical frequency. Opt. Express 2012, 20, 14871–14878. [Google Scholar] [CrossRef] [PubMed]
  96. Cui, Y.; Fung, K.H.; Xu, J.; Ma, H.; Jin, Y.; He, S.; Fang, N.X. Ultrabroadband Light Absorption by a Sawtooth Anisotropic Metamaterial Slab. Nano Lett. 2012, 12, 1443–1447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  97. Lobet, M.; Lard, M.; Sarrazin, M.; Deparis, O.; Henrard, L. Plasmon hybridization in pyramidal metamaterials: A route towards ultra-broadband absorption. Opt. Express 2014, 22, 12678–12690. [Google Scholar] [CrossRef] [PubMed]
  98. Sakurai, A.; Zhao, B.; Zhang, Z.M. Resonant frequency and bandwidth of metamaterial emitters and absorbers predicted by an RLC circuit model. J. Quant. Spectrosc. Radiant. Transf. 2014, 149, 33–40. [Google Scholar] [CrossRef]
  99. Adomanis, B.M.; Watts, C.M.; Koirala, M.; Liu, X.; Tyler, T.; West, K.G.; Starr, T.; Bringuier, J.N.; Starr, A.F.; Jokerst, N.M.; et al. Bi-layer metamaterials as fully functional near-perfect infrared absorbers. Appl. Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
  100. Wu, D.; Liu, C.; Liu, Y.; Yu, L.; Yu, Z.; Chen, L.; Ma, R.; Ye, H. Numerical study of an ultra-broadband near-perfect solar absorber in the visible and near-infrared region. Opt. Lett. 2017, 42, 450–453. [Google Scholar] [CrossRef] [PubMed]
  101. Üstün, K.; Turhan-Sayan, G. Broadband LWIR and MWIR metamaterial absorbers with a simple design topology: Almost perfect absorption and super-octave band operation in MWIR band. J. Opt. Soc. Am. B 2017, 34, D86–D94. [Google Scholar] [CrossRef]
  102. Hubarevich, A.; Kukhta, A.; Demir, H.V.; Sun, X.; Wang, H. Ultra-thin broadband nanostructured insulator-metal-insulator-metal plasmonic light absorber. Opt. Express 2015, 23, 9753–9761. [Google Scholar] [CrossRef] [PubMed]
  103. Wu, C.; Shvets, G. Design of metamaterial surfaces with broadband absorbance. Opt. Lett. 2012, 37, 308–310. [Google Scholar] [CrossRef] [PubMed]
  104. Harris, L.; McGinnies, R.T.; Siegel, B.M. The Preparation and Optical Properties of Gold Blacks. J. Opt. Soc. Am. 1948, 38, 582–589. [Google Scholar] [CrossRef]
  105. Harris, L. The Transmittance and Reflectance of Gold Black Deposits in the 15- to 100-Micron Region. J. Opt. Soc. Am. 1961, 51, 80–82. [Google Scholar] [CrossRef]
  106. Li, G.X.; Chen, S.M.; Wong, W.H.; Pun, E.Y.B.; Cheah, K.W. Highly flexible near-infrared metamaterials. Opt. Express 2012, 20, 397–402. [Google Scholar] [CrossRef] [PubMed]
  107. Ji, T.; Wang, Y.; Cui, Y.; Lin, Y.; Hao, Y.; Li, D. Flexible broadband plasmonic absorber on moth-eye substrate. Mater. Today Energy 2017, 5, 181–186. [Google Scholar] [CrossRef]
  108. Walia, S.; Shah, C.M.; Gutruf, P.; Nili, H.; Chowdhury, D.R.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Flexible metasurfaces and metamaterials: A review of materials and fabrication processes at micro- and nano-scales. Appl. Phys. Rev. 2015, 2. [Google Scholar] [CrossRef]
  109. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
  110. Sun, Z.; Chang, H. Graphene and Graphene-like Two-Dimensional Materials in Photodetection: Mechanisms and Methodology. ACS Nano 2014, 8, 4133–4156. [Google Scholar] [CrossRef] [PubMed]
  111. Cai, Y.; Zhu, J.; Liu, Q.H. Tunable enhanced optical absorption of graphene using plasmonic perfect absorbers. Appl. Phys. Lett. 2015, 106. [Google Scholar] [CrossRef]
  112. Pan, Q.; Hong, J.; Zhang, G.; Shuai, Y.; Tan, H. Graphene plasmonics for surface enhancement near-infrared absorptivity. Opt. Express 2017, 25, 16400–16408. [Google Scholar] [CrossRef] [PubMed]
  113. Jariwala, D.; Davoyan, A.R.; Tagliabue, G.; Sherrott, M.C.; Wong, J.; Atwater, H.A. Near-Unity Absorption in van der Waals Semiconductors for Ultrathin Optoelectronics. Nano Lett. 2016, 16, 5482–5487. [Google Scholar] [CrossRef] [PubMed]
  114. Ogawa, S.; Shimatani, M.; Fukushima, S.; Okuda, S.; Matsumoto, K. Graphene on metal-insulator-metal-based plasmonic metamaterials at infrared wavelengths. Opt. Express 2018, 26. [Google Scholar] [CrossRef] [PubMed]
  115. Huang, H.; Xia, H.; Xie, W.; Guo, Z.; Li, H.; Xie, D. Design of broadband graphene-metamaterial absorbers for permittivity sensing at mid-infrared regions. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
  116. Low, T.; Chaves, A.; Caldwell, J.D.; Kumar, A.; Fang, N.X.; Avouris, P.; Heinz, T.F.; Guinea, F.; Martin-Moreno, L.; Koppens, F. Polaritons in layered two-dimensional materials. Nat. Mater. 2017, 16, 182–194. [Google Scholar] [CrossRef] [PubMed]
  117. Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically tunable metasurface perfect absorbers for ultrathin mid-infrared optical modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef] [PubMed]
  118. Su, X.; Wei, Z.; Wu, C.; Long, Y.; Li, H. Negative reflection from metal/graphene plasmonic gratings. Opt. Lett. 2016, 41, 348–351. [Google Scholar] [CrossRef] [PubMed]
  119. Miao, Z.; Wu, Q.; Li, X.; He, Q.; Ding, K.; An, Z.; Zhang, Y.; Zhou, L. Widely Tunable Terahertz Phase Modulation with Gate-Controlled Graphene Metasurfaces. Phys. Rev. X 2015, 5, 041027. [Google Scholar] [CrossRef]
  120. Sherrott, M.C.; Hon, P.W.C.; Fountaine, K.T.; Garcia, J.C.; Ponti, S.M.; Brar, V.W.; Sweatlock, L.A.; Atwater, H.A. Experimental Demonstration of >230° Phase Modulation in Gate-Tunable Graphene–Gold Reconfigurable Mid-Infrared Metasurfaces. Nano Lett. 2017, 17, 3027–3034. [Google Scholar] [CrossRef] [PubMed]
  121. Aieta, F.; Kats, M.A.; Genevet, P.; Capasso, F. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef] [PubMed]
  122. Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Roques-Carmes, C.; Mishra, I.; Capasso, F. Visible Wavelength Planar Metalenses Based on Titanium Dioxide. IEEE J. Sel. Top. Quantum Electron. 2017, 23. [Google Scholar] [CrossRef]
  123. Zhang, S.; Kim, M.-H.; Aieta, F.; She, A.; Mansuripur, T.; Gabay, I.; Khorasaninejad, M.; Rousso, D.; Wang, X.; Troccoli, M.; et al. High efficiency near diffraction-limited mid-infrared flat lenses based on metasurface reflectarrays. Opt. Express 2016, 24, 18024–18034. [Google Scholar] [CrossRef] [PubMed]
  124. Lee, J.; Tymchenko, M.; Argyropoulos, C.; Chen, P.-Y.; Lu, F.; Demmerle, F.; Boehm, G.; Amann, M.-C.; Alù, A.; Belkin, M.A. Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions. Nature 2014, 511, 65–69. [Google Scholar] [CrossRef] [PubMed]
  125. Lu, X.; Zhang, L.; Zhang, T. Nanoslit-microcavity-based narrow band absorber for sensing applications. Opt. Express 2015, 23, 20715–20720. [Google Scholar] [CrossRef] [PubMed]
  126. Lassiter, J.B.; Chen, X.; Liu, X.; Ciracì, C.; Hoang, T.B.; Larouche, S.; Oh, S.-H.; Mikkelsen, M.H.; Smith, D.R. Third-Harmonic Generation Enhancement by Film-Coupled Plasmonic Stripe Resonators. ACS Photonics 2014, 1, 1212–1217. [Google Scholar] [CrossRef]
  127. Huang, Y.-W.; Lee, H.W.H.; Sokhoyan, R.; Pala, R.A.; Thyagarajan, K.; Han, S.; Tsai, D.P.; Atwater, H.A. Gate-Tunable Conducting Oxide Metasurfaces. Nano Lett. 2016, 16, 5319–5325. [Google Scholar] [CrossRef] [PubMed]
  128. Sabah, C.; Esat, V.; Obaidullah, M. Polarization independent triple-band (5,4) semiconducting carbon nanotube metamaterial absorber design for visible and ultraviolet regions. J. Nanophotonics 2017, 11, 046011. [Google Scholar] [CrossRef]
  129. Diem, M.; Koschny, T.; Soukoulis, C. Wide-angle perfect absorber/thermal emitter in the terahertz regime. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
  130. Tao, H.; Bingham, C.; Strikwerda, A.; Pilon, D.; Shrekenhamer, D.; Landy, N.; Fan, K.; Zhang, X.; Padilla, W.; Averitt, R. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication, and characterization. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
  131. Alves, F.; Grbovic, D.; Karunasiri, G. Investigation of microelectromechanical systems bimaterial sensors with metamaterial absorbers for terahertz imaging. Opt. Eng. 2014, 53. [Google Scholar] [CrossRef]
  132. Yahiaoui, R.; Hanai, K.; Takano, K.; Nishida, T.; Miyamaru, F.; Nakajima, M.; Hangyo, M. Trapping waves with terahertz metamaterial absorber based on isotropic Mie resonators. Opt. Lett. 2015, 40, 3197–3200. [Google Scholar] [CrossRef] [PubMed]
  133. Landy, N.; Sajuyigbe, S.; Mock, J.; Smith, D.; Padilla, W. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
  134. Zhou, W.; Wang, P.; Wang, N.; Jiang, W.; Dong, X.; Hu, S. Microwave metamaterial absorber based on multiple square ring structures. AIP Adv. 2015, 5. [Google Scholar] [CrossRef]
  135. Ding, F.; Cui, Y.; Ge, X.; Jin, Y.; He, S. Ultra-broadband microwave metamaterial absorber. Appl. Phys. Lett. 2012, 100, 103506. [Google Scholar] [CrossRef]
Materials 11 00458 g001 550
Figure 1. Schematic illustrations and reflectance of resonant absorbers: (a,b) the Salisbury screen; (c,d) the Jaumann absorber; and (e,f) the circuit analog CA absorber. “d” represents the quarter-wavelength gap [6].
Figure 1. Schematic illustrations and reflectance of resonant absorbers: (a,b) the Salisbury screen; (c,d) the Jaumann absorber; and (e,f) the circuit analog CA absorber. “d” represents the quarter-wavelength gap [6].
Materials 11 00458 g001
Materials 11 00458 g002 550
Figure 2. Schematic illustrations of metal-insulator-metal-based plasmonic metamaterial absorbers (MIM-PMAs); oblique view of (a) two-dimensional (2D) and (b) one-dimensional (1D) periodic micropatches. Cross-sectional views of (c) continuous and (d) isolated middle dielectric layers.
Figure 2. Schematic illustrations of metal-insulator-metal-based plasmonic metamaterial absorbers (MIM-PMAs); oblique view of (a) two-dimensional (2D) and (b) one-dimensional (1D) periodic micropatches. Cross-sectional views of (c) continuous and (d) isolated middle dielectric layers.
Materials 11 00458 g002
Materials 11 00458 g003 550
Figure 3. (a) Schematic illustration of the operating principle of MIM-PMAs. E, H, and p represent the electric displacement vector, magnetic field, and current, respectively. Calculated results: (b) magnetic field; (c) electric field; and (d) power distribution. The color maps represents the amplitude of each distribution. (b–d) are reprinted from Reference [41] with the permission of AIP Publishing.
Figure 3. (a) Schematic illustration of the operating principle of MIM-PMAs. E, H, and p represent the electric displacement vector, magnetic field, and current, respectively. Calculated results: (b) magnetic field; (c) electric field; and (d) power distribution. The color maps represents the amplitude of each distribution. (b–d) are reprinted from Reference [41] with the permission of AIP Publishing.
Materials 11 00458 g003
Materials 11 00458 g004 550
Figure 4. Calculated spectra for (a) absorption, reflection, and transmission; (b) Comparison of the measured and calculated absorption spectra; (c) Absorbance as a function of the wavelength and the micropatch size (w) in the near-IR wavelength region; (d) Relation between the micropatch size and the absorption wavelength in the IR wavelength region. (a,b) are adapted with permission from Reference [38]. © 2010 American Physical Society. (c) is reprinted from Reference [41] with the permission of AIP Publishing.
Figure 4. Calculated spectra for (a) absorption, reflection, and transmission; (b) Comparison of the measured and calculated absorption spectra; (c) Absorbance as a function of the wavelength and the micropatch size (w) in the near-IR wavelength region; (d) Relation between the micropatch size and the absorption wavelength in the IR wavelength region. (a,b) are adapted with permission from Reference [38]. © 2010 American Physical Society. (c) is reprinted from Reference [41] with the permission of AIP Publishing.
Materials 11 00458 g004
Materials 11 00458 g005 550
Figure 5. Calculated absorption for the (a) transverse-electric (TE) and (b) transverse-magnetic (TM) modes. Figures are adapted with permission from Reference [22]. © 2010 American Chemical Society.
Figure 5. Calculated absorption for the (a) transverse-electric (TE) and (b) transverse-magnetic (TM) modes. Figures are adapted with permission from Reference [22]. © 2010 American Chemical Society.
Materials 11 00458 g005
Materials 11 00458 g006 550
Figure 6. Schematic illustration of the LC equivalent circuit for MIM-PMAs. Figures were adapted with permission from Reference [40]. © 2013 Optical Society of America.
Figure 6. Schematic illustration of the LC equivalent circuit for MIM-PMAs. Figures were adapted with permission from Reference [40]. © 2013 Optical Society of America.
Materials 11 00458 g006
Materials 11 00458 g007a 550Materials 11 00458 g007b 550
Figure 7. Schematic illustration of an MIM-PMA with asymmetric cross-shaped micropatches for dual-band operation. (a) Electric field distribution for modes I and II; and (b) the corresponding reflectance spectrum. (c) Schematic illustration and (d) SEM image of an MIM-PMA with an elliptical nanodisk array. Calculated absorbance for (e) TE and (f) TM modes. (a,b) are adapted with permission from Reference [52]. © 2012 American Chemical Society. (c–f) are adapted with permission from Reference [47]. © 2011 Optical Society of America.
Figure 7. Schematic illustration of an MIM-PMA with asymmetric cross-shaped micropatches for dual-band operation. (a) Electric field distribution for modes I and II; and (b) the corresponding reflectance spectrum. (c) Schematic illustration and (d) SEM image of an MIM-PMA with an elliptical nanodisk array. Calculated absorbance for (e) TE and (f) TM modes. (a,b) are adapted with permission from Reference [52]. © 2012 American Chemical Society. (c–f) are adapted with permission from Reference [47]. © 2011 Optical Society of America.
Materials 11 00458 g007aMaterials 11 00458 g007b
Materials 11 00458 g008 550
Figure 8. Schematic illustrations of MIM-PMAs with multi-size micropatches having (a,b) 1D and (c) 2D periodic configurations. (d) Calculated and measured absorption spectra for the 2D periodic configuration. (a,b) are reprinted from Reference [65] with the permission of AIP Publishing. (c,d) are adapted with permission from Reference [66]. © 2012 Optical Society of America.
Figure 8. Schematic illustrations of MIM-PMAs with multi-size micropatches having (a,b) 1D and (c) 2D periodic configurations. (d) Calculated and measured absorption spectra for the 2D periodic configuration. (a,b) are reprinted from Reference [65] with the permission of AIP Publishing. (c,d) are adapted with permission from Reference [66]. © 2012 Optical Society of America.
Materials 11 00458 g008
Materials 11 00458 g009 550
Figure 9. (a) Schematic illustration of a multi-layer MIM-PMA and (b) the calculated absorption spectrum. Figures are adapted with permission from Reference [95]. © 2012 Optical Society of America.
Figure 9. (a) Schematic illustration of a multi-layer MIM-PMA and (b) the calculated absorption spectrum. Figures are adapted with permission from Reference [95]. © 2012 Optical Society of America.
Materials 11 00458 g009
Materials 11 00458 g010 550
Figure 10. (a) Schematic illustration and (b) SEM image of a flexible MIM-PMA. Figures are adapted with permission from Reference [86]. © 2011 American Chemical Society.
Figure 10. (a) Schematic illustration and (b) SEM image of a flexible MIM-PMA. Figures are adapted with permission from Reference [86]. © 2011 American Chemical Society.
Materials 11 00458 g010
Materials 11 00458 g011 550
Figure 11. Schematic illustration of a graphene-coated MIM-PMA.
Figure 11. Schematic illustration of a graphene-coated MIM-PMA.
Materials 11 00458 g011
Materials 11 00458 g012 550
Figure 12. (a) Schematic illustration of a flat metalens using MIM-PMAs. (b) Schematic illustration of the unit cell of a reflector array lens. (c) SEM image of the metalens surface. Figures are adapted with permission from Reference [123]. © 2016 Optical Society of America.
Figure 12. (a) Schematic illustration of a flat metalens using MIM-PMAs. (b) Schematic illustration of the unit cell of a reflector array lens. (c) SEM image of the metalens surface. Figures are adapted with permission from Reference [123]. © 2016 Optical Society of America.
Materials 11 00458 g012
Table
Table 1. Properties of metals used in MIM-PMAs. Adapted with permission from Reference [43]. © 2017 American Chemical Society. (CMOS: complementary metal oxide semiconductor).
Table 1. Properties of metals used in MIM-PMAs. Adapted with permission from Reference [43]. © 2017 American Chemical Society. (CMOS: complementary metal oxide semiconductor).
MaterialMelting Point (°C)Electrical Conductivity (×107 S/m @20 °C)Plasma Frequency (×1015 Hz)Thermal Expansion Coefficient (CTE; ×10−6 K−1)Young’s Modulus (E; GPa)CMOS Compatibility
Al660 3.53.572470yes
Au10004.522.21478no
Pt17700.9441.258.8168no
TiN29300.871.849.35251yes
Mo26201.91.84.8329yes
Table
Table 2. Properties of insulators used in MIM-PMAs. Adapted with permission from Reference [43]. © 2017 American Chemical Society.
Table 2. Properties of insulators used in MIM-PMAs. Adapted with permission from Reference [43]. © 2017 American Chemical Society.
MaterialMelting Point (°C)Young’s Modulus (E; GPa)Poisson Ratio (μ)CTE (×10−6 K−1)Thermal Conductivity (W/m·K)
AlN2200344.80.2874.6285
SiO21600700.170.51.4
Al2O32072353.10.224.525.08

Share and Cite

MDPI and ACS Style

Ogawa, S.; Kimata, M. Metal-Insulator-Metal-Based Plasmonic Metamaterial Absorbers at Visible and Infrared Wavelengths: A Review. Materials 2018, 11, 458. https://doi.org/10.3390/ma11030458

AMA Style

Ogawa S, Kimata M. Metal-Insulator-Metal-Based Plasmonic Metamaterial Absorbers at Visible and Infrared Wavelengths: A Review. Materials. 2018; 11(3):458. https://doi.org/10.3390/ma11030458

Chicago/Turabian Style

Ogawa, Shinpei, and Masafumi Kimata. 2018. "Metal-Insulator-Metal-Based Plasmonic Metamaterial Absorbers at Visible and Infrared Wavelengths: A Review" Materials 11, no. 3: 458. https://doi.org/10.3390/ma11030458

APA Style

Ogawa, S., & Kimata, M. (2018). Metal-Insulator-Metal-Based Plasmonic Metamaterial Absorbers at Visible and Infrared Wavelengths: A Review. Materials, 11(3), 458. https://doi.org/10.3390/ma11030458

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop