Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete
Abstract
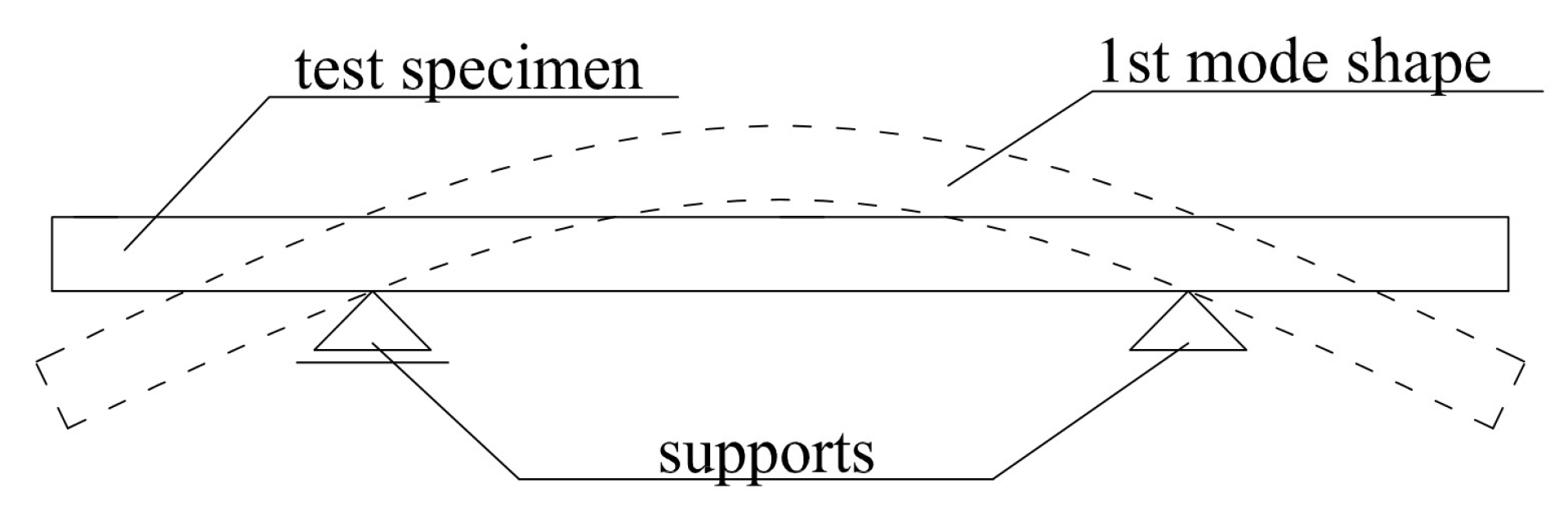
:1. Introduction
2. Materials and Methods
3. Experimental Results and Discussion
4. Relationship between Elastic Modulus and Compressive Strength
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Wang, Z.; Man, X.T.C.; Finch, R.D.; Jansen, B.H. The Dynamic Behavior and Vibration Monitoring of Reinforced Concrete Beams. J. Test. Eval. 1998, 26, 405–419. [Google Scholar]
- Azenha, M.; Ramos, L.F.; Aguilar, R.; Granja, J.L. Continuous monitoring of concrete E-modulus since casting based on modal identification: case study for in situ application. Cem. Concr. Res. 2012, 34, 881–890. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete, 4th ed.; Polski Cement: Cracow, Poland, 2000. (In Polish) [Google Scholar]
- American Concrete Institute. ACI manual of concrete practice Part 3: Use of concrete in buildings—Design, specifications, and related topics. In ACI 318-95 Building Code Requirements for Structural Concrete; American Concrete Institute: Detroit, MI, USA, 1996. [Google Scholar]
- European Commitee for Standardization. EN 1992-1-1 Eurocode 2: Design of Concrete Structures Part 1—NA, 1. General Rules and Rules for Buildings; European Commitee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- American Concrete Institute. ACI 363R-08 State of the Art Report on High Strength Concrete; American Concrete Institute: Detroit, MI, USA, 2008. [Google Scholar]
- Noguchi, T.; Tomosawa, F.; Nemati, K.M.; Chiaia, B.M.; Fantilli, A.P. A Practical Equation for Elastic Modulus of Concrete. ACI Struct. J. 2009, 106, 690–696. [Google Scholar]
- British Standards Institution. British Standard BS 8110-2: 1985 Structural Use of Concrete. Part 2: Code of Practice for Special Circumstances; British Standards Institution: London, UK, 1985. [Google Scholar]
- CSA Technical Committee. Reinforced Concrete Design, A23.3-04, Design of Concrete Structures; Canadian Standards Association: Rexdale, ON, Canada, 2004. [Google Scholar]
- Standards New Zealand. NZS 3101:2006 The Design of Concrete Structures; New Zealand Standard, Concrete Structures Standard; Standards New Zealand: Wellington, New Zealand, 2006. [Google Scholar]
- Jurowski, K.; Grzeszczyk, S. The influence of concrete composition on Young’s modulus. Procedia Eng. 2015, 108, 584–591. [Google Scholar] [CrossRef]
- Nikbin, I.M.; Beygi, M.H.A.; Kazemi, M.T.; Vaseghi, A.J.; Rahmani, E.; Rabbanifar, S.; Eslami, M. A comprehensive investigation into the effect of aging and coarse aggregate size and volume on mechanical properties of self-compacting concrete. Mater. Des. 2014, 59, 199–210. [Google Scholar] [CrossRef]
- Tasdemir, M.A.; Karihaloo, B.L. Effect of type and volume fraction of aggregate on the fracture properties of concrete. Mech. Concr. Struct. 2001, 123–129. [Google Scholar]
- Bilir, T. Investigation of performances of some empirical and composite models for predicting the modulus of elasticity of high strength concretes incorporating ground pumice and silica fume. Constr. Build. Mater. 2016, 127, 850–860. [Google Scholar] [CrossRef]
- Behnood, A.; Olek, J.; Glinicki, A. Predicting modulus elasticity of recycled aggregate concrete using M5’ model tree. Constr. Build. Mater. 2015, 94, 137–147. [Google Scholar] [CrossRef]
- Wang, Y.; Witten, I.H. Induction of Model Trees for Predicting Continuous Classes; Working Paper Series 96/23; University of Waikato: Hamilton, New Zealand, 1996. [Google Scholar]
- Logan, A.; Choi, W.; Mirmiran, A.; Rizkalla, S.; Zia, P. Short-Term Mechanical Properties of High-Strength Concrete. ACI Mater. J. 2009, 106, 413–418. [Google Scholar]
- Ross, A.; Tedesco, J.W.; Kuennen, S.T. Effects of strain rate on concrete strength. ACI Mater. J. 1995, 92, 37–47. [Google Scholar]
- Popovics, J.S.; Zemajtis, J.; Shkolnik, I. A Study of Static and Dynamic Modulus of Elasticity of Concrete; American Concrete Institute: Detroit, MI, USA, 2008. [Google Scholar]
- Lyndon, F.D.; Balendran, R.V. Some observations on elastic properties of plain concrete. Cem. Concr. Res. 1986, 16, 314–324. [Google Scholar] [CrossRef]
- Popovics, S. Verification of relationships between mechanical properties of concrete-like materials. Mater. Constr. 1975, 8, 183–191. [Google Scholar] [CrossRef]
- British Standards Institution. CP 110-1:1972 Code of Practice for the Structural Use of Concrete. Design, Materials and Workmanship; British Standards Institution: London, UK, 1972. [Google Scholar]
- Lee, B.J.; Kee, S.H.; Oh, T.; Kim, Y.Y. Effect of Cylinder Size on the Modulus of Elasticity and Compressive Strength of Concrete from Static and Dynamic Tests. Adv. Mater. Sci. Eng. 2015, 2015, 580638. [Google Scholar] [CrossRef]
- Salman, M.M.; Al-Amawee, A.H. The Ratio between Static and Dynamic Modulus of Elasticity in Normal and High Strength Concrete. J. Eng. Dev. 2006, 10, 163–174. [Google Scholar]
- Plachy, T.; Padevet, P.; Polak, M. Comparison of Two Experimental Techniques for Determination of Young’s Modulus of Concrete Specimens. In Proceedings of the 5th WSEAS International Conference on Applied and Theoretical Mechanics (MECHANICS ’09), Puerto De La Cruz, Spain, 14–16 December 2009; pp. 68–71. [Google Scholar]
- Shkolnik, I.E. Effect of nonlinear response of concrete on its elastic modulus and strength. Cem. Concr. Compos. 2005, 27, 747–757. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, J.; Sun, Z.; Qu, W. A fundamental study on compressive strength, static and dynamic elastic moduli of young concrete. Constr. Build. Mater. 2015, 98, 137–145. [Google Scholar] [CrossRef]
- Brunarski, L. Recommendations for use of resonance methods for testing concrete. Meteriaux Constr. 1969, 2, 269–273. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Bunke, N. Prüfung von Beton, Empfehlungen und Hinweise als Ergänzung zu DIN 1048; Deutscher Ausschauss für Stahlbeton: Berlin, Germany, 1991. (In German) [Google Scholar]
- International Organization for Standardization. EN ISO 12680-1 Methods of Test for Refractory Products—Part 1: Determination of Dynamic Young’s Modulus (MOE) by Impulse Excitation of Vibration; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Jurowski, K.; Kokot, S.; Bobra, P.; Grzeszczyk, S. The method of dynamic elastic modulus of concrete testing using impulse excitation of vibration and the modal analysis. Inżynieria i Budownictwo 2016, 11, 612–615. (In Polish) [Google Scholar]









| Cement/Additive | SiO2 | Al2O3 | Fe2O3 | CaO | MgO | K2O | Na2O | SO3 | TiO2 |
|---|---|---|---|---|---|---|---|---|---|
| (%) | |||||||||
| CEM I | 17.9 | 5.8 | 2.9 | 63.1 | 1.2 | 0.8 | 0.1 | 2.1 | - |
| CEM III | 28.8 | 6.9 | 1.8 | 51.0 | 5.3 | 0.6 | 0.3 | 1.9 | - |
| Metakaolin | 52.7 | 40.6 | 1.93 | 0.3 | 0.3 | 1.6 | 0.0 | - | 0.4 |
| Concrete | Binder | Water | Natural Aggregate | Basalt Aggregate | SP | |||
|---|---|---|---|---|---|---|---|---|
| CEM I | CEM III | Metakaolin | Silica Fume | |||||
| M1 | 500 | - | - | - | 200 | 1600 | - | - |
| M2 | - | 501 | - | - | 200 | 1600 | - | - |
| M3 | 387 | - | 97 | - | 193 | 1600 | - | 0.5 |
| M4 | - | 582 | - | - | 232 | - | 1692 | 2.0 |
| M5 | - | 585 | - | - | 202 | 1493 | - | 2.0 |
| M6 | 500 | - | - | 50 | 135 | - | 2008 | 1.25 |
| Concrete | Age (days) | Compressive Strength fc,cube | Static Elastic Modulus | Dynamic Elastic Modulus ED | |
|---|---|---|---|---|---|
| Initial | Stabilized | ||||
| (MPa) | (GPa) | (GPa) | (GPa) | ||
| M1, CEM I, natural aggregate | 4 | 47.5 | 33.1 | 36.8 | 40.1 |
| 7 | 52.7 | 34.1 | 37.7 | 41.3 | |
| 14 | 55.8 | 35.5 | 38.2 | 42.6 | |
| 21 | 57.2 | 35.4 | 38.5 | 43.2 | |
| 28 | 58.1 | 36.3 | 39.4 | 43.6 | |
| M2, CEM III, natural aggregate | 4 | 27.3 | 25.3 | 27.8 | 34.7 |
| 7 | 36.0 | 29.9 | 31.9 | 39.4 | |
| 14 | 45.1 | 33.9 | 36.2 | 42.3 | |
| 21 | 49.9 | 35.3 | 38.5 | 43.5 | |
| 28 | 52.5 | 38.2 | 39.1 | 43.9 | |
| M3, CEM I + metakaolin, natural aggregate | 4 | 34.7 | 26.3 | 29.3 | 34.0 |
| 7 | 41.5 | 30.2 | 32.7 | 37.9 | |
| 14 | 50.5 | 32.3 | 35.1 | 40.6 | |
| 21 | 52.2 | 33.7 | 36.8 | 41.8 | |
| 28 | 53.9 | 36.6 | 37.7 | 41.8 | |
| M4, CEM III, basalt aggregate | 7 | 36.9 | 33.9 | 35.9 | 40.8 |
| 14 | 51.5 | 39.8 | 41.2 | 44.3 | |
| 28 | 62.4 | 42.9 | 43.7 | 46.7 | |
| M5, CEM III, natural aggregate | 7 | 40.4 | 29.3 | 31.9 | 37.6 |
| 14 | 52.9 | 31.4 | 34.0 | 39.7 | |
| 28 | 64.6 | 35.4 | 37.3 | 42.1 | |
| M6, CEM I + silica fume, basalt aggregate | 7 | 84.8 | 53.1 | 55.0 | 56.9 |
| 14 | 98.3 | 56.6 | 59.3 | 60.3 | |
| 28 | 106.5 | 57.8 | 59.5 | 60.5 | |
| Concrete | Aggregate | Binder | Concrete Density | Volume Content of Aggregate | Coefficients Determined Using Least Squares Method | |
|---|---|---|---|---|---|---|
| M1 | Natural | CEM I | 2360 | 0.61 | 0.926 | 0.001 |
| M2 | Natural | CEM III A | 2340 | 0.61 | 0.926 | 0.090 |
| M3 | Natural | CEM I + metakaolin | 2310 | 0.61 | 0.926 | 0.039 |
| M4 | Basalt | CEM III A | 2560 | 0.55 | 0.964 | 0.090 |
| M5 | Natural | CEM III A | 2320 | 0.55 | 0.926 | 0.090 |
| M6 | Basalt | CEM I + silica fume | 2650 | 0.65 | 0.964 | 0.004 |
| Binder | |
|---|---|
| CEM I 42.5R | 2.31 |
| CEM III A 42.5N | 2.09 |
| CEM I + metakaolin | 2.19 |
| CEM I + silica fume | 2.76 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurowski, K.; Grzeszczyk, S. Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete. Materials 2018, 11, 477. https://doi.org/10.3390/ma11040477
Jurowski K, Grzeszczyk S. Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete. Materials. 2018; 11(4):477. https://doi.org/10.3390/ma11040477
Chicago/Turabian StyleJurowski, Krystian, and Stefania Grzeszczyk. 2018. "Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete" Materials 11, no. 4: 477. https://doi.org/10.3390/ma11040477
APA StyleJurowski, K., & Grzeszczyk, S. (2018). Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete. Materials, 11(4), 477. https://doi.org/10.3390/ma11040477




