Theoretical Investigations of the Hexagonal Germanium Carbonitride
Abstract
:1. Introduction
2. Theoretical Methods
3. Results and Discussion
3.1. Structural Properties
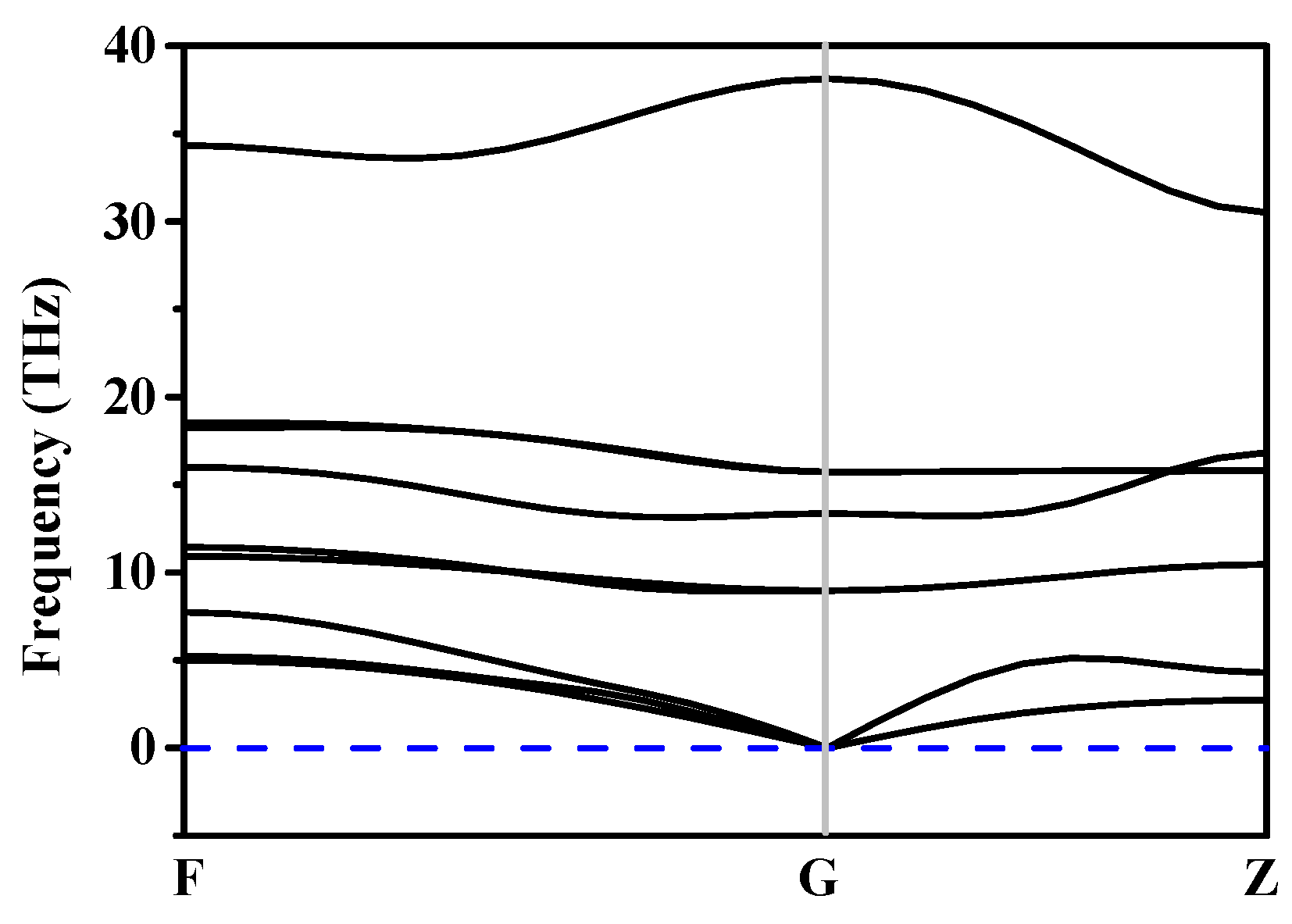
3.2. Stability and Mechanical Properties
3.3. Elastic Anisotropy Properties
3.4. Electronic Properties
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Zhang, M.G.; Yan, H.Y.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Imm2- and I m2-BCN. Comput. Mater. Sci. 2015, 97, 6–13. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Yan, H.Y.; Zhang, M.G.; Lin, Z.Z.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Structural, mechanical, and electronic properties of P3m1-BCN. J. Phys. Chem. Solids 2015, 79, 89–96. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wang, Y.C.; Lv, J.; Zhu, C.Y.; Li, Q.; Zhang, M.; Li, Q.; Ma, Y. First-principles structural design of superhard materials. J. Chem. Phys. 2013, 138, 114101. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhao, Z.S.; Luo, K.; Hu, M.; Ma, M.D.; He, J.L. Superhard orthorhombic phase of B2CO compound. Diam. Relat. Mater. 2017, 73, 87–92. [Google Scholar] [CrossRef]
- Wang, S.N.; Oganov, A.R.; Qian, G.R.; Zhu, Q.; Dong, H.F.; Dong, X.; Mahdi, D.E. Novel superhard B–C–O phases predicted from first principles. Phys. Chem. Chem. Phys. 2016, 18, 1859–1863. [Google Scholar] [CrossRef] [PubMed]
- Qiao, L.P.; Zhao, J. Two B-C-O compounds: structural, mechanical anisotropy and electronic properties under pressure. Materials 2017, 10, 1413. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.G.; Yan, H.Y.; Zheng, B.B.; Wei, Q. Influences of carbon concentration on crystal structures and ideal strengths of B2CxO compounds in the B-C-O system. Sci. Rep. 2015, 5, 15481. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.Y.; Yan, F.; Wang, S.X.; Jia, Q.Q.; Yu, X.H.; Shi, C.L. Mechanical, elastic, anisotropy, and electronic properties of monoclinic phase of 𝑚-Si𝑥Ge3−xN4. Chin. Phys. B 2017, 26, 126105. [Google Scholar] [CrossRef]
- Han, C.X.; Chai, C.C.; Fan, Q.Y.; Yang, J.H.; Yang, Y.T. Structural, electronic, and thermodynamic properties of tetragonal t-SixGe3−xN4. Materials 2018, 11, 397. [Google Scholar] [CrossRef] [PubMed]
- Miao, N.X.; Pu, C.Y.; He, C.Z.; Zhang, F.W.; Lu, C.; Lu, Z.W.; Zhou, D.W. Mechanical and thermodynamic properties of the monoclinic and orthorhombic phases of SiC2N4 under high pressure from first principles. Chin. Phys. B 2014, 23, 127101. [Google Scholar] [CrossRef]
- Wang, H.B.; Li, Q.; Wang, H.; Liu, H.Y.; Cui, T.; Ma, Y.M. Design of superhard ternary compounds under high pressure: SiC2N4 and Si2CN4. J. Phys. Chem. C 2010, 114, 8609. [Google Scholar] [CrossRef]
- Du, H.J.; Guo, L.C.; Li, D.C.; Yu, D.L.; He, J.L. First-principles calculations of phase transition and stability of Si2CN4 under high pressure. Chin. Phys. Lett. 2009, 26, 016403. [Google Scholar] [CrossRef]
- Hart, J.N.; Claeyssens, F.; Allan, N.L.; May, P.W. Carbon nitride: Ab initio investigation of carbon-rich phases. Phys. Rev. B 2009, 80, 174111. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Chen, Z.W.; Du, H.J.; Yang, C.; Ma, M.Z.; He, J.L.; Tian, Y.J.; Liu, R.P. Structural, elastic, and thermal properties of Laves phase ZrV2 under pressure. J. Appl. Phys. 2008, 103, 083533. [Google Scholar] [CrossRef]
- Xing, M.J.; Li, B.H.; Yu, Z.T.; Chen, Q. Structural, elastic and thermodynamic properties of the tetragonal structure of germanium Carbonitride. J. Phys. Chem. Solids 2016, 91, 106–113. [Google Scholar] [CrossRef]
- Liu, X.L.; Kang, J.Y. Structure prediction of ternary Ge-C-N System. In Proceedings of the 2004 13th International Conference on Semiconducting and Insulating Materials (SIMC-XIII-2004), Beijing, China, 20–25 September 2004; pp. 210–213. [Google Scholar]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Du, Z. A first-principles study of the properties of four predicted novel phases of AlN. J. Phys. Chem. Solids 2017, 104, 68–78. [Google Scholar] [CrossRef]
- Liu, C.; Hu, M.; Luo, K.; Cui, L.; Yu, D.L.; Zhao, Z.S.; He, J.L. Novel high-pressure phases of AlN: A first-principles study. Comput. Mater. Sci. 2016, 117, 496–501. [Google Scholar] [CrossRef]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Zhang, D.Y. First-principles study on phases of AlP. Solid State Commun. 2017, 267, 23–28. [Google Scholar] [CrossRef]
- Xu, L.F.; Bu, W. Mechanical and thermodynamic properties of AlX (X = N, P, As) compounds. Int. J. Mod. Phys. B 2017, 31, 1750167. [Google Scholar] [CrossRef]
- Liu, C.; Ma, M.D.; Yuan, X.H.; Sun, H.; Ying, P.; Xu, B.; Zhao, Z.S.; He, J.L. Metastable phases, phase transformation and properties of AlAs based on first-principle study. Comput. Mater. Sci. 2017, 128, 337–342. [Google Scholar] [CrossRef]
- Mujica, A.; Rubio, A.; Muñoz, A.; Needs, R.J. High-pressure phases of group-IV, III–V, and II–VI compounds. Rev. Mod. Phys. 2003, 75, 863–912. [Google Scholar] [CrossRef]
- Dos Santos, R.B.; de Brito Mota, F.; Rivelino, R.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Van der Waals stacks of few-layer h-AlN with graphene: An ab initio study of structural, interaction and electronic properties. Nanotechnology 2016, 27, 145601. [Google Scholar] [CrossRef] [PubMed]
- Freitas, R.R.Q.; de Brito Mota, F.; Rivelino, R.; de Castilho, C.M.C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Spin-orbit-induced gap modification in buckled honeycomb XBi and XBi3 (X = B, Al, Ga, and In) sheets. J. Phys.: Condens. Matter 2015, 27, 485306. [Google Scholar] [CrossRef] [PubMed]
- Freitas, R.R.Q.; de Brito Mota, F.; Rivelino, R.; de Castilho, C.M.C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Tuning band inversion symmetry of buckled III-Bi sheets by halogenation. Nanotechnology 2016, 27, 055704. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Wang, Q.Q.; Xu, B.; Yu, D.L.; Liu, Z.Y.; Tian, Y.J.; He, J.L. Prediction of novel SiCN compounds: First-principles calculations. J. Phys. Chem. C 2013, 117, 21943–21948. [Google Scholar] [CrossRef]
- Badzian, A. Stability of silicon carbonitride phases. J. Am. Ceram. Soc. 2002, 85, 16–20. [Google Scholar] [CrossRef]
- Raj, R.; An, L.; Shah, S.; Riedel, R.; Fasel, C.; Kleebe, H.J. Oxidation kinetics of an amorphous silicon carbonitride ceramic. J. Am. Ceram. Soc. 2001, 84, 1803–1810. [Google Scholar] [CrossRef]
- He, X.M.; Taylor, T.N.; Lillard, R.S.; Walter, K.C.; Nastasi, M. Bonding structure and properties of ion enhanced reactive magnetron sputtered silicon carbonitride films. J. Phys. Condens. Matter 2000, 12, L591. [Google Scholar] [CrossRef]
- Xiao, X.C.; Li, Y.W.; Song, L.X.; Peng, X.F.; Hu, X.F. Structural analysis and microstructural observation of SiCxNy films prepared by reactive sputtering of SiC in N2 and Ar. Appl. Surf. Sci. 2000, 156, 155–160. [Google Scholar] [CrossRef]
- Chen, L.C.; Chen, K.H.; Wei, S.L.; Kichambare, P.D.; Wu, J.J.; Lu, T.R.; Kuo, C.T. Crystalline SiCN: A hard material rivals to cubic BN. Thin Solid Films 1999, 355, 112–116. [Google Scholar] [CrossRef]
- Bendeddouche, A.; Berjoan, R.; Bêche, E.; Hillel, R. Hardness and stiffness of amorphous SiCxNy chemical vapor deposited coatings. Surf. Coat. Technol. 1999, 111, 184–190. [Google Scholar] [CrossRef]
- An, L.; Riedel, R.; Konetschny, C.; Kleebe, H.J.; Raj, R. Newtonian viscosity of amorphous silicon carbonitride at high temperature. J. Am. Ceram. Soc. 1998, 81, 1349–1352. [Google Scholar] [CrossRef]
- Chen, L.C.; Chen, C.K.; Wei, S.L.; Bhusari, D.M.; Chen, K.H.; Chen, Y.F.; Jong, Y.C.; Huang, Y.S. Crystalline silicon carbon nitride: A wide band gap semiconductor. Appl. Phys. Lett. 1998, 72, 2463–2465. [Google Scholar] [CrossRef]
- Machorro, R.; Samano, E.C.; Soto, G.; Cota, L. SiCxNy thin films alloys prepared by pulsed excimer laser deposition. Appl. Surf. Sci. 1998, 127, 564–568. [Google Scholar] [CrossRef]
- Riedel, R.; Greiner, A.; Miehe, G.; Dressler, W.; Fuess, H.; Bill, J.; Aldinger, F. The First crystalline solids in the ternary Si-C-N system. Angew. Chem., Int. Ed. 1997, 36, 603–606. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. Crystal structure prediction via particle swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Inorganic Crystal Structure Database. ICSD Collection Code 28391. Available online: http://icsd.fiz-karlsruhe.de (accessed on 19 April 2018).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892R–7895R. [Google Scholar] [CrossRef]
- Shanno, D.F.; Kettler, P.C. Optimal conditioning of quasi-newton methods. Math. Comput. 1970, 24, 657–664. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.J.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- Xing, M.J.; Li, B.H.; Yu, Z.T.; Chen, Q. C2/m-carbon: structural, mechanical, and electronic properties. J. Mater. Sci. 2015, 50, 7104–7114. [Google Scholar] [CrossRef]
- Voigt, W. Lehrburch der Kristallphysik; Teubner, B.G., Ed.; Johnson Reprint Corp.: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behavior of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823. [Google Scholar] [CrossRef]
- Lewandowski, J.J.; Wang, W.H.; Greer, A.L. Intrinsic plasticity or brittleness of metallic glasses. Philos. Mag. Lett. 2005, 85, 77. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Panda, K.B.; Ravi, K.S. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory. Comput. Mater. Sci. 2006, 35, 134–150. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.Y.; Han, Z.; Yu, X.H.; Wang, D.Y.; Tian, Y. Pnma-BN: Another boron nitride polymorph with interesting physical properties. Nanomaterials 2017, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T. The mechanical and electronic properties of carbon-rich silicon carbide. Materials 2016, 9, 333. [Google Scholar] [CrossRef] [PubMed]

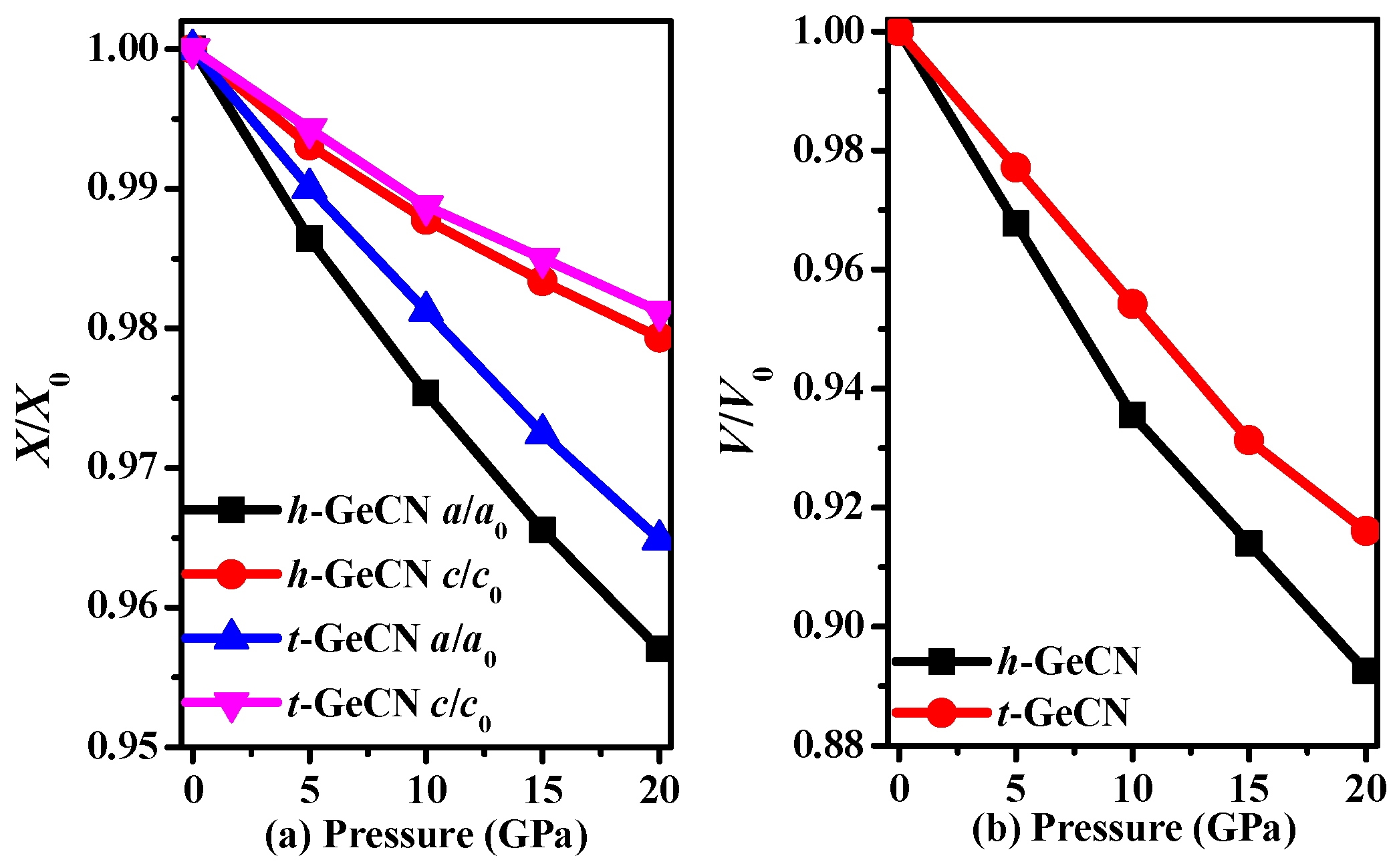


| Material | Methods | Pressure | a | c | V | ρ |
|---|---|---|---|---|---|---|
| h-GeCN | GGA | 0 | 3.165 | 10.701 | 92.819 | 5.292 |
| 5 | 3.122 | 10.627 | 89.687 | 5.477 | ||
| 10 | 3.087 | 10.570 | 87.207 | 5.633 | ||
| 15 | 3.056 | 10.523 | 85.100 | 5.772 | ||
| 20 | 3.029 | 10.480 | 83.270 | 5.899 | ||
| t-GeCN | GGA | 0 | 4.326 | 7.046 | 131.861 | 4.967 |
| 0 1 | 4.323 | 7.037 | 131.490 | 4.981 | ||
| LDA | 0 | 4.216 | 6.993 | 124.298 | 5.269 | |
| 0 1 | 4.205 | 6.892 | 121.836 | 5.376 |
| Material | Pressure | C11 | C12 | C13 | C14 | C24 | C33 | C44 | C56 | C66 |
|---|---|---|---|---|---|---|---|---|---|---|
| h-GeCN | 0 | 232 | 77 | 21 | 4 | −4 | 512 | 42 | 4 | 78 |
| 5 | 282 | 95 | 48 | −7 | 7 | 586 | 60 | −7 | 93 | |
| 10 | 329 | 106 | 68 | −20 | 20 | 644 | 65 | −20 | 112 | |
| 15 | 361 | 126 | 91 | −27 | 27 | 694 | 68 | −27 | 117 | |
| 20 | 380 | 158 | 109 | −33 | 33 | 741 | 59 | −33 | 111 | |
| t-GeCN | 0 1 | 263 | 143 | 94 | - | - | 492 | 151 | - | 167 |
| Material | Pressure | B | G | B/G | E | v | AU |
|---|---|---|---|---|---|---|---|
| h-GeCN | 0 | 130 | 77 | 1.688 | 193 | 0.253 | 2.112 |
| 5 | 165 | 95 | 1.737 | 239 | 0.258 | 1.463 | |
| 10 | 193 | 104 | 1.856 | 264 | 0.272 | 1.722 | |
| 15 | 219 | 107 | 2.047 | 276 | 0.290 | 1.950 | |
| 20 | 244 | 98 | 2.490 | 259 | 0.323 | 3.021 | |
| t-GeCN | 0 | 183 | 129 | 1.42 | 313 | 0.210 | 0.925 |
| Materials | Pressure | vp | vs | vm | ΘD |
|---|---|---|---|---|---|
| h-GeCN | 0 | 6631 | 3814 | 4236 | 506 |
| 5 | 7297 | 4165 | 4628 | 559 | |
| 10 | 7673 | 4297 | 4783 | 583 | |
| 15 | 7916 | 4306 | 4803 | 590 | |
| 20 | 7970 | 4076 | 4566 | 565 |
| Material | P | [100] | [001] | ||||
|---|---|---|---|---|---|---|---|
| [100]vl | [010]vt1 | [001]vt2 | [001]vl | [100]vt1 | [010]vt2 | ||
| h-GeCN | 0 | 3827 | 4682 | 1992 | 6955 | 1992 | 1992 |
| 5 | 4132 | 5074 | 2340 | 7314 | 2340 | 2340 | |
| 10 | 4449 | 5404 | 2402 | 7561 | 2402 | 2402 | |
| 15 | 4512 | 5592 | 2427 | 7754 | 2427 | 2427 | |
| 20 | 4338 | 5675 | 2236 | 7925 | 2236 | 2236 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Ma, Z.; Suriguge; Wang, P. Theoretical Investigations of the Hexagonal Germanium Carbonitride. Materials 2018, 11, 655. https://doi.org/10.3390/ma11050655
Yu X, Ma Z, Suriguge, Wang P. Theoretical Investigations of the Hexagonal Germanium Carbonitride. Materials. 2018; 11(5):655. https://doi.org/10.3390/ma11050655
Chicago/Turabian StyleYu, Xinhai, Zhenyang Ma, Suriguge, and Peng Wang. 2018. "Theoretical Investigations of the Hexagonal Germanium Carbonitride" Materials 11, no. 5: 655. https://doi.org/10.3390/ma11050655
APA StyleYu, X., Ma, Z., Suriguge, & Wang, P. (2018). Theoretical Investigations of the Hexagonal Germanium Carbonitride. Materials, 11(5), 655. https://doi.org/10.3390/ma11050655




