Effect of Cementite on the Hydrogen Diffusion/Trap Characteristics of 2.25Cr-1Mo-0.25V Steel with and without Annealing
Abstract
:1. Introduction
2. Experimental Method
2.1. Materials
2.2. Hydrogen Electrochemical Permeation Experiments
2.2.1. Preparation
2.2.2. Hydrogen Electrochemical Permeation Tests
2.3. Analysis of the Hydrogen Permeation Tests
2.4. Microstructure Characterization
3. Results
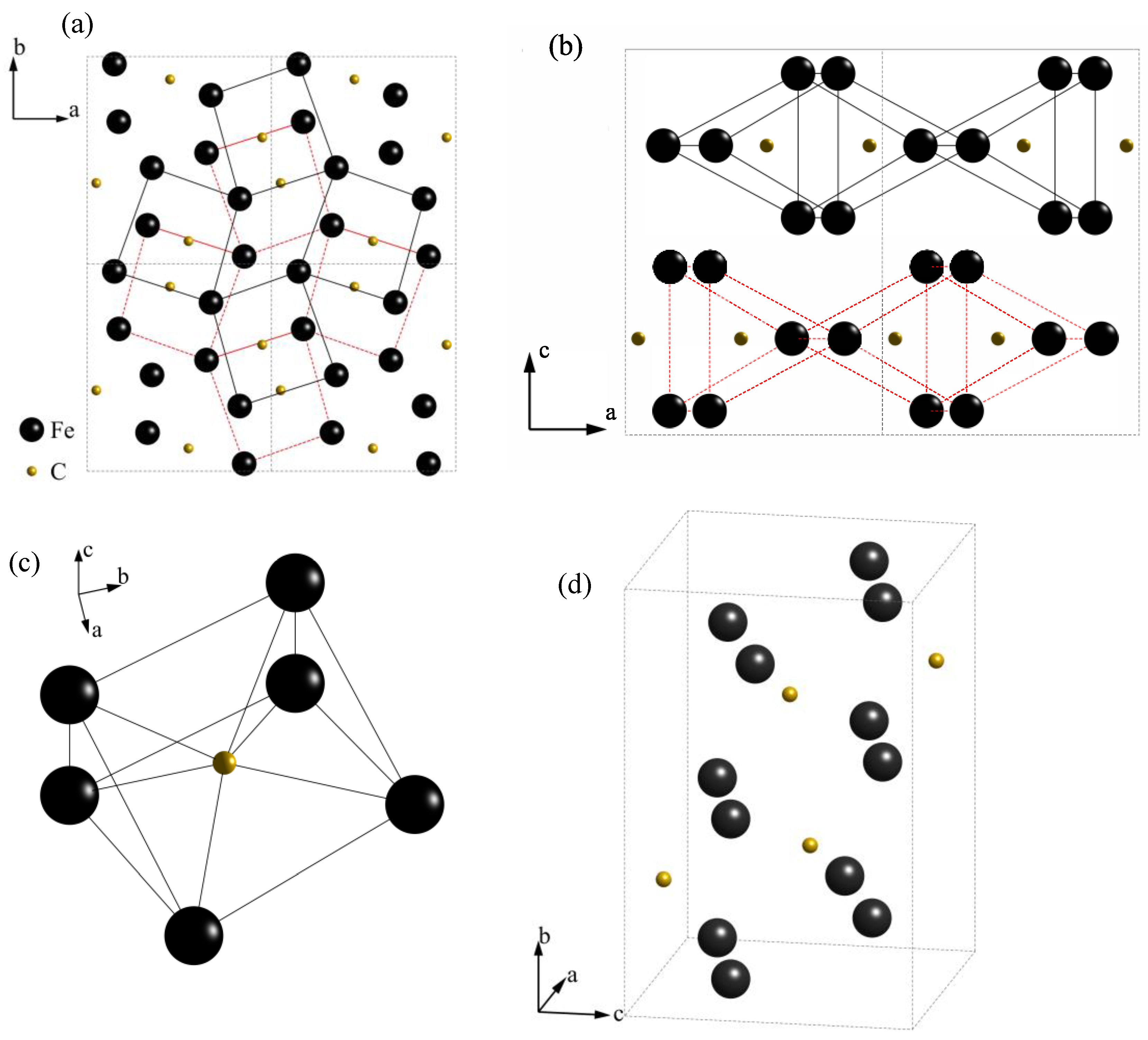
3.1. Microstructure Characterization
3.2. Hydrogen Electrochemical Permeation Tests
4. Discussion
4.1. Macroscopic Characterization of Hydrogen Trap
4.2. Microscopic Mechanism for Hydrogen Trap
5. Conclusions
- According to the electrochemical permeation test results, cementite located at the grain boundaries and at the interfaces of lath ferrite acted as a kind of hydrogen trap, mostly as an irreversible hydrogen trap.
- According to the diffusion thermodynamics and the Lennard–Jones potential theories, the interaction between hydrogen atoms and other atoms in cementite is larger than that in ferrite, thus, hydrogen diffusion from ferrite to cementite is up-hill diffusion and hydrogen atoms will be collected around the cementite, making the cementite a hydrogen trap.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- García, T.E.; Rodríguez, C.; Belzunce, F.J.; Cuesta, I.I. Effect of hydrogen embrittlement on the tensile properties of crmov steels by means of the small punch test. Mater. Sci. Eng. A 2016, 664, 165–176. [Google Scholar] [CrossRef]
- Song, Y.; Chai, M.; Wu, W.; Liu, Y.; Qin, M.; Cheng, G. Experimental investigation of the effect of hydrogen on fracture toughness of 2.25cr-1mo-0.25v steel and welds after annealing. Materials 2018, 11, 499. [Google Scholar] [CrossRef] [PubMed]
- Mohtadi-Bonab, M.A.; Szpunar, J.A.; Razavi-Tousi, S.S. A comparative study of hydrogen induced cracking behavior in api 5l x60 and x70 pipeline steels. Eng. Fail. Anal. 2013, 33, 163–175. [Google Scholar] [CrossRef]
- Mohtadi-Bonab, M.A.; Eskandari, M. A focus on different factors affecting hydrogen induced cracking in oil and natural gas pipeline steel. Eng. Fail. Anal. 2017, 79, 351–360. [Google Scholar] [CrossRef]
- Troiano, A.R. The role of hydrogen and other interstitials in the mechanical behavior of metals. Metallogr. Microstruct. Anal. 2016, 5, 557–569. [Google Scholar] [CrossRef]
- Martin, M.L.; Robertson, I.M.; Sofronis, P. Interpreting hydrogen-induced fracture surfaces in terms of deformation processes: A new approach. Acta Mater. 2011, 59, 3680–3687. [Google Scholar] [CrossRef]
- Birnbaum, H.K.; Sofronis, P. Hydrogen-enhanced localized plasticity—a mechanism for hydrogen-related fracture. Mater. Sci. Eng. A 1994, 176, 191–202. [Google Scholar] [CrossRef]
- Frappart, S.; Feaugas, X.; Creus, J.; Thebault, F.; Delattre, L.; Marchebois, H. Study of the hydrogen diffusion and segregation into fe–c–mo martensitic hsla steel using electrochemical permeation test. J. Phys. Chem. Solids 2010, 71, 1467–1479. [Google Scholar] [CrossRef]
- Cui, Q.Q.; Wu, J.S.; Xie, D.H.; Wu, X.G.; Huang, Y.H.; Li, X.G. Effect of nanosized nbc precipitates on hydrogen diffusion in x80 pipeline steel. Materials 2017, 10, 10. [Google Scholar] [CrossRef] [PubMed]
- Frappart, S.; Feaugas, X.; Creus, J.; Thebault, F.; Delattre, L.; Marchebois, H. Hydrogen solubility, diffusivity and trapping in a tempered fe–c–cr martensitic steel under various mechanical stress states. Mater. Sci. Eng. A 2012, 534, 384–393. [Google Scholar] [CrossRef]
- Huang, F.; Liu, J.; Deng, Z.J.; Cheng, J.H.; Lu, Z.H.; Li, X.G. Effect of microstructure and inclusions on hydrogen induced cracking susceptibility and hydrogen trapping efficiency of x120 pipeline steel. Mater. Sci. Eng. A 2010, 527, 6997–7001. [Google Scholar] [CrossRef]
- Park, G.T.; Koh, S.U.; Jung, H.G.; Kim, K.Y. Effect of microstructure on the hydrogen trapping efficiency and hydrogen induced cracking of linepipe steel. Corros. Sci. 2008, 50, 1865–1871. [Google Scholar] [CrossRef]
- Ágren, J. A note on the theoretical treatment of uphill diffusion in compound welds. Metall. Trans. A 1983, 14, 2167–2170. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields. II. From the equation of state of a gas. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Zheng, Y.P. Effects of absorption and desorption on hydrogen permeation—I. Theoretical modeling and room temperature verification. Acta Mater. 1998, 46, 5023–5033. [Google Scholar] [CrossRef]
- Devanathan, M.A.V.; Stachurski, Z. The adsorption and diffusion of electrolytic hydrogen in palladium. Proc. R. Soc. Lond. A 1962, 270, 90–102. [Google Scholar] [CrossRef]
- Xue, H.B.; Cheng, Y.F. Characterization of inclusions of x80 pipeline steel and its correlation with hydrogen-induced cracking. Corros. Sci. 2011, 53, 1201–1208. [Google Scholar] [CrossRef]
- Doyle, D.M.; Palumbo, G.; Aust, K.T.; El-Sherik, A.M.; Erb, U. The influence of intercrystalline defects on hydrogen activity and transport in nickel. Acta Metallurgica Materialia 1995, 43, 3027–3033. [Google Scholar] [CrossRef]
- Krauss, G.; Thompson, S.W. Ferritic microstructures in continuously cooled low and ultralow-carbon steels. ISIJ Int. 1995, 35, 937–945. [Google Scholar] [CrossRef]
- Yen, S.K.; Huang, I.B. Critical hydrogen concentration for hydrogen-induced blistering on aisi 430 stainless steel. Mater. Chem. Phys. 2003, 80, 662–666. [Google Scholar] [CrossRef]
- Oriani, R.A. The diffusion and trapping of hydrogen in steel. Acta Metall. 1970, 18, 147–157. [Google Scholar] [CrossRef]
- Araújo, D.F.; Vilar, E.O.; Palma Carrasco, J. A critical review of mathematical models used to determine the density of hydrogen trapping sites in steels and alloys. Int. J. Hydrog. Energy 2014, 39, 12194–12200. [Google Scholar] [CrossRef]
- Dong, C.F.; Liu, Z.Y.; Li, X.G.; Cheng, Y.F. Effects of hydrogen-charging on the susceptibility of x100 pipeline steel to hydrogen-induced cracking. Int. J. Hydrog. Energy 2009, 34, 9879–9884. [Google Scholar] [CrossRef]
- Gibala, R.; DeMiglio, D.S. Hydrogen in iron and steels: Interactions, traps and crack paths. In Hydrogen Effects in Metals: Proceedings of the Third International Conference on Effect of Hydrogen on Behavior of Materials; Thompson, A.W., Bernstein, I.M., Eds.; Metallurgical Society of AIME: Warrendale, PA, USA, 1981; pp. 113–122. [Google Scholar]
- Pressouyre, G.M. A classification of hydrogen traps in steel. Metall. Trans. A 1979, 10, 1571–1573. [Google Scholar] [CrossRef]
- Elliott, J.R.; Lira, C.T. Introductory Chemical Engineering Thermodynamics; Prentice Hall: Upper Saddle River, NJ, USA, 2012; p. 912. ISBN 978-0136068549. [Google Scholar]
- Rayne, J.A.; Chandrasekhar, B.S. Elastic constants of iron from 4.2 to 300°K. Phys. Rev. 1961, 122, 1714–1716. [Google Scholar] [CrossRef]
- Jiang, C.; Srinivasan, S.G.; Caro, A.; Maloy, S.A. Structural, elastic, and electronic properties of fe3c from first principles. J. Appl. Phys. 2008, 103, 043502. [Google Scholar] [CrossRef]
- Nikolussi, M.; Shang, S.L.; Gressmann, T.; Leineweber, A.; Mittemeijer, E.J.; Wang, Y.; Liu, Z.K. Extreme elastic anisotropy of cementite, Fe3C: First-principles calculations and experimental evidence. Scr. Mater. 2008, 59, 814–817. [Google Scholar] [CrossRef]
- Lv, Z.Q.; Zhang, F.C.; Sun, S.H.; Wang, Z.H.; Jiang, P.; Zhang, W.H.; Fu, W.T. First-principles study on the mechanical, electronic and magnetic properties of Fe3C. Comp. Mater. Sci. 2008, 44, 690–694. [Google Scholar] [CrossRef]
- Henriksson, K.O.E.; Sandberg, N.; Wallenius, J. Carbides in stainless steels: Results from ab initio investigations. Appl. Phys. Lett. 2008, 93, 191912. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Zhang, X.; Hickel, T.; Rogal, J.; Fähler, S.; Drautz, R.; Neugebauer, J. Structural transformations among austenite, ferrite and cementite in fe–c alloys: A unified theory based on ab initio simulations. Acta Mater. 2015, 99, 281–289. [Google Scholar] [CrossRef]









| Element | C | Si | Mn | P | S | Cr | Mo | V | Al |
|---|---|---|---|---|---|---|---|---|---|
| Percentage | 0.15 | 0.1 | 0.54 | 0.009 | 0.01 | 2.3 | 0.98 | 0.3 | 0.05 |
| Material | Time of Experiment | Hydrogen Flux (10−11 mol·m−2·s−1) | Effective Hydrogen Diffusivity (10−7 cm2·s−1) | Apparent Hydrogen Diffusivity (10−7 cm2·s−1) | Subsurface Hydrogen Concentration (10−5 mol·cm−3) |
|---|---|---|---|---|---|
| RS | 1st | 30.84 | 284.36 | 201.37 | 1.63 |
| 2nd | 13.27 | 673.39 | 578.03 | 0.27 | |
| AS | 1st | 28.34 | 329.38 | 255.18 | 1.36 |
| 2nd | 25.48 | 790.27 | 660.94 | 0.51 |
| Material | Hydrogen Trap Density for 1st Permeation | Hydrogen Trap Density for 2nd Permeation | Reversible Hydrogen Trap Density | Irreversible Hydrogen Trap Density |
|---|---|---|---|---|
| RS | 11.62 | 0.55 | 0.55 | 11.07 |
| AS | 8.58 | 0.77 | 0.77 | 7.81 |
| Research Scholars | Method | C11 | C22 | C33 | C12 | C23 | C13 | C44 | C55 | C66 | E | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jiang et al. [28] | Relaxed, energy-strain | 388 | 345 | 322 | 156 | 162 | 164 | 15 | 134 | 134 | 224 | 249 |
| Relaxed, stress-strain | 395 | 347 | 325 | 158 | 163 | 169 | 18 | 134 | 135 | 227 | 252 | |
| Nikolussi et al. [29] | Relaxed, stress-strain | 385 | 341 | 316 | 157 | 167 | 162 | 13 | 131 | 131 | 224 | 243 |
| Lv et al. [30] | Relaxed, stress-strain | 393 | 340 | 319 | 144 | 149 | 141 | -60 | 145 | 118 | 213 | 218 |
| Henriksson et al. [31] | Unrelaxed, energy-strain | 394 | 412 | 360 | 157 | 166 | 146 | 83 | 133 | 136 | 234 | 301 |
| Structure | Cell Geometries | Lattice Constant (nm) [33] | Bulk Modulus (GPa) | ||
|---|---|---|---|---|---|
| a | b | c | |||
| Ferrite | BCC | 0.2863 | 0.2863 | 0.2863 | 173.4 [27] |
| Cementite | Orthorhombic | 0.5038 | 0.6727 | 0.4484 | 231.1 [28] |
| Microstructure | Octahedral Sites | Tetrahedral Sites | Random Position | ||
|---|---|---|---|---|---|
| Maximum | Minimum | Average | |||
| Ferrite | |||||
| Cementite | - | - | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Han, Z.; Chai, M.; Yang, B.; Liu, Y.; Cheng, G.; Li, Y.; Ai, S. Effect of Cementite on the Hydrogen Diffusion/Trap Characteristics of 2.25Cr-1Mo-0.25V Steel with and without Annealing. Materials 2018, 11, 788. https://doi.org/10.3390/ma11050788
Song Y, Han Z, Chai M, Yang B, Liu Y, Cheng G, Li Y, Ai S. Effect of Cementite on the Hydrogen Diffusion/Trap Characteristics of 2.25Cr-1Mo-0.25V Steel with and without Annealing. Materials. 2018; 11(5):788. https://doi.org/10.3390/ma11050788
Chicago/Turabian StyleSong, Yan, Zelin Han, Mengyu Chai, Bin Yang, Yilun Liu, Guangxu Cheng, Yun Li, and Song Ai. 2018. "Effect of Cementite on the Hydrogen Diffusion/Trap Characteristics of 2.25Cr-1Mo-0.25V Steel with and without Annealing" Materials 11, no. 5: 788. https://doi.org/10.3390/ma11050788
APA StyleSong, Y., Han, Z., Chai, M., Yang, B., Liu, Y., Cheng, G., Li, Y., & Ai, S. (2018). Effect of Cementite on the Hydrogen Diffusion/Trap Characteristics of 2.25Cr-1Mo-0.25V Steel with and without Annealing. Materials, 11(5), 788. https://doi.org/10.3390/ma11050788





