Analytical Solutions for Stochastic Vibration of Orthotropic Membrane under Random Impact Load
Abstract
:1. Introduction
2. Theoretical Study
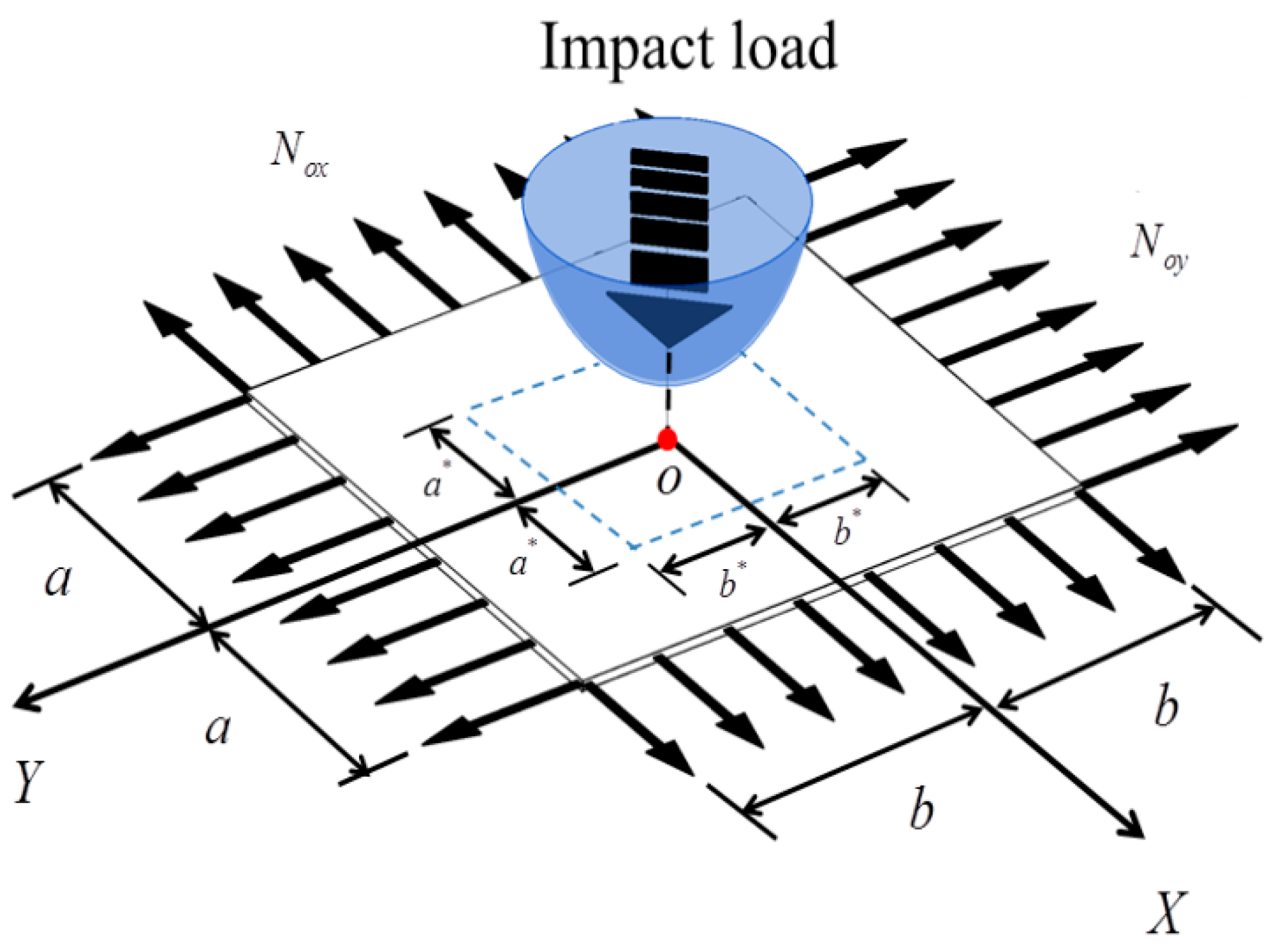
2.1. Model Description
- (1)
- Both membrane and impact load are symmetric. Furthermore, the center of impact load coincides with the center of membrane, namely (0,0);
- (2)
- The impact load is the mass of homogeneous intensity and area with the length of and the width of ;
- (3)
- The space distribution of impact load is symmetric and non-uniform;
- (4)
- According to the central limit theorem, the amplitude of impact load follows a Gaussian distribution;
- (5)
- The applied area of impact load can be defined as .
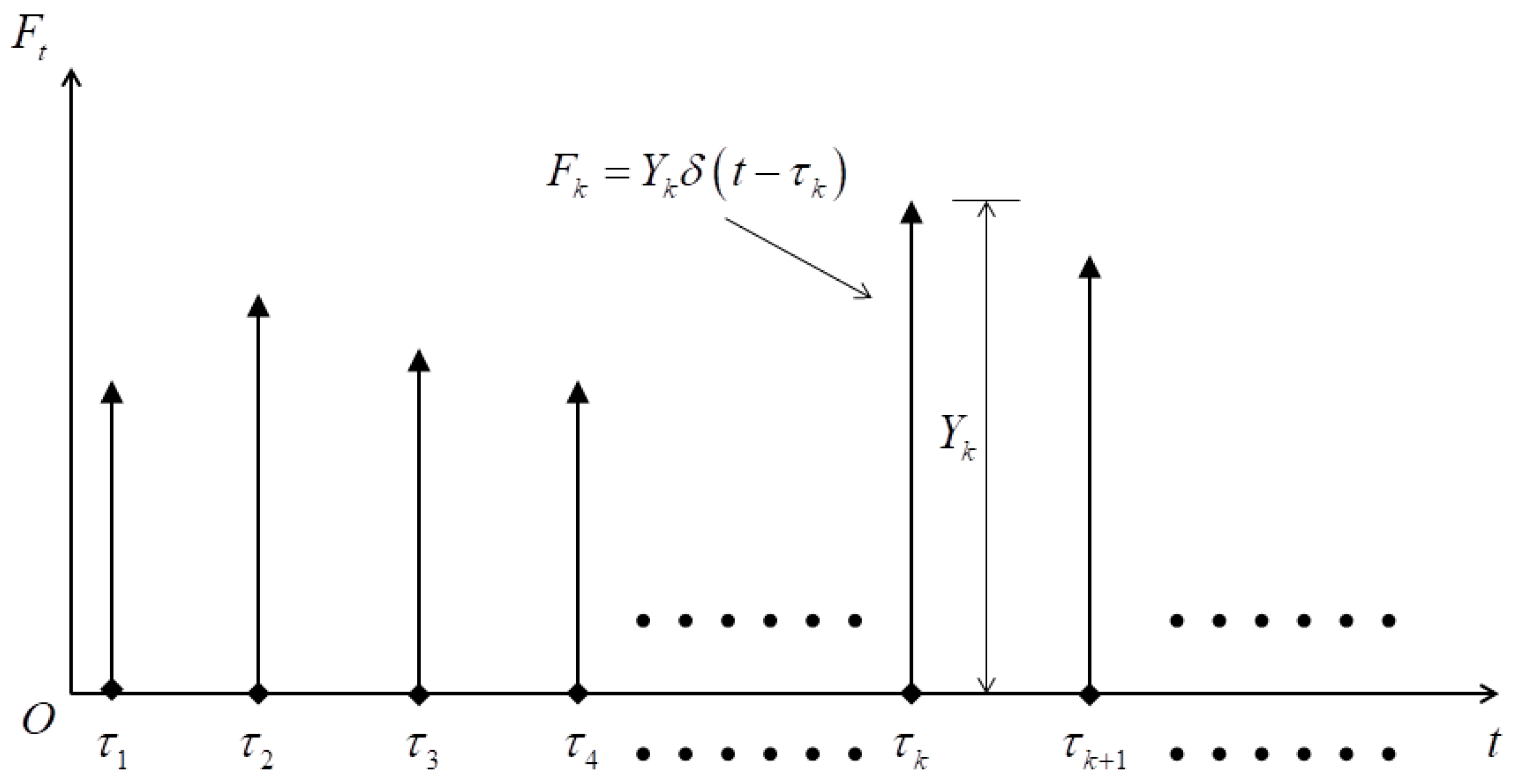
2.2. Statistical Characteristics of Impact Load
2.3. Establishing the FPK Equation
2.4. Solving the FPK Equation
3. Experimental Study
3.1. Experimental System
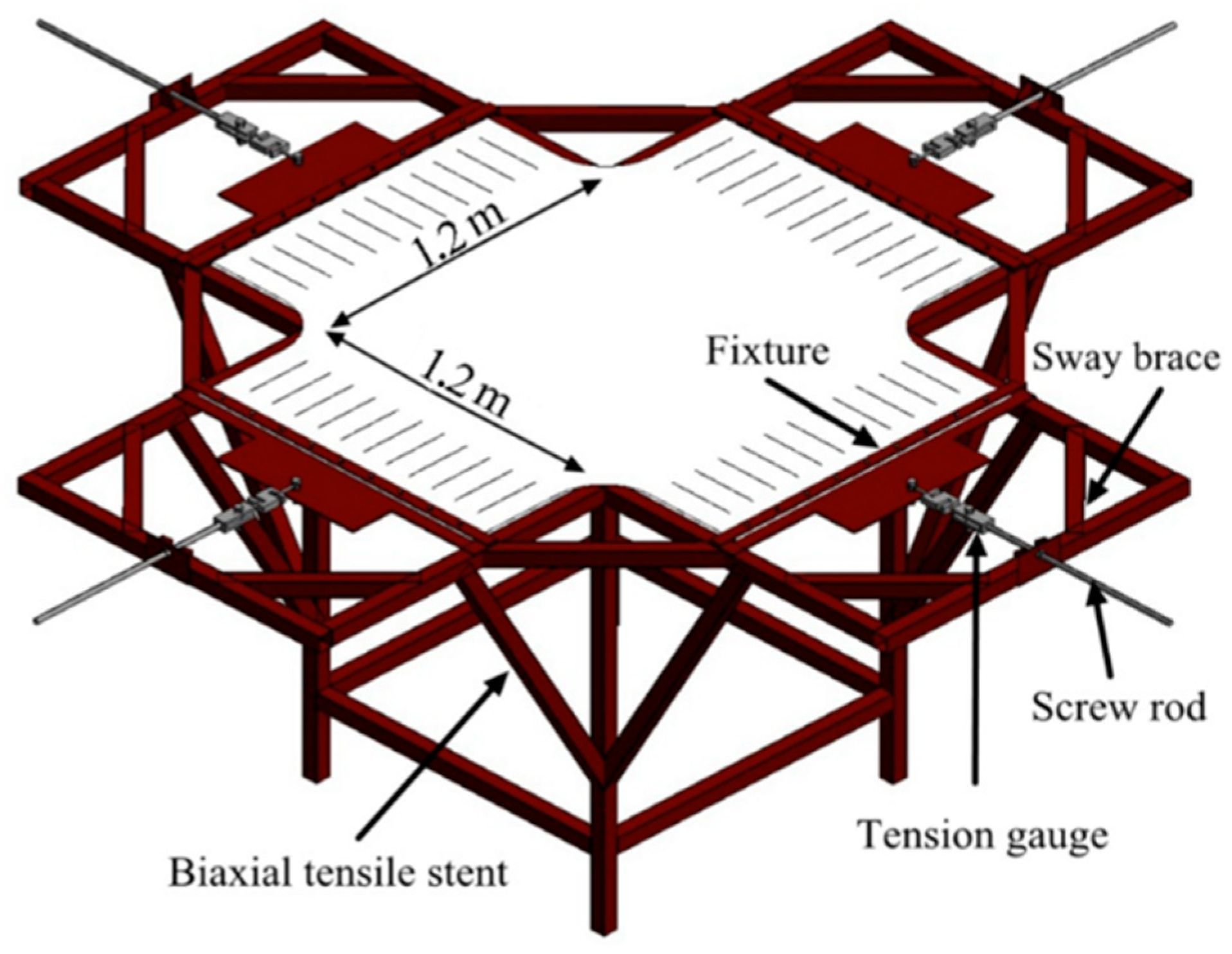
3.1.1. Experimental Pretension Device
3.1.2. Load Device
3.1.3. Data Collection Device
3.2. Experimental Schedule
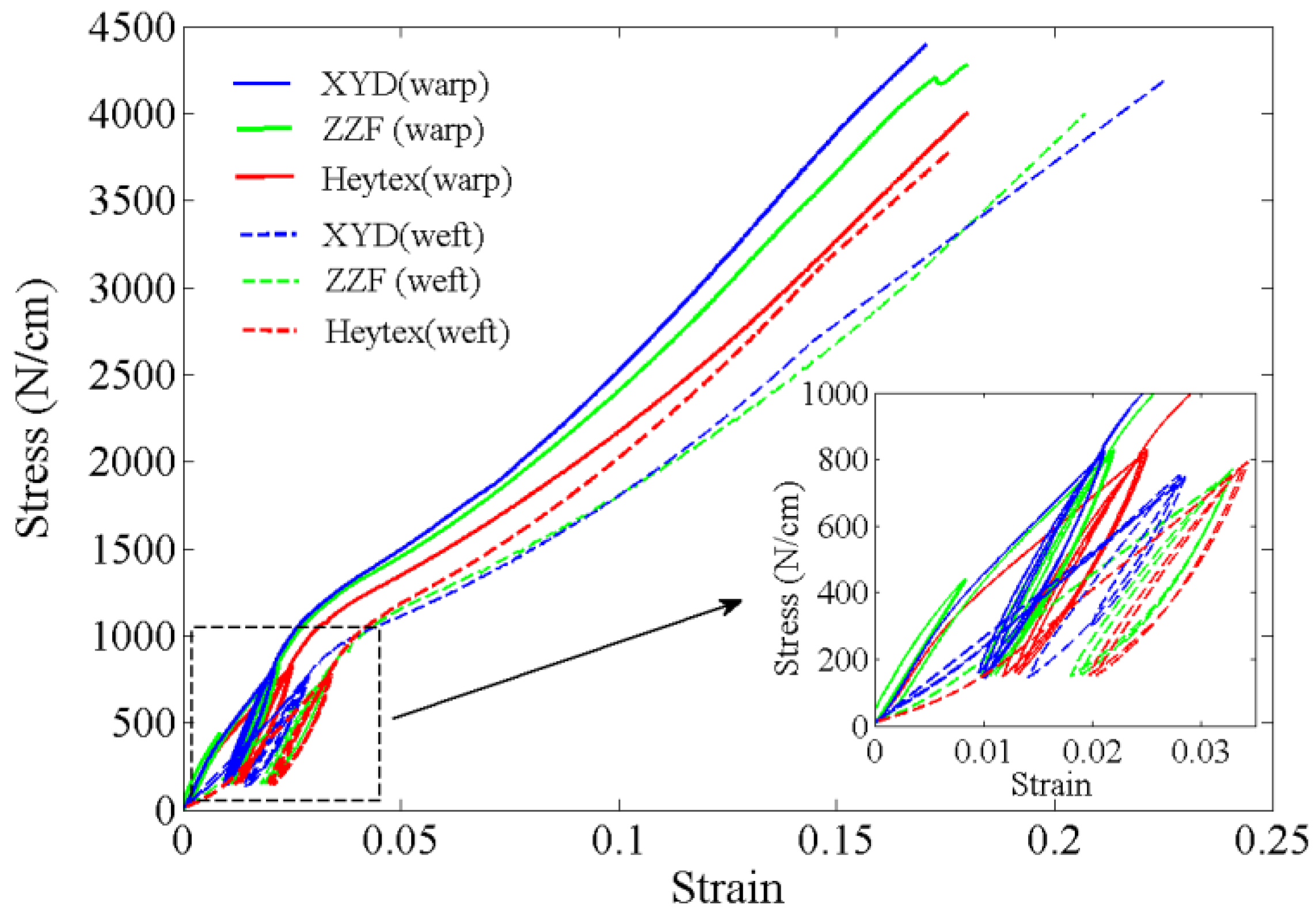
3.2.1. Experimental Samples
3.2.2. Load Program
3.2.3. Measurement Parameters
4. Validation of Theoretical Model
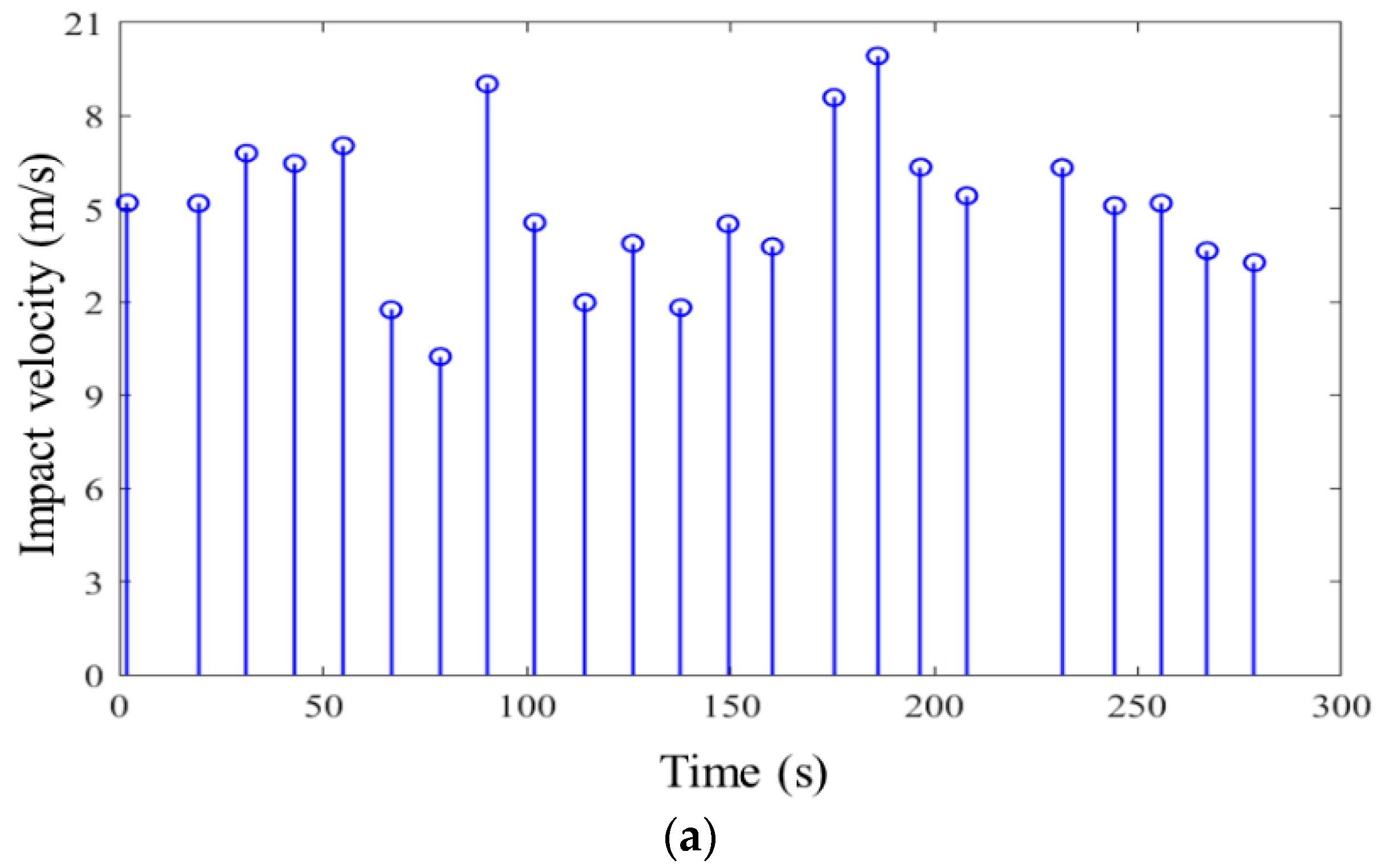
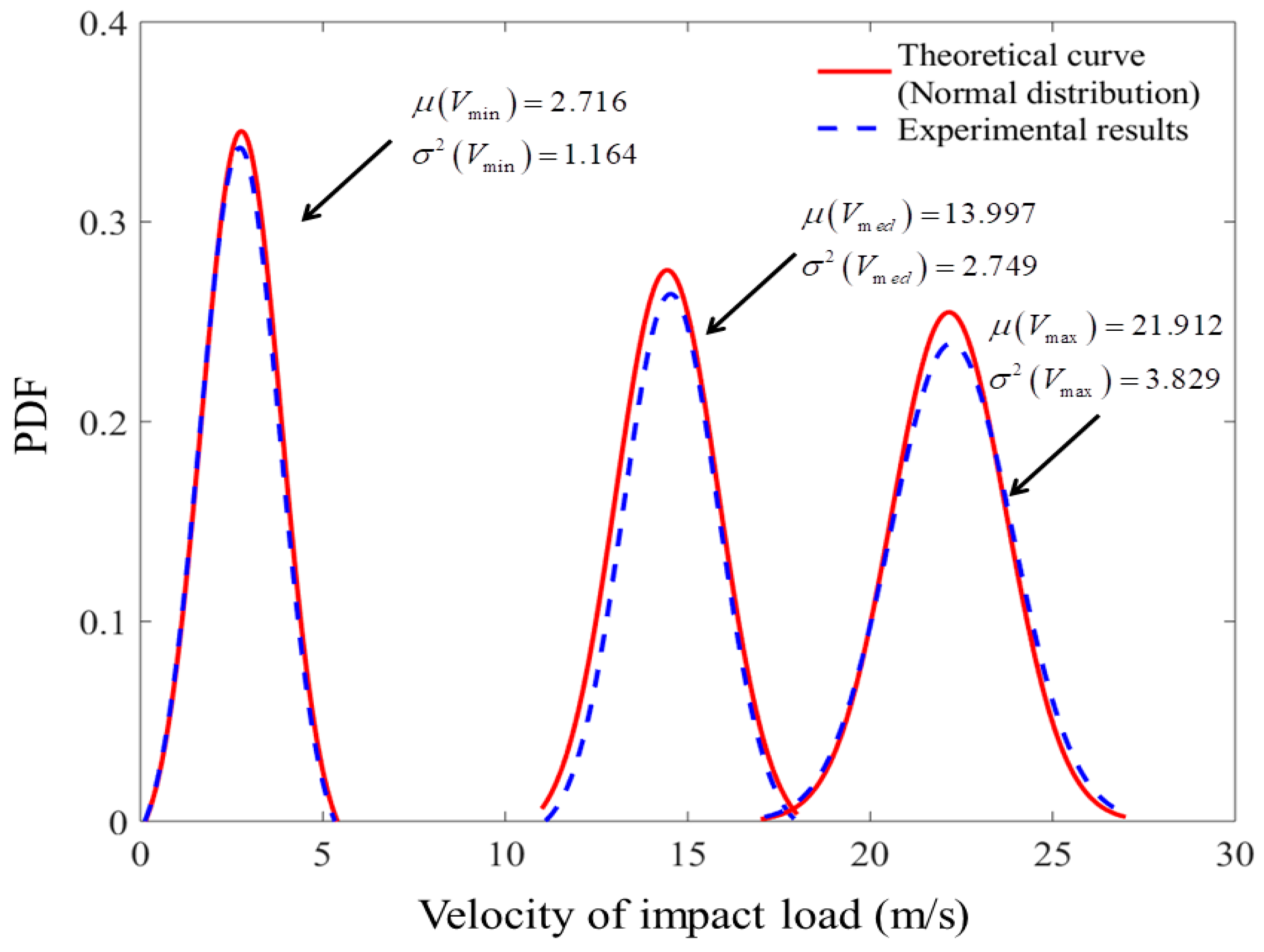
4.1. Impact Load
4.2. Stochastic Vibration Characteristic
5. Results and Discussions
5.1. Effect of Pretension Force
5.1.1. Effect of Pretension Force on Mean Value of Displacement
5.1.2. Effect of Pretension Force on Variance Value of Displacement
5.2. Effect of Velocity of Impact Load
5.2.1. Effect of Velocity of Impact Load on Mean Value of Displacement
5.2.2. Effect of Velocity of Impact Load on Variance Value of Displacement
5.3. Effect of Membrane Material
5.3.1. Effect of Membrane Material on Mean Value of Displacement
5.3.2. Effect of Membrane Material on Variance Value of Displacement
6. Conclusions
- The theoretical model proposed can predict the stochastic dynamic characteristics of the membrane accurately subjected to random impact load;
- When the strong stochastic vibration with obvious nonlinearity occurs, membrane will function as the nonlinear filter system, with the PDF results of dynamic response prone to approximate the Rayleigh Distribution. However, when the stochastic vibration proves weak, membrane will function as the linear filter system, with the corresponding PDF results more likely to follow the Gaussian distribution.
- The developed experimental system and program paves a way to study the stochastic vibration problem of membrane subjected to random impact load;
- The mean and variance value declines nonlinearly with pretension force and elastic modulus increasing. However, it will rise with velocity of impact load increasing. Furthermore, pretension force affects stochastic vibration results most dominantly among different variables.
Author Contributions
Funding
Conflicts of Interest
References
- Li, X.; Sun, J.Y.; Dong, J.; He, X.T. One-dimensional and two-dimensional analytical solutions for functionally graded beams with different moduli in tension and compression. Materials 2018, 11, 830. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.D.; Nguyen, P.D. The dynamic response and vibration of functionally graded carbon nanotube-reinforced composite truncated conical shells resting on elastic foundations. Materials 2017, 10, 1194. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.C.; Lourenco, P.B.; Milani, G. Rigid block and spring homogenized model (HRBSM) for masonry subjected to impact and blast loading. Int. J. Impact Eng. 2017, 109, 14–28. [Google Scholar] [CrossRef]
- Wang, C.G.; Liu, Y.P.; Lan, L.; Tan, H.F. Free transverse vibration of a wrinkled annular thin film by using finite difference method. J. Sound Vib. 2016, 363, 272–284. [Google Scholar] [CrossRef]
- York, A.R.; Sulsky, D.; Schreyer, H.L. The material point method for simulation thin membranes. Int. J. Numer. Anal. Mod. 1999, 44, 1429–1456. [Google Scholar] [CrossRef]
- Phoenix, S.L.; Porwal, P.K. A new membrane model for the ballistic impact response and V50 performance of multi-ply fibrous systems. Int. J. Solids Struct. 2003, 40, 6723–6765. [Google Scholar] [CrossRef]
- Malla, R.B.; Gionet, T.G. Dynamic response of a pressurized frame-membrane lunar with regolith cover subjected to impact load. J. Aerosp. Eng. 2013, 26, 855–873. [Google Scholar] [CrossRef]
- Mostofi, T.M.; Babaei, H.; Alitavoli, M. Theoretical analysis on the effect of uniform and localized impulsive loading on the dynamic plastic behavior of fully clamped thin quadrangular plates. Thin-Wall. Struct. 2016, 109, 367–376. [Google Scholar] [CrossRef]
- Seide, P. Large deflections of rectangular membranes under uniform pressure. Int. J. Nonlinear Mech. 1977, 12, 397–406. [Google Scholar] [CrossRef]
- Steinmann, R.; Friemann, H.; Prescher, C.; Schellin, R. Mechanical behavior of micromachined sensor membranes under uniform external pressure affected by in-plane stresses using a Ritz method and Hermite polynomials. Sens. Actuators A Phys. 1995, 48, 37–46. [Google Scholar] [CrossRef]
- Liu, C.J.; Zheng, Z.L.; Yang, X.Y. Analytical and numerical studies on the nonlinear dynamic response of orthotropic membranes under impact load. Earthq. Eng. Eng. Vib. 2016, 15, 657–672. [Google Scholar] [CrossRef]
- Zheng, Z.L.; Lu, F.M.; He, X.T.; Sun, J.Y.; Xie, C.X.; He, C. Large displacement analysis of rectangular orthotropic membranes under stochastic impact load. Int. J. Struct. Stab. Dyn. 2016, 16, 928–936. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.L.; Tian, Y.; Sun, J.Y.; He, X.T.; Lu, Y. Stochastic nonlinear vibration and reliability of orthotropic membrane structure under impact load. Thin-Wall. Struct. 2017, 119, 247–255. [Google Scholar] [CrossRef]
- Guo, J.L.; Cai, J.; Chen, W.S. Inertial effect on RC beam subjected to impact load. Int. J. Struct. Stab. Dyn. 2017, 17, 1750053. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Hoo Fatt, M.S. Damage assessment of cylinders due to impact and explosive loading. Int. J. Impact Eng. 1993, 13, 215–241. [Google Scholar] [CrossRef]
- Balkan, D.; Mecitoglu, Z. Nonlinear dynamic behavior of viscoelastic sandwich composite plates under non-uniform blast load: Theory and experiment. Int. J. Impact Eng. 2014, 72, 85–104. [Google Scholar] [CrossRef]
- Aksoylar, C.; Omercikoglu, A.; Mecitoglu, Z.; Omurtag, M.H. Nonlinear transient analysis of FGM and FML plates under blast loads by experimental and mixed FE methods. Compos. Struct. 2012, 94, 731–744. [Google Scholar] [CrossRef]
- Moller, O.; Foschi, R.O.; Rubinstein, M.; Quiroz, L. Seismic structural reliability using different nonlinear dynamic response surface approximations. Struct. Saf. 2009, 31, 432–442. [Google Scholar] [CrossRef]
- Ma, L.; Chen, J.K.; Tang, W.; Yin, Z.P. Vibration-based estimation of tension for an axially travelling web in roll-to roll manufacturing. Meas. Sci. Technol. 2018, 29, 015102:1–015102:8. [Google Scholar] [CrossRef]
- Eduard, V.; Theodor, K. Thin Plates and Shells; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Eisley, J.G. Nonlinear vibration of beams and rectangular plates. Zeitschrift für angewandte Mathematik und Physik 1964, 15, 167–175. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.L.; Todd, M.D. Nonlinear vibration of orthotropic rectangular membrane structures including modal coupling. J. Appl. Mech. 2018, 85, 061004:1–061004:9. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Chakraborty, S. Stochastic dynamic sensitivity of uncertain structures subjected to random earthquake loading. J. Sound Vib. 2002, 249, 543–556. [Google Scholar] [CrossRef]
- Er, G.K. Methodology for the solutions of some reduced Fokker–Planck equations in high dimensions. Ann. Phys. 2011, 523, 247–258. [Google Scholar] [CrossRef]
- Ma, J.; Gao, W.; Wriggers, P.; Chen, J.J.; Sahraee, S. Structural dynamic optimal design based on dynamic reliability. Eng. Struct. 2011, 33, 468–476. [Google Scholar] [CrossRef]
- Levinson, S.E.; Rabiner, L.R.; Sondhi, M.M. An introduction to the application of the theory of probabilistic functions of a Markov process to automatic speech recognition. Bell Labs Tech. J. 1983, 62, 1035–1074. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.L.; Liu, C.Y.; Zhang, G.X.; Lian, Y.S.; Tian, Y.; Xiao, Y.; Xie, X.M. Dynamic response of rectangular prestressed membrane subjected to uniform impact load. Arch. Civ. Mech. Eng. 2017, 17, 586–598. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Zhang, Q.L.; Lei, K.; Kuai, B.L. Experimental analysis of tensile behaviors of polytetrafluoroethylene-coated fabrics subjected to monotonous and cyclic loading. Text. Res. J. 2014, 84, 231–245. [Google Scholar]
- Hurtado, J.E.; Barbat, A.H. Monte Carlo techniques in computational stochastic mechanics. Arch. Comput. Methods Eng. 1998, 5, 3–30. [Google Scholar] [CrossRef]
- Tanimura, S. Comparison of rate-dependent constitutive models with experimental data. Int. J. Impact Eng. 2014, 69, 104–113. [Google Scholar] [CrossRef]


















| Blower Type | Power (W) | Flow (m3/h) | Pressure (Pa) | Rotational Speed (r/s) |
|---|---|---|---|---|
| CZR-CZT | 1100 | 1140 | 1080 | 2800/60 |
| Y90L-2 | 2200 | 1191 | 2562 | 2840/60 |
| Y100L-2 | 3000 | 1704 | 3253 | 2880/60 |
| Type | Density (kg/m²) | Thickness (mm) | Poisson Ratio (Warp/Weft) | Elastic Modulus (Warp/Weft) (MPa) | Tensile Strength (Warp/Weft) (N/cm) |
|---|---|---|---|---|---|
| Hextex | 0.95 | 0.8 | 0.3/0.4 | 1520/1290 | 4000/3800/5 |
| ZZF | 0.95 | 0.8 | 0.3/0.4 | 1590/1360 | 4300/4000/5 |
| XYD | 0.95 | 0.8 | 0.3/0.4 | 1720/1490 | 4400/4200/5 |
| Wind Type | Mean Value | Variance Value | ||||
|---|---|---|---|---|---|---|
| Theory (m/s) | Experiment (m/s) | Error (%) | Theory (m2/s2) | Experiment (m2/s2) | Error (%) | |
| Minimum wind | 2.716 | 2.652 | 2.41 | 1.164 | 1.142 | 1.93 |
| Medium wind | 13.997 | 14.187 | −1.34 | 2.749 | 2.628 | 4.60 |
| Maximal wind | 21.912 | 22.017 | −0.48 | 3.829 | 3.874 | −1.16 |
| Position | Theory (mm) | Experiment (mm) | Error (%) |
|---|---|---|---|
| Point O | 3.035 | 2.983 | 1.743 |
| Point A1 | 1.994 | 1.982 | 0.605 |
| Point A2 | 2.457 | 2.408 | 2.035 |
| Point B1 | 1.248 | 1.224 | 1.961 |
| Point B2 | 1.368 | 1.342 | 1.937 |
| Point C | 1.952 | 1.974 | 1.114 |
| Position | Theory (mm2) | Experiment (mm2) | Error (%) |
|---|---|---|---|
| Point O | 0.033 | 0.031 | 6.452 |
| Point A1 | 0.031 | 0.029 | 5.969 |
| Point A2 | 0.032 | 0.030 | 5.864 |
| Point B1 | 0.018 | 0.017 | 3.053 |
| Point B2 | 0.024 | 0.023 | 4.013 |
| Point C | 0.030 | 0.028 | 6.078 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zheng, Z.-L.; Yang, R.; Zhang, P. Analytical Solutions for Stochastic Vibration of Orthotropic Membrane under Random Impact Load. Materials 2018, 11, 1231. https://doi.org/10.3390/ma11071231
Li D, Zheng Z-L, Yang R, Zhang P. Analytical Solutions for Stochastic Vibration of Orthotropic Membrane under Random Impact Load. Materials. 2018; 11(7):1231. https://doi.org/10.3390/ma11071231
Chicago/Turabian StyleLi, Dong, Zhou-Lian Zheng, Rui Yang, and Peng Zhang. 2018. "Analytical Solutions for Stochastic Vibration of Orthotropic Membrane under Random Impact Load" Materials 11, no. 7: 1231. https://doi.org/10.3390/ma11071231
APA StyleLi, D., Zheng, Z.-L., Yang, R., & Zhang, P. (2018). Analytical Solutions for Stochastic Vibration of Orthotropic Membrane under Random Impact Load. Materials, 11(7), 1231. https://doi.org/10.3390/ma11071231





