Experimental Parametric Relationships for Chip Geometry in Dry Machining of the Ti6Al4V Alloy
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
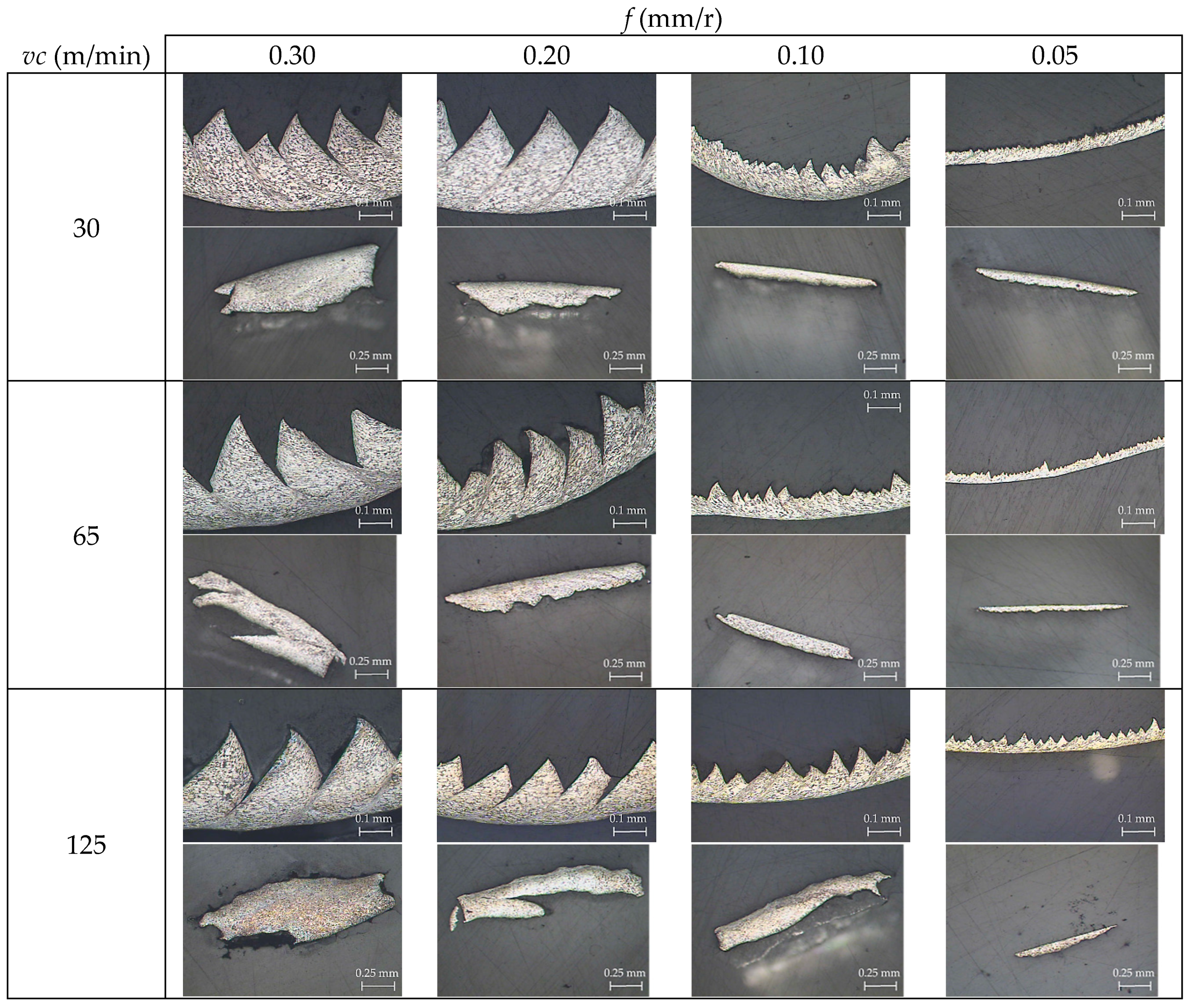
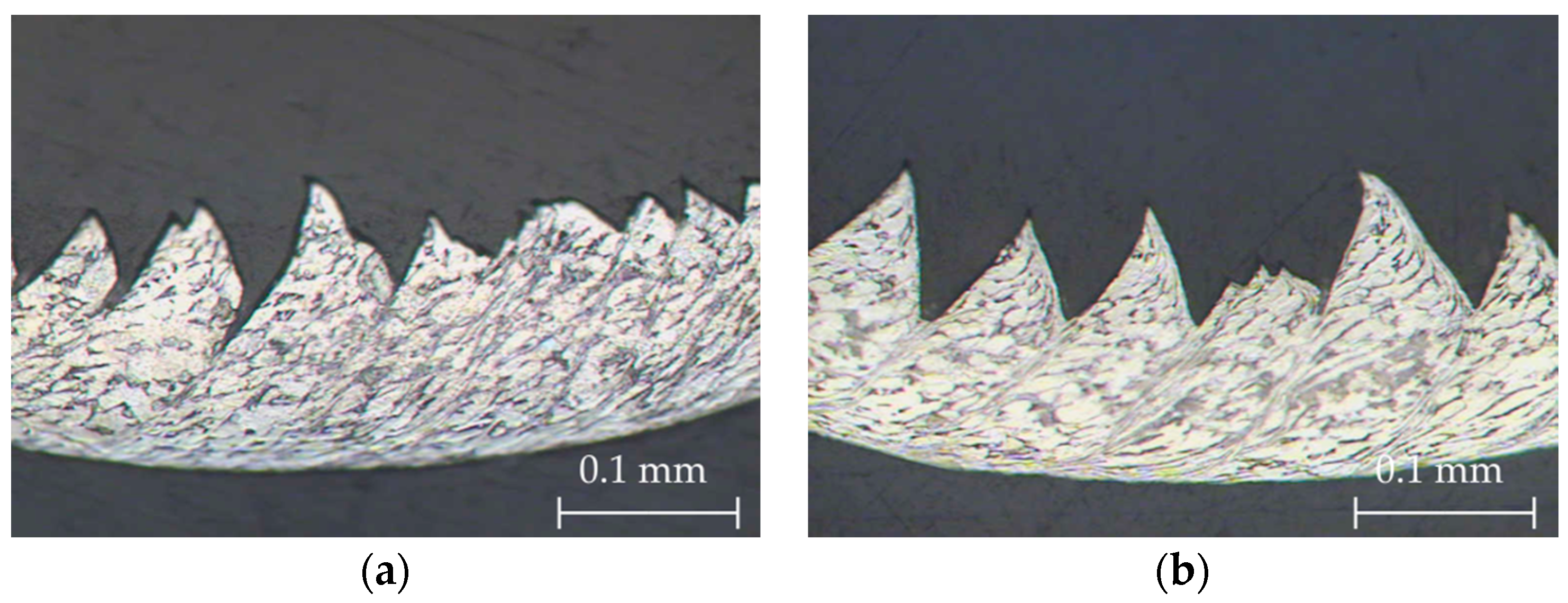
3.1. Chip Morphology and Microstructure
3.2. Geometric Parameters
3.3. Parametric Relantioships
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ezugwu, E.; Bonney, J.; Yamane, Y. An overview of the machinability of aeroengine alloys. J. Mater. Process. Technol. 2003, 134, 233–253. [Google Scholar] [CrossRef]
- Niknam, S.A.; Khettabi, R.; Songmene, V. Machinability and Machining of Titanium Alloys: A Review. In Machining of Titanium Alloys; Springer: Berlin, Germany, 2014; Chapter 1; pp. 1–30. ISBN 978-3-662-43901-2. [Google Scholar]
- Veiga, C.; Davim, J.P.; Loureiro, A.J.R. Review on machinability of titanium alloys: The process perspective. Rev. Adv. Mater. Sci. 2013, 34, 148–164. [Google Scholar]
- Arrazola, P.-J.; Garay, A.; Iriarte, L.-M.; Armendia, M.; Marya, S.; Le Maître, F. Machinability of titanium alloys (Ti6Al4V and Ti555.3). J. Mater. Process. Technol. 2009, 209, 2223–2230. [Google Scholar] [CrossRef]
- López de lacalle, L.; Pérez, J.; Llorente, J.; Sánchez, J. Advanced cutting conditions for the milling of aeronautical alloys. J. Mater. Process. Technol. 2000, 100, 1–11. [Google Scholar] [CrossRef]
- Boyer, R.R.; Briggs, R.D. The use of β titanium alloys in the aerospace industry. J. Mater. Eng. Perform. 2013, 22, 2916–2920. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Zhang, H.; Yang, J.; Nia, A.B.; Chai, G.B. Mechanical behaviors of Ti/CFRP/Ti laminates with different surface treatments of titanium sheets. Compos. Struct. 2017, 163, 21–31. [Google Scholar] [CrossRef]
- Calamaz, M.; Coupard, D.; Girot, F. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2009, 48, 275–288. [Google Scholar] [CrossRef]
- Nouari, M.; Makich, H. Analysis of Physical Cutting Mechanisms and Their Effects on the Tool Wear and Chip Formation Process When Machining Aeronautical Titanium Alloys: Ti-6Al-4V and Ti-55531. In Machining of Titanium Alloys; Springer: Berlin, Germany, 2014; pp. 79–111. ISBN 978-3-662-43901-2. [Google Scholar]
- Nouari, M.; Makich, H. On the Physics of Machining Titanium Alloys: Interactions between Cutting Parameters, Microstructure and Tool Wear. Metals 2014, 4, 335–358. [Google Scholar] [CrossRef]
- Cotterell, M.; Byrne, G. Dynamics of chip formation during orthogonal cutting of titanium alloy Ti-6Al-4V. CIRP Ann. Manuf. Technol. 2008, 57, 93–96. [Google Scholar] [CrossRef]
- Pramanik, A. Problems and solutions in machining of titanium alloys. Int. J. Adv. Manuf. Technol. 2014, 70, 919–928. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.-B. On thermoplastic shear instability in the machining of a titanium alloy (Ti-6Al-4V). Metall. Mater. Trans. A 2002, 33, 2995–3010. [Google Scholar] [CrossRef]
- Wan, Z.P.; Zhu, Y.E.; Liu, H.W.; Tang, Y. Microstructure evolution of adiabatic shear bands and mechanisms of saw-tooth chip formation in machining Ti6Al4V. Mater. Sci. Eng. A 2012, 531, 155–163. [Google Scholar] [CrossRef]
- Sima, M.; Özel, T. Modified material constitutive models for serrated chip formation simulations and experimental validation in machining of titanium alloy Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2010, 50, 943–960. [Google Scholar] [CrossRef]
- Shokrani, A.; Dhokia, V.; Newman, S.T. Environmentally conscious machining of difficult-to-machine materials with regard to cutting fluids. Int. J. Mach. Tools Manuf. 2012, 57, 83–101. [Google Scholar] [CrossRef]
- Kelly, J.F.; Cotterell, M.G. Minimal lubrication machining of aluminium alloys. J. Mater. Process. Technol. 2002, 120, 327–334. [Google Scholar] [CrossRef]
- Yoshimura, H.; Toda, Y.; Moriwaki, T.; Shibasaka, T.; Okida, J. Study on near dry cutting of aluminum alloys. Mach. Sci. Technol. 2006, 10, 289–299. [Google Scholar] [CrossRef]
- Vinayagamoorthy, R.; Xavior, M.A. Dry machining of Ti-6Al-4V using PVD coated tools. Int. J. Appl. Eng. Res. 2013, 8, 1373–1381. [Google Scholar]
- Salguero, J.; Gerez, J.; Batista, M.; Garófano, J.E.; Marcos Bárcena, M. A Study of Macrogeometrical Deviations in the Dry Turning of UNS R56400 Ti Alloy. Appl. Mech. Mater. 2012, 152–154, 613–617. [Google Scholar] [CrossRef]
- Ginting, A.; Nouari, M. Surface integrity of dry machined titanium alloys. Int. J. Mach. Tools Manuf. 2009, 49, 325–332. [Google Scholar] [CrossRef]
- Trujillo, F.J.; Sevilla, L.; Marcos, M. Experimental Parametric Model for Indirect Adhesion Wear Measurement in the Dry Turning of UNS A97075 (Al-Zn) Alloy. Materials 2017, 10, 152. [Google Scholar] [CrossRef] [PubMed]
- Hua, J.; Shivpuri, R. Prediction of chip morphology and segmentation during the machining of titanium alloys. J. Mater. Process. Technol. 2004, 150, 124–133. [Google Scholar] [CrossRef]
- Molinari, A.; Soldani, X.; Miguélez, M.H. Adiabatic shear banding and scaling laws in chip formation with application to cutting of Ti–6Al–4V. J. Mech. Phys. Solids 2013, 61, 2331–2359. [Google Scholar] [CrossRef]
- Liang, J.; Bi, S.S. Experimental Studies for Burrs in Dry Drilling of Stacked Metal Materials. Adv. Mater. Res. 2010, 129–131, 959–963. [Google Scholar] [CrossRef]
- Yang, X.; Richard Liu, C. Machining Titanium and its Alloys. Mach. Sci. Technol. 1999, 3, 107–139. [Google Scholar] [CrossRef]
- Calamaz, M.; Coupard, D.; Girot, F. Numerical simulation of titanium alloy dry machining with a strain softening constitutive law. Mach. Sci. Technol. 2010, 14, 244–257. [Google Scholar] [CrossRef]
- Yameogo, D.; Haddag, B.; Makich, H.; Nouari, M. Prediction of the Cutting Forces and Chip Morphology When Machining the Ti6Al4V Alloy Using a Microstructural Coupled Model. Procedia CIRP 2017, 58, 335–340. [Google Scholar] [CrossRef]
- Vyas, A.; Shaw, M.C. Mechanics of saw-tooth chip formation in metal cutting. J. Manuf. Sci. Eng. 1999, 121, 163–172. [Google Scholar] [CrossRef]
- Barry, J.; Byrne, G.; Lennon, D. Observations on chip formation and acoustic emission in machining Ti-6Al-4V alloy. Int. J. Mach. Tools Manuf. 2001, 41, 1055–1070. [Google Scholar] [CrossRef]
- Komanduri, R.; Von Turkovich, B.F. New observations on the mechanism of chip formation when machining titanium alloys. Wear 1981, 69, 179–188. [Google Scholar] [CrossRef]
- Obikawa, T.; Usui, E. Computational machining of titanium alloy—Finite element modeling and a few results. J. Manuf. Sci. Eng. Trans. ASME 1996, 118, 208–215. [Google Scholar] [CrossRef]
- Bai, W.; Sun, R.; Roy, A.; Silberschmidt, V.V. Improved analytical prediction of chip formation in orthogonal cutting of titanium alloy Ti6Al4V. Int. J. Mech. Sci. 2017, 133, 357–367. [Google Scholar] [CrossRef]
- Joshi, S. Dimensional inequalities in chip segments of titanium alloys. Eng. Sci. Technol. Int. J. 2018, 21, 238–244. [Google Scholar] [CrossRef]
- Turley, D.M.; Doyle, E.D.; Ramalingam, S. Calculation of shear strains in chip formation in titanium. Mater. Sci. Eng. 1982, 55, 45–48. [Google Scholar] [CrossRef]
- Sutter, G.; List, G. Very high speed cutting of Ti-6Al-4V titanium alloy—Change in morphology and mechanism of chip formation. Int. J. Mach. Tools Manuf. 2013, 66, 37–43. [Google Scholar] [CrossRef]
- Joshi, S.; Tewari, A.; Joshi, S.S. Microstructural Characterization of Chip Segmentation under Different Machining Environments in Orthogonal Machining of Ti6Al4V. J. Eng. Mater. Technol. 2015, 137, 011055. [Google Scholar] [CrossRef]
- Baker, M.; Rosler, J.; Siemers, C. Finite Element Simulation of Segmented Chip Formation of Ti6Al4V. J. Manuf. Sci. Eng. 2002, 124, 485–488. [Google Scholar] [CrossRef]
- Zhang, Y.; Outeiro, J.C.; Mabrouki, T. On the selection of Johnson-Cook constitutive model parameters for Ti-6Al-4V using three types of numerical models of orthogonal cutting. Procedia CIRP 2015, 31, 112–117. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z. Shear localization sensitivity analysis for Johnson-Cook constitutive parameters on serrated chips in high speed machining of Ti6Al4V. Simul. Model. Pract. Theory 2015, 55, 63–76. [Google Scholar] [CrossRef]
- Ducobu, F.; Rivière-Lorphèvre, E.; Filippi, E. Material constitutive model and chip separation criterion influence on the modeling of Ti6Al4V machining with experimental validation in strictly orthogonal cutting condition. Int. J. Mech. Sci. 2016, 107, 136–149. [Google Scholar] [CrossRef]
- Batista, M.; Calamaz, M.; Girot, F.; Salguero, J.; Marcos, M. Using image analysis techniques for single evaluation of the chip shrinkage factor in orthogonal cutting process. Key Eng. Mater. 2012, 504–506, 1329–1334. [Google Scholar] [CrossRef]
- Dye, D.; Hu, F.; Jones, N.G. Microstructure Formation in Alpha-Beta Titanium Alloys. In Titanium; Springer: Berlin, Germany, 2011. [Google Scholar]
- Lütjering, G.; Williams, J.C. Alpha + Beta Alloys. In Titanium; Springer: Berlin, Germany, 2007; ISBN 978-3-540-73036-1. [Google Scholar]
- Molinari, A.; Musquar, C.; Sutter, G. Adiabatic shear banding in high speed machining of Ti-6Al-4V: Experiments and modeling. Int. J. Plast. 2002, 18, 443–459. [Google Scholar] [CrossRef]
- Grzesik, W. Advanced Machining Processes of Metallic Materials: Theory, Modelling and Applications; Elsevier: New York, NY, USA, 2008; ISBN 9780444637208. [Google Scholar]















| Alloy | C | Fe | N | O | Al | V | Ti |
|---|---|---|---|---|---|---|---|
| Part | 0.08 | 0.164 | 0.05 | 0.05 | 5.47 | 4.09 | Balance |
| Feed Rate, f (mm/r) | Cutting Speed, vc (m/min) | Cutting Depth, ap (mm) |
|---|---|---|
| 0.05 | 30 65 125 | 1 |
| 0.10 | ||
| 0.20 | ||
| 0.30 |
| Geometric Parameter (GP) | K | x | y | R2 |
|---|---|---|---|---|
| Height of peak (hp) | 1.38 | 0.02 | 1.01 | 0.98 |
| Height of valley (hv) | 1.20 | −0.05 | 0.98 | 0.97 |
| Chip thickness (tc) | 1.29 | −0.01 | 0.99 | 0.98 |
| Segment ratio (Gs) | 0.15 | 0.24 | 0.17 | 0.52 |
| Segment width (S) | 0.87 | −0.10 | 1.16 | 0.94 |
| Transverse area (A) | 0.94 | 0.02 | 0.95 | 0.92 |
| Shear angle (θ) | 28.43 | 0.06 | −0.03 | 0.67 |
| Shrinkage factor (ζ) | 0.77 | 0.15 | 0.02 | 0.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez Hernández, Y.; Trujillo Vilches, F.J.; Bermudo Gamboa, C.; Sevilla Hurtado, L. Experimental Parametric Relationships for Chip Geometry in Dry Machining of the Ti6Al4V Alloy. Materials 2018, 11, 1260. https://doi.org/10.3390/ma11071260
Sánchez Hernández Y, Trujillo Vilches FJ, Bermudo Gamboa C, Sevilla Hurtado L. Experimental Parametric Relationships for Chip Geometry in Dry Machining of the Ti6Al4V Alloy. Materials. 2018; 11(7):1260. https://doi.org/10.3390/ma11071260
Chicago/Turabian StyleSánchez Hernández, Yezika, Francisco Javier Trujillo Vilches, Carolina Bermudo Gamboa, and Lorenzo Sevilla Hurtado. 2018. "Experimental Parametric Relationships for Chip Geometry in Dry Machining of the Ti6Al4V Alloy" Materials 11, no. 7: 1260. https://doi.org/10.3390/ma11071260
APA StyleSánchez Hernández, Y., Trujillo Vilches, F. J., Bermudo Gamboa, C., & Sevilla Hurtado, L. (2018). Experimental Parametric Relationships for Chip Geometry in Dry Machining of the Ti6Al4V Alloy. Materials, 11(7), 1260. https://doi.org/10.3390/ma11071260







