Fatigue Crack Growth Behavior of the MIG Welded Joint of 06Cr19Ni10 Stainless Steel
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Specimen Preparation
2.2. The Fatigue Testing and Microstructure Observation
2.3. Simulation and Measurement of Welding Residual Stresses
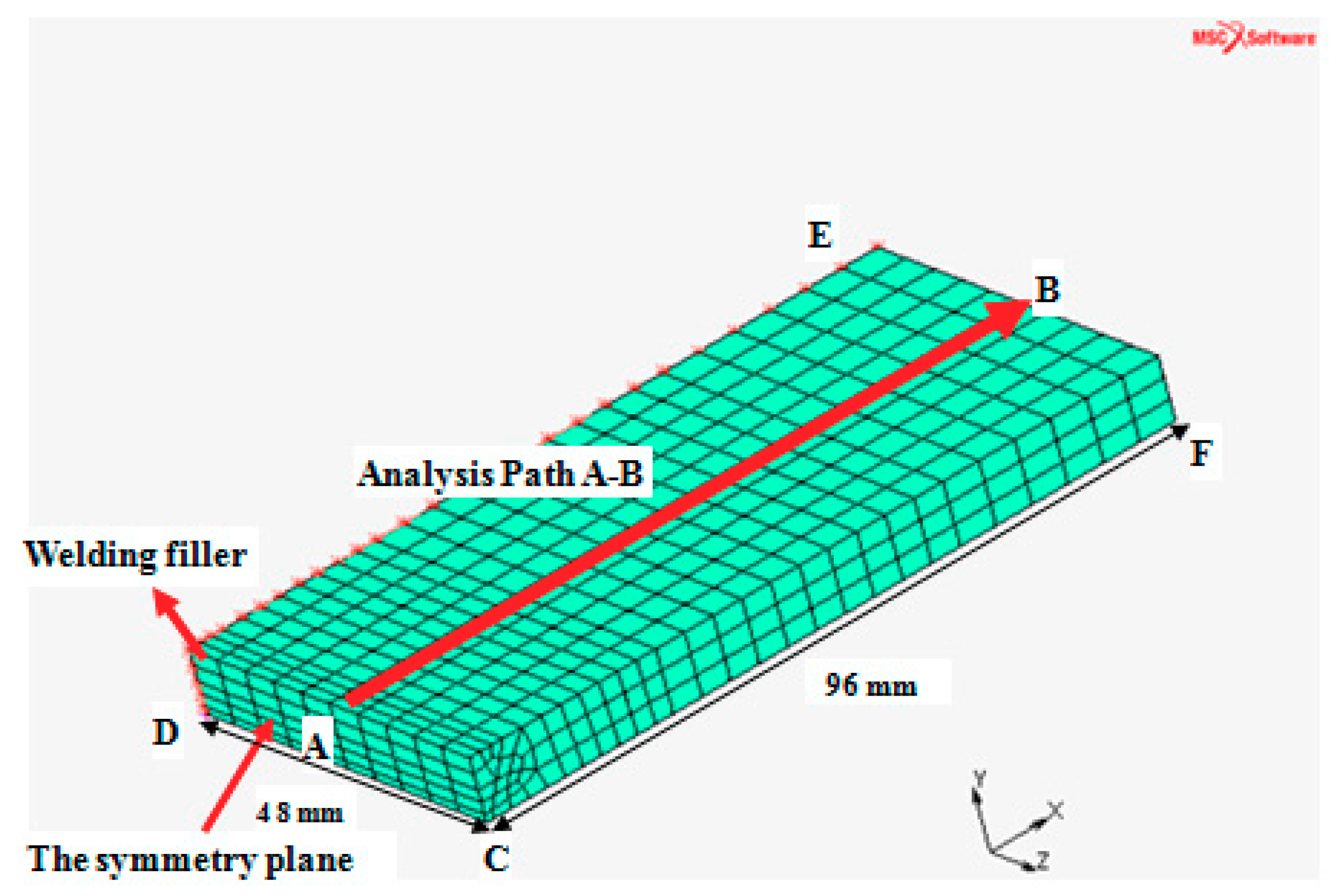
Residual Stress Simulation
3. Results and Discussions
3.1. FCG Paths
3.2. FCG Rate
3.3. Metallographic Microstructure
3.3.1. Metallographic Microstructure of the BM
3.3.2. Metallographic Microstructure of the Intermediate Zone
3.3.3. Metallographic Microstructure of the HAZ
3.4. Fracture Morphologies of the BM, the HAZ and the WM
3.4.1. FCG Region
3.4.2. Ultimate Fracture Region
3.5. Residual Stresses of the Welded Joint
4. Conclusions
- In the BM, HAZ and WM specimens, the original mixed-mode cracks changed into the mode I propagating crack. The specimen’s type and the crack location had a negligible effect on the FCG path in the weld joints.
- FCG test results indicated that the WM specimen had the largest FCG rate, followed by the HAZ specimen. The BM specimen had the lowest FCG rate.
- Metallographic analysis showed that the size and morphology of metallographic microstructures in the WM, the HAZ and the BM were significantly different, which could partially explain the reason for difference in FCG rates for the BM, HAZ and WM specimens.
- According to the fracture morphology, in the FCG area, the WM specimen had the largest striation spacing, followed by the HAZ specimen, and the BM had the lowest striation spacing. In the ultimate fracture area, depth of the dimple in the WM was shallower than that in the BM and the HAZ, implying larger plasticity of the material.
- The FE simulation and the XRD experiments showed that the high values of tensile residual stresses were found in the WM and the HAZ, which could be accounted for higher FCG rates of the WM and HAZ.
- The differences in fatigue crack growth behavior of the BM, WM, HAZ had been assumed to stem from the combination of microstructure difference and tensile residual stresses. However, the tensile residual stresses were considered to induce a more significant impact on the FCG rates of the welded joint.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | crack length (mm) |
| C | Paris material constant |
| BM | base metal |
| da/dN | crack growth rate (mm/cycle) |
| crystallographic d-spacing under stress-free condition (μm) | |
| dψ | crystallographic d-spacing under stress condition (μm) |
| E | the Young’s modulus (GPa) |
| FCG | fatigue crack growth |
| FEA | finite element analysis |
| h | crystal face exponent |
| HAZ | heat affected zone |
| k | crystal face exponent |
| l | crystal face exponent |
| m | Paris exponent |
| R | stress ratio |
| U | welding voltage (V) |
| υ | Poisson’s ratio |
| I | welding current (A) |
| XRD | X-Ray Diffraction |
| β | inclined angle of pre-crack (°) |
| σxx | transverse residual stress (MPa) |
| σeff | effective stress (MPa) |
| σys | yield strength (MPa) |
| σres | residual stress (MPa) σxx |
| the incident angle (°) | |
| ΔK | stress intensity factor (SIF) range |
| ΔKI | stress intensity factor range of mode I |
References
- Arora, P.; Singh, P.K.; Bhasin, V.; Rama Rao, A. Effect of dissolved oxygen and temperature on fatigue crack growth rate behaviour of SA312 Type 304L(N) material in water environment. Int. J. Fatigue 2017, 95, 204–215. [Google Scholar] [CrossRef]
- Wang, X.N.; Zhang, S.H.; Zhou, J.; Zhang, M.; Chen, C.J.; Misra, R.D.K. Effect of heat input on microstructure and properties of hybrid fiber laser-arc weld joints of the 800 MPa hot-rolled Nb-Ti-Mo microalloyed steels. Opt. Laser Eng. 2017, 91, 86–96. [Google Scholar] [CrossRef]
- Harati, E.; Karlsson, L.; Svensson, L.E. Neutron Diffraction Evaluation of Near Surface Residual Stresses at Welds in 1300 MPa Yield Strength Steel. Materials 2017, 10, 593. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Liu, X.; Berto, F. Low-Cycle Fatigue Behavior of 10CrNi3MoV High Strength Steel and Its Undermatched Welds. Materials 2018, 11, 661. [Google Scholar] [CrossRef] [PubMed]
- Yousefieh, M.; Shamanian, M.; Saatchi, A. Optimization of the pulsed current gas tungsten arc welding (PCGTAW) parameters for corrosion resistance of super duplex stainless steel (UNS S32760) welds using the Taguchi method. J. Alloys Compd. 2011, 509, 782–788. [Google Scholar] [CrossRef]
- Araque, O.; Arzola, N. Weld magnification factor approach in cruciform joints considering post welding cooling medium and weld size. Materials 2018, 11, 81. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.H.; Chen, K.; Guo, X.L.; Zhang, L.F. Fracture toughness of type 316L stainless steel weld joints. Mater. Sci. Eng. A 2017, 685, 107–114. [Google Scholar] [CrossRef]
- Tang, L.Q.; Qian, C.F.; Ince, A.; Li, H.F.; Zhang, X. The effect of strain strengthening on the mixed mode crack fatigue propagation in the HAZ of 06Cr19Ni10 stainless steel. Mater. Sci. Eng. A. 2017, 698, 341–347. [Google Scholar] [CrossRef]
- Parkes, D.; Xu, W.; Westerbaan, D.; Nayak, S.S.; Goodwin, F.; Bhole, S.; Chen, D.L. Microstructure and fatigue properties of fiber laser welded dissimilar joints between high strength low alloy and dual-phase steels. Mater. Des. 2013, 51, 665–675. [Google Scholar] [CrossRef]
- Qiao, J.N.; Lu, J.X.; Wu, S.K. Fatigue cracking characteristics of fiber Laser-VPTIG hybrid butt welded 7N01P-T4 aluminum alloy. Int. J. Fatigue 2017, 98, 32–40. [Google Scholar] [CrossRef]
- Tagawa, T.; Tahara, K.; Abe, E. Fatigue properties of cast aluminium joints by FSW and MIG welding. Weld. Int. 2014, 28, 21–29. [Google Scholar] [CrossRef]
- Basak, S.; Pal, T.K.; Shome, M. High-cycle fatigue behavior of MIG brazed galvanized DP600 steel sheet joint—Effect of process parameters. Int. J. Adv. Manuf. Technol. 2016, 82, 1197–1211. [Google Scholar] [CrossRef]
- Gaur, V.; Enoki, M.; Okada, T. A study on fatigue behavior of MIG-welded Al-Mg alloy with different filler-wire materials under mean stress. Int. J. Fatigue 2018, 107, 119–129. [Google Scholar] [CrossRef]
- Campanelli, S.L.; Casalino, G.; Casavola, C. Analysis and Comparison of Friction Stir Welding and Laser Assisted Friction Stir Welding of Aluminum Alloy. Materials 2013, 6, 5923–5941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, K.S. Roles of microstructure in fatigue crack initiation. Int. J. Fatigue 2010, 32, 1428–1447. [Google Scholar] [CrossRef]
- Cao, J.; Gong, Y.; Zhu, K.; Yang, Z.G.; Luo, X.M.; Gu, F.M. Microstructure and mechanical properties of dissimilar materials joints between T92 martensitic and S304H austenitic steels. Mater. Des. 2011, 32, 2763–2770. [Google Scholar] [CrossRef]
- Zerbst, U.; Mädler, K.; Hintze, H. Fracture mechanics in railway applications––An overview. Eng. Fract. Mech. 2005, 72, 163–194. [Google Scholar] [CrossRef]
- Zerbst, U.; Beretta, S. Failure and damage tolerance aspects of railway components. Eng. Fail. Anal. 2011, 18, 534–542. [Google Scholar] [CrossRef]
- Rozumek, D.; Macha, E. J-integral in the description of fatigue crack growth rate induced by different ratios of torsion to bending loading in AlCu4Mg1. Mater. Werkst. 2009, 40, 743–749. [Google Scholar] [CrossRef]
- Hobbacher, A. IIW Recommendations for fatigue design of welded joints and components, WRC Bulletin 520. In Welding Research Council; New York Google Scholar: New York, NY, USA, 2009; Volume 144, p. 3. [Google Scholar]
- Hou, C.Y. Fatigue analysis of welded joints with the aid of real three-dimensional weld toe geometry. Int. J. Fatigue 2007, 29, 772–785. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V.; Ayaso, F.J.; González, B.; Matos, J.C.; Vergara, D.; Lorenzo, M. Failure analysis of a lifting platform for tree pruning. Eng. Fail. Anal. 2010, 17, 739–747. [Google Scholar] [CrossRef]
- Jun, H.K.; Seo, J.W.; Jeon, I.S. Fracture and fatigue crack growth analyses on a weld-repaired railway rail. Eng. Fail. Anal. 2016, 59, 478–492. [Google Scholar] [CrossRef]
- Ngoula, D.T.; Beier, H.T.; Tchoffo Ngoula, D. Fatigue crack growth in cruciform welded joints, Influence of residual stresses and of the weld toe geometry. Int. J. Fatigue 2017, 101, 253–262. [Google Scholar] [CrossRef]
- Teng, T.L.; Chang, P.H. Effect of residual stresses on fatigue crack initiation life for butt-welded joints. J. Mater. Process. Technol. 2004, 145, 325–335. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Influence of transformation induced plasticity on simulated results of welding residual stress in low temperature transformation steel. Comp. Mater. Sci. 2013, 78, 55–62. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Luo, Q.; Jones, A.H. High-precision determination of residual stress of polycrystalline coatings using optimised XRD-sin2ψ technique. Surf. Coat. Technol. 2010, 205, 1403–1408. [Google Scholar] [CrossRef] [Green Version]
- Sander, M.; Richard, H.A. Experimental and numerical invesigations on the influence of the loading direction on the fatigue crack growth. Int. J. Fatigue 2006, 28, 583–591. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.B.; Recho, N.; Li, J. The mixed-mode investigation of the fatigue crack in CST metallic specimen. Int. J. Fatigue 2006, 28, 1780–1790. [Google Scholar] [CrossRef]
- Sander, M.; Richard, H.A. Fatigue crack growth under variable amplitude loading Part I: Experimental investigations. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 291–301. [Google Scholar] [CrossRef]
- Xie, X.F.; Ning, D.; Sun, J. Strain-controlled fatigue behavior of cold-drawn type 316 austenite stainless steel at room temperature. Mater. Charact. 2016, 120, 195–202. [Google Scholar] [CrossRef]
- Belattar, A.; Keller, C.; Taleb, L. Multiscale analysis of the pre-hardening effect on the cyclic behavior and fatigue life of 304L stainless steel. Mater. Sci. Eng. A 2016, 662, 468–480. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, X.; Zhou, F.; Xia, Z.; Zha, X.D.; Ma, Y.C.; Liu, K. Microstructure and mechanical properties of the welding joint of a new corrosion-resisting nickel-based alloy and 304 austenitic stainless steel. Acta Metall. Sin. 2014, 50, 1335–1342. [Google Scholar]
- Harjo, S.; Tomota, Y.; Ono, M. Measurements of thermal residual elastic strains in ferrite–austenite Fe–Cr–Ni alloys by neutron and X-ray diffractions. Acta Mater. 1998, 47, 353–362. [Google Scholar] [CrossRef]
- ElSawy, H.A. Characterization of the GTAW fusion line phases for superferritic stainless steel weldments. J. Mater. Process. Technol. 2001, 118, 127–131. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Z.; Kokawa, H.; Sato, Y.S. Reassessment of the effects of laser surface melting on IGC of SUS 304. Mater. Sci. Eng. A 2008, 474, 112–119. [Google Scholar] [CrossRef]
- Fan, X.G.; Jiang, D.M.; Zhong, L.; Wang, T.; Ren, S.Y. Influence of microstructure on the crack propagation and corrosion resistance of Al–Zn–Mg–Cu alloy 7150. Mater. Charact. 2007, 58, 24–28. [Google Scholar] [CrossRef]
- Chowdhury, P.B.; Sehitoglu, H.; Rateick, R.G.; Maier, H.J. Modeling fatigue crack growth resistance of nanocrystalline alloys. Acta Mater. 2013, 61, 2531–2547. [Google Scholar] [CrossRef]
- Hu, D.Y.; Mao, J.X.; Song, J.; Meng, F.C.; Shan, X.M.; Wang, R.Q. Experimental investigation of grain size effect on fatigue crack growth rate in turbine disc superalloy GH4169 under different temperatures. Mater. Sci. Eng. A 2016, 669, 318–331. [Google Scholar] [CrossRef]
- Miller, K.J. The two Thresholds of Fatigue Behavior. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 931–939. [Google Scholar] [CrossRef]
- Fan, J.L.; Guo, X.L.; Wu, C.W.; Zhao, Y.G. Research on fatigue behavior evaluation and fatigue fracture mechanisms of cruciform welded joint. Mater. Sci. Eng. A 2011, 528, 8417–8427. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.J.; Wang, J. Microstructure and low-temperature mechanical properties of 304 stainless steel joints by PAW + GTAW combined welding. J. Mater. Eng. Perform. 2016, 25, 4561–4573. [Google Scholar] [CrossRef]
- Forman, R.G.; Kearney, V.E.; Engle, R.M. Numerical analysis of crack propagation in cyclic-loaded structures. J. Basic Eng. Trans. 1967, 89, 463–464. [Google Scholar] [CrossRef]










| Cr | Ni | C | Si | Mn | S | Fe | |
|---|---|---|---|---|---|---|---|
| BM (06Cr19Ni10) | 17.2 | 8.10 | 0.043 | 0.46 | 1.12 | 0.001 | Remainder |
| Filler (ER308L) | 20.1 | 10.2 | 0.028 | 0.61 | 1.85 | 0.008 | Remainder |
| Parameter | Welding Voltage (V) | Welding Current (A) | Welding Speed (cm/min) | Filler Material | Shielding Gas Type |
|---|---|---|---|---|---|
| Value | 24.5 | 217 | 40 | ER308L | Argon, O2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Qian, C.; Ince, A.; Zheng, J.; Li, H.; Han, Z. Fatigue Crack Growth Behavior of the MIG Welded Joint of 06Cr19Ni10 Stainless Steel. Materials 2018, 11, 1336. https://doi.org/10.3390/ma11081336
Tang L, Qian C, Ince A, Zheng J, Li H, Han Z. Fatigue Crack Growth Behavior of the MIG Welded Joint of 06Cr19Ni10 Stainless Steel. Materials. 2018; 11(8):1336. https://doi.org/10.3390/ma11081336
Chicago/Turabian StyleTang, Lanqing, Caifu Qian, Ayhan Ince, Jing Zheng, Huifang Li, and Zhichao Han. 2018. "Fatigue Crack Growth Behavior of the MIG Welded Joint of 06Cr19Ni10 Stainless Steel" Materials 11, no. 8: 1336. https://doi.org/10.3390/ma11081336
APA StyleTang, L., Qian, C., Ince, A., Zheng, J., Li, H., & Han, Z. (2018). Fatigue Crack Growth Behavior of the MIG Welded Joint of 06Cr19Ni10 Stainless Steel. Materials, 11(8), 1336. https://doi.org/10.3390/ma11081336





