Mechanical Characteristics of Hybrid Composites with ±45° Glass and 0°/90° Stainless Steel Fibers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Reinforcing Fibers
Steel Reinforcement
Fiberglass Reinforcement
2.1.2. Resin Matrix
2.2. Manufacturing of Composite Specimens
2.3. Experimental Methodology
3. Results and Discussion
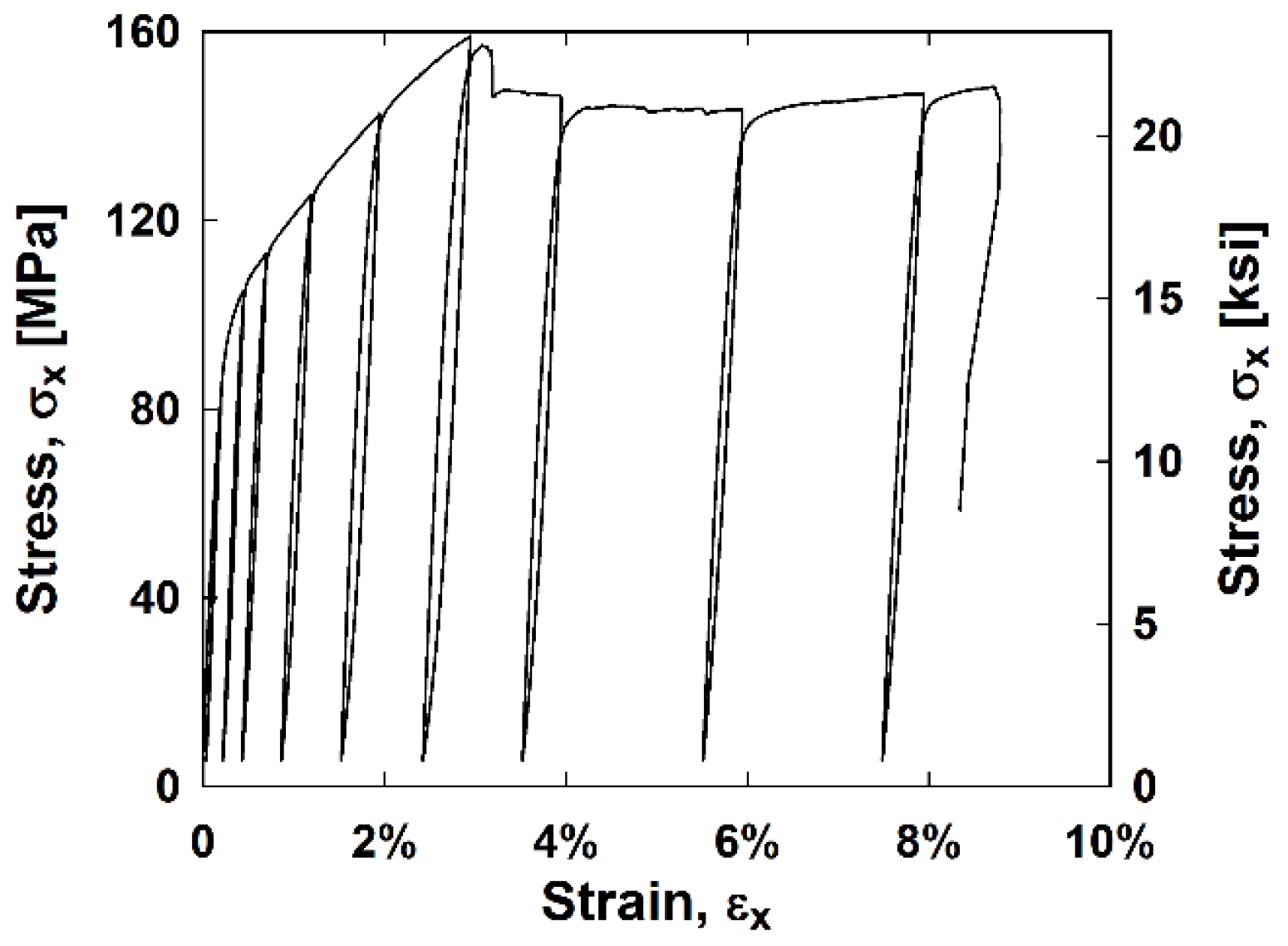
3.1. Tensile Properties
3.2. Failure Mechanisms
3.3. Modelling Hysteresis Experiments
3.3.1. Hybrid and Nonhybrid Glass Composite Model
3.3.2. Unidirectional Stainless Steel Composite Model
3.4. Simulated Hysteresis Behavior
3.4.1. Hybrid and Nonhybrid Glass Composite Model
3.4.2. Unidirectional Stainless Steel Composite Model
4. Conclusions and Future Work
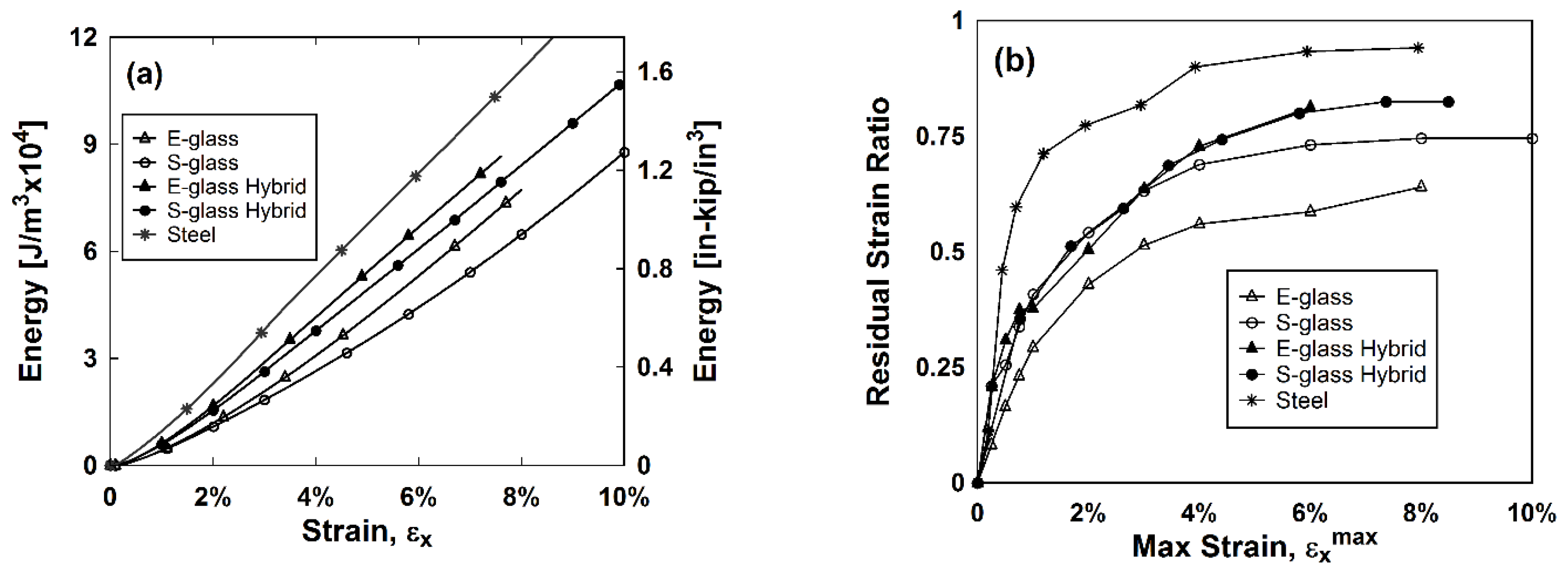
- Hybrid composites with glass and steel fibers had higher energy dissipation, stiffness, and strength when compared to their respective nonhybrid E-glass and S-glass composites;
- The hybrid composites with woven fiberglass subjected to in-plane shear in this study outperformed the UD hybrid composites tested by McBride et al. [18] in terms of energy dissipation and strain at failure;
- Geometry of woven materials is an important consideration when designing composites. The 4H modified twill weave outperformed the 8H satin weave in energy dissipation and had a lower residual strain ratio, thus reaching higher elastic strains;
- The S-glass composites did not reach their full shear strength potential, as the matrix was most likely too weak to support the higher strength of the S-glass fibers;
- The steel fibers did not reach their ultimate strain potential and their delamination from the composite was a major contribution to the failure mode of the hybrid samples. Fiber–matrix interface is an important consideration when designing a composite with desired mechanical properties. Callens et al. [17] improved the mechanical performance of their stainless steel fiber composites by modifying the adhesion of the stainless steel fibers with different silane treatments. The application of modified adhesion and use of a tougher matrix will be considered in future manufacturing of hybrid composites;
- In future work, the damage and failure modes of the hybrid composites should be investigated further. Jalalvand et. al [37] investigated the different damage modes of hybrid composites comprised of high strain material plies and low strain material plies as a function of absolute and relative thickness of the low strain material. By knowing the damage mode of a particular layup, one can improve the design and function of the composite;
- The nonlinear behavior of the composites when subjected to in-plane shear can be described as a degradation of the shear modulus and accumulation of permanent strain. The inelastic behavior of the stainless steel fibers altered the damage behavior of the hybrid composites compared to the all glass composites. The constitutive model developed in this study was robust enough to accurately model the additional plasticity that the stainless steel fibers contribute to the hybrid composites. The MATLAB® code described accurately predicts the hysteresis experiments as well as the energy dissipated in the experimental results. The Armstrong–Frederick model was able to accurately predict the behavior of the stainless steel fibers;
- The ability for one to investigate different hybrid composites designs by simulating their behavior is invaluable. Therefore, in future work, comparing superpositions of the steel fiber layers with the fiberglass layers will be investigated. By combining the Armstrong–Frederick model and the CDM model in finite element modelling (FEM), one can simulate different layups of the composites.
Author Contributions
Founding
Acknowledgments
Conflicts of Interest
References
- Zheng, M. The mechanical properties of composites reinforced with woven and braided fabrics. Compos. Sci. Tech. 2000, 60, 479–498. [Google Scholar]
- Chawla, K.K. Composite Materials: Science and Engineering, 3rd ed.; Springer: New York, NY, USA, 2012; ISBN 978-0-387-74365-3. [Google Scholar]
- Swolfs, Y.; Crauwels, L.; Van Breda, E.; Gorbatikh, L.; Hine, P.; Ward, I.; Verpoest, I. Tensile behaviour of intralayer hybrid composites of carbon fibre and self-reinforced polypropylene. Compos. A Appl. Sci. Manuf. 2014, 59, 78–84. [Google Scholar] [CrossRef]
- Taketa, I.; Ustarroz, J.; Gorbatikh, L.; Lomov, S.V.; Verpoest, I. Interply hybrid composites with carbon fiber reinforced polypropylene and self-reinforced polypropylene. Compos. A Appl. Sci. Manuf. 2010, 41, 927–932. [Google Scholar] [CrossRef]
- Sreekala, M.; George, J.; Kumaran, M.; Thomas, S. The mechanical performance of hybrid phenol-formaldehyde-based composites reinforced with glass and oil palm fibres. Compos. Sci. Tech. 2002, 62, 339–353. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Noorunnisa Khanam, P.; Mohan Reddy, M.; Raghu, K.; John, K.; Venkata Naidu, S. Tensile, flexural and compressive properties of sisal/silk hybrid composites. J. Reinf. Plas. Compos. 2007, 26, 1065–1070. [Google Scholar] [CrossRef]
- Priya, S.P.; Rai, S. Mechanical performance of biofiber/glass-reinforced epoxy hybrid composites. J. Indus. Text. 2006, 35, 217–226. [Google Scholar] [CrossRef]
- Thwe, M.M.; Liao, K. Effects of environmental aging on the mechanical properties of bamboo–glass fiber reinforced polymer matrix hybrid composites. Compos. A Appl. Sci. Manuf. 2002, 33, 43–52. [Google Scholar] [CrossRef]
- Thwe, M.M.; Liao, K. Durability of bamboo-glass fiber reinforced polymer matrix hybrid composites. Compos. Sci. Tech. 2003, 63, 375–387. [Google Scholar] [CrossRef]
- Callens, M.; Gorbatikh, L.; Verpoest, I. Tensile behaviour of ductile steel fibre/epoxy and steel fibre/polyamide composites. In Proceedings of the 10th International Conference on Durability of Composite Systems (DURACOSYS 2012), Brussels, Belgium, 17–19 September 2012. [Google Scholar]
- Callens, M.; Gorbatikh, L.; Verpoest, I. Tensile behaviour of ductile steel fibre/epoxy composites. In Proceedings of the 15th European Conference on Composite Materials(ECCM 15), Venice, Italy, 24–28 June 2012. [Google Scholar]
- Callens, M.; De Cuyper, P.; Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Hybridization of ductile steel fibre and self-reinforced composites. In Proceedings of the 9th International Conference on Composite Science and Technology ICCST, Sorrento, Italy, 24–26 April 2013; pp. 503–510. [Google Scholar]
- Callens, M. Development of ductile stainless steel fibre composites. 2014. Available online: https://www.mtm.kuleuven.be/Onderzoek/Composites/Research/micro_nano/projects/Nano-engineered_steel_fibres (accessed on 30 March 2018).
- Callens, M.; Gorbatikh, L.; Verpoest, I. Ductile steel fibre composites with brittle and ductile matrices. Compos. A Appl. Sci. Manuf. 2014, 61, 235–244. [Google Scholar] [CrossRef]
- Callens, M.G.; De Cuyper, P.; Gorbatikh, L.; Verpoest, I. Effect of fibre architecture on the tensile and impact behaviour of ductile stainless steel fibre polypropylene composites. Compos. Struct. 2015, 119, 528–533. [Google Scholar] [CrossRef]
- Callens, M.G.; Gorbatikh, L.; Bertels, E.; Goderis, B.; Smet, M.; Verpoest, I. Tensile behaviour of stainless steel fibre/epoxy composites with modified adhesion. Compos. A Appl. Sci. Manuf. 2015, 69, 208–218. [Google Scholar] [CrossRef]
- McBride, A. Mechanical behavior of hybrid glass/steel reinforced epoxy composites. Master’s Theses, University of Connecticut, Storrs, CT, USA, 2016. [Google Scholar]
- O’Brien, C.; McBride, A.; E Zaghi, A.; Burke, K.A.; Hill, A. Mechanical behavior of stainless steel fiber-reinforced composites exposed to accelerated corrosion. Materials 2017, 10, 772. [Google Scholar] [CrossRef] [PubMed]
- Allaer, K.; De Baere, I.; Lava, P.; Van Paepegem, W.; Degrieck, J. On the in-plane mechanical properties of stainless steel fibre reinforced ductile composites. Compos. Sci. Tech. 2014, 100, 34–43. [Google Scholar] [CrossRef]
- Thysen, S. Mechanical Behavior of Hybrid Steel and Glass Fibre Composites. Master’s Thesis, KU Leuven, Leuven, Belgium, 2013. [Google Scholar]
- Mosleh, Y.; Clemens, D.; Gorbatikh, L.; Verpoest, I.; van Vuure, A.W. Penetration impact resistance of novel tough steel fibre-reinforced polymer composites. J. Reinf. Plas. Compos. 2015, 34, 624–635. [Google Scholar] [CrossRef]
- Hannemann, B.; Backe, S.; Schmeer, S.; Balle, F.; Breuer, U.; Schuster, J. Hybridisation of cfrp by the use of continuous metal fibres (mcfrp) for damage tolerant and electrically conductive lightweight structures. Compos. Struct. 2017, 172, 374–382. [Google Scholar] [CrossRef]
- Ahmed, T. Hybrid Composite Structures: Multifunctionality through Metal Fibres. Doctoral Thesis, Delft University of Technology, Delft, The Netherlands, 2009. [Google Scholar]
- ASTM D3518/D3518M–13, Standard Test Method for in-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate; ASTM International: West Conshohocken, PA, USA, 2013. [CrossRef]
- Van Paepegem, W.; De Baere, I.; Degrieck, J. Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part i: Experimental results. Compos. Sci. Tech. 2006, 66, 1455–1464. [Google Scholar] [CrossRef]
- Van Paepegem, W.; De Baere, I.; Degrieck, J. Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part ii: Model development and finite element simulations. Compos. Sci. Tech. 2006, 66, 1465–1478. [Google Scholar] [CrossRef]
- Armstrong, P.J.; Frederick, C. A Mathematical Representation of the Multiaxial Bauschinger Effect; Internal Research Report for Central Electricity Generating Board and Berkeley Nuclear Laboratories, Research & Development Department Berkeley: London, UK, 1966; Volume 731. [Google Scholar]
- Halama, R.; Sedlák, J.; Šofer, M. Phenomenological modelling of cyclic plasticity. In Numerical Modelling; InTech: London, UK, 2012. [Google Scholar]
- Geerinck, S. Stainless Steel Filler Materials for Plastics; Bekaert Fiber Technologies: Zwevegem, Belgium, 2013. [Google Scholar]
- Resin, E. 828 Technical Datasheet; Hexion Inc.: Batesville, AR, Canada, 2005. [Google Scholar]
- Hexion, I. Epikure Curing Agent 3055 Technical Datasheet; Hexion Inc.: Batesville, AR, Canada, 2005. [Google Scholar]
- ASTM D638-14. Standard Test Method for Tensile Properties of Plastics; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- McBride, A.K.; Turek, S.L.; Zaghi, A.E.; Burke, K.A. Mechanical behavior of hybrid glass/steel fiber reinforced epoxy composites. Polymers 2017, 9, 151. [Google Scholar] [CrossRef]
- Lafarie-Frenot, M.; Touchard, F. Comparative in-plane shear behaviour of long-carbon-fibre composites with thermoset or thermoplastic matrix. Compos. Sci. Tech. 1994, 52, 417–425. [Google Scholar] [CrossRef]
- Kellas, S.; Morton, J.; Jackson, K.E. Damage and failure mechanisms in scaled angle-ply laminates. Compos. Mater. Fatigue Fract. 1993, 1156, 257. [Google Scholar]
- Jalalvand, M.; Czél, G.; Wisnom, M.R. Numerical modelling of the damage modes in ud thin carbon/glass hybrid laminates. Compos. Sci. Tech. 2014, 94, 39–47. [Google Scholar] [CrossRef]










| Composite | Composition | Layup |
|---|---|---|
| E-glass | 6 layers G±45 | [G±45]3s |
| S-glass | 6 layers G±45 | [G±45]3s |
| Stainless Steel | 6 layers S0 | [S0]3s |
| E-glass Hybrid | 6 layers G±45, 2 layers S0, 2 layers S90 | [G±45 G±45 S0 S90G±45]s |
| S-glass Hybrid | 6 layers G±45, 2 layers S0, 2 layers S90 | [G±45 G±45 S0 S90G±45]s |
| Sample | Thickness [mm (in)] | Length [cm (in)] | Glass Fiber Fraction [Theoretical % (TGA %)] | Steel Fiber Fraction [Theoretical % (TGA %)] | Total Fiber Volume Fraction [Theoretical % (TGA %)] |
|---|---|---|---|---|---|
| E-glass | 1.3 (0.0505) | 17.03 (6.706) | 51.08 (55.81) | -- | 51.08 (55.81) |
| S-glass | 1.45 (0.0571) | 17.14 (6.75) | 49.75 (52.82) | -- | 49.75 (52.82) |
| Stainless Steel | 1.592 (0.0627) | 19.05 (7.5) | -- | 27.38 (36.52) | 27.38 (36.52) |
| E-glass Hybrid | 2.277 (0.08963) | 17.86 (7.031) | 31.566 (32.98) | 12.67 (13.31) | 45.28 (46.29) |
| S-glass Hybrid | 2.486 (0.0979) | 16.51 (6.5) | 26.90 (32.81) | 10.80 (13.13) | 40.69 (45.94) |
| Composite | G120 [MPa] | Permanent Strain | Shear Damage | |||
|---|---|---|---|---|---|---|
| a | b | c | d | e | ||
| E-glass | 3624 | 2.366 | −8.574 | 0.6979 | 1.112 | −50.74 |
| S-glass | 4891 | 2.868 | −6.968 | 0.7170 | 1.432 | −93.02 |
| E-glass hybrid | 7900 | 2.743 | −3.360 | 0.4605 | 15.62 | −199.6 |
| S-glass hybrid | 6603 | 3.052 | −5.018 | 0.5326 | 9.995 | −111.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
O′Brien, C.; Zaghi, A.E. Mechanical Characteristics of Hybrid Composites with ±45° Glass and 0°/90° Stainless Steel Fibers. Materials 2018, 11, 1355. https://doi.org/10.3390/ma11081355
O′Brien C, Zaghi AE. Mechanical Characteristics of Hybrid Composites with ±45° Glass and 0°/90° Stainless Steel Fibers. Materials. 2018; 11(8):1355. https://doi.org/10.3390/ma11081355
Chicago/Turabian StyleO′Brien, Caitlin, and Arash E. Zaghi. 2018. "Mechanical Characteristics of Hybrid Composites with ±45° Glass and 0°/90° Stainless Steel Fibers" Materials 11, no. 8: 1355. https://doi.org/10.3390/ma11081355
APA StyleO′Brien, C., & Zaghi, A. E. (2018). Mechanical Characteristics of Hybrid Composites with ±45° Glass and 0°/90° Stainless Steel Fibers. Materials, 11(8), 1355. https://doi.org/10.3390/ma11081355





