1. Introduction
The forming limit curve (FLC) is used in expecting the forming range of sheet metal without material instabilities. The limits are expressed in terms of major and minor strain pairs at necking. A comprehensive summary of the FLC history can be found in Col [
1]. Nowadays the standard for the evaluation of the FLC is represented in Europe by the DIN EN ISO 12004-2 [
2]. The stretching tests used are according to the Nakajima [
3] and Marciniak [
4] setups. The sheet metal is clamped in a clamping unit and a punch, hemispherical or flat for the Nakajima or Marciniak test respectively, forms the specimen due to its vertical stroke until fractures occurs. The evaluation method suggested in the standard is based on the Bragard’s study in 1972 [
5] and it is known today as “cross-section” method. In this method, the strain distribution of the stage before crack is considered. Afterwards, sections perpendicular to the crack initiation are defined and the strain development on these sections is interpolated with a second-order polynomial, according to the common sense that the strain on such sections develops similar to a bell-shaped curve. In those years, the strain measurement techniques were based on putting circles patterns on the specimen surface before forming and measuring their diameter deformations after forming. However, it permitted only to identify the strain distribution on the last stage, without giving any information of the strain history.
In the 1990s, with the advent of the computer era, pictures could be digitalized during the deformation and analyzed with computer algorithms, based on digital image correlation techniques (DIC). The DIC correlates pictures of subsequent moments of the investigated test. Already in 1985 Chu et al. investigated the application of the DIC in experimental mechanics [
6] and in 1999 it was used for the evaluation of the FLCs [
7]. Due to using two cameras during Nakajima or Marciniak tests, the strain history on the surface can be measured. Although DIC allows an accurate and complete strain measurement, the standard method is still based only on the cross-section method. In addition, modern light materials such as high strength steels and aluminum alloys are characterized by multiple local strain maxima and sudden crack without necking phase. Consequently, for such materials the interpolation of the strain distribution with a second order function shows weaknesses [
8].
To address this limitation, several methods that take into account strain history during Nakajima tests, have been proposed. The so-called “line-fit” method proposed by Volk et al. [
9] or the correlation-coefficient method [
10] are an example of “time-dependent methods”. They consider the thickness reduction in the instability zone and evaluate the onset of necking as a sudden change in the thickness reduction. In particular, the line-fit method has shown promising results in good agreement with the experiments. Nevertheless, the time-dependent methods take into account the necking area and thus still focus the attention only on the instability zone.
In 2015 [
11] a new approach based on pattern recognition was proposed. The idea was to use machine learning for the pattern detection on Nakajima tests to incorporate new knowledge about the forming development. Conventional pattern recognition deals with the mathematical and technical aspects of automatic processing and evaluation of patterns [
12], where a physical signal e.g., images or speech are converted into appropriate compact characteristic representations. In a supervised pattern recognition setup these characteristic representations are often related e.g., to the visual perception of experts that have an excellent understanding of the underlying problem to be solved. These experts annotate the data to be associated with a certain class. Using a classification algorithm and a representative sub-sample of the data it is possible to learn a decision boundary based on the characteristic representation/label pairs, such that the underlying data can be separated into different classes. In this first approach in 2015, the pattern recognition method was used in a forming process for the prediction of the class “crack” for a DX54D steel. This classification approach has shown promise, with a 90% probability of predicting crack initiation, before it occurs. This analysis confirmed the validity of pattern recognition as a suitable tool to analyze material characteristics during Nakajima tests.
Nevertheless, while the class “crack” is easily definable, the onset of instability is challenging. Metallography analyses have shown that patterns related to localized necking are recognizable on the surface during instability for conventional deep drawing steel [
13] as well as dual phase steel [
14]. Therefore pattern recognition can be potentially used for the determination of forming limits. The consideration of the forming limit as classification problem becomes therefore a point of interest [
15]. In the present study, a supervised classification approach using experts’ opinions for the classification of diffuse necking, local necking and crack is presented. In order to qualify the validity of the proposed method for different material behaviors, three materials are investigated: the conventional deep drawing steel DX54D in two different thicknesses, the dual phase steel DP800 and the aluminum alloy AC170. The outcomes from the pattern recognition method are compared to the experts’ annotations and interpreted using the material characteristics. Additionally, multiple FLC candidates are created based on the classification results. These are compared with the conventional and the time-dependent FLC, and with the FLC created by majority voting, based on the experts annotations.
2. Experimental Procedure
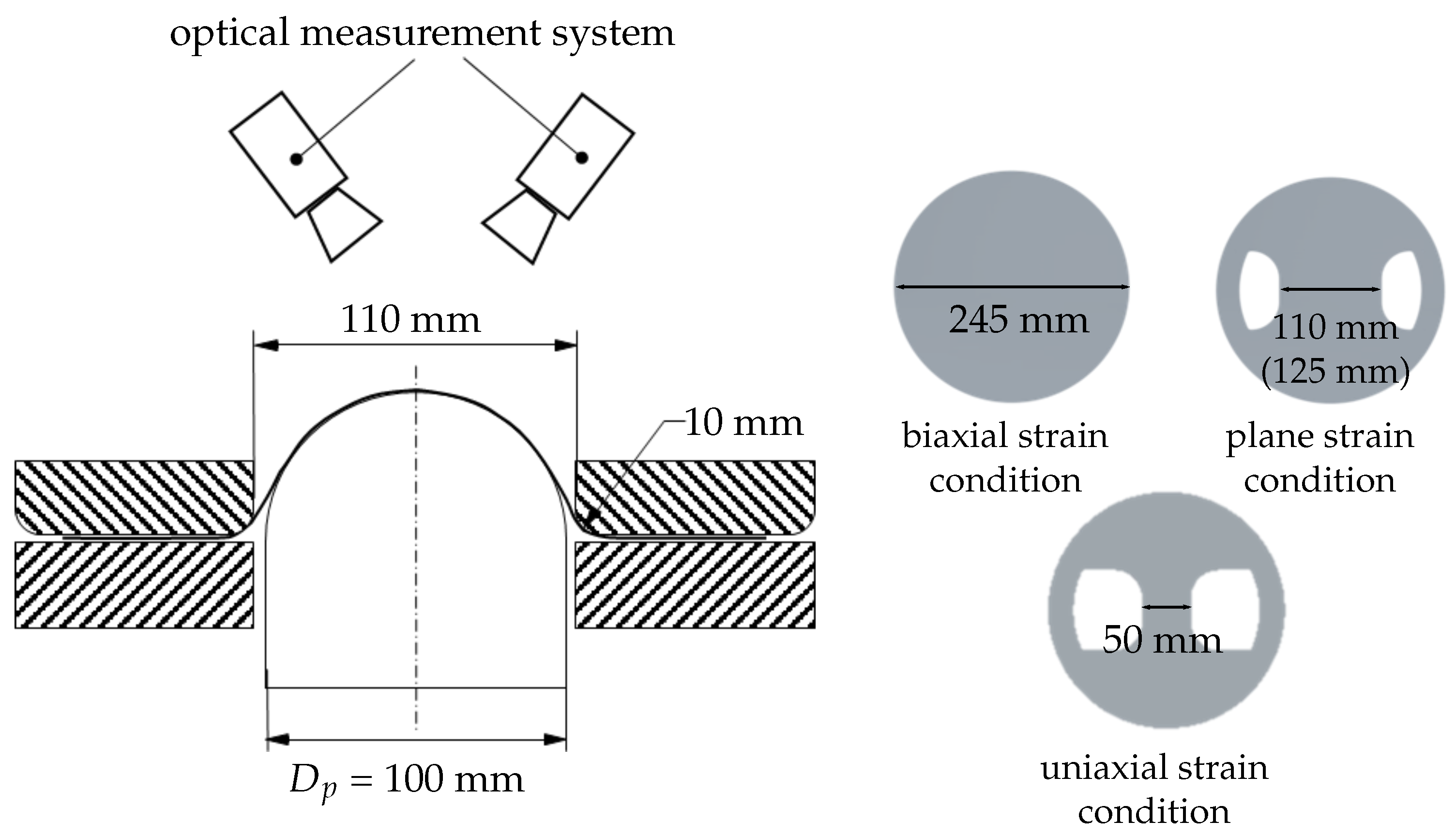
The used experimental Nakajima setup is depicted in
Figure 1. The system is composed by a clamping unit with a inner die diameter of 110 mm, a hemispherical punch with a diameter of 100 mm. The optical measurement system used is ARAMIS from gom GmbH. The two cameras take pictures of the surface from the beginning to the end of the test and the strain distributions are evaluated with the DIC technique. On the specimen surface a layer of white lacquer is applied, in order to minimize the metallic light reflection. Afterwards, a stochastic pattern of graphite is sprayed for the correlation of the pictures.
The investigated different strain paths are obtained by changing the specimen geometry from a full geometry to waisted blanks with a parallel shaft. The width of the remaining material defines the geometry’s name (for example: S050 has a width of 50 mm). Between punch and specimen a lubrication system according to the DIN EN ISO 12004-2 is used. The system is composed by multiple layers of grease, Teflon foil and soft PVC, in order to minimize the friction between punch and specimen and to achieve a crack at the top of the specimen. The frame rate as well as the punch velocity are varied for the different experiments. In order to have different combination of strain paths, materials and boundary conditions, the punch velocity varies from 1 to 2 mm/s and a frequency of 15 Hz, 20 Hz or 40 Hz. As long as the searched class is visible in the video data, the methodology is not dependent on the frame rate or punch velocity.
4. Methodology and Machine Classification of Failure Stages
As described in
Section 1, the evaluation of the onset of necking by conventional methods such as the cross-section method or time dependent methods, depends on the evaluation of limited areas or sections that are either based on an arbitrary threshold, require user interaction or focus only on one of the principle strains, such as major strain or thickness reduction. Instead of artificially decreasing the available information on a couple of pixels, the pattern recognition approach exploits the image information of all principle strains at the same time while focusing on the extremal region and its vicinity. To tackle the problem of detecting the three different failure classes, the method follows the conventional pattern recognition pipeline as illustrated in
Figure 7. The individual video sequences acquired of different materials and geometries (described in
Section 2) serve as inputs to the pipeline. These signals are preprocessed to aid in classification by reducing noise and interpolating missing data resulting from defect pixels. As the method follows the principle of supervised classification, expert knowledge is used to separate the different forming stages into distinct classes. This means each image of a video sequence receives a label from the experts which corresponds to a specific failure class. This procedure leads to a label vector for each sequence, used as ground truth for supervised classification. During
feature extraction the preprocessed images are transformed into another representation such that other characteristics besides the plain image intensity values can be used to describe the image and thus the current state of failure. This allows the generation of a compressed representation, a characteristic vector, of each image in feature space. The extracted features used in the method are closely related to the experts visual perception and therefore focus on the evaluation of greyscale and edge information or interactions between neighboring pixels and additionally support a comprehensive encoding of strain progression. This data processing sequence is valid for both, the classification and learning phase. To simulate a real-life scenario, that would use a learned classification model, the data set is divided into disjoint training and test sets. The training set is used within learning phase, whereas the test set is used for the simulation of the real-life scenario and thus corresponds to the classification phase. The extracted information, in form of the characteristic and ground truth vectors are used in the
classification step, wherein a classifier uses the training set to find an optimal solution, that separates instances to different classes. This separation hypothesis is evaluated using the disjoint test set, whereby the class assignments of the individual instances are compared to the corresponding ground truth labels, leading to a class probability
for each instance of the data. The separation hypothesis is quantitatively evaluated in terms of: the area under receiver operating characteristic curve (ROC) and precision or recall metrics. Subsequent sections describe each component of our classification pipeline in detail.
4.1. Preprocessing
The output of the optical measurement system ARAMIS is converted into a three channel (major strain, minor strain, thinning) image which serves as input to the algorithm. The high sampling rate or minor errors during probe preparation may adversely affect the DIC technique, such that it may temporarily be unable to correlate blocks on subsequent images and thus is unable to calculate strain values. This leads to temporal defect pixels rendering it impossible to apply e.g., a convolution with a kernel to extract edge information. As information of this nature is crucial to assess the localized necking state, missing values are interpolated using the temporal progression of individual strain values. In addition to the temporal missing values there exist static defect pixels that deliver no measurement signal during the whole forming procedure. These artifacts are removed by calculating the mean value using a square neighborhood. Besides these two types of artifacts defect, pixels may also be a sign of crack initiation, since just before or during material failure the DIC system is not able to further track the individual blocks, which leads to a sudden, increasing amount of defect pixels towards the end of the forming procedure. This indicator has been used by the experts to assign the failure class. As expert annotations are based on this kind of information, removing or interpolating values at these pixels would adversely affect the subsequent classification task. For this reason, defect pixels that do not recover during forming are replaced with a negative value to deliver e.g., a strong edge response that corresponds to material failure and thus crack initiation.
4.2. Feature Extraction
In the literature, material failure has been assessed using limited information from cross-sections or small areas, delineated based on an arbitrary threshold defined for one principal strain. Instead of focusing on a subjectively defined area, numerous areas of the available 2D image representations of strains, which include extremal regions and their vicinity. These images are encoded with local descriptors, the so called features, to reduce their dimensionality. The characteristic vector being used by the classification algorithm, is created by concatenating the extracted features of each principle strain, such that information from all three domains can be utilized simultaneously. The selection of suitable features is challenging as this is the first study to use pattern recognition methods to assess multiple stages of material failure. Consequently, we employ features that are considered suitable to capture the continuous progression of strain over time, and have been extensively investigated for various applications in medical image analysis and computer vision.
4.2.1. Histogram
In image processing a histogram represents the frequency of gray level occurrences of the whole image and may provide insight into the characteristics of the image. They do not consider any structural arrangement of pixels or a certain neighborhood and only provide information about the distribution of gray level intensities. The histogram is expected to change between the homogeneous forming phase and the inhomogeneous forming phase as higher intensities occur locally, affecting the skewness and the kurtosis of the distribution. To enable comparison, all histograms computed comprised 256 bins.
4.2.2. Homogeneity
Two types of image representations are evaluated using this feature extractor. The first information domain is the original greyscale (strain) distribution and the second information domain consists of the edge information. In the latter case, the intensities are converted into edge representation by convolution with a Sobel operator in x- and y-direction and calculation of their magnitude. Examples of both domains are depicted in
Figure 8a,b at different time steps showing the progression of strain and edges. Within both information domains the exact same features are computed. They consist of basic statistical moments up to the fourth order and assess the degree of homogeneity in image appearance. In addition to the statistical moments, the median, the minimum and the maximum values of both domains are considered. To evaluate changes within the structure of the material, the size of the top 10% and top 1% area with respect to the current maximum value of each domain are extracted, in addition to their fraction. Until the end of the homogeneous forming phase, the two areas are expected to progress evenly such that their fraction remains constant. If one of the two areas significantly changes regarding their expansion in size, their fraction will decrease. As these features are extracted for each principal strain, the characteristic vector consists of 60 features.
4.2.3. Local Binary Pattern
Another strategy to describe greyscale distributions are Local Binary Pattern (LBP) developed by Ojala et al. [
21]. The advantage of LBP is, that it is able to accommodate intensity variation within images, as one pixel is always evaluated in the context of its nearby neighborhood. Within the original approach by Ojala et al., a 3 × 3 (
) local neighborhood is considered to encode the central pixel using a binary weighting scheme. One drawback of LBPs is their rotation dependence, as the comparison of the central-pixel with its neighborhood will change when the image is rotated. Ojala et al. [
22] have extended this approach to become rotation invariant, using a circular neighborhood, with the possibility of varying the neighborhood and radius. They introduced uniform LBP (LBPu), as well as rotation-invariant uniform LBP (LBPriu), while the latter are a reduced version of LBPu which contain less information. A visualization of both features is depicted in
Figure 8, whereby (c) LBPu encode regions with the same color if the neighborhood with respect to the central-pixel behaves identical and (d) LBPriu highlight the extremal regions of the strain distribution. In the current method the LBPs, as well as an extended version which includes the variance as additional information [
23], are extracted with multiple radii and multiple neighborhoods (
,
).
4.2.4. Histogram of Oriented Gradients
In contrast to the introduced homogeneity feature, Histogram of Oriented Gradients [
24] exploit the gradient orientation, rather than the magnitude of the edges and were introduced in the scope of pedestrian detection. The idea behind the feature extractor is that humans in an upright position can be represented by the orientation of gradients of their outline with dependence on their pose. The degree of invariance to local geometric or human pose changes is addressed with the amount of orientation bins that affect the possible angular resolution. If the angular resolution is too fine, the resulting feature vector would be large and additionally, would result in a fine grained description of e.g., different poses of limbs which is unnecessary for pedestrian detection. In contrast to the original paper, dense sampling was omitted as well as the photometric normalization as the strain distributions are the result of optical measurement, and effects such as variation in illumination or contrast will not occur. Two different angular resolutions (5, 10 degree) are evaluated in a signed (360 degree) an unsigned (180 degree) manner.
4.3. Classification Using Random Forests
Random Forests [
25] belong to the category of ensemble learners based on the principle of decision trees. Within the training phase, a single decision tree is built with a part of the training data. At each node of the tree, starting from the top, the data is separated, in a binary best split manner based on a threshold value and the evaluation of the characteristic vector of each instance of the data. These comparisons are performed sequentially until no further separation of the data is possible. Within the classification phase, the individual instances of the held out test data are categorized into classes when reaching a leaf node based on the learned comparisons. Using the same input data for growing the classification tree would lead to the exact same classification tree and thus to the same classification result. Random Forest uses multiple strategies to introduce randomness and avoid over-fitting to the underlying data. During training, the data is sub-sampled with replacement and only a random subset of the characteristic vector is evaluated at each splitting node. In addition multiple decision trees are built with individual sub-samples of the training data, leading to different decision trees. Within the classification phase, the remaining instances are categorized based on a majority vote of the learned decision trees.
4.4. Experiments
4.4.1. Database
The different failure stages of each material and their distribution is shown in
Table 1. Overall, the localized necking and crack class is underrepresented by a large magnitude in all materials in contrast to the homogeneous and diffuse necking class. In general a classifier should be trained in such a way, that it reaches best classification results e.g., best accuracy. Due to the presence of a large imbalance in data (cf.
Table 1), a trained classifier would be biased towards the majority class rather than the crack class. On the one hand this can be addressed using a weighting scheme but on the other hand this solution does not increase the variance of the minority classes. To increase the variation of the minority classes data augmentation is used. Each dataset is artificially increased by a factor of 12, using vertical and horizontal flipping as well as small random rotations (2–12 degree). Besides increasing the variation of the dataset, the random rotations also address slight differences regarding the orientation of investigated probes that might occur during preparation. Overall, this procedure increases the data imbalance regarding the amount of instances per class. To address this imbalance, the data is randomly sub-sampled or up-sampled with respect to the amount of instances (50%) of the augmented localized necking class. In this way the variance of each class is increased and a uniformly distributed amount of data can be used for classification.
4.4.2. Inter-Rater-Reliability
The consistency among the annotations of the five raters is examined using the Fleiss’ kappa metric [
26]. This is a robust measure for agreement which considers the possibility of the agreement occurring by chance between multiple raters. Using this strategy it is possible to examine how consistent human experts are among each other in terms of their categorization into different failure stages. A value below 0 would correspond to no agreement, while a value between 0.41–0.61 corresponds to moderate agreement and 0.81–1.00 would be considered a perfect agreement.
4.4.3. Classification
To evaluate the performance of the classification algorithm, a Leave-One-Sequence-Out cross-validation (LOSO-CV) setup is carried out, while the majority vote over the experts’ annotations serve as ground truth. Furthermore to discount the influence of different geometries and materials, the LOSO-CV is evaluated geometry-wise for each material. In this way, the classifier is retrained three times within each geometry, such that two-thirds of the data are for training, while the left-out data set is used to asses the separation hypothesis. The number of decision trees used in the random forest classifier is fixed at 200, while suitable values for two other parameters, the maximum depth per tree as well as the minimum amount of samples per leaf are found via grid-search (15–30, 2–12, respectively) per trial of each geometry, in order to improve the generalization of the classifier. To address the unbalanced occurrence of uniaxial, biaxial and plane strain geometries and to generate an unbiased evaluation, the performance of the different features is assessed in two ways. The uniaxial to plane strain images are jointly evaluated using the S060, S080 and S100 geometry, or S050 and S110 if S080 and S100 are unavailable, as the images as well as the necking development appear comparable. The S245 geometry is evaluated independently, as the strain distribution appears very different in this geometry in comparison to the uniaxial to plane strain distributions and thus might require another evaluation area as well as feature for good separation. During training of the classifier, no particular class is preferred over the other, meaning that a miss-classification of the crack class or diffuse necking class has the same cost and thus no weighting scheme is used. Consequently, the general performance and quality of the four class classification problem is evaluated with the average area under ROC curve (AUC), which describes the capability of the classifier respecting all false positive rate thresholds without the need of choosing the best operating point, usually defined based on costs. This facilitates a comparison between the different features as only one value for each four class classification problem has to be considered. The individual best performing features of each material is then evaluated on the respective unrestricted dataset to asses the overall performance of the classification algorithm. In this case, the method is analyzed with a confusion matrix that corresponds to the 50% probability threshold and defines the class membership, such that the performance per class can be investigated in terms of miss-classifications. This allows class-wise assessment in terms of precision and recall.
Another aspect that needs clarification is the definition of an evaluation area. On the one hand it might be beneficial to focus only on local image details, but on the other hand there might be unused information in the surrounding area that may improve the classification process. For this reason three different patch extraction techniques are investigated that are visualized for DP800-S245 in
Figure 9. The first approach extracts multiple patches with an overlap of 50% with a side-length of 16–32 px and a step-size of 8 px, while the maximum value lays within the center (Patch-wise). The second approach covers the same area as the first one with only one patch that leads to a side-length of 24, 36 and 48 px (Single-patch). The third approach covers as much information as possible depending on the underlying sample geometry. As the size of the image may change over time, the evaluation area is defined on the last image without a defect pixel. In contrast to the other two approaches it is not possible to use the maximum value as center pixel as it will lead to image patches that include non-comparable image information e.g., imagine the maximum value lying next to the image border in one sequence and close to center within another sequence. This would lead to a comparison between patches containing unequal information. For this reason the center of mass is used as center of the evaluation area (Centered). A direct comparison of the patch-wise approach with the other strategies is not possible, as each of the nine patches is classified with its own individual probability. To allow a comparison the average image probability is calculated as the mean probability over the individual patches.
6. Discussion
The determination of necking using pattern recognition requires a clear definition of failure classes. For this reason, in the present study, a novel approach for categorizing forming processes into multiple failure classes based on pattern recognition has been presented. The strain distribution during the Nakajima tests was measured using digital image correlation (DIC) with an optical measurement system. The strain distribution characterized by the major strain, minor strain and thickness reduction was used by experts to visually assess forming sequences.
The expert annotations highlighted the heterogeneity of necking behavior for the different materials and strain conditions. While the crack class is well defined and easily recognizable, the diffuse and local necking can be differently interpreted. Focusing on the difference between the strain distribution (
Figure 10), it can be observed, that for the local and diffuse necking classes the experts’ knowledge shows low deviation for the geometry S050, while the diffuse necking class strongly deviates for the S110 and S245 geometries, confirming the heterogeneous material behavior under different strain condition. The geometry S050 is under a near uniaxial strain behavior. The negative minor strain and the diffuse necking along the width could be well evaluated from the experts. The test specimens under near plane strain (S110) and the specimens under biaxial condition (S245) show discrepancies between the experts decision regarding the diffuse necking. In addition, the number of images of homogeneous strain distribution are more than the stages in which an instability is observed. This demonstrates that the onset of instability of Nakajima tests occurs few millimeters of punch displacement before crack initiation, according to the definition of instability by the line-fit method [
9]. The most challenging geometry is represented by the S245 specimen under biaxial stretching. The biaxial stretching affects the whole evaluation area with a homogeneous thinning. Independently from the material, the strain distribution develops gradually causing different pronounced degrees of severe thinning until a crack occurs. Therefore, the experts have recognized a local necking only a few stages prior to crack initiation, while diffuse necking is considered to start at very early stages. It has also to be noted, that the guidelines used by experts for the general definition of diffuse necking and local necking were based on the tensile test. In this simple test, the stress can be considered uniaxial and it can be easily described by considering only the planar components. However, in Nakajima test with higher widths, the stress conditions are more complex. Therefore, while for small sample width in which the strain distribution is similar to the uniaxial tensile test, the general definition of necking is well defined and easy to detect, with wider samples the stress conditions cause more complex strain developments which are not directly detectable as general diffuse and local necking.
Also the material structure seems to play an important role, even if the general consideration about the differences due to different strain paths are valid for all investigated materials. Based on
Figure 10 depicting the experts’ decisions for the geometry under near plane strain condition for the investigated material, it can be observed that the diffuse and local necking classes were differently interpreted by the experts for the different materials. This is also emphasized by the Fleiss-Kappa values in
Table 2 as the quality of agreement decreases starting from S110 while reaching its minimum at S245. This degeneration is mainly introduced due to the low consistency of the homogeneous and diffuse necking classes as they dominate the forming process and thus negatively affect the measure. Additionally, it might also be a side effect of the localized necking behavior as it is not focusing on a small area but occurs distributed over larger parts of the image and thus renders it more difficult for experts to find the exact point in time, when the onset of necking takes place. This phenomenon also explains the consistently low Fleiss-Kappa values of DX54D (0.75 mm) as the ductility of the material coupled with a high frequency intensifies the problem for the experts to distinguish homogeneous state from diffuse necking, and diffuse necking from localized necking. In contrast, when using a low sampling rate (AC170 and DX54D (2.00 mm)) or analyzing a less-ductile material (DP800) a moderate to good agreement between the experts is achieved.
Figure 10 emphasizes that the annotations for localized necking are consistent among experts even in the case of a low kappa-value for the specimen under biaxial loading (S245). The consistently good agreement within the localized necking class might be the consequence of the graphical user interface that supported the rater with the possibility of drawing virtual cross sections along the specimen reducing the variance between the experts.
Overall, the classification results (cf.
Figure 3) emphasize that coupling expert knowledge with a classification algorithm, is a suitable approach to assess the failure behavior of sheet metals. This is particularly true for the detection of localized necking, as the ability of the experts to differentiate between different failure states by visual inspection, was a valuable source of information, as highlighted by the 85% recall for all materials. As the classification algorithm is influenced by the ground truth of the rater majority, the low consistency among experts and thus the high sampling rate also affects the classification performance. Inconsistent annotation of sequences thus lead to higher miss-classifications in the transition areas from one class to the other. This is highlighted by the lower recall for diffuse necking in comparison to the localized necking in all materials with the exception of DX54D (2.00 mm). Of course this under-performance might also be a limitation of the chosen feature space, as they are focusing on edge information that seems better suited to the localized necking state, but the inconsistency between experts renders this impossible to evaluate with certainty.
Three different evaluation strategies were investigated. The patch-wise strategy turned out to be the superior approach when evaluating uniaxial to plane strain geometries with a patch size of 24 px or 32 px using Homogeneity or HoG features. In contrast, for the biaxial condition S245 a larger evaluation area was found to be beneficial, using either a single-patch that is centered around the maximum of the last valid stage or based on the centered approach that uses the point of mass. For optimal classification results the evaluation strategy would have to be applied separately depending on the specimen geometry, but as the the uniaxial geometries dominate the data distribution only the best performing features were investigated. Additionally it is more important to have consistent and precise annotations regarding the point in time when necking occurs rather than the choice of feature.
The forming limit curves of the experts coincide very well with the candidates of the classification algorithm (cf.
Figure 14). This is particularly true for the localized necking candidate, which exhibits a high correlation. This is reasonable as the decision of the experts for this class were made using the graphical user interface that supported the rater with on-line virtual sections along the strain distribution and thus e.g., a sudden increase in the strain distribution could easily be detected, which might also explain the good agreement with the ISO determined forming limit curve. Additionally, this observation explains why the Homogeneity feature or HoG outperform the LBP features, as the latter are not able to capture rising intensity differences without being extended by variance as only binary comparisons are possible. Despite the encouraging results achieved in this study, the proposed method still has several limitations: (1) one has to decide to use a specific feature in advance or try all of the possible features rendering the method time consuming; (2) selection of the evaluation area is ambiguous, while for uniaxial geometries patch-wise evaluation seems appropriate, biaxial geometries require a large evaluation area, for best results a mixed evaluation strategy would be reasonable; (3) geometry wise evaluation and restriction to one material excludes side effects that might be beneficial for the classification process as the data is very imbalanced and limited with this setup, which was partly addressed with augmentation; (4) generation of ground truth annotations is expensive as multiple experts need to be consulted to asses the failure behavior based on visual inspection for every new material investigated; (5) lack of consistency between experts’ annotations for the diffuse necking class. The main drawback of the presented method is the dependence on expert knowledge (4), that could be addressed using unsupervised classification algorithms which focus only on the localized necking criteria and thus omit the low consistency of the diffuse necking class. If the experts would be able to define a consistent point in time within the strain distributions, the pattern recognition system would easily be able to separate classes, as within feature space the trials of each geometry are comparable. The classification performance is thus limited to the expected error of the experts and therefore an improvement of the ground truth, maybe based on metallographic examinations, should be pursued. Metallography investigations on the DX54D [
13] and on the DP800 [
14] suggested an improvement of consistency by using metallography outcomes with a better understanding of the material behavior during Nakajima tests. Despite these limitations, the presented work highlights the potential of conventional pattern recognition methods and allows staging the failure behavior of sheet metals based on image information. In particular, it has been shown that experts are able to assess the failure status of specimen during sheet metal forming processes, that their knowledge can be transfered and used to create a forming limit curve that consists of multiple failure stages, without the restriction of a limited evaluation area and the necessity to decide on a distinct principle strain. This study enables future work on other materials with more complex necking behavior and highlights the applicability of pattern recognition methods.