Light Concentration by Metal-Dielectric Micro-Resonators for SERS Sensing
Abstract
:1. Introduction
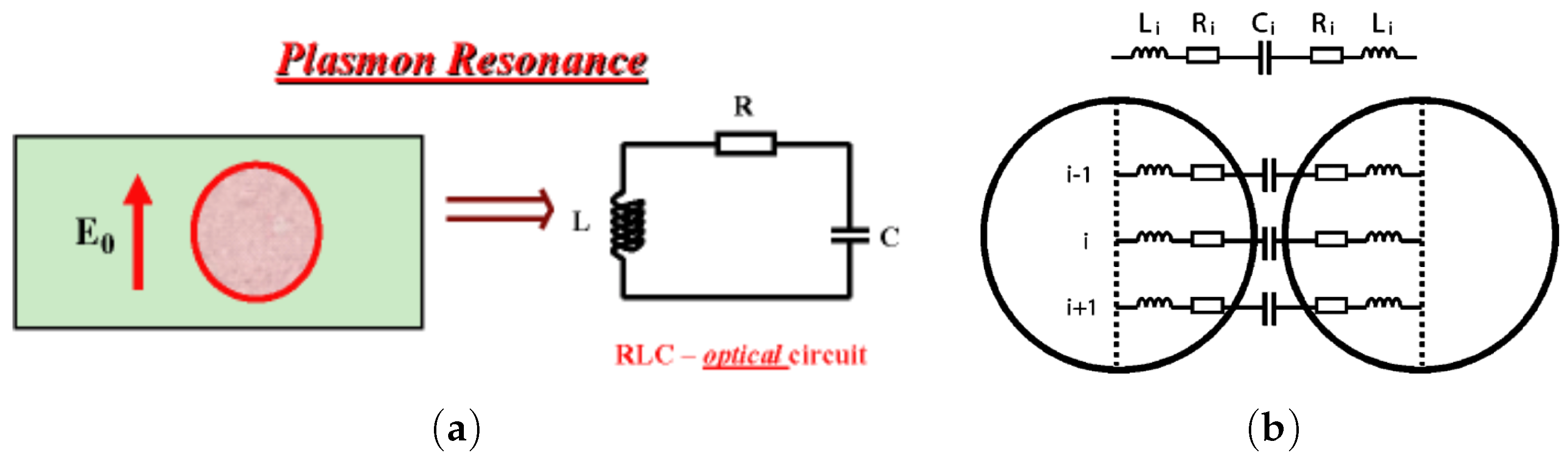
2. Plasmon Resonance and Field Enhancement
3. Surface Enhanced Raman Scattering (SERS)
4. Field Enhancement in Dielectric Resonators
5. Metal-Dielectric Resonances
6. Metal-Dielectric SERS Metasurfaces
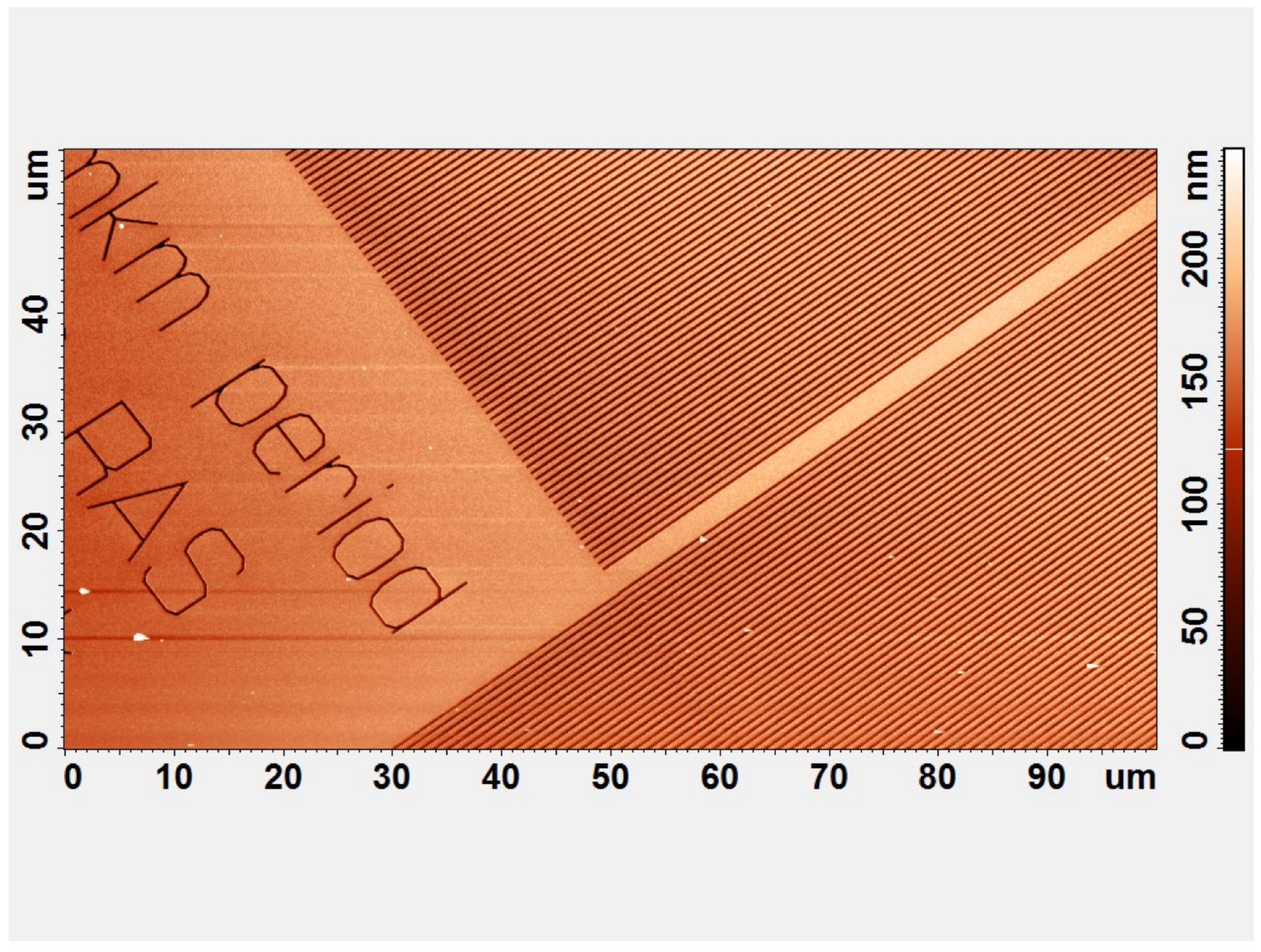
6.1. Periodic Bars
6.2. Periodic Blocks
7. 3D Dielectric Resonators for Surface Field Enhancement
7.1. WGM Resonators
7.2. Cone-Shaped Resonator
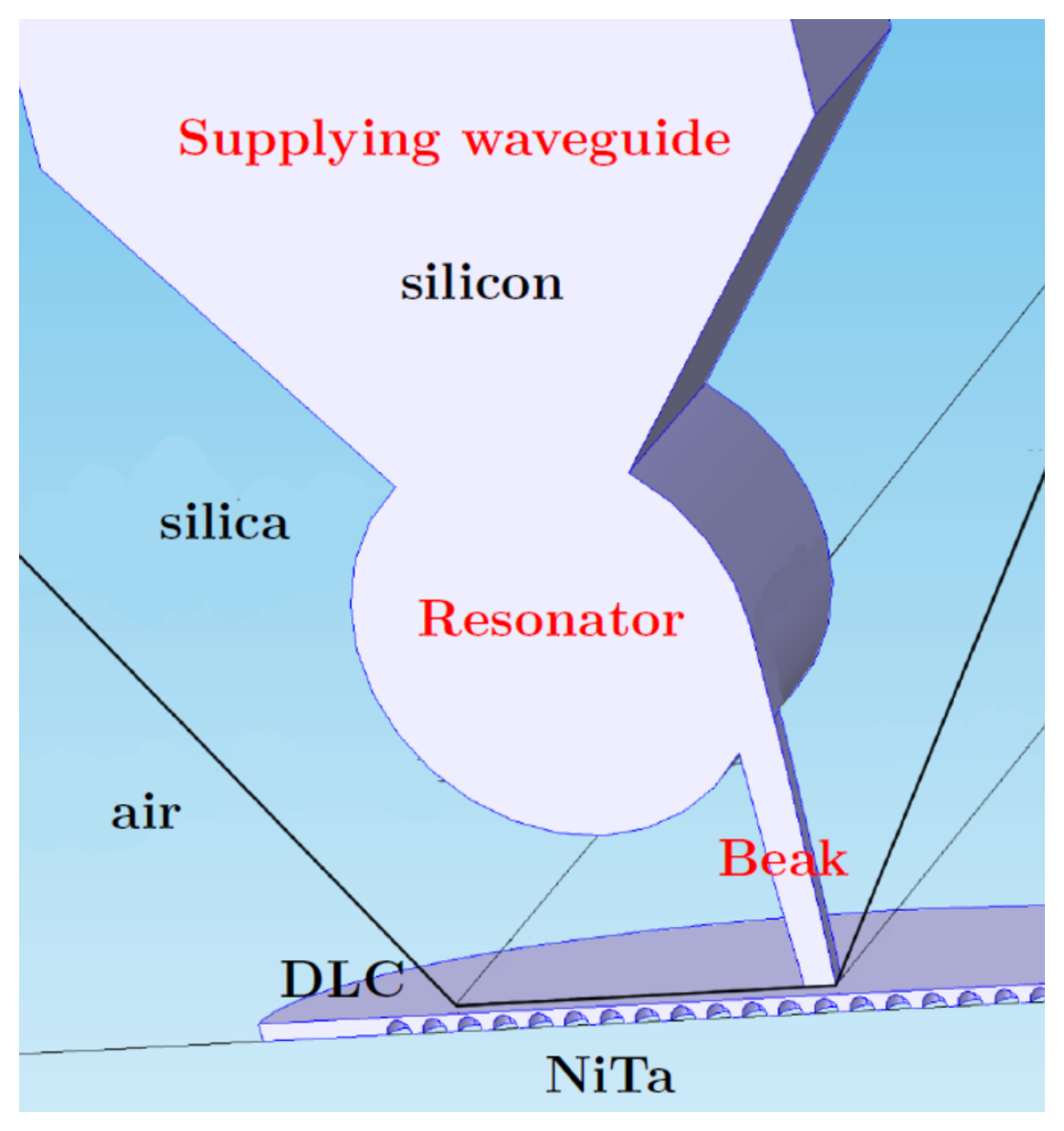
8. Local-Field Dielectric Transducer (LFDT)
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| ASNOM | Apertureless scanning near-field optical microscopy |
| AuNP | Gold nanoparticle |
| DLC | Diamond like carbon |
| DTNB | 5,5-Dithiobis-(2-nitrobenzoic acid) |
| EM | Electromagnetic |
| HAMR | Heat-assisted magnetic recording |
| LFDT | Local field dielectric transducer |
| PMMA | Polymethylmethacrylate |
| QED | Quantum electrodynamics |
| R & D | Research and development |
| SEM | Scanning electron microscopy |
| SERS | Surface-enhanced Raman scattering |
| SNOM | Scanning near-field optical microscopy |
| SP | Surface plasmon |
| TERS | Tip-enhanced Raman scattering |
| TNT | Trinitrotoluene |
| WGM | Whispering gallery mode |
References
- Faraday, M. Experimental relations of gold (and other metals) to light. Philos. Trans. R. Soc. Lond. 1857, 147, 145–181. [Google Scholar]
- Garnett, J.C.M. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. 1904, 203, 385. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S. The problem of the whispering gallery. Philos. Mag. 1910, 20, 1001–1004. [Google Scholar] [CrossRef]
- Armani, A.M.; Kulkarni, R.P.; Fraser, S.E.; Flagan, R.C.; Vahala, K.J. Label-free, single-molecule detection with optical microcavities. Sci. Mag. 2007, 317, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Challener, W.; Peng, C.; Itagi, A.; Karns, D.; Peng, W.; Peng, Y.; Yang, X.; Zhu, X.; Gokemeijer, N.; Hsia, Y.; et al. Heat-assisted magnetic recording by a near-field transducer with efficient optical energy transfer. Nat. Photonics 2009, 3, 220–224. [Google Scholar] [CrossRef]
- Vedantam, S.; Lee, H.; Tang, J.; Conway, J.; Staffaroni, M.; Yablonovitch, E. A plasmonic dimple lens for nanoscale focusing of light. Nano Lett. 2009, 9, 3447–3452. [Google Scholar] [CrossRef]
- Aoki, T.; Dayan, B.; Wilcut, E.; Bowen, W.P.; Parkins, A.S.; Kippenberg, T.J.; Vahala, K.J.; Kimble, H.J. Observation of strong coupling between one atom and a monolithic micro-resonator. Nature 2006, 443, 671–674. [Google Scholar] [CrossRef]
- Solano, M.; Faryad, M.; Hall, A.S.; Mallouk, T.E.; Monk, P.B.; Lakhtakia, A. Optimization of the absorption efficiency of an amorphous-silicon thin-film tandem solar cell backed by a metallic surface-relief grating. Appl. Opt. 2013, 52, 966–979. [Google Scholar] [CrossRef]
- Gresillon, S.; Aigouy, L.; Boccara, A.C.; Rivoal, J.C.; Quelin, X.; Desmarest, C.; Gadenne, P.; Shubin, V.A.; Sarychev, A.K.; Shalaev, V.M. Experimental observation of localized optical excitations in random metal-dielectric films. Phys. Rev. Lett. 1999, 82, 4520–4523. [Google Scholar] [CrossRef]
- Ivanov, A.V.; Shalygin, A.N.; Saryhev, A.K. TE-wave propagation through 2D array of metal nanocylinders. Solid State Phenom. 2012, 190, 577–580. [Google Scholar] [CrossRef]
- Ivanov, A.; Shalygin, A.; Lebedev, V.; Vorobev, V.; Vergiles, S.; Sarychev, A.K. Plasmonic extraordinary transmittance in array of metal nanorods. Appl. Phys. A 2012, 107, 17–21. [Google Scholar] [CrossRef]
- Ivanov, A.V.; Vaskin, A.V.; Lagarkov, A.N.; Sarychev, A.K. The field enhancement and optical sensing in the array of almost adjoining metal and dielectric nanorods. In Plasmonics: Metallic Nanostructures and Their Optical Properties XII; SPIE: Bellingham, WA, USA, 2014; p. 91633C. [Google Scholar] [CrossRef]
- Kurochkin, I.S.; Ryzhikov, I.A.; Sarychev, A.K.; Afanasiev, K.N.; Budashov, I.A.; Sedova, M.S.; Boginskaya, I.A.; Amitonov, S.; Lagarkov, A.N. New SERS-active junction based on cerium dioxide facet dielectric films for biosensing. Adv. Electromagn. 2014, 3, 57–60. [Google Scholar] [CrossRef]
- Afanasiev, K.N.; Boginskaya, I.A.; Budashov, I.A.; Ivanov, A.V.; Kurochkin, I.S.; Lagarkov, A.N.; Ryzhikov, I.A.; Sarychev, A.K. Giant field fluctuations in dielectric metamaterials and Raman sensors. In Plasmonics: Metallic Nanostructures and Their Optical Properties XII; SPIE: Bellingham, WA, USA, 2015; p. 95441Y1. [Google Scholar] [CrossRef]
- Ivanov, A.V.; Boginskaya, I.A.; Vaskin, A.V.; Afanas’ev, K.N.; Ryzhikov, I.A.; Lagarkov, A.N.; Sarychev, A. The field enhancement and optical sensing in the surface photonic chrystal. In Proceedings of the 2015 Days on Diffraction (DD), St. Petersburg, Russia, 25–29 May 2015; pp. 146–149. [Google Scholar] [CrossRef]
- Lagarkov, A.; Budashov, I.; Chistyaev, V.; Ezhov, A.; Fedyanin, A.; Ivanov, A.; Kurochkin, I.; Kosolobov, S.; Latyshev, A.; Nasimov, D.; et al. SERS-active dielectric metamaterials based on periodic nanostructures. Opt. Express 2016, 24, 7133–7150. [Google Scholar] [CrossRef] [PubMed]
- Sarychev, A.K.; Lagarkov, A.N.; Ivanov, A.V.; Boginskaya, I.A.; Bykov, I.V.; Ryzhikov, I.A.; Sedova, M.V.; Vaskin, A.V.; Kurochkin, I.N.; Rodionov, I.A.; et al. Metal-dielectric resonances in tip silicon metasurface and SERS based nanosensors. In Plasmonics: Design, Materials, Fabrication, Characterization, and Applications XV; SPIE: Bellingham, WA, USA, 2017; p. 103460C. [Google Scholar] [CrossRef]
- Lagarkov, A.; Boginkaya, I.; Bykov, I.; Budashov, I.; Ivanov, A.; Kurochkin, I.; Ryzhikov, I.; Rodionov, I.; Sedova, M.; Zverev, A.; et al. Light localization and SERS in tip-shaped silicon metasurface. Opt. Express 2017, 25, 17021–17038. [Google Scholar] [CrossRef] [PubMed]
- Bryche, J.F.; Gillibert, R.; Barbillon, G.; Gogol, P.; Moreau, J.; Lamy de la Chapelle, M.; Bartenlian, B.; Canva, M. Plasmonic enhancement by a continuous gold underlayer: Application to SERS sensing. Plasmonics 2016, 11, 601–608. [Google Scholar] [CrossRef]
- Barbillon, G.; Sandana, V.E.; Humbert, C.; Belier, B.; Rogers, D.J.; Teherani, F.H.; Bove, P.; McClintock, R.; Razeghi, M. Study of Au coated ZnO nanoarrays for surface en-hanced Raman scattering chemical sensing. J. Mater. Chem. C 2017, 5, 3528–3535. [Google Scholar] [CrossRef]
- Barbillon, G.; Bijeon, J.L.; Lerondel, G.; Plain, J.; Royer, P. Detection of chemical molecules with integrated plasmonic glass nanotips. Surf. Sci. 2008, 602, L119–L122. [Google Scholar] [CrossRef]
- Barbillon, G. Plasmonic nanostructures prepared by soft UV nanoimprint lithography and their application in biological sensing. Micromachines 2012, 3, 21–27. [Google Scholar] [CrossRef]
- Ignatov, A.I.; Merzlikin, A.M.; Baryshev, A.V. Wood anomalies for s-polarized light incident on a one-dimensional metal gratingand their coupling with channel plasmons. Phys. Rev. A 2017, 95, 053843. [Google Scholar] [CrossRef]
- Maier, S.A.; Kik, P.G.; Atwater, H.A.; Meltzer, S.; Harel, E.; Koel, B.E.; Requicha, A.A.G. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nat. Mater. 2003, 2, 229–232. [Google Scholar] [CrossRef]
- Alu, A.; Engheta, N. Theory of linear chains of metamaterial/plasmonic particles as subdiffraction optical nanotransmission lines. Phys. Rev. B 2006, 74, 205436. [Google Scholar] [CrossRef]
- Markel, V.; Sarychev, A. Propagation of surface plasmons in ordered and disordered chains of metal nanospheres. Phys. Rev. B 2007, 75, 1–11. [Google Scholar] [CrossRef]
- Hadad, Y.; Steinberg, B.Z. Green’s function theory for infinite and semi-infinite particle chains. Phys. Rev. B 2011, 84, 125402. [Google Scholar] [CrossRef]
- Auguie, B.; Barnes, W.L. Collective resonances in gold nanoparticle arrays. Phys. Rev. Lett. 2008, 101, 143902. [Google Scholar] [CrossRef] [PubMed]
- Weber, D.; Albella, P.; Alonso-Gonzalez, P.; Neubrech, F.; Gui, H.; Nagao, T.; Hillenbrand, R.; Aizpurua, J.; Pucci, A. Longitudinal and transverse coupling in infrared gold nanoantenna arrays: Long range versus short range interaction regimes. Opt. Express 2011, 19, 15047–15061. [Google Scholar] [CrossRef]
- Shalaev, V.M.; Cai, W.; Chettiar, U.; Yuan, H.K.; Sarychev, A.K.; Drachev, V.P.; Kildishev, A.V. Negative index of refraction in optical metamaterials. Opt. Lett. 2005, 30, 3356–3358. [Google Scholar] [CrossRef] [PubMed]
- Kildishev, A.V.; Cai, W.; Chettiar, U.; Yuan, H.K.; Sarychev, A.K.; Drachev, V.P.; Shalaev, V.M. Negative refractive index in optics of metal-dielectric composites. J. Opt. Soc. Am. B Opt. Phys. 2006, 23, 423–433. [Google Scholar] [CrossRef]
- Jen, Y.J.; Lakhtakia, A.; Yu, C.W.; Lin, C.T. Vapor-deposited thin films with negative real refractive index in the visible regime. Opt. Express 2009, 17, 7784–7789. [Google Scholar] [CrossRef]
- Ivanov, A.V.; Shalygin, A.N.; Galkin, V.Y.; Vedyayev, A.V.; Ivanov, V.A. Metamaterials from amorphous ferromagnetic microwires: interaction between microwires. Solid State Phenom. 2009, 152–153, 357–360. [Google Scholar] [CrossRef]
- Malyuzhinets, G.D. A note on the radiation principle. Sov. Phys. Tech. Phys. 1951, 21, 940–942. [Google Scholar]
- Veselago, V. The electrodynamics of substances with simultaneously negative values of ϵ and μ. Sov. Phys. Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bliokh, Y.P. Optical magnus effect as a consequence of berry phase anisotropy. JETP Lett. 2004, 79, 519–522. [Google Scholar] [CrossRef]
- Ivanov, A.V.; Shalygin, A.N.; Vedyaev, A.V.; Ivanov, V.A. Optical magnus effect in metamaterials fabricated from ferromagnetic microwires. JETP Lett. 2007, 85, 565–569. [Google Scholar] [CrossRef]
- Ono, A.; Kato, J.I.; Kawata, S. Subwavelength optical imaging through a metallic nanorod array. Phys. Rev. Lett. 2005, 95, 267407. [Google Scholar] [CrossRef] [PubMed]
- Shvets, G.; Trendafilov, S.; Pendry, J.; Sarychev, A. Guiding, focusing, and sensing on the subwavelength scale using metallic wire arrays. Phys. Rev. Lett. 2007, 99, 053903. [Google Scholar] [CrossRef] [PubMed]
- Ikonen, P.; Simovski, C.; Tretyakov, S.; Belov, P.; Hao, Y. Magnification of subwavelength field distributions at microwavefrequencies using a wire medium slab operating in the canalization regime. Appl. Phys. Lett. 2007, 91, 104102. [Google Scholar] [CrossRef]
- Belov, P.A.; Zhao, Y.; Tse, S.; Ikonen, P.; Silveirinha, M.G.; Simovski, C.R.; Tretyakov, S.; Hao, Y.; Parini, C. Transmission of images with subwavelength resolution to distances of several wavelengthsin the microwave range. Phys. Rev. B 2008, 77, 193108. [Google Scholar] [CrossRef]
- Kawata, S.; Ono, A.; Verma, P. Subwavelength colour imaging with a metallic nanolens. Nat. Photonics 2008, 2, 438–442. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.; Gong, Q. Metal-insulator-metal nanorod arrays for subwavelength imaging. Opt. Express 2009, 17, 2818–2825. [Google Scholar] [CrossRef] [PubMed]
- Silveirinha, M.G. Additional boundary conditions for nonconnected wire media. New J. Phys. 2009, 11, 113016. [Google Scholar] [CrossRef] [Green Version]
- Genov, D.; Sarychev, A.K.; Shalaev, V.M.; Wei, A. Resonant field enhancements from metal nanoparticle arrays. Nano Lett. 2004, 4, 153–158. [Google Scholar] [CrossRef]
- Le, F.; Brandl, D.W.; Urzhumov, Y.A.; Wang, H.; Kundu, J.; Halas, N.J.; Aizpurua, J.; Nordlander, P. Metallic nanoparticle arrays: A common substrate for both surface-enhanced Raman scattering and surface-enhanced infrared absorption. ACS Nano 2008, 2, 707–718. [Google Scholar] [CrossRef] [PubMed]
- Aubry, A.; Lei, D.; Maier, S.; Pendry, J.P. Broadband plasmonic device concentrating the energy at the nanoscale: The crescent-shaped cylinder. Phys. Rev. B 2010, 82, 125430. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Min, B.; Ostby, E.; Sorger, V.; Ulin-Avila, E.; Yang, L.; Zhang, X.; Vahala, K. High-Q surface plasmon polariton whispering gallery microcavity. Nature 2009, 457, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Tureci, H.; Schwefe, H.; Jacquod, P.; Stone, D. Modes of wave-chaotic dielectric resonators. Prog. Opt. 2005, 47, 75–108. [Google Scholar] [CrossRef]
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-high-Q toroid microcavityon a chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Mirgorodskiy, I.; Lihachev, G.; Gorodetsky, M.L.; Kippenberg, T.J. Mode Spectrum and temporal soliton formation in optical microresonators. Phys. Rev. Lett. 2014, 113, 123901. [Google Scholar] [CrossRef]
- Savchenkov, A.A.; Matsko, A.B.; Ilchenko, V.S.; Maleki, L. Optical resonators with ten million finesse. Opt. Express 2007, 15, 6768–6773. [Google Scholar] [CrossRef]
- Dumeige, Y.; Trebaol, S.; Ghisa, L.; Nguyen, T.K.; Tavernier, H.; Feron, P. Determination of coupling regime of high-Q resonators and optical gain of highly selective amplifiers. J. Opt. Soc. Am. B Opt. Phys. 2008, 25, 2073–2080. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453–455. [Google Scholar] [CrossRef] [PubMed]
- Sumetsky, M. Mode localization and the Q-factor of a cylindrical microresonator. Opt. Lett. 2010, 35, 2385–2387. [Google Scholar] [CrossRef]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing: Label-free detection down to single molecules. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef]
- Dantham, V.R.; Holler, S.; Kolchenko, V.; Wan, Z.; Arnold, S. Taking whispering gallery-mode single virus detection and sizing to the limit. Appl. Phys. Lett. 2012, 101, 043704. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Wiersig, J. Dielectric microcavities: Model systems for wave chaos and non-Hermitian physics. Rev. Mod. Phys. 2015, 87, 61–111. [Google Scholar] [CrossRef] [Green Version]
- Albella, P.; Ameen Poyli, M.; Schmidt, M.K.; Maier, S.A.; Moreno, F.; Saenz, J.J.; Aizpurua, J. Low-loss electric and magnetic field-enhanced spectroscopy with subwavelength silicon dimers. J. Phys. Chem. C 2013, 117, 13573–13584. [Google Scholar] [CrossRef]
- Bakker, R.M.; Permyakov, D.; Yu, Y.F.; Markovich, D.; Paniagua-Dominguez, R.; Gonzaga, L.; Samusev, A.; Kivshar, Y.; Luk’yanchuk, B.; Kuznetsov, A.I. Magnetic and Electric Hotspots with Silicon Nanodimers. Nano Lett. 2015, 15, 2137–2142. [Google Scholar] [CrossRef] [PubMed]
- Krasnok, A.E.; Miroshnichenko, A.E.; Belov, P.A.; Kivshar, Y.S. All-dielectric optical nanoantennas. Opt. Express 2012, 20, 20599–20604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, Y.; Pourmand, M.; Boriskina, S.V.; Reinhard, B.M. Enhanced light focusing in self-assembled optoplasmonic clusters with subwavelength dimensions. Adv. Mater. 2013, 25, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Qiu, Y.; Chen, T.; Reinhard, B.M. Rational assembly of optoplasmonic hetero-nanoparticle arrays with tunable photonic-plasmonic resonances. Adv. Funct. Mater. 2014, 24, 739–746. [Google Scholar] [CrossRef] [PubMed]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Jahani, S.; Jacob, Z. Transparent subdiffraction optics: Nanoscale light confinement without metal. Optica 2014, 1, 96–100. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Zhu, Z.; Yuan, X.; Qin, S. Strong field enhancement and light-matter interactions with all-dielectric metamaterials based on split bar resonators. Opt. Express 2014, 22, 30889–30898. [Google Scholar] [CrossRef]
- Maslov, A.V.; Astratov, V.N. Imaging of sub-wavelength structures radiating coherently near microspheres. Appl. Phys. Lett. 2016, 108, 051104. [Google Scholar] [CrossRef] [Green Version]
- Shorokhov, A.S.; Melik-Gaykazyan, E.V.; Smirnova, D.A.; Hopkins, B.; Chong, K.E.; Choi, D.Y.; Shcherbakov, M.R.; Miroshnichenko, A.E.; Neshev, D.N.; Fedyanin, A.A.; et al. Multifold enhancement of third-harmonic generation in dielectric nanoparticles driven by magnetic Fano resonances. Nano Lett. 2016, 16, 4857–4861. [Google Scholar] [CrossRef]
- Kim, S.J.; Fan, P.; Kang, J.H.; Brongersma, M.L. Creating semiconductor metafilms with designer absorption spectra. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Kurochkin, I.N.; Sarychev, A.K.; Ryzhikov, I.A.; Budashov, I.A.; Maklakov, S.S.; Boyarintsev, S.O.; Lagarkov, A.N. Surface-enhanced Raman scattering-based biosensors. In Portable Biosensing of Food Toxicants and Environmental Pollutants; Series in Sensors; CRC Press-Taylor & Francis Group: Boca Raton, FL, USA, 2014; pp. 97–121. [Google Scholar]
- Xu, H.; Aizpurua, J.; Kall, M.; Apell, P. Electromagnetic contributions to single-molecule sensitivity in surface-enhanced Raman scattering. Phys. Rev. E 2000, 62, 4318. [Google Scholar] [CrossRef]
- Kiran, M.S.; Itoh, T.; Yoshida, K.I.; Kawashima, N.; Biju, V.; Ishikawa, M. Selective Detection of HbA1c Using Surface Enhanced Resonance Raman Spectroscopy. Anal. Chem. 2010, 82, 1342–1348. [Google Scholar] [CrossRef]
- Sarychev, A.K.; Shalaev, V.M. Electrodynamics of Metamaterials; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2007; pp. 1–247. [Google Scholar]
- Brouers, F.; Blacher, S.; Lagarkov, A.N.; Sarychev, A.K.; Gadenne, P.; Shalaev, V.M. Theory of giant raman scattering from semicontinuous metal films. Phys. Rev. B 1997, 55, 13234–13245. [Google Scholar] [CrossRef]
- Genov, D.; Shalaev, V.; Sarychev, A. Surface plasmon excitation and correlation- induced localization-delocalization transition in semicontinuous metal films. Phys. Rev. B 2005, 72, 113102. [Google Scholar] [CrossRef]
- Seal, K.; Sarychev, A.K.; Noh, H.; Genov, D.A.; Yamilov, A.; Shalaev, V.M.; Ying, Z.C.; Cao, H. Near-field intensity correlations in semicontinuous metal-dielectric films. Phys. Rev. Lett. 2005, 94, 226101. [Google Scholar] [CrossRef] [PubMed]
- Seal, K.; Genov, D.A.; Sarychev, A.K.; Noh, H.; Shalaev, V.M.; Ying, Z.C.; Zhang, X.; Cao, H. Coexistence of localized and delocalized surface plasmon modes in percolating metal films. Phys. Rev. Lett. 2006, 97, 206103. [Google Scholar] [CrossRef] [PubMed]
- Sarychev, A.K.; Boyarintsev, S.O.; Rakhmanov, A.L.; Kugel, K.I.; Sukhorukov, Y.P. Collective volume plasmons in manganites with nanoscale phase separation: Simulation of the measured infrared spectra of La0.7Ca0.3MnO3. Phys. Rev. Lett. 2011, 107, 267401. [Google Scholar] [CrossRef] [PubMed]
- Raman, C.V.; Krishnan, K.S. A New Type of Secondary Radiation. Nature 1928, 121, 501–502. [Google Scholar] [CrossRef]
- Landsberg, G.; Mandelstam, L. Eine neue erscheinung bei der lichtzertreuung. Die Naturwissenschaften 1928, 16, 557–558. [Google Scholar]
- Landsherg, G.S.; Mandelstam, L.I. Uber die lichtzerstrenung in kristallen. Z. Fur. Phys. 1928, 50, 769–780. [Google Scholar] [CrossRef]
- Balcytis, A.; Nishijima, Y.; Krishnamoorthy, S.; Kuchmizhak, A.; Stoddart, P.R.; Petruskevicius, R.; Juodkazis, S. From fundamental toward applied SERS: Shared principlesand divergent approaches. Adv. Opt. Mater. 2018, 6, 1800292. [Google Scholar] [CrossRef]
- Fleischmann, M.; Hendra, P.; McQuillan, A. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166. [Google Scholar] [CrossRef]
- Zrimsek, A.B.; Wong, N.L.; Van Duyne, R.P. Single molecule surface-enhanced Raman spectroscopy: A critical analysis of the bianalyte vs. Isotopologue proof. J. Phys. Chem. C 2016, 120, 5133–5142. [Google Scholar] [CrossRef]
- Henry, A.I.; Ueltschi, T.W.; McAnally, M.O.; Van Duyne, R.P. Spiers memorial lecture surface-enhanced Raman spectroscopy: From single particle/molecule spectroscopy to angstrom-scale spatial resolution and femtosecond time resolution. Faraday Discuss. 2017, 205, 9–30. [Google Scholar] [CrossRef] [PubMed]
- Panneerselvam, R.; Liu, G.K.; Wang, Y.H.; Liu, J.Y.; Ding, S.Y.; Li, J.F.; Wu, D.Y.; Tian, Z.Q. Surface-enhanced Raman spectroscopy: Bottlenecks and future directions. Chem. Commun. 2018, 54, 10–25. [Google Scholar] [CrossRef]
- Ding, S.Y.; You, E.M.; Tian, Z.Q.; Moskovits, M. Electromagnetic theories of surface-enhanced Raman spectroscopy. Chem. Soc. Rev. 2017, 46, 4042–4076. [Google Scholar] [CrossRef]
- Le Ru, E.C.; Blackie, E.; Meyer, M.; Etchegoin, P.G. Surface enhanced Raman scattering enhancement Factors: A comprehensive study. J. Phys. Chem. C 2007, 111, 13794–13803. [Google Scholar] [CrossRef]
- Freeman, L.M.; Pang, L.; Fainman, Y. Maximizing the electromagnetic and chemical resonances of surface-enhanced Raman scattering for nucleic acids. ACS Nano 2014, 8, 8383–8391. [Google Scholar] [CrossRef] [PubMed]
- McNay, G.; Eustace, D.; Smith, W.; Faulds, K.; Graham, D. Surface-enhanced Raman scattering (SERS) and surface-enhanced resonance Raman scattering (SERRS): A review of applications. Appl. Spectrosc. 2011, 65, 825–837. [Google Scholar] [CrossRef]
- Morton, S.M.; Jensen, L. Understanding the molecule-surface chemical coupling in SERS. J. Am. Chem. Soc. 2009, 131, 4090–4098. [Google Scholar] [CrossRef]
- Laing, S.; Jamieson, L.E.; Faulds, K.; Graham, D. Surface-enhanced Raman spectroscopy for in vivo biosensing. Nat. Rev. Chem. 2017, 1, 1–19. [Google Scholar] [CrossRef]
- Sharma, B.; Frontiera, R.R.; Henry, A.I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Alessandri, I.; Lombardi, J.R. Enhanced Raman scattering with dielectrics. Chem. Rev. 2016, 116, 14921–14981. [Google Scholar] [CrossRef] [PubMed]
- McFarland, A.D.; Young, M.A.; Dieringer, J.A.; Van Duyne, R.P. Wavelength-scanned surface-enhanced Raman excitation spectroscopy. J. Phys. Chem. B 2005, 109, 11279–11285. [Google Scholar] [CrossRef] [PubMed]
- Perney, N.M.B.; Baumberg, J.J.; Zoorob, M.E.; Charlton, M.D.B.; Mahnkopf, S.; Netti, C.M. Tuning localized plasmons in nanostructured substrates for surface-enhanced Raman scattering. Opt. Express 2006, 14, 847–857. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Thubagere, A.; Premasiri, W.R.; Ziegler, L.D.; Negro, L.D.; Reinhard, B.M. Engineered SERS Substrates with Multiscale Signal Enhancement: Nanoparticle Cluster Arrays. ACS Nano 2009, 3, 1190–1202. [Google Scholar] [CrossRef]
- Fan, M.; Andrade, G.F.S.; Brolo, A.G. A review on the fabrication of substrates for surface enhanced Raman spectroscopy and their applications in analytical chemistry. Anal. Chim. Acta 2011, 693, 7–25. [Google Scholar] [CrossRef] [PubMed]
- Banaee, M.G.; Crozier, K.B. Mixed dimer double resonance substrates for surface-enhanced Raman spectroscopy. ACS Nano 2011, 5, 307–314. [Google Scholar] [CrossRef]
- Li, W.D.; Ding, F.; Hu, J.; Chou, S.Y. Three-dimensional cavity nanoantenna coupled plasmonic nanodots for ultrahigh and uniform surface-enhanced Raman scattering over large area. Opt. Express 2011, 19, 3925–3936. [Google Scholar] [CrossRef]
- Stolcova, L.; Proska, J.; Prochazka, M. Hexagonally ordered gold semishells as tunable SERS substrates. In Proceedings of the NANOCON, Brno, Czech Republic, 23–25 October 2012; pp. 225–229. [Google Scholar]
- Mattiucci, N.; D’Aguanno, G.; Everitt, H.O.; Foreman, J.V.; Callahan, J.M.; Buncick, M.C.; Bloemer, M.J. Ultraviolet surface-enhanced Raman scattering at the plasmonic band edge of a metallic grating. Opt. Express 2012, 20, 1868–1877. [Google Scholar] [CrossRef]
- Huang, J.A.; Zhao, Y.Q.; Zhang, X.J.; He, L.F.; Wong, T.L.; Chui, Y.S.; Zhang, W.J.; Lee, S.T. Ordered Ag/Si Nanowires Array: Wide-range surface-Enhanced Raman spectroscopy for reproducible biomolecule detection. Nano Lett. 2013, 13, 5039–5045. [Google Scholar] [CrossRef]
- Hu, F.; Lin, H.; Zhang, Z.; Liao, F.; Shao, M.; Lifshitz, Y.; Lee, S.T. Smart liquid SERS substrates based on Fe3O4/Au nanoparticles with reversibly tunable enhancement factor for practical quantitative detection. Sci. Rep. 2014, 4, 1–10. [Google Scholar] [CrossRef]
- Lee, J.; Hua, B.; Park, S.; Ha, M.; Lee, Y.; Fan, Z.; Ko, H. Tailoring surface plasmons of high-density gold nanostar assemblies on metal films for surface-enhanced Raman spectroscopy. Nanoscale 2014, 6, 616–623. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Liu, K.; Liu, Z.; Song, H.; Zeng, X.; Ji, D.; Cheney, A.; Jiang, S.; Gan, Q. Ultrabroadband Metasurface for Efficient Light Trapping and Localization: A Universal Surface-Enhanced Raman Spectroscopy Substrate for “All” Excitation Wavelengths. Adv. Mater. Interfaces 2015, 2, 1–7. [Google Scholar] [CrossRef]
- Jackson, J.B.; Westcott, S.L.; Hirsch, L.R.; West, J.L.; Halas, N.J. Controlling the surface enhanced Raman effect via the nanoshell geometry. Appl. Phys. Lett. 2003, 82, 257–259. [Google Scholar] [CrossRef]
- Campion, A.; Ivanecky, J.E.; Child, C.M.; Foster, M. On the mechanism of chemical enhancement in surface-enhanced Raman scattering. J. Am. Chem. Soc. 1995, 117, 11807–11808. [Google Scholar] [CrossRef]
- Kambhampati, P.; Child, C.M.; Foster, M.C.; Campion, A. On the chemical mechanism of surface enhanced Raman scattering: Experiment and theory. J. Chem. Phys. 1998, 108, 5013–5026. [Google Scholar] [CrossRef]
- Otto, A. The “chemical” (electronic) contribution to surface-enhanced Raman scattering. J. Raman Spectrosc. 2005, 36, 497–509. [Google Scholar] [CrossRef]
- Jensen, L.; Aikens, C.; Schatz, G. Electronic structure methods for studying surface-enhanced Raman scattering. Chem. Soc. Rev. 2008, 37, 1061–1073. [Google Scholar] [CrossRef]
- Jahn, M.; Patze, S.; Hidi, I.; Knipper, R.; Radu, A.; Muhlig, A.; Yuksel, S.; Peksa, V.; Weber, K.; Mayerhofer, T.; Cialla-May, D.; Popp, J. Plasmonic nanostructures for surface enhanced spectroscopic methods. Analyst 2016, 141, 756–793. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, X.; Lee, S.; He, Y. Silicon nanohybrid-based surface-enhanced Raman scattering sensors. Small 2014, 10, 4455–4468. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, X.; Zhou, H.; Shao, M.; Antonio Zapien, J.; Wong, N.; Lee, S. A high-efficiency surface-enhanced Raman scattering substrate based on silicon nanowires array decorated with silver nanoparticles. J. Phys. Chem. C 2010, 114, 1969–1975. [Google Scholar] [CrossRef]
- Galopin, E.; Barbillat, J.; Coffinier, Y.; Szunerits, S.; Patriarche, G.; Boukherroub, R. Silicon nanowires coated with silver nanostructures as ultrasensitive interfaces for surface-enhanced Raman spectroscopy. ACS Appl. Mater. Interfaces 2009, 1, 1396–1403. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Hubner, J.; Boisen, A. Large Area Fabrication of Leaning Silicon Nanopillars for Surface Enhanced Raman Spectroscopy. Adv. Mater. 2012, 24, OP11–OP18. [Google Scholar] [CrossRef] [PubMed]
- Bryche, J.F.; Belier, B.; Bartenlian, B.; Barbillon, G. Low-cost SERS substrates composed of hybrid nanoskittles for a highly sensitive sensing of chemical molecules. Sens. Actuators B 2017, 239, 795–799. [Google Scholar] [CrossRef]
- Magno, G.; Belier, B.; Barbillon, G. Gold thickness impact on the enhancement of SERS detection in low-cost Au/Si nanosensors. J. Mater. Sci. 2017, 52, 13650–13656. [Google Scholar] [CrossRef]
- Magno, G.; Belier, B.; Barbillon, G. Al/Si nanopillars as very sensitive SERS substrates. Materials 2018, 11, 1534. [Google Scholar] [CrossRef] [PubMed]
- Sinha, G.; Depero, L.; Alessandri, I. Recyclable SERS substrates based on Au-coated ZnO nanorods. ACS Appl. Mater. Interfaces 2011, 3, 2557–2563. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Hogan, T.; Shanker, B. Gold-coated zinc oxide nanowire-based substrate for surface-enhanced Raman spectroscopy. J. Raman Spectrosc. 2009, 40, 1539–1545. [Google Scholar] [CrossRef]
- Cheng, C.; Yan, B.; Wong, S.; Li, X.; Zhou, W.; Yu, T.; Shen, Z.; Yu, H.; Fan, H. Fabrication and SERS performance of silver-nanoparticle-decorated Si/ZnO nanotrees in ordered arrays. ACS Appl. Mater. Interfaces 2010, 2, 1824–1828. [Google Scholar] [CrossRef] [PubMed]
- Cui, S.; Dai, Z.; Tian, Q.; Liu, J.; Xiao, X.; Jiang, C.; Wu, W.; Roy, V. Wetting properties and SERS applications of ZnO/Ag nanowire arrays patterned by a screen printing method. J. Mater. Chem. C 2016, 4, 6371–6379. [Google Scholar] [CrossRef]
- Shan, Y.; Yang, Y.; Cao, Y.; Fu, C.; Huang, Z. Synthesis of wheatear-like ZnO nano arrays decorated with Ag nanoparticles and its improved SERS performance through hydrogenation. Nanotechnology 2016, 27, 145502. [Google Scholar] [CrossRef] [PubMed]
- Vo-Dinh, T.; Allain, L.R.; Stokes, D.L. Cancer gene detection using surface-enhanced Raman scattering (SERS). J. Raman Spectrosc. 2002, 33, 511–516. [Google Scholar] [CrossRef]
- Gniadecka, M.; Philipsen, P.A.; Sigurdsson, S.; Wessel, S.; Nielsen, O.F.; Christensen, D.H.; Hercogova, J.; Rossen, K.; Thomsen, H.K.; Gniadecki, R.; Hansen, L.K.; Wulf, H.C. Melanoma Diagnosis by Raman Spectroscopy and Neural Networks: Structure Alterations in Proteins and Lipids in Intact Cancer Tissue. J. Investig. Dermatol. 2004, 122, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Kim, J.S.; Choi, H.; Lee, S.M.; Jun, B.H.; Yu, K.N.; Kuk, E.; Kim, Y.K.; Jeong, D.H.; Cho, M.H.; Lee, Y.S. Nanoparticle probes with surface enhanced Raman spectroscopic tags for cellular cancer targeting. Anal. Chem. 2006, 78, 6967–6973. [Google Scholar] [CrossRef] [PubMed]
- Sha, M.; Xu, H.; Natan, M.J.; Cromer, R. Surface-enhanced Raman scattering tags for rapid and homogeneous detection of circulating tumor cells in the presence of human whole blood. J. Am. Chem. Soc. 2008, 130, 17214–17215. [Google Scholar] [CrossRef]
- Qian, X.; Peng, X.H.; Ansari, D.O.; Yin-Goen, Q.; Chen, G.Z.; Shin, D.M.; Yang, L.; Young, A.N.; Wang, M.D.; Nie, S. In vivo tumor targeting and spectroscopic detection with surface-enhanced Raman nanoparticle tags. Nat. Biotechnol. 2008, 26, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Chon, H.; Lee, S.; Son, S.; Oh, C.H.; Choo, J. Highly sensitive immunoassay of lung cancer marker carcinoembryonic antigen using surface-enhanced Raman scattering of hollow gold nanospheres. Anal. Chem. 2009, 81, 3029–3034. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Singh, A.K.; Khan, S.A.; Senapati, D.; Yu, H.; Ray, P.C. Gold Nano-popcorn-based targeted diagnosis, nanotherapy treatment, and in situ monitoring of photothermal therapy response of prostate cancer cells using surface-enhanced Raman spectroscopy. J. Am. Chem. Soc. 2010, 132, 18103–18114. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Qian, X.; Beitler, J.J.; Chen, Z.G.; Khuri, F.R.; Lewis, M.M.; Shin, H.J.; Nie, S.; Shin, D.M. Detection of circulating tumor cells in human peripheral blood using surface-enhanced Raman scattering nanoparticles. Cancer Res. 2011, 71, 1526–1532. [Google Scholar] [CrossRef] [PubMed]
- Samanta, A.; Maiti, K.K.; Soh, K.S.; Liao, X.; Vendrell, M.; Dinish, U.S.; Yun, S.W.; Bhuvaneswari, R.; Kim, H.; Rautela, S.; et al. Ultrasensitive near-infrared Raman reporters for SERS-based in vivo cancer detection. Angew. Chem. Int. Ed. 2011, 50, 6089–6092. [Google Scholar] [CrossRef]
- Lin, D.; Feng, S.; Pan, J.; Chen, Y.; Lin, J.; Chen, G.; Xie, S.; Zeng, H.; Chen, R. Colorectal cancer detection by gold nanoparticle based surface-enhanced Raman spectroscopy of blood serum and statistical analysis. Opt. Express 2011, 19, 13565–13577. [Google Scholar] [CrossRef]
- Song, J.; Zhou, J.; Duan, H. Self-assembled plasmonic vesicles of SERS-encoded amphiphilic gold nanoparticles for cancer cell targeting and traceable intracellular drug delivery. J. Am. Chem. Soc. 2012, 134, 13458–13469. [Google Scholar] [CrossRef] [PubMed]
- Maiti, K.K.; Dinish, U.S.; Samanta, A.; Vendrell, M.; Soh, K.S.; Park, S.J.; Olivo, M.; Chang, Y.T. Multiplex targeted in vivo cancer detection using sensitive near-infrared SERS nanotags. Nano Today 2012, 7, 85–93. [Google Scholar] [CrossRef]
- Jokerst, J.V.; Cole, A.J.; Van de Sompel, D.; Gambhir, S.S. Gold nanorods for ovarian cancer detection with photoacoustic imaging and resection guidance via Raman Imaging in living mice. ACS Nano 2012, 6, 10366–10377. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Lin, D.; Lin, J.; Li, B.; Huang, Z.; Chen, G.; Zhang, W.; Wang, L.; Pan, J.; Chen, R.; Zeng, H. Blood plasma surface-enhanced Raman spectroscopy for non-invasive optical detection of cervical cancer. Analyst 2013, 138, 3967–3974. [Google Scholar] [CrossRef]
- Vendrell, M.; Maiti, K.K.; Dhaliwal, K.; Chang, Y.T. Surface-enhanced Raman scattering in cancer detection and imaging. Trends Biotechnol. 2013, 31, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Mert, S.; Ozbek, E.; Otunctemur, A.; Culha, M. Kidney tumor staging using surface-enhanced Raman scattering. J. Biomed. Opt. 2015, 20, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Velicka, M.; Urboniene, V.; Ceponkus, J.; Pucetaite, M.; Jankevicius, F.; Sablinskas, V. Detection of cancerous biological tissue areas by means of infrared absorption and SERS spectroscopy of intercellular fluid. Proc. SPIE 2015, 9550, 95500A. [Google Scholar] [CrossRef]
- Granger, J.H.; Schlotter, N.E.; Crawford, A.C.; Porter, M.D. Prospects for point-of-care pathogen diagnostics using surface-enhanced Raman scattering (SERS). Chem. Soc. Rev. 2015, 45, 3865–3882. [Google Scholar] [CrossRef] [PubMed]
- Rong, Z.; Wang, C.; Wang, J.; Wang, D.; Xiao, R.; Wang, S. Magnetic immunoassay for cancer biomarker detection based on surface-enhanced resonance Raman scattering from coupled plasmonic nanostructures. Biosens. Bioelectron. 2016, 84, 15–21. [Google Scholar] [CrossRef]
- Pazos, E.; Garcia-Algar, M.; Penas, C.; Nazarenus, M.; Torruella, A.; Pazos-Perez, N.; Guerrini, L.; Vazquez, M.; Garcia-Rico, E.; Mascarenas, J.; et al. Surface-Enhanced Raman Scattering Surface Selection Rules for the Proteomic Liquid Biopsy in Real Samples: Efficient Detection of the Oncoprotein c-MYC. J. Am. Chem. Soc. 2016, 138, 14206–14209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oseledchyk, A.; Andreou, C.; Wall, M.A.; Kircher, M.F. Folate-targeted surface-enhanced resonance Raman scattering nanoprobe ratiometry for detection of microscopic ovarian cancer. ACS Nano 2016, 11, 1488–1497. [Google Scholar] [CrossRef] [PubMed]
- Litti, L.; Amendola, V.; Toffoli, G.; Meneghetti, M. Detection of low-quantity anticancer drugs by surface-enhanced Raman scattering. Anal. Bioanal. Chem. 2016, 408, 2123–2131. [Google Scholar] [CrossRef] [PubMed]
- Schurmann, R.; Bald, I. Decomposition of DNA Nucleobases by laser irradiation of gold nanoparticles monitored by surface- enhanced Raman scattering. J. Phys. Chem. C 2016, 120, 3001–3009. [Google Scholar] [CrossRef]
- Andreou, C.; Neuschmelting, V.; Tschaharganeh, D.F.; Huang, C.H.; Oseledchyk, A.; Iacono, P.; Karabeber, H.; Colen, R.R.; Mannelli, L.; Lowe, S.W.; et al. Imaging of liver tumors using surface-enhanced Raman scattering Nanoparticles. ACS Nano 2016, 10, 5015–5026. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Pan, F.; Liu, J.; Wang, K.; Zhang, C.; Cheng, S.; Lu, L.; Zhang, W.; Zhang, Z.; et al. Breath analysis based on surface-enhanced Raman scattering sensors distinguishes early and advanced gastric cancer patients from healthy persons. ACS Nano 2016, 10, 8169–8179. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ren, J.Q.; Zhang, X.G.; Wu, D.Y.; Shen, A.G.; Hu, J.M. Alkyne-modulated surface-enhanced Raman scattering-palette for optical interference-free and multiplex cellular imaging. Anal. Chem. 2016, 88, 6115–6119. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Choi, N.; Wang, R.; Lee, S.; Moon, K.C.; Yoon, S.Y.; Chen, L.; Choo, J. Simultaneous detection of dual prostate specific antigens using surface-enhanced Raman scattering-based immunoassay for accurate diagnosis of prostate cancer. ACS Nano 2017, 11, 4926–4933. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Z.; Zhu, B.; Ma, Y.; Lin, B.; Liu, R.; Song, Y.; Lin, H.; Tu, S.; Yang, C.J. Surface-enhanced Raman Scattering active plasmonic nanoparticles with ultrasmall interior nanogap for multiplex quantitative detection and cancer cell imaging. Anal. Chem. 2016, 88, 7828–7836. [Google Scholar] [CrossRef]
- Kneipp, J. Interrogating cells, tissues, and live animalswith new generations of surface-enhanced raman scattering probes and labels. ACS Nano 2017, 11, 1136–1141. [Google Scholar] [CrossRef]
- Harmsen, S.; Wall, M.A.; Huang, R.; Kircher, M.F. Cancer imaging using surface-enhanced resonance Raman scattering nanoparticles. Nat. Protoc. 2017, 12, 1400–1414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.; Bjerneld, E.J.; Kall, M.; Borjesson, L. Spectroscopy of single hemoglobin molecules by surface enhanced Raman Scattering. Phys. Rev. Lett. 1999, 83, 4357–4360. [Google Scholar] [CrossRef]
- Dingari, N.C.; Horowitz, G.L.; Kang, J.W.; Dasari, R.R.; Barman, I. Raman spectroscopy provides a powerful diagnostic tool for accurate determination of albumin glycation. PLoS ONE 2012, 7, e32406. [Google Scholar] [CrossRef] [PubMed]
- Barman, I.; Dingari, N.C.; Kang, J.W.; Horowitz, G.L.; Dasari, R.; Feld, M.S. Raman spectroscopy- based sensitive and specific detection of glycated hemoglobin. Anal. Chem. 2012, 84, 2474–2482. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Lin, J.; Huang, Z.; Lu, P.; Wang, J.; Wang, X.; Chen, R. Raman Spectroscopy of human hemoglobin for diabetes detection. J. Innov. Opt. Health Sci. 2014, 7, 1350051. [Google Scholar] [CrossRef]
- Das, G.; Mecarini, F.; Angelis, F.D.; Prasciolu, M.; Liberale, C.; Patrini, M.; Fabrizio, E.D. Attomole (amol) myoglobin Raman detection from plasmonic nanostructures. Microelectron. Eng. 2008, 85, 1282–1285. [Google Scholar] [CrossRef]
- Benford, M.E.; Wang, M.; Kameoka, J.; Cote, G.L. Detection of Cardiac Biomarkers Exploiting Surface Enhanced Raman Scattering (SERS) using a Nanofluidic Channel Based Biosensor towards Coronary Point-of-Care Diagnostics. In Plasmonics in Biology and Medicine VI; SPIE: Bellingham, WA, USA, 2009; p. 719203. [Google Scholar]
- Chon, H.; Lee, S.; Yoon, S.Y.; Lee, E.K.; Chang, S.l.; Choo, J. SERS-based competitive immunoassay of troponin I and CK-MB markers for early diagnosis of acute myocardial infarction. Chem. Commun. 2014, 50, 1058–1060. [Google Scholar] [CrossRef]
- Wang, R.; Chon, H.; Lee, S.; Cheng, Z.; Hong, S.H.; Yoon, Y.H.; Choo, J. Highly sensitive detection of hormone estradiol E2 using SERS-based immunoassays for the clinical diagnosis of precocious puberty. ACS Appl. Mater. Interfaces 2016, 8, 10665–10672. [Google Scholar] [CrossRef]
- Bodelon, G.; Montes-Garcia, V.; Lopez-Puente, V.; Hill, E.H.; Hamon, C.; Sanz-Ortiz, M.N.; Rodal-Cedeira, S.; Costas, C.; Celiksoy, S.; Perez-Juste, I.; et al. Detection and imaging of quorum sensing in Pseudomonas aeruginosa biofilm communities by surface-enhanced resonance Raman scattering. Nat. Mater. 2016, 15, 1203–1211. [Google Scholar] [CrossRef] [Green Version]
- Duan, N.; Chang, B.; Zhang, H.; Wang, Z.; Wu, S. Salmonella typhimurium detection using a surface-enhanced Raman scattering-based aptasensor. Int. J. Food Microbiol. 2016, 218, 38–43. [Google Scholar] [CrossRef]
- Duan, N.; Yan, Y.; Wu, S.; Wang, Z. Vibrio parahaemolyticus detection aptasensor using surface-enhanced Raman scattering. Food Control 2016, 63, 122–127. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Z.; Zhao, B.; Hou, R.Y.; Kinchla, A.; Clark, J.M.; He, L. Real-time and in situ monitoring of pesticide penetration in edible leaves by surface-enhanced Raman scattering mapping. Anal. Chem. 2016, 88, 5243–5250. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Y.; Kannan, P.; Zhang, L.; Lin, Z.; Zhang, J.; Chen, T.; Guo, L. Flexible and adhesive SERS Active tape for rapid detection of pesticide residues in fruits and vegetables. Anal. Chem. 2016, 88, 2149–2155. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Meng, G.; Wu, N.; Zhou, N.; Chen, B.; Li, F.; Huang, Q. Dipping into a drink: Basil-seed supported silver nanoparticles as surface-enhanced Raman scattering substrates for toxic molecule detection. Sens. Actuators B 2016, 223, 447–452. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Jiang, Q.; Liu, K.K.; Luan, J.; Naik, R.R.; Singamaneni, S. Bacterial nanocellulose- based flexible surface enhanced Raman scattering substrate. Adv. Mater. Interfaces 2016, 3, 1–8. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, H.; Hu, Z.; Yu, G.; Yang, D.; Zhao, J. Label and label-free based surface-enhanced Raman scattering for pathogen bacteria detection: A review. Biosens. Bioelectron. 2017, 94, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Ding, P.; Shi, Y.; Jin, T.; Su, Y.; Wang, H.; He, Y. Portable and reliable Surface-Enhanced raman scattering silicon chip for signal-on detection of trace trinitrotoluene explosive in real systems. Anal. Chem. 2017, 89, 5072–5078. [Google Scholar] [CrossRef] [PubMed]
- Hakonen, A.; Rindcevicius, T.; Schmidt, M.S.; Andresson, P.O.; Juhlin, L.; Svedendahl, M.; Boisen, A.; Kall, M. Detection of nerve gases using surface-enhanced Raman scattering substrates with high droplet adhesion. Nanoscale 2016, 8, 1305–1308. [Google Scholar] [CrossRef] [Green Version]
- Boyarintsev, S.O.; Sarychev, A.K. Computer simulation of surface-enhanced Raman scattering in nanostructured metamaterials. J. Exp. Theor. Phys. 2011, 113, 963–971. [Google Scholar] [CrossRef]
- Ma, R.M.; Ota, S.; Li, Y.; Yang, S.; Zhang, X. Explosives detection in a lasing plasmon nanocavity. Nat. Nanotechnol. 2014, 9, 600–604. [Google Scholar] [CrossRef] [PubMed]
- Soteropulos, C.E.; Hunt, H.K.; Armani, A.M. Determination of binding kinetics using whispering gallery mode microcavities. Appl. Phys. Lett. 2011, 99, 103703. [Google Scholar] [CrossRef]
- Shopova, S.I.; Rajmangal, R.; Holler, S.; Arnold, S. Plasmonic enhancement of a whispering-gallery-mode biosensor for single nanoparticle detection. Appl. Phys. Lett. 2011, 98, 243104. [Google Scholar] [CrossRef]
- Ozer, N. Optical properties and electrochromic characterization of sol-gel deposited ceria films. Sol. Energy Mater. Sol. Cells 2001, 68, 391–400. [Google Scholar] [CrossRef]
- Patsalas, P.; Logothetidis, S.; Metaxa, C. Optical performance of nanocrystalline transparent ceria films. Appl. Phys. Lett. 2002, 81, 466–468. [Google Scholar] [CrossRef]
- Krogman, K.; Druffel, T.; Sunkara, M. Anti-reflective optical coatings incorporating nanoparticles. Nanotechnology 2005, 16, S338–S343. [Google Scholar] [CrossRef] [PubMed]
- Verma, A.; Karar, N.; Bakhshi, A.K.; Chander, H.; Shivaprasad, S.M.; Agnihotry, S.A. Structural, morphological and photoluminescence characteristics of sol-gel derived nano phase CeO2 films deposited using citric acid. J. Nanopart. Res. 2007, 9, 317–322. [Google Scholar] [CrossRef]
- Mansilla, C. Structure, microstructure and optical properties of cerium oxide thin films prepared by electron beam evaporation assisted with ion beams. Solid State Sci. 2009, 11, 1456–1464. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Sundari, S.T.; Kuppusami, P.; Mohan, P.C.; Srinivasan, M.; Mohandas, E.; Ganesan, V.; Sastikumar, D. A study of microstructural and optical properties of nanocrystalline ceria thin films prepared by pulsed laser deposition. Thin Solid Films 2011, 519, 2520–2526. [Google Scholar] [CrossRef]
- Oh, T.S.; Tokpanov, Y.S.; Hao, Y.; Jung, W.; Haile, S.M. Determination of optical and microstructural parameters of ceria films. J. Appl. Phys. 2012, 112, 103535. [Google Scholar] [CrossRef] [Green Version]
- Murugan, R.; Vijayaprasath, G.; Mahalingam, T.; Hayakawa, Y.; Ravi, G. Effect of RF power on the properties of magnetron sputtered CeO2 thin films. J. Mater. Sci. Mater. Electron. 2015, 26, 2800–2809. [Google Scholar] [CrossRef]
- Tribelsky, M.I.; Luk’yanchuk, B.S. Anomalous light scattering by small particles. Phys. Rev. Lett. 2006, 97, 263902–263906. [Google Scholar] [CrossRef]
- Vergeles, S.S.; Sarychev, A.K.; Tartakovsky, G.T. All-dielectric light concentrator to subwavelength volume. Phys. Rev. B 2017, 95, 085401. [Google Scholar] [CrossRef]
- Ru, E.C.L.; Etchegoin, P.G. Principles of Surface-Enhanced Raman Spectroscopy and Related Plasmonic Effects; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Rahmani, M.; Lukyanchuk, B.; Ng, B.; Tavakkoli, A.K.G.; Liew, Y.F.; Hong, M. Generation of pronounced Fano resonances and tuning of subwavelength spatial light distribution in plasmonic pentamers. Opt. Express 2011, 19, 4952–4956. [Google Scholar] [CrossRef]
- Li, K.; Stockman, M.I.; Bergman, D.J. Self-Similar Chain of Metal Nanospheres as an Efficient Nanolens. Phys. Rev. Lett. 2003, 91, 227402. [Google Scholar] [CrossRef] [PubMed]
- Schultz, D.A. Plasmon Resonant particles for biological detection. Curr. Opin. Biotech. 2003, 14, 13–22. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Kristensen, A.; Yang, J.K.W.; Bozhevolnyi, S.I.; Link, S.; Nordlander, P.; Halas, N.J.; Mortensen, N.A. Plasmonic colour generation. Nat. Rev. Mater. 2016, 2, 16088. [Google Scholar] [CrossRef]
- Hong, Y.; Reinhard, B.M. Collective photonic-plasmonic resonances in noble metal-dielectric nanoparticle hybrid arrays. Opt. Mat. Express 2014, 4, 2409–2422. [Google Scholar] [CrossRef]
- Pi, S.; Zeng, X.; Zhang, N.; Ji, D.; Chen, B.; Song, H.; Cheney, A.; Xu, Y.; Jiang, S.; Sun, D.; Song, Y.; Gan, Q. Dielectric-grating-coupled surface plasmon resonance from the back side of the metal film for ultrasensitive sensing. IEEE Photonics J. 2016, 8, 1–7. [Google Scholar] [CrossRef]
- Santiago-Cordoba, M.A.; Boriskina, S.V.; Vollmer, F.; Demirel, M.C. Nanoparticle-based protein detection by optical shift of a resonant microcavity. Appl. Phys. Lett. 2011, 99, 073701. [Google Scholar] [CrossRef]
- Gromova, M.S.; Sigolaeva, L.V.; Fastovets, M.A.; Evtushenko, E.G.; Babin, I.A.; Pergushov, D.V.; Amitonov, S.V.; Eremenko, A.V.; Kurochkin, I.N. Improved adsorption of choline oxidase on a polyelectrolyte LBL film in the presence of iodide anions. Soft Matter. 2011, 7, 7404–7409. [Google Scholar] [CrossRef]
- Tamer, U.; Boyaci, I.; Temur, E.; Zengin, A.; Dincer, I.; Elerman, Y. Fabrication of magnetic gold nanorod particles for immunomagnetic separation and SERS application. J. Nanopart. Res. 2011, 13, 3167–3176. [Google Scholar] [CrossRef]
- Bandarenka, H.V.; Girel, K.V.; Bondarenko, V.P.; Khodasevich, I.A.; Panarin, A.Y.; Terekhov, S.N. Formation regularities of plasmonic silver nanostructures on porous silicon for effective surface-enhanced Raman scattering. Nanoscale Res. Lett. 2016, 11, 262. [Google Scholar] [CrossRef] [PubMed]
- Cottat, M.; Lidgi-Guigui, N.; Tijunelyte, I.; Barbillon, G.; Hamouda, F.; Gogol, P.; Aassime, A.; Lourtioz, J.M.; Bartenlian, B.; Lamy de la Chapelle, M. Soft UV nanoimprint lithography-designed highly sensitive substrates for SERS detection. Nanoscale Res. Lett. 2014, 9, 623. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hentschel, M.; Saliba, M.; Vogelgesang, R.; Giessen, H.; Alivisatos, A.P.; Liu, N. Transition from isolated to collective modes in plasmonic oligomers. Nano Lett. 2010, 10, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Atay, T.; Song, J.H.; Nurmikko, A. Strongly interacting plasmon nanoparticles: From dipole interaction to conductively coupled regime. Nano Lett. 2004, 4, 1627–1631. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mat. 2013, 25, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Swiontek, S.; Faryad, M.; Lakhtakia, A. Surface plasmonic polaritonic sensor using a dielectric columnar thin film. J. Nanophotonics 2014, 8, 083986. [Google Scholar] [CrossRef]
- Lakhtakia, A.; Faryad, M. Theory of optical sensing with Dyakonov-Tamm waves. J. Nanophotonics 2014, 8, 083072. [Google Scholar] [CrossRef]
- Sumetsky, M. Whispering-gallery-bottle microcavities: The three-dimensional etalon. Opt. Lett. 2004, 29, 8–10. [Google Scholar] [CrossRef]
- Sumetsky, M. Localization of light on a cone: Theoretical evidence and experimental demonstration for an optical fiber. Opt. Lett. 2011, 36, 145–147. [Google Scholar] [CrossRef]
- Barannik, A.A.; Bunyaev, S.A.; Cherpak, N.T. Conical quasioptical dielectric resonator. Tech. Phys. Lett. 2005, 31, 811–812. [Google Scholar] [CrossRef]
- Kishk, A.A.; Yin, Y.; Glisson, A.W. Conical dielectric resonator antennas for wide-band applications. IEEE Trans. Antennas Propag. 2002, 50, 469–474. [Google Scholar] [CrossRef]
- Kishk, A.A.; Zhang, X.; Glisson, A.W.; Kajfez, D. Numerical analysis of stacked dielectric resonator antennas excited by a coaxial probe for wideband applications. IEEE Trans. Antennas Propag. 2003, 51, 1996–2006. [Google Scholar] [CrossRef]
- Chern, G.D.; Tureci, H.E.; Stone, A.D.; Chang, R.K.; Kneissl, M.; Johnson, N.M. Unidirectional lasing from InGaN multiple-quantum-well spiral-shaped micropillars. Appl. Phys. Lett. 2003, 83, 1710–1712. [Google Scholar] [CrossRef]
- Gmachl, C.; Capasso, F.; Narimanov, E.E.; Nockel, J.U.; Stone, A.D.; Faist, J.; Sivco, D.L.; Cho, A.Y. High-Power Directional Emission from Microlasers with Chaotic Resonators. Science 1998, 280, 1556–1564. [Google Scholar] [CrossRef] [Green Version]
- Gmachl, C.; Narimanov, E.E.; Capasso, F.; Baillargeon, J.N.; Cho, A.Y. Kolmogorov-Arnold-Moser transition and laser action on scar modes in semiconductor diode lasers with deformed resonators. Opt. Lett. 2002, 27, 824–826. [Google Scholar] [CrossRef]
- Fang, W.; Cao, H.; Podolskiy, V.A.; Narimanov, E.E. Dynamical localization in microdisk lasers. Opt. Express 2005, 13, 5641–5652. [Google Scholar] [CrossRef] [PubMed]
- Bykov, V.; Gologanov, A.; Shevyakov, V. Test structure for SPM tip shape deconvolution. Appl. Phys. A 1998, 66, 499–502. [Google Scholar] [CrossRef]
- Green, M.A.; Keevers, M.J. Optical Properties of Intrinsic Silicon at 300 K. Prog. Photovolt. 1995, 3, 189–192. [Google Scholar] [CrossRef]
- Hussain, S.; Bhatia, C.S.; Yang, H.; Danner, A.J. Characterization of C-apertures in a successful demonstration of heat-assisted magnetic recording. Opt. Lett. 2015, 40, 3444–3447. [Google Scholar] [CrossRef] [PubMed]
- Schuller, J.; Barnard, E.; Cai, W.; Jun, Y.; White, J.; Brongersma, M. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Novotny, L.; Hulst, N. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Fedorov, I.A.; Parfenyev, V.M.; Vergeles, S.S.; Tartakovsky, G.T.; Sarychev, A.K. Allowable number of plasmons in nanoparticle. JETP Lett. 2014, 100, 530–534. [Google Scholar] [CrossRef]
- Vergeles, S.S.; Sarychev, A.K. Silicon plasmonics and optical field concentration at nanometer scale. In Metamaterials, Metadevices, and Metasystems 2015; SPIE: Bellingham, WA, USA, 2015; p. 954415. [Google Scholar]
- Yuan, G.; Rogers, E.; Roy, T.; Shen, Z.; Zheludev, N. Flat super-oscillatory lens for heat-assisted magnetic recording with sub-50 nm resolution. Opt. Express 2014, 22, 6428–6437. [Google Scholar] [CrossRef] [PubMed]
- Bohn, J.L.; Nesbitt, D.J.; Gallagher, A. Field enhancement in apertureless near-field scanning optical microscopy. JOSA A 2001, 18, 2998–3006. [Google Scholar] [CrossRef]
- Bouhelier, A.; Beversluis, M.; Hartschuh, A.; Novotny, L. Near- Field Second- Harmonic Generation Induced by Local Field Enhancement. Phys. Rev. Lett. 2003, 90, 013903. [Google Scholar] [CrossRef]
- Cancado, L.; Hartschuh, A.; Novotny, L. Tip-enhanced Raman spectroscopy of carbon nanotubes. J. Raman Spectrosc. 2009, 40, 1420–1426. [Google Scholar] [CrossRef]
- Gerton, J.M.; Wade, L.A.; Lessard, G.A.; Ma, Z.; Quake, S.R. Tip-enhanced fluorescence microscopy at 10 nanometer resolution. Phys. Rev. Lett. 2004, 93, 180801. [Google Scholar] [CrossRef] [PubMed]
- Kato, S.; Chonan, S.; Aoki, T. High-numerical-aperture microlensed tip on an air-clad optical fiber. Opt. Lett. 2014, 39, 773–776. [Google Scholar] [CrossRef]
- Wang, Y.; Du, Z.; Park, Y.; Chen, C.; Zhang, X.; Pan, L. Quasi-3D plasmonic coupling scheme for near-field optical lithography and imaging. Opt. Lett. 2015, 40, 3918–3921. [Google Scholar] [CrossRef]
- Song, Q.; Ge, L.; Redding, B.; Cao, H. Channeling Chaotic Rays into Waveguides for Efficient Collection of Microcavity Emission. Phys. Rev. Lett. 2012, 108, 243902. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Mizusawa, A.; Ishida, K.; Seki, T.; Shima, T.; Takanashi, K. Magneto-Optical Spectra of Ordered and Disordered FePt Films Prepared at Reduced Temperatures. Trans. Magn. Soc. Jpn. 2004, 4, 297–300. [Google Scholar] [CrossRef]
- Bergmann, J.; Heusinger, M.; Andra, G.; Falk, F. Temperature dependent optical properties of amorphous silicon for diode laser crystallization. Opt. Express 2012, 20, A856–A863. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Pandey, M.; Chand, N.; Biswas, A.; Bhattacharya, D.; Dash, S.; Tyagi, A.; Dey, R.; Kulkarni, S.; Patil, D. Optical and mechanical properties of diamond like carbon films deposited by microwave ECR plasma CVD. Bull. Mater. Sci. 2008, 31, 813–818. [Google Scholar] [CrossRef]
- Mednikarov, B.; Spasov, G.; Babeva, T.; Pirov, J.; Sahatchieva, M.; Popova, C.; Kulischa, W. Optical properties of diamond-like carbon and nanocrystalline diamond films. J. Optoelectron. Adv. Mater. 2005, 7, 1407–1413. [Google Scholar]
- Almeida, V.R.; Xu, Q.; Barrios, C.A.; Lipson, M. Guiding and confining light in void nanostructure. Opt. Lett. 2004, 29, 1209–1211. [Google Scholar] [CrossRef] [PubMed]
- Koos, C.; Vorreau, P.; Vallaitis, T.; Dumon, P.; Bogaerts, W.; Baets, R.; Esembeson, B.; Biaggio, I.; Michinobu, T.; Diederich, F.; et al. All-optical high-speed signal processing with silicon-organic hybrid slot waveguides. Nat. Photonics 2009, 3, 216–219. [Google Scholar] [CrossRef]
- Liu, Q.; Tu, X.; Kim, K.W.; Kee, J.S.; Shin, Y.; Han, K.; Yoon, Y.J.; Lo, G.Q.; Park, M.K. Highly sensitive Mach-Zehnder interferometer biosensor based on silicon nitride slot waveguide. Sens. Actuators B 2013, 188, 681–688. [Google Scholar] [CrossRef]
- Mongia, R.K.; Bhartia, P. Dielectric resonator antennas-A review and general design relations for resonant frequency and bandwidth. Int. J. Microw. Millim.-Wave Comput.-Aided Eng. 1994, 4, 230–247. [Google Scholar] [CrossRef]
- Permyakov, D.; Sinev, I.; Markovich, D.; Ginzburg, P.; Samusev, A.; Belov, P.; Valuckas, V.; Kuznetsov, A.I.; Lukanchuk, B.S.; Miroshnichenko, A.E.; et al. Probing magnetic and electric optical responses of silicon nanoparticles. Appl. Phys. Lett. 2015, 106, 171110. [Google Scholar] [CrossRef]
- Weller, D.; Mosendz, O.; Parker, G.; Pisana, S.; Santos, T.S. L1 0 FePtX-Y media for heat-assisted magnetic recording. Phys. Status Solidi (a) 2013, 210, 1245–1260. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Cher, K.M.; Varghese, B.; Xu, B.; Lim, C.; Shi, J.; Chen, Y.; Ye, K.; Zhang, J.; An, C.; et al. FePt-based hamr media with a function layer for better thermal control. IEEE Trans. Magn. 2016, 52, 1–6. [Google Scholar] [CrossRef]


































| Au-NP Localization | Signal (Counts) | Au-NP Number | Normalized Signal |
|---|---|---|---|
| Pyramid side | 786 | 1 | 786 |
| Between pyramids | 553 | 30 | 18.4 |
| Outside of grating | 553 | 89 | 6.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarychev, A.K.; Ivanov, A.; Lagarkov, A.; Barbillon, G. Light Concentration by Metal-Dielectric Micro-Resonators for SERS Sensing. Materials 2019, 12, 103. https://doi.org/10.3390/ma12010103
Sarychev AK, Ivanov A, Lagarkov A, Barbillon G. Light Concentration by Metal-Dielectric Micro-Resonators for SERS Sensing. Materials. 2019; 12(1):103. https://doi.org/10.3390/ma12010103
Chicago/Turabian StyleSarychev, Andrey K., Andrey Ivanov, Andrey Lagarkov, and Grégory Barbillon. 2019. "Light Concentration by Metal-Dielectric Micro-Resonators for SERS Sensing" Materials 12, no. 1: 103. https://doi.org/10.3390/ma12010103
APA StyleSarychev, A. K., Ivanov, A., Lagarkov, A., & Barbillon, G. (2019). Light Concentration by Metal-Dielectric Micro-Resonators for SERS Sensing. Materials, 12(1), 103. https://doi.org/10.3390/ma12010103






