Studies on Pitting Corrosion of Al-Cu-Li Alloys Part II: Breakdown Potential and Pit Initiation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Passive Film Characterization
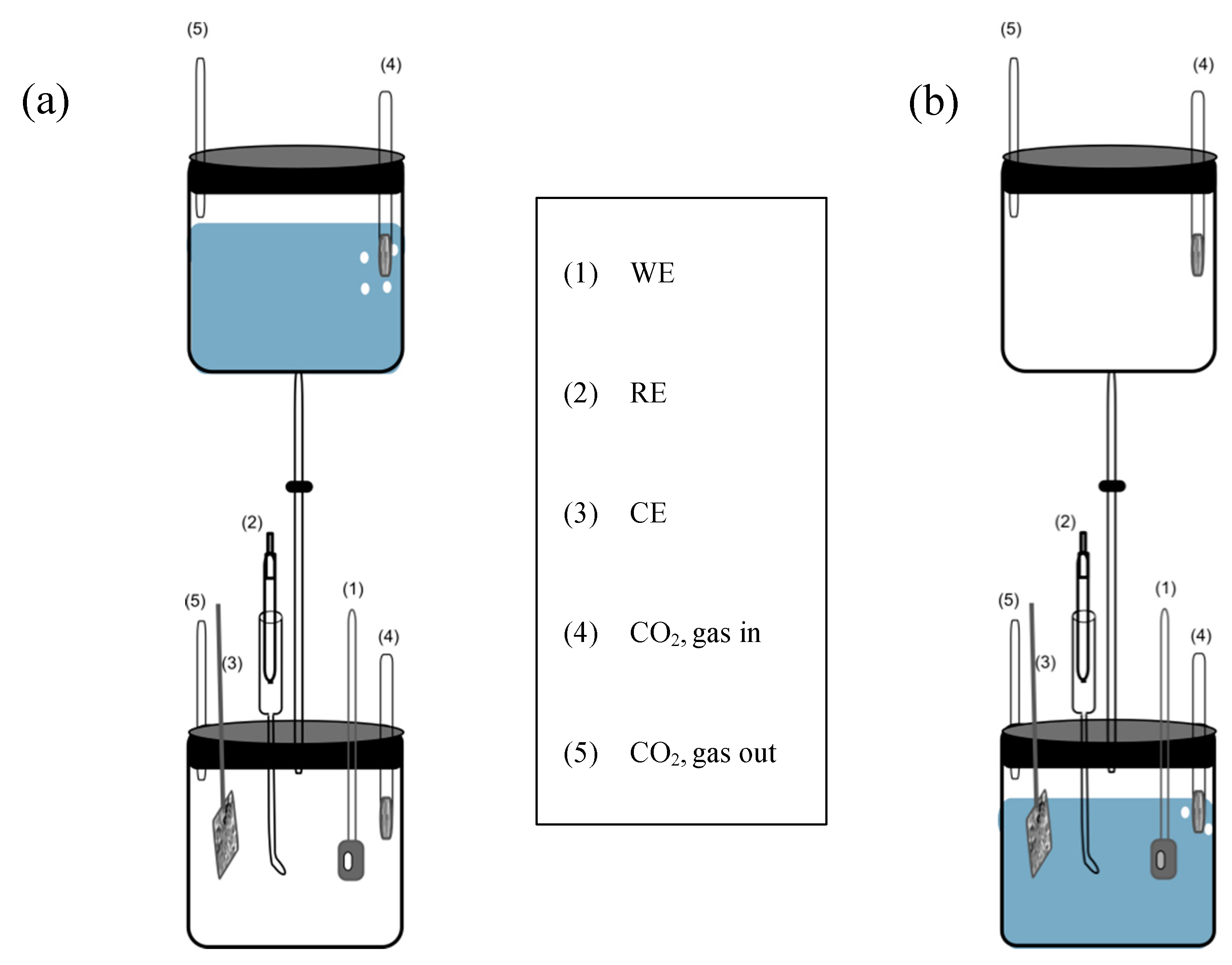
2.3. Electrochemical Measurements
3. Results
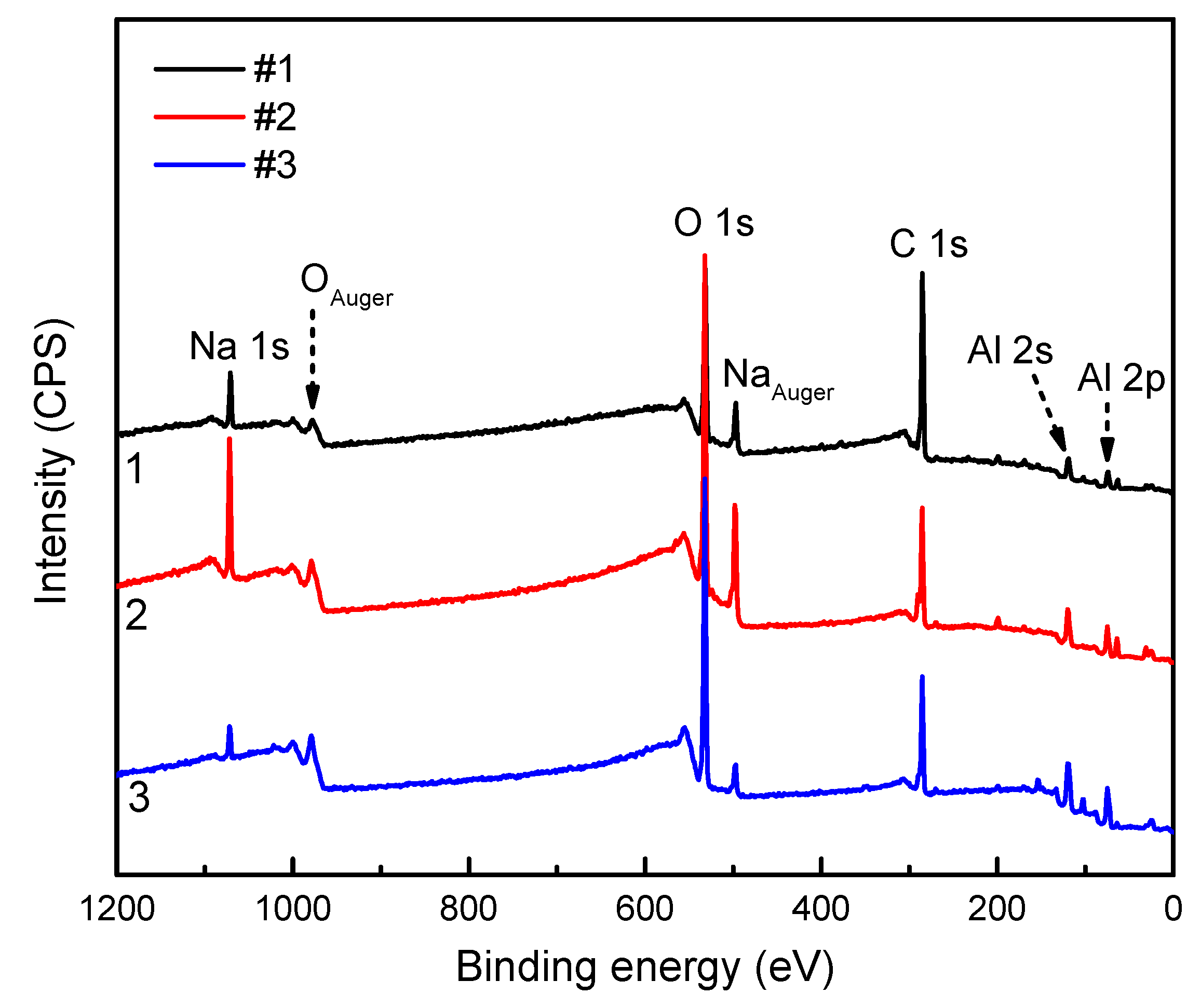
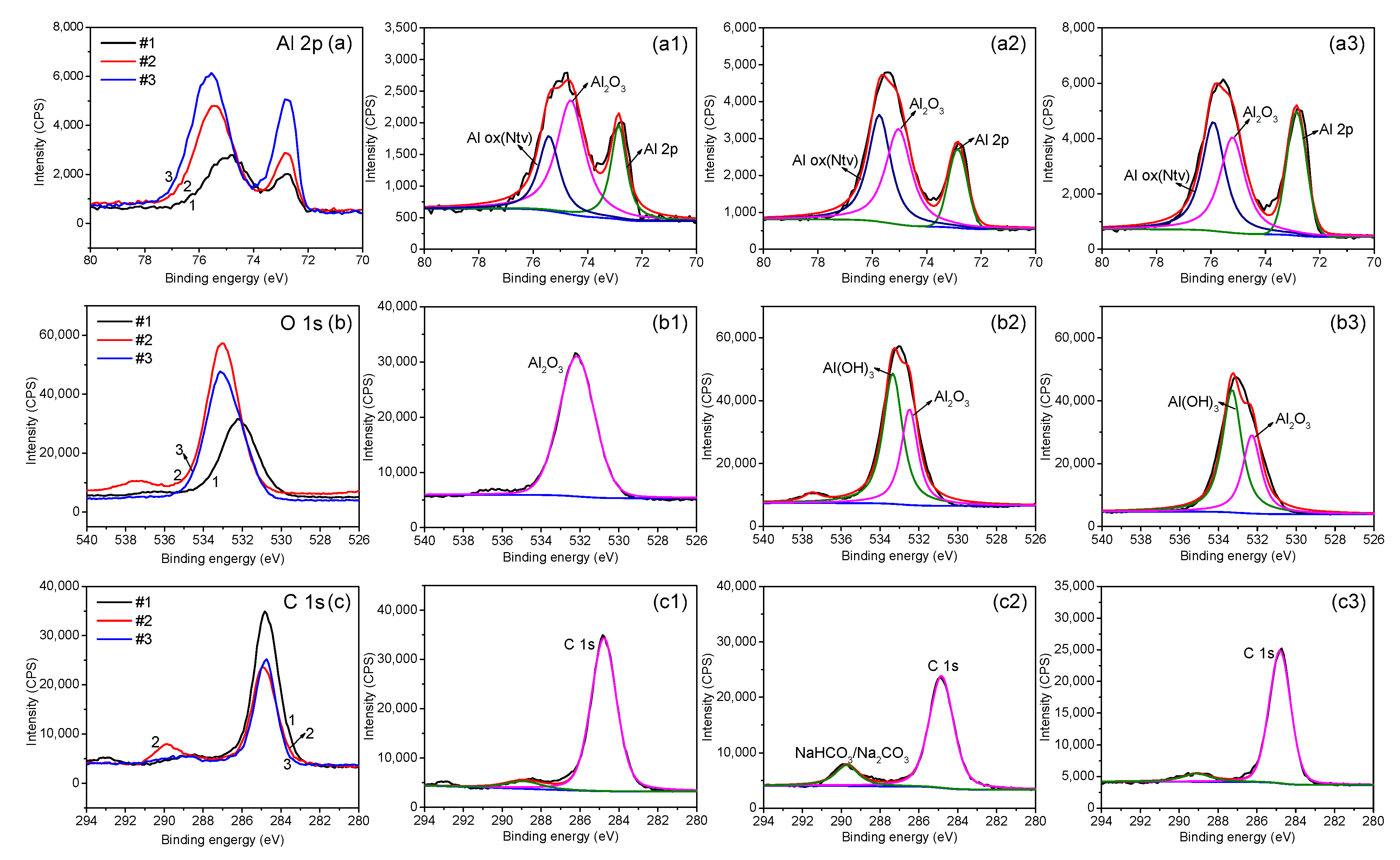
3.1. XPS Analysis of the Passive Film
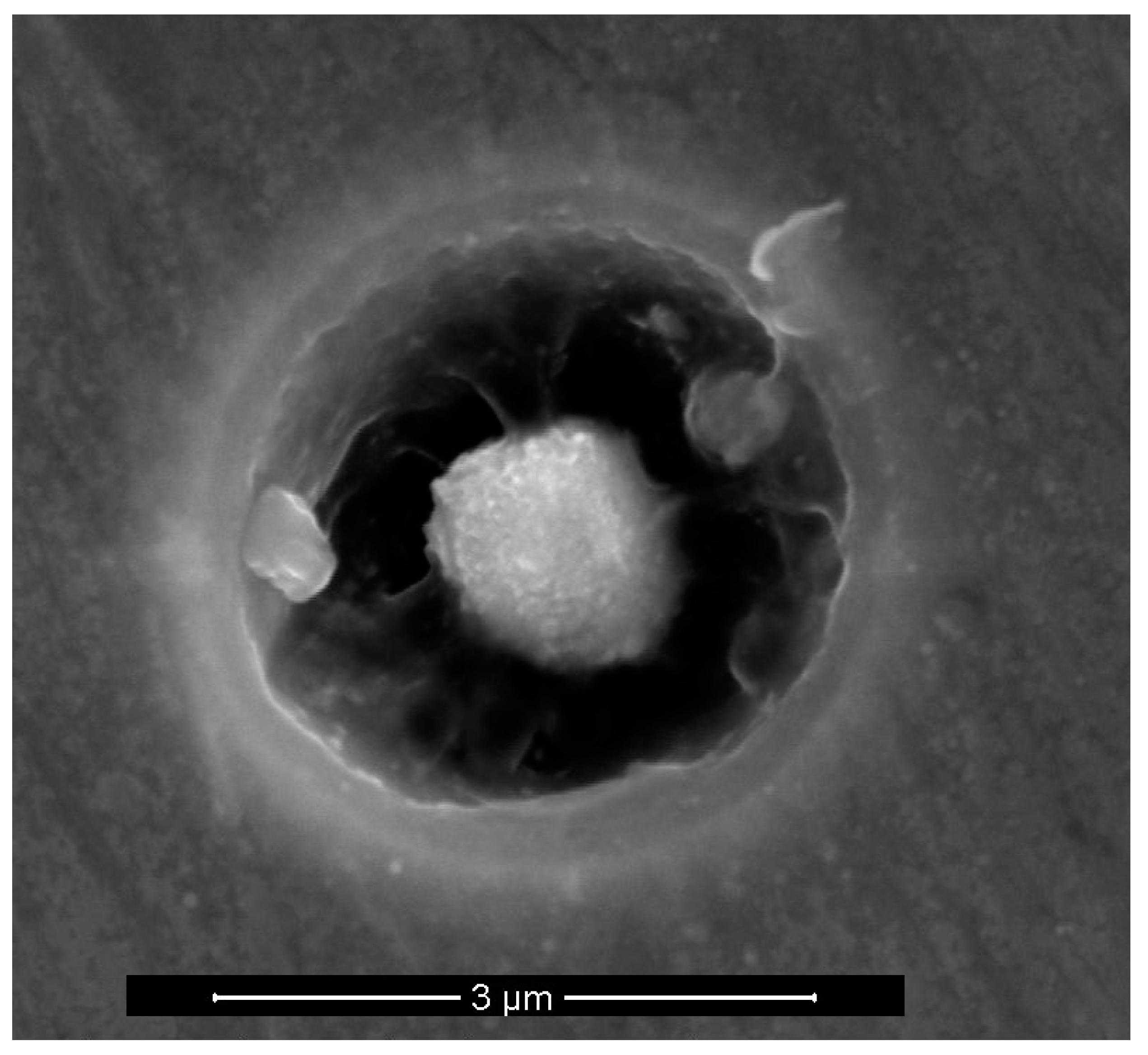
3.2. Precipitates, Particles and Pit Nucleation
3.3. Potentiodynamic Polarization
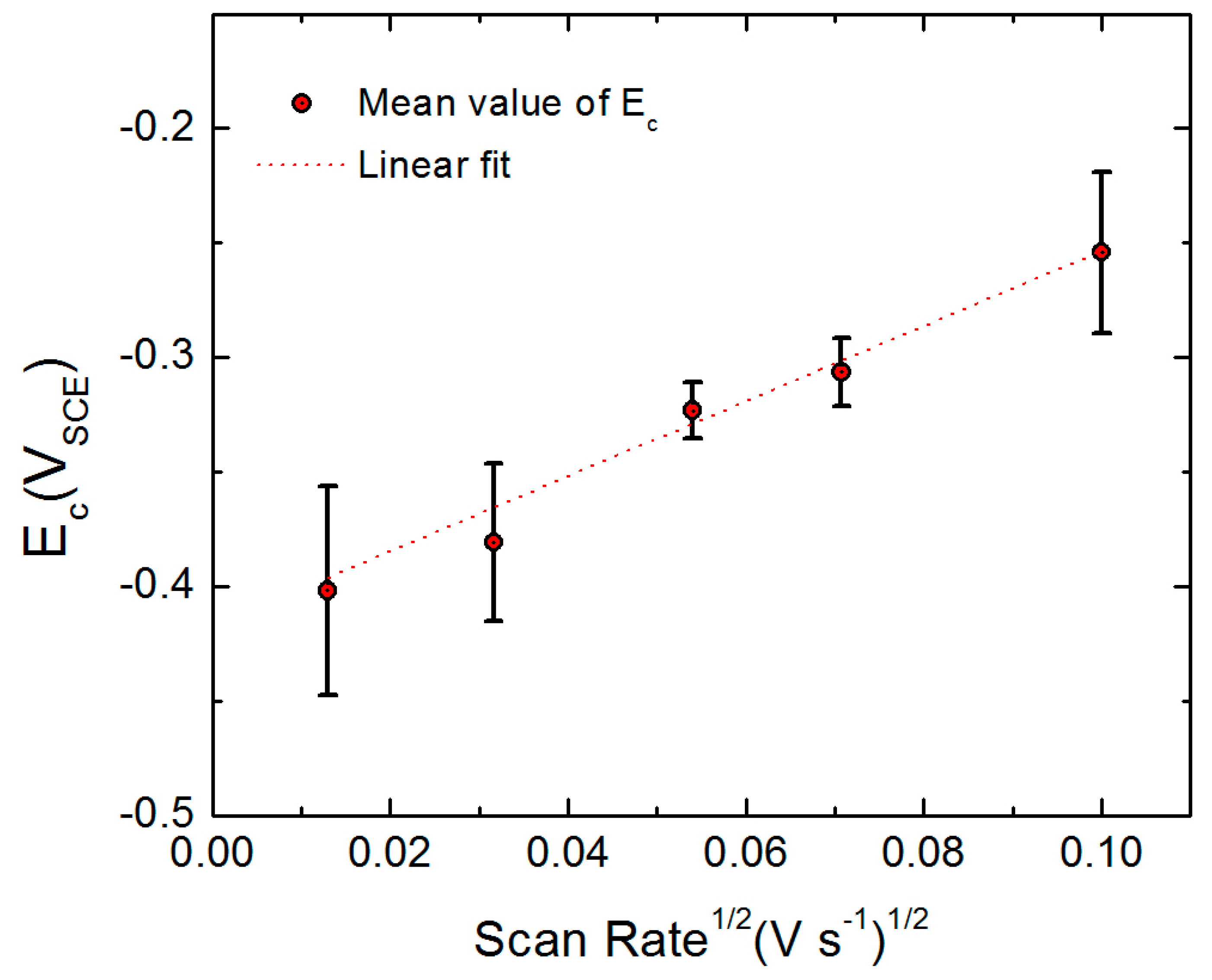
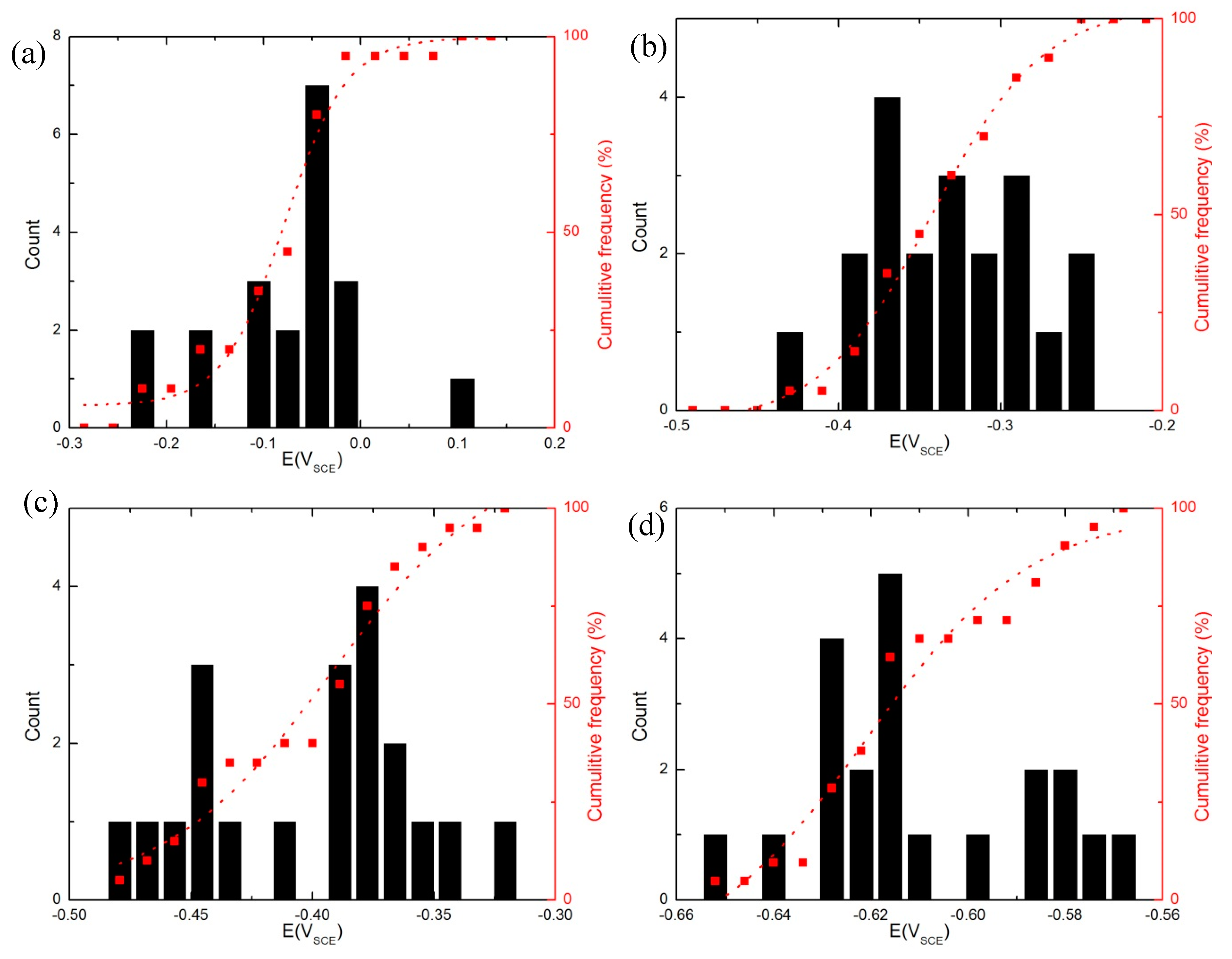
3.4. Critical Breakdown Potential of AA2098-T851
3.5. Passivity Breakdown of AA2098-T851
4. Discussion
4.1. Passivity Breakdown of AA2098-T851 Based on the PDM
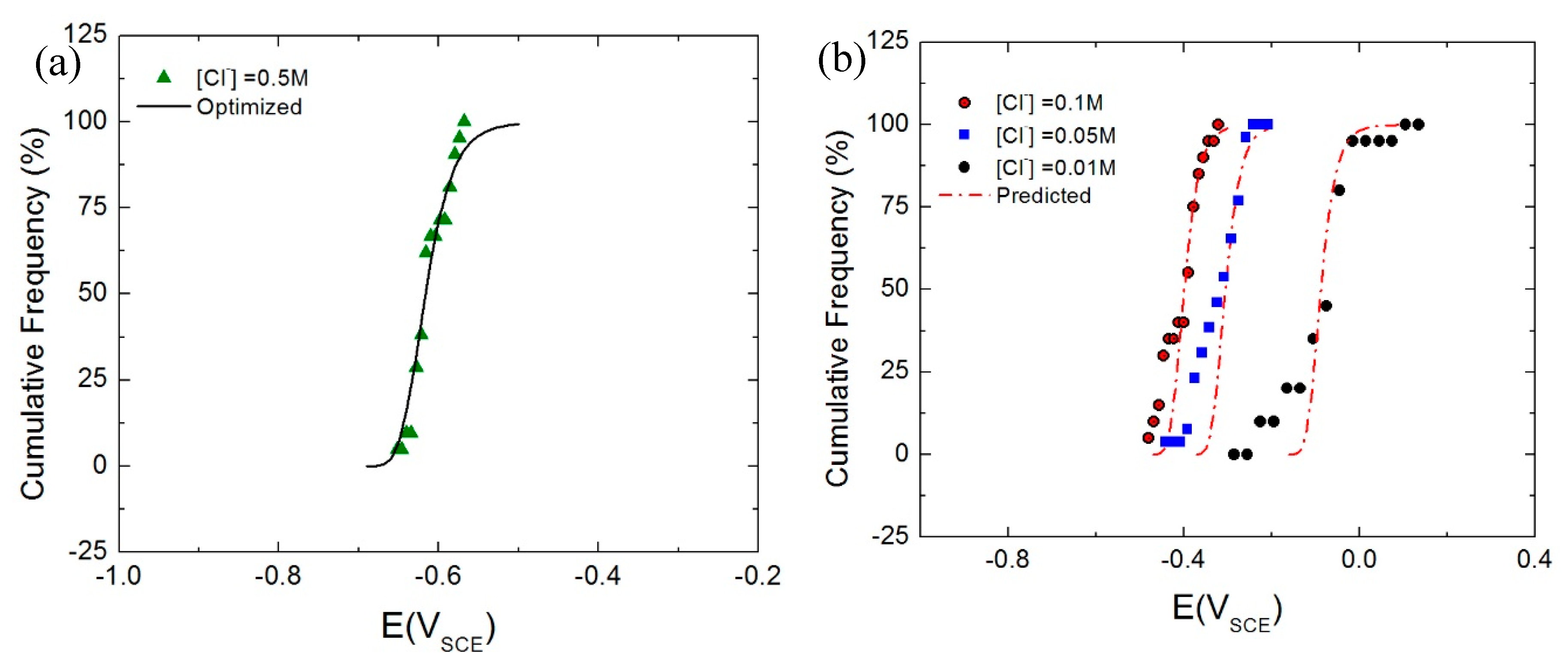
4.2. Cumulative Probabilities of the Ec
5. Summary and Conclusions
- The linear dependence of Ec on the logarithm of the chloride activity, on the pH, and on the square root of the voltage scan rate (ʋ1/2) agree well with the predictions of the PDM.
- From the experimental results, using the PDM, some characteristic parameters, such as (α, β, Jm and ξ) were extracted which were later employed in the optimization of the near-normal distribution of Ec.
- Satisfactory agreement between ξ that was obtained from the experiment with that estimated theoretically from the passive layer/metal structure validates the predictions made by the PDM.
- By numerical analysis (optimization) of the theoretical cumulative probability function, as given by the PDM, on the experimental breakdown potential data for a single chloride concentration (0.5 M), values for various model parameters were derived.
- The derived model parameters satisfactorily account for the cumulative probability functions measured at other chloride concentrations.
- The above findings can be used to predict the passivity breakdown and failure of the AA2098-T851 in different pH, [Cl−] and temperature and similarly, the methodology could be extended to other alloys as well.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Prasad, N.; Eswara, A.G.; Wanhill, R.J.H. Aluminum-Lithium Alloys: Processing, Properties, and Applications; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Kobayashi, K.; Ohsaki, S.K.A.; Tsuji, Y. Effect of Zn Addition on Corrosion Resistance of 2090 and 2091 Alloys; Peters, M., Winkler, P.-J., Eds.; Aluminum-Lithium, Informationsgesellschaft, Verlag: New York, NY, USA, 1991; Volume 2, pp. 673–678. [Google Scholar]
- Zhang, R.; Knight, S.P.; Holtz, R.L.; Goswami, R.; Davies, C.H.J.; Birbilis, N. A survey of sensitization in 5xxx series aluminum alloys. Corrosion 2015, 72, 144–159. [Google Scholar] [CrossRef]
- Gupta, R.K.; Zhang, R.; Davies, C.H.J.; Birbilis, N. Influence of Mg content on the sensitization and corrosion of Al-xMg(-Mn) alloys. Corrosion 2013, 69, 1081–1087. [Google Scholar] [CrossRef]
- Zhang, R.; Gupta, R.K.; Davies, C.H.J.; Hodge, A.M.; Tort, M.; Xia, K.; Birbilis, N. The influence of grain size and grain orientation on sensitization in AA5083. Corrosion 2015, 72, 160–168. [Google Scholar]
- Holroyd, N.H.; Scamans, G.M. Stress corrosion cracking in Al-Zn-Mg-Cu aluminum alloys in saline environments. Metall. Mater. Trans. A 2013, 44, 1230–1253. [Google Scholar] [CrossRef]
- Birbilis, N.; Zhang, R.; Lim, M.L.C.; Gupta, R.K.; Davies, C.H.J.; Lynch, S.P.; Scully, J.R. Quantification of sensitization in AA5083-H131 via imaging Ga-embrittled fracture surfaces. Corrosion 2012, 69, 396–402. [Google Scholar] [CrossRef]
- Ding, Q.; Zhang, D.; Zuo, J.; Hou, S.; Zhuang, L.; Zhang, J. The effect of grain boundary character evolution on the intergranular corrosion behavior of advanced Al-Mg-3wt% Zn alloy with Mg variation. Mater. Charact. 2018, 146, 47–54. [Google Scholar] [CrossRef]
- Luo, C.; Albu, S.P.; Zhou, X.; Sun, Z.; Zhang, X.; Tang, Z.; Thompson, G.E. Continuous and discontinuous localized corrosion of a 2xxx aluminium–copper–lithium alloy in sodium chloride solution. J. Alloys Compd. 2016, 658, 61–70. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, Y.; Zhang, W. Intergranular corrosion and exfoliation corrosion of Al_Li_alloys. Mater. Sci. Forum 2000, 331, 1671–1676. [Google Scholar] [CrossRef]
- Liang, W.J.; Pan, Q.; He, Y.; Zhou, Y.; Lu, C. Effect of ageing on mechanical properties and corrosion susceptibility of Al–Cu–Li–Zr alloy containing scandium. Rare Met. 2008, 27, 146–152. [Google Scholar] [CrossRef]
- Jiang, N.; Li, J.F.; Zheng, Z.; Wei, X.Y.; Li, Y.F. Effect of ageing on mechanical properties and localized corrosion behaviors of Al–Li–Cu alloy. Trans. Non-Ferrous Met. Soc. China 2005, 15, 23–29. [Google Scholar]
- Yue, X.U.; Xiaojing, W.A.N.G.; Zhaotong, Y.A.N.; Jiaxue, L.I. Corrosion properties of light-weight and high-strength 2195 Al-Li alloy. Chin. J. Aeronaut. 2011, 24, 681–686. [Google Scholar]
- Rinker, J.G.; Marek, M.; Sanders, T.H., Jr. Microstructure, toughness and stress corrosion cracking behavior of aluminum alloy 2020. Mater. Sci. Eng. 1984, 64, 203–221. [Google Scholar] [CrossRef]
- Meletis, E.I. Microstructure and stress-corrosion cracking relationship in an Al-Li-Cu-Zr alloy. Mater. Sci. Eng. 1987, 93, 235–245. [Google Scholar] [CrossRef]
- Dorward, R.C.; Hasse, K.R. Stress corrosion characteristics of AlCuLi AA 2090 alloy. Corrosion 1988, 44, 932–941. [Google Scholar] [CrossRef]
- Buchheit, R.G., Jr.; Moran, J.P.; Stoner, G.E. Localized corrosion behavior of alloy 2090—The role of microstructural heterogeneity. Corrosion 1990, 48, 610–617. [Google Scholar] [CrossRef]
- Buchheit, R.G.; Wall, F.D.; Stoner, G.E.; Moran, J.P. Anodic dissolution-based mechanism for the rapid cracking, preexposure phenomenon demonstrated by aluminum-lithium-copper alloys. Corrosion 1995, 51, 417–428. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, X.; Huang, W.; Thompson, G.E.; Zhang, X.; Luo, C.; Sun, Z. Localized corrosion in AA2099-T83 aluminum–lithium alloy: The role of intermetallic particles. Mater. Chem. Phys. 2015, 161, 201–210. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, R.; Liu, D.; Xu, Y.; Li, J.; Chen, Y.; Zhang, X.; Zheng, Z. Correlation between artificial aging and intergranular corrosion sensitivity of a new Al-Cu-Li alloy sheet. Mater. Corros. 2017, 68, 65–76. [Google Scholar] [CrossRef]
- Buchheit, R.G.; Grant, R.P.; Hlava, P.F.; McKenzie, B.; Zender, G.L. Local dissolution phenomena associated with S phase (Al2CuMg) particles in aluminum alloy 2024-T3. J. Electrochem. Soc. 1997, 44, 2621–2628. [Google Scholar] [CrossRef]
- Buchheit, R.G.; Martinez, M.A.; Montes, L.P. Evidence for Cu Ion Formation by Dissolution and Dealloying the Al2CuMg Intermetallic Compound in Rotating Ring-Disk Collection Experiments. J. Electrochem. Soc. 2000, 147, 119–124. [Google Scholar] [CrossRef]
- Macdonald, D.D. Passivity–the key to our metals-based civilization. Pure Appl. Chem. 1999, 71, 951–978. [Google Scholar] [CrossRef]
- Kowal, K.; DeLuccia, J.; Josefowicz, J.Y.; Laird, C.; Farrington, G.C. In Situ Atomic Force Microscopy Observations of the Corrosion Behavior of Aluminum-Copper Alloys. J. Electrochem. Soc. 1996, 143, 2471–2481. [Google Scholar] [CrossRef]
- Rynders, R.M.; Paik, C.H.; Ke, R.; Alkire, R.C. Use of in situ atomic force microscopy to image corrosion at inclusions. J. Electrochem. Soc. 1994, 141, 1439–1445. [Google Scholar] [CrossRef]
- Lei, X.; Saatchi, A.; Ghanbari, E.; Dang, R.; Li, W.; Wang, N.; Macdonald, D.D. Studies on Pitting Corrosion of Al-Cu-Li Alloys Part I: Effect of Li Addition by Microstructural, Electrochemical, In-situ, and Pit Depth Analysis. Materials (Basel) 2019, 12, 1600. [Google Scholar] [CrossRef] [PubMed]
- Li, J.F.; Birbilis, N.; Liu, D.Y.; Chen, Y.L.; Zhang, X.H.; Cai, C. Intergranular corrosion of Zn-free and Zn-microalloyed Al–xCu–yLi alloys. Corros. Sci. 2016, 105, 44–57. [Google Scholar] [CrossRef]
- Gao, C.; Luan, Y.; Yu, J.; Ma, Y. Effect of thermo-mechanical treatment process on microstructure and mechanical properties of 2A97 Al-Li alloy. Trans. Nonferrous Met. Soc. China 2014, 24, 2196–2202. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, X.; Liao, Y.; Chen, X.; Zhang, C.; Wu, H.; Huang, W. Effect of Anodizing Parameters on Film Morphology and Corrosion Resistance of AA2099 Aluminum-Lithium Alloy. J. Electrochem. Soc. 2016, 163, C369–C376. [Google Scholar] [CrossRef] [Green Version]
- Carrick, D.M.; Hogg, S.C.; Wilcox, G.D. Influence of Li additions on the microstructure and corrosion response of 2XXX series aluminium alloys. Mater. Sci. Forum Trans. 2014, 794, 193–198. [Google Scholar] [CrossRef]
- Hatch, J.E. Aluminum: Properties and Physical Metallurgy; ASM International: Metals Park, OH, USA, 1984. [Google Scholar]
- Verwey, E. Electrolytic conduction of a solid insulator at high fields The formation of the anodic oxide film on aluminium. Physica 1935, 2, 1059–1063. [Google Scholar] [CrossRef]
- Vetter, K.J.; Gorn, F. Kinetics of layer formation and corrosion processes of passive iron in acid solutions. Electrochim. Acta 1973, 18, 321–326. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.; Wang, F. Electrochemical corrosion behaviour of microcrystalline aluminium in acidic solutions. Corros. Sci. 2007, 49, 2071–2082. [Google Scholar] [CrossRef]
- Zhao, X. Exfoliation Corrosion Kinetics of High Strength Aluminum Alloys. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2006. [Google Scholar]
- Chao, C.Y.; Lin, L.F.; Macdonald, D.D. A point defect model for anodic passive films I. Film growth kinetics. J. Electrochem. Soc. 1981, 128, 1187–1194. [Google Scholar] [CrossRef]
- Lin, L.F.; Chao, C.Y.; Macdonald, D.D. A point defect model for anodic passive films II. Chemical breakdown and pit initiation. J. Electrochem. Soc. 1981, 128, 1194–1198. [Google Scholar] [CrossRef]
- Fattah-Alhosseini, A.; Shojae, S.T. Immersion time and passive potential role on the passive and electrochemical response of tantalum in 0.1 M HNO3 solution. Mater. Res. Express 2018, 5, 116512. [Google Scholar] [CrossRef]
- Gupta, R.K.; Sukiman, N.L.; Cavanaugh, M.K.; Hinton, B.R.W.; Hutchinson, C.R.; Birbilis, N. Metastable pitting characteristics of aluminium alloys measured using current transients during potentiostatic polarisation. Electrochim. Acta 2012, 66, 245–254. [Google Scholar] [CrossRef]
- Karayan, A.I.; Jata, K.; Velez, M.; Castaneda, H. On exfoliation corrosion of alloy 2060 T8E30 in an aggressive acid environment. J. Alloys Compd. 2016, 657, 546–558. [Google Scholar] [CrossRef]
- Ott, N.; Yan, Y.; Ramamurthy, S.; Kairy, S.; Birbilis, N. Auger electron spectroscopy analysis of grain boundary microchemistry in an Al–Cu–Li alloy. Scr. Mater. 2016, 119, 17–20. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Urquidi-Macdonald, M. Distribution functions for the breakdown of passive films. Electrochim. Acta 1986, 31, 1079–1086. [Google Scholar] [CrossRef]
- Shibata, T.; Takeyama, T. Stochastic theory of pitting corrosion. Corrosion 1977, 33, 243–251. [Google Scholar] [CrossRef]
- Pride, S.T.; Scully, J.R.; Hudson, J.L. Metastable pitting of aluminum and criteria for the transition to stable pit growth. J. Electrochem. Soc. 1994, 141, 3028–3040. [Google Scholar] [CrossRef]
- Kim, Y.; Buchheit, R.G. A characterization of the inhibiting effect of Cu on metastable pitting in dilute Al–Cu solid solution alloys. Electrochim. Acta 2007, 52, 2437–2446. [Google Scholar] [CrossRef]
- Pistorius, P.C.; Burstein, G.T. Metastable pitting corrosion of stainless steel and the transition to stability. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1992, 341, 531–559. [Google Scholar]
- Pistorius, P.C.; Burstein, G.T. Aspects of the effects of electrolyte composition on the occurrence of metastable pitting on stainless steel. Corros. Sci. 1994, 36, 525–538. [Google Scholar] [CrossRef]
- Burstein, G.T.; Pistorius, P.C.; Mattin, S.P. The nucleation and growth of corrosion pits on stainless steel. Corros. Sci. 1993, 35, 57–62. [Google Scholar] [CrossRef]
- Cui, N.; Ma, H.Y.; Luo, J.L.; Chiovelli, S. Use of scanning reference electrode technique for characterizing pitting and general corrosion of carbon steel in neutral media. Electrochem. Commun. 2001, 3, 716–721. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Luo, J.L. Metastable pitting of carbon steel under potentiostatic control. J. Electrochem. Soc. 1999, 146, 970–976. [Google Scholar] [CrossRef]
- Sharifi-Asl, S.; Macdonald, D.D.; Almarzooqi, A.; Kursten, B.; Engelhardt, G.R. A comprehensive electrochemical impedance spectroscopic study of passive carbon steel in concrete pore water. J. Electrochem. Soc. 2013, 160, C316–C325. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Peiper, J.C.; Busey, R.H. Thermodynamic properties of aqueous sodium chloride solutions. J. Phys. Chem. Ref. Data 1984, 13, 1–102. [Google Scholar] [CrossRef]
- Ghanbari, E.; Saatchi, A.; Lei, X.; Kovalov, D.; Macdonald, D.D. Passivity Breakdown and Pitting Corrosion of Al- Li Aerospace Alloys. In Proceedings of the 2017 DoD Allied Nations Technical Corrosion Conference, Birmingham, AL, USA, 7–10 August 2017. [Google Scholar]
- Sharifi-Asl, S.; Mao, F.; Lu, P.; Kursten, B.; Macdonald, D.D. Exploration of the effect of chloride ion concentration and temperature on pitting corrosion of carbon steel in saturated Ca(OH)2 solution. Corros. Sci. 2015, 98, 708–715. [Google Scholar] [CrossRef]
- Szklarska-Smialowska, Z. Pitting corrosion of aluminum. Corros. Sci. 1999, 41, 1743–1767. [Google Scholar] [CrossRef]
- Macdonald, D.D. The point defect model for the passive state. J. Electrochem. Soc. 1992, 139, 3434–3449. [Google Scholar] [CrossRef]
- Mao, F.; Dong, C.; Sharifi-Asl, S.; Lu, P.; Macdonald, D.D. Passivity breakdown on copper: Influence of chloride ion. Electrochim. Acta 2014, 144, 391–399. [Google Scholar] [CrossRef]
- Zhang, Y.; Macdonald, D.D.; Urquidi-Macdonald, G.R.; Engelhardt, M.; Dooley, R.B. Passivity breakdown on AISI Type 403 stainless steel in chloride-containing borate buffer solution. Corros. Sci. 2006, 48, 3812–3823. [Google Scholar] [CrossRef]
- Szauer, T.; Jakobs, J. The pitting corrosion of low alloy and mild steels. Corros. Sci. 1976, 16, 945–949. [Google Scholar] [CrossRef]
- Broli, A.; Holtan, H. Use of potentiokinetic methods for the determination of characteristic potentials for pitting corrosion of aluminium in a deaerated solution of 3% NaCl. Corros. Sci. 1973, 13, 237–246. [Google Scholar] [CrossRef]
- Schwenk, W. Theory of stainless steel pitting. Corrosion 1964, 20, 129t–137t. [Google Scholar] [CrossRef]
- Haruna, T.; Macdonald, D.D. Theoretical prediction of the scan rate dependencies of the pitting potential and the probability distribution in the induction time. J. Electrochem. Soc. 1997, 144, 1574–1581. [Google Scholar] [CrossRef]
- Bastidas, J.M.; Polo, J.L.; Torres, C.L.; Cano, E. A stochastic approach to study localized corrosion of AISI 304L and AISI 316L stainless steels as a function of potential scan rate. Corrosion 2001, 57, 666–669. [Google Scholar] [CrossRef]
- Szklarska-Smialowska, Z. Pitting and Crevice Corrosion; NACE Int.: Houston, TX, USA, 2005. [Google Scholar]
- Fonseca, I.T.; Lima, N.; Rodrigues, J.A.; Pereira, M.I.S.; Salvador, J.C.S.; Ferreira, M.G. Passivity breakdown of Al 2024-T3 alloy in chloride solutions: A test of the point defect model. Electrochem. Commun. 2002, 4, 353–357. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Engelhardt, G.R. Predictive Modeling of Corrosion. Shreir’s Corros. 2010, 2, 1630–1679. [Google Scholar]
- Ghanbari, E.; Saatchi, A.R.; Kovalov, D.; Kursten, B.; Macdonald, D. The Influence of Halide Ions on the Passivity Breakdown of Carbon Steel Based on the Point Defect Model; NACE International: Phoenix, AZ, USA, 2018. [Google Scholar]
- Bargeron, C.B.; Benson, R.C. Analysis of the gases evolved during the pitting corrosion of aluminum in various electrolytes. J. Electrochem. Soc. 1980, 127, 2528–2530. [Google Scholar] [CrossRef]
- Bargeron, C.B.; Givens, R.B. Localized corrosion of aluminum: Blister formation as a precursor of pitting. J. Electrochem. Soc. 1977, 124, 1845–1848. [Google Scholar] [CrossRef]
- Bargeron, C.B.; Givens, R.B. Source of oscillations in the anode current during the potentiostatic pitting of aluminum. J. Electrochem. Soc. 1977, 124, 1230–1232. [Google Scholar] [CrossRef]
- Bargeron, C.B.; Givens, R.B. A signature in the current during early events in the pitting corrosion of aluminum. J. Electrochem. Soc. 1982, 129, 340–341. [Google Scholar] [CrossRef]
- McCafferty, E. Sequence of steps in the pitting of aluminum by chloride ions. Corros. Sci. 2003, 45, 1421–1438. [Google Scholar] [CrossRef]
- McCafferty, E. The electrode kinetics of pit initiation on aluminum. Corros. Sci. 1995, 37, 481–492. [Google Scholar] [CrossRef]
- Natishan, P.M.; O’grady, W.E.; McCafferty, E.; Ramaker, D.E.; Pandya, K.; Russell, A. Chloride Uptake by Oxide Covered Aluminum as Determined by X-Ray Photoelectron and X-Ray Absorption Spectroscopy. J. Electrochem. Soc. 1999, 146, 1737–1740. [Google Scholar] [CrossRef]
- Lu, P.; Engelhardt, G.R.; Kursten, B.; Macdonald, D.D. The kinetics of nucleation of metastable pits on metal surfaces: The Point Defect Model and its optimization on data obtained on stainless steel, carbon steel, iron, aluminum and Alloy-22. J. Electrochem. Soc. 2016, 163, C156–C163. [Google Scholar] [CrossRef]
- Zhu, Y.; Frankel, G. Effect of Major Intermetallic Particles on Localized Corrosion of AA2060-T8. Corrosion 2019, 75, 29–41. [Google Scholar] [CrossRef]
- Schmutz, P.; Frankel, G.S. Corrosion study of AA2024-T3 by scanning kelvin probe force microscopy and in situ atomic force microscopy scratching. J. Electrochem. Soc. 1998, 145, 2295–2306. [Google Scholar] [CrossRef]
- Schmutz, P.; Frankel, G.S. Characterization of AA2024-T3 by scanning Kelvin probe force microscopy. J. Electrochem. Soc. 1998, 7, 2285–2295. [Google Scholar] [CrossRef]
- Zhao, Z.; Frankel, G.S. On the first breakdown in AA7075-T6. Corros. Sci. 2007, 49, 3064–3088. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, K.; Frankel, G.S. Intermetallic Phases in Aluminum Alloys and Their Roles in Localized Corrosion. J. Electrochem. Soc. 2018, 165, C807–C820. [Google Scholar] [CrossRef]
- Dong, C.; Mao, F.; Gao, S.; Sharifi-Asl, S.; Lu, P.; Macdonald, D.D. Passivity breakdown on copper: Influence of temperature. J. Electrochem. Soc. 2016, 163, C707–C717. [Google Scholar] [CrossRef]
- Zhong, J.; Mao, F.; Ghanbari, E.; Macdonald, D.D. Passivity breakdown on 300 M and S280 ultra-high strength steels in borate buffer solutions containing chloride ion. Electrochim. Acta 2017, 251, 324–335. [Google Scholar] [CrossRef]
- Shibata, T. 1996 WR Whitney Award lecture: Statistical and stochastic approaches to localized corrosion. Corrosion 1996, 52, 813–830. [Google Scholar] [CrossRef]
- Zhang, Y.; Urquidi-Macdonald, M.; Engelhardt, G.R.; Macdonald, D.D. Development of localized corrosion damage on low pressure turbine disks and blades: I. Passivity. Electrochim. Acta 2012, 69, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Urquidi-Macdonald, M.; Engelhardt, G.R.; Macdonald, D.D. Development of localized corrosion damage on low pressure turbine disks and blades: II. Passivity breakdown. Electrochim. Acta 2012, 69, 12–18. [Google Scholar] [CrossRef]
- Macdonald, D.D. On the existence of our metals-based civilization I. Phase-space analysis. J. Electrochem. Soc. 2006, 153, B213–B224. [Google Scholar] [CrossRef]
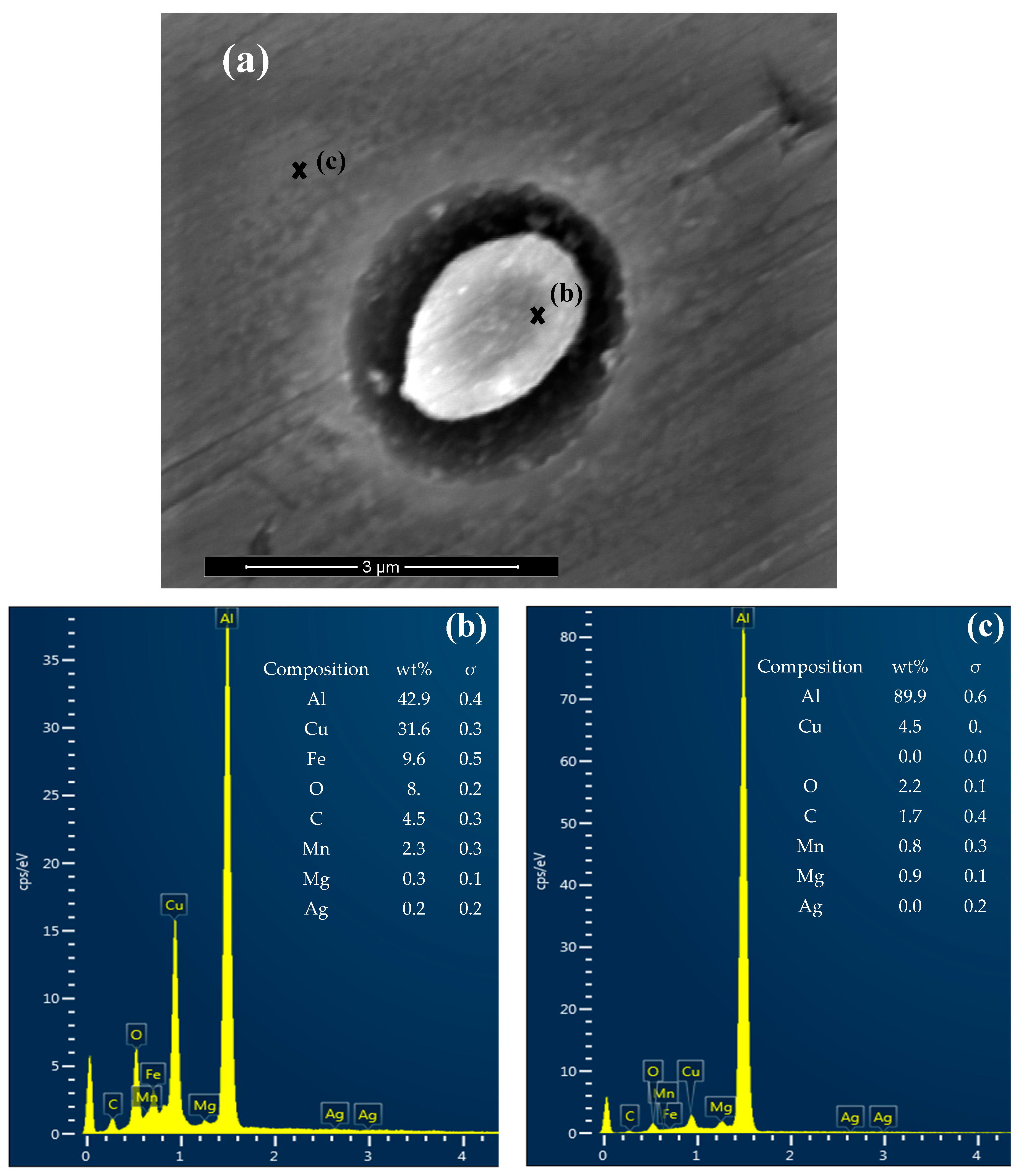
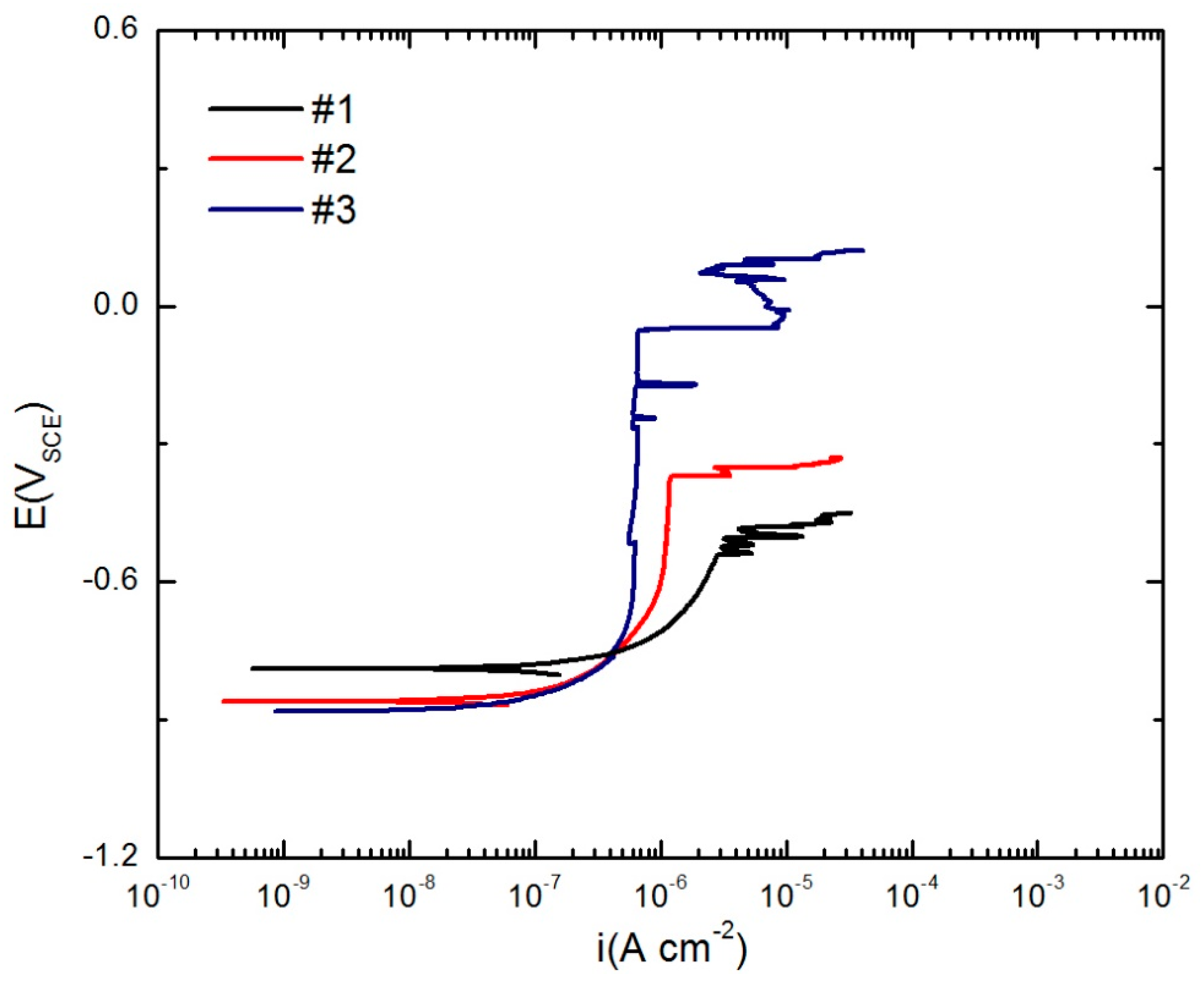
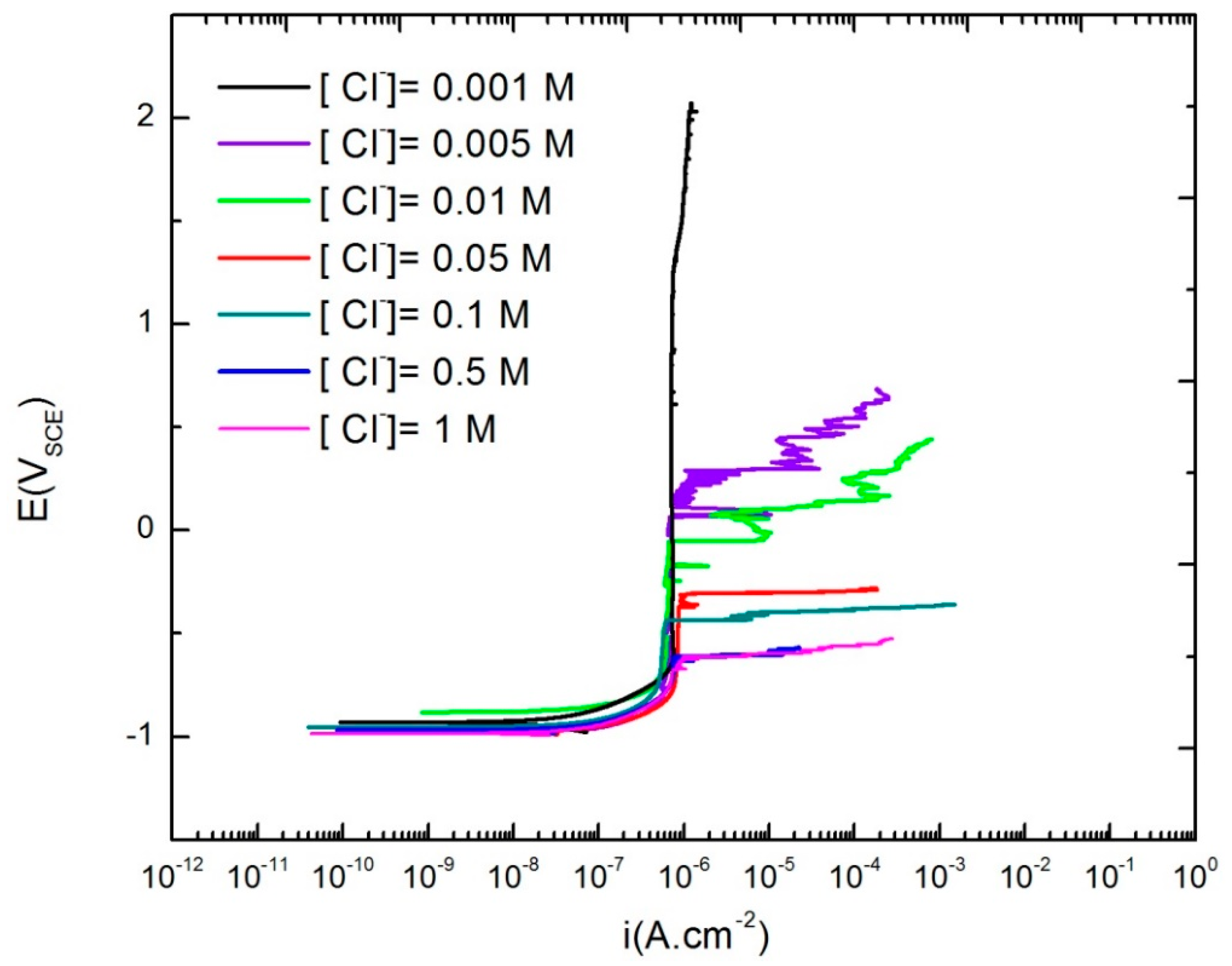
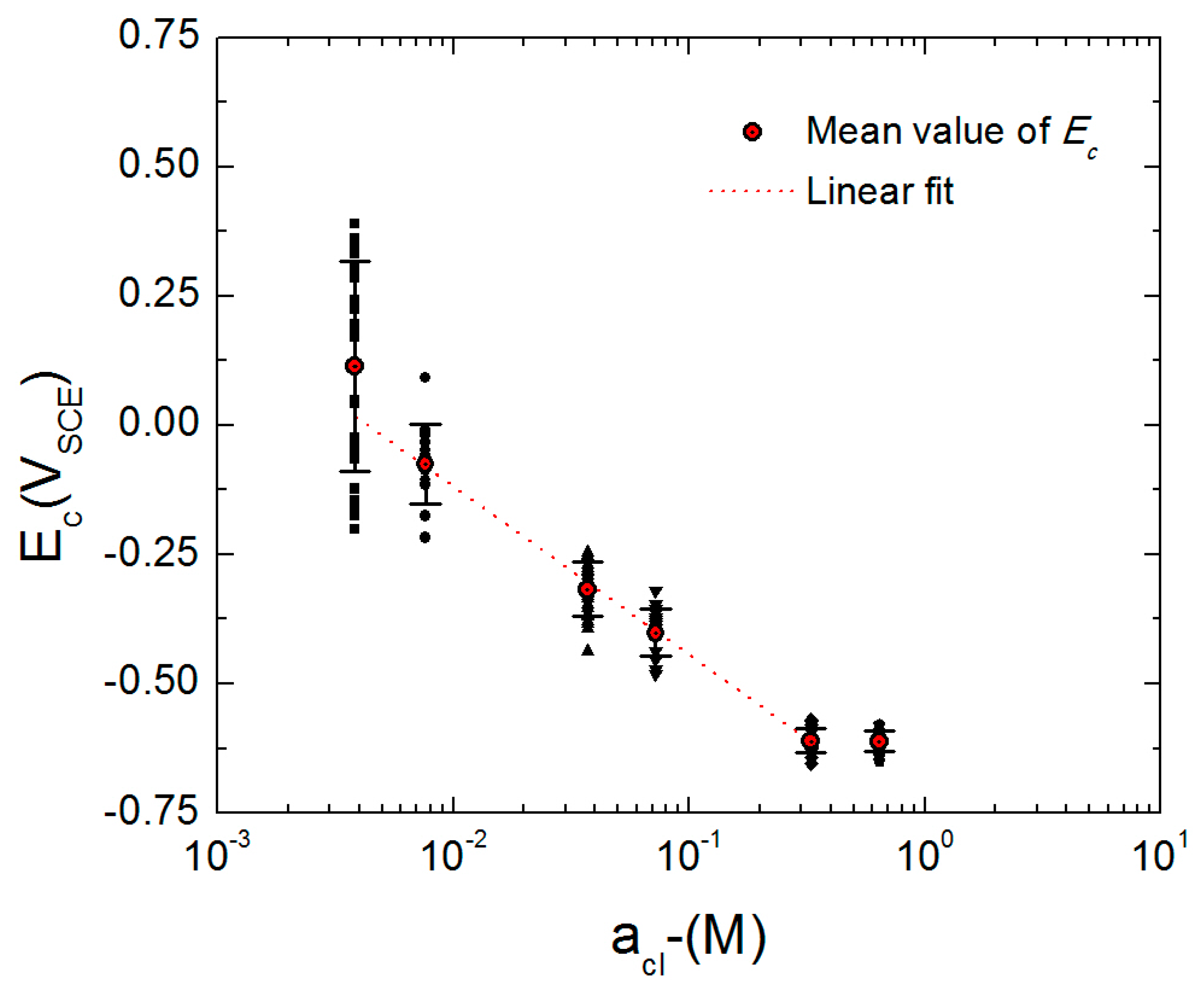

| Number | Material | Cu | Li | Mg | Mn | Ag | Zr | Zn | Al |
|---|---|---|---|---|---|---|---|---|---|
| 2029-T8 (S1) | 2029-T8 | 3.46 | - | 0.80 | 0.26 | 0.04 | - | 0.01 | Bal. |
| 2060-T8 (S2) | 2060-T8 | 3.63 | 0.78 | 0.67 | 0.25 | 0.04 | 0.06 | 0.29 | Bal. |
| 2098-T851 (S3) | 2098-T851 | 3.71 | 1.29 | 0.26 | 0.03 | 0.03 | 0.06 | 0.01 | Bal. |
| Parameter | Definition | Value | Source |
|---|---|---|---|
| α | Polarizability of bl/ol Interface | 0.19 | From Figure 10 |
| β | Dependence of the potential drop across bl/ol upon pH | −0.014 V | From Figure 11 |
| ε | Electric Field Strength | 3 × 106 V cm−1 | Assumed |
| χ | Oxidation state | 3 | Assigned |
| Ω | Molar volume of oxide per cation | 12.91 cm3 mol−1 | From density |
| The mean diffusivity of cation vacancy | 3.5 × 10−18 cm2 s−1 | From fitting | |
| The standard deviation for | 1.05 × 10−18 cm2 s−1 | From fitting | |
| ξ | The critical vacancy concentration | 5.6 × 1013 cm−2 | From Figure 12 |
| Jm | The critical vacancy flux | 2.08 × 1012 cm−2 s−1 | From Figure 9 |
| ω | The energy term | −24888 J mol−1 | From Figure 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanbari, E.; Saatchi, A.; Lei, X.; Macdonald, D.D. Studies on Pitting Corrosion of Al-Cu-Li Alloys Part II: Breakdown Potential and Pit Initiation. Materials 2019, 12, 1786. https://doi.org/10.3390/ma12111786
Ghanbari E, Saatchi A, Lei X, Macdonald DD. Studies on Pitting Corrosion of Al-Cu-Li Alloys Part II: Breakdown Potential and Pit Initiation. Materials. 2019; 12(11):1786. https://doi.org/10.3390/ma12111786
Chicago/Turabian StyleGhanbari, Elmira, Alireza Saatchi, Xiaowei Lei, and Digby D. Macdonald. 2019. "Studies on Pitting Corrosion of Al-Cu-Li Alloys Part II: Breakdown Potential and Pit Initiation" Materials 12, no. 11: 1786. https://doi.org/10.3390/ma12111786
APA StyleGhanbari, E., Saatchi, A., Lei, X., & Macdonald, D. D. (2019). Studies on Pitting Corrosion of Al-Cu-Li Alloys Part II: Breakdown Potential and Pit Initiation. Materials, 12(11), 1786. https://doi.org/10.3390/ma12111786





